Abstract
The dynamics of acoustic cavitation bubbles hold significant importance in ultrasonic cleaning, biomedicine, and chemistry. Utilizing an in-situ normal pressure bubble generation and observation system that was developed, this study examined the translational behavior of micrometer-scale normal pressure bubble pairs with initial radius ratio of 1:1 and 2:1 under ultrasonic field excitation. A velocity-distance curve was proposed to quantify the secondary Bjerknes forces during various interaction stages of the bubbles. The findings revealed that equal-sized bubbles underwent an acceleration phase, a deceleration phase, and a velocity jump phase during attraction in both strong and weak acoustic fields. In contrast, bubbles of unequal sizes, due to different oscillation frequencies, experienced multiple acceleration and deceleration phases, presenting asynchronous behaviors. The study further explored the effects of the initial bubble radius, shape oscillation, and volume oscillations on the attraction speed. Results showed that the velocity of the bubble’s centroid decreased with an increase in the initial radius, while intensified volume oscillations increased the secondary Bjerknes force, thereby increasing the centroid’s velocity. Moreover, strong acoustic fields were more likely to induce severe volume and shape oscillations in bubbles than weak fields. The irregular shape oscillations in twin bubbles resulted in shortened durations of acceleration and deceleration phases, reduced peak velocities of acceleration phase, and diminished acceleration during the velocity jump phase. The research provided some mechanical explanations for acoustic cavitation dynamics and its applications.
Keywords: Ultrasonic wave, Bubble pair, Secondary Bjerknes force
1. Introduction
When ultrasonic waves (with frequencies above 20 kHz) are applied, microbubbles (cavitation nuclei) in liquids undergo a series of dynamic process, including translation, oscillation, and collapse. These phenomena are termed as acoustic cavitation [1], [2], [3], [4]. Acoustic cavitation has a wide range of applications in fields such as ultrasonic cleaning [5], [6], [7], [8], [9], biomedicine [10], [11], [12], [13], [14], and chemistry [15], [16], [17], [18], [19]. The study of bubble dynamics includes not only the individual behaviors of bubbles, but also the interactions between bubbles. The force exerted by the flow field pressure changes due to a bubble’s own oscillation on other bubbles is known as the secondary Bjerknes force [20]. This force is of significant importance to many acoustic phenomena and applications, especially in microfluidic technologies [21], [22], [23], [24], [25]. To further investigate the dynamic characteristics of cavitation bubbles, researchers have conducted extensive studies. Crum [25] proposed the theory of the secondary Bjerknes force, explaining the interactive forces between bubbles in a low-amplitude acoustic field. In the context of Crum’s research, it is posited that the secondary Bjerknes force is derived under the assumption of linear bubble oscillation. Following a period of acoustic frequency oscillation, a time-averaging procedure is employed to yield a simplified expression for the force in question. The study concludes that two bubbles oscillating in synchrony would be subject to an attractive force, whereas two bubbles oscillating with phase opposition would experience a repulsive force. Marston [26] and colleagues observed in experiments that bubbles aggregate but do not coalesce in the acoustic field, a phenomenon that reveals the limitations of the classical secondary Bjerknes theory in explaining the behavior of bubbles in actual acoustic fields.
In the realm of numerical computation, Doinikov [27] conducted numerical simulations to study the translational motion of bubbles in a plane standing wave, including the coupled vibration and translation patterns of the bubbles. These results are of significant importance for understanding the irregular bubble motion observed in experiments under strong acoustic fields. Huang et al. [28], [29] used the boundary element method (BEM) based on potential flow theory to explore the two microbubble system (TMS) under ultrasonic excitation. They conducted a parametric study of the two bubble system’s behavior based on the amplitude and direction of the ultrasonic wave, as well as the size and separation distance of the two bubbles. Three states of TMS dynamic behavior were identified based on the pressure amplitude of the ultrasonic wave. Shen [30] studied the impact of bubble–bubble interactions on the spherical pulsation of bubbles. By comparing numerical simulation results with and without considering bubble–bubble interactions, they found that the suppression or amplification effect of bubble–bubble interactions on the bubble expansion ratio mainly depends on ultrasonic parameters, the radius of surrounding bubbles, bubble spacing, and the number of bubbles. This study provided a deeper understanding of the interactions between bubbles. Zhang [31] and colleagues established a theoretical model based on the unified bubble equation to calculate the coupling effects of multiple bubbles in an acoustic field. This model can predict the trend of changes in the secondary Bjerknes force between two bubbles in different types of acoustic fields, providing theoretical support for the study of bubble cluster dynamics in acoustic fields.
In the experimental studies, Mettin [32] experimentally investigated the secondary Bjerknes force between small-sized bubbles in a strong acoustic field, finding significant differences between the interactive forces of the bubbles and the predictions of linear theory under strong acoustic fields. Mettin’s findings reveal the importance of nonlinear effects in the interactions between bubbles. Yoshida and Fujikawa [33] utilized a high-speed camera imaging system to observe the behavior of two bubbles in an ultrasonic standing wave, discovering that at a certain separation distance between the bubbles, the forces were in opposite directions. Bai [34] and colleagues employed a high-speed cinematography system to conduct experimental research on the hitherto unobserved phenomenon of bubbles circling near a wall. The focus was on the translation trajectory of the free bubbles, the arrangement process of the wall-adherent bubbles, the origin of the bubbles, and the nuances of bubble vibration. The experimental results revealed that the translation paths of the circling bubbles exhibited characteristics of instability, irregularity, and asperity. Wang [35] experimentally investigated the coupled motion of bubbles in an ultrasonic field, finding that the interactive forces between bubbles significantly affected their vibrational properties, providing empirical data to support the understanding of bubble dynamics within ultrasonic fields.
In summary, the research conducted by scholars has primarily focused on the numerical simulation and experimental studies of acoustic bubble dynamics. Due to the randomness and uncontrollable nature of cavitation bubbles formed through the evolution of gas nuclei in an ultrasonic field, quantitative experimental studies on bubble dynamics in ultrasonic fields are relatively lacking. To address this, the present study developed an in-situ atmospheric pressure bubble generation, excitation, and observation device within the acoustic field, aiming to delve deeper into the translation behavior of bubbles in the field. Section 2 of this paper provides a detailed introduction to the experimental setup, while Section 3 offers a thorough analysis of the translation characteristics of two types of bubbles (equal-sized and unequal-sized) in the ultrasonic field. Conclusions are presented in Section 4.
2. Experimental setup
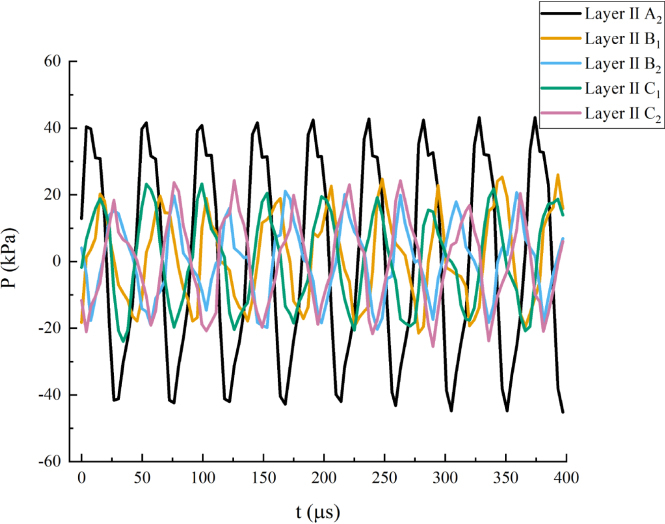
The water tank used in this experiment is composed of acrylic plates with a thickness of 3, with dimensions of 248 in length, 130 in width, and 152 in height. A circular hole with a diameter of 7 was drilled on one side of the water tank wall along the direction of the longer edge, with the centroid of the hole 54 from the bottom of the tank. A syringe needle with an inner diameter of 5 was inserted into the water tank through the circular hole, and the other end of the needle was connected to a rubber tube, which in turn was connected to a microflow pump to serve as a bubble generation device. Water with a height of 125 was poured into the water tank, the emitting end of the ultrasonic transmitter (Sonopilot Ultrasonic Levitator-SonoRh-1, Nanjing Sound Force Technology Co., Ltd., China) was submerged 3 below the water surface, with the transducer port plane kept horizontal. The ultrasonic frequency was set at 20500, with a rated power of 1000 W, and an experimental power of 30 W was utilized. On the opposite side of the water tank, a Phantom VEO 710 high-speed industrial camera (Vision Research, USA) was positioned, the images captured during the experiment were transmitted to a laptop via an optical fiber, with a resolution set at 512 × 256 and a frame rate of 48000 frames per second (fps); A flat light source measuring 82.5 by 250 was placed laterally to the Phantom VEO 710 high-speed industrial camera to serve as a supplementary lighting device for the image capture system. A schematic diagram of the experimental setup is depicted in Fig. 1. Considering the distribution of sound pressure in the water tank, we have installed an experimental setup to measure the sound pressure distribution within a water tank and have selected ten measurement points for this purpose (Figs. 2 and 3). We have collected sound pressure data from these ten points and plotted the corresponding time-domain graphs (Figs. 4 and 5). We found that: The pressure distribution in the ultrasonic field is relatively stable, and the flow field at point A meets the requirements of our experiment.
Fig. 1.
Schematic diagram of the experimental setup.
Fig. 2.
Schematic diagram of the experimental setup for measuring the acoustic pressure distribution in a water tank.
Fig. 3.
Three views of the ten measurement points (with the positions of the transducer and the needle indicated in the diagram).
Fig. 4.
The sound pressure–time data graph for measurement points Layer I.
Fig. 5.
The sound pressure–time data graph for measurement points Layer II.
Here, and represent the radii of the two bubbles, respectively, and represents the distance between the centroid of the two bubbles, represents the horizontal distance between the axis of the ultrasonic transducer and the centroid of . represents the distance between the face of the ultrasonic transducer and the line connecting the centroid of the bubbles. represents the angle between the line connecting the centroid of the two-bubble system and the face of the ultrasonic transducer. The ultrasonic transducer is vertically immersed in water. When = 0, the two bubbles are horizontal distributed. Fig. 6b shows the bubble behavior observed at different moments using a long-focus microlens at a resolution of 256 × 128 pixels and a recording rate of 4.8 × 104 frames per second. The left side of the image is the syringe needle for generating in-situ atmospheric pressure bubbles, and the right side shows the attraction process of the generated bubble pair. In the equal-sized two-bubble experimental images, the bubble on the left is labeled as B1, and the one on the right is labeled as B2. In the unequal-sized two-bubble experimental images, the larger bubble is labeled as B1. To obtain more precise measurement data, the Mega Speed AVI Player tool is used to measure the size of the bubbles, with the inner diameter of the syringe needle used in the experiment being 5, and the initial radius of the generated bubbles being 10–20. Concurrently, we perform binarization on the image data obtained from the high-speed camera and apply morphological opening operation for noise reduction, and then use an algorithm to locate the centroid of the two bubbles [36], the calculation expression for the bubble centroid is as follows:
| (1) |
| (2) |
Here, is the x-coordinate of the centroid. is the y-coordinate of the centroid. A is the area of the connected region, which is the number of pixel points within the region. and are the and coordinates of the th pixel point in the region, respectively. To better observe the translation characteristics of the two-bubble system in the acoustic field, the distance between the two bubbles is expressed in a dimensionless form as , where represents the dimensionless distance between the centroid of the two bubbles, and represents the initial radius of bubble . According to the linear theory [37], [38], [39], when the driving frequency is greater than or less than the resonance frequency of the two bubbles, bubbles will exhibit a phenomenon of attraction. Based on the relationship between the resonance frequency and the resonance size of the bubbles, as given by Eq. (3) [40], it can be known that the resonance frequency of bubbles with an initial radius of less than 20 is much higher than the frequency of the sound waves used in the experiment. Consequently, it was found that the translation characteristics of the two bubbles in the experiment always exhibit attraction.
| (3) |
Here, the initial bubble radius 20, represents the ratio of specific heats of the gas with a value of 1.4, the fluid density is 999 kg/m3, represents the initial gas pressure inside the bubble, which is 1.013 × 105 Pa and the surface tension is 0.073 N/m.
Fig. 6.
Schematic and experimental images of the two bubble system. (a) B1 and B2 are two atmospheric pressure bubbles injected through a microneedle into the water. (b) The scale bar represents a length of 10.
3. Results and discussions
3.1. Interaction between equal-sized two bubbles
Considering the oscillation of two spherical bubbles in an incompressible liquid driven by an acoustic field, in this study, the distance between the two bubbles (on the order of 100) is much greater than the equilibrium radius of the bubbles (on the order of 10). Thus, under the condition that the distance is large and the acoustic driving is weak, higher-order spherical harmonics can be neglected, and the bubbles are considered to remain spherically stable [32], [41]. The motion of the liquid around bubble also has spherical symmetry, and its velocity can be expressed as
| (4) |
r is the radial coordinate of the bubble, the rate of change of the bubble radius over time is , according to Euler’s theorem, the pressure field generated by bubble 1 in the surrounding liquid can be expressed as
| (5) |
is the fluid density, is the acoustic pressure radiated by the vibration of bubble 1 in the liquid. The offset term in Eq. (5) is negligible and thus omitted, integrating Eq. (4) into Eq. (5) yields the radiated acoustic pressure of bubble as
| (6) |
According to the expression of the primary Bjerknes force, under the influence of a pressure gradient field , a bubble with volume will be subjected to:
| (7) |
By substituting Eq. (6) into Eq. (7), the force exerted by bubble on bubble can be obtained as
| (8) |
is the distance between the two bubbles, and are the volumes of bubble 1 and bubble 2, respectively, represents the unit vector of the spherical motion of the bubble. Since the bubbles undergo periodic vibration in the acoustic field, the force acting on the second bubble is the time average of the force over a period. This net radiative force acting between adjacent spherical bubbles is referred to as the secondary Bjerknes force between the bubbles.
By performing a double integral on Eq. (8), the expression for the secondary Bjerknes force can be obtained.
| (9) |
Here, represents taking the average value over a period of wave, where indicates attraction and indicates repulsion.
Fig. 6(b) illustrates the translation process of two bubbles recorded by a high-speed camera. The system recorded initial bubble radii ranging from 5 to 20, and the radius difference between the two bubbles was controlled within 8%, considered equal, that is, . If two bubbles satisfy 0 at the initial moment of attraction, we consider them to be a pair of horizontal micro double bubbles, and the bubble pairs discussed in the following text are all horizontal micro double bubbles. In the case of 100, 117, we recorded the interaction of two bubbles and selected typical data to plot distance–velocity graphs, with corresponding high-speed photography images attached for each phase (initial, acceleration, deceleration, contact) (left bubble as B1, right bubble as B2). In the experiment, B2 was first out from the needle and moved to the right. Subsequently, B1 moved towards B2 with the initial velocity imparted by the needle pressure. We simulated the approach of the two bubbles in a stationary state by subtracting the initial velocity imparted to B1 by the needle injection pressure. The first data point in the graph marks the moment when the two bubbles began to attract each other from a stationary state.
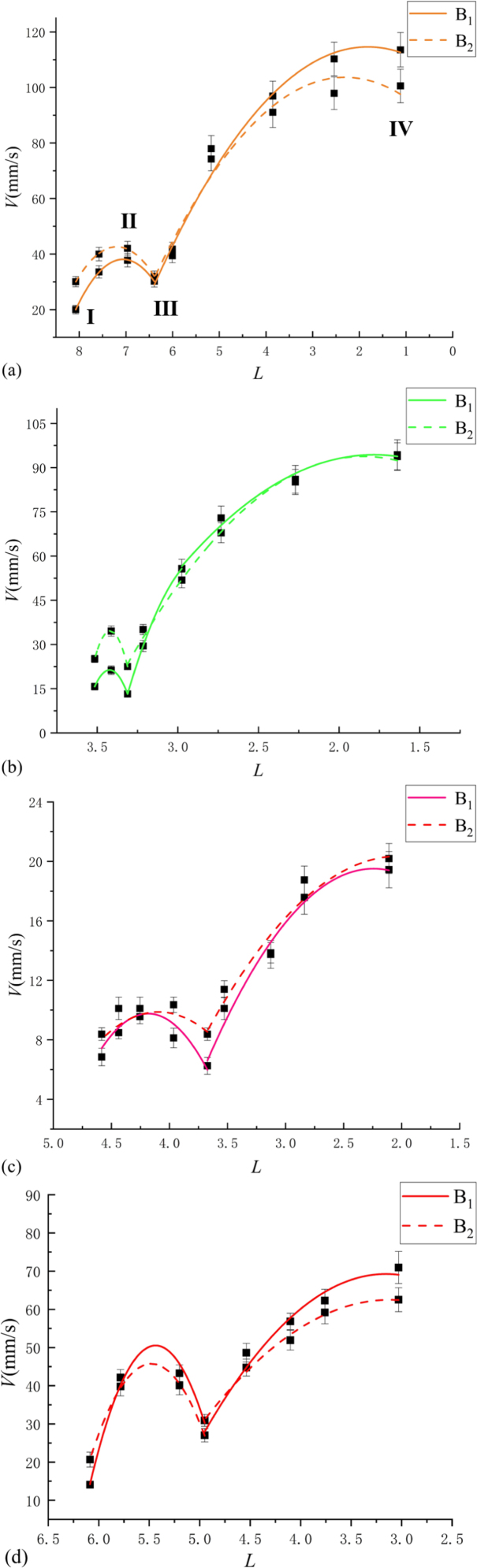
Fig. 7 illustrates that the attraction between bubbles can be divided into three stages: acceleration, deceleration, and a velocity jump. In the first case, the initial dimensionless distance between B1 and B2 was 8.1, with initial velocities of 20 mm/s and 30 mm/s, respectively. As the distance decreased to 6.9, the velocities reached the first peak at 38 mm/s and 42 mm/s, respectively, indicating that the secondary Bjerknes force became dominant. Subsequently, the bubbles entered the deceleration phase, which lasted for 1.8 dimensionless distances, during which the bubble radii increased, leading to increased fluid resistance and a decrease in translation speed. When the distance was reduced to 6.3, the velocities were 32 mm/s and 30 mm/s, respectively, marking the end of deceleration. Then, within the distance from 6.3 to 1.1, the bubbles’ acceleration and velocity increased sharply, forming a parabolic growth. Fig. 8a shows that under the acoustic field, the bubble volume increased, and according to Eq. (9), the secondary Bjerknes force increased accordingly. At contact, the velocities of B1 and B2 were 113 mm/s and 100 mm/s, respectively.
Fig. 7.
Two-bubble distance–velocity plot with , 100, 117. (a) Spherical oscillating bubbles separated by 8. (b) Spherical oscillating bubbles separated by 3.6. (c) Spherically oscillating bubbles. (d) High-order oscillating bubbles.
Fig. 8.
Images of two bubbles translation with , 100, 117. (a) Image of spherically oscillating bubbles separated by 8. (b) Image of spherically oscillating bubbles separated by 3.6. (c) Image of spherically oscillating bubbles. (d) Image of high-order oscillating bubbles. The Roman numerals in frame (a) correspond to the initial moment of the two bubbles, the first peak velocity during the acceleration phase, the velocity nadir during the deceleration phase, and the contact moment between the bubbles in Fig. 6, respectively.
Figs. 7b and 8b demonstrate that two bubbles undergoing spherical oscillation experience three phases: acceleration, deceleration, and a velocity jump, ultimately colliding. The periods of acceleration and deceleration are short, and according to Eq. (8), the interactive force between bubbles is inversely proportional to the distance. By analyzing the results of previous experiments, we found that the duration of the acceleration and deceleration phases of the bubbles is related to the initial dimensionless distance; the greater the distance, the longer the duration of these phases. In Fig. 7c, the velocity change trend of the two bubbles is similar to the first two cases, but the overall velocity is smaller, due to the small bubble radius (Fig. 8c), high Laplace pressure, which leads to weak volume oscillation, and consequently a smaller secondary Bjerknes force. In the fourth case, the bubbles exhibit higher-order oscillations during the attraction process, as shown in Fig. 8d. Nevertheless, their motion trends are consistent with the previous sets of conditions, all experiencing stages of acceleration, deceleration, and velocity jump. The difference lies in the fact that from 0–83, the two bubbles transition from spherical oscillation to third-order oscillation, maintaining this shape until collision, with a relatively low contact velocity. This indicates that the high-order oscillations of the two bubbles are closely related to their interactive dynamic behavior.
Under strong acoustic field ( 117, 0), the secondary Bjerknes force between the two bubbles significantly increases, leading to a greater acceleration during the velocity jump phase. This is clearly observable during the velocity jump phase of the two bubbles, as shown in Figs. 9a and 9b for B1 and B2, where the significant increase in velocity indicates that the secondary Bjerknes force has a more pronounced effect on bubble motion in a strong acoustic field. The first velocity peak image in Fig. 10c shows that under the influence of the secondary Bjerknes force, B1 transitions from spherical oscillation to a collapse oscillation towards B2. B1’s velocity is initially greater than B2’s, and at the end of the deceleration phase, the radii of both bubbles increase, but the intensity of the oscillation decreases. During the velocity jump phase, due to the oscillation difference in the radii of the two bubbles, the velocity difference is maintained at approximately 20 mm/s. Upon collision, the velocities of the two bubbles reach the maximum values of 136 mm/s and 124 mm/s, with the bubble morphology exhibiting non-spherical oscillation. The experimental results indicate that the secondary Bjerknes force between the two bubbles varies with the rate of change of bubble volume, consistent with the theoretical research of Eq. (9) [32]. The periods of acceleration and deceleration phases shown in Fig. 9d are shorter than the previous two sets, and the difference between the velocity peak and initial velocity is also smaller. In Fig. 10d, the bubbles exhibit irregular oscillation. The acceleration during the velocity jump phase is reduced compared to Figs. 9a and 9b, and the two bubbles collide at 2.2. We believe that the irregular shape oscillation caused by changes in the acoustic field leads to a shortening of the acceleration and deceleration phases, a reduction in amplitude, and a decrease in acceleration during the velocity jump phase. This is because the irregularly oscillating bubbles have a larger surface area, increasing the resistance during translation.
Fig. 9.
Two-bubble distance–velocity plot with , 0, 117. (a) Spherical oscillating bubbles separated by 6.5. (b) Spherical oscillating bubbles separated by 4.6. (c) Non-spherical oscillating bubbles. (d) Irregular-shaped oscillating bubbles.
Fig. 10.
Images of two bubbles translation with , 0, 117. (a) Image of bubbles separated by a distance 6.5. (b) Image of bubbles separated by a distance 4.6. (c) Image of non-spherical oscillating bubbles. (d) Image of irregularly shaped oscillating bubbles. The Roman numerals in frame (a) correspond to the initial moment, the first peak velocity during the acceleration phase, the velocity nadir during the deceleration phase, and the contact moment of the bubbles in Fig. 8, respectively.
Overall, in a strong acoustic field with 0, two bubbles undergo acceleration, deceleration, and velocity jump phases during their attraction process. The non-spherical oscillation of the bubbles significantly affects the variation of the secondary Bjerknes force. Additionally, strong acoustic fields are more likely to induce irregular shape oscillations and non-spherical oscillations in the bubbles, where the increased translation resistance due to irregular shape oscillations is the main reason for the shortened duration of acceleration and deceleration phases, reduced velocity peak values, and decreased acceleration during the velocity jump phase.
Under cases of 0 and 100, we studied the translation characteristics of equal-sized two bubbles. In Fig. 11,  represent bubbles under the condition of 100, while
represent bubbles under the condition of 100, while  represent bubbles under the condition of 0. By comparing these conditions, the changes in bubble translation velocity under different acoustic field intensities can be directly observed. The image shows that the velocity of two bubbles reaches a peak upon contact. We observed that the translation velocity of the bubbles decreases with increasing initial radius, but this decrease is not linear. Specifically, bubbles with an initial radius of 4 (as shown in Fig. 8c) have a lower translation velocity, mainly because their large Laplace pressure results in a small volume change rate, thereby causing a smaller secondary Bjerknes force. In contrast, bubbles with an initial radius of 14 (as shown in Fig. 10c) have a higher translation velocity due to their intense oscillation and large volume change rate, thus experiencing a greater secondary Bjerknes force. The images also reveal that a strong acoustic field ( 0) is more likely to induce bubble volume oscillations and increase the secondary Bjerknes force compared to a weak acoustic field ( 100), which may lead to the translation velocity of larger bubbles in a strong acoustic field approaching or even exceeding that of smaller bubbles in a weak acoustic field.
represent bubbles under the condition of 0. By comparing these conditions, the changes in bubble translation velocity under different acoustic field intensities can be directly observed. The image shows that the velocity of two bubbles reaches a peak upon contact. We observed that the translation velocity of the bubbles decreases with increasing initial radius, but this decrease is not linear. Specifically, bubbles with an initial radius of 4 (as shown in Fig. 8c) have a lower translation velocity, mainly because their large Laplace pressure results in a small volume change rate, thereby causing a smaller secondary Bjerknes force. In contrast, bubbles with an initial radius of 14 (as shown in Fig. 10c) have a higher translation velocity due to their intense oscillation and large volume change rate, thus experiencing a greater secondary Bjerknes force. The images also reveal that a strong acoustic field ( 0) is more likely to induce bubble volume oscillations and increase the secondary Bjerknes force compared to a weak acoustic field ( 100), which may lead to the translation velocity of larger bubbles in a strong acoustic field approaching or even exceeding that of smaller bubbles in a weak acoustic field.
Fig. 11.
Equal-sized two-bubble velocity plot. (the -axis represents the initial radius, and the -axis represents the velocity).  represent bubbles in the 100 acoustic field, and
represent bubbles in the 100 acoustic field, and  represent bubbles in the 0 acoustic field. Each set of points on a vertical line represents the velocities of two bubbles in an experiment.
represent bubbles in the 0 acoustic field. Each set of points on a vertical line represents the velocities of two bubbles in an experiment.
3.2. Interaction between unequal-sized two bubbles
In practical applications, bubble sizes are often inconsistent. Utilizing the aforementioned experimental setup, we generated double bubbles of unequal sizes in water, to study their translation behavior in an ultrasonic field. By comparing and analyzing multiple sets of experimental data images, we explored the translation characteristics of these bubbles.
The high-speed camera captured bubbles generated by micro-needles at the micrometer scale, with initial radii ranging from 5 to 20, and the radius ratio of the double bubbles was approximately 2:1.
The bubble behavior and velocity-distance graph observed using a long-focus microlens at a resolution of 256 × 128 pixels and a recording rate of 4.8 × 104 frames per second are shown in Fig. 12, with initial radii ranging from 5 to 20, and the radius ratio of the double bubbles was approximately 2:1. When the percentage difference in the initial radii of the bubbles / is no more than 10% ( represents the initial radius value of B1 in the attraction stage, represents the initial radius value of B2 in the attraction stage, B1 represents bubbles with larger radii, and B2 represents bubbles with smaller radii), we consider the initial radii of the two bubbles to be in a 2:1 ratio, denoted as : 2:1. In the study of the interaction between equal-sized bubbles, we found that the position of the acoustic field significantly affects the stability and oscillation of the bubbles. Similarly, in the study of the interaction between bubbles with a 2:1 size ratio, we also considered the position of the acoustic field () as an independent variable.
Fig. 12.
Two-bubble distance–velocity plot : 2:1, 100, 117. (a) High-order oscillating bubbles. (b) High-order oscillating bubbles. (c) Spherical oscillating bubbles. (d) High-order oscillating bubbles. The Roman numerals in frame (a) denote the initial moment, the velocity nadir during the deceleration phase, and the moment of contact between the two bubbles.
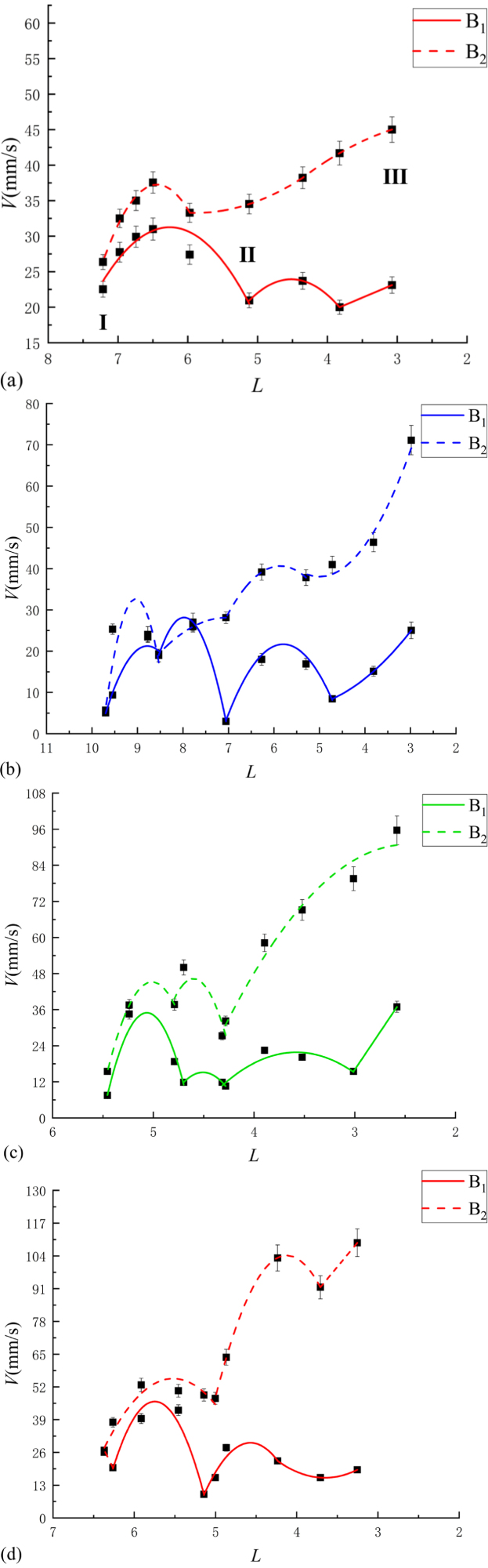
In the first two experimental cases, a translation process of two bubbles with higher-order oscillations was observed. The third case demonstrated spherical oscillations of the two bubbles; while in the fourth case, the bubbles exhibited irregular shape oscillations. As shown in Fig. 12, the velocity curve of the two bubbles went through multiple fluctuations, including several stages of acceleration and deceleration, which significantly differs from the interaction between equal-sized bubbles.
In Fig. 12a, B1 displays third-order oscillation traits. At a distance 6.6, B1 and B2 achieve their initial peak velocities. Thereafter, at 5.2, B1’s velocity diminishes while B2’s velocity persists in increasing. In the moments preceding contact, the velocities of both bubbles escalate; notably, B2 transitions from decelerating to accelerating, signifying a surge in the secondary Bjerknes force.
In Fig. 12b, the velocity profiles of B1 and B2 exhibit multiple rounds of acceleration and deceleration. At 6.7, B1 undergoes deceleration, reaching its minimum velocity, while B2’s velocity increases, preemptively entering an acceleration phase. Unlike equal-sized two bubbles, the acceleration and deceleration behaviors of unequal-sized bubbles during attraction are not entirely synchronized, as also observed in Figs. 11c and 11d. This asynchrony may stem from differences in the expansion and contraction timings associated with their distinct initial radii. In the final moments before contact, the secondary Bjerknes force increases due to the expanding volumes and rising volume change rates of the bubbles, which governs their attraction. At this juncture, B2’s velocity trend shifts from deceleration to acceleration, with an acceleration magnitude approaching that of B1. Throughout the interaction, B1’s velocity fluctuates within a certain range, whereas B2 does not exhibit a significant velocity surge, primarily attributed to the size discrepancy between the two bubbles.
In Figs. 12c and 13c, the two bubbles undergo spherical oscillation. At 4.1, B2 is nearing the end of its deceleration phase, while B1 has completed deceleration and begun the velocity jump phase. It is observed that the acceleration of the two bubbles during the velocity jump phase just before contact is greater than that of the higher-order oscillating bubbles, which may indicate a stronger secondary Bjerknes force between the spherically oscillating bubbles.
Fig. 13.
Images of two bubbles translation : 2:1, 100, 117. (a) Image of high-order oscillating bubbles. (b) Image of high-order oscillating bubbles. (c) Image of spherical oscillating bubbles. (d) Image of irregular-shaped oscillating bubbles. The Roman numerals in frame (a) denote the initial moment of the two bubbles, the lowest velocity point during the deceleration phase, and the moment of contact between the bubbles.
Fig. 13d illustrates the transition from third-order oscillation to irregular shape oscillation as the distance between the bubbles decreases. This evolution significantly affects the velocity of the two bubbles, especially in Fig. 12d, where B2 has a very low acceleration just before contact, and B1 exhibits an abnormal change in velocity during the velocity jump phase. These phenomena indicate that higher-order modal oscillations and irregular shape oscillations increase the resistance to bubble translation, and may also alter the direction of the secondary Bjerknes force between spherical bubbles due to non-spherical effects, potentially magnifying it by several times [42], [43], [44], thereby affecting the interactive dynamics between the two bubbles.
In the experiment, we observed that when the sound source is located directly above the bubbles ( 0) rather than at a distance ( 100), the increase in local sound pressure amplitude begins to induce higher-order oscillations and irregular shape oscillations of the bubbles, thereby altering the velocity trend of the bubbles. As shown in Figs. 14a and 15a, in the early stages of bubble generation, they maintain spherical oscillations. At 5.2, 4.9, and 3.2, the acceleration and deceleration of the two bubbles are not synchronized, primarily due to the differences in expansion and contraction cycles caused by the different sizes of the bubbles. In the final moments before contact, bubble B1 transitions from deceleration to acceleration, with an acceleration similar to that of B2. The velocity curve of Fig. 14b is similar to that of Fig. 14a, indicating that the acceleration and deceleration behaviors of the two bubbles are not synchronized. Fig. 15c clearly shows the non-spherical oscillations of the bubbles, while in Fig. 14c, bubble B1 only experienced two stages of acceleration and deceleration. Just before the two bubbles are about to touch, the velocity change trend of B1 is still deceleration, while B2 enters the velocity jump stage at 6.4, indicating an increase in the secondary Bjerknes force acting on B2. However, the non-spherical oscillations of B1 increase the translation resistance, leading to a decrease in its velocity. In Fig. 15d, due to the change in the position of the sound source, B1 begins non-spherical oscillations at the initial moment. At 4.5 and 3.9, due to the difference in bubble sizes, the acceleration and deceleration behaviors once again exhibit asynchrony. Before the two bubbles touch, the irregular oscillations of B1 result in a lower acceleration compared to B2. By analyzing these images, we find that the non-spherical and irregular oscillations of the bubbles affect the interaction between the two bubbles, especially at close distances, increasing fluid resistance and affecting the translation characteristics of the bubbles.
Fig. 14.
Two-bubble distance–velocity plot : 2:1, 0, 117. (a) Spherical oscillating bubbles. (b) Spherical oscillating bubbles. (c) Non-spherical oscillating bubbles. (d) Non-spherical oscillating bubbles. The Roman numerals in frame (a) denote the initial moment, the velocity nadir during the deceleration phase, and the moment of contact between the two bubbles.
Fig. 15.
Images of two bubbles translation : 2:1, 0, 117. (a) Image of spherical oscillating bubbles. (b) Image of spherical oscillating bubbles. (c) Image of non-spherical oscillating bubbles. (d) Image of non-spherical oscillating bubbles. The Roman numerals in frame (a) correspond to the initial moment of the two bubbles, the velocity nadir during the deceleration phase, and the moment of contact between the two bubbles.
To thoroughly investigate the translation characteristics of bubbles of unequal sizes in strong and weak acoustic fields, we used the bubble radius as the horizontal axis to study the translation of the bubble pair under conditions of 0 and 100. As shown in Fig. 16,  represent bubbles in the 100 acoustic field, and
represent bubbles in the 100 acoustic field, and  represent bubbles in the 0 acoustic field.
represent bubbles in the 0 acoustic field.
Fig. 16.
Unequal-sized velocity plot. (the -axis represents the initial radius, and the -axis represents the velocity).  represent bubbles in the 100 acoustic field, and
represent bubbles in the 100 acoustic field, and  represent bubbles in the 0 acoustic field. Each set of points on a vertical line represents the velocities of two bubbles in an experiment.
represent bubbles in the 0 acoustic field. Each set of points on a vertical line represents the velocities of two bubbles in an experiment.
To study the translation characteristics of unequal-sized bubbles under different acoustic field intensities, we analyzed using the initial radius of the smaller bubble in each set of conditions as the horizontal axis. Observational results indicate that the translation velocity of smaller bubbles is generally faster than that of larger bubbles, reaching a peak upon contact. In a strong acoustic field ( 0), the difference in bubble velocities is more pronounced compared to a weak acoustic field ( 100). This is primarily because a strong acoustic field is more likely to induce volume oscillations and irregular shape oscillations of the bubbles, where volume oscillations enhance the secondary Bjerknes force, while irregular shape oscillations increase translation resistance. Among bubbles of different sizes, larger bubbles are more prone to irregular oscillations due to their lower Laplace pressure [45], [46], resulting in significant differences in velocity between the two bubbles. As shown in Fig. 15c, when the radius of the smaller bubble is 8.4, the irregular oscillations are weaker, resulting in a relatively smaller difference in velocities, which validates our research findings. Furthermore, we found that the contact velocity of bubbles with unequal initial radii differs more significantly from that of equal-sized bubbles, indicating that the initial radius of the bubble is an important factor affecting its translation characteristics, with the translation velocity changing as its radius increases.
4. Conclusions
This study developed an in-situ atmospheric pressure bubble generation system to investigate the translation characteristics of horizontal micro-scale two-bubble systems in a 20 kHz acoustic field, overcoming the stochastic nature of cavitation bubble formation and enabling a detailed analysis of the secondary Bjerknes force through a proposed bubble velocity–distance curve. The conclusions are as follows:
1. The pressure within the ultrasonic field is relatively stable, with the impact of the two layers on the sound pressure amplitude being negligible. The sound pressure at the central measurement point in the water tank is consistently around 40 kPa, while the sound pressure at the four surrounding measurement points (, and , ) is comparable but less than 40 kPa.
2. The interaction of two bubbles with the same radius in different acoustic fields, and observed a three-stage attraction process: acceleration, deceleration, and velocity jump. In stronger acoustic fields, the bubbles exhibit more irregular oscillations, which shorten the pulsation cycle experienced by the bubbles as they approach each other, reduce peak velocities, and decrease acceleration during the velocity jump phase due to increased surface area and resistance.
3. In two-bubble systems with an initial radius ratio of 2:1, the bubbles experience asynchronous acceleration and deceleration stages due to differences in their expansion and contraction cycles. Bubbles with larger initial radii exhibit slower migration speeds; intense volume oscillations slow down bubble movement. Irregular oscillations before contact can reduce their acceleration during the velocity jump phase.
These findings have implications for biomedicine, ultrasonic cleaning, and other fields where understanding the complex dynamics of interacting cavitation bubbles is crucial.
CRediT authorship contribution statement
Xiao Huang: Supervision, Funding acquisition, Conceptualization. Peng-Bo Liu: Methodology, Data curation. Guang-Yun Niu: Writing – original draft, Resources, Methodology, Formal analysis, Data curation. Hai-Bao Hu: Supervision.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Thanks to the support of the National Natural Science Foundation of China (Nos. 52101373, 52471345), the Shenzhen Science and Technology Program, China (No. JCYJ20230807145621043), the Postdoctoral Science Foundation of Chinahttp://dx.doi.org/10.13039/501100002858 (No. 2021M692629), and the Innovation Capability Support Program of Shaanxi, China (No. 2024RS-CXTD-15), this research was made possible.
References
- 1.Huang X., Niu G., Xie Y., Chen X., Hu H., Pan G. Application of ultrasonic cavitation in ship and marine engineering. J. Mar. Sci. Appl. 2024;23(1):23–38. [Google Scholar]
- 2.Plesset M.S., Prosperetti A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977;9:145–185. [Google Scholar]
- 3.Brennen C.E. Cambridge University Press; 2014. Cavitation and Bubble Dynamics. [Google Scholar]
- 4.Lauterborn W., Kurz T. vol. 73. IOP Publishing; 2010. Physics of bubble oscillations. (Reports on Progress in Physics). [Google Scholar]
- 5.Salimi M., Livadas M., Teyeb A., El Masri E., Gan T.-H. Biofouling removal using a novel electronic system for driving an array of high power marinised transducers. Appl. Sci. 2023;13(6):3749. [Google Scholar]
- 6.Guo S., Khoo B.C., Teo S.L.M., Zhong S., Lim C.T., Lee H.P. Effect of ultrasound on cyprid footprint and juvenile barnacle adhesion on a fouling release material. Colloids Surf. B. 2014;115:118–124. doi: 10.1016/j.colsurfb.2013.11.020. [DOI] [PubMed] [Google Scholar]
- 7.Mazue G., Viennet R., Hihn J., Carpentier L., Devidal P., Albaïna I. Large-scale ultrasonic cleaning system: design of a multi-transducer device for boat cleaning (20 kHz) Ultrason. Sonochemistry. 2011;18(4):895–900. doi: 10.1016/j.ultsonch.2010.11.021. [DOI] [PubMed] [Google Scholar]
- 8.Zhong X., Dong J., Liu M., Meng R., Li S., Pan X. Experimental study on ship fouling cleaning by ultrasonic-enhanced submerged cavitation jet: A preliminary study. Ocean Eng. 2022;258 [Google Scholar]
- 9.Mat-Shayuti M.S., Tuan Ya T.M.Y.S., Abdullah M.Z., Othman N.H., Alias N.H. Exploring the effect of ultrasonic power, frequency, and load toward remediation of oil-contaminated beach and oilfield sands using ANOVA. Environ. Sci. Pollut. Res. 2021;28(41):58081–58091. doi: 10.1007/s11356-021-14776-8. [DOI] [PubMed] [Google Scholar]
- 10.ur Rehman H., Shuaib M., Ismail E.A., Li S. Enhancing medical ultrasound imaging through fractional mathematical modeling of ultrasound bubble dynamics. Ultrason. Sonochemistry. 2023;100 doi: 10.1016/j.ultsonch.2023.106603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Siebenmorgen C., Poortinga A., van Rijn P. Sono-processes: Emerging systems and their applicability within the (bio-) medical field. Ultrason. Sonochemistry. 2023 doi: 10.1016/j.ultsonch.2023.106630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu M., Ouyang Y., Wang Z., Zhang R., Huang P.-H., Chen C., Li H., Li P., Quinn D., Dao M., et al. Isolation of exosomes from whole blood by integrating acoustics and microfluidics. Proc. Natl. Acad. Sci. 2017;114(40):10584–10589. doi: 10.1073/pnas.1709210114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guo F., Mao Z., Chen Y., Xie Z., Lata J.P., Li P., Ren L., Liu J., Yang J., Dao M., et al. Three-dimensional manipulation of single cells using surface acoustic waves. Proc. Natl. Acad. Sci. 2016;113(6):1522–1527. doi: 10.1073/pnas.1524813113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sun R., Xu W., Xiong L., Jiang N., Xia J., Zhu Y., Wang C., Liu Q., Ma Y., Luo H. The combined effects of ultrasound and plasma-activated water on microbial inactivation and quality attributes of crayfish during refrigerated storage. Ultrason. Sonochemistry. 2023;98 doi: 10.1016/j.ultsonch.2023.106517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Muruganandham M., Sivasubramanian K., Velmurugan P., Kumar S.S., Arumugam N., Almansour A.I., Kumar R.S., Manickam S., Pang C.H., Sivakumar S. An eco-friendly ultrasound approach to extracting yellow dye from cassia alata flower petals: Characterization, dyeing, and antibacterial properties. Ultrason. Sonochemistry. 2023;98 doi: 10.1016/j.ultsonch.2023.106519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jan R., Gani A., Dar M.M., Bhat N.A. Bioactive characterization of ultrasonicated ginger (Zingiber officinale) and licorice (Glycyrrhiza glabra) freeze dried extracts. Ultrason. Sonochemistry. 2022;88 doi: 10.1016/j.ultsonch.2022.106048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang Z., Liang W., Guo X., Liu L. Inactivation of scrippsiella trochoidea cysts by different physical and chemical methods: Application to the treatment of ballast water. Marine Poll. Bull. 2018;126:150–158. doi: 10.1016/j.marpolbul.2017.11.002. [DOI] [PubMed] [Google Scholar]
- 18.Zhang Q., Liu J., Xia H., Xu Y., Zhang L. Effective removal of as from a high arsenic-bearing ZnSO4 solution by ultrasonic enhanced ozonation in a one-pot method. Ultrason. Sonochemistry. 2024;102 doi: 10.1016/j.ultsonch.2023.106748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boateng I.D., Kumar R., Daubert C.R., Flint-Garcia S., Mustapha A., Kuehnel L., Agliata J., Li Q., Wan C., Somavat P. Sonoprocessing improves phenolics profile, antioxidant capacity, structure, and product qualities of purple corn pericarp extract. Ultrason. Sonochemistry. 2023;95 doi: 10.1016/j.ultsonch.2023.106418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ida M., Naoe T., Futakawa M. Suppression of cavitation inception by gas bubble injection: A numerical study focusing on bubble-bubble interaction. Phys. Rev. E. 2007;76(4) doi: 10.1103/PhysRevE.76.046309. [DOI] [PubMed] [Google Scholar]
- 21.Baresch D., Thomas J.-L., Marchiano R. Observation of a single-beam gradient force acoustical trap for elastic particles: acoustical tweezers. Phys. Rev. Lett. 2016;116(2) doi: 10.1103/PhysRevLett.116.024301. [DOI] [PubMed] [Google Scholar]
- 22.Tran S., Marmottant P., Thibault P. Fast acoustic tweezers for the two-dimensional manipulation of individual particles in microfluidic channels. Appl. Phys. Lett. 2012;101(11) [Google Scholar]
- 23.Rabaud D., Thibault P., Raven J.-P., Hugon O., Lacot E., Marmottant P. Manipulation of confined bubbles in a thin microchannel: Drag and acoustic Bjerknes forces. Phys. Fluids. 2011;23(4) [Google Scholar]
- 24.Ozcelik A., Rufo J., Guo F., Gu Y., Li P., Lata J., Huang T.J. Acoustic tweezers for the life sciences. Nature Methods. 2018;15(12):1021–1028. doi: 10.1038/s41592-018-0222-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crum L.A. Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 1975;57(6):1363–1370. [Google Scholar]
- 26.Marston P.L., Trinh E.H., Depew J., Asaki T.J. Response of bubbles to ultrasonic radiation pressure: Dynamics in low gravity and shape oscillations. Bubble Dynamics and Interface Phenomena: Proceedings of an IUTAM Symposium Held in Birmingham; UK, 6–9 September 1993; Springer; 1994. pp. 343–353. [Google Scholar]
- 27.Doinikov A.A. Translational motion of a spherical bubble in an acoustic standing wave of high intensity. Phys. Fluids. 2002;14(4):1420–1425. [Google Scholar]
- 28.Huang X., Wang Q.-X., Zhang A.-M., Su J. Dynamic behaviour of a two-microbubble system under ultrasonic wave excitation. Ultrason. Sonochemistry. 2018;43:166–174. doi: 10.1016/j.ultsonch.2018.01.012. [DOI] [PubMed] [Google Scholar]
- 29.Huang X., Hu H., Li S., Zhang A.-M. Nonlinear dynamics of a cavitation bubble pair near a rigid boundary in a standing ultrasonic wave field. Ultrason. Sonochemistry. 2020;64 doi: 10.1016/j.ultsonch.2020.104969. [DOI] [PubMed] [Google Scholar]
- 30.Shen Y., Zhang L., Wu Y., Chen W. The role of the bubble–bubble interaction on radial pulsations of bubbles. Ultrason. Sonochemistry. 2021;73 doi: 10.1016/j.ultsonch.2021.105535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang A., Li S.-M., Cui P., Li S., Liu Y.-L. A unified theory for bubble dynamics. Phys. Fluids. 2023;35(3) [Google Scholar]
- 32.Mettin R., Akhatov I., Parlitz U., Ohl C., Lauterborn W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. Phys. Rev. E. 1997;56(3):2924. [Google Scholar]
- 33.Yoshida K., Fujikawa T., Watanabe Y. Experimental investigation on reversal of secondary Bjerknes force between two bubbles in ultrasonic standing wave. J. Acoust. Soc. Am. 2011;130(1):135–144. doi: 10.1121/1.3592205. [DOI] [PubMed] [Google Scholar]
- 34.Li-Chun B., Jin-Guang S., Yan-Dong G. High-speed photography and image analysis of orbital motion of gas bubbles in ultrasonic field. Acta Phys. Sin. 2021;70(5):223–229. [Google Scholar]
- 35.Wang C., Lin S. The coupled motion of bubbles in ultrasonic field. Shengxue Xuebao(Acta Acustica) 2011;36(3):325–331. [Google Scholar]
- 36.R.C. Gonzalez, Digital Image Processing, Coursesmart eTextbook, 3/E.
- 37.Reddy A.J., Szeri A.J. Coupled dynamics of translation and collapse of acoustically driven microbubbles. J. Acoust. Soc. Am. 2002;112(4):1346–1352. doi: 10.1121/1.1502899. [DOI] [PubMed] [Google Scholar]
- 38.Bjerknes V. Columbia University Press; 1906. Fields of Force: Supplementary Lectures, Applications to Meteorology; A Course of Lectures in Mathematical Physics Delivered December 1 to 23, 1905. [Google Scholar]
- 39.Doinikov A.A. Effects of the second harmonic on the secondary Bjerknes force. Phys. Rev. E. 1999;59(3):3016. [Google Scholar]
- 40.Minnaert M. XVI. On musical air-bubbles and the sounds of running water. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1933;16(104):235–248. [Google Scholar]
- 41.Wang X., Ning Z., Lv M., Yao J., Sun C. The secondary bjerknes force between two bubbles in ultrasonic field. J. Phys. Soc. Japan. 2022;91(1) [Google Scholar]
- 42.Ma Y., Zhang G., Ma T. Interaction of two bubbles with distortion in an acoustic field. Ultrason. Sonochemistry. 2022;84 doi: 10.1016/j.ultsonch.2022.105953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hilgenfeldt S., Lohse D., Brenner M.P. Phase diagrams for sonoluminescing bubbles. Phys. Fluids. 1996;8(11):2808–2826. [Google Scholar]
- 44.Yan M., Shu-Yu L., Jie X., Yi-Fan T. Influnece of nonspherical effects on the secondary Bjerknes force in a strong acoustic field. Acta Phys. Sin. 2016;65(23) [Google Scholar]
- 45.Klapcsik K., Hegedűs F. Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochemistry. 2019;54:256–273. doi: 10.1016/j.ultsonch.2019.01.031. [DOI] [PubMed] [Google Scholar]
- 46.Kalmár P., Hegedűs F., Klapcsik K. A comparative study of measurements and numerical simulations of acoustically excited non-spherical bubbles oscillation. Int. J. Multiph. Flow. 2024;179 [Google Scholar]