Abstract
In solid-state NMR, dipolar-based heteronuclear polarization transfer has been extensively used for sensitivity enhancement and multidimensional correlations, but its efficiency often suffers from undesired spin interactions and hardware limitations. Herein, we propose a novel dipolar-echo edited R-symmetry (DEER) sequence, which is further incorporated into the INEPT-type scheme, dubbed DEER-INEPT, for achieving highly efficient heteronuclear polarization transfer. Numerical simulations and NMR experiments demonstrate that DEER-INEPT offers significantly improved robustness, enabling efficient polarization transfer under a wide range of MAS conditions, from slow to ultrafast rates, outperforming existing methods. Its high efficiency leads to noticeably enhanced sensitivity in both 1H → X and X → 1H transfers, applicable to both spin-1/2 and spin-half-integer quadrupolar nuclei. DEER-INEPT is expected to be widely used in various systems, offering advantages in both sensitivity enhancement and structural analysis.
A novel dipolar-echo edited R-symmetry (DEER) sequence is proposed, which is further incorporated into the INEPT-type scheme, dubbed DEER-INEPT, for achieving highly efficient heteronuclear polarization transfer under a wide range of MAS rates.
Introduction
As a powerful and irreplaceable technique, solid-state NMR has been widely used for revealing the atomic level structures in a variety of materials including liquid crystals and microcrystalline and amorphous solid materials. Its versatility stems largely from the high sensitivity to the surrounding chemical environment around nuclear spins, mediated by interactions such as scalar, dipolar, and quadrupolar couplings.1–5 Among these, the dipolar coupling interaction is of particular importance in solid-state NMR, linking two spins through a direct dipole–dipole interaction. The strength of this interaction, defined by the dipolar coupling constant (DCC), depends on the gyromagnetic ratios (γ) of the coupled spins and their distance, DCC ∝ γ1γ2/r3, making it a critical parameter for structural studies. Furthermore, the anisotropic nature of dipolar coupling, which can be reduced or even averaged out by molecular motions, offers valuable insights into the dynamic behavior of materials.3,6–8
One of the key applications of the dipolar coupling interaction is its role in heteronuclear polarization transfer, where the polarization from a high-γ spin (e.g., 1H/19F, denoted as I) is transferred to a low-γ spin (e.g., 13C/17O/15N, denoted as S). This process enhances the detection sensitivity of low-γ nuclei and facilitates the establishment of multi-dimensional NMR correlation spectroscopy, being site-specific and encoded with internuclear distances, and hence provides valuable information for materials sciences.9–11
Efficient polarization transfer becomes even more important for quadrupolar nuclei (spin >1/2), since they constitute over 75% of the elements in the periodic table and are widely present in materials such as oxides, zeolites, metal–organic frameworks, etc.5,12–16 However, achieving efficient transfer involving quadrupolar nuclei is challenging due to the complex spin dynamics involving both central (CT) and satellite transitions (ST), which are further complicated by the mutual interferences arising from unavoidable hardware imperfections and unwanted spin interactions.
Currently, most solid-state NMR experiments are conducted under magic-angle spinning (MAS) to achieve high spectral resolution. Conventional methods, such as CPMAS (Cross Polarization under MAS) routinely used for spin-1/2 systems (1H, 13C, 15N, 19F, 29Si, etc.), often exhibit limited efficiency for quadrupolar nuclei because of the high sensitivity to radiofrequency (rf) inhomogeneity and the ineffective spin-locking of quadrupolar magnetization under MAS.17–21 For polarization transfer between one spin-1/2 nucleus and one half-integer-spin quadrupolar nucleus, a simple strategy is to minimize the number of rf pulses on the quadrupolar nucleus and to use soft CT-selective pulses for only manipulating the central transition. Accordingly, through-space polarization transfer can be established by applying heteronuclear dipolar recoupling sequences on the spin-1/2 nucleus, while applying only a few π/2 and/or π pulses on the quadrupolar nucleus.22,23 The most representative approaches include D-RINEPT (Dipolar-based Refocused Insensitive Nuclei Enhanced by Polarization Transfer)24–26 and PRESTO (Phase-shifted Recoupling Effects a Smooth Transfer of Order),27,28 which employ zero-quantum and single-quantum heteronuclear dipolar recoupling sequences, respectively. Among these, D-RINEPT is more versatile than PRESTO since it allows both forward (I → S) and backward (S → I) transfers. However, the transfer efficiency of the D-RINEPT sequence is hampered by the delays in spin echoes, particularly at slow MAS frequencies.26 Moreover, the dipolar recoupling sequences used in D-RINEPT, such as R3 and SR412/RNnν symmetry-based sequences, often exhibit unstable performances due to the aforementioned interferences.26,27,29–33
In this contribution, we introduce a novel approach, termed DEER-INEPT (dipolar-echo edited R-symmetry INEPT), which combines PMRR (phase-modulated rotary resonance) recoupling34 and a unique dipolar-echo design. This new scheme enables highly efficient polarization transfer between spin-1/2 and quadrupolar nuclei. DEER-INEPT is adaptable to a wide range of MAS conditions, from slow to ultrafast spinning speed. Through comprehensive numerical simulations and experiments across various spinning speeds (10–60 kHz), we demonstrate the high robustness and superior transfer efficiency of DEER-INEPT. The high efficiency not only provides better sensitivity enhancement, but also allows efficient acquisitions of multidimensional correlation spectra, as exemplified by 2D 1H–71Ga and 1H–27Al DEER-INEPT correlation experiments.
Experimental
Materials
Ammonium dihydrogen phosphate (NH4H2PO4, ADP) was purchased from Shanghai Macklin Biochemical Technology Co., Ltd and used without further treatment; NaCl was purchased from Sinopharm Chemical Reagent Co., Ltd and was baked at 383 K for 3 h; γ-alumina was purchased from Alfa Aesar and used without further treatment; Ga(acac)3 was purchased from Shanghai Yuanye Bio-Technology Co., Ltd and used without further treatment. HY zeolite was purchased from Alfa Aesar and heated under vacuum at 673 K for 6 h and then loaded in a 3.2 mm rotor in a glove box filled with Ar.
Solid-state NMR experiments
1H → 31P polarization transfer experiments in ADP were used for revealing the effect of rf inhomogeneity on DEER-INEPT and SR4-D-RINEPT. The ADP powder was packed to 1 mm thick and located in 11 different positions in a 4 mm rotor (as shown in Fig. 2), while the rest of the rotor volume was packed with NaCl. NaCl was dehydrated at 383 K in an air oven. The rotor was spun to 10 kHz, with a 4 mm HX WVT probe in an Avance NEO 400 Bruker spectrometer with a 9.4 T Oxford magnet. For both DEER-INEPT and SR4-D-RINEPT, the rf amplitudes of 1H π/2 excitation pulses were 59.5 kHz, and those for 31P pulses were 64 kHz. For DEER-INEPT (fw = 0) and SR4-D-RINEPT, rf amplitudes (ν1) of PMRR and SR4 were both 20 kHz, while ν1 = 80 kHz was used for DEER-INEPT (fw = 0.75). For all 1H → 31P experiments, the total duration for dipolar recoupling (mixing time) was 0.4 ms from optimization, and 1.0 s recycle delay was used.
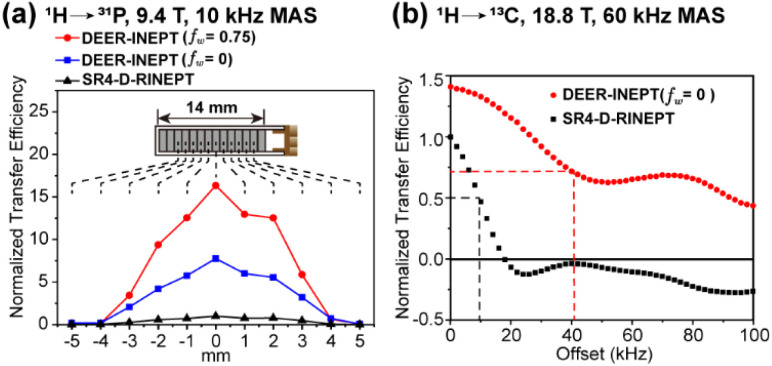
Fig. 2. Comparisons of experimental transfer efficiencies of DEER-INEPT, SR4-D-RINEPT and PRESTO. (a) 1H → 31P transfer in ADP with the sample packed at different rotor positions; (b) 1H → 13C transfer in 13Cα-glycine with varying 1H resonance offset. The methods, MAS frequencies and magnetic fields are denoted in each figure. The details of NMR experiments are provided in the ESI.†.
The experiments with γ-Al2O3, Ga(acac)3 and HY zeolite were performed on an 18.8 T Avance NEO Bruker NMR spectrometer, with a 3.2 mm HX probe for 10–20 kHz MAS and 1.3 mm HX probe for 40–60 kHz MAS. The parameters used in these experiments are summarized in Tables S1–S3.†
Simulations
All simulations are performed using the SIMPSON (v2.0) software. In the simulations of stability under rf mismatch and 1H–1H dipolar coupling, the spin systems are nonlinear 15N–1H⋯1H and tetrahedral 15N1H4, where all 15N–1H dipolar couplings are 4.0 kHz. In the nonlinear 15N–1H⋯1H spin system, the second 1H is not coupled to 15N and the angle ∠1H15N1H = 144.75°. In the 15N1H4 spin system, all 1H are coupled to 15N and each 1H is coupled to the rest three 1H spins. For calculating power averaging, the numbers of γ-angles are set between 10 and 20, and the numbers of (α, β)-angles are 100, using REPULSION partition scheme. In the comparisons between DEER-INEPT and SR4-D-RINEPT, both sequences use identical recoupling time. All interferences, e.g., rf mismatch, offset, chemical shift anisotropy (CSA) and homonuclear dipolar coupling, are only set to 1H spin, for which magnetization starts at the x direction. All simulated transfer efficiencies are normalized by the maximum value from an identical spin system with no interference.
For simulating the stability of DEER-INEPT with varied window modification, the spin system and simulation parameters are kept identical to those described above. Since larger window modification leads to a larger scaling factor of PMRR and, consequently, faster polarization transfer, the transfer efficiencies are normalized using the maximum value with an identical spin system and window modification without any interference.
Results and discussion
The core design of DEER-INEPT is the use of two dipolar-echoes that replace the two spin-echoes in conventional D-RINEPT. As shown in Fig. 1a–c, the two dipolar echoes are placed before and after the central π/2-pulses. As the heteronuclear dipolar recoupling also reintroduces CSA of the irradiated spin, both types of echoes can refocus the CSA and allow the heteronuclear dipolar interactions alone to mediate the transfer.
Fig. 1. The pulse scheme of (a) DEER, (b) DEER-INEPT with and without window modification and (c) SR4-D-RINEPT scheme where the repetitive unit of the SR4 sequence is [πyπ−yπyπ−y][π−yπyπ−yπy] spanning 2τr. The white/grey/brown rectangles denote π-pulses with different phases, and the blue rectangles denote the π/2-pulses used to transfer the magnetization. The π/2-pulses marked by black triangles in (b) have the same rf amplitude as their neighbouring π-pulses. In (c), τ1 = τR, τ2 = τR − τπ/2, τ3 = τR − τπ/2/2, and total delay is ca. 8τr for rotor-synchronization with finite durations of π- and π/2-pulses. (d–f) The simulated polarization transfer efficiency of 1H → 15N for DEER-INEPT as functions of rf mismatch, offset and 1H–1H homonuclear coupling, compared with SR4-D-RINEPT. Simulations in (d) and (e) were performed at 60 kHz MAS and (f) at 20 kHz MAS. More details of simulations are described in the ESI.†.
In the conventional D-RINEPT, such as the version shown in Fig. 1c using SR412 dipolar recoupling (SR4-D-RINEPT), delays τi (i = 1, 2, 3) are incorporated into the two spin-echoes to compromise between rotor synchronization of the recoupling sequence and the finite length of the refocusing π pulses.24,26 However, these delays, with each duration being ca. one rotor cycle (τr), are detrimental to polarization transfer efficiency because they cause redundant transverse relaxation (T2) decay and allow free evolution of interferences.35
The dipolar-echo, on the other hand, can circumvent the use of such delays. As discovered by Gan et al., 30,36 a central delay in the rotary resonance recoupling can invert the sign of the recoupled anisotropic spin interactions, provided that the delay has the same duration as that of the π-pulse. During this central delay, the heteronuclear dipolar Hamiltonians continue to evolve and are inverted by the physical rotation (i.e. MAS) of rotor, allowing an echo to occur. A similar refocusing effect, named rotational-echo, can also be found in the REDOR method proposed by Gullion et al.37 Given that the PMRR sequence is based on the rotary resonance phenomenon,34 a dipolar-echo can therefore be constructed by shifting the π-pulses by τr/8 and omitting the central and the last π-pulses, as illustrated in Fig. 1a. The I–S dipolar coupling (IzSz) is then restored using a central π-pulse applied on S spin. Note that in DEER-INEPT, the central π/2-pulse (marked by black triangles in Fig. 1b) on spin I is not only used to transfer the magnetization from I to S nuclei, but also a part of the recoupling scheme. Hence, it must have the same rf amplitude as other π-pulses, resulting in a duration of τr/8. As a consequence, there is no need in DEER-INEPT to introduce additional intervals to maintain the rotor-synchronization of the recoupling sequence (Fig. 1b). In contrast, a total delay of ca. 8τr is used in the SR4-D-RINEPT scheme (Fig. 1c).
In addition to its more compact design, DEER-INEPT can be adapted to a wide range of MAS conditions by using an adjustable window in the PMRR recoupling. For example, at slow spinning speed, PMRR with a large window can perform more efficiently than that without a window, as it effectively suppresses interferences such as homonuclear dipolar couplings. The window modification can be described by the window fraction fw, which is the total window duration (τw) in one rotor period (τr) of PMRR recoupling, i.e., fw = τw/τr.34
Fig. 1d and e show the numerical simulations using SIMPSON software38,39 comparing DEER-INEPT to SR4-D-RINEPT in terms of rf mismatch and offset at 60 kHz spinning speed. As the results indicate, under varying rf mismatch and resonance offset (Fig. 1d and e) at 60 kHz MAS, DEER-INEPT (fw = 0) shows significantly higher stability than SR4-D-RINEPT. Specifically, the former can maintain >50% transfer efficiency with rf mismatch ranging from −64% to + 33% (corresponding to rf amplitudes from 44 to 160 kHz) and resonance offset up to 28 kHz. The higher robustness to rf mismatch and offset can make DEER-INEPT more efficient across larger sample volumes and across wider bandwidth. In contrast, SR4-D-RINEPT is much less robust under these conditions. Improvements are also observed when multiple interferences exist simultaneously, such as rf mismatch combined with 1H–1H coupling, or resonance offset combined with CSA, as shown in Fig. S1.† These significantly improved performances of DEER-INEPT can be attributed to continuous spin lock on 1H spin during the entire polarization transfer process (see detailed discussion in the ESI Fig. S2 and S3†), a feature that is not achievable with SR4-D-RINEPT due to interruptions caused by delays τi. However, SR4-D-RINEPT is compatible with frequency selective transfer,40 whereas DEER-INEPT can only achieve broadband transfer, as the sign inversion in the dipolar-echo is achieved by sample rotation which is inherently frequency non-selective.
Another crucial interference in 1H–X polarization transfer is homonuclear (1H–1H) dipolar coupling. Strong 1H–1H dipolar coupling can be destructive to transfer efficiency, especially at slower spinning speed. As shown in Fig. 1f, at 20 kHz MAS, large window modification (fw = 0.5) for DEER-INEPT reduces the efficiency loss to only 15%, compared to a 70% loss for DEER-INEPT (fw = 0) and SR4-D-RINEPT. Similar results can be obtained in a proton-bath (tetrahedral 15NH4) spin system, as shown in Fig. S4.† The simulations indicate that, in real experiments, larger fw is always preferred for minimizing the interference from 1H–1H dipolar coupling. The improved stability with larger fw comes from enhanced performances of windowed PMRR recoupling sequences.34 In the following, experiments on proton-rich samples will further reveal that, with enhanced stability, DEER-INEPT can produce significantly stronger signal intensity, even though these two methods possess identical theoretical transfer efficiency (0.52γI/γS for I → S transfer).
First, the stability and transfer efficiency of the DEER-INEPT scheme are examined in model samples with 1/2-spin pairs, including 1H → 31P in ammonium dihydrogen phosphate (ADP) and 1H → 13C in 13Cα-glycine, as presented in Fig. 2. To evaluate the impact of rf inhomogeneity from the detection coil, the samples in rotor were packed at different fixed positions along the rotating axis. At a slow MAS frequency of 10 kHz, 1H → 31P polarization transfer experiments on ADP reveal significantly enhanced efficiencies of DEER-INEPT over SR4-D-RINEPT, across a large volume of sample. A large window fraction (fw = 0.75) leads to further enhanced 31P signal intensity, as clearly demonstrated in Fig. 2a. For the centrally packed ADP sample, the 31P signal intensities from DEER-INEPT with fw = 0 and fw = 0.75 are 7.8 and 16.3 times higher, respectively, than those with SR4-D-RINEPT. These large enhancement factors are likely attributed to two factors: first, the removal of delays τi discussed above, which eliminates redundant T2 relaxation decays; second, large windows, which elevate the rf amplitude and effectively suppress the undesired interferences from rf mismatch, resonance offset and others.
Next, the performance with the presence of 1H–1H dipolar coupling and offset is evaluated, via1H → 13C transfer in 13Cα-glycine at an ultrafast MAS rate of 60 kHz, as demonstrated in Fig. 2b. In this case, the enhancement factor of DEER-INEPT is reduced to 1.4. This lower enhancement factor is understandable because at higher spinning frequencies, the τi delays in SR4-D-RINEPT become shorter and less harmful to transfer efficiency. However, in the presence of strong 1H–1H dipolar coupling (e.g. 18 kHz in the CH2 group), the transfer efficiency of SR4-D-RINEPT decreases rapidly with increasing 1H offset. A 50% drop in 13C signal intensity is observed as the 1H offset equals 9 kHz, and the signal is barely detectable with an offset over 16 kHz. In contrast, DEER-INEPT maintains 50% transfer efficiency with 41 kHz 1H offset, and yet, still retains 31% signal intensity at 100 kHz offset. Similar trends of 1H → 31P transfer efficiency in 1H offset tolerance are observed in the ADP sample at 10 kHz MAS, as presented in Fig. S5.† The enhanced stability to offset is especially important in high magnetic fields, or for nuclei with a broad chemical shift range, such as 19F and 31P.
To evaluate the performance of DEER-INEPT in quadrupolar spin systems, the polarization transfers from 1H to 27Al, 71Ga, and 17O are examined in γ-Al2O3, Ga(acac)3 and Ca(17OH)2, respectively. As shown in Fig. 3a and b, DEER-INEPT consistently outperforms both SR4-D-RINEPT and PRESTO across MAS rates ranging from 10 to 60 kHz, in both forward (1H → 27Al) and reversed (71Ga → 1H) transfers. The transferred signal intensities with DEER-INEPT are 1.3–5.9 times greater than those with SR4-D-RINEPT, depending on the sample and MAS frequency. Generally, higher transfer efficiencies are obtained with larger fw, and larger performance differences are observed with lower spinning speeds. The most significant improvements are observed under slow MAS conditions (10–20 kHz) with larger windows (fw ≥ 0.5). This trend of transfer enhancement is universal regardless of the transfer direction, as similar results are observed in the reversed transfer experiments (i.e., 1H → 71Ga and 27Al → 1H, Fig. S6†).
Fig. 3. (a) 1H → 27Al transfer in γ-Al2O3 and (b) 71Ga → 1H transfer in Ga(acac)3 under various MAS conditions. (c) {1H}17O NMR spectra by various methods in 17O enriched Ca(OH)2. (d) 2D 1H–71Ga correlation spectrum of Ga(acac)3via71Ga → 1H as in (b). (e) Column projections showing 71Ga spectra extracted at δiso(1H) = 2.2 ppm in (d), in comparison with the one-pulse 71Ga NMR spectrum. The 1D NMR spectra in (a and b) and 2D SR4-D-RINEPT spectra for comparisons in (d and e) are presented in the ESI.† The experiments are operated at 18.8 T, and (c and d) are operated at 20 kHz MAS. The NMR spectra in (a and b) are presented in Fig. S7.†.
In addition to improving the transfer efficiency, DEER-INEPT also performs better in preserving the intrinsic quadrupolar lineshapes in which the valuable bonding or coordinating information is encoded. Apart from the direct acquisition via1H → X transfer, e.g.1H → 17O in Fig. 3c, indirect (proton) detection is preferred for samples possessing a long 1H longitudinal (T1) relaxation, as in the 71Ga → 1H experiments presented in Fig. 3d and e. Superiority is most pronounced in the case of 1H → 17O transfer, in which the 17O lineshape obtained by DEER-INEPT is nearly identical to that from a one-pulse 17O NMR experiment, whereas those acquired by PRESTO and SR4-D-RINEPT are severely distorted. In the proton-detected 2D 71Ga → 1H experiment (Fig. 3d), the quadrupolar lineshapes of the 71Ga nucleus can be extracted along the indirect dimension. As shown in Fig. 3e, the 71Ga signal by DEER-INEPT not only has higher S/N than that by SR4-D-RINEPT (92 versus 39), but also a lineshape closer to that of the one-pulse 71Ga spectrum. According to the above simulations, the better preservation of quadrupolar lineshapes from DEER-INEPT is likely due to a more homogeneous and less interfered transfer process. The high efficiency and well-preserved lineshapes are important for material research. Indeed, they allow for a more accurate determination of structural and dynamics parameters, such as the quadrupolar coupling constant (QCC) and asymmetry factor.
The examples presented above, although using standard samples, clearly revealed the robustness and high transfer efficiency of DEER-INEPT under complex conditions, such as proton-rich environments, a broad range of MAS rates, and both forward and backward polarization transfers. To further highlight its practical utility, we demonstrate the DEER-IENPT's performance with a more realistic material, HY zeolite, a solid-acid catalyst extensively used in industry. The exact structure of its active sites, i.e., precise protonic species in Brønsted acid sites (BAS, Si–OH–Al) and defects (SiOH, Al–OH), are not clear to date.41–45 HY zeolite in the dehydrated form was chosen due to its dense proton environment and strong 1H–1H dipolar couplings among the protonic species,45,46 in which 27Al → 1H transfer was used for the benefit of proton detection. Fig. 4 compares the sensitivity enhancement of 1D and 2D DEER-INEPT spectra over SR4-D-RINEPT, recorded at a MAS rate of 20 kHz. Overall, a 1.5-fold sensitivity increase is obtained, as shown with the 1D spectra in Fig. 4a. Notably, Fig. 4a–c reveal a new signal at 8.2 ppm using DEER-INEPT, which was not detected by SR4-D-RINEPT or SR4-D-HMQC (Fig. S8†). This discrepancy likely indicates a complex hydrogen-bonding environment with strong homonuclear 1H–1H dipolar coupling for such a species. In addition, given the correlated 27Al signal at ca. 60 ppm, this species can be unambiguously attributed to tetrahedrally coordinated Al species surrounded by defect structures such as Al–OH or Si–OH, which are of general interest in the catalysis field.46,47 Furthermore, the 1H–27Al DCCs are measured via fitting the buildup curves with increasing recoupling times (Fig. 4d and S9†). The 1H–27Al DCCs measured by DEER-INEPT agree well with the previously reported results in BAS of low acid density zeolites (2.0 kHz and 2.5 Å internuclear distances48–50). In contrast, the SR4-D-RINEPT scheme is subject to the interferences of strong 1H–1H dipolar coupling at such MAS rates, leading to overestimated 1H–27Al distances (∼2.70 Å).
Fig. 4. Experiments on dehydrated HY zeolites. (a) 1D 1H{27Al} spectra and deconvolution of the 1H signals. The proton-detected 2D 1H–27Al correlation spectra from (b) DEER-INEPT (fw = 0.5) and (c) SR4-D-RINEPT. (d) 1H–27Al distance measurements by fitting the signal buildup curves at δiso(1H) = 3.6 ppm. The experiments are operated at 18.8 T and 20 kHz MAS, with details provided in the ESI.†.
Conclusions
The DEER-INEPT sequence, developed for efficient heteronuclear polarization transfer between spin-1/2 and quadrupolar nuclei, presents significantly improved performance over existing methods such as SR4-D-RINEPT and PRESTO. Numerical simulations reveal that the dipolar-echo design and windowed PMRR recoupling sequence can efficiently suppress the common interferences in DEER-INEPT, including rf inhomogeneity, resonance offset and homonuclear dipolar coupling. As verified on various proton-rich samples involving 1H–X spin pairs (X = 13C, 31P, 17O, 27Al, 71Ga), DEER-INEPT achieves polarization transfer efficiencies from 1.4 to 16 times greater than those from conventional SR4-D-RINEPT and PRESTO methods, across a wide range of MAS frequencies from 10 kHz to 60 kHz. This method is particularly advantageous at relatively slow MAS rates (≤20 kHz), where an adjustable window modification can further improve the performance. Additionally, DEER-INEPT yields distortion-free quadrupolar lineshapes in both direct and indirect detection of half-integer-spin quadrupolar nuclei. Its successful application in HY zeolite underscores DEER-INEPT's versatility and effectiveness for site-selective spectral editing, multi-dimensional correlation spectroscopy, and precise distance measurements, positioning it as a powerful tool for exploring local structural details in a wide variety of solid materials.
Data availability
The data supporting this article have been included as part of the ESI.†
Author contributions
G. H. conceived the research project, and participated in the experimental design, data analysis, discussion and the revision of manuscript. L. L. participated in the experimental design, accomplished all simulations and experimental data acquisitions, all fitting and the data analysis as well as writing of original draft. K. C. participated in the discussion and the revision of manuscript.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work was financially supported by the National Key R&D Program of China (No. 2021YFA1502803), the National Natural Science Foundation of China (Grant No. 22325405, 22432005, 22404159, 22472166, and 22321002), the Liaoning Revitalization Talents Program (XLYC2203134), and DICP I202406.
Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc07965e
References
- Reif B. Ashbrook S. E. Emsley L. Hong M. Solid-state NMR Spectroscopy. Nat. Rev. Methods Primers. 2021;1:1–23. doi: 10.1038/s43586-020-00002-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shcherbakov A. A. Medeiros-Silva J. o. Tran N. Gelenter M. D. Hong M. From Angstroms to Nanometers: Measuring Interatomic Distances by Solid-state NMR. Chem. Rev. 2021;122:9848–9879. doi: 10.1021/acs.chemrev.1c00662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang L. Ji Y. Chen K. Gao P. Zhao Z. Hou G. Solid-State NMR Dipolar and Chemical Shift Anisotropy Recoupling Techniques for Structural and Dynamical Studies in Biological Systems. Chem. Rev. 2022;122:9880–9942. doi: 10.1021/acs.chemrev.1c00779. [DOI] [PubMed] [Google Scholar]
- Nishiyama Y. Hou G. Agarwal V. Su Y. Ramamoorthy A. Ultrafast Magic Angle Spinning Solid-state NMR Spectroscopy: Advances in Methodology and Applications. Chem. Rev. 2022;123:918–988. doi: 10.1021/acs.chemrev.2c00197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien P.-H. Griffith K. J. Liu H. Gan Z. Hu Y.-Y. Recent Advances in Solid-state Nuclear Magnetic Resonance Techniques for Materials Research. Annu. Rev. Mater. Res. 2020;50:493–520. doi: 10.1146/annurev-matsci-091019-011049. [DOI] [Google Scholar]
- Ji Y. Liang L. Bao X. Hou G. Recent Progress in Dipolar Recoupling Techniques under Fast MAS in Solid-state NMR Spectroscopy. Solid State Nucl. Magn. Reson. 2021;112:101711. doi: 10.1016/j.ssnmr.2020.101711. [DOI] [PubMed] [Google Scholar]
- Ahlawat S. Mote K. R. Lakomek N.-A. Agarwal V. Solid-State NMR: Methods for Biological Solids. Chem. Rev. 2022;122:9643–9737. doi: 10.1021/acs.chemrev.1c00852. [DOI] [PubMed] [Google Scholar]
- Krushelnitsky A. Reichert D. Saalwachter K. Solid-state NMR Approaches to Internal Dynamics of Proteins: from Picoseconds to Microseconds and Seconds. Acc. Chem. Res. 2013;46:2028–2036. doi: 10.1021/ar300292p. [DOI] [PubMed] [Google Scholar]
- Perras F. A. Viger-Gravel J. Burgess K. M. Bryce D. L. Signal Enhancement in Solid-State NMR of Quadrupolar Nuclei. Solid State Nucl. Magn. Reson. 2013;51–52:1–15. doi: 10.1016/j.ssnmr.2012.11.002. [DOI] [PubMed] [Google Scholar]
- Molugu T. R. Lee S. Brown M. F. Concepts and Methods of Solid-State NMR Spectroscopy Applied to Biomembranes. Chem. Rev. 2017;117:12087–12132. doi: 10.1021/acs.chemrev.6b00619. [DOI] [PubMed] [Google Scholar]
- Vasa S. K. Rovó P. Linser R. Protons as Versatile Reporters in Solid-state NMR Spectroscopy. Acc. Chem. Res. 2018;51:1386–1395. doi: 10.1021/acs.accounts.8b00055. [DOI] [PubMed] [Google Scholar]
- Xu J. Wang Q. Deng F. Metal Active Sites and Their Catalytic Functions in Zeolites: Insights from Solid-state NMR Spectroscopy. Acc. Chem. Res. 2019;52:2179–2189. doi: 10.1021/acs.accounts.9b00125. [DOI] [PubMed] [Google Scholar]
- Casabianca L. B. Solid-state Nuclear Magnetic Resonance Studies of Nanoparticles. Solid State Nucl. Magn. Reson. 2020;107:101664. doi: 10.1016/j.ssnmr.2020.101664. [DOI] [PubMed] [Google Scholar]
- Li S. Lafon O. Wang W. Wang Q. Wang X. Li Y. Xu J. Deng F. Recent Advances of Solid-State NMR Spectroscopy for Microporous Materials. Adv. Mater. 2020;32:2002879. doi: 10.1002/adma.202002879. [DOI] [PubMed] [Google Scholar]
- Smith M. E. Recent Progress in Solid-state Nuclear Magnetic Resonance of Half-Integer Spin Low-γ Quadrupolar Nuclei Applied to Inorganic Materials. Magn. Reson. Chem. 2021;59:864–907. doi: 10.1002/mrc.5116. [DOI] [PubMed] [Google Scholar]
- Wang W. Xu J. Deng F. Recent Advances in Solid-state NMR of Zeolite Catalysts. Natl. Sci. Rev. 2022;9:nwac155. doi: 10.1093/nsr/nwac155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vega A. J. MAS NMR Spin Locking of Half-Integer Quadrupolar Nuclei. J. Magn. Reson. 1992;96:50–68. [Google Scholar]
- Vega A. J. CPMAS of Quadrupolar S= 3/2 Nuclei. Solid State Nucl. Magn. Reson. 1992;1:17–32. doi: 10.1016/0926-2040(92)90006-U. [DOI] [PubMed] [Google Scholar]
- Ashbrook S. E. Wimperis S. Spin-Locking of Half-Integer Quadrupolar Nuclei in Nuclear Magnetic Resonance of Solids: Creation and Evolution of Coherences. J. Chem. Phys. 2004;120:2719–2731. doi: 10.1063/1.1638995. [DOI] [PubMed] [Google Scholar]
- Ashbrook S. E. Wimperis S. Spin-Locking of Half-Integer Quadrupolar Nuclei in Nuclear Magnetic Resonance of Solids: Second-Order Quadrupolar and Resonance Offset Effects. J. Chem. Phys. 2009;131:194509. doi: 10.1063/1.3263904. [DOI] [PubMed] [Google Scholar]
- Gupta R. Hou G. Polenova T. Vega A. J. RF Inhomogeneity and How It Controls CPMAS. Solid State Nucl. Magn. Reson. 2015;72:17–26. doi: 10.1016/j.ssnmr.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kao H.-M. Grey C. P. INEPT Experiments Involving Quadrupolar Nuclei in Solids. J. Magn. Reson. 1998;133:313–323. doi: 10.1006/jmre.1998.1455. [DOI] [PubMed] [Google Scholar]
- Amoureux J.-P. Trébosc J. Wiench J. Pruski M. HMQC and Refocused-INEPT Experiments Involving Half-Integer Quadrupolar Nuclei in Solids. J. Magn. Reson. 2007;184:1–14. doi: 10.1016/j.jmr.2006.09.009. [DOI] [PubMed] [Google Scholar]
- Trébosc J. Hu B. Amoureux J.-P. Gan Z. Through-Space R3-HETCOR Experiments Between Spin-1/2 and Half-Integer Quadrupolar Nuclei in Solid-state NMR. J. Magn. Reson. 2007;186:220–227. doi: 10.1016/j.jmr.2007.02.015. [DOI] [PubMed] [Google Scholar]
- Martineau C. Bouchevreau B. Taulelle F. Trébosc J. Lafon O. Amoureux J. P. High-Resolution Through-Space Correlations Between Spin-1/2 and Half-Integer Quadrupolar Nuclei using the MQ-D-R-INEPT NMR Experiment. Phys. Chem. Chem. Phys. 2012;14:7112–7119. doi: 10.1039/C2CP40344G. [DOI] [PubMed] [Google Scholar]
- Giovine R. Trebosc J. Pourpoint F. Lafon O. Amoureux J.-P. Magnetization Transfer from Protons to Quadrupolar Nuclei in Solid-state NMR using PRESTO or Dipolar-mediated Refocused INEPT Methods. J. Magn. Reson. 2019;299:109–123. doi: 10.1016/j.jmr.2018.12.016. [DOI] [PubMed] [Google Scholar]
- Zhao X. Hoffbauer W. Schmedt auf der Gunne J. Levitt M. H. Heteronuclear Polarization Transfer by Symmetry-Based Recoupling Sequences in Solid-State NMR. Solid State Nucl. Magn. Reson. 2004;26:57–64. doi: 10.1016/j.ssnmr.2003.11.001. [DOI] [PubMed] [Google Scholar]
- Gómez J. S. Rankin A. G. Trébosc J. Pourpoint F. Tsutsumi Y. Nagashima H. Lafon O. Amoureux J.-P. Improved NMR Transfer of Magnetization from Protons to Half-Integer Spin Quadrupolar Nuclei at Moderate and High MAS Frequencies. Magn. Reson. 2021:1–29. doi: 10.5194/mr-2-447-2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oas T. G. Griffin R. G. Levitt M. H. Rotary Resonance Recoupling of Dipolar Interactions in Solid-state Nuclear Magnetic Resonance Spectroscopy. J. Chem. Phys. 1988;89:692–695. doi: 10.1063/1.455191. [DOI] [Google Scholar]
- Gan Z. Grant D. M. R E. R. NMR Chemical Shift Anisotropy Measurements by RF Driven Rotary Resonance. Chem. Phys. Lett. 1996;21:349–357. doi: 10.1016/0009-2614(96)00268-0. [DOI] [Google Scholar]
- Brinkmann A. Kentgens A. P. Proton-selective 17O-1H Distance Measurements in Fast Magic-angle-spinning Solid-state NMR Spectroscopy for the Determination of Hydrogen Bond Lengths. J. Am. Chem. Soc. 2006;128:14758–14759. doi: 10.1021/ja065415k. [DOI] [PubMed] [Google Scholar]
- Chen L. Wang Q. Hu B. Lafon O. Trebosc J. Deng F. Amoureux J. P. MEASUREMENT of Hetero-nuclear Distances using a Symmetry-based Pulse Sequence in Solid-state NMR. Phys. Chem. Chem. Phys. 2010;12:9395–93405. doi: 10.1039/B926546E. [DOI] [PubMed] [Google Scholar]
- Levitt M. H., Symmetry-Based Pulse Sequences in Magic-Angle Spinning Solid-State NMR, in Encyclopedia in Nuclear Magnetic Resonance, ed. Grant, D. M. and Harris, R. K., Wiley, Chichester, 2002, vol. 9, pp. 165–196 [Google Scholar]
- Liang L. Ji Y. Zhao Z. Quinn C. M. Han X. Bao X. Polenova T. Hou G. Accurate Heteronuclear Distance Measurements at All Magic-angle Spinning Frequencies in Solid-state NMR spectroscopy. Chem. Sci. 2021;12:11554–11564. doi: 10.1039/D1SC03194E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagashima H. Trébosc J. Kon Y. Sato K. Lafon O. Amoureux J.-P. Observation of Low-γ Quadrupolar Nuclei by Surface-enhanced NMR Spectroscopy. J. Am. Chem. Soc. 2020;142:10659–10672. doi: 10.1021/jacs.9b13838. [DOI] [PubMed] [Google Scholar]
- Gan Z. Rotary Resonance Echo Double Resonance for Measuring Heteronuclear Dipolar Coupling under MAS. J. Magn. Reson. 2006;183:235–41. doi: 10.1016/j.jmr.2006.08.014. [DOI] [PubMed] [Google Scholar]
- Gullion T. Schaefer J. Rotational-Echo Double-Resonance NMR. J. Magn. Reson. 1989;81:196–200. doi: 10.1016/j.jmr.2011.09.003. [DOI] [PubMed] [Google Scholar]
- Bak M. Rasmussen J. T. Nielsen N. C. SIMPSON A. General Simulation Program for solid-state NMR Spectroscopy. J. Magn. Reson. 2000;147:296–330. doi: 10.1006/jmre.2000.2179. [DOI] [PubMed] [Google Scholar]
- Juhl D. W., Tošner Z. and Vosegaard T., Versatile NMR Simulations using SIMPSON, in Annu. Rep. NMR Spectrosc., Elsevier, 2020, vol. 100, pp. 1–59 [Google Scholar]
- Bajaj V. S. Mak-Jurkauskas M. L. Belenky M. Herzfeld J. Griffin R. G. DNP Enhanced Frequency-selective TEDOR Experiments in Bacteriorhodopsin. J. Magn. Reson. 2010;202:9–13. doi: 10.1016/j.jmr.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng L. Chupas P. J. Grey C. P. Measuring Brønsted Acid Densites in Zeolite HY with Diphosphine Molecules and Solid-state NMR Spectroscopy. J. Am. Chem. Soc. 2004;126:12254–12255. doi: 10.1021/ja0467519. [DOI] [PubMed] [Google Scholar]
- Peng L. Liu Y. Kim N. Readman J. E. Grey C. P. Detection of Brønsted Acid Sites in Zeolite HY with High-field 17O-MAS-NMR Techniques. Nat. Mater. 2005;4:216–219. doi: 10.1038/nmat1332. [DOI] [PubMed] [Google Scholar]
- Li S. Zheng A. Su Y. Zhang H. Chen L. Yang J. Ye C. Deng F. Brønsted/Lewis Acid Synergy in Dealuminated HY Zeolite: a Combined Solid-state NMR and Theoretical Calculation Study. J. Am. Chem. Soc. 2007;129:11161–11171. doi: 10.1021/ja072767y. [DOI] [PubMed] [Google Scholar]
- Primo A. Garcia H. Zeolites as Catalysts in Oil Refining. Chem. Soc. Rev. 2014;43:7548–7561. doi: 10.1039/C3CS60394F. [DOI] [PubMed] [Google Scholar]
- Schroeder C. Hansen M. R. Koller H. Ultrastabilization of Zeolite Y Transforms Brønsted–Brønsted Acid Pairs into Brønsted–Lewis Acid Pairs. Angew. Chem., Int. Ed. 2018;57:14281–14285. doi: 10.1002/anie.201808395. [DOI] [PubMed] [Google Scholar]
- Chen K. Horstmeier S. Nguyen V. T. Wang B. Crossley S. P. Pham T. Gan Z. Hung I. White J. L. Structure and Catalytic Characterization of A Second Framework Al(IV) Site in Zeolite Catalysts Revealed by NMR at 35.2 T. J. Am. Chem. Soc. 2020;142:7514–7523. doi: 10.1021/jacs.0c00590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravi M. Sushkevich V. L. van Bokhoven J. A. Towards A Better Understanding of Lewis Acidic Aluminum in Zeolites. Nat. Mater. 2020;19:1047–1056. doi: 10.1038/s41563-020-0751-3. [DOI] [PubMed] [Google Scholar]
- Hunger M. Freude D. Fenzke D. Pfeifer H. 1H Solid-state NMR Studies of the Geometry of Brønsted Acid Sites. J. Magn. Reson. 1992;191:391–395. [Google Scholar]
- Chen K. Gan Z. Horstmeier S. White J. L. Distribution of Aluminum Species in Zeolite Catalysts: 27Al NMR of Framework, Partially-Coordinated Framework, and Non-Framework Moieties. J. Am. Chem. Soc. 2021;143:6669–6680. doi: 10.1021/jacs.1c02361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji Y. Chen K. Han X. Bao X. Hou G. Precise Structural and Dynamical Details in Zeolites Revealed by Coupling-Edited 1H–17O Double Resonance NMR Spectroscopy, Partially-Coordinated Framework, and Non-Framework Moieties. J. Am. Chem. Soc. 2024;146:11211–11224. doi: 10.1021/jacs.3c14787. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting this article have been included as part of the ESI.†