Organic carbon dry deposition outpaces atmospheric processing with unaccounted implications for air quality and freshwater ecosystems

Abstract

Dry deposition is an important yet poorly constrained process that removes reactive organic carbon from the atmosphere, making it unavailable for airborne chemical reactions and transferring it to other environmental systems. Using an aircraft-based measurement method, we provide large-scale estimates of total gas-phase organic carbon deposition rates and fluxes. Observed deposition rates downwind of large-scale unconventional oil operations reached up to 100 tC hour⁻¹, with fluxes exceeding 0.1 gC m⁻² hour⁻¹. The observed deposition lifetimes (τ_dep) were short enough (i.e., 4 ± 2 hours) to compete with chemical oxidation processes and affect the fate of atmospheric reactive carbon. Yet, much of this deposited organic carbon cannot be accounted for using traditional gas-phase deposition algorithms used in regional air quality models, signifying underrepresented, but influential, chemical-physical surface properties and processes. Furthermore, these fluxes represent a major unaccounted contribution of reactive carbon to downwind freshwater ecosystems that outweigh terrestrial sources, necessitating the inclusion of dry deposition in aquatic carbon balances and models.

Dry deposition of gaseous organic carbon is rapid and provides an important atmospheric input to aquatic ecosystems.

INTRODUCTION

Historically, investigation into the processes and impacts associated with both wet and dry deposition has focused on the deposition of inorganic species (i.e., SO_X, NO_X, NH₃, and O₃) as routes to acidification (1), eutrophication (2), or agricultural crop damage (3), with wet deposition (i.e., precipitation) playing an especially prominent role in particle scavenging and acid rain (4, 5). However, comparatively little attention has been paid to the deposition of gaseous organic compounds, especially via dry deposition. Gas-phase organic carbon, including volatile, intermediate-volatility, and semivolatile organic compounds (VOCs, IVOCs, and SVOCs), are emitted from a diverse array of anthropogenic and biogenic sources globally. They represent an extensive pool of reactive chemicals in the atmosphere, with multigenerational oxidation reactions transforming emitted hydrocarbons or less-oxygenated compounds (containing mostly carbon and hydrogen) to highly oxygenated molecules. On timescales ranging from hours to days, oxidative processing generally results in these gaseous compounds becoming more water soluble and/or less volatile, properties which are considered controlling factors in both dry deposition to surfaces and secondary organic aerosol (SOA) formation. Algorithms describing gas-phase dry deposition in regional air quality models, in contrast to small-scale equilibrium partitioning models used in the agricultural community (6, 7), assume that the dry deposition process is controlled in part by oxidation reactions and/or aqueous dissolution of the gases at the surface they are in contact with (e.g., leaves, soil) [(8, 9) and references therein]. Therefore, depositing organic compounds or their precursors must be either soluble or reactive to result in appreciable regional deposition. In contrast, the assumed mechanism historically underlying the formation of SOA from lower volatility oxidized gases is mainly absorptive partitioning, wherein molecular properties (e.g., vapor pressure) largely determine equilibrium partitioning between the gas and particle phase (10). Hence, in regional air quality models, the fate of gas-phase organic carbon is largely determined by a series of gas-phase oxidation reactions forming compounds that, in comparison to the precursor gases, are more prone to partitioning to the condensed phase in aerosols and/or to surface deposition.

Dry deposition to Earth’s surface represents a removal of carbon, which would otherwise be available for SOA and ozone formation. Thus, deposition plays an underappreciated, yet central, role in air quality, climate, and ecosystem health through the lifetimes and relative distribution of airborne versus deposited pollutants. To fully understand and model the fate of organic carbon in the atmosphere on regional to global scales, the relative timescales associated with both oxidation and removal via dry deposition are required but are recognized as a major knowledge gap (11, 12). While several studies have investigated the oxidative chemistry of organic carbon and estimated its lifetimes with respect to OH radical oxidation (11, 13–15), comparatively little information exists on the competing organic carbon depositional timescales. Quantitative dry deposition of organic compounds have only recently been investigated, usually through eddy flux measurement approaches for select VOCs (16, 17) within biogenic environments. These studies have suggested that the deposition of select individual VOCs can be very fast (16, 17). Model results have also suggested that deposition of oxidized species may compete with their removal by atmospheric oxidation (18–21), and that current global dry deposition losses may be underpredicted. Despite these advances, deposition studies are often limited to a subset of relatively small–molecular weight molecules over small spatial scales (16, 17, 22), though there is evidence for deposition of diverse, more-oxidized sets of molecules as more advanced instrumentation is applied (22–24). They may also be based solely on unverified model simulations, which depend on anthropogenic emissions estimates (18–21). Without a measurement-based estimate of total gas-phase organic carbon (TGOC) deposition, it remains unclear whether the previously measured deposition flux for some instrument defined, and/or low–molecular mass species (16, 17, 22–24) are representative of the diverse array of TGOC emitted and chemically transformed in the atmosphere or whether TGOC depositional lifetimes are competitive with gaseous oxidation lifetimes.

TGOC dry deposition represents both an atmospheric end point, and a potential starting point for surface ecosystem chemistry and impacts. In particular, carbon in the form of dissolved organic carbon (DOC) plays a key role in freshwater ecosystems, where it acts as an energy source for aquatic organisms (25, 26) and affects their ecological functions (27, 28). DOC has been implicated as delaying the recovery of aquatic ecosystems from recent inorganic acidification (29), with levels that have been increasing over the past several decades (30)—catalyzing research efforts to understand and model the various carbon fluxes into (and out of) freshwater systems (31–34). Atmospheric dry deposition is a carbon flux with the potential to contribute to freshwater DOC because atmospheric oxidation transforms most carbonaceous species to highly soluble compounds (11, 35), as well as oxidation in surrounding environmental media following deposition (36) (i.e., oxidation in soil with subsequent runoff). Carbon flux models used to represent the carbon balance in freshwater systems generally assume negligible inputs of atmospheric carbon via dry deposition compared to terrestrial inputs (wet deposition is also typically very small), and it is thus ignored (31–34). Therefore, quantifying the total dry deposition of gas-phase organic carbon represents a critical first step in assessing its importance for aquatic ecosystem processes.

Recent developments in the ability to quantify large-scale deposition via aircraft measurements (37), as well as advances in both TGOC measurements and molecular speciation, now enable an evaluation of the highly uncertain magnitude of TGOC dry deposition, which has implications for both fundamental atmospheric processes and wide-reaching ecosystem impacts. The Athabasca Oil Sands region of Alberta Canada features intensive unconventional oil extraction and processing, with a large source of gas-phase organic carbon (38) and pollutant plumes that can be transported for hundreds of kilometers downwind with continued oxidation (39). This sharp gradient from concentrated anthropogenic emissions into the surrounding boreal forest ecosystem provides a distinct opportunity to examine carbon fluxes to the surrounding boreal ecosystem, while examining its importance relative to other competing atmospheric loss processes.

RESULTS

Total gas-phase organic carbon deposition rates

Airborne measurements of TGOC mixing ratios (parts per million carbon) were obtained during two consecutive campaigns in the Athabasca Oil Sands Region of northern Alberta, Canada (April and June, 2018; fig. S1), and were used to estimate TGOC dry deposition rates (tonnes C hour⁻¹), deposition fluxes (tonnes C m⁻² hour⁻¹), and deposition velocities (cm s⁻¹) as shown schematically in fig. S2. The instrumentation used during the study measured gas-phase organic carbon regardless of its oxidation state, molecular size, or volatility, while excluding CH₄, CO, CO₂, and particle-phase organic carbon (see Materials and Methods) such that it represented the measured total of carbon-containing compounds and not the summation of measured individual organic species. From the mixing ratio data, TGOC deposition rates and fluxes were determined using the Top-down Emissions Rate Retrieval Algorithm (TERRA) (40), adapted to provide estimates of deposition flux, as previously demonstrated for total oxidized sulfur and nitrogen (37) (see Materials and Methods).

This aircraft-based approach has the advantage of investigating TGOC deposition over large spatial scales (3000 to 6000 km²) that have not been previously attainable via traditional ground based flux measurements (37). It should also be noted that while there would be large uncertainties for fluxes of individual species derived in this manner (e.g., due to gas-phase transformation sources/sinks, OH reaction rates, OH concentration assumptions, etc.), TGOC is a parameter that is fully inclusive of all gas-phase organic carbon, such that loss or production of individual compounds are both considered, and hence, total carbon is inherently conserved within the chemical boundary conditions of the calculation. In this way, the TGOC approach may overcome the limitations of attempting to measure total organic fluxes based on the aggregate of individual compounds (23, 24).

Seven flights across two seasons were used in the analysis (table S1), wherein large-scale plumes were repeatedly sampled at increasing distances downwind of oil sands operations in a semi-Lagrangian manner, under clear-sky conditions, absent any low-lying cloud cover or precipitation. TGOC mixing ratios were measured along level flight tracks at multiple altitudes perpendicular to the wind direction. When stacked vertically, the flight tracks were used to create virtual screens that encompass the entire plume and include the effects of mixing from entrainment and dispersion. TGOC concentrations were interpolated across the screens and multiplied by the corresponding normal wind vectors to determine the TGOC horizontal fluxes through each virtual screen using TERRA (see Materials and Methods). When integrated over the spatial extent of the plumes, this resulted in a total gaseous organic carbon mass transfer rate (T_TGOC; tonnes C hour⁻¹) across each screen as demonstrated previously (39, 41, 42) (fig. S2). Given the near-Lagrangian nature of these flights resulting in screens that encompass the impacts of dilution, mixing, and chemical oxidation, the difference in T_TGOC between successive screens (ΔT_TGOC) quantifies the decreasing TGOC transfer rates with increasing downwind distance and thus represents the measured deposition rate (D_TGOC; tonnes C hour⁻¹) between screens [see Supplementary Materials and fig. S2] (37). Over the complete downwind flight patterns, the total measured hourly deposition rate occurring across the flight area is equal to the sum of D_TGOC between all screens (i.e., $\sum D_{\mathit{\text{TGOC}}}$).

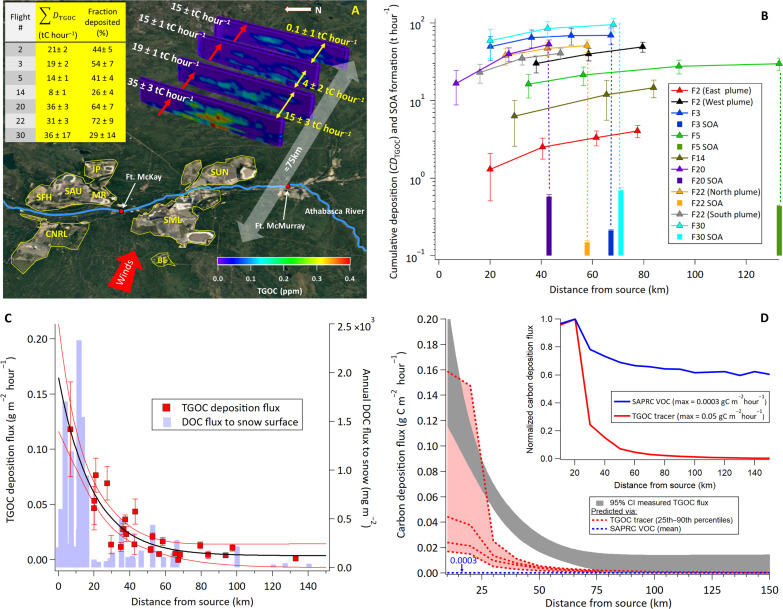
An example of the derived virtual flight screens and associated transfer rates (T_TGOC) is shown in Fig. 1A for flight 3 (additional transfer rates across screens shown in fig. S3). The entirety of the large-scale plumes was captured in the screens, with a clear decrease observed in the transfer rates through successive downwind screens. This results in a $\sum D_{\mathit{\text{TGOC}}}$ of 19 ± 2 tC hour⁻¹ for flight 3 (Fig. 1A) and a range of 8(±1) to 36(±17) tC hour⁻¹ across all flights (inset table of Fig. 1A). The measured $\sum D_{\mathit{\text{TGOC}}}$ across all flights accounted for 26 to 72% (mean, 48 ± 20%) of the TGOC transferred through the first screens (inset table of Fig. 1A), representing a sizable fraction of the large organic carbon emissions from oil sands facilities (41, 43). Monotonic decreases in T_TGOC across screens were observed in all of the investigated flights (fig. S3) and were used to estimate the deposition rates occurring in the area between the source(s) and the first screen of each flight, by extrapolating the TGOC transfer rates back to the source location (T_TGOC,0) (see Materials and Methods) (37). The cumulative deposition rates (CD_TGOC) from the source to the final screen (i.e., 75 to 100 km downwind) were then estimated (Fig. 1B), showing that CD_TGOC can be large (up to ~100 tC hour⁻¹), with large variation (e.g., 10 to 100 tC hour⁻¹) depending on the number and size of facilities upwind of the screens (Fig. 1B and table S1). Together, the results indicate that the majority of TGOC deposition (50 to 80%) occurred within ~100 km of the source(s) (Fig. 1B).

Fig. 1. Transport and deposition of measured and modeled TGOC.

(A) TGOC transfer rates (T_TGOC; white values; tC hour⁻¹) through the virtual screens of flight 3 downwind of oil sands surface mining operations, shown with differences between screens (yellow values). Inset: Sum of deposition rates between screens $(\sum D_{\mathit{\text{TGOC}}})$ for all flights where the fraction deposited is relative to the transfer rate through the first screen. (B) Cumulative TGOC deposition rates (${\mathit{CD}}_{\mathit{\text{TGOC}}};$ markers) compared to cumulative SOA formation rates from available flights (bars) with dotted lines showing differences between deposition and SOA formation for the specific flight. (C) Measured under-plume TGOC deposition flux as a function of source distance across all flights, where distance from source is taken from the midpoint between screens. Red lines represent 95% confidence interval (CI) of an exponential fit to the data (black line). The measured flux decreases exponentially with distance, spatially consistent with the total measured DOC flux to snow (blue bars). (D) Simulated GEM-MACH carbon deposition using both the TGOC tracer approach and the SAPRC volatile organic carbon (VOC) method. Inset: GEM-MACH estimates of SAPRC VOC and TGOC tracer dry deposition normalized by their maximum values. The value of 0.0003 represents the maximum carbon deposition flux (grams per square meter per hour) predicted by GEM-MACH using the SAPRC VOC method described in the text.

In principle, the formation of SOA during the examined flights, or the partitioning of existing organic mass to particles, may also represent a loss of organic carbon from the gas-phase, which could potentially be misinterpreted as a depositional loss. However, the cumulative SOA formation rates across the same flight screens (Fig. 1B) indicate that SOA formation, while large, was minimal by comparison to the TGOC lost via deposition (<1% of CD_TGOC; see Supplementary Materials) and comparable to the SOA observed in previous work (41). This small contribution from SOA formation was nonetheless subtracted from the deposition rates where SOA formation data was available (i.e., the four flights in Fig. 1B), which would be inclusive of any other organic partitioning to aerosols. In these evolving oil sands plumes that are continuously being oxidized over short time and spatial scales, the dominant process is expected to be condensation to particle surfaces and not evaporation, which is consistent with the observations of continually increasing SOA mass here. Regardless, an evaporated organic aerosol (OA) mass equivalent to the SOA mass formed would also be very small relative to the deposited mass and would imply that the deposition rates were underestimated. Similarly, any biogenic gas-phase organic carbon emissions between screens could partially offset the observed TGOC loss between screens, leading to underestimates of TGOC deposition rates and fluxes. However, three of the seven flights (table S1) were conducted in early spring, when the ground was covered with snow, before the onset of elevated terrestrial emissions, and observed depositional losses were similar to those during the summer period flights. Moreover, the TGOC levels within the anthropogenic plumes were much higher (up to >1 ppmC) than the biogenic “background” TGOC levels (<100 ppbC), suggesting only minor impacts on the TGOC deposition rate estimated from the anthropogenic plumes.

Measured and modeled TGOC dry deposition fluxes

While the observed deposition rates represented a large fraction of the emissions, the flux of carbon to the surface is the critical parameter affecting ecological systems. Using D_TGOC values, the average dry deposition fluxes of TGOC (F_TGOC) (in gC m⁻² hour⁻¹), were calculated by dividing D_TGOC by the plume footprint surface areas (743 to 5674 km²; table S1), estimated by extending the plume edges to the surface (see fig. S2). The TGOC dry deposition fluxes, shown in Fig. 1C, ranged from 0.01 to 0.1 gC m⁻² hour⁻¹, monotonically decreasing with e-folding distances of 20 to 100 km (Fig. 1C). The calculated decrease in estimated F_TGOC with distance is qualitatively similar to the drop-off observed in the annual deposition flux of DOC inferred from snow samples collected at ground-based sites across the region (Fig. 1C) (see Supplementary Materials). Although measured DOC in snow represents a combination of the wet and dry deposition of a subset of carbon molecules, over a fraction of the year, the similarity in the spatial scale of the decrease in snow DOC (Fig. 1C) nonetheless indicates that dry deposition to the surface (as a fraction of DOC) occurs rapidly with downwind distance, consistent with the spatial extent of the aircraft dry deposition flux observations. However, the absolute magnitude of the DOC flux in Fig. 1C is not expected to match that of the TGOC flux, given that they represent different subsets of molecules (DOC versus TGOC), snow is just one of many surfaces under the aircraft across all flights (i.e., foliage, soil, water, etc.), and the TGOC flux measured during flights specifically quantifies the deposition from concentrated downwind plumes, rather than deposition to snow averaged over a longer time period across broader spatial scales.

These measured TGOC dry deposition fluxes were representative of the surface areas downwind from the studied oil sands facilities during each of the flights, while the magnitude of deposition fluxes across the broader region will vary with distance and time of the year, particularly with greater distances from sources. Hence, the Global Environmental Multiscale–Modelling Air-quality and CHemistry (GEM-MACH) chemical transport model (44) was used to estimate the spatial distribution of the total organic deposition fluxes for a larger region over an entire year and to compare with measured TGOC flux estimates. The model, which included a number of updates as described in the methods and SI, was used to estimate annual total organic carbon dry deposition fluxes in two distinct ways.

In the first approach, GEM-MACH was used with its native oil sands VOC emissions, the California Statewide Air Pollution Research Center (SAPRC11) VOC reaction mechanism (45), and the existing deposition algorithm based on a modified resistance method (46) (henceforth referred to as “SAPRC VOC deposition”). The annual dry deposition fluxes of organic carbon via this approach were derived using hourly modeled carbon deposition fluxes for each VOC in the SAPRC11 mechanism generated from a 12-month simulation (1 November 2017 to 31 October 2018), which were summed to create a net VOC carbon flux (assuming in this case that ΣVOC carbon = TGOC).

In the second approach, the annual total organic carbon fluxes were estimated by explicitly using the observed TGOC emissions in GEM-MACH as a single variable (i.e., a “tracer”) and allowing it to dry deposit (henceforth referred to as “TGOC tracer deposition”). The TGOC emissions in this case were based on measurements of TGOC emissions from individual flights around the four largest oil sands surface mining facilities estimated using TERRA (see Materials and Methods) (38). For the purposes of deriving model deposition estimates, the TGOC tracer deposition approach assumed that the physical/chemical properties of TGOC were equivalent to those of pyruvic acid. The deposition parameters of pyruvic acid were chosen as a surrogate for the complex mixture of TGOC, because the deposition velocities modeled/calculated for pyruvic acid and measured for TGOC were empirically very similar (see below), though we acknowledge the variations in molecular features of VOCs-SVOCs. The annual modeled deposition flux fields from these two approaches (SAPRC VOC and TGOC tracer deposition) were then displayed at 15° intervals and at successive 10-km radii centered on the village of Fort McKay (Fig. 1D). The resulting average TGOC deposition values are compared to the measured deposition fluxes in Fig. 1C. Average deposition fluxes using both the approaches were also normalized by their maximum values (426 and 2.6 gC m⁻² year⁻¹, respectively; Fig. 1D, inset).

The simulated deposition fluxes via the time-averaged TGOC tracer method approached those of the measured downwind fluxes (Fig. 1D), even though TGOC emissions in the model were instantaneously diluted into a 2.5-km model grid cell and noting that the absolute time-averaged (i.e., annual) model values were also lower than the measured in-plume fluxes. When considering the more concentrated conditions of a plume, rather than an annual average, a comparison to the 90th percentile of modeled TGOC flux values shown in Fig. 1D was similar to the measured fluxes with some variations during downwind transport. Conversely, the deposition fluxes estimated via the SAPRC VOC approach underestimated the measurement-based TGOC deposition fluxes by more than two orders of magnitude (Fig. 1D). This underestimate partly reflects uncertainties in the underlying VOC emissions inventory data. For example, the sum of all VOC emissions from the surface mining oil sands facilities used in the model ranged from 2.2 to 3.7 tC hour⁻¹ (43) while the aircraft-based estimates were 2.5 to 38.5 tC hour⁻¹ (38), indicating that at least part of the discrepancy in absolute fluxes is due to the VOC emissions inventory underestimating the TGOC gas emissions.

However, while the net deposited organic carbon mass was underestimated, the observed rapid downwind decrease in fluxes was also not captured by the SAPRC VOC method, as shown in the normalized comparison (Fig. 1D, inset). This may suggest that the chemical and physical properties of the SAPRC11’s gas-phase speciation do not adequately represent the average chemical and physical properties of depositing organic compounds and/or that the associated resistances to surface deposition in the model is insufficiently parameterized. In the case of this SAPRC-based approach, the discrepancies may be contributed to by the fact that gaseous organic compounds in emissions inventories focus mainly on VOCs with relatively low molecular weight with most of the VOCs in SAPRC11 having carbon numbers less than C₁₀, as do their oxidation products. However, most of the measured TGOC emitted from the oil sands sources were composed of larger–molecular weight hydrocarbons (i.e., IVOCs-SVOCs) (38), with a large proportion of condensing SOA mass composed of such compounds and their oxidation products (41). Neither the I/SVOC precursors nor their oxidized products are resolved in typical emissions inventories or VOC reaction mechanisms and hence may be a potential source of additional organic carbon for surface deposition not currently well represented in models.

Speciated organic carbon contributions to observed TGOC deposition

Regional and global modeling of deposition relies on accurate parameterization of deposition velocities (V_d), and hence, the absence of a modeled rapid decrease in deposition flux with increasing distance (Fig. 1D) suggests that the model dry deposition velocities may be underestimated. This may be manifested as V_d underestimates for the individual SAPRC11 organic species used in the model and/or the lack of a suitable V_d for high–molecular mass organic species (comprising much of the measured TGOC but not included in SAPRC11); both of these scenarios are explored below through comparisons with measured TGOC V_d values and available speciated measurements. TGOC deposition velocities were estimated from aircraft observations by dividing the F_TGOC by the estimated TGOC concentrations at 40 m above ground (V_d = F_TGOC/[TGOC]_40m), resulting in an average V_d across all flights of 3.3 ± 1.0 cm s⁻¹ (see Materials and Methods).

Contributions from oxidized compounds

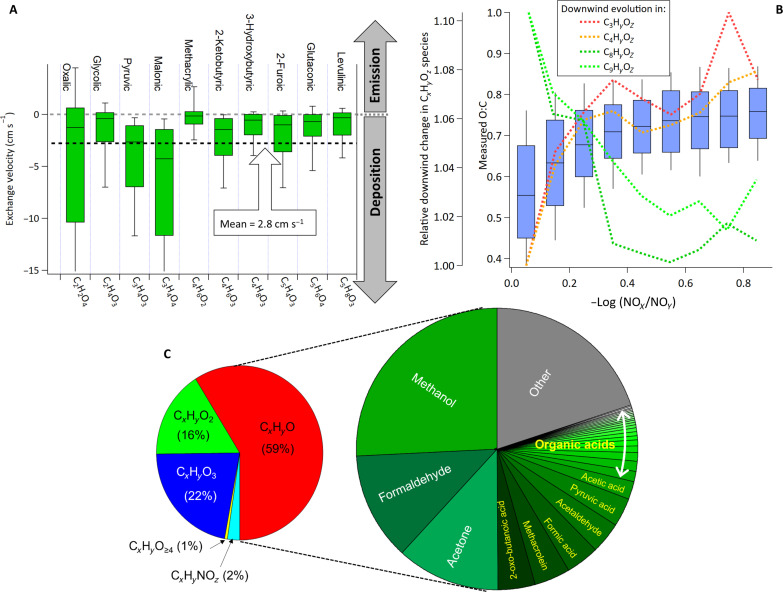
The average aircraft-estimated TGOC V_d was similar to that measured previously for select oxidized species in temperate forests such as organic hydroperoxides, peroxyacids, and some aldehydes (16, 17). While analogous measurements of V_d for oxidized anthropogenic species (relevant to this region) do not exist, the TGOC V_d was nonetheless consistent with modeling predictions of V_d for molecules with two to five oxidized functional groups (18) and similar to the V_d derived from ground-based gradient flux measurements (see Supplementary Materials) of select organic acids in the oil sands region (Fig. 2A; mean V_d = 3 cm s⁻¹). A number of oxidized compounds (including organic acids) were also formed during the in-plume evolution of oil sands emissions, observed during both spring and summer flights. Measurements of this oxidized carbon (see Materials and Methods) suggested that the oxidation process within these plumes was relatively fast even in early spring. For example in flight 2, this was indicated by rapid increases in the measured gas-phase O:C ratio (a metric for oxidative evolution) (35) with increasing photochemical age (estimated as −log(NO_X/NO_Y) (47); Fig. 2B). The overall measured O:C ratio increased by ~30% over the first 2 hours of transport (median O:C from 0.55 to 0.7) with the second flight screen corresponding to a NO_X/NO_Y-derived photochemical age of approximately 0.4 (Fig. 2B). This is partly attributed to the oxidation-induced fragmentation of larger molecules to smaller, more oxidized species. This multigenerational oxidation was evident in the relative increase of C₃ and C₄ oxidized compounds (i.e., C₃H_yO_z and C₄H_yO_z species), while the carbon associated with larger oxidation products (e.g., C₈ and C₉) became progressively less important to the total measured oxidized carbon mass from all C_xH_yO_z species as the air mass aged (Fig. 2B). The relative decrease in larger oxidation products (C₈ and C₉) was also due in part to the formation SOA that removed them from the gas phase. While dry deposition was also likely occurring, it is expected to affect higher O:C species (i.e., smaller highly functionalized molecules in Fig. 2B) to a greater extent than C₈/C₉ molecules, which is not apparent in the data of Fig. 2B.

Fig. 2. Oxidized organic carbon speciation, evolution, and surface exchange.

(A) Net exchange velocities, including deposition and emissions/production, for select organic acids measured during a ground-based gradient flux study at 30 m over a tailing ponds in the oil sands region (see Materials and Methods). Negative values represent net deposition (i.e., deposition velocities). Dashed line represents the mean of ground-based observations (2.8 cm s⁻¹) which are consistent with the overall TGOC V_d observed in aircraft data (3.3 cm s⁻¹). (B) Average in-flight gas-phase O:C ratio for all detected species via proton-transfer and chemical ionization mass spectrometer measurements (see Supplementary Materials) as a function of photochemical age [i.e., −log(NO_x/NO_y)] for a representative flight in early spring (flight 2; blue bars representing quartiles). Dotted lines display changes in the relative downwind change in C_xH_yO_z species (far left axis) normalized to the shortest photochemical age where a decrease in the C₈-C₉ normalized fraction and increase in the C₃-C₄ normalized fraction suggests multigenerational photochemistry/molecular fragmentation leading to smaller, more polar species available for deposition. (C) Mean (in-plume) relative contribution of different oxidized chemical families (left) during flight 20 and the breakdown of individual compounds for the top 30 species by mass (right), which is similar across all transformation flights.

While a deconvolution of dry deposition from oxidative formation for individual oxidized products was impossible (i.e., only the net effect is observed), the rapid multigenerational oxidation observed here (Fig. 2B) is consistent with previous observations within oil sands plumes (39, 41). This suggests that the oxidation rate was sufficiently rapid (even in the spring) to form small, highly functionalized gas-phase species on the timescales of these flights, as potential contributors to the observed TGOC deposition. The available speciated measurements indicated that about 40% of the measured oxidized carbon mass within the first hour of evolution was composed of molecules containing two to four oxygen atoms (Fig. 2C), a fraction of which had organic acid functional groups, and hence considerable solubility. These characteristics are considered to be important for parameterizing deposition under existing gas-phase deposition theory (9).

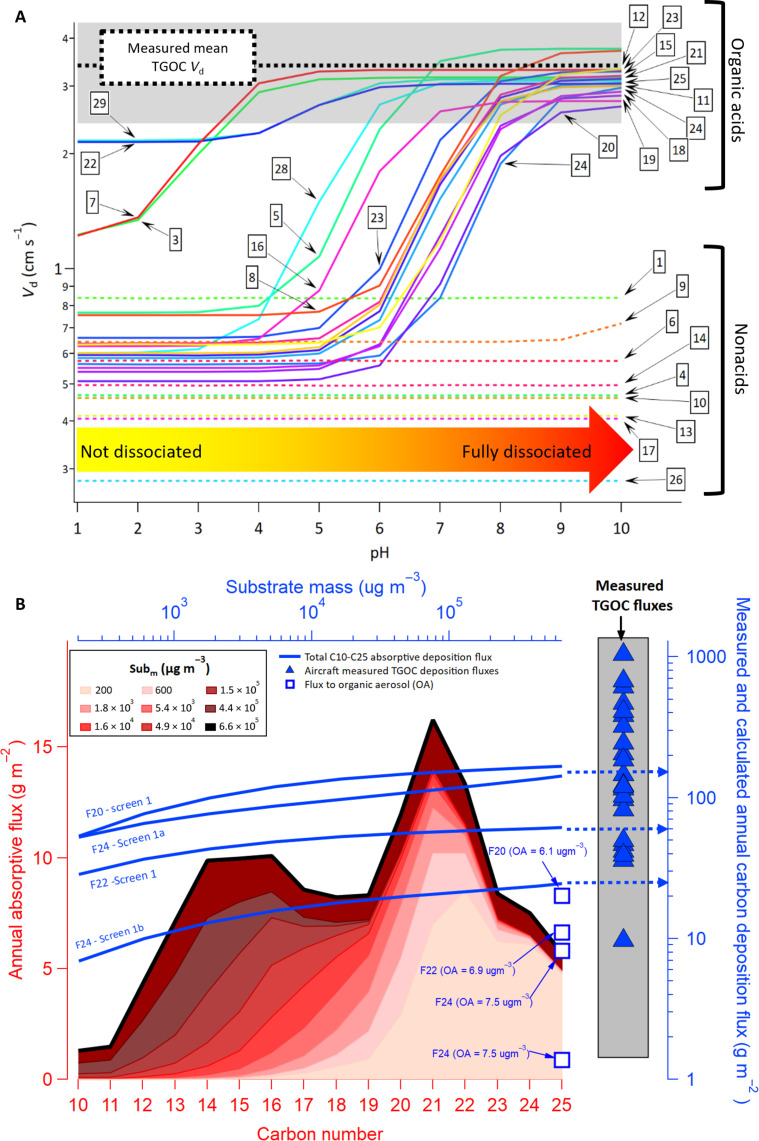
However, dry deposition velocities calculated via a Monte Carlo simulation using field-standard resistance terms for the 30 most abundant measured oxidized species (by carbon mass; Fig. 2C and table S2) indicates that most of the observed species have calculated deposition velocities that are slower than the observed TGOC V_d when estimated under neutral pH conditions and the range of observed flight conditions (Fig. 3A; see Materials and Methods and SI) (37). These neutral conditions along with the parameterization of V_d in these simulations are used in most air quality models, including in GEM-MACH. Recent regional modeling has also shown that explicitly simulating the Henry’s law dissociation of SO₂ for non-neutral surfaces increased deposition (37). Similarly, increased surface pH resulted in an increase in the simulated V_d for measured ionizable organic acids, approaching that of the aircraft measurement-based TGOC V_d (Fig. 3A), particularly for pH >8. The established importance of base cation deposition (46), possibly resulting in alkaline surfaces near the sources of fugitive dust in the oil sands region, suggests that acid dissociation may affect deposition rates via increases in V_d. However, it can only explain the minor portion of the observed TGOC V_d that is composed of dissociating species and would require highly basic surfaces (Fig. 3A), an assumption that has which not been experimentally verified. Despite the observation of gas-phase organic acids and some other highly functionalized compounds within oil sands plumes, their abundance remains extremely low relative to the measured TGOC (38), which is incongruent with the magnitude of observed TGOC deposition.

Fig. 3. Simulated deposition velocities and fluxes using traditional absorption and deposition theory.

(A) Monte Carlo simulations of deposition velocities (V_d; using a resistance model parametrization) for the top 30 organic species in Fig. 2C as a function of surface pH, under representative conditions for the region (mode value shown; see Supplementary Materials). Measured TGOC V_d (mean ± SD) is shown as a black dashed line and gray shading, and number labels indicate the individual species in table S2, which make up only a small fraction of the measured TGOC. (B) Estimated annual absorptive deposition fluxes for observed IVOCs-SVOCs (flight 20, screen 1) as a function of carbon number and increasing forest substrate mass (Sub_m) where darker shaded red areas indicate larger substrate mass available for absorptive partitioning (see Supplementary Materials). The calculated deposition flux total for >C₁₀ species (blue lines) is also shown for several flights as a function of forest substrate mass (top axis) and compared to the measured TGOC deposition fluxes across all flights (blue triangles) and shown with the flux to OA during flights (blue squares).

Contributions from nonpolar hydrocarbons

While approximately 40% of the TGOC mass in the downwind transformation flights studied here contained oxidized carbon species, only a small fraction was likely highly soluble and thus able to appreciably dry deposit according to conventional theory. Conversely, the vast majority of the emitted TGOC mass (i.e., 60%) had lower oxygenation levels or no oxygenation (38), raising the possibility of additional deposition pathways. The current understanding of organic carbon dry deposition and subsequent parametrizations within regional air quality models rely primarily on solubility and reactivity of oxidized compounds (9, 18), which for most of the I/SVOCs here would result in deposition velocities <0.1 cm s⁻¹. However, the relatively large amount of gas-phase IVOC and SVOC mass measured during these flights (38) suggests that these nonpolar compounds likely also contributed to the observed TGOC deposition fluxes via absorptive deposition to surfaces.

Equilibrium absorptive partitioning as an approach to estimating gas-surface condensation/volatilization has frequently been used to study the fate of contaminants on indoor surfaces (48) and of pesticides on agricultural surfaces at the field scale (6, 7). Such models typically calculate a local equilibrium between air, soil, and water compartments, using observation-based air-soil and air-water coefficients for individual pesticides (49). The near-leaf equilibrium concentration is derived making use of these partitioning coefficients, which in turn is used to generate a flux of pesticide lost from the foliage to the bulk atmosphere. While pesticide models have successfully been evaluated against measured leaf-scale dissipation rates from field experiments, they are not fully applicable to regional air quality models, where depositing/condensing species span a wide range of volatilities and functionalities, for which surface equilibrium constants are generally unknown. Here, the potential importance of surface absorption was investigated using the measurements of gaseous I/SVOC compounds, together with an absorption partitioning model wherein Raoult’s law for high-concentration solutions is used to determine partitioning (10). The calculated fluxes were then estimated in a manner analogous to prior bidirectional flux parametrizations for ammonia (50) (see Materials and Methods and SI for full description). In this approach, the substrate available for I/SVOC absorptive partitioning was assumed to be the boreal forest foliage surface (predominantly jack pine species), which are known to be coated with liquid/semisolid layers of nonpolar epicuticular waxes (i.e., C₁₆-C₃₅ alkanes) present throughout the year (51). On the basis of the estimated vapor pressures of measured I/SVOCs and a range of applicable surface substrate mass within the forest canopy (i.e., from one monolayer to the full needle thickness; see Supplementary Materials), the deposition flux of I/SVOCs for this region can be qualitatively estimated (Fig. 3B). We note that the relative rates of adsorptive partitioning of organic gases to solid surfaces versus absorptive partitioning of gases to liquid/solid surfaces largely favors the latter as the dominating process, and hence, we have considered absorptive partitioning alone in our estimates of deposition.

The results show that absorptive partitioning of nonpolar hydrocarbons to vegetated surfaces may contribute appreciably to TGOC deposition, even for single monolayers of epicuticular wax, especially for species with carbon numbers greater than C₁₉ (Fig. 3B). Species with carbon numbers as low as C₁₀ may also absorptively partition to foliage if a greater proportion of the leaf is assumed to be available as a substrate for partitioning. In addition, the total I/SVOC absorptive deposition flux (summed across all carbon numbers as the blue lines in Fig. 3B) estimated for several flights was within the range of measured TGOC deposition fluxes (blue triangles), indicating the potential for absorptive partitioning to make a relevant contribution to the overall carbon deposition flux (e.g., up to ~30% of the measured TGOC flux for the same flights). This total calculated I/SVOC absorptive flux was relatively insensitive to the estimated forest substrate mass available. Sensitivity simulations varying the available absorbing medium by four orders of magnitude showed only minor variations in the calculated total I/SVOC deposition flux (i.e., by a factor of ~2). Similarly, sensitivity analyses of other absorptive partitioning parameters indicated that they minimally affected the estimated flux (table S4), while the single largest impact on absolute fluxes was associated with the observed range of I/SVOC carbon concentrations across flights. While the existing OA during flights could also act as a competing absorbing sink, the calculated I/SVOC flux to OA in Fig. 3B (using the average in-plume OA measurements) was much lower than the flux to even a single monolayer of absorbing forest surface. In principle, here or in other locations, the depositing organic mass itself could, over time, also act as an absorbing medium, provided that a sufficient amount accumulates in surface-accessible layers, though a sizable fraction can be expected to migrate to other reservoirs (i.e., plant tissues, soil, and water) over time. While the quantity of such species on vegetative surfaces in the area has not been measured, the relatively large regional deposition flux of TGOC here suggests that this could represent an additional non-negligible reservoir in some cases, provided the mass of accumulated long-term anthropogenic substrate deposited is in the upper range of that estimated for plant waxes (i.e., Fig. 3B) (see Supplementary Materials). However, as noted above, the effect of thicker substrates on modeled deposition fluxes is not proportional. This is also consistent with results showing the propensity of accumulated urban surface films to act as reservoirs for absorptive partitioning (52, 53).

Given the observations here, it is notable that the role of deposition via sorptive partitioning has been more considered in the context of indoor air contaminants and agricultural pesticide fate and their associated models (6, 7, 48). We note that the single-component approach used in that context would accurately represent single gas partitioning, given sufficient observational data for individual vegetation and surface types. However, these mixtures of atmospheric gases span wide ranges of concentrations, molecular masses, and vapor pressures, so the complex TGOC mixture is collectively better represented via a fundamental approach such as the use of Raoult’s law for high-concentration TGOC solutions here, similar to collective gas-to-OA partitioning approaches. Our results suggest that the direct absorptive deposition of I/SVOC species, while not currently implemented in GEM-MACH or other air quality models, is important to consider in future dry deposition algorithms within chemical transport models, especially for regions with large I/SVOC emissions.

Deposition versus oxidation lifetimes

The impact of rapid organic carbon deposition on air quality–related processes is predicated on the notion that removal of carbon from the atmosphere prevents the deposited fraction of the mass from participating in further atmospheric chemistry, ultimately affecting the formation of ozone, oxidized gases, and secondary particulate matter (PM). An approach to evaluating the competition between dry deposition and oxidative chemistry is the comparison of deposition lifetimes (τ_dep) to the average OH oxidation lifetimes (τ_OH). In most cases, oxidation does not remove organic carbon from the atmosphere (with the exception of CO, CO₂, and SOA formation) but transforms them into oxidation by-products that remain airborne and often reactive. However, oxidation leads to more polar species that should deposit more readily. This implies that the comparison of lifetimes (τ_dep versus τ_OH) represents a lower limit to the relative contribution of dry deposition to overall removal of organic carbon from the atmosphere, because the cumulative (i.e., multigeneration) oxidative lifetime for TGOC is likely to be longer in most cases than estimated here on the basis of the collection of individually measured species. Nonetheless, the comparison provides quantitative context for the competition between these two processes. Although τ_OH is a commonly derived metric, the magnitude of τ_dep for TGOC has not been examined through a measurement-based approach until now. Normalizing the cumulative plume deposition curves (Fig. 1B) by the extrapolated TGOC transfer rates at the sources (T_TGOC,0; fig. S3) provides a measure of the fraction of the initial emitted mass that is deposited as a function of distance (fig. S4). Interpolating this cumulative deposition fraction to 63.2% led to e-folding distances (d_1/e) ranging 20 to 100 km. The measured d_1/e were consistent with the d_1/e values from regional model estimates of TGOC deposition (d_1/e = 12 to 48 km within 40 to 250 km of sources) using deposition properties for pyruvic acid, whose V_d empirically matched that measured for TGOC. These measured e-folding distances were used to derive τ_dep for TGOC using the average horizontal wind speed during individual fights (U)

$${\mathrm{\tau }}_{\text{dep}}=\frac{d_{1/\mathrm{e}}}{U}$$

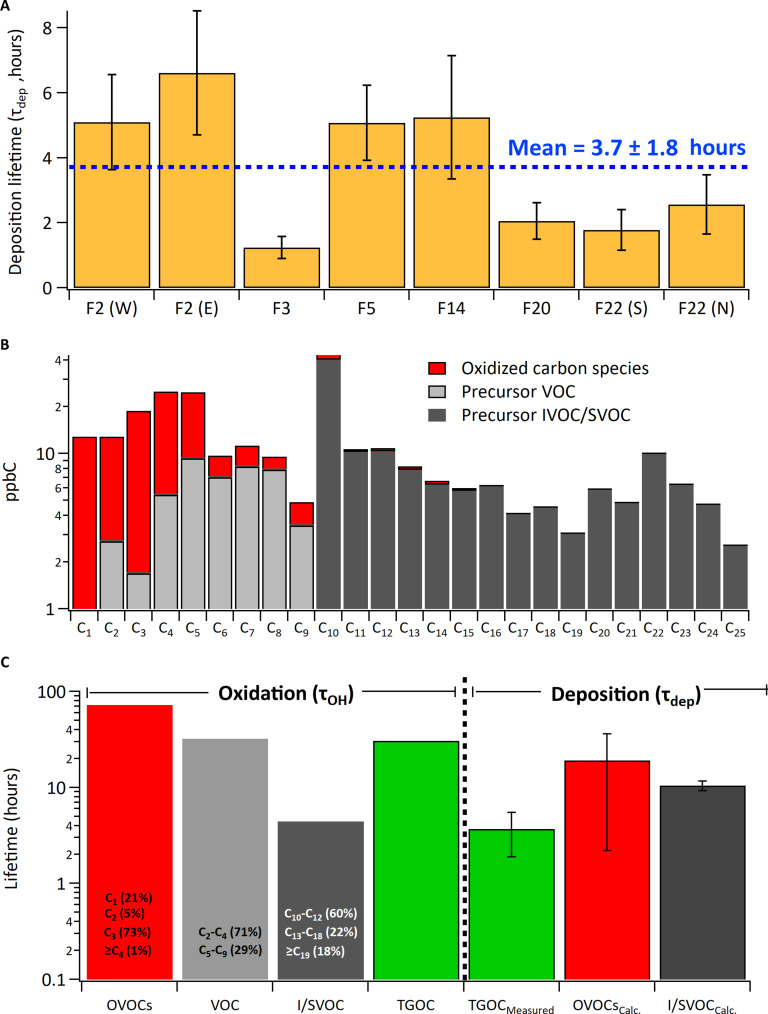
This resulted in estimated τ_dep that ranged from 1.2 to 6.6 hours (mean, 4 ± 2 hours) (Fig. 4A). This is very short when compared to the limited τ_dep estimates for single species that exist, which ranged from 19 hours for H₂O₂ (54) to >30 hours for a highly oxygenated organic gas (55). The estimated range of τ_dep values derived through measurements here was also much shorter than those modeled for even the most highly soluble oxidation products of biogenic precursors (minimum ~7 hours) and orders of magnitude shorter than wet deposition lifetimes (i.e., 80 to 200 hours) (21). As noted above and shown in Figs. 3B and 4A, detailed offline measurements in concert with high-resolution online total organic carbon measurements indicated that I/SVOCs made a major contribution to the speciated carbon mass (38, 56). Combining the speciated measurements of I/SVOCs with the speciated measurements of oxidized and VOC carbon mass for the first screen of flight 20, which in this instance achieved carbon closure within uncertainties (i.e., 100 ± 50%) of the measured TGOC, allowed a carbon-weighted τ_OH to be estimated (for both precursors and oxidation products). Accordingly, the longest τ_OH values were associated with small oxidized molecules (>60 hours; Fig. 4C), consistent with previous work (11, 13), and much longer than the observed TGOC deposition lifetimes for all flights (τ_dep). Conversely, the shortest τ_OH were associated with hydrocarbons ≥C₁₀ (including I/SVOCs; Fig. 4C), because of their high OH rate constants (k_OH) (see Materials and Methods). Despite their relatively high reactivity, this lower volatility range of carbon was associated with a carbon mass–weighted τ_OH that is comparable to the average τ_dep for TGOC across all flights (Fig. 4C), and a factor 2 longer than that estimated specifically for flight 20 (2 ± 0.6 hours; Fig. 4A). Considering all forms of organic carbon together [i.e., VOCs, I/SVOCs, and oxidized VOCs (OVOCs); green bar in Fig. 4C] also resulted in an overall carbon-weighted τ_OH that is almost an order of magnitude greater than the average measured deposition lifetime, τ_dep for TGOC.

Fig. 4. Assessing competition between oxidation and deposition.

(A) Estimated deposition lifetime (τ_dep) for total measured gaseous carbon (TGOC) across all applicable flights where E, W, and N indicate East, West, and North plumes for those flights, respectively. (B) Measured organic carbon distribution for the nearest screen in flight 20 using proton transfer reaction mass spectrometry and chemical ionization mass spectrometry (PTR-MS and CIMS for oxidized organics), whole air samples (hydrocarbon VOCs), and adsorbent tube samples (I/SVOC), respectively (see Materials and Methods and SI). (C) Estimated carbon-weighted oxidative lifetime (τ_OH) for oxidized VOCs (OVOCs), VOC, I/SVOC, and total carbon distribution summarized in (B), compared with the deposition lifetimes (τ_dep) of total carbon from (A) (TGOC_Measured), the top 30 oxidized species in Fig. 2C (OVOCs_Calc.), and I/SVOC carbon (I/SVOC_Calc.) estimated via absorptive partitioning (see Materials and Methods and SI). Note, the percentages on the first three carbon-weighted bars indicate the fraction of carbon mass driving the overall lifetime calculation, where the total bar size is the lifetime for each compound class.

The measured depositional lifetimes for TGOC (Fig. 4A), which were derived at in-flight altitudes, were also considerably shorter than the calculated τ_DEP for select molecular types observed in plumes. Specifically, modeling of the deposition lifetimes for the top 30 oxidized species measured (OVOC; Fig. 2C) and the I/SVOC species (Fig. 4B) at a mean altitude of 1000 m above sea level and governed by resistance terms R_a, R_b, and R_c (see Supplementary Materials) resulted in modeled τ_DEP for these species that ranged from 10 to 17 hours (Fig. 4C), three to five times longer than that measured for TGOC, but consistent with previous modeling studies (21). The long calculated deposition lifetimes for each molecular type (Fig. 4C), which is in contrast to the observed high TGOC deposition velocities and short measured τ_dep, indicate rapid and/or nonlimiting surface kinetics for the wide range of chemical species comprising TGOC, with reduced surface resistances (R_c) that approach transport-limited deposition velocities (i.e., governed by R_a + R_b only) downwind of the source(s) (fig. S5A). The measured short deposition lifetimes are also in relative agreement with vertical turbulent eddy diffusivity (Kz) theory (i.e., K theory) estimates of deposition velocity from an altitude within the mixed boundary layer, (e.g., the aircraft altitude) to the canopy reference height where R_a and R_b are more typically calculated within the constant flux layer (see Supplementary Materials). Last, the measured short deposition lifetimes and high deposition velocity for TGOC is also consistent with theoretical work that suggests that organic compounds in the atmosphere should be subjected to considerably faster removal based on molecular property estimations (57–59).

Contribution to freshwater ecosystems

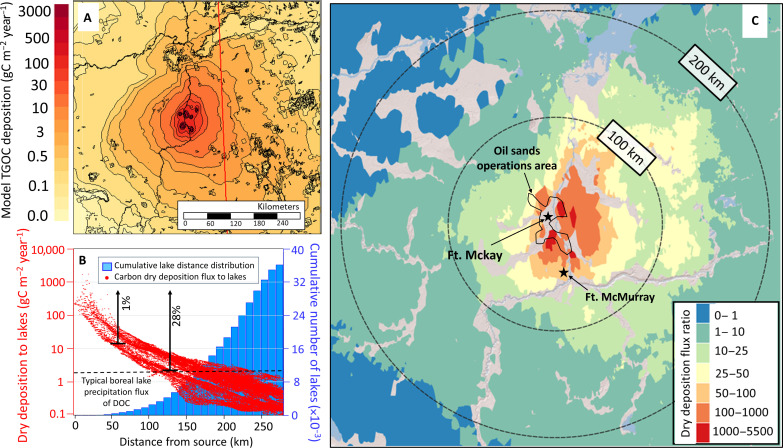
While the deposition fluxes derived from in-plume measurements are large (Fig. 1C), over the course of a year, surrounding ecosystems are not constantly exposed to concentrated oil sands plumes. Thus, the GEM-MACH regional air quality model was used to estimate spatially resolved annual TGOC deposition fluxes (gC m⁻² year⁻¹) for 2017–2018 using the TGOC tracer method described above, which best approximated the observed fluxes (Fig. 5A; see Materials and Methods). Figure 5 indicates that annual carbon deposition fluxes are highest near the sources (> 3000 gC m⁻² year⁻¹), decreasing rapidly beyond 200 km to less than 1 gC m⁻² year⁻¹. The magnitude of the annual TGOC deposition fluxes outside of the immediate source area ranged <1 to 10 gC m⁻² year⁻¹ (Fig. 5A), which is similar to measured net biogenic carbon deposition fluxes reported previously for a small vegetated area at a US site (sum of >500 species extrapolated annually) (22). This implies the sum of TGOC deposition in the currently modeled domain will be even larger when considering the emissions of the underlying boreal forest and its oxidative evolution (i.e., not only the TGOC of oil sands origin in Fig. 5A).

Fig. 5. Determining the impact of TGOC deposition on freshwater lakes in the region.

(A) Model estimated annual dry deposition carbon flux based on the GEM-MACH TGOC approach (see Materials and Methods and SI) near oil sands sources, with circles radiating outward from Fort McKay. (B) Cumulative histogram of distance from oil sands source(s) to the >36,000 lakes within 275 km of Fort McKay (blue bars), and the GEM-MACH estimated TGOC dry deposition flux for the grid cells containing those lakes (red data points). Percentages (1 and 28%) denote the fraction of lakes which receive TGOC deposition fluxes greater than 20 and 2 gC m⁻² year⁻¹, respectively. (C) Dry deposition flux ratio (DDFR = Dry deposition flux / lake catchment DOC flux) (see main text), as a measure of the contribution of atmospheric organic carbon to the overall catchment DOC balance.

Within 275 km of Fort McKay, which sits near the center of surface mining operations, there are more than 36,000 individual freshwater lakes, which have been studied for exceedances of aquatic critical loads of ecosystem acidity in previous work (Fig. 5B) (60). Yet, a much larger number of acid-sensitive ecosystems may be found further from the sources [Fig. 5A; see also (46)]. The carbon dry deposition fluxes estimated in Fig. 5A that are specifically associated with the grid cells containing the 36,000 lakes were extracted and are shown in Fig. 5B as a function of distance from Fort McKay. The typical measured annual flux of carbon from precipitation (i.e., wet deposition) to boreal lakes is in the range of <1 to 2 gC m⁻² year⁻¹ (31, 32, 61) or is sometimes assumed to be negligible. Our dry deposition estimates suggest that 28% of the lakes within 275 km of Fort McKay receive TGOC deposition fluxes greater than 2 gC m⁻² year⁻¹, and around 1% of these lakes receive greater than 20 gC m⁻² year⁻¹ (Fig. 5B). Therefore, for many lakes, the dry deposition of gas-phase organic carbon was larger than the established observational estimates from wet deposition in typical boreal lakes located away from these sources (31, 32, 61).

However, precipitation represents only one flux of organic carbon to lake ecosystems. A more relevant comparison is between our estimated TGOC gas dry deposition flux and the total annual DOC fluxes entering/exiting individual lake catchments [“DOC catchment flux” (DCF)] from all airborne, terrestrial, and aquatic (i.e., within-lake) sources. This DOC flux into and out of the lake catchments along with DOC concentrations within the lake water was estimated for the domain of fig. S6 [(46, 60) and SI]. These DCF values were compared to the TGOC dry deposition fluxes estimated here. We note that the exact chemical composition (i.e., at the molecular level) of both DOC and deposited TGOC is unknown, and hence, there is uncertainty with respect to the fraction of the depositing TGOC that would be representative of DOC. Assuming that 100% of the deposited TGOC is representative of DOC as an upper limit, the relative importance of dry deposition can be estimated as the dry deposition flux ratio (DDFR), the ratio of the atmospheric dry deposition flux (Fig. 5A) to the output DCF. The DDFR over the current domain (Fig. 5C) is a measure of the potential importance of atmospheric input to previous estimates of the DOC balance, where the atmospheric DOC inputs have generally been assumed to be negligible and hence have been omitted from past ecosystem mass balance assessments (31–34). In contrast, we have found here that across the entire domain for which lake deposition fluxes have been calculated (60), the mean and median DDFR were 1.9 and 0.2, respectively, with increasing DDFR values closer to the sources. Within ~200 km of the source area, the DDFR is usually >1 (Fig. 5C), with the maximum DDFR greater than a factor of 5500. These high TGOC deposition fluxes relative to DCF suggests retention or uptake of the TGOC carbon in the catchment, similar to the deposition of other nutrients (i.e., nitrogen or phosphorus) (62). A lower-limit scenario assumes that only the oxygenated fraction of TGOC (i.e., red bars in Fig. 4B) contributes to DOC. In this case, the DDFR values would be reduced by a factor of 0.4 but nonetheless remain an important carbon input flux to these lakes and greater than DCF.

Uncertainties, assumptions, and opportunities for future research

The implications of TGOC dry deposition described here rely on the depositional flux estimates derived from aircraft measurements and hence the uncertainties and assumptions involved therein. These uncertainties include those associated with the TGOC measurement itself (estimated accuracy of ±10%; see Materials and Methods), the estimate of geographic area (km²) influenced under the measured plumes (e.g., ~10%), and, in the case of the total deposition (CD_TGOC), the extrapolation of transfer rates (T_TGOC) back to the source region (e.g., ±10 to 20%). Additional uncertainties are also associated with the outputs of the TERRA mass transfer model (see Materials and Methods), which is largely influenced by the method of extrapolation chosen for TGOC concentrations below the lowest flight altitude (e.g., ~20 to 30%). The uncertainties from the TERRA output and other parameters noted above are propagated through the calculation of the depositional flux, resulting in overall uncertainties in deposition rates and deposition fluxes of approximately ±14 to 75% as shown in Fig. 1 (B and C).

There are additional assumptions underlying the approach applied here, and while they cannot be explicitly quantified, they must be acknowledged. One important assumption is the representativeness of the finite number of flights (seven) used to model the deposition flux for all times of the year and for regions outside of the aircraft flight domain. While this assumption cannot be tested, it does not negate the specific fluxes derived during in-plume flights, which were conducted in at least two distinct seasons and downwind of multiple sets of facilities. In addition, while the flights were assumed to be near-Lagragian in nature, fully Lagrangian plume intercepts are virtually impossible, despite some plume centers having been intercepted in subsequent screens within several minutes of their wind speed–derived arrival time (63). Regardless, Lagrangian plume intercepts are not a strict prerequisite of calculating fluxes via this airborne approach provided that at source emissions are constant, which is expected for oil sands facilities where emissions are usually associated with near-constant production (particularly over the course of a 2- to 4-hour flight).

While many surface flux measurement approaches make use of a vertical gradient in pollutant concentrations, such a gradient below the lowest flight altitude could not be measured here. Rather, the heterogeneity of the plumes and thus the varied vertical profiles to the surface is accounted for through the TERRA algorithm, which represents the largest uncertainty within TERRA (40). Regardless, the downwind concentration gradient clearly demonstrates the depletion of an airborne reservoir of gas-phase organic carbon, as other TGOC sinks (i.e., gas-to-particle partitioning) cannot account for the downwind differences, such that the calculated TGOC losses and associated conclusions are not solely reliant on knowing the structure of the vertical profile in this region. Last, while the average TGOC deposition velocity is reported here, it should be noted that this mixture is composed of species with a range of deposition velocities, which will each vary with molecular structure.

There are valuable future opportunities to further refine the methods applied here and better constrain the associated uncertainties and assumptions. For example, coupled aircraft and ground-based tower TGOC flux measurements (using gradient methods) represent the best direct comparison/evaluation of the airborne approach, while also providing information on the applicability of the extrapolations used for below the lowest flight altitude. The deposition of TGOC observed here suggests that many of the individual species measured should also be present on the underlying surfaces (foliage, soil, water, etc.), and hence, in-field surface material collection and analysis could offer an additional means of verifying the exact species that make up the deposited mass. Deposition fluxes for individual organic species (rather than TGOC) could also be targeted in future aircraft missions. Because the perceived loss from screen to screen of any single species will be the net effect of atmospheric formation and oxidative destruction (an effect not relevant to TGOC), this would require measurements of all precursors and in-plume oxidant concentrations in real time. Together with models of formation and loss, the deposition velocity of individual species could be computed and compared with those derived via ground-based eddy covariance, as a further evaluation of these TGOC aircraft-based methods. The approach to TGOC deposition determination here further suggests that similar flights targeting other sources including urban areas or wildfire plumes would be valuable, providing previously inaccessible experimental data for those regions and observations of TGOC deposition across more diverse environments. Last, this work suggests that absorptive partitioning could be incorporated more completely into regional air quality models as a complimentary approach to the resistance algorithms currently implemented, which could improve model performance.

DISCUSSION

Implications for air quality modeling

Despite uncertainties associated with estimating k_OH for the various species (see Supplementary Materials), these results indicate that TGOC dry deposition may be the primary atmospheric loss process, with OH oxidation taking a secondary role, for the bulk of compounds comprising TGOC. The measurements here, which represent the first estimates of the TGOC depositional lifetime over a large geographical region, are consistent with recent modeling studies (18, 19), which demonstrated that the deposition of oxidation products of short-chain anthropogenic precursors alone led to large reductions in modeled SOA (up to 40%). The current work implies that accounting for all precursors (including I/SVOCs), their emissions, their oxidation products, and losses through absorptive partitioning (or other surface uptake processes) may have an even larger impact on SOA formation and associated models. Ultimately, our results suggest that the formation of SOA in the oil sands region may currently be lower than what is possible based solely on emissions and chemistry, because dry deposition reduces the amount of organic carbon precursors available for SOA formation; this in turn could explain the relatively small contribution of SOA formation to the cumulative gas-phase carbon loss processes in Fig. 1B. Furthermore, while the absolute magnitude of both the emissions and observed deposition fluxes were very large, the observed deposition velocities and associated lifetimes are not exclusive to the oil sands region’s high TGOC concentrations, as deposition velocities show no correlation with TGOC concentrations (r = 0.09; fig. S5B).

Regional air quality models universally calculate deposition velocities using a resistance approach, whereby the resistance to surface mass transfer is governed by aerodynamic (R_a), boundary layer (R_b) and surface (R_c) resistances (9). Because aerodynamic and boundary layer resistances must always be present, the large TGOC deposition velocities observed in this study suggest that many of the TGOC constituents measured here, which will include a large I/SVOC fraction, experience little resistance to uptake at the surface itself, with surface resistances approaching R_c = 0, and that the aerodynamic and boundary layer resistances must dominate (see fig. S5A). Because no individual components of TGOC can have deposition velocities higher than for the case where R_c = 0 (fig. S5A), this mathematically infers that any TGOC constituent contributing to the depositional flux here also cannot experience appreciable surface resistance to deposition. This is in contrast to the conventional parameterizations used in regional air quality models, which would typically assign large surface resistances to many of the compounds known to contribute to TGOC in this, and most other regions. Such a result implies that additional or changes to current deposition algorithms may be necessary to reproduce TGOC deposition observations and that of its components, which will vary with molecular size and functionality. It is also noted that while the current work indicates measurement-model discrepancies exist for dry deposition, wet deposition may also be underestimated in models for water-soluble gases. While beyond the scope of work here, the extent of impact would also be dependent on a number of factors related to both molecular properties and precipitation parameterizations, which have begun to be investigated as described previously (21).

Collectively, these results emphasize that both near and far downwind of oil sands and other sources, future research must include better understanding and parameterization of underlying absorptive reservoirs, multiphase surface characteristics and chemical processes across the diverse range of environmental conditions (e.g., pH, relative humidity, and temperature), and the ultimate fate of deposited organic carbon. Doing so ensures that dry deposition and its underlying influential variables are accurately accounted for in models, with validation using additional deposition measurements of total gas-phase carbon and its individual components, particularly downwind of anthropogenic source regions.

Implications for downwind freshwater ecosystems

With respect to the impact on freshwater systems, the large DDFR for this region indicates that atmospheric dry deposition of organic carbon has the potential to make important contribution to the overall freshwater ecosystem carbon balance, in contrast to current freshwater carbon budget models, which assume a nonexistent or negligible contribution from atmospheric deposition (31–34). These inputs of atmospheric carbon may influence several freshwater processes, the impacts of which have not been considered in previous work. For example, the fraction of organic acid functionality that comprises TGOC (Fig. 2C) may be an important input to acid-sensitive lakes, with the potential to drive these lakes into a critical load exceedance regime or delay the recovery from previous inorganic acidification. This is particularly relevant for regions downwind of the oil sands, with known acid sensitivity (46, 64). In addition, deposited forms of organic carbon, including organic acids and hydrocarbons, are metabolized by microbial communities in lake ecosystems (65, 66), with unknown impacts to those communities. This microbial food source from the atmosphere will ultimately be metabolized with the potential to increase lake primary productivity through an increase in dissolved CO₂ (67), owing to the increase in nutrient availability (68). Furthermore, the atmospheric contribution of organic carbon, particularly that of the IVOCs/SVOCs observed here as part of TGOC (Fig. 4B), is consistent with the historical increase in polycyclic aromatic hydrocarbon levels in lake sediments in the oil sands region, which have caused those lake ecosystems to enter new ecological states distinct from those of previous centuries (69). The impact of dry deposition of organic carbon may not be limited to aquatic systems. While the dry deposition of atmospheric nitrogen and particulate black carbon can make important contributions to the total deposition to forest/vegetated ecosystems (17, 70, 71), the impact of atmospheric TGOC dry deposition to these systems is entirely unknown. Given that DOC is such an important factor in freshwater energy budgets, the results here demonstrate that atmospheric dry deposition of gaseous organic carbon needs to be properly represented and parameterized to fully understand and model carbon cycling. Beyond the industrial sources studied here, this work clearly demonstrates the importance of better understanding the influential role of deposition across a broader range of spatial scales and sources—thereby fully capturing their impacts across the atmosphere, terrestrial biosphere, and aquatic ecosystems.

MATERIALS AND METHODS

Flight campaign

Two airborne campaigns were conducted in the Athabasca Oil Sands region of Alberta, Canada (April and June–July 2018), aboard the National Research Council of Canada (NRC) Convair 580, with the primary goals of quantifying pollutant emissions from oil sands operations and investigating their subsequent downwind evolution (including deposition). Thirty separate flights were conducted, 7 of which were designed as near-Lagrangian to track pollutant plumes downwind of the source area, which are thus used in the current analysis (table S1 and fig. S1). A comprehensive suite of trace gas, particle, and meteorology measurements were conducted at high time resolution and sensitivity and that have been deployed on previous oil sands campaigns that have been described in detail elsewhere (72) and in the SI. Additional instrumental details are provided here for measurements relevant to the current analysis and/or for modifications from previous deployments.

Airborne measurement methods

Total gas-phase organic carbon

TGOC measurements were made aboard the aircraft by difference, using a pair of cavity ring-down (CRD) absorption instruments (Picarro G2401-m) which measured CO₂, CO, CH₄, and H₂O. The TGOC system and its application on the aircraft have been described in detail previously (38, 72). Briefly, one of the CRD instruments was used to sample behind a heated (650°C) platinum catalyst (Shimadzu Inc.), which quantitatively converted all carbonaceous species into CO₂ as described previously (13, 73, 74) such that TGOC (parts per million carbon) was obtained as the difference between the CRD-measured species as

$$\mathit{\text{TGOC}}=∆{\text{CO}}_2-(∆{\text{CH}}_4+∆\text{CO})$$

where Δ refers to the difference between with and without catalyst sample streams. Given that the heating and combustion occurred outside of the aircraft, with no inlet, loses on inlet tubing were negligible, while the rear-facing nature of the inlet was designed to sample negligible particle mass. Calibrations using two different concentration mixtures of CO, CO₂, and CH₄ (National Institute of Standards and Technology–referenced) were performed simultaneously for both instruments at the beginning and end of each flight. The detection limit for the TGOC system was evaluated using in-flight data during a zero period, resulting in an estimated detection limit of ~60 ppbC at the 3σ level. Laboratory experiments before the study were conducted indicating that the conversion efficiency of ethane across the catalyst was ≈100%, which is expected to be the most challenging species to combust aside from methane, which is concurrently measured by the CRDs. Additional laboratory experiments using a range of hydrocarbons (>C₂) including aromatics and alkanes also exhibited ≈100% conversion efficiency (75), and it is expected that oxygenated compounds are even more readily decomposed/combusted at reduced temperatures. While there was no evidence of the catalyst efficiency degrading with time, it was nonetheless replaced four times during the study.

Application of TERRA for deposition calculations

The use of TERRA to derive deposition fluxes have been described in great detail previously for total oxidized sulfur and total oxidized nitrogen (37). The first step in deriving TGOC deposition fluxes is the estimation of mass transfer rates (T_TGOC; tonnes C hour⁻¹) across the flight screens (Fig. 1A) using an extension of TERRA that was originally developed for emission rate determination using aircraft measurements (40). TERRA was originally developed to estimate pollutant emission rates based on the divergence theorem, which equates the change in mass within a control volume to the integrated mass flux through the walls of the control volume [i.e., a three-dimensional (3D) flight box]. Consequently, as described previously (40), the emission rate of a given chemical (E_C) is defined via a mass balance across the control volume as

$$E_{\mathrm{C}}=E_{\mathrm{C},\mathrm{H}}+E_{\mathrm{C},\text{HT}}+E_{\mathrm{C},\mathrm{V}}+E_{\mathrm{C},\text{VT}}+E_{\mathrm{C},\text{VD}}-E_{\mathrm{C},\mathrm{M}}-E_{\mathrm{C},\mathrm{X}}$$

where E_C,H is the horizontal advective flux through the box walls that is ultimately equated to the transfer rate through a given flight screen (T_TGOC). Other terms above include E_C,HT, the horizontal turbulent flux through the “box’s” sides; E_C,V, the advective flux through the box top; E_C,VT, the turbulent flux through the box top; E_C,VD, the deposition to the surface; E_C,M, the increase in mass within the volume due to a change in air density; and E_C,X, the increase in mass due to chemical changes of the compound within the box volume (i.e., oxidation). The modified TERRA used in this study uses screen flights (2D) rather than box flights (3D), which results in the nonapplicability of the terms E_C,V, E_C,VT, E_C,VD, E_C,M, and E_C,X in the above equation, while the horizontal turbulent flux through the screen has been found to be negligible (40). Hence, integration of the horizontal fluxes across the within-screen plumes results in T_TGOC calculated via

$$T_{\text{TGOC}}=E_{\mathrm{C}}=E_{\mathrm{C},\mathrm{H}}={\displaystyle \underset{s_1}{\overset{s_2}{\int }}}{\displaystyle \underset{z_1}{\overset{z_2}{\int }}}C(s,z)u_n(s,z)\mathit{\text{dsdz}}$$

where $C(s,z)$ is the background subtracted concentration at screen coordinate s and z, which represent the horizontal and vertical axes of the screen, and $u_n(s,z)$ is the horizontal wind speed normal to the screen, resulting in a transfer rate in units of t hour⁻¹. T_TGOC was estimated with TERRA using virtual screens (via Kriging), after subtracting a TGOC background concentration. The TGOC background concentration was derived as a moving box-car average of the fifth percentile of data for a given flight, using an approach described elsewhere (76). The data were extrapolated below the lowest flight track to the surface as described previously (40), with the variation in results between multiple extrapolation approaches (5 to 20%) included in the uncertainty estimates. The uncertainty for a single screen is estimated at 4% for elevated sources and ~20% for ground based emissions, driven largely by the extrapolation to the ground (40). TGOC data were also extrapolated linearly to background values from the highest-altitude flight track upwards to the top of the mixed layer, which was determined from vertical profiles of TGOC and NO_x mixing ratios, temperature, and dew point (table S1) but typically resulted in a small upwards extrapolation of less 100 to 200 m. The TGOC deposition rate, equal to the differences in the transfer rates between screens (ΔT_TGOC), was calculated as the differences in T_TGOC between pairs of virtual screens, with uncertainties in ΔT_TGOC (tonnes C hour⁻¹) estimated between 15 and 35% as supported by emission rate uncertainties determined for box flights (40). The uncertainty analysis for box flights is applicable to ΔT_TGOC here, as both account for uncertainties with an upwind and a downwind screen. The ΔT_TGOC uncertainties were propagated through subsequent calculations. As opposed to previous work on the deposition of total sulfur (37), chemical loss in TGOC via OH or ozone oxidation does not need to be considered, as all forms of carbon are included in the measurement of TGOC. As noted previously, SOA formation could potentially be misinterpreted as loss of TGOC; however, as shown in Fig. 1B, formation rates are negligible compared to the loss of TGOC between screens. Other assumptions in deriving a deposition flux using this approach as outlined in fig. S2 include that (i) there are negligible emissions between flight screens (shown above), (ii) there is no precipitation occurring for the duration of a given flight, (iii) diffusion outside of the edges of the screens is negligible and most of the plume is contained within a given screen, (iv) source emission rates are near constant, and (v) the boundary layer is quasi-stationary. These assumptions have been described here and previously (40) and found to be valid under most circumstances.

Dry deposition fluxes (F_TGOC) (gC m⁻² hour⁻¹) were obtained by dividing the deposition rates, D_TGOC by the footprint surface area of the plume between two adjacent screens, estimated as the area under the plume extending to where concentrations fell to background levels (ΔTGOC ≈ 0 ppm), and with an estimated uncertainty of 10%. Dry deposition fluxes between the sources and the first screen were also estimated by extrapolating the transfer rates (T_TGOC) back to the source region, with the uncertainties in the exponential fit parameters (10 to 20%) propagated through the calculation of the cumulative deposition rates of Fig. 1B. The uncertainty in the surface area for the source extrapolated fluxes was approximately 15%. The furthest extent from the source area for determination of fluxes and deposition rates was defined as the midpoint between screens.

Spatially averaged dry deposition velocities (V_d) based on the aircraft measurements were determined over the surface area between screens using average plume concentrations across pairs of screens estimated for 40 m above the ground (to compare with modeled V_d that is also computed at 40 m) such that V_d = F_TGOC/[TGOC]. The largest source of uncertainty in V_d calculated in this manner was the determination of concentration at 40 m, as the measurements were extrapolated from the lowest aircraft altitude to the surface. Estimates of V_d between the screens of each flight were similar, with the final reported V_d taken as the mean of all V_d estimates across all flights and screens. Despite uncertainties in the estimated TGOC concentrations, the large average deposition velocity is consistent with the large measured and modeled fluxes for TGOC. The calculated V_d here represents the bulk deposition velocity for all carbon-based molecules, with those of individual species being dependent on molecular structure. The measurement-derived mean V_d was compared with those from the air quality model GEM-MACH, which uses inferential methods.

Carbon-weighted oxidation lifetimes

The atmospheric lifetime with respect to OH radical oxidation (τ_OH) for a given compound (C_i) is calculated as

$${\mathrm{\tau }}_{\text{OH}}={(k_{C_i+\text{OH}}\overline{[\text{OH}]})}^{-1}$$

using an average OH concentration of 3.0 × 10⁶ molecules cm⁻³, consistent with OH derived from flights using the evolution of various VOC ratios (37), and similar to modeled OH levels in oil sands plumes estimated using GEM-MACH. This provides a reasonable estimate of τ_OH, representative of daytime, in-plume oxidation. The average carbon-weighted lifetime for the compound categories of Fig. 4C (OVOC, VOC, and I/SVOC) was calculated on the basis of the estimated carbon concentrations of species within those categories (or for the total carbon from all species), such that

$${\mathrm{\tau }}_{\text{OH},\text{CWA}}=\frac{\sum ({\mathrm{\tau }}_{\text{OH},i}·C_i)}{\sum C_i}$$

where ${\mathrm{\tau }}_{\text{OH},\text{CWA}}$ is the carbon-weighted average for a group of organic species in Fig. 4C, ${\mathrm{\tau }}_{\text{OH},i}$ is the τ_OH of species i, and C_i is the carbon concentration of species i. The underlying OH reaction rate constants (k_Ci+OH, a.k.a., k_OH) used in deriving the lifetime for compounds of known chemical structure were obtained from the National Institute of Standards and Technology Chemical Kinetics Database (77) and relevant literature (78). This includes rate constants for hydrocarbon VOC species measured with discrete whole-air samples and select OVOCs measured by proton transfer reaction time-of-flight mass spectrometry (PTR-ToF-MS and chemical ionization time-of-flight mass spectrometry (CI-ToF-MS). The k_Ci+OH for gas-phase oxidation products of unknown chemical structure measured by the PTR-ToF-MS and CI-ToF-MS were estimated from their elemental formulas (i.e., n_C, n_O, and O/C ratio) using an approach described previously (79). OH rate constants for organic species in the I/SVOC volatility range measured with adsorbent tubes were estimated on the basis of k_Ci+OH for surrogate species with similar carbon number and double bond equivalency (DBE). Increases in DBE for a given carbon number were generally accounted for by increasing the number of ring structures in the surrogate species chosen, while increases in carbon number at a given DBE value were accounted for by adding an increasing number of carbon substituents to the ring structures as needed. The rate constants for these surrogates were calculated using group contribution methods (80) and are shown in table S3.

GEM-MACH annual carbon fluxes

GEM-MACH’s implementation for the oil sands region has been described elsewhere; here, we provide an overview of model components updated relative to previous work (36). GEM-MACH is an online regional air quality model, incorporating the following key process representations: (i) Gas-phase chemistry was simulated using a modified SAPRC11 reaction mechanism (45) resulting in a total of 162 gas-phase species and 476 reactions; (ii) SOA formation is carried out with a revised yield approach (81); particle species representation was via a 12-size bin sectional approach with 14 particle species (SO₄, NO₃, NH₄, Ca, Mg, Na, K, Cl, Fe, Mn, SOA, primary OA, black carbon, and crustal material); (iii) gas-phase dry deposition used a modified Wesely approach (9, 46), using Henry’s law partitioning and reactivity coefficients obtained from the literature or calculated using group methods (as described above with pH assumed to be neutral in this implementation), land use–dependent deposition parameters being used to account for different surface resistance values to different vegetation types (82), and satellite observations to provide monthly varying leaf area index values (83); (iv) particle inorganic chemistry was carried out with a modified algorithm based on ISORROPIA2 (84); (v) large stack emissions were distributed in the vertical using a modified Briggs approach incorporating latent heat release from combustion plumes (85); (vi) the online model incorporated direct and indirect effect feedbacks between weather and model-generated particulate matter (86); improved cloud processing included snow and rain scavenging (87); (vii) the model included subgrid scale parameterizations for turbulence and shading within forest canopies (88, 89); and (vii) the impact of vehicle-induced turbulence on pollutant mixing was also included (89). Hourly emissions of TGOC and NOx were generated from aircraft observations of box flights around specific facilities using the TERRA algorithm, from which emission ratios (TGOC/NO_X) were calculated (table S5). The emissions ratios were found to be relatively consistent for a given facility and were used to generate hourly TGOC emissions using reported NO_X emissions as a surrogate. While emission ratios were not possible for all oil sands facilities, the largest facilities with the highest TGOC emissions [Syncrude Mildred Lake (SML), Suncor (SUN), and Canadian Natural Resources Limited (CNRL)], were included in emissions estimates used here. A full description of TGOC emissions from oil sands facilities is described elsewhere (38). VOC emissions were generated by making use of multiple data sources, including continuous emissions monitoring, emissions reporting, and aircraft and settling pond observations (90). Deposition of VOC for all SAPRC11 depositing gas species were summed and converted to a cumulative SAPRC11 VOC carbon deposition value for comparison to the deposition flux of TGOC resulting from aircraft-derived TGOC emissions. Model deposition fluxes of all SAPRC11 species for the 12-month simulation period were converted to units of tC year⁻¹ and summed for the comparison in Fig. 5.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S6

Tables S1 to S5

References