Abstract
Co-occurrence of metal oxo-anions (e.g., arsenate) in drinking water pose human health risks. To understand and predict competition and breakthrough for individual or mixtures of oxo-anions in continuous-flow packed bed adsorption systems, we linked equilibrium surface complexation models (SCMs) with a Pore Surface Diffusion Model (PSDM). After parameterization using data for two commercial adsorbents, the SCM and PSDM predicted well the adsorption isotherm data and column breakthrough curves, respectively, for single-solute (arsenate) and bi-solute water chemistries (arsenate, vanadate) as well as chromatographic displacement of previously adsorbed arsenate by vanadate. Surface- and pore- diffusivities for both commercial adsorbents were 3.0 to 3.5 x10−12 cm2/s and 1.1 to 0.8 x10−6 cm2/s, respectively. After validation, the SCM+PSDM was used in silico to evaluate adsorbent media characteristics, variable water chemistries, and reactor configurations. When contrasting hypothetical crystalline versus amorphous metal (hydr)oxide adsorbents, increasing surface site density resulted in higher Freundlich isotherm capacity (KF) but didn’t impact 1/n. Increasing surface binding affinities beneficially impacted both KF and 1/n isotherm and would improve performance of point-of-use (POU) adsorbent system applications. In silico simulation results suggest prioritizing enhancing adsorbent capacity (q) through improved surface reactivity in the design of new POU adsorbent materials rather than focusing on reducing mass transport limitations through intraparticle pore design. For municipal-scale adsorption systems, the PSDM simulation of the mass transfer zone shape was evaluated for hypothetical adsorbent pore designs (i.e., intraparticle porosity (εp) and tortuosity) and demonstrated that εp control was a key strategy to improve performance.
Keywords: Adsorption, Mass Transport, Modeling, Oxo-Anion, Water Treatment
1. Introduction
Drinking water utilities serving smaller population communities have the highest rates of regulatory violations, and arsenic is among the ten most common reasons for these violations in the United States of America (USA).1–3 Small systems (i.e., serving 500 or fewer consumers) often remove arsenic using packed bed adsorption systems with iron-(hydr)oxide granules.4–6 Larger sized water treatment systems (i.e., serving at least 501 consumers) more commonly use precipitation with iron salts to remove arsenic from drinking water supplies. The United States Environmental Protection Agency (USEPA) Maximum Contaminant Level (MCL) for arsenic is 10 ppb, but this MCL is above the 106 excess cancer risk set for many drinking water carcinogenic contaminants. Risk analysis suggests arsenic may pose among the greatest health risks in drinking water in the USA today.7,8 There is no safe level of arsenic in drinking water, and many homes served by compliant municipal water employ point of use (POU) to further reduce risks.1 POU technologies are also often used by homeowners using private, non-regulated wells for drinking water. Therefore, designing and predicting the lifespan of adsorbents that reduce arsenic in drinking water to below the MCL is key to reducing health risk.
Adsorption of arsenic and other oxo-anions onto metal (hydr)oxide adsorbents occurs by (i) physisorption through London-van der Waals forces as outer-sphere complexes or (ii) chemisorption as inner-sphere complexes through the sharing of electrons. The capacity of an adsorbent (e.g., μg As/mg sorbent) depends on the water chemistry and physical and chemical sorbent properties, including surface area (SA, m2/g), surface site density (SSD, sites/nm2), and binding affinities of hydroxide or oxo-anions to the surface, which are represented by conditional stability constants (i.e., log KEQ ).9,10 When used in a continuous-flow packed-bed water treatment system, the dynamic removal of arsenate is influenced by its maximum adsorption capacity plus mass transport across the bulk stagnant film around the adsorbent media outer surface (e.g., film diffusion) followed by pore and surface diffusion within the adsorbent particle.11 Full-scale packed bed systems operate through porous media, with empty bed contact times (EBCTs) of 2 to 10 minutes, while POU systems have EBCTs of only 10 to 60 seconds. Adsorbent particle size and flowrate through the packed bed impact hydraulic pressure losses (e.g., headloss) as well as Reynolds, Schmidt, and other dimensionless numbers that represent mass transport mechanisms.12 While many studies seek to create new adsorbents to improve the arsenic adsorption capacity, uncertainty exists for tradeoffs between adsorbent capacity and mass transport within porous media.
Arsenic is a polyprotic oxo-anion that occurs in drinking water supplies as arsenate and arsenite . Elevated pH and co-occurring oxo-anions such as vanadate, tungstate, phosphate, and silicate vary geographically and compete against arsenic for surface binding sites on adsorbents.10,13,14 Higher pH increases deprotonation of surface binding sites and causes undesirable electrostatic repulsion for anionic oxo-anions such as arsenic.10 Experimental approaches to predict adsorbent media performance suffer from the limited ability to extrapolate adsorbent performance in water chemistries beyond those employed in laboratory or pilot tests.13,15–17 Therefore, strategies are needed to apriori design new adsorbents that exceed the removal capabilities of existing media without extensive lab- or pilot-based experiments. Recently, several in-silico models have simulated arsenic removal performance of commercial media but have not been used to apriori improve design of adsorbent granular media.13,18 Our work builds on these homogeneous surface diffusion based modeling efforts for individual adsorbents by systematically varying material properties, aiming to discern the net effects of changes and significance of material attributes to design new sorbents.
This study aimed to improve our understanding of adsorbent properties and water quality on packed bed water treatment processes to inform design of enhanced adsorbents. This was achieved by developing and validating an equilibrium surface complexation model (SCM) linked with dynamic mass transport pore-surface diffusion models (PSDMs) for arsenic in multi-solute systems across a pH range. First, SCMs were parameterized using previous batch equilibrium adsorption experiments for two different commercial adsorbents in several water matrices containing arsenate, varying pH, and competing anions (e.g., carbonate, vanadate). Second, a MATLAB® code was developed to convert SCM outputs of equilibrium solid and liquid phase oxo-anion concentrations into Freundlich isotherm parameters , which are required inputs into a MATLAB® version of the PSDM component. Third, linked SCM+PSDM simulations of arsenate breakthrough were validated against column test data. Fourth, the linked models were employed with predictive capabilities to explore new media properties applied to full-scale or POU applications.
2. Data Sources and Models
2.1. Commercial Sorbent Properties
Two commercially available iron-based porous adsorbents that are widely used in packed-bed treatment systems to remove arsenic from drinking waters were used. They are referred to by the acronyms E33 (developed by Bayer AG and marketed in the USA by Severn Trent Service) or GFH (Granular Ferric Hydroxide distributed by US Filter or others).19–22 Manufacturers and papers often report BET surface areas for E33 and GFH between 125 and 300 m2/g.23 However, because N2 BET surface area underestimates the actual specific surface area because even at low room temperature, the surface structure may be altered by the evolution of chemisorbed water.24,25 Therefore, as previously published26 the surface areas of the adsorbents were adjusted such that the surface charge densities as a function of were similar for the commercially available adsorbents and the reference crystalline oxides, and these surface area estimates were used for all subsequent analyses. The surface areas obtained using this approach are 350 and 600 m2/g for E33 and GFH, respectively. Thus, within this work, all surface areas, site densities and charge densities are internally consistent.23,27 Adsorption experiments determined surface site densities for E33 and GFH are 0.385 and 0.826 sites/nm2, respectively, based on maximum anion adsorption (MAA) .23 Resulting point of zero charge for E33 and GFH are 8.4 and 7.8, respectively, based upon our prior work.23 The characterization measurements were obtained in CO2 free the water in a nitrogen purged glove box, and all sorption experiments were evaluated through NaHCO3 addition for sorbate complexation affinities.
2.2. Surface Complexation & Isotherm Models
An equilibrium surface complexation model (Visual MinteQ, ver 3.1) was parameterized using conditional stability constants (Table 1) using the 2 pK double layer model (DLM) from previous experimental studies.23 The prior experiments were conducted using bottle-point-adsorption tests with 0 to 100 mg/L of sorbent in CO2 purged batch reactors for ten days across a range of water quality conditions.23 Equations 1–6 in Table 1 describe key speciation reactions and equilibrium constants for arsenate (As(V)) and vanadate (V(V)) within a 10 mM NaHCO3 water matrix. Preliminary experiments conducted at 100 μg/L initial As(V) did not significantly impact As(V) competition; however, it is possible that lower As(V) concentrations could be impacted by the presence of carbonate.28 Future efforts may explicitly incorporate carbonate surface complexation species in SCMs, but this would require additional competitive adsorption modeling. Thus, because natural waters contain carbonate alkalinity, we opted to implicitly embed impacts of low carbonate in the SCM modeling parameters As(V) and other solutes through apparent complexation affinities. V(V) was selected as a model competitive oxo-anion to As(V) because of its isostructural configuration and similar pKa.29
Table 1.
Surface equilibrium equations and sorbate protonation equations used in the SCM for two commercial adsorbents (E33 and GFH) based on prior work.23
| Equation Number | Equation | Log (KEQ) | |
|---|---|---|---|
| 1 |
|
||
| 2 |
|
||
| 3 |
|
||
| 4 |
|
||
| 5 |
|
||
| 6 |
|
||
| 7 |
|
|
|
| 8 |
|
|
|
| 9 |
|
||
| 10 |
|
|
|
| 11 |
|
Equations 7–11 represent As(V) or V(V) adsorption to iron hydroxide surfaces (E33 or GFH) based on prior fitting using FITEQL of conditional stability constants (K7-10,E33 or K7-8,10-11,GFH).23 These values were consistent with other reported values for iron (hydr)oxide adsorbents.30,31 Fitted surface complexation constants (Table 1) for Eq. 7 and 8 for E33 were and ,23 where the standard deviations represent variance in experimental data and fitting of data over a wide pH range of 4 to 12. Visual MinteQ requires a single fixed KEQ value, rather than a range. Through an optimization method to fit data of environmental relevance between pH 7 to 10, final values were and (Table 1). A similar process was used for GFH. Table 1 represents a “tableau” approach to write equilibrium surface complexation reactions. Parameter fitting to parameterize the DLM used experimental data and four different monodentate complexation reactions shown in Table 1.23,32 SCM output data simulated both equilibrium liquid and solid-phase oxo-anion concentrations for several adsorbent masses (e.g., dosages), which were then used as inputs to obtain Freundlich isotherm parameters KF and 1/n. A MATLAB® script was used to post-process the data because Freundlich isotherm parameters KF and 1/n were required PSDM inputs.
2.3. Pore Surface Diffusion Model (PSDM) Parameterization
The PSDM simulates solute mass transfer for adsorbents in a packed bed reactor by accounting for external film and intraparticle pore or surface diffusion. A custom MATLAB® PSDM code developed by Ron Hofmann and reported elsewhere was used (https://github.com/ebriese1/PSDM).33,34 Mass transport coefficients including film pore , and surface diffusivity constants were initially estimated for uniform spherical particles using the Gnielinski equation (Eq. 12) and equations 13–14.35–37 Tortuosity , or the labyrinth factor, was additionally calculated using intraparticle porosity in Eq. 15.12
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Equations 12–15 utilize the porosity of the packed bed (dimensionless), the liquid diffusivity DL (cm2/s), the Reynolds number Re, the Schmidt number Sc, the intraparticle porosity of the particle (dimensionless), the influent concentration (C0, mg/L), the surface pore diffusion flux ratio (SPDFR, the apparent adsorbent density , and the adsorbent phase concentration in equilibrium with influent concentration qe (mg As / g wet media).
After initial estimation for spherical adsorbent particles (e.g., Gnielinski Eq. 12), parameterization of the PSDM mass transport variables were fit to experimental packed bed breakthrough curves. This fitting was essential because the commercial adsorbents (E33 and GFH) are non-spherical and have a range of particle diameters between different mesh sizes. The fitting process is discussed in results section 3.2. Previous reported packed bed experimental results were used, based upon rapid small scale column tests (RSSCTs) designed with V0 loading rate of 15 m/hr and geometric mean media radius of 64 μm (100x140 mesh) for E33 or GFH (see Text S1 Table S1).16,23
3. Results and Discussion
3.1. Validation of SCM and Simulation of Freundlich Isotherm Parameters
Arsenate adsorption experimental values across a relevant drinking water pH range were accurately predicted by the parameterized SCM and successfully used to generate Freundlich isotherm parameters. Figure 1a shows the SCM for a single sorbent dosage of 0.01 g/L does the best at predicting the percentage adsorbed arsenate around pH 8.5. Figure 1b confirms the SCM predictions (hashed symbols) are within the 95% confidence intervals of experimental data performed over a range of sorbent dosages. Because of the better data fits near pH 8.5, much of the subsequent simulations were performed in thereabouts. Data in Figure 1a did not have error bars on the experimental data for the single-point adsorption data. The inherent variability of experimental data was illustrated in Figure 1b using multiple sorbent dosages. Regressions through the GFH and E33 experimental data, and the 95% confidence intervals on the slopes, showed no difference at pH 8.5 between E33 and GFH. Because GFH has a slightly higher number of surface binding sites (4.96x1020 sites/g) compared to E33 (35x1020 sites/g), SCM simulations in Figure 1b showed slightly higher arsenate adsorption by GFH. Overall, SCM simulations and experimental data at multiple sorbent dosages all fell within the 95% confidence interval of the GFH adsorption isotherm.
Figure 1.

Experimental (solid symbols) and SCM predictions (hash-marks) for arsenate adsorbed onto E33 or GFH (10 mM NaHCO3, 100 ppb As(V)). (a) Arsenate adsorption onto the surface is higher for GFH in experimental or SCM predictions across the range of equilibrium pH levels. (b) Plots at pH 8.5 of experimental data (solid symbols) and SCM predicted data (hash-marks) to yield fit Freundlich values with 95% confidence intervals (solid lines) (KF = 8.6 and 8.9 (mg/g)(L/mg)(1/n) and 1/n = 0.21 and 0.26 for SCM and experimental E33 data, respectively, for a sorbent weight range of 5 to 30 mg/L wet media; KF = 12.1 and 12.2 (mg/g)(L/mg)(1/n) and 1/n = 0.24 and 0.23, for SCM and experimental GFH data, respectively, for a weight range of 2 to 26 mg/L wet media for As(V)).
Figure 1b shows isotherms for GFH and E33 from experimental data and SCM simulated data using a range of adsorbent dosages at a single elevated pH of 8.5. Both datasets are nearly linear on the log-log plot and were fit well by the Freundlich model. The simulated isotherm data fell within the 95% CI of experimental data and therefore validated this general modeling approach. Freundlich isotherm parameters varied by <10% between experimental data and SCM predictions. Overall, using only equilibrium constants for arsenate complexes (Eq. 7 and 8), isotherm parameters were reasonably predicted in this single-solute (arsenate) system for the drinking water relevant pH range.
Bi-solute As(V) and V(V) adsorption isotherm plots (Figure S1) also showed good agreement between experimental data and SCM simulations using the conditional stability constants in Table 1. Table 2 summarizes KF and 1/n for single- and bi-solute conditions for two different initial molar concentrations (0.134 or 1.34 μM) of each solute. Equimolar concentrations of As(V) and V(V) were compared for these oxo-anions to represent molecular competition of the oxo-anions for adsorbent binding sites. Arsenate has slightly more favorable adsorption energy trends (e.g., lower 1/n) on GFH than E33.15 However, E33 exhibited a higher adsorption capacity (e.g., higher KF) than GFH for pH 8.5. In bi-solute systems containing As(V) and V(V), KF values were lower for arsenate and vanadate together compared with parallel single-solute systems as competition for similar binding sites occurred. Adsorption site competition among the two oxo-anions had only a slight impact on the adsorption energies (e.g., slightly less favorable, and higher 1/n). Overall, the SCM represented well the key changes in water quality (pH, presence of competing sorbents), and a MATLAB® post-processing add-on was able to generate equilibrium the Freundlich isotherm parameters (KF, 1/n) that were required inputs for the PSDM.
Table 2.
Freundlich Isotherm coefficients obtained for several water chemistries using baseline conditions in the SCM (pH = 8.5, 10 mM NaHCO3) with two different sorbents (E33 and GFH) and several initial arsenate and/or vanadate concentrations.
| Sorbent material | Initial Arsenate Concentration (μM) | Initial Vanadate Concentration (μM) | Freundlich Isotherm Values for arsenate (vanadate values shown in parentheses) |
|
|---|---|---|---|---|
| KF [ (mg/g)(L/mg)1/n ] | 1/n | |||
| 1.34 (100 ppb) | 0 | 8.6 | 0.21 | |
| 0.134 (10 ppb) | 0 | 14.4 | 0.28 | |
| E33 | 0.134 (10 ppb) | 0.134 (6.8 ppb) | 7.0 (17.6) | 0.22 (0.31) |
| 1.34 (100 ppb) | 1.34 (68 ppb) | 6.4 (10.9) | 0.21 (0.25) | |
| 0 | 1.34 (68 ppb) | -- (11.5) | -- (0.20) | |
|
| ||||
| 1.34 (100 ppb) | 0 | 12.1 | 0.24 | |
| 0.134 (10 ppb) | 0 | 18.2 | 0.37 | |
| GFH | 0.134 (10 ppb) | 0.134 (6.8 ppb) | 9.8 (29.3) | 0.33 (0.47) |
| 1.34 (100 ppb) | 1.34 (68 ppb) | 7.4 (14.6) | 0.27 (0.38) | |
| 0 | 1.34 (68 ppb) | -- (33.1) | -- (0.41) | |
3.2. Packed Bed Simulations of Experimental Data
Using KF and 1/n generated from the SCM data, the PSDM accurately simulated experimental As(V) and V(V) packed bed column breakthrough data. Through a sequential parameterization process, single-solute arsenate experimental breakthrough data were fit to obtain the film diffusion coefficient (kf) and intraparticle surface (Ds) and pore (Dp) diffusivities. First, the liquid diffusivity for arsenate in water (DL = 1.05x10−5 cm2/s) and previously reported surface diffusivity (Ds) of 3x10−12 cm2/s 23 for E33 were used as initial fitting values for both adsorbents.23 Second, arsenate breakthrough curves were iteratively fit over the first 10,000 bed volumes (BV) treated by varying kf. Fitted values for kf were 0.0015 and 0.0025 cm/s for GFH and E33, respectively. Third, using breakthrough data beyond 10,000 BV, DS and DP were iteratively varied to fit the slope and curvature of the breakthrough curve (see SI Text S2, Table S2). Final DS values for GFH and E33 were 3.0x10−12 and 3.5x10−12 cm2/s, respectively. DP values for GFH and E33 were 1.1x10−6 and 8.4x10−7 cm2/s, respectively, which are similar to values found in literature.36 As expected, DS values were orders of magnitude lower than DP. The calculated surface to pore diffusion flux ratio (SPDFR, Eq. 16) was 4x10−6 and 3x10−6 for E33 and GFH, respectively, and within literature reported ranges.37 Because diffusivities were obtained from RSSCT and existing literature, limitations arise when extrapolating and simulating highly porous or diffusive materials. The sequential parameterization process led to obtaining PSDM mass transport parameters for the purpose of simulated oxo-anion breakthrough curves.
Figure 2 shows that linked SCM+PSDM simulations reasonably fit single-solute arsenate breakthrough in packed beds containing GFH or E33 sorbents. The breakthrough curves showed a gradual lag resulting from intraparticle diffusion in single-solute systems before arsenate breakthrough occurred more rapidly (at 15,000 BV). GFH and E33 had similar arsenate breakthrough curves, reaching 60% breakthrough at around 46,000 and 34,000 BV, respectively. Coefficients of determination (R2) obtained for the three modeled datasets were 0.97, 0.97, and 0.94 for single solute E33, single solute GFH, and bi-solute E33, respectively. To facilitate comparison of breakthrough data, we introduce a design metric termed “BV10” to quantify the number of bed volumes treated until the effluent of a packed bed reactor reached the arsenic MCL of 10 ppb. For experiments in Figure 2, which utilized 100 ppb influent arsenate, BV10 occurred at 11,100 and 10,200 for GFH and E33, respectively. Overall, the SCM+PSDM accurately simulated both single- and bi-solute arsenate breakthrough curves for experimental RSSCT column data.
Figure 2.

Experimental data (symbols) and SCM+PSDM simulated (lines) breakthrough curves for an RSSCT in two different single-solute (solid lines) and one bi-solute (dashed line) system. Influent water chemistry was pH 8.5 containing 100 ppb As(V) alone or in combination, for bi-solute experiment, with 68 ppb V(V). Column dimensions were 4.0 cm long and 1.1 cm diameter. Column was operated at a surface loading of 0.385 cm/s, which resulted in an RSSCT EBCT of 0.17 min.
For the bi-solute system, we assumed similar mass transfer parameters for both arsenate and vanadate because of their comparable hydration state and radii. To validate this assumption, Figure 2 shows a bi-solute system (depicted by green symbols and lines); without any additional fitting of variables, PSDM predictions accurately fit the arsenate breakthrough curve for a packed bed of E33. Arsenate breakthrough occurred faster (i.e., fewer BV) in the bi-solute system with equimolar concentrations (1.34 μM) of arsenate (100 ppb) and vanadate (68 ppb) at pH 8.5 than in the single-solute system of only 100 ppb arsenate. Because E33 equilibrium Freundlich isotherm coefficients (KF, 1/n) were lower for bi- than single-solute systems (Table 2), surface binding sites reached saturation at fewer BV treated compared against a single-solute system of As(V) through the packed column. Overall, the ability for the SCM+PSDM linked models was demonstrated using packed bed experimental data.
Figure 2 shows experimental data for the RSSCT, which used a high column flow rate and small adsorbent particle diameter. Previous studies have demonstrated the ability of RSSCT to accurately predict full-scale arsenic removal in real groundwaters.20,23,34 By using the fitted mass transfer parameters, the PSDM was applied to full scale treatment systems with larger adsorbent particles within similar Re*Sc regions. We previously showed that RSSCTs with an EBCT of 17 seconds simulates well the arsenic removal performance of a full-scale wellhead packed bed system with an EBCT of 5 minutes.17,38,39 RSSCTs and full-scale systems have different particle diameters and flowrates, but the same adsorbent media. This was an important validation step. Next, we sought to simulate, but not experimentally validate, the performance of separate POU system which uses E33 material of a different diameter than used in either RSSCTs or wellhead packed bed system. The under-the-sink E33 POU system had an EBCT of 0.42 minutes based upon recommended operating condition and physical dimensions (Figure S2). This POU system reached breakthrough in fewer bed volumes than a full-scale wellhead treatment (EBCT of 5 minutes). This was attributed to being able to capture the entire mass transfer zone in the system with a longer EBCT. Moreover, this demonstrates the benefits of in silico SCM+PSDM approaches in potentially improving POU designs. Therefore, subsequent sections employed the SCM+PSDM linking modeling approach across various water quality, adsorbent media, and reactor conditions.
3.3. Simulating Effects of Water Chemistry Using Linked SCM+PSDM
In contrast to experimental data, which is only applicable to the specific water quality conditions under which it was acquired, parameterized SCMs can simulate equilibrium isotherm values across various water chemistry conditions. Table 3 presents an orthogonal matrix design approach used for in silico experiments to simulate the effects of pH and competing ion concentrations on arsenic breakthrough in a full-scale packed bed system.
Table 3.
Orthogonal experimental matrix for five levels of parameters that influence water quality, sorbent material property or hydraulic packed bed column operating conditions for E33. Matrix conditions were used with the linked SCM+PSDM to simulate pollutant breakthrough curves.
| Factor | Parameter | Parameter Values |
||||
|---|---|---|---|---|---|---|
| Lowest | Low | Average | High | Highest | ||
| Water Quality | pH | 6.5 | 7 | 7.5 | 8 | 8.5 |
| As(V) (ppb) | 15 | 25 | 50 | 75 | 100 | |
| V(V) (ppb) | 0 | 0 | 34 | 51 | 68 | |
|
| ||||||
| Sorbent Material Property | εpore | 0.1 | 0.2 | 0.25 | 0.5 | 0.75 |
| SSD (sites/nm2) | 0.25 | 0.325 | 0.385 | 0.425 | 0.5 | |
| Log(K8, E33) | - | - | 11.9 | 12 | 12.08 | |
| Log(K7, E33) | - | - | 27.11 | 27.21 | 27.29 | |
| Log(K9, E33) | 15.61 | 15.79 | 15.91 | - | - | |
| Log(K10, E33) | 8.6 | 8.78 | 8.9 | - | - | |
|
| ||||||
| Hydraulic Operating Condition | Loading Rate (m/h) [gpm/ft2] | 7.3 [3] | 8.6 [3.5] | 9.8 [4] | 11.0 [4.5] | 12.2 [5] |
| Resulting EBCT (min) | 1 | 2 | 3 | 6 | 8 | |
Reducing pH using acid is a commonly employed strategy to enhance the performance of arsenic removal from groundwater in packed beds.40,41 This was easily simulated using the SCM. Table S3 presents Freundlich isotherm values derived from the SCM model simulations using GFH or E33 for pH from 6 to 8.5. Figure 3a shows that simulated arsenate breakthrough at lower pH resulted in more bed volumes (BVs) treated for the same mass of adsorbent in the packed beds; this is equivalent to higher throughput expressed as liters of water treated per unit sorbent mass. Therefore the x-axis in Figure 3 can be converted to throughput (L/kg) by accounting for the water flowrate, bed volume and mass of adsorbent in the packed bed. Throughput is often used in the water industry to scale RSSCTs to full-scale performance, as an alternative to # BV treated. For example, the throughput to reach 10 ppb arsenate (C/C0 = 0.1 for an influent of 100 ppb) in the E33 column effluent (BV10) increased from 13,500 L/kg to 26,000, 51,000, 100,000, 160,000, and 180,000 L/kg as influent pH was reduced from 8.5 to 6 in 0.5 pH increments. The same trend was observed for GFH. Overall, the linked modeling method demonstrated the flexibility to simulate pH control in a variety of influent water chemistries.
Figure 3.
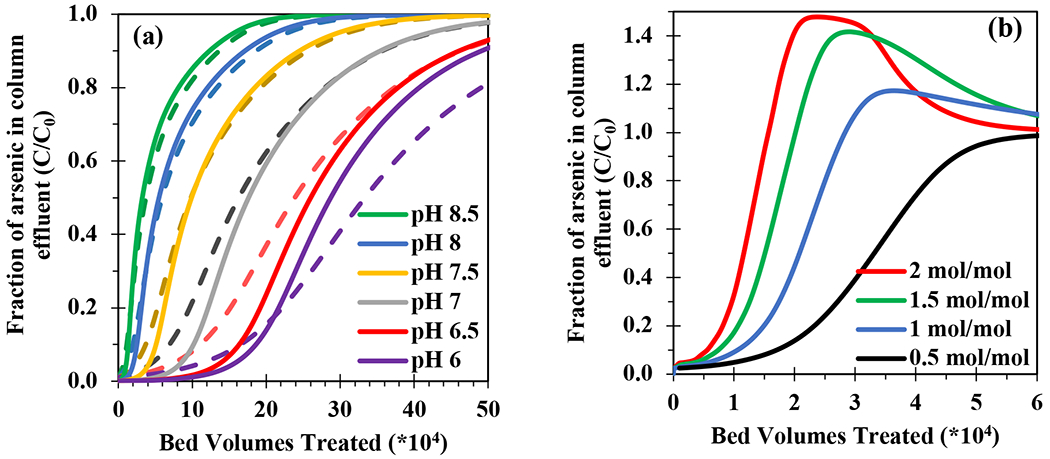
SCM+PSDM simulated arsenate breakthrough curves for (a) E33 (solid lines) and GFH (dashed lines) with a fixed influent single-solute arsenate concentration (100 ppb As(V) in 10mM of NaHCO3) for column dimensions of 4.0x1.1 cm, a surface loading of 0.385 cm/s, and an EBCT of 0.17 min for influent pH ranging from 6.0 to 8.5, and (b) influent vanadate to arsenate molar ratios of 0.5 to 2.0 mole V(V)/mole As(V) (pH 8.5) for E33.
Vanadate co-occurrence with arsenate results in competition among the solutes for the same surface binding sites. Because fluctuations in groundwater chemistry are common, the robustness of the SCM approach was examined by simulating the effects of different vanadate-to-arsenate molar ratios in the influent water. Figure 3b shows that vanadate competition for binding sites caused earlier arsenate breakthrough. Additional co-occurrence of vanadate caused chromatographic displacement of previously adsorbed arsenate, which agrees with experimental data in Figure 2 (i.e., C/C0 values for arsenic exceeded unity in column effluent). Figure S4 shows the vanadate breakthrough data, where no chromatographic displacement of previously sorbed vanadate occurs. Chromatographic displacement occurs because the vanadate binding affinities (Eq. 9–10) are greater than those of arsenate (Eq. 7–8) for equivalent protonation states. Therefore, our modeling approach proved flexible and able to predict the influence of competing sorbates and their removal by packed bed media.
3.4. Simulating Sorbent Material Improvements to Enhance Arsenate Removal
3.4.1. Engineering Adsorbent Surface Reactivity.
Many studies previously aimed to enhance arsenic removal through synthesizing new materials with modified surface site density (sites/nm2) or altered energetics of surface binding sites.10 We adopted an in silico method to discern the significance of material attributes, including surface reactivity (Equations 7–11) and binding site density (see Table 3) on arsenate breakthrough. Simulations were performed for an influent arsenate concentration of 100 ppb at pH 8.5 for varied surface site density, surface area, and binding affinity of target and competing oxo-anions. After varying these parameters in the SCM, output data were applied to the PSDM to generate arsenate breakthrough curves.
As an example of enhancing arsenate adsorption, crystal facet engineering (i.e., adjusting the degree of crystallinity) was explored to modify amorphous metal (hydr)oxide binding sites.42–44 Figure S5 shows simulations using SSD of 0.385 to 0.462 sites/nm2 for E33 and 0.826 to 0.991 sites/nm2 for GFH, which are in the ranges of ferrihydrite and goethite found in literature using maximum adsorption densities.45–48 For both GFH and E33, the resulting BV10 was 67% higher with only a 20% increase in SSD. Higher SDD values in the SCM also influenced Freundlich isotherm coefficients. A 20% SSD increase increased Freundlich KF constant by 39% with a negligible change in the exponent (1/n) (see Table S4). This was expected because the selectivity (or affinity) was not increased; only the binding site availability increased, which only increased the interaction capacity. Further simulations were conducted to understand the complex interaction of varied binding affinities independently and with varied SSD.
To simulate the effects of surface complex formation energy and competing ion adsorption, binding affinity was varied and simulated in the SCM using KEQ (Table 3). Previous studies have highlighted the ability of increasingly amorphous materials to have more favorable adsorption isotherms, often attributed to increased binding site availability or binding affinity. To simulate selective oxyanion removal, binding affinities were varied to exploit this phenomenon observed experimentally in literature.34,49,50 First, a 50% reduction in KEQ (not log KEQ) for vanadate adsorption (K9, E33 and K10, E33) was simulated to decrease competition with arsenate for binding sites, resulting in only a 7–8% decrease in both KF and 1/n. This also decreased BV10 for arsenate by 4% (Figure S6a). Second, in an attempt to simulate high arsenate selective surface binding sites, binding affinities for arsenate (K7, E33 and K8, E33) were increased while maintaining baseline vanadate binding affinities. Figure S6b shows that a 50% increase in arsenate binding affinities (K7, E33 and K8, E33) increased KF by 10% and 1/n by less than 1%, which resulted in a 6% increase in BV10. The minimal changes in 1/n indicate only minor alterations in binding affinity or surface reactivity (e.g., selectivity). To observe the effects of surface reactivity and selectivity at a large magnitude, arsenate binding affinities (K7, E33 and K8, E33) were increased by 200%, resulting in 24% and 7% increases in KF and 1/n, respectively, which also increased BV10 by 36%. Therefore, selectivity for arsenate adsorption can be greatly exploited with increased binding affinity of the target oxo-anion.
Prior literature found that increasing amorphous nature of adsorbent surfaces increased capacity and provided more arsenate binding sites and surface area, creating a strategy to increase SSD available to adsorbents.34,51 Specifically, increasing the amorphous content of the adsorbent increases binding site density and energy of complex formation corresponded to an increase in SSD and decrease in 1/n.51,52 To simulate the increased amorphous nature of an adsorbent, SSD was increased by 120% along with a 200% increase in binding affinity for arsenate complex formation (K7, E33 and K8, E33). The resulting BV10 was 93% higher and reflected a 76% increase in adsorption capacity (KF) and an 8.6% increase in the energy of the complex formation (1/n) compared to baseline conditions (Figure S6b). Overall, improvements in equilibrium arsenate binding by in silico simulated amorphous metal (hydr)oxide adsorbents caused a favorable delay in breakthrough (i.e., sorbent treated more bed volumes and increased operational life).
3.4.2. Engineering Sorbent Morphology to Improve Packed Bed Performance.
All breakthrough curves are S-shaped (i.e., sigmoidal-shaped), where “sharper sigmoidal” shaped breakthrough curves more closely approach ideal plug-flow like shapes because of less intraparticle mass transport diffusion limitations. The shape of a breakthrough curve was represented as the equivalent length of the mass transfer zone (MTZ), or the operational time when the fraction of pollutant in the packed bed effluent (i.e., C/C0) ranges from 0.05 to 0.95.53 Reduced MTZ values have sharper sigmoidal-shaped breakthrough curves and allow a single packed-bed adsorption column to operate for an extended period (e.g., higher throughput) or with a shorter bed length while producing very low effluent arsenate. The breakthrough curve shape is crucial in full-scale system operations involving multiple packed-beds arranged in series or in parallel (see SI Text S3). As a result, shorter MTZs help maximize adsorbent utilization (i.e., higher L/kg throughput). 54
Adsorbent pore design can provide an opportunity to engineer material with a shorter MTZ by varying the intraparticle porosity of the material. To reduce intraparticle mass transport limitations, the intraparticle porosity of the adsorbent particle was increased to explore its impact on adsorbent performance. Increasing εp changed the breakthrough curve MTZ shape from a sigmoidal to a sharper sigmoidal shape, enabling a higher volume of water (BV10) to be treated in a shorter adsorbent column (e.g., a POU device). For the data presented in Figure 4, varying εp from 0.2 to 0.9 shortened the MTZ from 110,000 to only 26,000 bed volumes and increased BV10 from 9,100 to 31,600 bed volumes. Other highly porous adsorbents have been designed to maximize intraparticle porosity with the intention of minimizing the intraparticle mass transport limitations. For example, in prior work, ZrO2 spherical adsorbents with an εp of 0.92 achieve rapid mass transport for arsenate in packed bed adsorption columns.36 However, those authors observed a low structural integrity, specifically the friability of the highly porous adsorbent. Overall, while recognizing operational limitations (e.g., friability of highly porous sorbent), the consequence of increasing εp from 0.2 to 0.9 was a change from a sigmoidal to a sharper sigmoidal breakthrough curve shape, correlating with a 76% reduction in MTZ and a 71% increase in BV10.
Figure 4.

(a) Arsenate breakthrough curves for varied intraparticle porosity (εp) and tortuosity (τ), and (b) the interdependent relationship between bed volumes in the MTZ, BV10, DP, and εP for 100 ppb As(V), 10mM NaHCO3, and pH 8.5, simulated for an RSSCT design (4.0x1.1 cm) with a surface loading of 0.385 cm/s and an EBCT of 0.17 min.
Material scientists have created adsorbents with hierarchical pores, wherein porosity is controlled across length scales in hierarchical structures to induce advective flow through the adsorbent itself. This creates shorter length scales for diffusion into smaller-sized pores, and overall minimizing apparent intraparticle mass transport limitations.55–57 The SPDFR (Eq. 16) relationship links surface to pore diffusion, and low resulting SPDFR values indicate control by pore diffusion. While the PSDM accounts for advective flow outside particles within the packed bed, the PSDM does not simulate intraparticle convective flow improvements created by some hierarchical pore designs. However, to account for the net shorter diffusion paths the concept of enhanced intraparticle mass transport through strategies such as hierarchical designs was represented in silico using tortuosity (τ, Eq. 15) or labyrinth factor, which estimates the length of one path of pore space relative to the total length of potential paths.35 The interdependent relationship between MTZ, BV10, DP, and εp is shown in Figure 4b where increasing εp correlated with increasing BV10, BV in MTZ, and DP values. Figure S7 shows MTZ values from simulated breakthrough curves where both εp and τ varied. A 10x to 50x increase in DP (1.27x10−7 cm2/s (εp of 0.2) to 6.90x10−6 cm2/s (εp of 0.9)) changed the MTZ shape and resulted in a sharper sigmoidal breakthrough curve with a higher BV10. Overall, increasing intraparticle porosity mitigated intraparticle mass transport limitations with more favorable mass transport and thus created a productive pathway for improved adsorbent design for shorter column lengths such as in POU modules.
3.5. Impacts of Media Diameter and Hydraulic Loading Rate
More rapid intraparticle mass transport of arsenate can be achieved by using small diameter adsorbent media but comes at the expense of increased hydraulic pressure as water flows through packed beds. Increasing headloss can raise pumping energy requirements or cause physical compression of media with reduced material permeability.36,58 Figure S8a shows how headloss rapidly increased as media particle size decreased based on Darcy’s law for a range of hydraulic loading rates. Smaller particle diameters are often used in POU packed bed arsenic treatment systems (e.g., Model AD2710S 25cm long with 60x80 mesh size for E33) to limit headloss to less than 0.55 bar (8 psi). Larger particles (8x20 mesh size) used in full-scale drinking water systems for arsenic removal at higher flowrates have similar headloss of 0.34 bar (5 psi). Thus, within common operational flowrates selected to minimize headloss, a narrow range in adsorbent granular diameters were simulated in silico to understand mass transfer implications on arsenate breakthrough. Subsequent sections employ a pathway to maintain consistent bed volumes treated for a decreased column length, however pressure loss limitations must be considered.
To better understand how particle diameter influences breakthrough, Figure S8b shows arsenate breakthrough as function of particle diameter for 0.02 mm (60x80 mesh size) to 0.14 mm (8x20 mesh size) in a pilot scale system. The adsorbent mass in the column was constant for each simulation, resulting in constant capacity μg As/mg adsorbent). Smaller particle sizes (60x80 mesh size) achieved a BV10 value of 103,000 compared to 86,800 BV10 for larger particles (8x20 mesh size). The simulated effects of 60x80 vs 8x20 mesh size resulted in MTZ increase from 22,200 to 147,000 bed volumes. The smaller adsorbent granular size used in POU devices changed the breakthrough curve shape from a sigmoidal to a sharper sigmoidal shape, enabling more bed volumes treated for the same quantity of media within a shorter POU column.
Insights gained from these in silico simulations can be used to refine POU arsenic adsorbent devices for the purpose of rapid oxyanion removal to increase the number of BVT until reaching breakthrough. Physical design conditions for these new POU modules are shown in Figure S9. Figure 5a shows that engineering new adsorbents that can achieve double and triple the volume of water treated before reaching BV10 would require an increase in capacity (q) of 36% and 53%, respectively. An adsorbent material can also undergo intraparticle pore design, modifying the mass transport mechanism while maintaining a constant capacity. To understand how structural design, including porosity or particle diameter, could increase the baseline BV10 through mass transport kinetics, DP was increased to the maximum possible value (i.e., set DP=DL). This resulted in only a 1.6x increase in BV10 (see Text S4). SCM+PSDM simulated breakthrough curves for a POU system with an EBCT of 0.42 minutes (25 ppb As(V) and pH 8.5) showed that two to three times more bed volumes of water could be treated before exceeding an effluent 10 ppb arsenate level (i.e., BV10) by slightly increasing adsorbent capacity. Therefore, the simulation results suggest prioritizing enhancing adsorbent capacity (q) through improved surface reactivity in the design of new POU adsorbent materials rather than focusing on reducing mass transport limitations through intraparticle pore designs.
Figure 5.
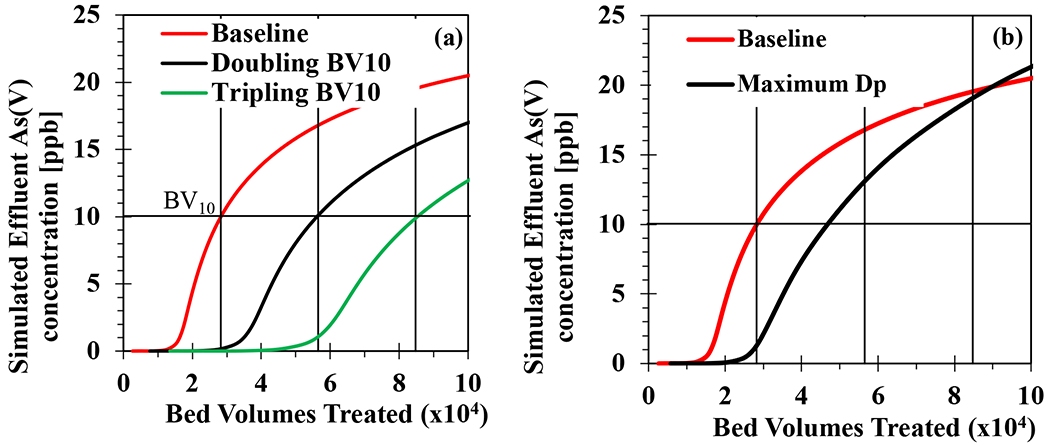
Simulated breakthrough curves for mesh size of 60x80 in a water chemistry of 25 ppb As(V) and pH 8.5 for a POU system with an EBCT of 0.42 minutes, configured to double and triple the bed volumes treated to achieve BV10 by (a) increasing adsorbent capacity and (b) increasing pore diffusivity (DP).
4. Summary and Conclusion
An in silico approach was successfully applied to commercial and new, yet-to-be synthesized, arsenate adsorbents by linking equilibrium SCM and mass transport simulating PSDMs. The models were validated with experimental data for commercial adsorbents E33 and GFH. Effects of pH and competing ions were well simulated for experimental batch and continuous flow packed bed data. The models accurately represented chromatographic displacement of more weakly bound surface complexes (As(V)) when in the presence of stronger complex formation (V(V)), which other studies have observed experimentally. Our in silico approach allowed rapid exploration of the most desirable material properties and found that increasing the site density by only 20% increased the capacity by 38%. By modifying a combination of SSD, surface area, and arsenate binding affinity, adsorbent capacity was 70% higher and almost doubled the BV10 compared to the baseline. Higher adsorbent capacities, like those simulated in our study, can be engineered by increasing SSD or increasing binding affinity of the target contaminant through synthesis of amorphous metal (hydr)oxide surface complexes.
The linked SCM+PSDM enabled exploration into the role of intraparticle pore design to minimize the MTZ and increase the volume treated until reaching regulatory limits for arsenic. We found that maximizing pore diffusion could increase BV10 by 1.6x for a POU system. Strategies to improve intraparticle mass transport limitation emerged as a critical factor for the design of adsorbent materials.59 Researchers should continue to pursue exploiting favorable mass transport dynamics through increased intraparticle porosity and hierarchical pore designs. Comparatively, adsorbent capacity only would require a 36% increase to double the amount of bed volumes treated. Because of the findings in this study, we recommend that adsorbent engineers pursue exploiting capacity through surface reactivity over intraparticle pore design to reduce mass transport limitations to achieve rapid oxyanion removal.
Our in silico approach can mitigate the need to demonstrate the impact of pH or changing water chemistries with a large number of batch and column tests. Our ongoing research a priori uses this in silico approach to determine amorphous metal (hydr)oxide mass loading into ceramic-like activated carbon block filters before conducting synthesis and experimental testing across a wide pH range. However, this integrated SCM+PSDM in silico approach still relies upon experimentation to fit surface complexation constants (Table 1) which have some inherent variability relative to experimental data (Figure 1). Therefore, the frontier of our in silico modeling will be to a priori select novel metal (hydr)oxide materials (e.g., mixed titanium plus rare earth element (hydr)oxides) by using molecular dynamics and density functional theory to a priori predict KEQ and protolysis constants (pK+, pK−) for Eq. 7– 11. This approach would be totally in silico and potentially revolutionize adsorbent design.
Supplementary Material
6. Acknowledgements
This work was partially funded by the Ira A. Fulton School of Engineering Dean’s Fellowship at Arizona State University, The National Institute of Environmental Health Sciences through the Metals and metal mixtures: Cognitive aging, remediation, and exposure sources (MEMCARE) center (#P42ES030990), and the Nanotechnology Enabled Water Treatment Center (NEWT) through the National Science Foundation (NSF) award (EEC-1449500). The original PSDM MATLAB® code was developed by Ron Hofmann (University of Toronto). Experimental batch, isotherm, and RSSCT data was provided by Lynn E. Katz (University of Texas at Austin) and Gerald E. Speitel (University of Texas at Austin). Laurel Passantino provided technical editing.
Footnotes
7. Supporting Information
Additional experimental and PSDM breakthrough curves, adsorption isotherms and Freundlich isotherm coefficients, parametrized PSDM input values, POU system configuration, and details on the Biot number.
5. Conflicts of Interest
The authors declare no conflict of interest.
8. References
- (1).Ramsay L; Petersen MM; Hansen B; Schullehner J; Van Der Wens P; Voutchkova D; Kristiansen SM Drinking Water Criteria for Arsenic in High-Income, Low-Dose Countries: The Effect of Legislation on Public Health. Environ Sci Technol 2021, 55 (6), 3483–3493. 10.1021/acs.est.0c03974. [DOI] [PubMed] [Google Scholar]
- (2).Allaire M; Wu H; Lall U National Trends in Drinking Water Quality Violations. Proc Natl Acad Sci U S A 2018, 115 (9), 2078–2083. 10.1073/pnas.1719805115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Brown KG; Ross GL Arsenic, Drinking Water, and Health: A Position Paper of the American Council on Science and Health. Regulatory Toxicology and Pharmacology 2002, 36 (2), 162–174. 10.1006/rtph.2002.1573. [DOI] [PubMed] [Google Scholar]
- (4).Höll WH Mechanisms of Arsenic Removal from Water. Environ Geochem Health 2010, 32 (4), 287–290. 10.1007/s10653-010-9307-9. [DOI] [PubMed] [Google Scholar]
- (5).Hering JG; Chen P-Y; Wilkie JA; Elimelech M; Liang S Arsenic Removal by Ferric Chloride. J Am Water Works Assoc 1996, 88 (4), 155–167. 10.1002/j.1551-8833.1996.tb06541.x. [DOI] [Google Scholar]
- (6).US EPA. 2006 Community Water System Survey Volume I: Overview; 2009. https://nepis.epa.gov/Exe/ZyPDF.cgi/P1009JJI.PDF?Dockey=P1009JJI.PDF. [Google Scholar]
- (7).Alfredo KA; Seidel C; Ghosh A; Roberson JA Using a Relative Health Indicator (RHI) Metric to Estimate Health Risk Reductions in Drinking Water. Environ Monit Assess 2017, 189 (3), 1–11. 10.1007/s10661-017-5815-8. [DOI] [PubMed] [Google Scholar]
- (8).Rosenblum JS; Liethen A; Miller-Robbie L Prioritization and Risk Ranking of Regulated and Unregulated Chemicals in US Drinking Water. Environ Sci Technol 2024, 58 (16), 6878–6889. 10.1021/acs.est.3c08745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Rudel HE; Lane MKM; Muhich CL; Zimmerman JB Toward Informed Design of Nanomaterials: A Mechanistic Analysis of Structure-Property-Function Relationships for Faceted Nanoscale Metal Oxides. ACS Nano 2020, 14 (12), 16472–16501. 10.1021/acsnano.0c08356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Pincus LN; Rudel HE; Petrović PV; Gupta S; Westerhoff P; Muhich CL; Zimmerman JB. Exploring the Mechanisms of Selectivity for Environmentally Significant Oxo-Anion Removal during Water Treatment: A Review of Common Competing Oxo-Anions and Tools for Quantifying Selective Adsorption. Environ Sci Technol 2020, 54 (16), 9769–9790. 10.1021/acs.est.0c01666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Badruzzaman M; Westerhoff P; Knappe DRU Intraparticle Diffusion and Adsorption of Arsenate onto Granular Ferric Hydroxide (GFH). Water Res 2004, 38 (18), 4002–4012. 10.1016/j.watres.2004.07.007. [DOI] [PubMed] [Google Scholar]
- (12).Hristovski KD; Markovski J Engineering Metal (Hydr)Oxide Sorbents for Removal of Arsenate and Similar Weak-Acid Oxyanion Contaminants: A Critical Review with Emphasis on Factors Governing Sorption Processes. Science of the Total Environment 2017, 598, 258–271. 10.1016/j.scitotenv.2017.04.108. [DOI] [PubMed] [Google Scholar]
- (13).Dabizha A; Bahr C; Kersten M Predicting Breakthrough of Vanadium in Fixed-Bed Absorbent Columns with Complex Groundwater Chemistries: A Multi-Component Granular Ferric Hydroxide–vanadate–arsenate–phosphate–silicic Acid System. Water Res X 2020, 9, 100061. 10.1016/j.wroa.2020.100061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Xu T; Wang Q; Wang Z; Catalano JG Effects of Phosphate Competition on Arsenate Binding to Aluminum Hydroxide Surfaces. ACS Earth Space Chem 2021, 5 (11), 3140–3149. 10.1021/acsearthspacechem.1c00239. [DOI] [Google Scholar]
- (15).Luo J; Yu D; Hristovski KD; Fu K; Shen Y; Westerhoff P; Crittenden JC Critical Review of Advances in Engineering Nanomaterial Adsorbents for Metal Removal and Recovery from Water: Mechanism Identification and Engineering Design. Environ Sci Technol 2021, 55 (8), 4287–4304. 10.1021/acs.est.0c07936. [DOI] [PubMed] [Google Scholar]
- (16).Nguyen VL; Chen W-H; Young T; Darby J Effect of Interferences on the Breakthrough of Arsenic: Rapid Small Scale Column Tests. Water Res 2011, 45 (14), 4069–4080. 10.1016/j.watres.2011.04.037. [DOI] [PubMed] [Google Scholar]
- (17).Badruzzaman M; Westerhoff P The Application of Rapid Small-Scale Column Tests in Iron-Based Packed Bed Arsenic Treatment Systems. In Advances in Arsenic Research; ACS Symposium Series, 2005; Vol. 915, pp 268–283. 10.1021/bk-2005-0915.ch019. [DOI] [Google Scholar]
- (18).Sperlich A; Schimmelpfennig S; Baumgarten B; Genz A; Amy G; Worch E; Jekel M Predicting Anion Breakthrough in Granular Ferric Hydroxide (GFH) Adsorption Filters. Water Res 2008, 42 (8–9), 2073–2082. 10.1016/j.watres.2007.12.019. [DOI] [PubMed] [Google Scholar]
- (19).Driehaus W; Jekel M; Hildebrandt U Granular Ferric Hydroxide—a New Adsorbent for the Removal of Arsenic from Natural Water. Journal of Water Supply: Research and Technology—AQUA 1998, 47 (1), 30–35. 10.2166/aqua.1998.0005. [DOI] [Google Scholar]
- (20).Westerhoff P; De Haan M; Martindale A; Badruzzaman M Arsenic Adsorptive Media Technology Selection Strategies. Water Quality Research Journal 2006, 41 (2), 171–184. 10.2166/wqrj.2006.020. [DOI] [Google Scholar]
- (21).Lalley J; Han C; Mohan GR; Dionysiou DD; Speth TF; Garland J; Nadagouda MN Phosphate Removal Using Modified Bayoxide® E33 Adsorption Media. Environ Sci (Camb) 2015, 1 (1), 96–107. 10.1039/c4ew00020j. [DOI] [Google Scholar]
- (22).Badruzzaman M. Mass Transport Scaling and the Role of Silica on Arsenic Adsorption onto Porous Iron Oxide (Hydroxide). Annu Rev Plant Biol 2005, 42 (1), 665–700. 10.1146/annurev-arplant-050718-100353. [DOI] [Google Scholar]
- (23).Speitel G; Katz L; Chen C-CC; Stokes S; Westerhoff PK; Shafieian P Surface Complexation and Dynamic Transport Modeling of Arsenic Removal on Adsorptive Media. Water Research Foundation 2010. [Google Scholar]
- (24).Yates DE The Structure of the Oxide/Aqueous Electrolyte Interface, 1975. http://hdl.handle.net/11343/39411 (accessed 2024-07-20).
- (25).van den Hul HJ; Lyklema J Determination of Specific Surface Areas of Dispersed Materials. Comparison of the Negative Adsorption Method with Some Other Methods; UTC, 1968; Vol. 281. https://pubs.acs.org/sharingguidelines. [Google Scholar]
- (26).Nomaan SM; Stokes SN; Han J; Katz LE Application of Spectroscopic Evidence to Diffuse Layer Model (DLM) Parameter Estimation for Cation Adsorption onto Ferrihydrite in Single- and Bi-Solute Systems. Chem Geol 2021, 573, 120199. 10.1016/j.chemgeo.2021.120199. [DOI] [Google Scholar]
- (27).Davis JA; Leckie JO Surface Ionization and Complexation at the Oxide/Water Interface II. Surface Properties of Amorphous Iron Oxyhydroxide and Adsorption of Metal Ions. J Colloid Interface Sci 1978, 67 (1), 90–107. 10.1016/0021-9797(78)90217-5. [DOI] [Google Scholar]
- (28).Radu T; Subacz JL; Phillippi JM; Barnett MO Effects of Dissolved Carbonate on Arsenic Adsorption and Mobility. Environ Sci Technol 2005, 39 (20), 7875–7882. 10.1021/es050481s. [DOI] [PubMed] [Google Scholar]
- (29).Williams R. PKa Values in Water Compilation. ACS Division of Organic Chemistry 2022, 1–33. [Google Scholar]
- (30).Kersten M; Karabacheva S; Vlasova N; Branscheid R; Schurk K; Stanjek H Surface Complexation Modeling of Arsenate Adsorption by Akageneite (β-FeOOH)-Dominant Granular Ferric Hydroxide. Colloids Surf A Physicochem Eng Asp 2014, 448 (1), 73–80. 10.1016/j.colsurfa.2014.02.008. [DOI] [Google Scholar]
- (31).Nelson H; Sjöberg S; Lövgren L Surface Complexation Modelling of Arsenate and Copper Adsorbed at the Goethite/Water Interface. Applied Geochemistry 2013, 35, 64–74. 10.1016/j.apgeochem.2013.03.007. [DOI] [Google Scholar]
- (32).Dzombak D; Morel F Surface Complexation Modeling: Hydrous Ferric Oxide; John Wiley & Sons, 1990. [Google Scholar]
- (33).Sperlich A; Werner A; Genz A; Amy G; Worch E; Jekel M Breakthrough Behavior of Granular Ferric Hydroxide (GFH) Fixed-Bed Adsorption Filters: Modeling and Experimental Approaches. Water Res 2005, 39 (6), 1190–1198. 10.1016/j.watres.2004.12.032. [DOI] [PubMed] [Google Scholar]
- (34).Farsad A; Niimi K; Ersan MS; Gonzalez-Rodriguez JR; Hristovski KD; Westerhoff P Mechanistic Study of Arsenate Adsorption onto Different Amorphous Grades of Titanium (Hydr)Oxides Impregnated into a Point-of-Use Activated Carbon Block. ACS ES&T Engineering 2023, 3 (7), 989–1000. 10.1021/acsestengg.3c00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Sontheimer H; Frick BR; Fettig J; Hubele C; Zimmer G Activated Carbon for Water Treatment, 2nd Editio.; DVGW-Forschungsstelle, 1988. [Google Scholar]
- (36).Hristovski KD; Westerhoff PK; Crittenden JC; Olson LW Arsenate Removal by Nanostructured ZrO2 Spheres. Environ Sci Technol 2008, 42 (10), 3786–3790. 10.1021/es702952p. [DOI] [PubMed] [Google Scholar]
- (37).Dale S; Markovski J; Hristovski KD Modeling Packed Bed Sorbent Systems with the Pore Surface Diffusion Model: Evidence of Facilitated Surface Diffusion of Arsenate in Nano-Metal (Hydr)Oxide Hybrid Ion Exchange Media. Science of the Total Environment 2016, 563-564, 965–970. 10.1016/j.scitotenv.2015.11.176. [DOI] [PubMed] [Google Scholar]
- (38).Hand DW; Crittenden JC; Thacker WE Simplified Models for Design of Fixed-Bed Adsorption Systems. Journal of Environmental Engineering 1984, 110 (2), 440–456. 10.1061/(ASCE)0733-9372(1984)110:2(440). [DOI] [Google Scholar]
- (39).Crittenden JC; Berrigan JK; Hand DW; Lykins B Design of Rapid Fixed-Bed Adsorption Tests for Nonconstant Diffusivities. Journal of Environmental Engineering 1987, 113 (2), 243–259. 10.1061/(asce)0733-9372(1987)113:2(243). [DOI] [Google Scholar]
- (40).Jain A; Sharma VK; Mbuya OS Removal of Arsenite by Fe(VI), Fe(VI)/Fe(III), and Fe(VI)/Al(III) Salts: Effect of PH and Anions. J Hazard Mater 2009, 169 (1–3), 339–344. 10.1016/j.jhazmat.2009.03.101. [DOI] [PubMed] [Google Scholar]
- (41).Klas S; Kirk DW Advantages of Low PH and Limited Oxygenation in Arsenite Removal from Water by Zero-Valent Iron. J Hazard Mater 2013, 252-253, 77–82. 10.1016/j.jhazmat.2013.02.044. [DOI] [PubMed] [Google Scholar]
- (42).Huang X; Hou X; Song F; Zhao J; Zhang L Facet-Dependent Cr(VI) Adsorption of Hematite Nanocrystals. Environ Sci Technol 2016, 50 (4), 1964–1972. 10.1021/acs.est.5b05111. [DOI] [PubMed] [Google Scholar]
- (43).Zheng C; Zhong W; Yan L; Jing C Facet-Dependent Atomic Distances Shape Vanadate Adsorption Complexes on Hematite Nanocrystals. Langmuir 2023, 39 (3), 949–956. 10.1021/acs.langmuir.2c02192. [DOI] [PubMed] [Google Scholar]
- (44).Cao S; Zhang X; Huang X; Wan S; An X; Jia F; Zhang L Insights into the Facet-Dependent Adsorption of Phenylarsonic Acid on Hematite Nanocrystals. Environ Sci Nano 2019, 6 (11), 3280–3291. 10.1039/c9en00879a. [DOI] [Google Scholar]
- (45).Pierce ML; Moore CB Adsorption of Arsenite and Arsenate on Amorphous Iron Hydroxide. Water Res 1982, 16 (7), 1247–1253. 10.1016/0043-1354(82)90143-9. [DOI] [Google Scholar]
- (46).Chen H; Davis CC; Edwards M Using Surface Complexation Modeling to Assess the Role of Silica in Arsenate Adsorption onto Metal Oxides. Journal of Water Supply: Research and Technology-Aqua 2005, 54 (6), 339–348. 10.2166/aqua.2005.0032. [DOI] [Google Scholar]
- (47).Buerge-Weirich D; Behra P; Sigg L Adsorption of Copper, Nickel, and Cadmium on Goethite in the Presence of Organic Ligands. Aquat Geochem 2003, 9 (2), 65–85. 10.1023/B:AQUA.0000019455.82756.ac. [DOI] [Google Scholar]
- (48).Gunneriusson L; Sjoberg S Surface Complexation in the H+ −Goethite (a-FeOOH) - Hg(II) - Chloride System. J Colloid Interface Sci 1993, 156, 121–128. [Google Scholar]
- (49).Hameed AM Synthesis of Si/Cu Amorphous Adsorbent for Efficient Removal of Methylene Blue Dye from Aqueous Media. J Inorg Organomet Polym Mater 2020, 30 (8), 2881–2889. 10.1007/s10904-019-01436-1. [DOI] [Google Scholar]
- (50).Gai WZ; Zhang SH; Yang Y; Zhang X; Deng ZY Separation of Excess Fluoride from Water Using Amorphous and Crystalline AlOOH Adsorbents. ACS Omega 2021, 6 (25), 16488–16497. 10.1021/acsomega.1c01620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Sujana MG; Soma G; Vasumathi N; Anand S Studies on Fluoride Adsorption Capacities of Amorphous Fe/Al Mixed Hydroxides from Aqueous Solutions. J Fluor Chem 2009, 130 (8), 749–754. 10.1016/j.jfluchem.2009.06.005. [DOI] [Google Scholar]
- (52).Yokoyama T; Ueda A; Kato K; Mogi K; Matsuo S A Study of the Alumina-Silica Gel Adsorbent for the Removal of Silicic Acid from Geothermal Water: Increase in Adsorption Capacity of the Adsorbent Due to Formation of Amorphous Aluminosilicate by Adsorption of Silicic Acid. J Colloid Interface Sci 2002, 252 (1), 1–5. 10.1006/jcis.2002.8382. [DOI] [PubMed] [Google Scholar]
- (53).Al Mesfer MK; Danish M; Khan MI; Ali IH; Hasan M; Jery A. El. Continuous Fixed Bed CO2 Adsorption: Breakthrough, Column Efficiency, Mass Transfer Zone. Processes 2020, 8 (10), 1–16. 10.3390/pr8101233. [DOI] [Google Scholar]
- (54).Kearns J; Krupp A; Diek E; Mitchell S; Dossi S; Hartman S Lead-Lag Series and Staged Parallel Operational Strategies Improve the Performance and Cost-Effectiveness of Bonechar for Control of Fluoride in Groundwater. Journal of Water Sanitation and Hygiene for Development 2018, 8 (4), 777–784. 10.2166/washdev.2018.111. [DOI] [Google Scholar]
- (55).Yang XY; Chen LH; Li Y; Rooke JC; Sanchez C; Su BL Hierarchically Porous Materials: Synthesis Strategies and Structure Design. Chemical Society Reviews. Royal Society of Chemistry January 21, 2017, pp 481–558. 10.1039/c6cs00829a. [DOI] [PubMed] [Google Scholar]
- (56).Ouimet JA; Xu J; Flores - Hansen C; Phillip WA; Boudouris BW Design Considerations for Next-Generation Polymer Sorbents: From Polymer Chemistry to Device Configurations. Macromol Chem Phys 2022, 223 (16). 10.1002/macp.202200032. [DOI] [Google Scholar]
- (57).Xu J; Slykas C; Braegelman AS; Alvarez KG; Kasl T; Boudouris BW; Webber MJ; Sharma V; Phillip WA Heavy Metal Removal Using Structured Sorbents 3D Printed from Carbon Nanotube-Enriched Polymer Solutions. Matter 2022, 5 (10), 3432–3451. 10.1016/j.matt.2022.07.012. [DOI] [Google Scholar]
- (58).Worch E. Adsorption Technology in Water Treatment; De Gruyter, 2012. 10.1515/9783110240238. [DOI] [Google Scholar]
- (59).Furusawa T; Smith JM Intraparticle Mass Transport in Slurries by Dynamic Adsorption Studies. AIChE Journal 1974, 20 (1), 88–93. 10.1002/aic.690200111. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


