Effect of magnetized water on the fundamental grouting properties of cement grout under varying magnetization conditions

Abstract

The development and modification of grouting materials constitute crucial factors influencing the effectiveness of grouting. Given the pivotal role of water in the hydration of cement-based composite materials and construction processes, this study proposes an exploratory approach using green, economical magnetized water technology to enhance the performance of cement grouts. The research systematically investigates the effects of magnetized water on the fundamental grouting properties (stability, rheological behavior, and stone body strength) of cement grouts, prepared under varying magnetization conditions (including magnetic intensity, water flow speed, and cycle times). Through the conduct of specific physicochemical tests on water, the study elucidates the mechanism through which magnetized water influences these properties. The results indicate that magnetized water positively impacts the stability of cement grouts, significantly reducing their absolute viscosity, apparent viscosity, plastic viscosity, and yield stress, thus markedly affecting the rheological characteristics of the cement grouts. Additionally, magnetized water notably enhances the flexural and compressive strength of the cement grout stone body, with a particularly significant improvement in early strength. From a quantum mechanics perspective, a magnetization mechanism based on the competition between the strengthening of hydrogen bonds between water molecule clusters and the weakening or breaking of hydrogen bonds within clusters is introduced, providing a theoretical basis for explaining the variability observed in water magnetization experiments.

Introduction

Grouting technology plays a crucial role in various engineering fields, including civil engineering, water conservancy, transportation, mining, and environmental remediation^1–4. This technology is widely applied in civil engineering due to its practicality, safety, cost-effectiveness, minimal equipment requirements, short construction period, and low environmental impact. Applications range from tunnel rock reinforcement and structural enhancement to foundation treatment and building lifting and rectification^5–7. One of the key factors influencing grouting effectiveness is the choice of grouting materials, whose development and modification are essential for the continuous advancement of grouting technology. To meet the diverse performance requirements in engineering practice, various grouting materials, including cement-based, chemical, and biological types, have been developed. Examples include cement grouts, polymer-modified cement grouts, chemical solutions, and microbial grouting materials^8–11. Among these, cement-based grouting materials are the most widely used in civil engineering¹², due to their low cost, abundant availability, and simple preparation process.

Cement-based grouting materials aim to improve grout performance, expand engineering applications, and enhance grouting effectiveness while adhering to the principles of green economic sustainability. The development of environmentally friendly and high-performance grouting materials is a key focus in this field. To enhance the grouting performance of cement-based materials, extensive research has been conducted, yielding significant results^13–21. Nguyen et al.¹⁴ emphasized that high stability, fluidity, and hardened strength are fundamental performance requirements for cement-based grouts in various engineering applications. Improving the rheological and stability properties of grout is crucial for the continuous advancement of grouting technology^22. Additionally, numerous studies on the rheological properties of cement-based grouts have demonstrated their critical impact on grouting effectiveness. For instance, references^23,24 indicate that the bleeding and settlement stability of cement grouts should be well-controlled, as excessive bleeding and settlement instability can lead to incomplete grouting, thereby compromising reinforcement and seepage control. Cinar et al.^25,26 found that the rheological properties of cement-based grouts determine their final diffusion state within the soil or rock mass, and that these rheological parameters are crucial for grouting design and effectiveness prediction²⁷, serving as prerequisites for successful grouting design and implementation²⁸. In the context of seepage control and reinforcement, the compressive strength of the cement grout stone body is a key factor in evaluating the mechanical properties, durability, and overall effectiveness of the grouted composite structure, as well as in selecting construction design parameters. The importance of stone body strength, as a core mechanical indicator for assessing the performance of cement-based grouting materials, cannot be overlooked²⁹. In practical applications of grouting technology, clearly and accurately assessing the strength of cement-based material grout stone is a crucial step to ensure the effectiveness of engineering applications, optimize construction designs, and enhance the quality and durability of the project. Therefore, stability, rheological properties, and strength of cement-based grout are essential grouting properties that cement-based grout must possess in grouting engineering. The determination of these properties is a crucial step in engineering applications.

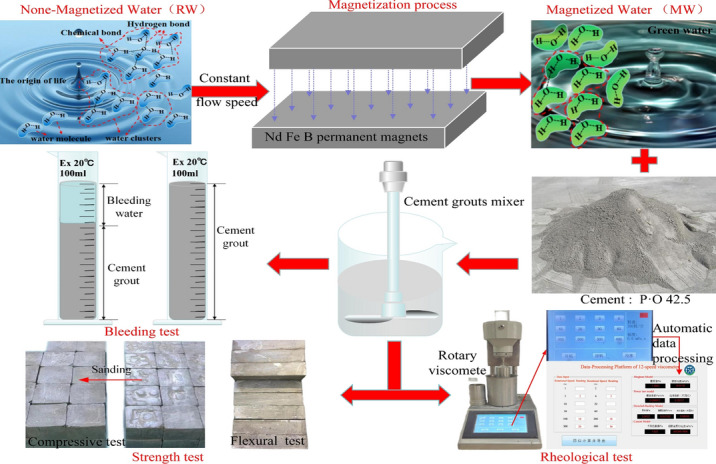
Water plays a crucial role in the hydration of cement and the construction process of cement-based composites. Typically, easily accessible and clean tap water (TW) is used as mixing water. The scarcity of water for cement-based materials highlights the importance of optimizing water usage. The chemical and physical structure of water directly affects the mechanical properties of cement-based materials, including workability and compressive strength, which has become a key issue of global concern³⁰. Magnetized water (MW), as a green technology, has been widely applied in various engineering fields^31,32. When water is exposed to a static magnetic field or passes through a magnetic field at a certain speed, its physical and chemical properties change, resulting in MW^33–35. In the field of civil engineering, extensive research has shown that concrete mixed with MW exhibits advantages such as improved workability, higher strength, reduced environmental pollution, lower costs, and reduced use of chemical admixtures^36–44. For instance, Ghorbani et al. used MW to prepare foamed concrete, and the results showed significant improvements in the stability, mechanical properties, and durability of cement-based composites^40,41. Similarly, The preparation of self-compacting concrete containing volcanic ash using MW, as demonstrated by Gholhaki et al., not only enhances the workability and strength of the concrete but also reduces the usage of water-reducing agents by up to 45%⁴². Wei et al. found that ordinary concrete mixed with MW exhibited improved crack resistance, compressive strength, splitting tensile strength, and fluidity⁴³. Additionally, some studies have pointed out that placing cement paste in a static magnetic field can accelerate the hydration rate of cement, resulting in a denser cement stone structure with higher compressive strength⁴⁴. Given that magnetic fields or MW can enhance the workability and strength of cement-based materials, using magnetically treated water as a means to improve the performance of cement-based composites is economical, environmentally friendly, and straightforward. Compared to the use of complex, expensive, and potentially environmentally harmful admixtures or additives, mixing cement-based slurry with low-cost, simple-to-process green MW has become a focus for in-depth exploration regarding changes in fundamental grouting performance. However, to the author’s knowledge, research on the use of MW to mix cement-based grout is extremely scarce. Therefore, this research, based on the widespread application of cement-based slurry materials in grouting engineering, proposes an exploratory study of the use of MW to prepare cement grout (without admixtures) and investigates the impact of MW on the fundamental grouting properties of cement grout.

A comprehensive review of the literature on the magnetization of water and its effects on the performance of cement-based materials reveals that magnetic induction intensity, magnetization duration, and water flow speed are key factors influencing the magnetization effect^{30–34,45–47}. Additionally, previous research indicates that understanding the stability, rheological properties, and strength of cement grout is fundamental for its application in grouting, as well as for grouting design, quality control, and performance prediction. This research focuses on the impact of MW, prepared under various magnetization conditions (including magnetic induction strength, water flow velocity, and cycle times), on the stability and rheological properties of cement grouts with different water-to-cement (w/c) ratios, as well as the strength of the cement grout stone body at different curing ages. Furthermore, by combining the physicochemical characteristics of MW under various conditions with the current understanding of magnetization mechanisms, the influence mechanism of MW on cement grout is explored. The aim is to provide a scientific basis for the application of MW in grouting engineering.

Experimental design

Materials

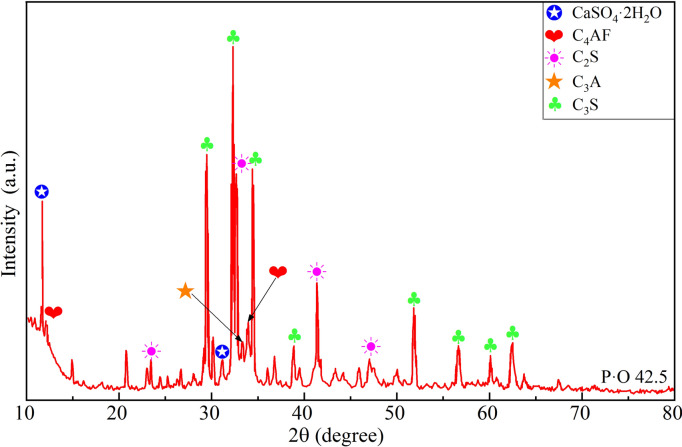
The cement used in this research was P.O 42.5 ordinary Portland cement from the same batch produced by Southern Cement Co., Ltd. (Changsha, China). To ensure the quality of the cement remained unaffected by environmental factors, it was stored in vacuum-sealed bags. The performance parameters of this cement are listed in Table 1. As shown in Fig. 1, the X-ray diffraction (XRD) pattern of the cement indicates that the total content of the minerals C₃S, C₂S, C₃A, and C₄AF exceeds 95%, with C₃S being the most abundant, comprising approximately half of the total mineral content. The harmful components SO₃ and Cl^– in this cement are present at levels of 1.25% and 0.03%, respectively. Laser particle size analysis reveals that the particle size of the cement ranges from 0.5 to 187.65 μm, with a majority of particles concentrated in the 1–80 μm range, and over 99% of the particles are smaller than 80 μm.

Table 1.

Partial performance parameters of P.O 42.5 Portland cement.

	Specific surface area (m2/kg)	Loss on ignition (%)	Slag content (%)	Alcoholamine grinding aids (%)	Initial setting time (min)	Final setting time (min)	Alkali content (%)	Soundness
P.O 42.5	356	2.76	9.5	0.1	176	335	0.4	Qualified
Standard	≥ 300	≤ 5.0	5.0 ~ 20.0	≤ 0.5	≥ 45	≤ 600	0.6	Qualified

Fig. 1.

The XRD pattern of P.O 42.5 Portland Cement.

The water used in the experiments was sourced from the tap water (TW) supply at Central South University. It was stored in a reservoir bucket and left to stand in a temperature-controlled room for over 48 h to ensure a constant water temperature, allow for the settling of impurities, and the removal of chlorine. The water quality parameters of the tap water are provided in Table 2.

Table 2.

The quality of TW.

Items	Turbidity (NTU)	Free residual chlorine (mg/L)	Total Hardness (CaCO3)	Oxygen consumption (mg/L)	PH	Iron content (mg/L)	Manganese content (mg/L)	Aluminum content (mg/L)	Colority
Test value	0.16	0.18	107	0.99	7.14	< 0.05	< 0.05	0.035	< 5
Standard	< 3	0.3 ~ 4	< 450	< 5	6.5 ~ 8.5	< 0.3	< 0.1	< 0.2	< 15

Oxygen consumption was calculated by O₂ using CODMn method; Lead content < 0.004 (mg/L); Cadmium content < 0.0002 (mg/L); Mercury content < 0.0001 (mg/L); Selenium content < 0.001 (mg/L); Arsenic content: 0.001 (mg/L). The standard is the Chinese standard.

The Magnetization system

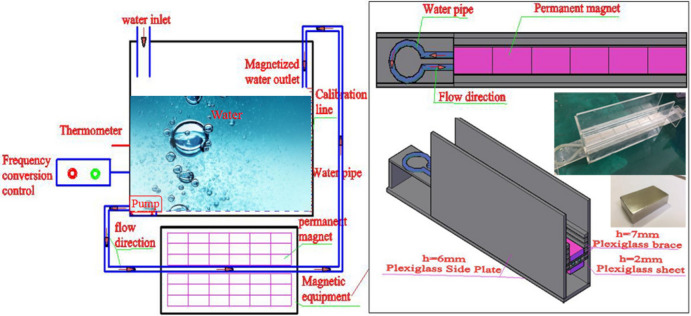
As evident from reviews^30–34, MW can be obtained via placement of water in a static magnetic field or via passage of water through the magnetic field area in the form of a water flow. In most studies on the engineering applications of MW, the magnetization of water for mixing cement-based materials is achieved by passing water through a magnetic field. Control conditions such as water flow velocity, magnetic induction intensity, cycle times, or magnetization time are adjusted to study the effects of MW on the engineering performance of cement-based materials^{35,39–43,47}. The authors of this paper have successfully developed magnetization equipment and applied it in preliminary research, as illustrated in Fig. 2. For more specific details, refer to references^48,49.

Fig. 2.

The magnetization system^48,49.

Experimental parameter design

In the magnetization treatment of water, magnetic induction intensity, water flow speed, circulation frequency, and magnetization time can all be controlled variables. Based on previous research findings, this study selects magnetic induction strength (B), water flow speed (v), and cycle times (n) as the key control parameters for MW, with specific magnetization conditions detailed in Table 3. It is important to note that the control values listed in Table 3 are not necessarily used in every test; the specific values are chosen based on the research requirements and will be emphasized and explained in the testing procedure section. To assess the impact of MW on cement grout and its physicochemical properties, results from tests using non-magnetized water (regular tap water) and its corresponding cement grouts are used as control groups. Given the significant effect of temperature on the performance of grout, all experiments are conducted in a temperature-controlled room, maintaining the environmental temperature at 20 ± 1 °C, and the actual temperature of the cement slurry is recorded for each test.

Table 3.

Experimental parameters.

Magnetic intensity B (mT)	Flow speed v (m/s)	Cycle times n	Water/cement ratio w/c
0	0	0	0.5/ 0.8/ 1.0
136	0.75	1
261	1.5	5
656	2.75	10

Testing methods and procedures for fundamental grouting performance

The preparation method of grout has a significant impact on the test results of slurry performance. An NJ-160A planetary cement mixer (manufactured in Jiangsu, China) was used to mix the cement slurry. The mixer was set to automatic mixing, which involved pouring cement into the mixing container after adding water, followed by initial rapid mixing (with revolution and rotation speeds of 125 ± 10 and 285 ± 10 r/min, respectively) for 120 s. There was a 15-s pause to scrape the slurry splashed onto the container walls back into the container, and then slow mixing (with revolution and rotation speeds of 62 ± 5 and 140 ± 10 r/min, respectively) for another 120 s. The specific performance parameters of the mixer can be found in the authors’ previous research reports^48,49.

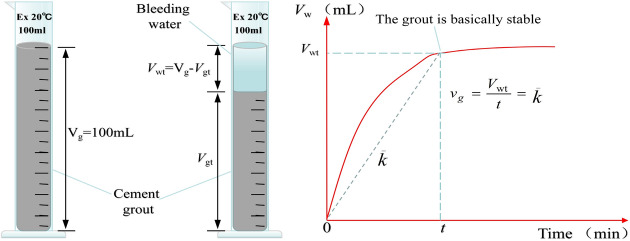
The stability of the cement grouts was evaluated through a bleeding test. Grouts with w/c = 0.5 and 1.0 were used to represent high-consistency and low-consistency grouts, respectively. This approach was employed to investigate the effects of MW under different conditions on the stability performance of cement grouts with varying consistencies. Upon completion of mixing the cement grout, it was immediately poured through a funnel into a 100 mL graduated cylinder (with a graduation value of 1 mL) to the 100 mL mark (Fig. 3). The particles in the grout began to settle, and the thickness of the clear water layer gradually increased from top to bottom. A stopwatch was used to time the process, ensuring that the ambient temperature remained at 20 ± 1 °C. The volume of water (V_w) was recorded every 10 min until it stabilized, at which point the test was concluded. The average measurement from five samples was taken as the final test result, and the data were plotted as a bleed water volume-time growth curve. All the bleed water volume-time growth curves exhibit two main characteristics: the growth curve passes through the origin; there is a rapid increase in the early stages, followed by a slower growth rate, eventually stabilizing into a semi-"C" shape. For more detailed information, refer to the author’s previous research⁴⁹. Swiss scholar Lombardi was the first to propose a classification standard for grout types⁵⁰, a standard that has been consistently applied in grouting engineering. This standard categorizes grouts into two types based on stability; however, it does not quantify the degree of stability, meaning it cannot differentiate the stability levels within stable or unstable grouts. Currently, there are various methods for evaluating grout stability, which presents challenges when selecting stability assessment indicators⁵¹. These methods can be broadly categorized into two types: direct measurement methods, which strictly adhere to the definition of grout stability by using the final bleed time (or its equivalent, such as the bleed rate) as the evaluation criterion, with the bleed test being the most classic method; and indirect measurement methods, which typically use the bleed rate or sedimentation rate as indicators of grout stability. From the strict definition of grout stability, indirect measurement methods are not directly applicable for evaluating grout stability. However, some scholars argue that the parameters selected by indirect methods are directly related to grout stability⁵², and can be considered equivalent to time-based direct measurement methods, though this hypothesis lacks scientific validation. Therefore, in this study, the bleed rate (v_g) is used to reflect the stability of the grout, calculated as the ratio of the stabilized bleed water volume to the corresponding time, with the unit expressed as mL/min. As shown in Fig. 4, the v_g is determined by the average slope of the relatively stable portion of the bleed water volume-time curve. The smaller the bleed rate, the better the stability of the grout. To better assess the impact of MW on the stability of the cement grout, the relative variation ratio (θ) is introduced as an indicator, which can be expressed as:

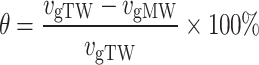1

Fig. 3.

The performance testing of cement grouts.

Fig. 4.

Determination of the water bleeding rate of the grout.

Here, v_gTW and v_gRW represent the bleed rates of the grout prepared with regular TW and MW, respectively. A positive θ value indicates that MW has a positive effect on the stability of the cement grout, whereas a negative value suggests an adverse impact.

The determination of the rheological properties of cement grout primarily involves identifying its flow behavior (the relationship between shear stress and shear rate, expressed through a mathematical equation), plastic viscosity, apparent viscosity, and yield stress. Cement-based grout materials can be categorized into different rheological models based on various constitutive equations, including the Bingham model, Power Law model, Herschel-Bulkley model, and Carson model⁵³. The rotational viscometer method is the most widely used technique for measuring the rheological properties of cement-based grouts (such as apparent viscosity, absolute viscosity, plastic viscosity, yield stress, dynamic yield stress, and static yield stress)^12,22,25. The test results can be used to evaluate the viscosity, rheology, and thixotropy of the grout. Therefore, this study employs the ZNN-12D digital rotational viscometer with rotational speeds set at 1, 2, 3, 6, 10, 20, 30, 60, 100, 200, 300, and 600 r/min (Fig. 3). The well-mixed slurry was poured into the rheological test measuring cup, and gently stirred with a glass rod to prevent segregation of the high w/c ratio slurry. The measuring cup was then quickly installed to commence the rheological test, ensuring that the slurry reached a relatively stable state before testing. Considering the impact of the hydration process of the freshly mixed slurry on its rheological properties and parameters, it was necessary to minimize the testing time. Therefore, we accurately controlled the duration for each shear rate according to the experimental protocol. The test at a specific shear rate was completed when the viscosity value stabilized for 5 s or the fluctuation was within ± 2 mPa·s after reaching that shear rate, followed immediately by the viscosity test at the next shear rate. This viscometer enables precise measurement of various rheological parameters for non-Newtonian fluids, and the data obtained from multiple measurements can be used to plot rheological curves to determine the flow behavior of cement grout during the flow process. Therefore, a data fitting and parameter determination platform based on Matlab software was independently developed for the ZNN-12D digital viscometer, as shown in Fig. 3. This platform allows for the rapid acquisition of rheological parameters and the goodness of fit for various rheological models based on the viscometer’s test readings. Data fitting was performed for the Bingham model, Power–Law model, Herschel–Bulkley (H–B) model, and Carson model, with each data value representing the mean of three independent parallel test results. A comparative analysis was conducted to evaluate the fitting performance of each model, and the impact of MW on the rheological parameters of the cement grout was determined.

Currently, in the field of grouting engineering, there is no standardized method or guideline for testing the strength of cement-based grout bodies. Referring to ASTM-C438 and ASTM-C439, compressive and flexural strength tests were conducted on the cement grout stone. After the cement grout is mixed, it is poured into cement mortar cube molds (with dimensions of 70.7 mm × 70.7 mm × 70.7 mm) and prism molds (with dimensions of 40 mm × 40 mm × 160 mm) to form the test specimens, as shown in Fig. 5a. These specimens are then placed in a standard curing chamber for curing according to standard procedures, as shown in Fig. 5b. After demolding, the specimens are kept in the standard curing room until they reach the specified curing ages of 3, 7, and 28 days, after which the strength tests are conducted. During the solidification of the cement grout, due to significant bleeding and natural settlement under atmospheric pressure, the height of the molded specimens varies and is often less than 70.7 mm and 40 mm for different w/c. Additionally, when the grout is relatively thin, the upper surface of the specimens may be rough and uneven. Therefore, for specimens with the same w/c, sandpaper or a steel saw blade is used to grind them to uniform dimensions, and the dimensions of the specimens are measured with a caliper. For cube and prism specimens with w/c of 0.5, 0.8, and 1.0, the ground dimensions were determined through experimentation. Specifically, the ground heights for cube and prism specimens with a w/c of 0.5 are 68 mm and 38 mm, respectively; for a w/c of 0.8, the heights are 55 mm and 31 mm; and for a w/c of 1.0, the heights are 48 mm and 27 mm, respectively. Six parallel specimens were prepared under each condition for analysis. After grinding, the specimen surfaces were kept moist but free of visible water before immediately conducting the flexural and compressive strength tests, as shown in Fig. 5c.

Fig. 5.

Strength testing process.

The rheological properties and grout stone strength of cement grout with w/c of 0.5, 0.8, and 1.0 were studied to investigate the effects of MW on these properties under different magnetization conditions. The rheological behavior and strength performance of cement grout prepared with MW were compared with those of cement grout (mixed with TW) with the same w/c, which served as the control group. The preparation methods for both the MW cement grout and the control group were identical. The magnetization control conditions and parameter values for the water are detailed in Table 3. An orthogonal experimental design was employed, using an L9(3⁴) orthogonal array with three factors and three levels, as shown in Table 4. Experiments were conducted to assess the rheological properties and strength performance of cement grout prepared with MW under various magnetization control conditions.

Table 4.

Orthogonal experiment design for magnetic treatment of tap water.

No.	Magnetization control conditions			Specific Magnetization Parameters B (mT); v (m/s); n
	Magnetic intensity B (mT)	Flow speed v (m/s)	Cycle times n
1	1 (B1)	1 (v1)	1 (n1)	B1 = 136; v1 = 0.75; n1 = 1
2	1 (B1)	2 (v2)	2 (n2)	B1 = 136; v2 = 1.50; n2 = 5
3	1 (B1)	3 (v3)	3 (n3)	B1 = 136; v3 = 2.75; n3 = 10
4	2 (B2)	1 (v1)	2 (n2)	B2 = 261; v1 = 0.75; n2 = 5
5	2 (B2)	2 (v2)	3 (n3)	B2 = 261; v2 = 1.50; n3 = 10
6	2 (B2)	3 (v3)	1 (n1)	B2 = 261; v3 = 2.75; n1 = 1
7	3 (B3)	1 (v1)	3 (n3)	B3 = 656; v1 = 0.75; n3 = 10
8	3 (B3)	2 (v2)	1 (n1)	B3 = 656; v2 = 1.50; n1 = 1
9	3 (B3)	3 (v3)	2 (n2)	B3 = 656; v3 = 2.75; n2 = 5

Testing methods and procedures for the physicochemical properties of water

The current research on MW indicates that there are numerous physicochemical property indicators. In this study, we focus on testing the physicochemical properties that are relatively easy to obtain and hold significant reference value. These include the measurement of electrical conductivity, pH value, salt solubility, and the constant temperature evaporation rate.Existing research has pointed out that the magnetic memory effect of water can last from a few hours to several days^30,31. Therefore, the resting time of MW (3–10 min) can be considered negligible in its impact on the physicochemical properties. Given that temperature significantly affects the physicochemical properties of water, it is essential to ensure that the temperature difference of the water samples remains below 0.2 °C during testing. Five cups of MW and five cups of TW were used to create a total of 10 test samples. The samples were labeled at the bottom of the cups, randomized, and placed on the test bench for blind testing of physicochemical properties. The tests were conducted in the following order: electrical conductivity, pH value, and salt solubility. Additionally, another set of five cups of MW and five cups of TW were used for the blind test of constant temperature evaporation. The mean values of the evaporation rates for both MW and TW were calculated separately and used as the final test results.

The current methods for testing water’s electrical conductivity, pH value, and salt solubility are quick, reliable, and accurate, making them suitable for verifying changes in water’s properties after magnetization. For the electrical conductivity test, the CT3030 conductivity meter (Shenzhen, China) with automatic temperature compensation was used. The pH value was measured using the 818 type pH meter (Dongguan, China), which also features automatic temperature compensation. The salt solubility of water was represented by the measured salt concentration, determined using the MH212-ATC T/L optical salinity analyzer. The measurement of salt concentration is based on the principle of light refraction, where the ratio of the sine values of the angles of incidence and refraction remains constant, and in a given environment, the salt content in the solution is directly proportional to the refractive index. By measuring the refractive index of the salt solution, the salt concentration can be calculated. In this experiment, table salt (Changsha, Hunan) was used, with each 100 g of table salt containing 38,238 mg of sodium. An excess amount of table salt was added to the water, stirred thoroughly, and left to stand until the temperature of each sample stabilized before testing the salt solubility. In this study, the constant temperature evaporation capacity m of MW and TW were tested at different temperatures (50 °C and 80 °C) to explore whether the evaporation capacity changes after magnetization. The study analyzed the evaporation rate of TW under different magnetization conditions. The experimental methods and procedures can be found in the author’s previous research⁴⁸. It is important to note that, due to the extensive research on the physicochemical properties of MW, the magnetization conditions for the water in this study were controlled at B = 261 mT and 656 mT, with n = 5 and 10, and v = 0.75 m/s, 1.5 m/s, and 2.75 m/s. These results, combined with the results from cement grout performance tests, were used to explain the mechanisms of the magnetization effects.

Results and discussion

The impact of MW on the stability performance of cement grout

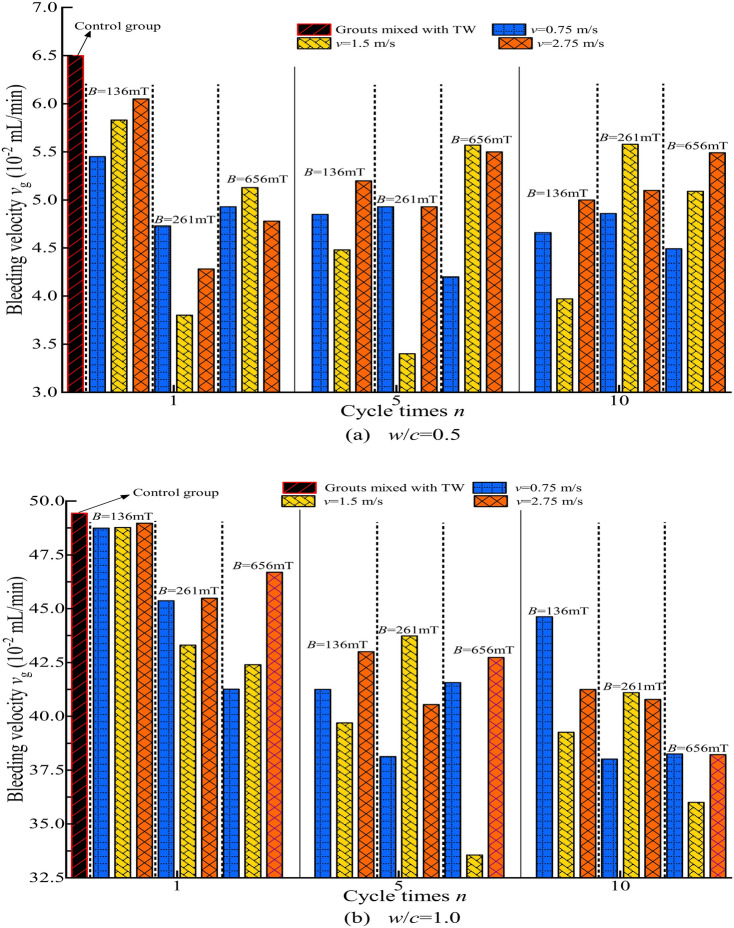
The stability of cement grout was evaluated based on bleeding tests, using the mean values from five parallel experiments to plot the water bleeding volume V_w−T curves. These curves were used to determine the basic stabilization time and the amount of bleeding for the cement grout, from which the bleeding velocity (v_g) was calculated, as shown in Fig. 6. The Fig. 6 illustrates the v_g of cement grouts under different conditions. Compared to the cement grout prepared with TW (shown as the control group), the v_g of cement grouts with w/c = 0.5 and 1.0 were lower when MW was used. This indicates that MW reduced the bleeding velocity of the cement grout, demonstrating a positive effect on the grout’s stability, which is consistent with similar findings in previous studies on cement-based materials^40,41,48,49. The influence of MW on the stability of cement grout did not show a clear pattern under different magnetization conditions, and the effects also varied with different w/c. Some existing research also suggests that the impact of magnetization conditions on the properties of water and the performance of cement-based materials mixed with MW does not follow a consistent pattern with changes in magnetization conditions^41,54. The presence of multiple extreme values observed in many studies aligns with the conclusions of this research.

Fig. 6.

The bleeding velocity of cement grouts under different magnetization conditions.

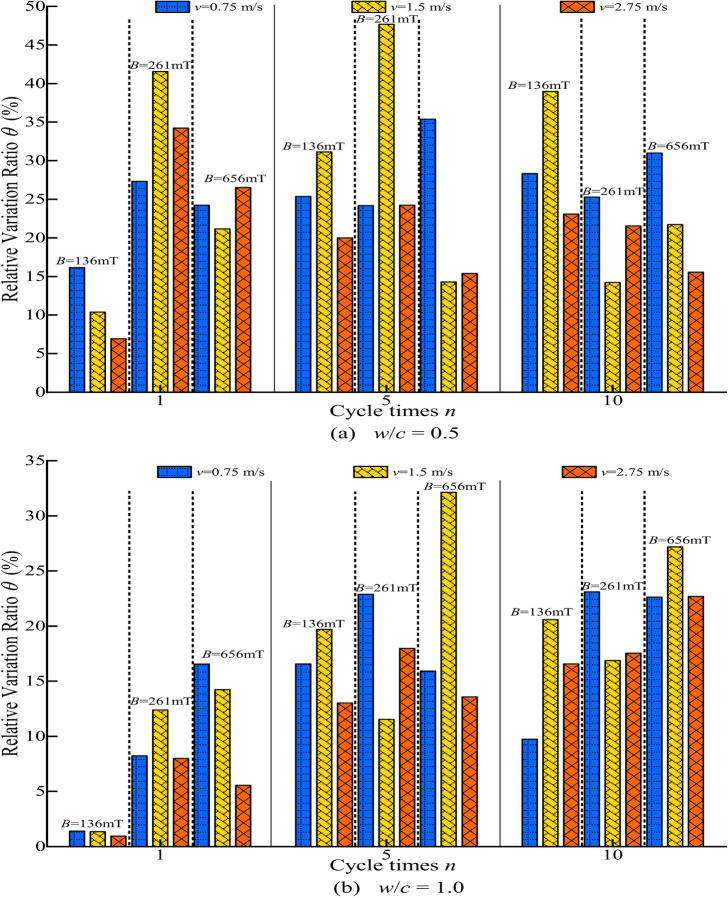
To quantify the positive effect of MW on the stability of cement grout, the relative variation ratio (θ) of stability under different magnetization conditions was calculated using Eq. (1). The results are presented in Fig. 7. A higher value indicates a greater improvement in the stability of the cement grout. As clearly shown in Fig. 7, the θ are all positive, indicating that MW enhances the stability of the cement grout. However, the pattern of change in the relative variation ratio with varying magnetization conditions is not consistent. The range of θ at w/c = 0.5 and 1.0 are 6.92% to 47.69% and 0.95% to 32.13%, respectively.

Fig. 7.

The relative variation ratio θ of cement grouts under different magnetization conditions.

The impact of MW on the rheological properties of cement grout

Rheological performance tests were conducted on cement grouts with different magnetization conditions (No.1 to No.9) and different w/c (0.5, 0.8, and 1.0). Using a developed data processing platform, the optimal flow model for each condition was fitted, and the corresponding rheological parameters were determined. The platform was also used to fit and analyze the experimental data, yielding the rheological equations and parameters for cement grout mixed with TW under four classic rheological models. Additionally, the goodness of fit R² for the rheological curves of the cement grouts under different models was statistically analyzed. The R² reflects the overall relationship between the dependent variable and all independent variables, indicating how well the model fits the data. An R² value closer to 1 suggests that the model provides a better fit for the experimental data; conversely, a lower R² value indicates a poorer fit. Figure 8 illustrates the fitting results of different rheological models for cement grout mixed with TW.

Fig. 8.

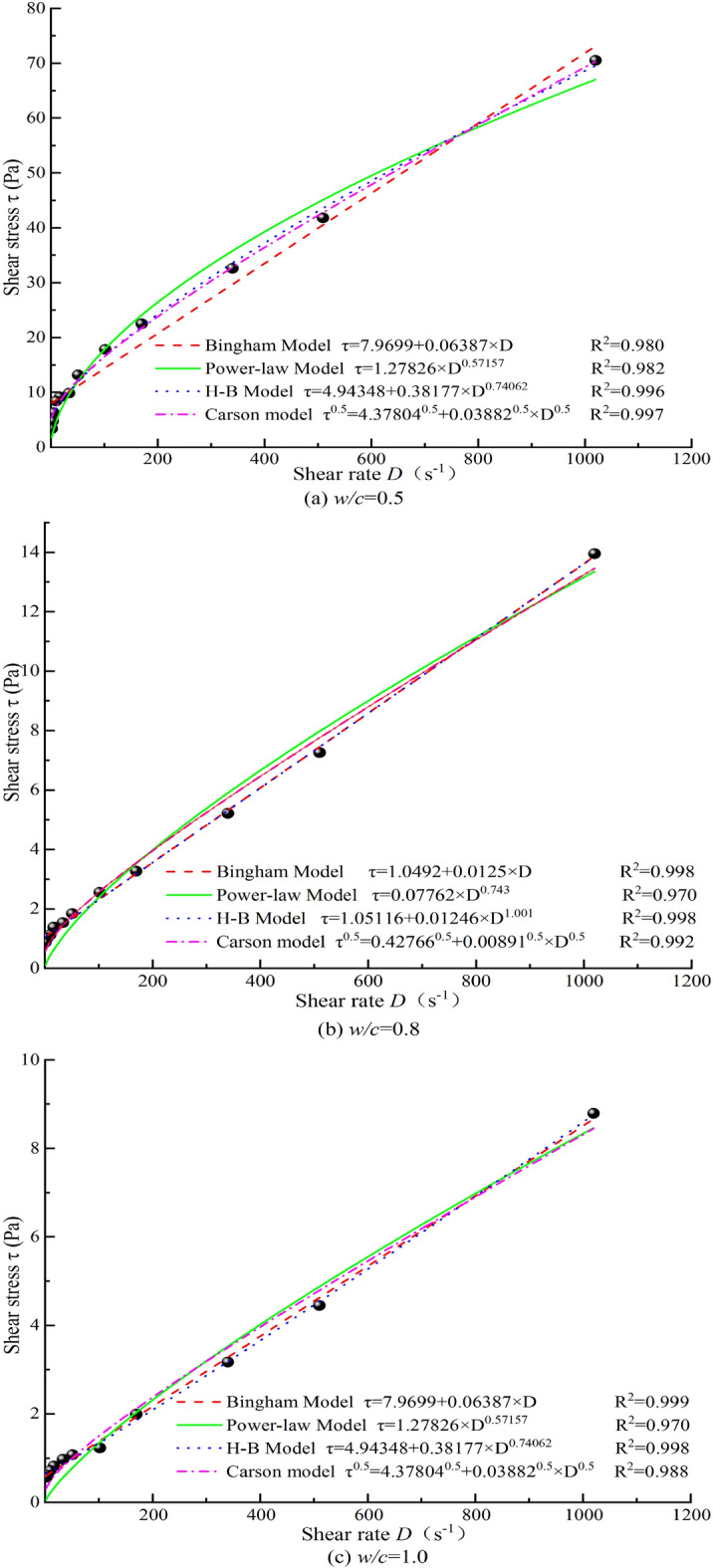
Rheological curve fitting results of cement grouts mixed with TW.

As shown in Fig. 8, the (H-B) model has a broader applicable range across different w/c (with a goodness of fit R² consistently greater than 0.99). In contrast, the Power Law model demonstrates relatively lower goodness of fit across different w/c, indicating it is not suitable for characterizing the rheological behavior of cement grout.

For a w/c = 0.5, there are significant differences in the rheological curves fitted by the four models. As the w/c increases to 0.8, these differences diminish, and at w/c = 1.0, the differences in the fitted rheological curves become minimal. This suggests that at w/c = 1.0, the shear-thinning characteristic of the grout is not prominent, and the grout can be considered a simple Bingham fluid. For w/c ≤ 0.8, the fitted rheological curves show significant differences, with pronounced shear-thinning characteristics, indicating that the grout behaves as a pseudoplastic fluid. The H–B model is well-suited for representing the rheological behavior of cement grouts across different w/c. Specifically, the Carson model is the best fit for the rheological behavior of cement grout at a low w/c. For w/c = 0.8 and 1.0, both the Bingham and H–B models can adequately represent the rheological curves. When comparing cement grouts prepared with MW to those with TW, the optimal representation model remains unchanged, but the rheological equation parameters show noticeable differences. Figure 9 illustrates the fitted rheological test curve results under magnetization condition No.4 (only this curve is shown due to the consistency of the conclusions across multiple figures).

Fig. 9.

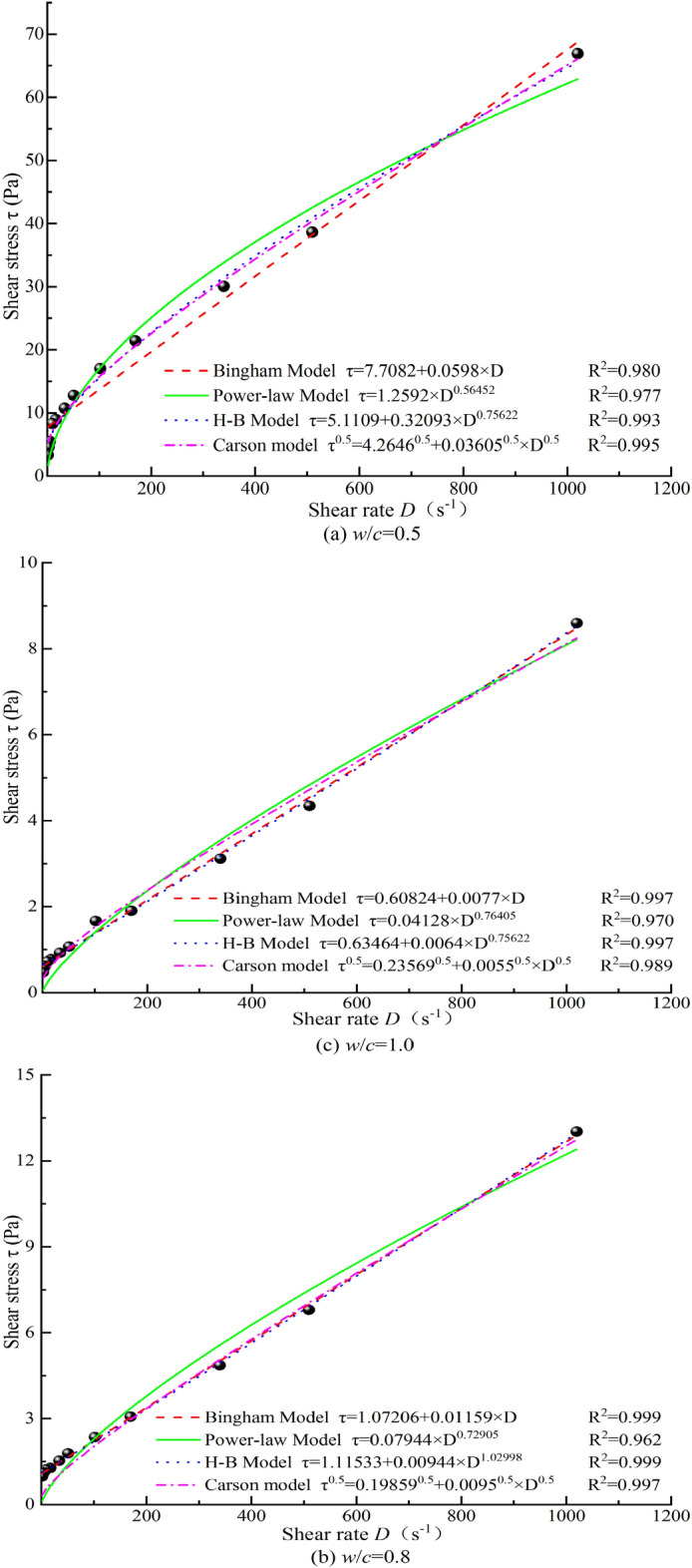
Rheological curves of cement grouts mixed with MW under the condition No. 4

The Carson model is the most suitable representation for the rheological behavior of cement grout with w/c = 0.5. Therefore, for cement grout with w/c = 0.5, the influence of MW on its rheological properties is investigated using key parameters of the Carson model, such as yield stress and asymptotic viscosity, along with rheological performance parameters obtained according to standards. For cement grouts with w/c = 0.8 and 1.0, both the Bingham and H-B models adequately represent the rheological curves, with the H–B flow index values being close to 1. Consequently, the simpler Bingham model’s key parameters-yield stress and plastic viscosity-are used to explore the effects of MW on the rheological properties of these grouts.

Generally, grouts with lower viscosity exhibit better flowability, and the relative change ratio of viscosity is used to assess the effectiveness of MW in influencing the rheological properties of the cement grout. For yield stress, there is no absolute better or worse; its optimal value depends on the specific engineering application and geological conditions. Therefore, the relative change ratio of yield stress is used to reflect the strength of the influence of MW on the grout, without implying a qualitative judgment of better or worse.

To compare the degree of change in the rheological performance parameters of cement grout after magnetization, the relative change ratio of each rheological parameter was calculated based on the results of the rheological tests. The relative change ratio is expressed as the percentage difference between the parameter value of the cement grout prepared with TW and that of the cement grout prepared with MW, relative to the parameter value of the cement grout mixed with TW. A negative relative change ratio indicates that the parameter value for the MW has improved relative to the TW.

The following table provides an orthogonal analysis of the relative change ratios of the rheological performance parameters for cement grout with w/c = 0.5 under different magnetization conditions. This analysis helps in understanding how various magnetization conditions affect the rheological properties of the cement grout compared to its non-magnetized counterpart.

Table 5 indicates that the relative change ratios for absolute viscosity η_J, apparent viscosity η_A, and dynamic yield stress τ_d under different magnetization conditions are all positive, suggesting that MW effectively reduces the absolute viscosity, apparent viscosity, and dynamic yield stress of cement grout. For the key rheological parameters of the Carson model (Carson yield stress τ₀ and asymptotic viscosity η_∞), most of the values are positive, with only a few negative values. This overall trend indicates that MW generally reduces the Carson yield stress and asymptotic viscosity. However, the plastic viscosity η_P shows a prevalence of negative values, indicating an increase in plastic viscosity relative to ordinary cement grout. This increase might be attributed to the way η_P is defined in the standards as the difference in readings at 600 r/min and 300 r/min. Since the grout with w/c = 0.5 is relatively thick, it was often observed during the experiments that a substantial amount of aggregated cement adhered to the viscometer rotor after completing the measurement at 600 r/min. This likely caused a significant deviation in the readings at 600 r/min, leading to a larger experimental error. Compared to cement grout mixed with TW, MW can reduce the absolute viscosity by up to 9.73%, the apparent viscosity by up to 5.61%, and the plastic viscosity by up to 2.85%. The dynamic yield stress varies between 5.4 and 32.30%, the asymptotic viscosity can be reduced by up to 8.84%, and the Carson yield stress varies between − 6.22 and 19.10%.

Table 5.

Relative change ratios of rheological parameters for cement grout with w/c = 0.5

No.	Magnetization control conditions			Relative change ratio of indicator values (%)
	B (mT)	v (m/s)	n	ηJ	ηA	ηp	τd	τ0	η∞
1	1(136)	1(0.75)	1(1)	2.06	1.45	0.21	5.40	− 0.71	2.52
2	1	2	2	5.64	4.64	2.85	11.11	3.75	5.67
3	1	3	3	6.86	2.39	− 4.45	31.35	19.10	− 2.34
4	2(261)	1	2(5)	7.40	5.13	1.49	19.84	2.59	7.14
5	2	2(1.5)	3	6.52	2.93	− 2.62	26.15	7.51	2.52
6	2	3	1	6.37	3.51	− 1.00	22.06	5.45	3.68
7	3(656)	1	3(10)	2.75	1.25	− 1.28	10.95	− 6.22	4.33
8	3	2	1	3.48	1.56	− 1.49	14.01	− 4.22	4.28
9	3	3(2.75)	2	9.73	5.61	− 0.71	32.30	1.60	8.84

In the table, the absolute viscosity η_J, apparent viscosity η_A, dynamic yield stress τ_d, plastic viscosity η_p, Carson yield stress τ₀ , and asymptotic viscosity η_∞ are all calculated based on experimental test results.

Similarly, the relative change ratios of rheological performance parameters for cement grout with w/c = 0.8 under different magnetization conditions were determined. Table 6 shows that under various magnetization conditions, the relative change ratios of the plastic viscosity, a key parameter of the Bingham model, are all positive, indicating that MW effectively reduces the plastic viscosity of the cement grout. The relative change ratios of yield stress, another key parameter of the Bingham model, are mostly negative, with the exception of a positive value under magnetization condition No.9. This suggests that MW generally increases the yield stress in the Bingham model. Compared to cement grout mixed with TW, MW can reduce the plastic viscosity of cement grout with w/c = 0.8 by up to 9.44%, while the yield stress varies within a range of − 20.02% to 5.72%.

Table 6.

Relative change ratios of rheological parameters for cement grout with w/c = 0.8

No.	Magnetization control conditions			Relative change ratio of indicator values (%)
	B (mT)	v (m/s)	n	Dynamic yield stress	Plastic viscosity ηp
1	1 (136)	1 (0.75)	1 (1)	− 2.10	4.00
2	1	2	2	− 8.58	5.28
3	1	3	3	− 12.11	4.00
4	2 (261)	1	2 (5)	− 2.19	7.28
5	2	2 (1.5)	3	− 14.01	9.44
6	2	3	1	− 6.77	5.84
7	3 (656)	1	3 (10)	− 6.77	6.48
8	3	2	1	− 20.02	8.24
9	3	3 (2.75)	2	5.72	7.44

As shown in Table 7, the relative change ratios of rheological parameters for cement grout with w/c = 1.0 under different magnetization conditions were analyzed. The relative change ratios of the plastic viscosity, a key parameter of the Bingham model, are predominantly positive, indicating that MW effectively reduces the plastic viscosity of the cement grout. For the yield stress, another key parameter of the Bingham model, the relative change ratios are mostly negative, suggesting that MW generally increases the yield stress in the Bingham model. Compared to cement grout mixed with TW, MW can reduce the plastic viscosity of cement grout with w/c = 1.0 by up to 4.79%, while the yield stress varies within a range of − 26.05% to 7.44%.

Table 7.

Relative change ratios of rheological parameters for cement grout with w/c = 1.0

No.	Magnetization control conditions			Relative change ratio of indicator values (%)
	B (mT)	v (m/s)	n	Dynamic yield stress	Plastic viscosity ηp
1	1 (136)	1 (0.75)	1 (1)	3.98	0.76
2	1	2	2	− 20.56	2.65
3	1	3	3	− 5.07	0.13
4	2 (261)	1	2 (5)	− 4.41	2.65
5	2	2 (1.5)	3	− 12.31	2.14
6	2	3	1	− 31.20	2.27
7	3 (656)	1	3 (10)	7.44	0.25
8	3	2	1	− 22.10	2.52
9	3	3 (2.75)	2	− 26.05	4.79

The rheological performance test data were selected under the magnetization conditions that resulted in the greatest reduction in viscosity for the best-fitting model at each w/c. For w/c = 0.5, the data were determined according to the asymptotic viscosity from the Carson model. For w/c = 0.8 and 1.0, the data were determined according to the plastic viscosity from the Bingham model. The rheological curves were then plotted based on the model with the highest goodness of fit, as shown in Fig. 10. It can be observed that MW causes noticeable changes in the rheological curves of cement grout with w/c = 0.5 and 0.8. However, for w/c = 1.0, the rheological curves of cement grout mixed with TW and cement grout mixed with MW do not show significant differences. This is likely because the grout with w/c = 1.0 is relatively dilute, resulting in lower shear stress, and thus, the changes in the rheological curves are less pronounced.

Fig. 10.

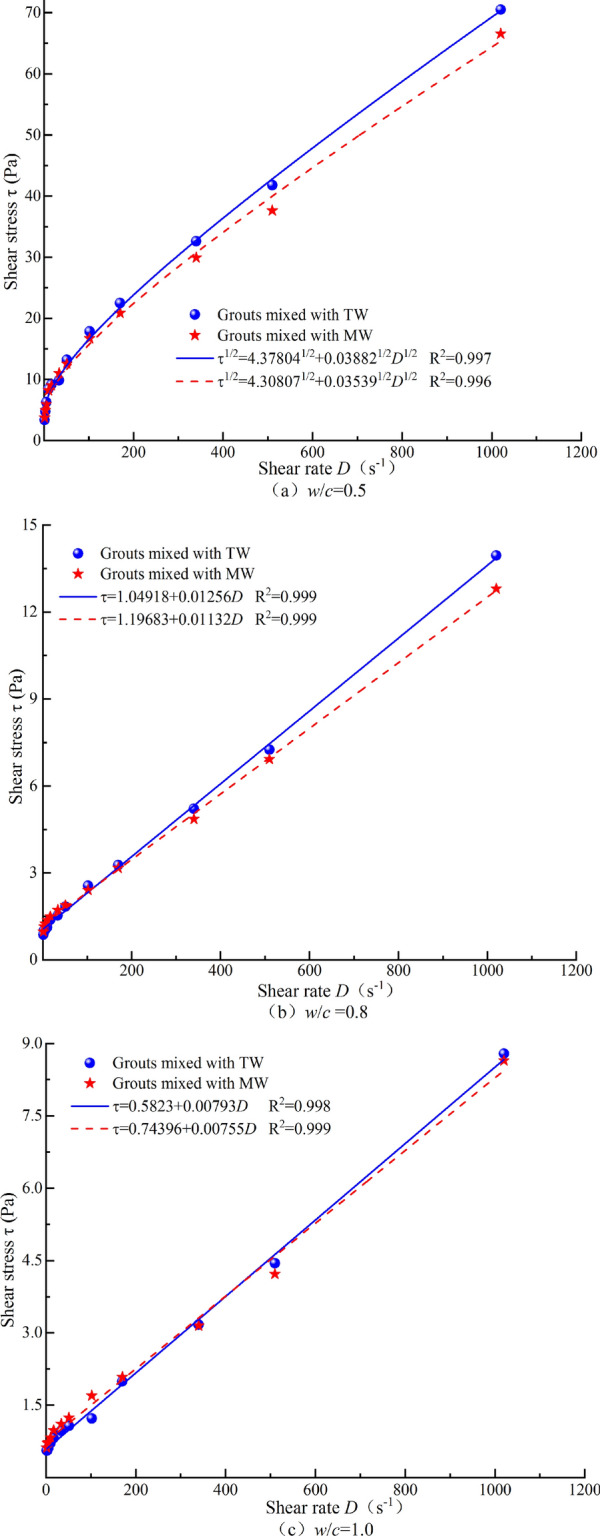
Optimal fitted rheological models of cement grout prepared with MW and TW at different w/c.

The impact of MW on the strength of cement grout stone

The average strength value of the six specimens under each condition (at the same curing age) was taken as the strength test result for that curing age. To more intuitively assess whether MW affects the flexural strength and compressive strength of the cement grout stone at different curing ages (3, 7, 28 days), the test results for the flexural strength and compressive strength of the cement grout stone at different w/c were generated, as shown in Figs. 11 and 12.

Fig. 11.

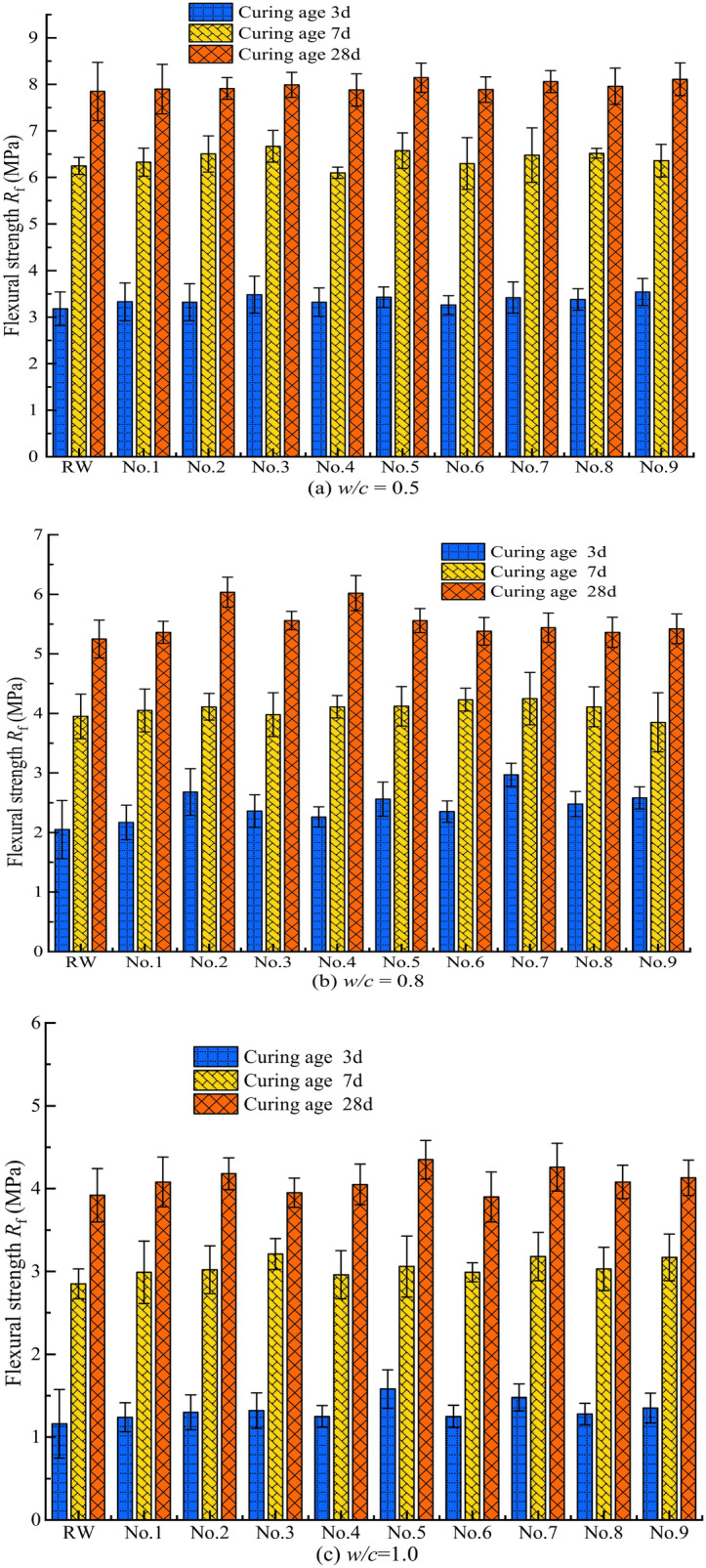
Flexural strength of cement grout stone under different conditions.

Fig. 12.

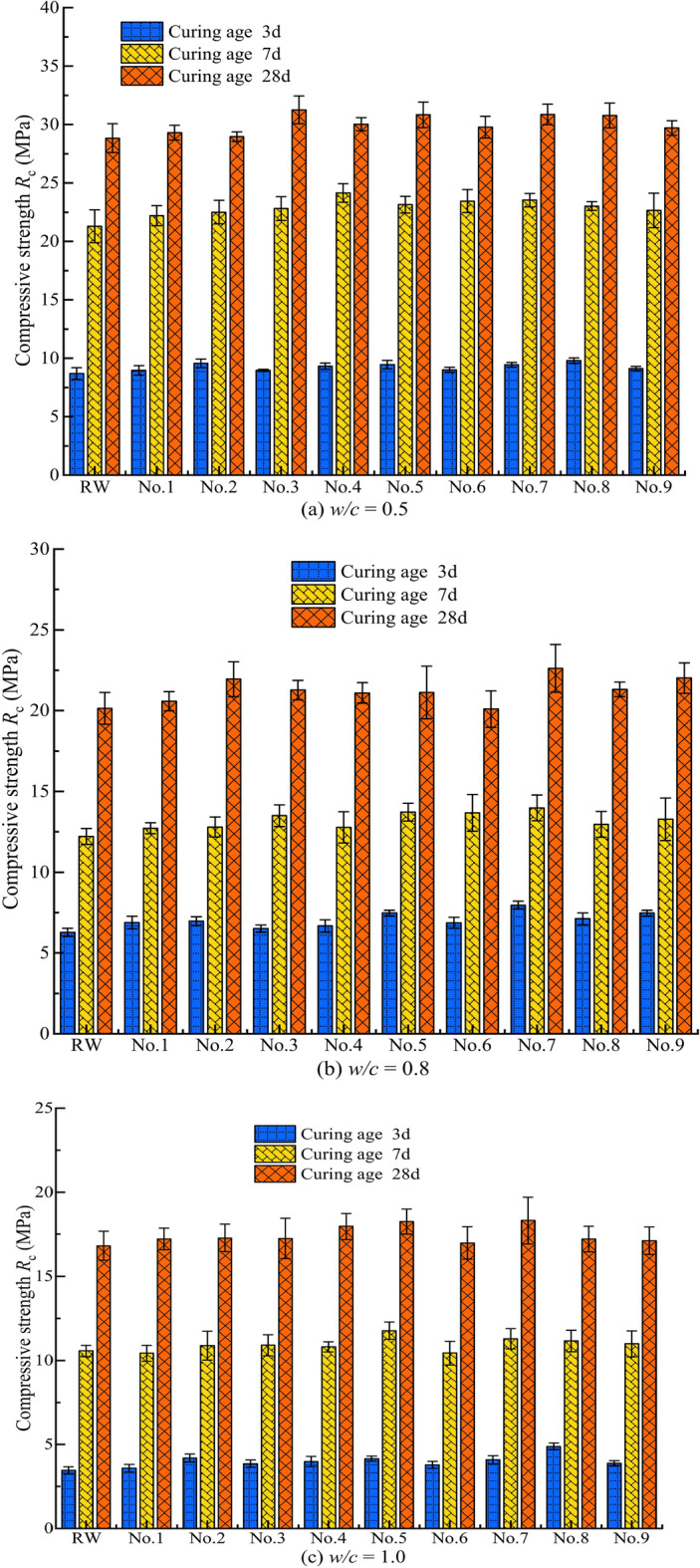
Compressivel strength of cement grout stone under different conditions.

As seen in Figs. 11 and 12, the flexural and compressive strengths of cement grout bodies at different curing ages (for w/c = 0.5, 0.8, and 1.0) vary significantly across different conditions (cement grout mixed TW and MW). This indicates that MW has a noticeable impact on the flexural and compressive strengths of cement grout bodies with different w/c. To quantify the impact of MW on the flexural and compressive strengths of the cement grout stone under different magnetization conditions, the flexural strength change ratio λ_f(%) and the compressive strength relative change rate λ_c(%) are introduced, as shown in Eqs. (2) and (3).

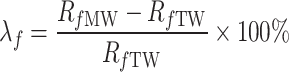2

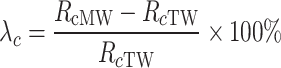3

where, R_{f MW} and R_{c MW} respectively represent the flexural and compressive strength of the cement grout stones mixed with MW, while R_{f TW} and R_{c TW} represents the flexural and compressive strength of the cement grout stones prepared with TW. Clearly, when λ_f and λ_c are positive, it indicates that MW has increased the flexural and compressive strength of the cement grout stones, respectively. Conversely, if λ_f and λ_c are negative, it indicates that MW has an adverse effect on the flexural and compressive strength. The larger the absolute values of λ_f and λ_c, the greater the impact of MW on the strength properties of the cement grout stone.

Figure 13 shows that all λ_f values are positive, indicating that MW improves the flexural strength of the cement grout stone. Additionally, the λ_f values vary significantly under different magnetization conditions. MW exhibits a beneficial effect on the flexural strength of the cement grout stone at all curing ages across different w/c. Specifically, for w/c = 0.5, the maximum relative change ratios in flexural strength for curing ages of 3d, 7d, and 28d are 11.32%, 6.72%, and 3.75%, respectively. At w/c = 0.8, the maximum relative change ratios for these curing ages are 44.48%, 7.59%, and 14.95%, respectively. Lastly, for w/c = 1.0, the maximum relative change ratios for the same curing ages are 36.21%, 12.63%, and 10.97%, respectively.

Fig. 13.

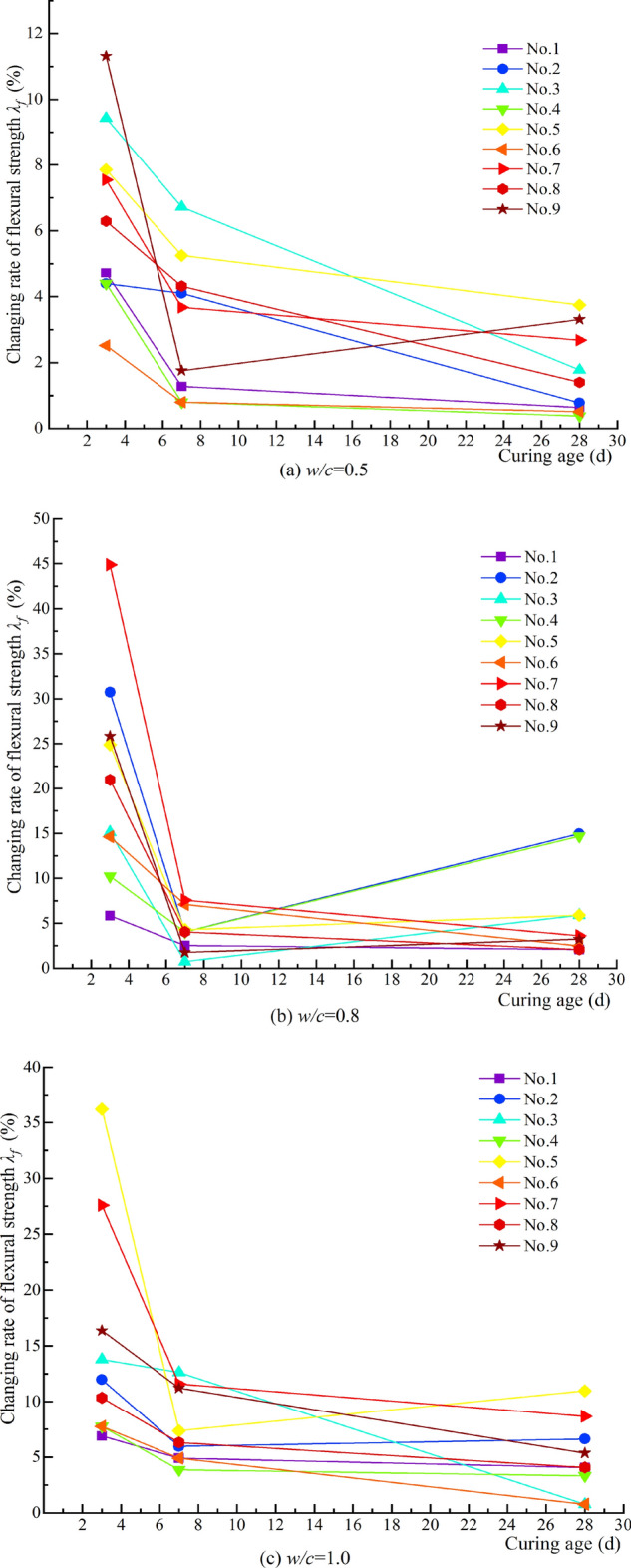
Relative change ratio of flexural strength under different magnetization conditions.

Figure 14 indicates that the λ_c values are positive, suggesting that MW can enhance the compressive strength of cement grout bodies. For cement grout bodies with different w/c, MW exhibits a positive effect on compressive strength at all curing ages. Specifically, when w/c = 0.5, the maximum relative change ratios in compressive strength for curing ages of 3, 7, and 28 days are 12.66%, 13.41%, and 9.33%, respectively; when w/c = 0.8, the ratios are 26.75%, 12.32%, and 12.31%, respectively; and when w/c = 1.0, the ratios are 30.01%, 11.46%, and 8.94%, respectively. Together with Fig. 13, it is evident that the relative change ratios in flexural and compressive strength of cement grout bodies with different w/c exhibit similar trends with curing age, generally decreasing, indicating that MW is more beneficial for enhancing the early-age strength of cement grout bodies.

Fig. 14.

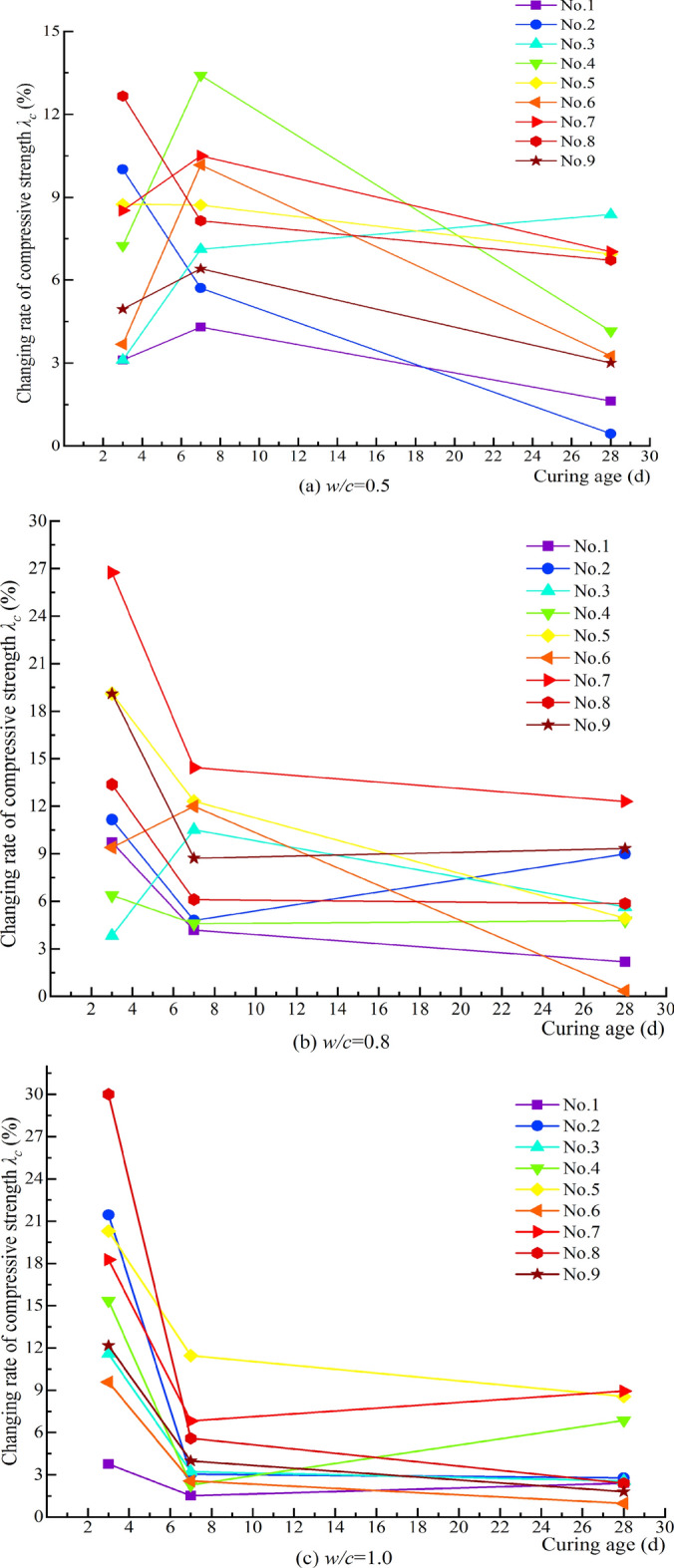
Relative change ratio of compressive strength under different magnetization conditions.

Quantum mechanics-based explanation of the mechanism of magnetization effects

Analysis of the physicochemical properties of MW

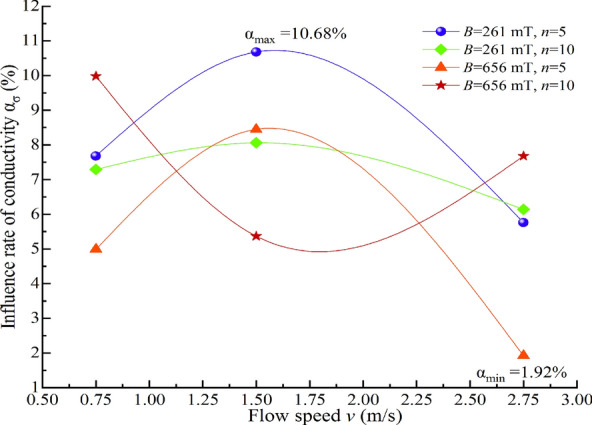
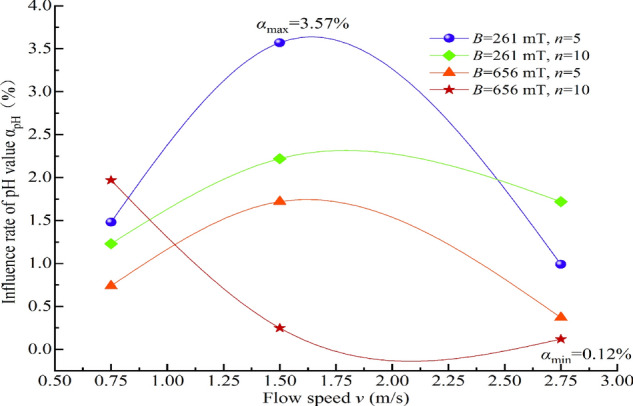
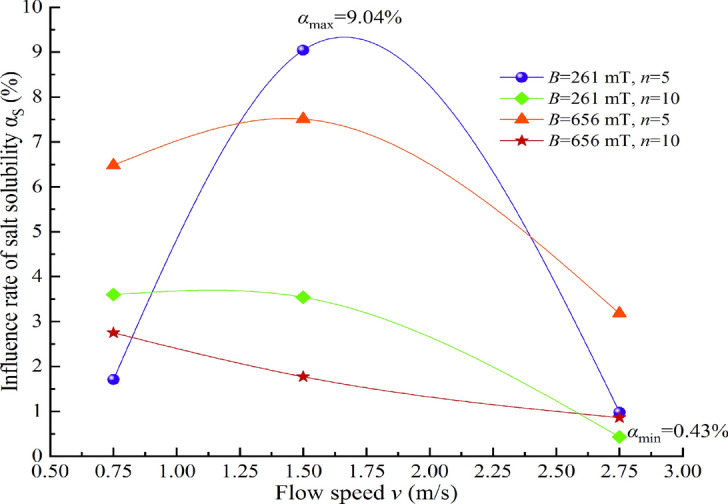
To further analyze the extent of the impact of magnetization conditions on the physicochemical properties of water and, on this basis, investigate the mechanism of magnetization effects on water, the percentage difference between the physicochemical property characterization values of water under different magnetization conditions and those of non-magnetized water, relative to the characterization values of the corresponding non-magnetized water, is defined as the impact ratio α. Specifically, α represents the extent of change in physicochemical properties due to magnetization, with the unit being %. A positive value of α indicates an increase. The relationships between the impact ratios α_σ, α_pH, α_S, and α_m of the conductivity σ, pH value, salt solubility S, and constant temperature evaporation m of MW and the water flow speed v are plotted, as shown in Figs. 15, 16, 17, 18.

Fig. 15.

Relationship between the influence ratio of α_σ and water flow speed.

Fig. 16.

Relationship between the influence ratio of α_pH and water flow speed.

Fig. 17.

Relationship between the influence ratio of α_S and water flow speed.

Fig. 18.

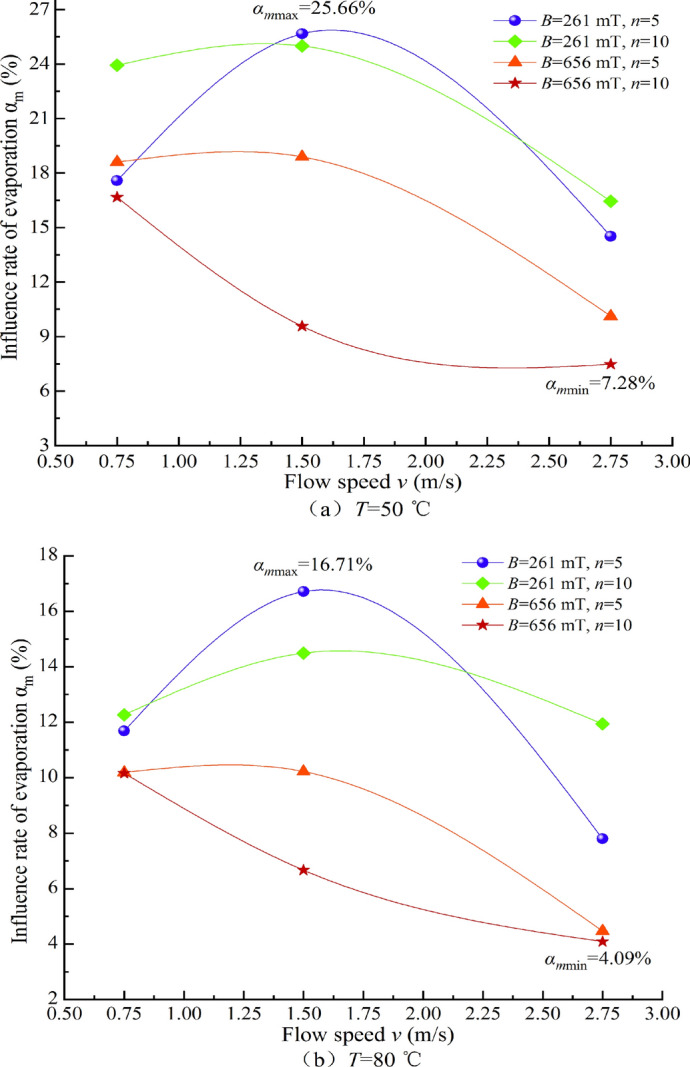
Relationship between the influence ratio of α_m and water flow speed.

It is evident from Figs. 15, 16, 17, 18 that the impact ratio α of the physicochemical properties of TW after magnetization is positive, indicating that the conductivity σ, pH value, salt solubility S, and constant temperature evaporation m of the water increase after magnetization. The ranges of impact rate α for conductivity σ, pH value, salt solubility S, and constant temperature evaporation m at 50 °C and 80 °C under different magnetization conditions are 1.92–10.68%, 0.12–3.57%, 0.43–9.04%, 7.48–25.66%, and 4.09–16.71%, respectively.

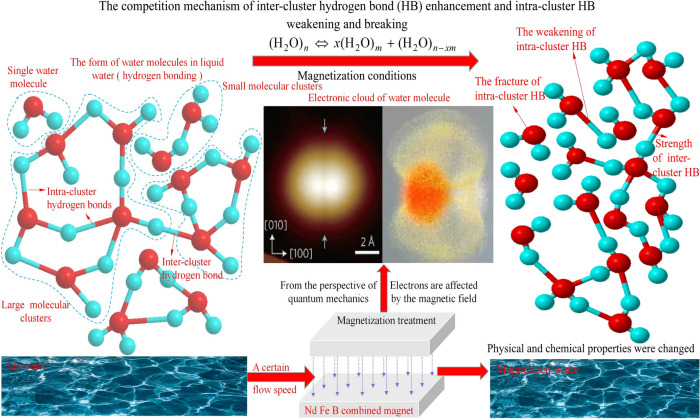
The magnitude of the impact rate α reflects the degree of change in the physicochemical properties of water under different magnetization conditions. It is evident that there are significant differences in the degree of impact on water under different magnetization conditions, but the physicochemical properties of water do change after magnetic treatment. A series of studies on water have shown that the occurrence state of water (the chemical bonds of water molecules, water clusters, and the hydrogen bond network between them, as well as the thermal motion of water molecules) determines its physicochemical properties, indicating that magnetic treatment alters the occurrence state of water. Currently, there is no consensus on the magnetization mechanism of water, but it is a consensus of years of research that the physicochemical properties of water change after magnetization. Based on the consensus of experimental research results, it is generally believed that magnetization of water alters the larger associated molecular clusters and the hydrogen bond network between them. Due to differences in experimental results, there are certain discrepancies in the explanation of the magnetization mechanism, even contradictory^30–32. The mechanistic explanations for magnetically treated water are all based on the hydrogen bond breakage theory (the majority of research results) and the hydrogen bond enhancement theory (a minority of results) and have developed from these. No single mechanistic explanation can be applied to analyze all experimental results of magnetically treated water. The key to elucidating the mechanism of magnetization effects and the focus of contradiction lie in the fact that the work done by the magnetic field during the magnetization process is far less than the bond energy of hydrogen bonds, so how do hydrogen bonds break? But if only the hydrogen bond enhancement theory is considered, many experimental results of MW cannot be explained.

In nature, liquid water exists in the form of a few individual water molecules and numerous water clusters stabilized by hydrogen bonding^55,56. Meanwhile, Brownian motion is constantly occurring in liquid water. Research published in Nature has successfully observed the “quantum tug” phenomenon in the hydrogen bond network of pure water⁵⁷, further enhancing our understanding of the microscopic hydrogen bond dynamics of water. Liquid water is composed of a macroscopically connected, random hydrogen bond network, where hydrogen bonds are constantly deforming, breaking, and undergoing topological reorganization⁵⁸. Hydrogen bonding is a special type of van der Waals force between water molecules, but it is distinguished by its directionality and saturation, and it is also different from the chemical bonds firmly established within water molecules. As an intermolecular force in liquid water, hydrogen bonding constantly forms, breaks, or experiences “quantum tug” phenomena among water associates, which can be represented by the following dynamic equilibrium equation: 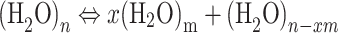, where m = 1 represents a single water molecule, and 1 < m < n represents smaller water clusters.

TW is composed of a mixture of individual water molecules, water clusters, soluble salts, and ions that constitute these salts. As previously mentioned, the physicochemical properties of water are determined by its state of existence. Assuming that TW passes through a magnetic field, its main components, water molecules and water clusters, undergo changes in the motion of individual electrons and the outer electrons of water clusters under the influence of the external magnetic field. Macroscopically, these changes prompt the electrons to form an “electron cloud” and undergo polarization. As a result, the magnetic moment and torque generated by the magnetized electrons are oriented opposite to the direction of the external magnetic field. For TW, which is composed of a macroscopically connected, random hydrogen bond network⁵⁹, its hydrogen bonds are constantly deforming, breaking, and undergoing topological reorganization. The hydrogen bond dynamics of TW determine its physicochemical properties. The protons (hydrogen nuclei) in water molecules undergo transfer along with hydrogen bonds, and this transfer process of hydrogen nuclei (with extremely small mass) exhibits significant nuclear quantum effects, such as quantum tunneling and zero-point motion, in water. It is noteworthy that the protons in the hydrogen bond network of water molecules are not independent; they exhibit strong correlations with each other. Under the influence of an external magnetic field, the process of hydrogen bond vibrational deformation (stretching, compression, bending) or local breakage is affected by the external magnetic field. The transfer of protons within the hydrogen bond network involves understanding the limited many-body quantum behavior⁶⁰. This quantum effect leads to changes in the physicochemical properties of water. Meanwhile, under the influence of an external magnetic field, the outer electrons of various impurities and hydrated ions in water are affected by the magnetic field, leading to relative displacements of their molecular groups. This is also one of the factors influencing the changes in water properties. Studies on magnetized different aqueous solutions have also confirmed this effect. For example, the changes in kinetic and potential energy of Ca²⁺ ions in water due to magnetic fields, based on M. Faraday’s electromagnetic effect theory, indicate that water with certain electrical conductivity, when subjected to an external force and passing through a magnetic field, cuts magnetic field lines. A large number of particles in the water undergo spiral circular motion through the magnetic field region and acquire new energy in the magnetic field. According to the Born–Oppenheimer approximation regarding particles, when studying the motion of electrons, the nuclei are approximately considered static, and the inter-nuclear distances are also constant. Taking the atom as the unit, one can establish the Hamiltonian for the electron and the corresponding fundamental equation in quantum mechanics proposed by Schrödinger. Furthermore, the Hamiltonian and Schrödinger equation for MW can be derived. Regarding the solution of the Hamiltonian and Schrödinger equation, advanced quantum mechanics indicates the use of the Ritz method for solving the ground state wave function. From the perspective of quantum mechanics, this magnetization of water changes the potential and kinetic energies of the particles in the water, which further affects the vibrational deformation (stretching, compression, bending) or local breakage of hydrogen bonds in the water. As a result, this dynamic process is influenced by the magnetic field, prompting different changes in hydrogen bonds in the water, including their enhancement and breakage. Therefore, numerous studies have shown that under the influence of a magnetic field, hydrogen bonds are enhanced, even forming more hydrogen bonds⁶¹, while other studies have reported a weakening of hydrogen bonds in water⁶².

As aforementioned, hydrogen bonds exhibit directionality and saturation. The magnetic field influences the potential and positional energies of particles in water, subsequently leading to variations in the effects of hydrogen bonds. Specifically, changes in potential and positional energies enhance hydrogen bonds between water clusters while weakening or breaking those within clusters. Hence, the magnetic field induces such differences in its effects on water. Existing research has experimentally demonstrated the enhancement of inter-cluster hydrogen bonds and the weakening or breakage of intra-cluster hydrogen bonds⁶³, yet the mechanism underlying this process remains unexplained. Meanwhile, numerous uncontrollable factors in the magnetization process, such as impurities in water, the amount of dissolved oxygen, and variations in magnetization conditions, render the experimental effects merely supportive evidence for the magnetization mechanism and contribute to significant discrepancies in its interpretation. From a quantum mechanical perspective, the magnetic field alters the potential and kinetic energies of particles in water, subsequently influencing the competition between the strengthening of inter-cluster hydrogen bonds and the weakening or breakage of intra-cluster hydrogen bonds. If the enhancement of hydrogen bonds dominates, the experimental results favor the mechanistic explanation supporting hydrogen bond strengthening; conversely, they support the argument for hydrogen bond weakening or breakage. Furthermore, differences exist in the impact of intra-cluster and inter-cluster hydrogen bonds on water properties⁶⁴, consequently, some physicochemical indicators of water tend to support the explanation of hydrogen bond enhancement, while others lean towards the argument for hydrogen bond weakening or breakage.

Based on the quantum mechanical explanation of the magnetization mechanism discussed earlier, this section explores the effects of different magnetization conditions on the electrical conductivity σ, pH value, salt solubility S, and constant-temperature evaporation capacity m of water. TW exhibits conductivity due to its ability to facilitate the decomposition of impurities into positive and negative ions and undergo weak ionization. After magnetization treatment, the competition between the strengthening and weakening or disruption of hydrogen bonds in TW becomes unbalanced. Under the magnetization conditions employed in this study, the breakage of hydrogen bonds in water molecules dominates, leading to the generation of more small water clusters and individual water molecules, indicating increased water activity and enhanced affinity for ions in water. This, in turn, enhances the decomposition of impurities into ions and the ionization of water, thereby increasing the electrical conductivity of TW. Correspondingly, the increased number of ionized H⁺ ions in MW results in a higher pH value. The water after magnetization exhibits a stronger ability to hydrolyze various impurities, which promotes the ionization and hydrolysis of salt, and the dissolved salt in water is less prone to precipitation, leading to an increase in the material solubility of MW. Water evaporation is a gradual process involving the detachment of individual water molecules from the liquid phase. A greater number of individual water molecules, smaller water clusters (indicating higher water activity), and more intense Brownian motion facilitate water evaporation. Weaker hydrogen bonds and smaller inter-molecular van der Waals forces accelerate water evaporation, resulting in a larger cumulative evaporation capacity per unit time. Since hydrogen bonds are the primary inter-molecular forces that keep water molecules in the liquid phase, evaporation necessarily involves the breakage of hydrogen bonds in water. Regardless of how hydrogen bonds in water are affected by the magnetic field, their changes will undoubtedly impact water evaporation: the strengthening of hydrogen bonds inhibits water evaporation, while their weakening and breakage promote it. The experimental results of this study demonstrate that under the magnetization conditions employed, the evaporation capacity of MW increases, providing evidence for the dominance of hydrogen bond breakage. Furthermore, previous research has confirmed that magnetization treatment weakens van der Waals forces⁶⁵, and since the van der Waals forces between water molecules are weaker than hydrogen bonds, the weakening of van der Waals forces is also one of the reasons for the increased water evaporation capacity.

Discussion on the impact of MW on the properties of cement grout

The magnetization effect mechanism of MW on the stability of cement grout can be well explained based on Stokes’ law, as detailed in the author’s previous research⁴⁹. Considering the variations in plastic viscosity and consistency coefficient of cement grout under different w/c, cement grout exhibits fluid behavior with a certain spatial network structural strength. When the applied shear stress exceeds this strength, the grout undergoes shear deformation. Lower grout consistency leads to stronger molecular attractions, particle aggregation, uneven distribution, and consequently higher grout viscosity. From a quantum mechanics perspective, MW alters the potential and kinetic energies of particles in water, influencing the vibrational deformation (stretching, compression, bending) or local breakage of hydrogen bonds in water. This dynamic process is influenced by the magnetic field, causing various changes in hydrogen bonds, including strengthening, weakening, or breakage, with a competitive mechanism governing these transformations. Under the magnetization experimental conditions described in this study, the weakening or breakage of hydrogen bonds within water clusters dominates. After magnetization, the number of individual water molecules or small water clusters increases, indicating enhanced activity. The weakening or breakage of hydrogen bonds in water leads to a reduction in surface tension and altered electrical attractions. During cement grout mixing, a thin layer of MW molecules aligns on the surface of cement particles, maintaining a uniform spacing between cement colloidal particles. This enhances the dispersion of the cement solid phase, inhibiting the formation of cement flocculation aggregates. Fine cement particles in the medium are evenly dispersed, and changes in electric potential increase repulsion between cement particles. Therefore, the viscosity of the cement grout decreases, and the strength of the network structure between cement grouts is weakened. Consequently, MW exhibits overall effects of viscosity reduction and shear stress reduction.

A comparison of the SEM micrographs and and quantitative chemical element analysis of cement grouts cured for 28 days, prepared with MW and TW, is presented in Fig. 19. The SEM images reveal that the cement paste prepared with MW exhibits a higher number of hydration crystals, resulting in a denser filling of the spaces between cement particles, fewer and smaller voids, a compact structure, and numerous contact points. Consequently, the compressive strength of the cement paste specimens prepared with MW is higher than that of specimens prepared with non-magnetized water, which is consistent with the findings of previous studies on concrete mixed with MW^36–44, as shown in Fig. 19. This indicates that passing water through a magnetic field at a certain flow rate improves its physicochemical properties, enhancing its reactivity with cement. From the perspective of quantum mechanics, considering the competitive mechanism of inter-cluster hydrogen bond strengthening and intra-cluster hydrogen bond weakening or breakage, water passing through a magnetic field at a certain flow rate becomes magnetized. Under the magnetization conditions described in this study, intra-cluster hydrogen bond weakening or breakage dominates, leading to an increased number of individual water molecules and small water clusters in the MW. When cement is mixed with this highly reactive MW, it accelerates the early hydration reaction of the cement^40,41,45,46, resulting in higher early strength. Additionally, it enhances the depth of cement hydration, promotes the formation of more hydration products, and leads to a denser cement paste structure, ultimately improving both the compressive and flexural strengths of the cement grout stone.

Fig. 19.

SEM images and elemental analysis of 28 days cured cement grout stone.

The physicochemical property test results of MW indicate that the magnetic field influences the competitive mechanism between the enhancement of inter-cluster hydrogen bonds and the weakening or breakage of intra-cluster hydrogen bonds within water clusters. Specifically, under the magnetization conditions presented in this study, the magnetic field weakens the stronger intra-cluster hydrogen bonds, disrupts larger water clusters, and forms smaller clusters with stronger inter-cluster hydrogen bonds, thereby achieving a new arrangement of water clusters. In this process, the weakening or breakage of intra-cluster hydrogen bonds dominates, leading to the physicochemical properties of MW manifesting as hydrogen bond breakage. In summary, the explanation of the magnetization influence mechanism from a quantum mechanics perspective is shown in Fig. 20.

Fig. 20.

Explanation of magnetization mechanism based on quantum mechanics.

Conclusion

1. The bleeding velocity is an effective indicator for characterizing the stability of cement grout, and MW can enhance the stability of cement grout. When the w/c = 0.5 and 1.0, the variation range of the relative change ratio of stability under different magnetization conditions is 6.92–47.69% and 0.95–32.13%, respectively.

2. MW can significantly alter the rheological curves of cement grouts with w/c = 0.5 and 0.8. For cement grouts with w/c = 0.5, the Casson model is the optimal representation of their rheological curves. Under different magnetization conditions, the effects of MW on this cement grout are as follows: the absolute viscosity can be reduced by up to 9.73%, the apparent viscosity by up to 5.61%, the plastic viscosity by up to 2.85%, the dynamic yield stress varies within a range of 5.4–32.30%, the limiting viscosity can be reduced by up to 8.84%, and the Casson dynamic yield stress varies within a range of–6.22% to 19.10%.

3. Both the Bingham model and the H-B model provide good representations of the rheological curves of cement grouts with w/c = 0.8 and 1.0. For cement grouts with w/c = 0.8, MW can reduce the key parameter of the Bingham model—plastic viscosity, with a maximum reduction of 9.44%, and the dynamic yield stress varies within a range of –20.02% to 5.72%. For cement grouts with w/c = 1.0, MW can also reduce the key parameter of the Bingham model—plastic viscosity, with a maximum reduction of 4.79%, and the dynamic yield stress varies within a range of –26.05% to 7.44%.

4. MW can enhance the flexural strength and compressive strength of cement grout stones, particularly beneficial for improving their early-stage strength. Specifically, for cement grout stones with w/c = 0.5, 0.8, and 1.0, MW can increase their flexural strength in the early stage (3 days) with maximum increases of 11.32%, 44.48%, and 36.21%, respectively. Similarly, MW can also increase their compressive strength in the early stage with maximum increases of 12.66%, 26.75%, and 30.01%, respectively.

5. Under different magnetization conditions, multiple physicochemical properties of TW have undergone changes. The conductivity varies within a range of 1.92–10.68%, the pH value varies within a range of 0.12% to 3.57%, the salt solubility varies within a range of 0.43–9.04%, and the evaporation rate at constant temperatures of 50 °C and 80 °C varies within ranges of 7.48–25.66% and 4.09–16.71%, respectively.

6. From a quantum mechanical perspective, authors tentatively propose a mechanistic explanation: the magnetic field influences the competitive mechanism between the enhancement of inter-cluster hydrogen bonds and the weakening or breakage of intra-cluster hydrogen bonds in water clusters.

Author contributions

Chao Deng: Conceptualization, Methodology, Investigation, Writing – review & editing, Resources, Data curation, Funding acquisition. Liuxi Li: Validation, Formal analysis, Investigation, Writing. Huanxiao Hu: Conceptualization, Validation, Funding acquisition, Project administration, Supervision. Zhichao Xu: Validation,Investigation, Funding acquisition. Yi Zhou: Data curation, Validation, Investigation. Quan Yin: Validation, Investigation, Funding acquisition. Juan Chen: Validation, Investigation, Funding acquisition. All authors reviewed the manuscript.

Data availability

Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.