Abstract
Recent advances in Light Emitting Diode (LED) technology have enabled a more affordable high frame rate photoacoustic imaging (PA) alternative to traditional laser-based PA systems that are costly and have slow pulse repetition rate. However, a major disadvantage with LEDs is the low energy outputs that do not produce high signal-to-noise ratio (SNR) PA images. There have been recent advancements in integrating deep learning methodologies aimed to address the challenge of improving SNR in LED-PA images, yet comprehensive evaluations across varied datasets and architectures are lacking. In this study, we systematically assess the efficacy of various Encoder-Decoder-based CNN architectures for enhancing SNR in real-time LED-based PA imaging. Through experimentation with in vitro phantoms, ex vivo mouse organs, and in vivo tumors, we compare basic convolutional autoencoder and U-Net architectures, explore hierarchical depth variations within U-Net, and evaluate advanced variants of U-Net. Our findings reveal that while U-Net architectures generally exhibit comparable performance, the Dense U-Net model shows promise in denoising different noise distributions in the PA image. Notably, hierarchical depth variations did not significantly impact performance, emphasizing the efficacy of the standard U-Net architecture for practical applications. Moreover, the study underscores the importance of evaluating robustness to diverse noise distributions, with Dense U-Net and R2 U-Net demonstrating resilience to Gaussian, salt and pepper, Poisson, and Speckle noise types. These insights inform the selection of appropriate deep learning architectures based on application requirements and resource constraints, contributing to advancements in PA imaging technology.
Keywords: LED based photoacoustic imaging, Deep-learning, Convolutional neural networks, U-Net architectures, Signal-to-noise ratio
1. Introduction
Photoacoustic (PA) imaging, stemming from the pioneering work of Bell [1], is a non-invasive and label-free technique that capitalizes on the synergy between laser and ultrasound technologies, offering high-resolution visualization of biological tissues with excellent optical contrast. PA imaging holds immense promise for clinical applications, such as in cancer theranostics [2], [3], [4], [5], owing to its capability to probe functional and physiological functions in the body at considerable tissue depth [5], [6], [7], [8]. Conventionally, PA imaging employs nanosecond pulse laser systems irradiating tissues at specific wavelengths tailored to tissue optical properties [9], [10]. However, the traditional reliance on these costly lasers, such as the Nd-YAG pumped optical parametric oscillator lasers, has posed challenges regarding mobility and cost-effectiveness. Recent strides have been made towards mitigating these limitations with pulsed laser diode [11], [12] or light emitting diode (LED)-based illumination systems [13], [14]. Specifically, in LED-based systems, despite their advantages in terms of cost-effectiveness and portability, LED arrays face constraints (∼400 ) in delivering high fluence outputs comparable to lasers (∼40–100 ), necessitating compensatory strategies such as high frame averaging [15]. Moreover, the high number of averages needed leads to prolonged acquisition times, impeding real-time imaging crucial for understanding dynamic biological processes in vivo.
Recent advances in PA imaging have witnessed a convergence with deep learning methodologies. For example, numerous significant investigations, including recent reviews [16], [17], [18], [19], in the realm of deep learning applied to laser-based systems have addressed the challenge of under-sampled data sparsity arising from a restricted number of detectors. While various studies have showcased their findings using numerically simulated data and in vitro phantoms [20], [21], [22], [23], [24], [25], [26], only a few have ventured into testing their deep-learning models on in vivo preclinical or clinical data. Moreover, in instances where in vivo data were utilized, both the training and testing datasets were drawn from similar in-class samples (e.g., training and testing conducted on similar phantoms or in vivo vasculature datasets) [27], [28], [29], [30], [31], [32]. This methodology ultimately imposes constraints on the generalizability of the deep networks. Furthermore, it is important to highlight that while most existing studies focus on laser-based PA systems, which are known for their high signal-to-noise ratio (SNR), LED-based PA imaging systems are often underrated due to their lower SNR, despite offering the advantage of a higher image acquisition speed. In our previous work, we demonstrated that SNR in LED-PA imaging can be enhanced with Encoder-Decoder-based Convolutional Neural Network (CNN), specifically U-Net architecture. The network improved the quality of low number of frame average (LA) images by transforming them to a distribution similar to that of high number of frame average (HA) images. The performance was evaluated using no-reference image quality metrics, including SNR, Peak SNR (PSNR), and Contrast-to-Noise Ratio. We also tested the architecture with out-of-class samples (Training data captured from in vitro phantoms, and test data consisted of in vivo mouse tumor samples) in our previous study [33]. However, the spatial resolution of this vanilla U-Net’s outcomes was not satisfactory, and it made the images blurry and also struggled to remove Salt & Pepper (S&P) noise.
In the U-Net-based models, the encoder part extracts feature from the input image by progressively reducing its spatial dimensions while increasing the number of feature maps. This process captures essential patterns and structures in the image, which are crucial for distinguishing noise from actual image content. The encoder captures broad contextual information from the input image, which helps in distinguishing between noise and meaningful signal (Fig. S1, Contextual feature extraction) [34], [35], [36], [37]. The decoder part reconstructs the denoised image from the encoded features by progressively increasing the spatial dimensions to produce a clean image that retains the important features extracted by the encoder while removing the noise (Fig. S1, Detail reconstruction) [34], [35], [36], [37]. The skip connections, also known as feature map concatenations (Fig. S1), help preserve spatial information lost during downsampling and make it easier for the decoder to reconstruct detailed and accurate images [38], [39]. The decoder, especially with the help of skip connections, focuses on integrating local details back into the image. This combination of global context and local details enables effective denoising, as the model can suppress noise while preserving important structures. The Encoder-Decoder architectures learn hierarchical representations of the input data, allowing the model to understand and process the image at multiple levels of abstraction [40] (Fig. S1, Multi-scale feature extraction). This capability is particularly useful for denoising, as noise can manifest at different scales and complexities. Advanced versions of the encoder-decoder-based architecture are needed to overcome the limitations of the original architecture, such as insufficient feature representation, poor gradient flow in deep networks, and lack of robustness to diverse noise types [41]. These limitations or gaps in application can be overcome by incorporating enhancements like deeper architectures, dense connections, and attention mechanisms etc. that are efficient and scalable for various image processing tasks [41], [42]. These architectures can be tailored and fine-tuned for different types of imaging conditions and noise distributions and thus were adapted to work with medical images, natural scenes, and other domains by training on relevant datasets [42], [43], [44], [45], [46], [47].
There is another class of deep learning model, known as Generative Adversarial Network (GAN) [48], [49], [50], which can produce highly realistic images. However, it can also inadvertently introduce artifacts resembling real structures [51], [52], [53], such as the spurious features like additional vessel-like patterns in PA imaging. These spurious features arise because the generator overlearns certain features in an attempt to fool the discriminator, leading to structures that resemble real vessels but are not present in the original image. Moreover, GANs, including Pix2Pix, sometimes suffer from mode collapse, where the generator produces limited variations of patterns, instead of accurately capturing the diversity of the dataset [54], [55], [56]. This limitation often causes the generator to replicate structures across different areas of an image, leading to artifacts that might look like duplicated anatomical features, such as vessel-like shapes appearing in regions without actual vessels. Since Pix2Pix relies heavily on the quality and diversity of paired training data, any noise or bias in the dataset can lead to incorrect generalizations. For LED-based PA imaging, where signals are often faint and susceptible to noise, the Pix2Pix GAN could misinterpret noise or faint signals, resulting in spurious outputs. Also, the discriminator in Pix2Pix is typically trained to classify between real and fake images at a global level and may not enforce pixel-perfect accuracy. This lack of fine-grained supervision can cause spurious artifacts to pass as realistic data, as long as the overall image appears plausible to the discriminator. Given these factors, careful validation is required when using Pix2Pix or GAN networks for tasks where pixel accuracy and the absence of spurious features are essential, making simpler models like U-Net and its variants more reliable for denoising tasks where spatial fidelity is crucial.
To date, no comprehensive study has compared various encoder-decoder-based deep learning architectures on a unified test platform to evaluate their effectiveness in enhancing the SNR on LED-based PA images. Here, we first compared basic convolutional autoencoder and U-Net architectures, discerning the impact of skip connections on image quality metrics. Subsequently, we investigated the influence of hierarchical depth variations within the U-Net framework on SNR enhancement. Next, we conducted a comparative analysis between the basic U-Net model and several advanced versions of U-Net. We also investigated whether introducing deeper layers or incorporating Attention, Dense, Residual, and Recurrent modules lead to any significant SNR enhancements for LED-based PA imaging. Lastly, the deep learning models trained with one type of noise distribution (obtained from LED-based PA system) were tested with datasets corrupted by different noise distribution types, namely Gaussian, Salt and pepper (S&P), Poisson and Speckle, to demonstrate noise type invariance of our networks. Overall, our study underscores the significance of impartial comparison of different encoder decoder-based deep learning architectures and emphasizes that simpler models, despite reduced denoising efficiency, are more practical to use due to their reduced computational complexity.
2. Methodology
2.1. Imaging platform
We captured all the imaging data using AcousticX LED-based PA system (Cyberdyne Inc, Japan). We used a linear array transducer with center frequency of 7 MHz and a −6 dB bandwidth of 80 %, comprising 128 elements. The illumination source consisted of LEDs emitting at a wavelength of 850 nm, delivering 30 nanoseconds pulse width with a pulse repetition frequency (PRF) of 4 kHz. The gain settings remained consistent throughout the experiment, ranging from 60 to 67 dB depending on whether in vitro or in vivo samples were examined. For mouse biology models and metal phantoms, the dynamic range was adjusted to 19 dB and 19–25 dB, respectively. High-frame rate acquisitions occurred at 30 Hz, with data averaging over 128 image frames (referred to as LA), while low frame rate acquisitions were conducted at a rate of 0.15 Hz, resulting in images generated from 25,600 frames (referred to as HA).
2.2. Deep learning coding platform
We performed all the computational tasks in our in-house processing computer built with GeForce RTX 3060 12 GB GPU, Intel(R) Core(TM) i7–11700 @ 2.5 GHz 8-Core processor, 64 GB CPU RAM. The deep learning codes are written in Python 3.9 (Spyder 5.5.1), leveraging the Keras 2.10.0 and TensorFlow 2.10.0 libraries for model implementation, training, and testing. For calculating the time complexity of a model, we used a custom callback function that captures the training time shown by model.fit() for each epoch. We considered either 10 or 30 as the epoch values (mentioned in Table 1) based on the corresponding loss values. Subsequent processing of the acquired beamformed images and implementing the analysis of image quality metrics involved custom-coded MATLAB (R2024a).
Table 1.
Computational complexity (Training and Testing) of different CNN-based deep learning architectures.
| Networks | # Params | Training time(s) / epoch | Test time(ms) | Total epoch |
|---|---|---|---|---|
| Conv AE | 27,891,584 | 21 ± 1 | 19 | 10 |
| UN - 1 layer | 403,328 | 8 ± 1 | 19 | 10 |
| UN - 2 layers | 1861,504 | 14 ± 1 | 20 | 10 |
| UN | 31,025,024 | 27 ± 2 | 20 | 10 |
| UN++ | 36,158,083 | 30 ± 1 | 21 | 10 |
| Dense-UN | 38,961,027 | 48 ± 2 | 21 | 10 |
| Res-UN | 33,158,351 | 33 ± 2 | 21 | 30 |
| Att-UN | 37,334,803 | 37 ± 1 | 21 | 30 |
| Att Res-UN | 39,090,515 | 48 ± 3 | 22 | 30 |
| R2-UN | 176,175,362 | 130 ± 3 | 24 | 10 |
| Double UN | 3760,899 | 25 ± 1 | 19 | 10 |
2.3. Datasets
Training data: Metal frames, wires of various shapes, and graphite rods were utilized in two distinct setups, employing low and high frame averaging for our training inputs and labels, respectively. Images captured by the LED Acoustic-X system were cropped accordingly and resized to 256 × 256 pixels. A total of 3200 snapshots of the objects were gathered at different spatial positions and depths. The dynamic range spanned from 19 to 25 dB, with the gain set at 64 dB.
Test data: Our test dataset is out-of-class data and comprised a diverse array of samples, including metal phantoms assumed to be in-class data distribution, ex vivo biological organs, and in vivo tumors in mice classified as out-of-class distributed data. Ex vivo organ imaging entailed capturing cross-sectional frames of the heart, lung, kidney, and liver tissue from mice. In the in vivo experiments, nude mice were subcutaneously injected with AsPC-1 human pancreatic cancer cells suspended in a mixture of Matrigel (BD Bioscience) and phosphate-buffered saline (1:1 v/v) as previously reported in [33]. Over a period of 55–60 days post-inoculation, the tumors were allowed to grow to a size of approximately 300–400 mm3, exhibiting a heterogeneous microenvironment comprising both vascular and avascular regions.
Prior to imaging, the mice were anesthetized with 2 % isoflurane and positioned on a specially designed platform submerged in a water bath, with their heads elevated above the water level for safety. The isoflurane concentration was then reduced to 1–1.5 % during the imaging procedure to maintain anesthesia. A total of 8 mice were included in the study. The mice had subcutaneous tumors of diameter 9–15 mm. Approximately 9–10 frames were captured at intervals of 1–2 mm for each tumor. The experimental protocols adhered to the guidelines set by The Institutional Animal Care and Use Committee of Tufts University.
Noise distribution details: To ensure noise distribution type invariance of our U-Net architectures, we distorted the ground truth (high number of frame average PA images) with the following types of noise:
-
•
Gaussian white noise[57], [58] constitutes an additive noise characterized by a probability density function (PDF) that adheres to a normal distribution with a variance which we assumed to be of 0.01–0.08 [59], [60], [61]. Mathematically, the PDF can be represented as: , where g is the gray value, mean is 0, and is the variance.
-
•
S&P noise[62], [63] is another sporadic impulse noise, and we considered its distribution with a density of either 5 % or 10 % for pixel destruction [64].
-
•
Speckle noise[65] is a type of multiplicative noise with uniform distribution having zero mean and 0.05 or 0.1 as variance [59], [60], [61].
-
•
Poisson noise[66] distribution depends on the input data type where the PDF for this noise type is given by , where N denotes the number of photons and is the expectation of N [59], [60], [61]. For practical implementation, the process depends on the input pixel values are interpreted as means of Poisson distribution with a scale-up factor of 1e12 if the datatype is double, 1e6 if the datatype is single precision, and uint8 or uint16 datatype values are directly used without scaling.
2.4. Deep learning architectures
Convolutional Auto-Encoder (Conv-AE):
We investigated a Conv-AE [67] architecture comprising four downsampling (Maxpooling layer) and for corresponding up-sampling layers (Conv2D-Transpose) each incorporating two stacks of conv2D filters. The filter stacks initiate with 64 filters and increase by a factor of 2 with each subsequent layer (Fig. 1(a)).
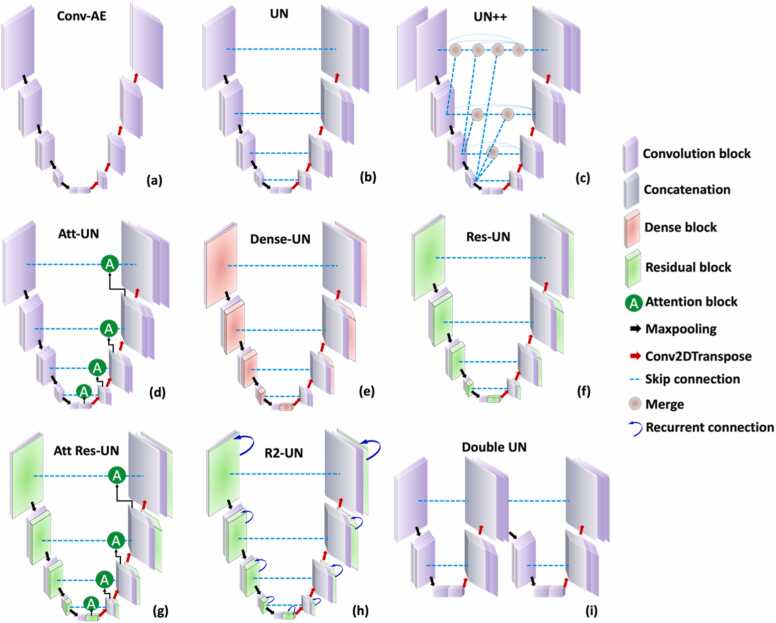
Fig. 1.
Different CNN-based deep learning architectures - Convolution block: conv - BN - ReLU - conv - BN - ReLU - Dropout (if enabled); Residual block: conv - BN - ReLU - conv - BN - shortcut - BN – shortcut + BN – ReLU; Dense block: Convolution block1 - concatenate(Input, Convolution block1) - Convolution block2 - concatenate(Input, Convolution block1, 2) - Convolution block3 - concatenate(Input, Convolution block1, 2, 3) - Convolution block4 - concatenate(Input, Convolution block1, 2, 3, 4); Where, Conv: Convolution; BN: Batch Normalization; ReLU: Activation.
Vanilla U-Net (UN):
We explored a U-Net architecture [68], consisting of an encoder-decoder structure with skip connections, for our investigation. The encoder portion comprises successive layers of Maxpooling, each equipped with two stacks of conv2D filters starting from 64, with the number doubling in subsequent layers. Conversely, the decoder section involves upscaling operations to reconstruct the input image resolution (Fig. 1(b)). In this study, we considered 1, 2 and 4 hierarchical layers of UN.
U-Net++ (UN++):
We opted for a U-Net++ architecture [69], a variant of the traditional U-Net model, renowned for its enhanced feature extraction capabilities through a more intricate skip connection scheme. Similar to the standard U-Net, the UN++ architecture comprises encoder and decoder sections, but with additional skip connections at multiple depths within each side of the network. The encoder portion incorporates successive layers of Maxpooling, with each layer containing two stacks of conv2D filters starting from 64, progressively increasing in number. Conversely, the decoder section utilizes upscaling operations to reconstruct the input image resolution while leveraging the skip connections for feature fusion (Fig. 1(c)).
Dense U-Net (Dense-UN):
In our study, we utilized a Dense UN architecture [28], which integrates Dense-Net blocks [70] into each hierarchical layer of the U-Net model. This novel architecture enhances feature propagation and reuse by establishing dense connections between layers within the network. Each layer in the encoder and decoder sections incorporates Dense-Net blocks, facilitating the direct flow of information from one layer to the next. Similar to the standard U-Net, the encoder section employs successive layers of Maxpooling, with each layer containing two stacks of conv2D filters starting from 64 and progressively increasing. Conversely, the decoder section utilizes upscaling operations to reconstruct the input image resolution while leveraging the dense connections for feature fusion (Fig. 1(d)).
Res U-Net (Res-UN) [71]:
We integrated Res-Net blocks [72] into each hierarchical layer of the U-Net model. This architecture incorporates residual connections within the network, facilitating the propagation of gradients and alleviating the vanishing gradient problem during training. Each layer in both the encoder and decoder sections contains Res-Net blocks, enabling the direct flow of information across layers. The encoder section employs successive layers of Maxpooling, with each layer containing two stacks of conv2D filters starting from 64 and progressively increasing. Conversely, the decoder section employs upscaling operations to reconstruct the input image resolution while leveraging the residual connections for feature fusion (Fig. 1(e)).
Attention U-Net (Att-UN):
We incorporated Attention blocks [73], [74] before each concatenation layer in the Upconvolution pathway of the U-Net model which is known as Attention U-Net [75]. This architecture enables the network to dynamically focus on informative regions of the feature maps. The Attention blocks facilitate the learning of spatial dependencies between feature maps, allowing the network to selectively emphasize relevant features while suppressing irrelevant ones. We used four downsampling and their corresponding upsampling hierarchical layers for our study (Fig. 1(f)).
Attention Res U-Net (Att Res-UN):
Combining both the architectural constructs of Residual and Attention mechanism (Fig. 1(g)), we implemented a four-layered encoder-decoder-based U-Net model, named as Attention Res-U-Net [76]. Residual connections within each convolutional block of both the encoder and decoder enhance gradient flow, feature propagation, and training speed by allowing the gradient to bypass certain layers, facilitating the training of deeper models, and enabling the network to learn more complex features. Attention mechanisms, specifically attention gates, are integrated into the skip connections to dynamically focus on the most relevant parts of the input image, suppressing irrelevant features and highlighting salient ones.
R2 U-Net (R2-UN):
We considered Recurrent Residual (R2) blocks at each layer of the U-Net model, known as R2-UN [77]. This architecture (Fig. 1(h)) combines the benefits of recurrent and residual connections to enhance the model's ability to capture temporal dependencies and preserve spatial information throughout the network. The R2 blocks introduce recurrent connections within each layer, allowing the network to iteratively refine feature representations by incorporating information from previous time steps. Additionally, residual connections are employed to facilitate the flow of gradients during training, mitigating the vanishing gradient problem and enabling more efficient optimization.
Double U-Net (Double UN):
We also considered a Double U-Net architecture [78], which involves connecting two U-Net models, each comprising two hierarchical U-Net networks. The Double U-Net architecture consists of two interconnected pathways, with each pathway comprising an encoder-decoder structure resembling a standard U-Net (Fig. 1(i)). The first pathway serves as the primary U-Net, responsible for extracting high-level features and generating initial predictions. Simultaneously, the second pathway, acting as the secondary U-Net, refines the predictions made by the primary pathway by incorporating additional contextual information and fine-grained details from intermediate feature maps. To optimize the network's performance, we employed the Adam solver [79] with an initial learning rate set to 1e−4, coupled with Mean Squared Error (MSE) loss function [80] for all the networks.
In our application to denoise PA images and improve SNR, it is important to facilitate superior feature learning and preservation of fine image details. As both denoising and segmentation rely on accurate feature extraction, we leveraged observations from a recent demonstration of various U-Net architectures to segment Optical Coherence Tomography images [42]. Though the U-Net variants mentioned above have demonstrated comparable (no statistically significant differences) performance in segmenting, we believe the architectural features provided by the advanced U-Nets will outperform the UN architecture, particularly in improving SNR of images corrupted with various distributions and levels of noise. Amongst the various U-Net architectures, Dense-UN and R2-UN might outperform other U-Net variants in denoising due to their advanced architectural features that enhance feature learning and detail preservation [81], [82], [83], [84]. Dense-UN utilizes DenseNet blocks in both the encoder and decoder, allowing each layer to receive input from all preceding layers within the same block [83], [84]. This continuous flow of information promotes efficient feature reuse, ensuring that fine details are preserved and preventing information degradation that can lead to blurring. The dense connections also improve gradient flow, which helps the network learn effectively, even in deeper layers, leading to more precise reconstructions [85], [86], [87]. On the other hand, R2-UN incorporates recurrent residual connections that iteratively refine feature representations [88], [89], [90]. This recurrent mechanism allows the network to repeatedly enhance its output, reducing blurring and smudging. The residual connections help retain essential input information while focusing on learning the differences between the input and the target, which helps maintain sharp features. Together, these features might make Dense-UN and R2-UN more robust to noise, improving their ability to generalize across different datasets and resulting in superior denoising performance compared to other U-Net variants.
2.5. Image quality metrics
To check the quality of the deep learning model-generated outcomes, we used two full reference image quality metrics which are generally believed to be critical parameters in the assessment.
PSNR: PSNR is a full reference quality metric [91], [92] measured in dB scale which is a ratio signal and into account and is expressed in logarithmic terms because signals sometimes might have a dynamic wide range. is defined as
, where is the maximum possible pixel value of image .
SSIM: Structural similarity index () [93], [94] is another full reference image quality metric ranging between 0 and 1 which measures the amount of distortion in a reconstructed image compared to the ground truth. is defined as
, where is the sample mean of , is the variance of , covariance of & , and () and () are determined based on and which are set as 0.01 and 0.03, respectively, and is the dynamic range.
3. Results and Discussions
3.1. Computational complexity
Table 1 provides insights into the complexity and computational efficiency of various neural network architectures based on their number of parameters, training time per epoch (300 as the steps per epoch), test time and total epochs. The computational time was calculated using TensorFlow Core’s fit() function (model.fit(data_set_details,steps_per_epoch=300,epochs=10,callbacks=model_checkpoint)). We used data generator (tf.data.Dataset) to load our training data in batches. The parameter ‘steps_per_epoch’ informed the model how many batches it should process before considering one epoch complete. Our models consider one epoch to be completed after processing 11 (3200/300) batches. Among the architectures evaluated, the Convolutional AE exhibits a moderate parameter count (27,891,584) and a shorter running time (21 ± 1 seconds) compared to the UN architecture with 4 layers that exhibits a moderate number of parameters (31,025,024) and a relatively short running time per epoch (27 ± 2 seconds). In comparison, the UN++ architecture, despite having a slightly higher parameter count (36,158,083), demonstrates a comparable running time (30 ± 1 seconds). Conversely, the Dense-UN architecture, with a higher parameter count (38,961,027), requires a significantly longer running time per epoch (48 ± 2 seconds), indicating increased computational complexity. Similarly, the Res-UN and Att-UN architectures show variations in parameter count and running time, with the former having slightly fewer parameters (33,158,351) and a shorter running time (33 ± 2 seconds) compared to the latter (37,334,803 parameters, 37 ± 1 seconds). The Att Res-UN architecture exhibits a higher parameter count (39,090,515) and a longer running time (48 ± 3 seconds) than both the Res-UN and Att-UN models. In contrast, the R2-UN architecture stands out with a significantly larger parameter count (176,175,362) and substantially longer running time (130 ± 3 seconds), indicating significantly higher computational demands. The Double UN architecture, composed of two layers each, demonstrates relatively low parameter count (3760,899) and a moderate running time (25 ± 1 seconds). Regarding training time performance, we found that among UN-4 layer, R2-UN, and Dense-UN, the UN-4 layer is the quickest to train, completing in 27 ± 2 seconds. Dense-UN requires 48 ± 2 seconds, while R2-UN takes the longest training time at 130 ± 3 seconds. We have also included the test times (per image) for all networks in Table 1. The test times were calculated using TensorFlow Core's predict_generator() function (model.predict_generator(test dataset, number of data, verbose=1)). The results show that there is negligible difference in running time (test) among these networks. From these results, we can infer that the deep learning networks are capable of real-time denoising.
3.2. Importance of skip connection and layer depth in encode-decoder architectures
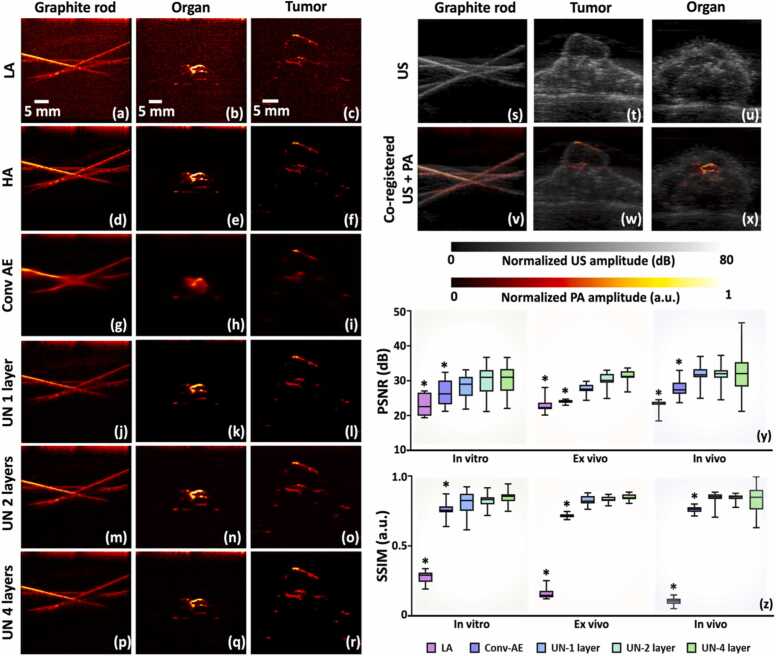
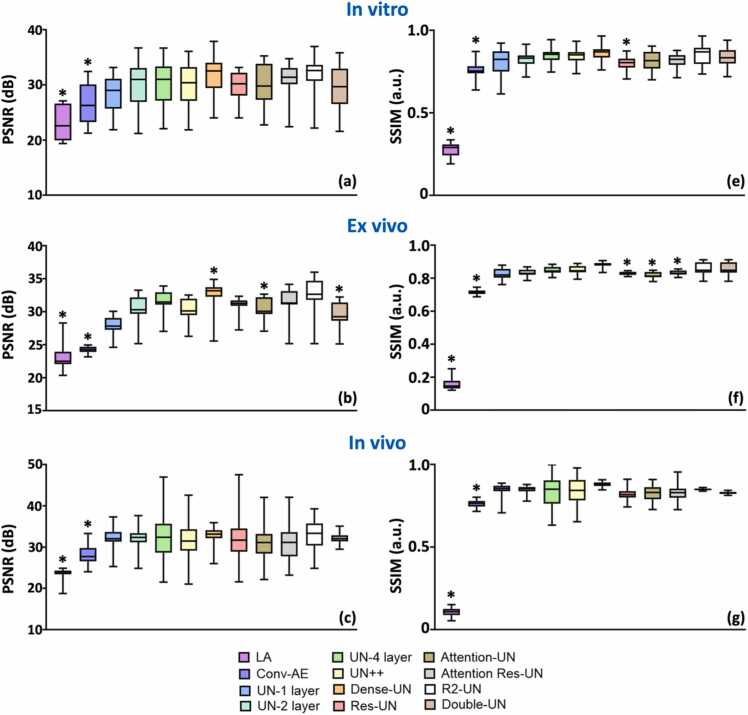
We conducted a comparison between Conv-AE and U-Net, both comprising 4 hierarchical layers, focusing on the significance of skip connections, as illustrated in Fig. 2. Our evaluation involved testing both deep learning architectures using in vitro phantoms, ex vivo mouse organs, and in vivo subcutaneous mouse tumors, as depicted in the respective columns in the left part of Fig. 2. First three rows and the last row of the Fig. displayed outcomes for LA (Fig. 2(a-c)), HA (Fig. 2(d-f)), Conv-AE (Fig. 2(g-i)), and UN with 4 layers (Fig. 2(p-r)), respectively. Specifically, the first column showcased a sample of a graphite rod embedded in a gelatin block representing in vitro phantoms, the second column displayed a cross-section of a mouse liver representing ex vivo organs, and the third column depicted a sample cross-section of in vivo subcutaneous mouse tumors. Our next focus was on examining the importance of hierarchical depth concerning downsampling in the UN architecture. We analyzed UN models with a depth of 1 layer, 2 layers, and 4 layers, displaying their respective results in Fig. 2(j-l), (m-o), and (p-r). We utilized the same three test datasets to evaluate the network depths. We presented the respective ultrasound (US) images in Fig. 2(s-u) and the co-registered US and PA images to demonstrate alignment of US morphology with the PA functional information. Fig. 2(y) and (z) depict box plots illustrating the PSNR and SSIM comparisons, respectively, among Conv-AE, and three UNs with varying hierarchical layers across three test scenarios: in vitro, ex vivo, and in vivo.
Fig. 2.
(a-r) Comparative analysis of Conv-AE and U-Net architectures with emphasis on skip connections and depth, evaluated across in vitro phantoms (First column), ex vivo mouse organs (2nd column), and in vivo subcutaneous mouse tumors (last column). (s-u) Ultrasound images of in vitro, ex vivo and in vivo objects. (v-x) The corresponding co-registered US+PA images include HA PA images in the foreground with US image in the background shown in gray scale. Additionally, box plots illustrate (y) PSNR and (z) SSIM comparisons across architectures and test scenarios (1st column – In vitro samples, 2nd column – Ex vivo tissue, and last column – In vivo tumor tissue). (*: p < 0.05).
The architecture of UN closely resembles that of the Convolutional Autoencoder, with the key distinction of including the skip residual connections from encoder to decoder pathways at each layer. Therefore, when assessing the denoising capabilities of both networks across various test image distributions, the superior performance of UN in terms of PSNR and SSIM (Fig. 2) underscores the importance of these skip connections. Skip connections enable the direct flow of information from the encoder to the decoder layers. This might have helped in preserving fine-grained spatial details that might otherwise get lost during the downsampling process. The skip connections also facilitated feature reuse, enabling the model to leverage both low-level and high-level features for better performance. These shortcut residual connections also helped alleviate the probable vanishing gradient problem in the Conv-AE network by providing additional paths for gradients to flow backward through the network [95], [96]. The residual connections also helped the network handle variations in the input data more effectively and allowed the network to access both abstract features and detailed features simultaneously. Our findings (Fig. 2 last three rows on the left side) regarding the importance of hierarchical depth in the UN architecture with 1, 2, and 4 layers indicate that increasing the hierarchical depth of the UN did not yield significant improvements in performance. Despite the additional layers, the higher-depth UN variants did not exhibit a considerable enhancement in image quality metrics, as illustrated by the PSNR and SSIM comparisons depicted in Fig. 2(y) and (z). Noise in images is typically a local phenomenon. Hence, effective denoising was achieved by capturing and reconstructing local features, which did not necessarily require very deep networks. Note that the standard UN consistently performed well across all the test scenarios. However, considering that the inference time for all network depths was not significantly different (in the order of ∼ for all of them), the standard UN emerges as a practical and effective solution. Additionally, we also trained the UNs with different depth layers using smaller number of datasets (200, 500, and 1000) whose quantitative outcomes are shown in supplementary Fig. S2 and table ST1. We found no statistically significant difference among the networks’ performance with respect to the two image quality metrics. One of the plausible reasons for such high performances of the networks even with smaller number of datasets might be the advantage of over-parameterized architectures where the training and test loss both reduce for the second time after the initial increment of test error, traditionally known as bias-variance trade-off [97], [98], [99], [100], [101], [102]. These results underscore the importance of carefully evaluating the hierarchical depth of neural network architectures to ensure optimal performance and efficiency in real-world applications. While depth can enhance the performance of U-Nets for tasks requiring complex feature hierarchies and high-level abstractions, it does not significantly impact the effectiveness of denoising tasks because denoising relies on capturing and reconstructing local, low-level features, which might sometimes be achieved with shallower architectures.
3.3. Evaluation of different deep learning architectures
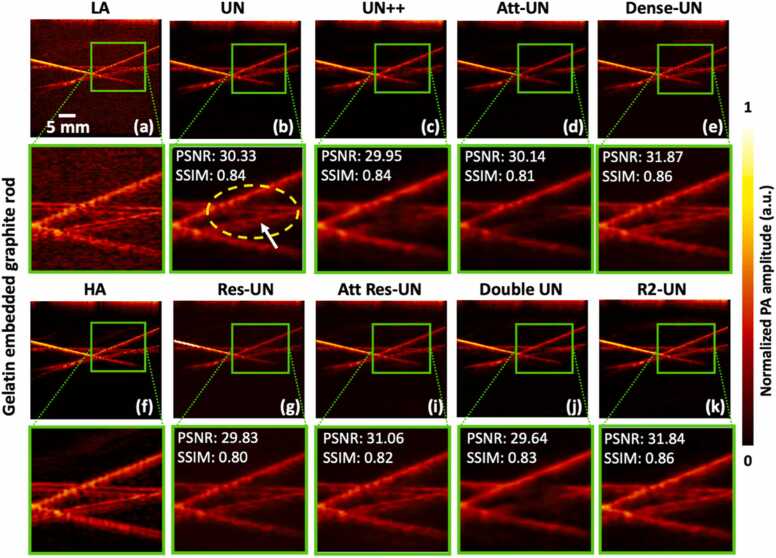
In this segment, we examined all the U-Net variations on in vitro phantoms. Fig. 3 illustrates the performance evaluation of these architectures in the first and third rows, while the zoomed-in view of the spatial reconstruction, highlighted by the green box, is presented in the second and fourth rows. As an example, we showcase the outcomes for a cross-section of the gelatin-embedded graphite rod phantom. In the zoomed-in section of Fig. 3(b), the white arrow highlights that the signal is preserved by the UN, Dense-UN, Res-UN, and R2-UN models while others were not able to do so. However, it is also evident that there is a degree of smudging or blurring around the yellow-dashed elliptical area in the results produced by all these networks, except for the Dense-UN and R2-UN models which reduce this degradation effect.
Fig. 3.
Showcasing SNR improvement for various U-Net variations on in vitro gelatin-embedded graphite rod phantom. First and third rows depict denoised images of the phantom by corresponding architectures; Second and fourth rows offer a zoomed-in view of spatial reconstruction, enclosed by the green box.
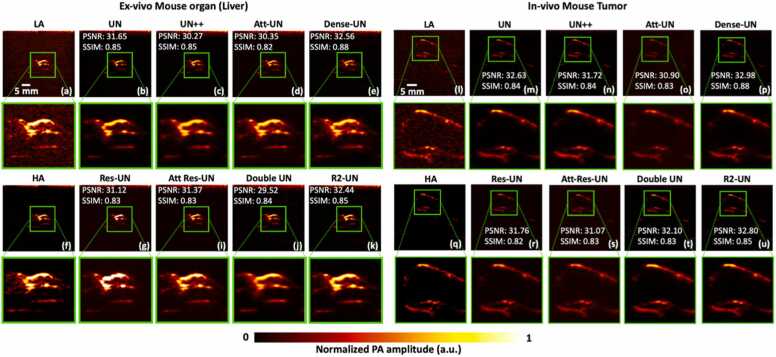
In the case of ex vivo mouse organs, Fig. 4(a-k) in the left half illustrates the comparative performance of all U-Net variants in the first and third rows. The second and fourth rows feature a zoomed-in view of the spatial reconstruction within the green boxed region for clearer observation. We opted to display a cross-section of a mouse liver for illustration purposes. On the right side, Fig. 4(l-u) presents identical scenario as Fig. 3 and Fig. 4(a-k), with the distinction that the test data pertains to a cross-section of an in vivo mouse subcutaneous tumor. For each type of test dataset, box plots were created to evaluate the performance of various U-Net variants focusing on the two metrics: PSNR and SSIM. These box plots, presented in Fig. 5(a) and (b) respectively, provide a visual representation of the distribution of PSNR and SSIM values for each model across different datasets. For the ex vivo organ, Res-UN was noted to over-saturate the outcome (Fig. 4g) as it amplified specific features and intensities. Conversely, for other outputs (Fig. 3g, and Fig. 4r), the network managed to balance the feature intensities appropriately, preventing the oversaturation.
Fig. 4.
(a-k) Depicting SNR improvement for various U-Net variations on ex vivo gelatin-embedded mouse liver. First and third rows depict denoised images of the phantom by corresponding architectures; Second and fourth rows offer a zoomed-in view of spatial reconstruction, enclosed by the green box. (l-u) Snapshot of SNR improvement for various U-Net variations on in vivo mouse subcutaneous tumor. First and third rows depict denoised images of the phantom by corresponding architectures; Second and fourth rows offer a zoomed-in view of spatial reconstruction, enclosed by the green box.
Fig. 5.
Statistical evaluation of SNR improvement and structural preservation for reconstructed images by various U-Net variations on in vitro, ex vivo, and in vivo test dataset. Comparing image quality metrics (a-c) PSNR (e-g) SSIM for different network’s performance. All the comparisons are done with respect to the 4-layered UN’s performance. (*: p < 0.05). Non-significant statistics are not represented in the graphs. Tabulated values are shown in Table ST2.
The results (Fig. 5, Fig. S3 and Table ST2) revealed that Dense-UN exhibited superior performance (better preservation of spatial structure and resolution) among all network variants, closely followed by R2-UN and UN-4 layers. Table ST2 represents the quantitative performance of different deep learning architectures summarizing the mean and standard deviation of PSNR and SSIM values for all types of test datasets. Similar data is also represented as percentage improvement of the image quality metrics of the U-Net variants’ outcomes relative to LA images in Fig. S3. The differences in the metric values between various U-Net architectures are not statistically significant for both percentage change and absolute quantitative values of PSNR and SSIM. Notably, the improvement in SSIM was more pronounced compared to the improvement in PSNR, with the scale of SSIM enhancement being more substantial. Interestingly, the increase in network complexity did not result in significant performance improvements, suggesting diminishing returns with higher complexity. Moreover, the introduction of an Attention module in UN-4 layers did not lead to substantial performance gains but inevitably increased network complexity. Adding more skip connections or Attention mechanisms to a U-Net does not automatically guarantee better denoising performance. Issues such as overloading the decoder with redundant information, diluting high-level contextual features, and potential reinforcement of noise due to the addition of extra skip connections can all contribute to the lack of improvement [103], [104]. On the other hand, noise confounding attention and task specificity of the Attention process might inherently limit its denoising capability [105]. More skip connections might also cause the model to prioritize low-level features (such as textures and edges) over high-level contextual features, which are crucial for effective denoising [106]. This can result in suboptimal denoising where the model focuses too much on reconstructing fine details and textures that might include noise, rather than leveraging broader context to remove noise. While attention mechanisms are powerful for tasks like segmentation or classification, they might not be inherently well-suited for denoising tasks.
Notably, R2-UN demonstrated slightly better results than UN, and Dense-UN performed better denoising than R2-UN, re-highlighting the significance of skip connections in improving denoising performance. The incorporation of R2 blocks enabled the network to leverage both short-term and long-term temporal dependencies in the input data, enhancing its ability to model complex relationships and patterns. By integrating R2 blocks into the UN architecture, our objective was to exploit their synergistic effects to improve feature learning and representation, thereby enhancing the model's performance in tasks such as image denoising and reconstruction. By capturing contextual dependencies, R2-UN achieved better performance in denoising, where understanding the context around each pixel was important. Residual connections also promoted feature reuse, making it easier for the network to learn and utilize complex patterns without requiring an excessively deep architecture. Overall, the combination of residual and recurrent layers enhances the network's robustness to noise and variations in the input data, improving its generalization capabilities across different datasets. For the Dense-UN architecture, each layer in the encoder and decoder sections incorporates Dense-Net blocks, facilitating the direct flow of information from one layer to the immediate next. This enabled efficient feature reuse and enhanced gradient flow throughout the network by ensuring that each layer receives the feature maps from all preceding layers within the same dense block. By concatenating feature maps from all previous layers, Dense-UN ensures that information flowed effectively throughout the network and this continuous flow of information helped the network maintain a comprehensive understanding of the input data. Each layer in Dense-UN had direct access to the gradients and features from all preceding layers, allowing it to learn a diverse set of features. The dense connections also had a regularizing effect, which helped prevent overfitting. This enhanced the network’s ability to generalize well to new, unseen data. Hence, Dense-UN resulted in somewhat best outcomes (if not statistically significant) with enhanced feature reuse, improved gradient flow, parameter efficiency, and strong generalization.
Additionally, we observed for a few scenarios (Fig. 5, in vitro and ex vivo) that the standard deviation of Dense-UN is higher compared to many other networks. The higher standard deviation in PSNR values for Dense UN, despite its higher mean, could be attributed to the network's sensitivity to certain image features or noise characteristics that cause greater variability in reconstruction quality across different samples [36], [107]. PSNR, which measures the ratio between the maximum possible power of a signal and the power of corrupting noise, is highly sensitive to even small differences in pixel intensity, especially in areas with high contrast or sharp edges. Dense-UN's complex architecture, which involves dense connections and deeper layers, may lead to better overall denoising performance (hence the higher mean PSNR) but also introduces variability in how it handles noise distribution characteristics or image structures, leading to a higher standard deviation. In contrast, SSIM measures structural similarity by focusing on changes in structural information, luminance, and contrast, making it more robust to small pixel-level variations that might significantly impact PSNR. Dense-UN's ability to effectively preserve and reconstruct the overall structure of images likely results in both higher mean SSIM values and lower or similar standard deviations. The network’s architecture is likely more consistent in maintaining structural integrity across different images, leading to less variability in SSIM compared to PSNR.
Another aspect to be noted on the Dense-UN and R2-UN architectures is their ability to avoid blurring of the PA images. In the case of Dense-UN architecture, due to the dense connection’s feature reuse property, low-level features can be directly passed through the network, enhancing fine detail preservation, and learning of diverse features without unnecessary redundancy [85], [86], [87]. By continuously passing fine-grained details throughout the network, Dense-UN reduces the risk of information degradation that could lead to blurring. The dense connections help ensure that the decoder has access to detailed, high-resolution features that are crucial for reconstructing sharp images. Also, the improvement of gradient flow during training mitigated vanishing gradients ensuring the deeper layers in the network to learn effectively. The better training dynamics contributed to a more precise reconstruction of image details, thus reducing smudging in the Dense-UN images. In the case of R2-UN architecture, the incorporation of recurrent residual connections refined feature representations iteratively, improving the network’s ability to correctly capture fine details [88], [89], [90]. The recurrent mechanism allows the network to reconsider and enhance its output multiple times, reducing the likelihood of blurring and smudging. The residual connections in R2-UN helped in retaining the original input’s information while focusing on learning the residuals (differences) between the input and the target. By focusing on the residuals, R2-UN maintained sharp features and preventing the loss of details that can lead to smudging or blurring.
3.4. Noise invariancy test for top performing deep learning networks
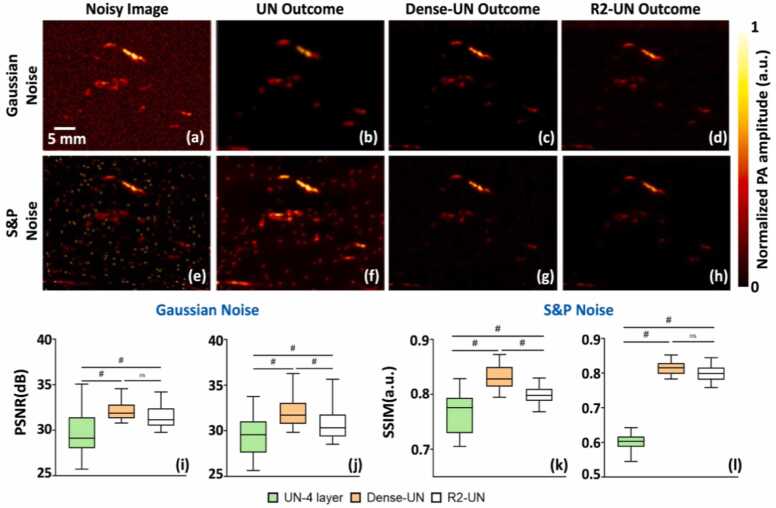
We assessed the robustness of the top-performing network to various types of noise distributions, including Gaussian, S&P, among others. Our comparative analysis included the UN, Dense-UN, and R2-UN deep learning frameworks. As depicted in the first column of Fig. 6, the top row presents an image corrupted with Gaussian white noise (variance = 0.01), while the second row displays an image corrupted with S&P noise (5 %-pixel destruction). The B-scan PA images shown in Fig. 6 are specifically from a subcutaneous mouse tumor. Subsequent columns illustrate respective outcomes generated by the UN, Dense-UN, and R2-UN architectures. The last row of Fig. 6 presents comprehensive PSNR and SSIM comparison for images reconstructed by the networks when subjected to Gaussian (Fig. 6i and k) and S&P (Fig. 6j and l) noise corruption. The results revealed that while the UN efficiently removed Gaussian white noise, it struggled to address S&P noise types effectively. In contrast, Dense-UN and R2-UN exhibited robustness in denoising both types of noise. Dense-UN tends to overfit less, which improves its generalization to unseen noise patterns. The integration of more residual and recurrent connections within the convolution blocks of R2-UN might have enhanced the model's resilience and versatility in handling multiple noise distributions. Its ability to integrate contextual information across iterations helped in understanding the structure of noise and signal. Overall, dense connections in Dense-UN ensure rich feature reuse and multi-scale information capture, while R2 layers in R2-UN enable iterative refinement and better gradient flow. These characteristics collectively contributed to their strong denoising capabilities and invariance to different types of noise.
Fig. 6.
Evaluation of noise invariancy for top-performing deep learning networks: (a) and (e): showcase images corrupted with Gaussian white noise (variance = 0.01) and S&P noise, derived from a subcutaneous mouse tumor cross-section. The outcomes produced by (b) and (f): UN, (c) and (g): Dense-UN, and (d) and (h): R2-UN architectures demonstrate their robustness to various noise distributions. Last row: PSNR comparison for the networks’ reconstructed images whose input was corrupted by (i) Gaussian and (j) S&P noise. SSIM for networks’ outcomes whose input was adulterated by (k) Gaussian and (l) S&P noise. (#: p < 0.001, ns: Not Significant).
Table 2, Table 3 summarize the performance of our networks on four different types of noise distributions with varying noise parameters based on the two image quality metrics. Specifically, removal of Gaussian, S&P, Speckle and Poisson noise is reported. In agreement with the images in Fig. 6, the results in the Table 2, Table 3, and Fig. S4 clearly demonstrated that the three DL networks—UN-4 layer, Dense-UN, and R2-UN—exhibited robustness across most noise distributions. However, all three networks showed a notable exception in their performance with S&P noise. Specifically, the UN-4 layer network struggled significantly when exposed to S&P noise (mean SSIM value is significantly less for UN-4 layer in Table 3 and Fig. S4), involving 5 %- and 10 %-pixel corruption, where a considerable portion of the image pixels were randomly altered. This led to a marked degradation in the network's ability to recover the original image, highlighting its vulnerability to this type of noise. In contrast, the Dense-UN and R2-UN networks displayed robust performance across all tested noise distributions, including the challenging S&P noise scenarios.
Table 2.
PSNR metric values for UN-4 layer, Dense-UN and R2-UN networks concerning different noise distribution types with certain parameters – Gaussian, S&P, Speckle and Poisson.
| Noise type | Noise Details | UN-4 layer | Dense-UN | R2-UN |
|---|---|---|---|---|
| Gaussian | 29.592.203 | 32.12 | 31.431.171 | |
| 29.370.875 | 31.081.108 | |||
| 28.54 | 30.95 | 30.59 | ||
| S&P | Pixel destruction = 5 % | |||
| Pixel destruction = 10 % | ||||
| Speckle | ||||
| Poisson |
Table 3.
SSIM metric values for UN-4 layer, Dense-UN and R2-UN networks concerning different noise distribution types with certain parameters – Gaussian, S&P, Speckle and Poisson.
| Noise type | Noise Details | UN-4 layer | Dense-UN | R2-UN |
|---|---|---|---|---|
| Gaussian | 0.035 | 0.83 | 0.800.015 | |
| 0.036 | ||||
| S&P | Pixel destruction = 5 % | |||
| Pixel destruction = 10 % | ||||
| Speckle | ||||
| Poisson |
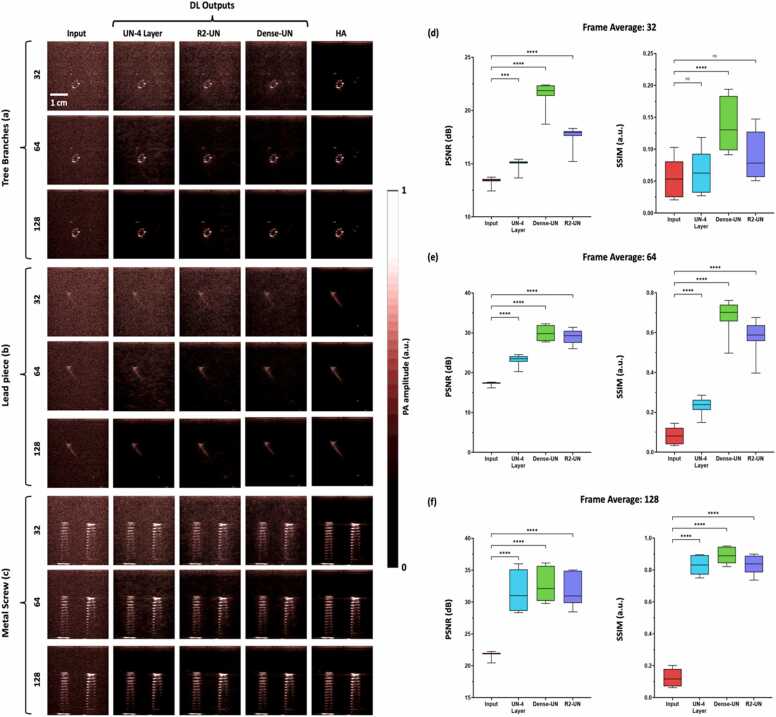
We further evaluated our best performing networks (UN-4 layer, Dense-UN, and R2-UN) ability to denoise images obtained with frame averages less than 128 frames. The lowest frame average data available on Acoustic-X LED system is 128 frames with 4 kHz PRF setting. To obtain lower frame averages, we lowered the PRF to 1 kHz to achieve 32- and 64-frame averages. Fig. 7 illustrates the outcomes of the networks on PA images obtained using three phantoms - tree branches, lead pieces, and metal screws. All the three networks had statistically significant higher PSNR and SSIM values compared to the 64-frame average inputs. Specifically in the 32-frame averaging images, residual noise in the outputs caused lower SSIM values, leading to non-significant SSIM improvements for UN-4 layer and R2-UN compared to the inputs (Fig. 7d, e, f, and Table ST3). Overall, Dense-UN still achieved significantly higher SSIM values and outperformed the other two models in the 32- and 64-frame average cases (Fig. 7d, e, f, and Table ST3). As frame averaging increased, image quality improvements plateaued, with all networks converging to similar performance, consistent with our previous findings.
Fig. 7.
Noise invariance testing of deep learning networks across varying noise levels and frame averaging - Noise-level invariance was evaluated using three phantom datasets: (a)tree branches, (b) lead pieces, and (c) metal screws. (d, e, f) Across all frame averaging cases, deep learning networks (UN-4 layer, R2-UN, and Dense-UN) demonstrated significantly higher PSNR values than their corresponding inputs. For 32-frame averaging, the residual noise in outputs led to non-significant SSIM improvements for UN-4 layer and R2-UN, but Dense-UN achieved significantly higher SSIM values. As frame averaging increased, image quality improvements plateaued, and the networks converged to similar performance observed in (f).
Assessing the performance of deep learning networks under various noise conditions is crucial for evaluating their robustness in real-world scenarios, where imaging may be constrained to different (and sometimes unknown beforehand) noise sources. Understanding a model's ability to generalize across diverse noise distributions provides valuable insights into its applicability and informs decisions regarding its deployment and potential enhancements. By evaluating how well a model performs in unseen, real-world situations, researchers, and practitioners can make informed choices about the suitability of the model for real-life applications and identify areas for further refinement. This understanding of a deep learning model's robustness to different noise distributions is essential for ensuring the effectiveness and reliability in real-world settings. Higher PSNR values across all datasets indicates that the networks, particularly Dense-UN, are capable of learning to denoise effectively, even in scenarios where the noise level exceeds that present in the training data. However, the SSIM performance was more variable, especially for the 32-frame averaging case, where the increased noise led to reduced structural similarity in the outputs. While both UN-4 layer and R2-UN failed to show significant SSIM improvements in this condition, Dense-UN maintained a statistically higher SSIM, likely due to its superior ability to preserve fine structural details. This advantage can be attributed to Dense-UN's dense connections, which facilitate better feature propagation and reuse, allowing the network to retain more contextual information about the image structure despite higher noise levels. Additionally, Dense-UN's richer representation of features makes it more robust to varying noise levels, as it can model both local and global patterns in the noisy data. R2-UN, with its recurrent connections, adds some advantage in handling repetitive structures, but it doesn't provide the same level of feature diversity as Dense-UN. The dense connections allow Dense-UN to learn a more diverse set of features across different scales and levels of abstraction. This makes it more adaptable to different levels of noise and variations in noise distribution, giving it a higher capacity to generalize under conditions that deviate significantly from the training data. The quality improvement performance converging across models suggests that once the noise level becomes sufficiently low, the advantages of more complex architectures like Dense-UN are less pronounced, as all models can adequately handle the remaining noise.
In addition to U-Net architectures, complex architectures such as GANs and Diffusion models are powerful and have been used in various image processing applications [49], [50], [108], [109], [110], [111], [112], [113], [114], [115], [116]. However, they can inadvertently introduce artifacts, such as spurious vessel-like patterns in PA imaging. These artifacts mainly arise because the GAN generator often emphasizes learned features to fool the discriminator, potentially creating patterns unrelated to the actual content. Issues like mode collapse and reliance on training data quality can further amplify this effect, leading to repetitive or incorrect structures in the output, particularly in noisy or low-signal environments like LED-based PA imaging [55], [56], [117]. Moreover, the specific requirements needed for enhancing SNR in LED-PA imaging, such as training stability, interpretability, task specificity, data requirements and computational complexity, also make U-Net variants more appropriate choice and we discuss each of these aspects in detail as below:
Training Stability and Interpretability: U-Net has been widely recognized as one of the most effective and interpretable architectures for various biomedical imaging tasks, including segmentation, denoising, and enhancement [118]. Advanced and complex GAN-based architectures face challenges associated with training, particularly in achieving a stable balance between the generator and discriminator [119]. This might lead to issues like mode collapse or unstable convergence, which require careful tuning and more computational resources. Diffusion models also involve complex stochastic processes that can make it harder to interpret and predict, especially in a clinical context where understanding the model's decisions is crucial. In contrast, U-Net is more straightforward architecture to implement and train, providing a more stable and reliable approach [120], [121], [122], [123], [124], [125], [126].
Specificity to the Task: U-Net based architectures are well-suited for capturing fine-grained details at multiple scales [127], [128], [129], [130], which is essential in tasks like LED-PA imaging where preserving spatial resolution and structural information is crucial and particularly well-suited for our SNR improvement task. While GANs excel in generating realistic images, they may introduce artifacts or lose detail in high-precision tasks where exactness is more important than realism [131], [132], [133].
Data Requirements and Computational Efficiency: The advanced learning networks such as GAN or Diffusion models generally require large amounts of data to train effectively [134], [135], [136], [137], [138], require more resources for both training and inference [139], [140], [141], [142], [143] to produce high-quality results compared to the U-Net variants. In the context of LED-PA imaging, data availability is limited, making U-Net architectures a more practical choice. For example, we demonstrated that even with low number of training samples, all variants of U-Net provided satisfactory PSNR and SSIM (Fig. S2), which is due to its efficient use of convolutional layers and skip connections that retained the detailed information.
Our findings revealed consistent denoising performance even with a reduced number of datasets (Table ST1). This could potentially be due to overparameterization, and our future work will involve understanding the underlying mechanisms, particularly the potential impact of over-parameterization and the role of data augmentation techniques. Additionally, our future studies will also involve a comprehensive evaluation of U-Net, Dense-UN, and R2-UN networks' robustness to noise, incorporating theoretical frameworks and rigorous statistical methods. We will create advanced synthetic noise models tailored specifically to LED-based PA imaging, using these models to simulate noise-augmented training data which will lead to more robust networks capable of handling various real-world noise conditions. To enhance the performance of the networks, we also aim to refine their architectures by integrating attention mechanisms or recurrent blocks with Dense networks, potentially combining the strengths of these approaches for superior denoising capabilities. With recent advances in Vision Transformers and hybrid CNN-Transformer models [144], [145], [146], [147], [148], exploring these architectures in PA imaging could provide new insights into handling complex spatial dependencies and improving noise reduction in challenging low-SNR settings. Furthermore, a detailed exploration of the interpretability and explainability of these networks is essential. This would involve a mathematical analysis of how individual architectural components impact denoising performance, providing insights into the specific contributions of different network features. To make denoising models more transparent, future research will also focus on explainability techniques such as Grad-CAM or saliency mapping to identify which features and structures are prioritized by the model [149], [150], [151], [152]. This would provide insights into how models differentiate between noise and meaningful signal. Finally, our future work will involve evaluating the platform independence nature of the networks on data obtained from photoacoustic imaging systems with various configurations (laser based, laser diode based, microscopy and tomography systems etc.).
In summary, our findings underscore the importance of selecting the appropriate deep learning architecture based on specific application requirements, training time, performance and resource constraints. Our analysis indicates a trade-off between these parameters simpler models are more computationally efficient, but advanced models like Dense-UN and R2-UN offer potentially better performance at the cost of higher complexity. While Dense-UN may be preferable for high-end resource-rich system environments, UN still remains a viable option for resource-constrained environments, delivering satisfactory denoising performance comparable to the state-of-the-art models. This study provides insights for optimizing model selection in practical settings, assessing both performance and resource considerations.
4. Conclusion
A comprehensive comparative study presented here provides a foundation for choosing robust architectures that deliver consistent performance, aiding in the clinical translation of PA imaging to point-of-care or bedside applications where reliability and speed are essential. We evaluated various Encoder-Decoder-based CNN architectures systematically to enhance the SNR in real-time LED-based PA imaging. First, we analyzed the computational complexity of all the models. Then we compared the basic convolutional autoencoder and U-Net architectures, discerning the impact of skip connections on image quality metrics. Next, we investigated the influence of hierarchical depth variations within the U-Net framework on SNR enhancement. Subsequently, we conducted a comparative analysis between the UN model and several advanced iterations of U-Net. We also conducted an evaluation of top-performing networks’ resilience to various noise type distributions (Gaussian, S&P, Poisson, and Speckle). Our experimental evaluations encompassed in vitro phantoms, ex vivo mouse organs, and in vivo subcutaneous mouse tumors. Our findings indicate that skip connections play a crucial role in preserving fine-grained spatial details and facilitating feature reuse, as demonstrated by the superior performance of UN compared to Convolutional Autoencoder in terms of PSNR and SSIM. Increasing the depth of the UN did not lead to significant improvements in performance. The performance is also invariant to the number of training samples as the noise is typically a local phenomenon, suggesting that the standard UN may be the optimal choice for practical applications due to its consistent performance across all test scenarios. Furthermore, our exploration of various U-Net architectures demonstrated that Dense-UN showcased superior performance based on the two image quality metrics – PSNR and SSIM (even though statistically not significant) compared to all other network variants, with R2-UN and UN following closely. Nevertheless, the upscaling of network complexity did not yield substantial enhancements in performance, suggesting diminishing returns as complexity increased. Finally, our research delved into assessing the resilience of the top-performing networks against various noise distributions. We found that Dense-UN and R2-UN demonstrated resilience in effectively reducing Gaussian, S&P, Poisson, and Speckle noise types, while UN encountered difficulties with S&P noise. These outcomes emphasize the significance of carefully choosing the appropriate deep learning architecture, tailored to specific application needs and resource constraints. Dense-UN might be preferred for well-resourced systems, whereas UN remains a feasible choice for environments with limited resources, offering satisfactory denoising performance akin to the state-of-the-art models. In essence, our investigation offers valuable insights for optimizing model selection in practical scenarios, considering both performance and resource constraints.
CRediT authorship contribution statement
Srivalleesha Mallidi: Writing – review & editing, Writing – original draft, Visualization, Supervision, Resources, Project administration, Methodology, Funding acquisition, Conceptualization. Avijit Paul: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to acknowledge support from Tufts School of Engineering, Tufts Data Intensive Science Center Pilot grant and Dr. Tayyaba Hasan for Subcontract funds on NIH grant 5R01CA231606. The authors would also like to acknowledge Dr. Marvin Xavierselvan for help with tumor implantation and Ms. Allison Sweeney for handling animal care.
Biographies
 Avijit Paul received the Bachelor of Technology degree in computer science and engineering from the KGEC, WBUT, India, in 2008, and the Masters in Intelligence Systems (CSE) degree from University of Sussex, U.K., in 2012. He has more than 11 years of experience as a software developer, a technical lead, and a project management lead in several MNCs in India. He is currently pursuing PhD in Biomedical Engineering from iBIT lab, Tufts University, USA. His present research interests include ML/DL learning applications for biomedical imaging and signal processing especially in Photoacoustics and Photodynamic therapy. He is also interested in understanding and analyzing computational aspects of the human visual system with ML/DL.
Avijit Paul received the Bachelor of Technology degree in computer science and engineering from the KGEC, WBUT, India, in 2008, and the Masters in Intelligence Systems (CSE) degree from University of Sussex, U.K., in 2012. He has more than 11 years of experience as a software developer, a technical lead, and a project management lead in several MNCs in India. He is currently pursuing PhD in Biomedical Engineering from iBIT lab, Tufts University, USA. His present research interests include ML/DL learning applications for biomedical imaging and signal processing especially in Photoacoustics and Photodynamic therapy. He is also interested in understanding and analyzing computational aspects of the human visual system with ML/DL.
 Dr. Srivalleesha Mallidi received her Masters and PhD Degree in Biomedical Engineering from the University of Texas at Austin. Her graduate work was on molecular specific photoacoustic imaging to understand nano-molecular interactions. After graduation, she joined Wellman Center for Photomedicine (WCP) at Massachusetts General Hospital (MGH), Harvard Medical School with a goal to translate the imaging techniques to clinic, and was a NIH Ruth L. Kirschstein postdoctoral fellow. She won several travel awards, poster awards and Young Investigator award at national and international conferences. Currently Dr. Mallidi is the Tiampo Family Assistant Professor at Department of Biomedical Engineering at Tufts University, Medford, MA and she directs the integrated Biofunctional Imaging and Therapeutics (iBIT) lab that focuses on developing nano-enabled ultrasound and photoacoustic imaging guided therapeutic strategies.
Dr. Srivalleesha Mallidi received her Masters and PhD Degree in Biomedical Engineering from the University of Texas at Austin. Her graduate work was on molecular specific photoacoustic imaging to understand nano-molecular interactions. After graduation, she joined Wellman Center for Photomedicine (WCP) at Massachusetts General Hospital (MGH), Harvard Medical School with a goal to translate the imaging techniques to clinic, and was a NIH Ruth L. Kirschstein postdoctoral fellow. She won several travel awards, poster awards and Young Investigator award at national and international conferences. Currently Dr. Mallidi is the Tiampo Family Assistant Professor at Department of Biomedical Engineering at Tufts University, Medford, MA and she directs the integrated Biofunctional Imaging and Therapeutics (iBIT) lab that focuses on developing nano-enabled ultrasound and photoacoustic imaging guided therapeutic strategies.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.pacs.2024.100674.
Appendix A. Supplementary material
Supplementary material
Data availability
Data will be made available on request.
References
- 1.Bell A.G. On the production and reproduction of sound by light. Am. J. Sci. 1880;3(118):305–324. [Google Scholar]
- 2.Gargiulo S., Albanese S., Mancini M. State-of-the-art preclinical photoacoustic imaging in oncology: recent advances in cancer theranostics. Contrast Media Mol. Imaging. 2019;2019(1):5080267. doi: 10.1155/2019/5080267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zare A., et al. Clinical theranostics applications of photo-acoustic imaging as a future prospect for cancer. J. Control. Release. 2022;351:805–833. doi: 10.1016/j.jconrel.2022.09.016. [DOI] [PubMed] [Google Scholar]
- 4.Mallidi S., et al. Prediction of tumor recurrence and therapy monitoring using ultrasound-guided photoacoustic imaging. Theranostics. 2015;5(3):289. doi: 10.7150/thno.10155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.John S., et al. Niche preclinical and clinical applications of photoacoustic imaging with endogenous contrast. Photoacoustics. 2023 doi: 10.1016/j.pacs.2023.100533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang L.V. Prospects of photoacoustic tomography. Med. Phys. 2008;35(12):5758–5767. doi: 10.1118/1.3013698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu M., Wang L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006;77(4) [Google Scholar]
- 8.Beard P. Biomedical photoacoustic imaging. Interface Focus. 2011;1(4):602–631. doi: 10.1098/rsfs.2011.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Attia A.B.E., et al. A review of clinical photoacoustic imaging: current and future trends. Photoacoustics. 2019;16 doi: 10.1016/j.pacs.2019.100144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Das D., et al. Another decade of photoacoustic imaging. Phys. Med. Biol. 2021;66(5):05TR01. doi: 10.1088/1361-6560/abd669. [DOI] [PubMed] [Google Scholar]
- 11.Upputuri P.K., Pramanik M. Pulsed laser diode based optoacoustic imaging of biological tissues. Biomed. Phys. Eng. Express. 2015;1(4) [Google Scholar]
- 12.Upputuri P.K., Pramanik M. Fast photoacoustic imaging systems using pulsed laser diodes: a review. Biomed. Eng. Lett. 2018;8(2):167–181. doi: 10.1007/s13534-018-0060-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xavierselvan M., Singh M.K.A., Mallidi S. In vivo tumor vascular imaging with light emitting diode-based photoacoustic imaging system. Sensors. 2020;20(16):4503. doi: 10.3390/s20164503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bulsink R., et al. Oxygen saturation imaging using LED-based photoacoustic system. Sensors. 2021;21(1):283. doi: 10.3390/s21010283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhu Y., et al. Towards clinical translation of LED-based photoacoustic imaging: a review. Sensors. 2020;20(9):2484. doi: 10.3390/s20092484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yang C., et al. Review of deep learning for photoacoustic imaging. Photoacoustics. 2021;21 doi: 10.1016/j.pacs.2020.100215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Deng H., et al. Deep learning in photoacoustic imaging: a review. J. Biomed. Opt. 2021;26(4) doi: 10.1117/1.JBO.26.4.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gröhl J., et al. Deep learning for biomedical photoacoustic imaging: a review. Photoacoustics. 2021;22 doi: 10.1016/j.pacs.2021.100241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rajendran P., Sharma A., Pramanik M. Photoacoustic imaging aided with deep learning: a review. Biomed. Eng. Lett. 2022:1–19. doi: 10.1007/s13534-021-00210-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lan, H., et al. Reconstruct the photoacoustic image based on deep learning with multi-frequency ring-shape transducer array. in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2019. IEEE. [DOI] [PubMed]
- 21.Feng J., et al. End-to-end Res-Unet based reconstruction algorithm for photoacoustic imaging. Biomed. Opt. Express. 2020;11(9):5321–5340. doi: 10.1364/BOE.396598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gutta S., et al. Deep neural network-based bandwidth enhancement of photoacoustic data. J. Biomed. Opt. 2017;22(11) doi: 10.1117/1.JBO.22.11.116001. [DOI] [PubMed] [Google Scholar]
- 23.Antholzer S., Haltmeier M., Schwab J. Deep learning for photoacoustic tomography from sparse data. Inverse Probl. Sci. Eng. 2019;27(7):987–1005. doi: 10.1080/17415977.2018.1518444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shan H., Wang G., Yang Y. Accelerated correction of reflection artifacts by deep neural networks in photo-acoustic tomography. Appl. Sci. 2019;9(13):2615. [Google Scholar]
- 25.Zhang H., et al. A new deep learning network for mitigating limited-view and under-sampling artifacts in ring-shaped photoacoustic tomography. Comput. Med. Imaging Graph. 2020;84 doi: 10.1016/j.compmedimag.2020.101720. [DOI] [PubMed] [Google Scholar]
- 26.Davoudi N., Deán-Ben X.L., Razansky D. Deep learning optoacoustic tomography with sparse data. Nat. Mach. Intell. 2019;1(10):453–460. [Google Scholar]
- 27.Jeon S., Kim C. in Photons plus ultrasound: Imaging and sensing 2020. SPIE; 2020. Deep learning-based speed of sound aberration correction in photoacoustic images. [Google Scholar]
- 28.Guan S., et al. Fully dense UNet for 2-D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health Inform. 2019;24(2):568–576. doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 29.Vu T., et al. A generative adversarial network for artifact removal in photoacoustic computed tomography with a linear-array transducer. Exp. Biol. Med. 2020;245(7):597–605. doi: 10.1177/1535370220914285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Farnia P., et al. High-quality photoacoustic image reconstruction based on deep convolutional neural network: towards intra-operative photoacoustic imaging. Biomed. Phys. Eng. Express. 2020;6(4) doi: 10.1088/2057-1976/ab9a10. [DOI] [PubMed] [Google Scholar]
- 31.Tong T., et al. Domain transform network for photoacoustic tomography from limited-view and sparsely sampled data. Photoacoustics. 2020;19 doi: 10.1016/j.pacs.2020.100190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guan S., et al. Limited-view and sparse photoacoustic tomography for neuroimaging with deep learning. Sci. Rep. 2020;10(1):8510. doi: 10.1038/s41598-020-65235-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Paul A., Mallidi S. U-Net enhanced real-time LED-based photoacoustic imaging. J. Biophotonics. 2024 doi: 10.1002/jbio.202300465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jia L., et al. Highly efficient encoder-decoder network based on multi-scale edge enhancement and dilated convolution for LDCT image denoising. Signal, Image Video Process. 2024:1–11. [Google Scholar]
- 35.Mohammadi K., Islam A., Belhaouari S.B. Zooming into clarity: image denoising through innovative autoencoder architectures. IEEE Access. 2024 [Google Scholar]
- 36.Jia, F., W.H. Wong, and T. Zeng. Ddunet: Dense dense u-net with applications in image denoising. in Proceedings of the IEEE/CVF international conference on computer vision. 2021.
- 37.Nasrin S., et al. 2019 IEEE national aerospace and electronics conference (NAECON) IEEE; 2019. Medical image denoising with recurrent residual u-net (r2u-net) base auto-encoder. [Google Scholar]
- 38.Couturier R., Perrot G., Salomon M. in Neural Information Processing: 25th International Conference, ICONIP 2018, Siem Reap, Cambodia, December 13–16, 2018, Proceedings, Part VI 25. Springer; 2018. Image denoising using a deep encoder-decoder network with skip connections. [Google Scholar]
- 39.Zhang J., et al. A novel denoising method for CT images based on U-net and multi-attention. Comput. Biol. Med. 2023;152 doi: 10.1016/j.compbiomed.2022.106387. [DOI] [PubMed] [Google Scholar]
- 40.Asadi A., Safabakhsh R. The encoder-decoder framework and its applications. Deep Learn.: Concepts Archit. 2020:133–167. [Google Scholar]
- 41.Siddique N., et al. U-net and its variants for medical image segmentation: a review of theory and applications. IEEE Access. 2021;9:82031–82057. [Google Scholar]
- 42.Kugelman J., et al. A comparison of deep learning U-Net architectures for posterior segment OCT retinal layer segmentation. Sci. Rep. 2022;12(1):14888. doi: 10.1038/s41598-022-18646-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ghaznavi A., et al. Comparative performance analysis of simple U-Net, residual attention U-Net, and VGG16-U-Net for inventory inland water bodies. Appl. Comput. Geosci. 2024;21 [Google Scholar]
- 44.Man N., et al. Multi-layer segmentation of retina OCT images via advanced U-net architecture. Neurocomputing. 2023;515:185–200. [Google Scholar]
- 45.Podorozhniak A., et al. Performance comparison of U-Net and LinkNet with different encoders for reforestation detection. Adv. Inf. Syst. 2024;8(1):80–85. [Google Scholar]
- 46.Saichandran, K.S., Ventricular Segmentation: A Brief Comparison of U-Net Derivatives. arXiv preprint arXiv:2401.09980, 2024.
- 47.Zhang F., et al. in Medical Imaging 2024: Image Processing. SPIE; 2024. A comparison of U-Net series for teeth segmentation in CBCT images. [Google Scholar]
- 48.Creswell A., et al. Generative adversarial networks: an overview. IEEE Signal Process. Mag. 2018;35(1):53–65. [Google Scholar]
- 49.Goodfellow I., et al. Generative adversarial networks. Commun. ACM. 2020;63(11):139–144. [Google Scholar]
- 50.Yi X., Walia E., Babyn P. Generative adversarial network in medical imaging: a review. Med. Image Anal. 2019;58 doi: 10.1016/j.media.2019.101552. [DOI] [PubMed] [Google Scholar]
- 51.Ahmad Z., et al. Understanding GANs: fundamentals, variants, training challenges, applications, and open problems. Multimed. Tools Appl. 2024:1–77. [Google Scholar]
- 52.Chen H. in Journal of Physics: Conference Series. IOP Publishing; 2021. Challenges and corresponding solutions of generative adversarial networks (GANs): a survey study. [Google Scholar]
- 53.Saxena D., Cao J. Generative adversarial networks (GANs) challenges, solutions, and future directions. ACM Comput. Surv. (CSUR) 2021;54(3):1–42. [Google Scholar]
- 54.Megahed M., Mohammed A. A comprehensive review of generative adversarial networks: fundamentals, applications, and challenges. Wiley Interdiscip. Rev.: Comput. Stat. 2024;16(1) [Google Scholar]
- 55.Thanh-Tung H., Tran T. 2020 International Joint Conference on Neural Networks (ijcnn) IEEE; 2020. Catastrophic forgetting and mode collapse in GANs. [Google Scholar]
- 56.Zhang Z., Li M., Yu J. On the convergence and mode collapse of GAN. SIGGRAPH Asia 2018 Tech. Briefs. 2018:1–4. [Google Scholar]
- 57.Lepskii O. On a problem of adaptive estimation in Gaussian white noise. Theory Probab. Appl. 1991;35(3):454–466. [Google Scholar]
- 58.Balakrishnan A., Mazumdar R.R. On powers of gaussian white noise. IEEE Trans. Inf. Theory. 2011;57(11):7629–7634. [Google Scholar]
- 59.Jain A., Bhateja V. A versatile denoising method for images contaminated with Gaussian noise. Proc. CUBE Int. Inf. Technol. Conf. 2012 [Google Scholar]
- 60.Mafi M., et al. Denoising of ultrasound images affected by combined speckle and Gaussian noise. IET Image Process. 2018;12(12):2346–2351. [Google Scholar]
- 61.Saxena C., Kourav D. Noises and image denoising techniques: a brief survey. Int. J. Emerg. Technol. Adv. Eng. 2014;4(3):878–885. [Google Scholar]
- 62.Chan R.H., Ho C.-W., Nikolova M. Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Trans. Image Process. 2005;14(10):1479–1485. doi: 10.1109/tip.2005.852196. [DOI] [PubMed] [Google Scholar]
- 63.Azzeh J., Zahran B., Alqadi Z. Salt and pepper noise: effects and removal. JOIV: Int. J. Inform. Vis. 2018;2(4):252–256. [Google Scholar]
- 64.Jiang Y., et al. Salt and pepper noise removal method based on the edge-adaptive total variation model. Front. Appl. Math. Stat. 2022;8 [Google Scholar]
- 65.Tur M., Chin K.-C., Goodman J.W. When is speckle noise multiplicative? Appl. Opt. 1982;21(7):1157–1159. doi: 10.1364/AO.21.001157. [DOI] [PubMed] [Google Scholar]
- 66.Hasinoff S.W. Photon, Poisson Noise. Comput. Vis. 2014;4 (A Reference Guide) [Google Scholar]
- 67.Zhang, Y. A better autoencoder for image: Convolutional autoencoder. in ICONIP17-DCEC. Available online: 〈http://users.cecs.anu.edu.au/Tom.Gedeon/conf/ABCs2018/paper/ABCs2018_paper_58.pdf〉 (accessed on 23 March 2017). 2018.
- 68.Ronneberger, O., P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. in Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18. 2015. Springer.
- 69.Zhou Z., et al. in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, September 20, 2018, Proceedings 4. Springer; 2018. Unet++: A nested u-net architecture for medical image segmentation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- G. Huang, Densely connected convolutional networks. in Proceedings of IEEE Conf. Comput. Vis. Pattern Recognit.2017.
- 71.Zhang Z., Liu Q., Wang Y. Road extraction by deep residual u-net. IEEE Geosci. Remote Sens. Lett. 2018;15(5):749–753. [Google Scholar]
- 72.K. He, Deep residual learning for image recognition. in Proceedings of IEEE Conf. Comput. Vis. Pattern Recognit.2016.
- 73.Niu Z., Zhong G., Yu H. A review on the attention mechanism of deep learning. Neurocomputing. 2021;452:48–62. [Google Scholar]
- 74.Liu X., Milanova M. Visual attention in deep learning: a review. Int Rob. Auto. J. 2018;4(3):154–155. [Google Scholar]
- 75.Oktay, O., et al., Attention u-net: Learning where to look for the pancreas. arXiv preprint arXiv:1804.03999, 2018.
- 76.Zhao S., et al. in IOP Conference Series: Earth and Environmental Science. IOP Publishing; 2020. Attention residual convolution neural network based on U-net (AttentionResU-Net) for retina vessel segmentation. [Google Scholar]
- 77.Alom, M.Z., et al., Recurrent residual convolutional neural network based on u-net (r2u-net) for medical image segmentation. arXiv preprint arXiv:1802.06955, 2018.
- 78.Farasin A., Colomba L., Garza P. Double-step u-net: A deep learning-based approach for the estimation of wildfire damage severity through sentinel-2 satellite data. Appl. Sci. 2020;10(12):4332. [Google Scholar]
- 79.Kingma, D.P. and J. Ba, Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
- 80.Wang Z., Bovik A.C. Mean squared error: love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009;26(1):98–117. [Google Scholar]
- 81.Majumdar S., et al. Metallographic image segmentation using feature pyramid based recurrent residual U-Net. Comput. Mater. Sci. 2024;244 [Google Scholar]
- 82.Siddique N., et al. in Pattern Recognition and Tracking XXXII. SPIE; 2021. Recurrent residual U-Net with EfficientNet encoder for medical image segmentation. [Google Scholar]
- 83.Xu W., et al. High-resolution u-net: preserving image details for cultivated land extraction. Sensors. 2020;20(15):4064. doi: 10.3390/s20154064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Yang Z., et al. A densely connected network based on U-Net for medical image segmentation. ACM Trans. Multimed. Comput., Commun., Appl. (TOMM) 2021;17(3):1–14. [Google Scholar]
- 85.Hess A. arXiv preprint. Explor. Feature reuse DenseNet Archit. 2018 arXiv:1806.01935, [Google Scholar]
- 86.Hou Y., et al. The application of improved densenet algorithm in accurate image recognition. Sci. Rep. 2024;14(1):8645. doi: 10.1038/s41598-024-58421-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Wan K., et al. 2019 IEEE 31st international conference on tools with artificial intelligence (ICTAI) IEEE; 2019. Reconciling feature-reuse and overfitting in densenet with specialized dropout. [Google Scholar]
- 88.Alaeddine H., Jihene M. Deep residual network in network. Comput. Intell. Neurosci. 2021;2021(1):6659083. doi: 10.1155/2021/6659083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Heinrich M.P., Stille M., Buzug T.M. Residual U-net convolutional neural network architecture for low-dose CT denoising. Curr. Dir. Biomed. Eng. 2018;4(1):297–300. [Google Scholar]
- 90.Zhang T., et al. arXiv preprint. Peeking Curtains Residual Learn. 2024 arXiv:2402.08645, [Google Scholar]
- 91.He H., et al. Importance of ultrawide bandwidth for optoacoustic esophagus imaging. IEEE Trans. Med. Imaging. 2017;37(5):1162–1167. doi: 10.1109/TMI.2017.2777891. [DOI] [PubMed] [Google Scholar]
- 92.Korhonen J., You J. 2012 Fourth International Workshop on Quality of Multimedia Experience. IEEE; 2012. Peak signal-to-noise ratio revisited: Is simple beautiful? [Google Scholar]
- 93.Dosselmann R., Yang X.D. A comprehensive assessment of the structural similarity index. Signal, Image Video Process. 2011;5:81–91. [Google Scholar]
- 94.Brunet D., Vrscay E.R., Wang Z. On the mathematical properties of the structural similarity index. IEEE Trans. Image Process. 2011;21(4):1488–1499. doi: 10.1109/TIP.2011.2173206. [DOI] [PubMed] [Google Scholar]
- 95.Wilm, F., et al., Rethinking U-net Skip Connections for Biomedical Image Segmentation. arXiv preprint arXiv:2402.08276, 2024.
- 96.Wu J., et al. Skip connection U-Net for white matter hyperintensities segmentation from MRI. IEEE Access. 2019;7:155194–155202. [Google Scholar]
- 97.Allen-Zhu Z., Li Y., Liang Y. Learning and generalization in overparameterized neural networks, going beyond two layers. Adv. Neural Inf. Process. Syst. 2019:32. [Google Scholar]
- 98.Chen, Z., et al., Over-parameterization and Adversarial Robustness in Neural Networks: An Overview and Empirical Analysis. arXiv preprint arXiv:2406.10090, 2024.
- 99.S.S. Du, , 2018arXiv:1810.02054,Gradient Descent. provably Optim. -Parameter Neural Netw. arXiv Prepr..
- 100.Liu H., et al. in International Conference on Machine Learning. PMLR; 2022. Benefits of overparameterized convolutional residual networks: Function approximation under smoothness constraint. [Google Scholar]
- 101.Martin S., Bach F., Biroli G. in International Conference on Artificial Intelligence and Statistics. PMLR; 2024. On the impact of overparameterization on the training of a shallow neural network in high dimensions. [Google Scholar]
- 102.Zou D., Gu Q. An improved analysis of training over-parameterized deep neural networks. Adv. Neural Inf. Process. Syst. 2019:32. [Google Scholar]
- 103.Wang H., et al. Narrowing the semantic gaps in U-Net with learnable skip connections: the case of medical image segmentation. Neural Netw. 2024;178 doi: 10.1016/j.neunet.2024.106546. [DOI] [PubMed] [Google Scholar]
- 104.Zhang X., et al. FAFS-UNet: redesigning skip connections in UNet with feature aggregation and feature selection. Comput. Biol. Med. 2024;170 doi: 10.1016/j.compbiomed.2024.108009. [DOI] [PubMed] [Google Scholar]
- 105.Kim J., et al. Limitations of deep learning attention mechanisms in clinical research: empirical case study based on the korean diabetic disease setting. J. Med Internet Res. 2020;22(12) doi: 10.2196/18418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Kamath A., et al. in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2023. Do We Really Need that Skip-Connection? Understanding Its Interplay with Task Complexity. [Google Scholar]
- 107.Acar V., Eksioglu E.M. Densely connected dilated residual network for image denoising: Ddr-net. Neural Process. Lett. 2023;55(5):5567–5581. [Google Scholar]
- 108.Alverson M., et al. Generative adversarial networks and diffusion models in material discovery. Digit. Discov. 2024;3(1):62–80. [Google Scholar]
- 109.Chakraborty T., et al. Ten years of generative adversarial nets (GANs): a survey of the state-of-the-art. Mach. Learn.: Sci. Technol. 2024;5(1) [Google Scholar]
- 110.Croitoru F.-A., et al. Diffusion models in vision: a survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023;45(9):10850–10869. doi: 10.1109/TPAMI.2023.3261988. [DOI] [PubMed] [Google Scholar]
- 111.Ghosheh G.O., Li J., Zhu T. A survey of generative adversarial networks for synthesizing structured electronic health records. ACM Comput. Surv. 2024;56(6):1–34. [Google Scholar]
- 112.Goodfellow I., et al. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014:27. [Google Scholar]
- 113.Guo Z., et al. Diffusion models in bioinformatics and computational biology. Nat. Rev. Bioeng. 2024;2(2):136–154. doi: 10.1038/s44222-023-00114-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Po R., et al. in Computer Graphics Forum. Wiley Online Library; 2024. State of the art on diffusion models for visual computing. [Google Scholar]
- 115.Saad M.M., O’Reilly R., Rehmani M.H. A survey on training challenges in generative adversarial networks for biomedical image analysis. Artif. Intell. Rev. 2024;57(2):19. [Google Scholar]
- 116.Yang L., et al. Diffusion models: a comprehensive survey of methods and applications. ACM Comput. Surv. 2023;56(4):1–39. [Google Scholar]
- 117.Ding Z., Jiang S., Zhao J. 2022 IEEE 2nd International Conference on Electronic Technology, Communication and Information (ICETCI) IEEE; 2022. Take a close look at mode collapse and vanishing gradient in GAN. [Google Scholar]
- 118.Williams C., et al. A unified framework for U-Net design and analysis. Adv. Neural Inf. Process. Syst. 2023;36:27745–27782. [Google Scholar]
- 119.Thanh-Tung, H., T. Tran, and S. Venkatesh, Improving generalization and stability of generative adversarial networks. arXiv preprint arXiv:1902.03984, 2019.
- 120.Koker T., et al. 2021 IEEE International Conference on Image Processing (ICIP) IEEE; 2021. U-noise: Learnable noise masks for interpretable image segmentation. [Google Scholar]
- 121.Poudel S., Lee S.-W. Explainable U-Net model forMedical image segmentation. Nord. Mach. Intell. 2021;1(1):41–43. [Google Scholar]
- 122.Sun J., et al. in Medical Image Computing and Computer Assisted Intervention–MICCAI 2020: 23rd International Conference, Lima, Peru, October 4–8, 2020, Proceedings, Part IV 23. Springer; 2020. Saunet: Shape attentive u-net for interpretable medical image segmentation. [Google Scholar]
- 123.Wang X., et al. Improving the Interpretability and Reliability of Regional Land Cover Classification by U-Net Using Remote Sensing Data. Chin. Geogr. Sci. 2022;32(6):979–994. [Google Scholar]
- 124.Zhang X., Chen T. 2020 IEEE international conference on bioinformatics and biomedicine (BIBM) IEEE; 2020. Attention u-net for interpretable classification on chest x-ray image. [Google Scholar]
- 125.Mei, S., U-Nets as Belief Propagation: Efficient Classification, Denoising, and Diffusion in Generative Hierarchical Models. arXiv preprint arXiv:2404.18444, 2024.
- 126.Pham N., Fomel S. Uncertainty and interpretability analysis of encoder-decoder architecture for channel detection. Geophysics. 2021;86(4):O49–O58. [Google Scholar]
- 127.Cui H., et al. Multiscale attention guided U-Net architecture for cardiac segmentation in short-axis MRI images. Comput. Methods Prog. Biomed. 2021;206 doi: 10.1016/j.cmpb.2021.106142. [DOI] [PubMed] [Google Scholar]
- 128.Liu C., Gu P., Xiao Z. Multiscale U-net with spatial positional attention for retinal vessel segmentation. J. Healthc. Eng. 2022;2022(1):5188362. doi: 10.1155/2022/5188362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Su R., et al. Msu-net: multi-scale u-net for 2d medical image segmentation. Front. Genet. 2021;12 doi: 10.3389/fgene.2021.639930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Wei Y., et al. Multiscale feature U-Net for remote sensing image segmentation. J. Appl. Remote Sens. 2022;16(1) [Google Scholar]
- 131.Borji A. Pros and cons of GAN evaluation measures. Comput. Vis. Image Underst. 2019;179:41–65. [Google Scholar]
- 132.Galteri L., et al. Deep universal generative adversarial compression artifact removal. IEEE Trans. Multimed. 2019;21(8):2131–2145. [Google Scholar]
- 133.Wang J., et al. From artifact removal to super-resolution. IEEE Trans. Geosci. Remote Sens. 2022;60:1–15. [Google Scholar]
- 134.Arora A., Arora A. Generative adversarial networks and synthetic patient data: current challenges and future perspectives. Future Healthc. J. 2022;9(2):190–193. doi: 10.7861/fhj.2022-0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Brock A. arXiv preprint. Large Scale GAN Train. High. Fidel. Nat. Image Synth. 2018 arXiv:1809.11096, [Google Scholar]
- 136.Jimenez F., et al. Generative adversarial network performance in low-dimensional settings. J. Res. Natl. Inst. Stand. Technol. 2021;126 doi: 10.6028/jres.126.008. (p. NA-NA) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Lim W., et al. Future of generative adversarial networks (GAN) for anomaly detection in network security: a review. Comput. Secur. 2024 [Google Scholar]
- 138.Wang Y., et al. Transferring gans: generating images from limited data. Proc. Eur. Conf. Comput. Vis. (ECCV) 2018 [Google Scholar]
- 139.Chen G., et al. Rethinking the unpretentious U-net for medical ultrasound image segmentation. Pattern Recognit. 2023;142 [Google Scholar]
- 140.Ho J., et al. in International conference on machine learning. PMLR; 2019. Flow++: Improving flow-based generative models with variational dequantization and architecture design. [Google Scholar]
- 141.Jena B., et al. Analysis of depth variation of U-NET architecture for brain tumor segmentation. Multimed. Tools Appl. 2023;82(7):10723–10743. [Google Scholar]
- 142.Maaløe L., et al. Biva: A very deep hierarchy of latent variables for generative modeling. Adv. Neural Inf. Process. Syst. 2019;32 [Google Scholar]
- 143.Vaswani A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017 [Google Scholar]
- 144.Khan A., et al. A survey of the vision transformers and their CNN-transformer based variants. Artif. Intell. Rev. 2023;56(3):2917–2970. [Google Scholar]
- 145.Khan S., et al. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022;54(10s):1–41. [Google Scholar]
- 146.Park, N. and S. Kim, How do vision transformers work? arXiv preprint arXiv:2202.06709, 2022.
- 147.Parvaiz A., et al. Vision Transformers in medical computer vision—A contemplative retrospection. Eng. Appl. Artif. Intell. 2023;122 [Google Scholar]
- 148.H. Wu, Cvt: Introducing convolutions to vision transformers. in Proceedings of IEEE/CVF Int. Conf. Comput. Vis.2021.
- 149.Chaddad A., et al. Generalizable and explainable deep learning for medical image computing: an overview. Curr. Opin. Biomed. Eng. 2024 [Google Scholar]
- 150.Salahuddin Z., et al. Transparency of deep neural networks for medical image analysis: a review of interpretability methods. Comput. Biol. Med. 2022;140 doi: 10.1016/j.compbiomed.2021.105111. [DOI] [PubMed] [Google Scholar]
- 151.Teng Q., et al. A survey on the interpretability of deep learning in medical diagnosis. Multimed. Syst. 2022;28(6):2335–2355. doi: 10.1007/s00530-022-00960-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Zhang Y., et al. An Interpretability optimization method for deep learning networks based on grad-CAM. IEEE Internet Things J. 2024 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material
Data Availability Statement
Data will be made available on request.