Abstract
To investigate the effect of the filter device on the cleanliness of molten steel and the flow field distribution within the tundish. The tundish filters were designed into five groups of pores with 20°, 25°, 30°, 35° and 40° elevation angles, and the flow field distribution and impurity removal rate of molten steel were calculated by Discrete Phase Model (DPM). The results showed that the removal rate of impurity in the molten steel could be significantly improved by using the tundish filter with elevation angle. When the elevation angle of the filter was 40°, the impurity removal rate reached 74.05%, and the flow field distribution would be more stable. The presence of the tundish filter caused the higher flow density of the molten steel before the filter inlet to decrease and become steadier after the filter, thereby enhancing the contact rate between impurities in the molten steel and the covering agent, ultimately achieving the highest impurity removal rate.
Keywords: Tundish filter, Removal rate of impurity, Elevation angle, Flow field distribution, Continuous casting
Subject terms: Computational methods, Materials science, Materials for devices
Introduction
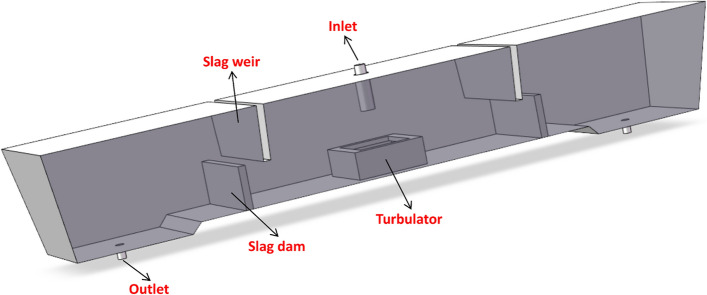
With the rapid development of high-performance steel products, the cleanliness requirements for molten steel in industrial applications have increased significantly, leading to the gradual adoption of tundishes as refined metallurgical reaction vessels1–4. Besides buffering the poured molten steel, tundish also plays a role in balancing the temperature of the molten steel and especially removing the impurity in the molten steel5,6. The tundish serves as a transitional vessel between the ladle and the continuous casting process7–15. The traditional tundish was composed of long nozzle under the ladle bottom, turbulence, slag dam, slag weir and immersion nozzle as shown in Fig. 1. The molten steel flowed into the tundish through the long nozzle, passed the buffer of the turbulator, flowed through the gap between the slag dam and the slag weir, and finally flowed out of the submerged nozzle, which had an positive effect on the removal of impurities in the molten steel16. As is well known, the purity of molten steel exiting the tundish directly affects the quality of the casting billet, indicating that tundish metallurgy plays a crucial role in the overall processing system17–19. Therefore, how to further improve the removal rate of impurities in the molten steel though the tundish had become the top priority20–22.
Fig. 1.
Three-dimensional model of traditional tundish.
Traditional filtration devices in the tundish, such as slag dams and slag weirs, are designed to intercept slag floating on the surface of molten steel23–27. These devices are primarily made from magnesia precast blocks28. As shown in Fig. 1, due to the limited contact area between the slag dam/weir and the molten steel, the flow direction and velocity of the molten steel cannot be accurately controlled, leading to an increased residual impurity load entering the crystallizer irreversibly29,30. A more effective method to remove impurities involves replacing slag dams and weirs with advanced ceramic filters. These filters, made from oxide compound materials similar to the impurities, can absorb inclusions from the molten steel31–35. By analyzing the tundish’s structural characteristics and its purification mechanisms, it has been found that the impurity removal rate can be enhanced through both the filter and tundish covering agent36. Additionally, during the impurity floating process, traditional ceramic filters can promote the collision and agglomeration of smaller inclusions, gradually increasing their size and accelerating their removal by the tundish covering agent, thereby improving the impurity removal efficiency37,38. Wang et al., discovered that porous tundish filters can modify the flow pattern and velocity of molten steel. As molten steel passes through the filters, inclusions are captured, purifying the steel and increasing the impurity removal rate from 65.3% to 72.0%39. Qin et al.40 explored the removal of inclusions of various sizes using tundish filters, showing that porous filters significantly enhance removal efficiency for inclusions smaller than 50 microns, with a removal rate of 64% for fine-sized inclusions. Quan et al., introduced flow control devices into the tundish to extend the residence time of molten steel. Their research revealed that controlling the flow velocity effectively increases the removal rate of inclusions, particularly for larger particles41. Huang et al., developed a vortex tundish, where inclusions are concentrated at the center of the vortex by centrifugal force. This mechanism causes smaller inclusions to agglomerate into larger particles, which then float to the surface and are absorbed by the tundish covering agent due to their buoyancy42. Currently, the pore distribution of most filters is designed to be horizontal and aligned with the molten steel flow direction43. Although using ceramic filters in the tundish results in better impurity removal compared to slag dams and weirs, the horizontal straight pore design is not ideal for industrial practice, as it cannot adequately guide the molten steel flow or enhance the contact between impurities and the tundish covering agent. Existing literature indicates a lack of fundamental and systematic research on the numerical simulation of tundish filters designed with specific elevation angles and their impact on impurity removal rates. Given the limitations of slag dams and weirs in impurity removal, the use of filters to replace them has gained significant attention in recent studies44,45. Research has also shown that when molten steel fully contacts the tundish covering agent, the separated impurities can be absorbed by the covering agent and walls, improving the impurity removal rate. Previous studies suggest that adjusting the elevation angle of the filters can improve impurity removal rates, but there remains a lack of research on the impact of different filter elevation angles on impurity removal rates for different particle sizes and flow field distribution46.
The primary contributions of this research are as follows.
Proposed a Novel Filter Elevation Angle Design: This study introduces a tundish filter with varying elevation angles to optimize molten steel flow and impurity removal. Unlike traditional straight-pore filters, the proposed design improves impurity capture by adjusting the elevation angle.
Numerical Simulation of Filter Elevation Angle Effects: The Discrete Phase Model (DPM) was used to systematically simulate the effects of different elevation angles on molten steel flow and impurity removal, providing quantitative support for optimizing the filter structure.
Comparative Study on Impurity Removal Efficiency: A comparative analysis of filters with different elevation angles showed that the 40° angle achieved the best impurity removal efficiency across all particle sizes, offering strong data support for tundish filter optimization.
Mechanism of Flow Field Regulation and Impurity Removal: The study analyzed changes in flow direction and velocity to reveal how filter elevation angles regulate flow stability and impurity flotation, providing a valuable basis for improving molten steel cleanliness.
Model description
Mathematical modelling
This paper employs numerical simulation to investigate the influence of filter elevation angle on the removal rate of impurities of various particle sizes and the flow field distribution in the tundish. In this study, the tundish filter was designed with 16 pores distributed according to a non-uniform pattern to optimize the molten steel flow field and enhance impurity removal efficiency. The distribution process involved dividing the filter into four equal quadrants using the center points of the top, bottom, left, and right edges as reference lines. Each quadrant was then further subdivided into four equal sections, resulting in a total of 16 sections. The pore area in each section was scaled proportionally, ensuring that the overall pore distribution was balanced while maintaining functional variability. This systematic design ensures a more targeted flow pattern for the molten steel passing through the filter.
To maintain consistency with traditional tundish designs, the total pore area of the filter was set equal to the cross-sectional area beneath the slag dam in a conventional tundish. This equivalence guarantees a comparable flow rate, providing a basis for analyzing the effects of the new filter design. The pores were arranged symmetrically along the central axis of the filter, ensuring equal distribution between the left and right sides.
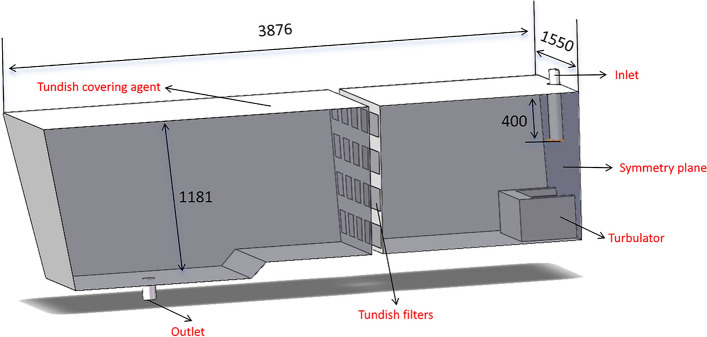
A key feature of the filter design in this study is the inclusion of an elevation angle for the pores. The inclined orientation of the pores plays a critical role in modifying the flow characteristics of molten steel. The elevation angle directs the flow toward specific regions of the filter, influencing both the residence time and the interaction with the filter surface. This design feature is central to this research, as it allows for the investigation of how pore elevation angle impacts impurity removal efficiency and flow field optimization. Due to the double-flow symmetry, the tundish was evenly divided into halves from the entrance. One side of the developed three-dimensional tundish model, which was used for numerical simulation, is presented in Fig. 2.
Fig. 2.
Three-dimensional model of developed tundish with elevation angle filter.
The tundish model consisted of envelop walls, long nozzle, submersed nozzle, turbulator and the porous filter with 16 pores. The top length and width of the tundish model steel level were 3876 mm (half of the tundish) and 1550 mm, the inner diameter of the long nozzle and the submersed nozzle were 120 mm and 90 mm. The height of the molten steel in the tundish was 1180 mm from the molten steel surface to the bottom of the tundish. The immersion depth of submersed nozzle in the molten steel was 400 mm.
Filter design
In summary, this experiment utilized porous filters to replace the slag dam and slag weir in the tundish, with the filter pores designed at specific elevation angles. The tundish was divided into two areas including area A and area B. Area A was the part of the molten steel from the entrance to the filter of the tundish, and area B was the part of the molten steel from the filter to the exit of the tundish, as shown in Fig. 3.
Fig. 3.
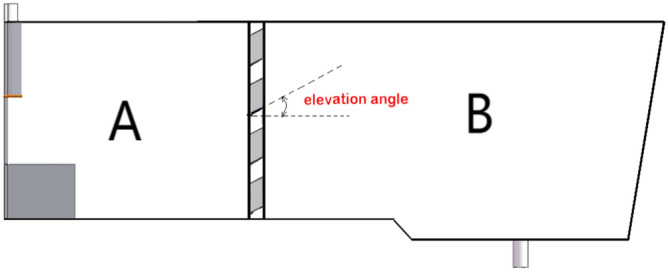
The right side of the tundish including area A and area B.
In this experiment, based on calculations regarding the proportion of the traditional slag dam to the bottom of the tundish, the molten steel channel was determined to occupy 36% of the tundish’s cross-sectional area. To maintain the flow rate of molten steel, the cross-sectional area of the porous filter was evenly divided into 16 pores, constituting the total pore proportion. The elevation angles of the filter channels were designed at 20°, 25°, 30°, 35°, and 40°, respectively. The influence of the elevation angles of filter pores on the flow field distribution and the removal rate of impurity in molten steel were studied by mathematical modelling.
Experimental methods
The standard k-epsilon turbulence model was selected for this study due to its robustness and computational efficiency in high Reynolds number flows. Previous studies have highlighted its suitability for complex flow scenarios involving dispersed media and multi-phase interactions, demonstrating reliable performance in similar systems. In particular, k-epsilon models have been effectively used in simulations of tundish systems, where they accurately predict macroscopic flow structures and particle dynamics. Moreover, comparative studies have shown that the k-epsilon model provides reasonable accuracy while maintaining computational efficiency, making it a suitable choice for engineering applications in multi-phase flows47,48.
Basic hypotheses.
Due to the geometric symmetry of continuous casting tundish, only one half of molten steel flow, was turbulent and incompressible viscous fluid, in tundish was numerically simulated. Tundish covering agent had no effect on molten steel flow, however had effect the impurities removal rate that was regarded as being absorbed by the covering agent. The impurity particles was considered to be spherical, not taken into counted collision among partials and growth of the impurity in the molten steel.
-
2.
Governing equation.
The molten steel flow in tundish adopts the standard k-epsilon equation. For this experiment, the molten steel phase flow steady followed the equation of continuity, the equation of momentum (N-S Equation) and equation of impurities movement.
 |
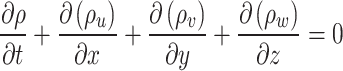1 |
where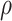 
was molten steel density (
), 
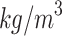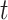was turbulence time (s), x, y, and z were the three-dimensional coordinate value (m), u, v, and w indicated the flow rate in the x, y, and z direction (m/s).
 |
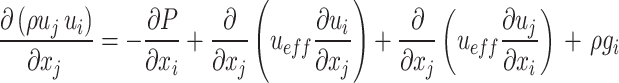2 |
where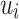 
and 
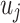was the average rate of the molten steel turbulence (m/s), 
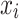and 
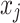was the value of i and j direction (m), P was the pressure value (Pa), 
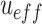was effective viscosity coefficient (pa·s), 
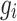was the acceleration of gravity.
The DPM discrete phase model was used to simulate the moving trajectory of the impurities in the tundish clad steel. In the simulation calculation, the density of impurity Alumina was 3970 kg/m3, and the average sizes of impurity Alumina were 20, 30, 40, 50, 60, 70, 80 μm. The specific equation was as follows.
 |
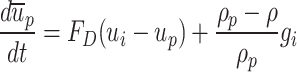3 |
 |
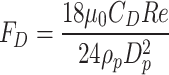4 |
where,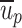 
was the average velocity of the impurities (m/s), 
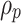was the density of the impurity (
),
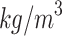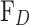was drag force caused by the viscosity of molten steel (N), 
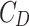was drag coefficient of molten steel.
-
3.
Inclusion motion.
The motion trajectories of inclusions in the molten steel of the tundish are calculated using the Discrete Phase Model (DPM). In the molten steel, inclusions are subjected to forces such as gravity, buoyancy, drag force, Saffman lift force, and pressure gradient force. In this study, impurities with a density of 3970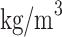 
and the particle sizes of 20 μm, 30 μm, 40 μm, 50 μm, 60 μm, 70 μm and 80 μm are simulated. Based on Newton’s second law, the equation of motion for the inclusions is given as follows:
 |
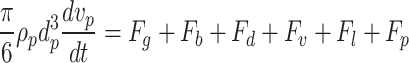5 |
Here,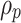 
represents the inclusion density, 
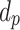is the inclusion particle diameter, and 
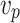is the inclusion velocity. 
, 
, 
, 
, 
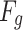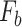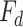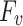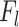, and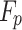 
represent the forces acting on the inclusion, including gravity, buoyancy, drag force, virtual mass force, Saffman lift force, and pressure gradient force, respectively.
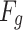gravity and 
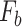buoyancy are both vertical forces, with gravity acting downward and buoyancy acting upward. Their resultant force is:
 |
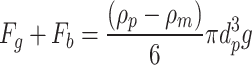6 |
In the equation,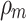 
represents the density of molten steel, with a unit of 
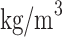, and g denotes the gravitational acceleration, which is 9.81 
.
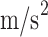The drag force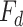 
, caused by the viscosity of molten steel, influences the motion trajectory of inclusions. Its magnitude is determined by the Reynolds number between the molten steel and the inclusions. The expression is given as:
 |
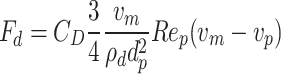7 |
In the equation,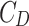 
represents the drag coefficient; 
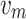is the velocity of the molten steel, with a unit of m/s; and 
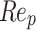is the Reynolds number associated with the surface of the inclusion.
The virtual mass force 
refers to the force exerted on a particle when its accelerated motion in a fluid causes the surrounding fluid to accelerate as well. This interaction results in a force acting on the particle, known as the virtual mass force. Its expression is given as:
 |
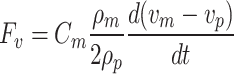8 |
where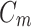 
is the virtual mass coefficient.
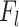represents the Saffman lift force. When a velocity gradient exists in the molten steel flow field, the fluid velocity varies at different points on the particle’s surface, resulting in a force acting perpendicular to the fluid flow direction. This force is known as the Saffman lift force. Its expression is as follows:
 |
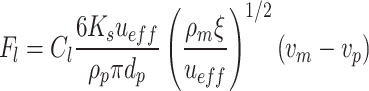9 |
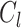represents the correction coefficient for the Saffman lift force; 
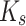is the Saffman lift force coefficient; and 
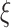denotes the velocity gradient of the molten steel fluid in a direction perpendicular to a specific axis.
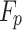represents the pressure gradient force. When a pressure gradient exists in the flow field, the particle is subjected to a force caused by the pressure variation. This force is referred to as the pressure gradient force, and its expression is as follows:
 |
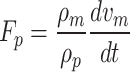10 |
Boundary condition
Suggested that sectional area of slab steel was 1.5 m × 0.6 m and average casting speed was 1.5 m/min, the value of molten steel at entrance would be 1.33 m/s. The flowing direction of molten steel was along to the long nozzle, and the boundary conditions at the molten steel outlet choose the outflow boundary condition to ensure the flow of molten steel. The inlet was set as the velocity inlet, and the impurities were uniformly distributed on the inlet boundary with the same velocity as the molten steel. The upper wall was set as trap. When the impurity touches the molten steel surface, it was considered that the inclusions was trapped by the tundish covering agent. The perimeter, bottom, turbulence and baffle of tundish were set to reflect, and the impurities were considered to be bounced when they contact the wall surfaces. The porous filter surfaces of all pores were set as trap considering the reaction absorption between the impurities and the filter surfaces. The exiting condition was set to escape. When the impurities move towards the exit, they enter the crystallizer. Setting the density of molten steel as 7020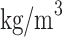 
, the viscosity as 0.0062 kg/m s.
Meshing
The computational domain was divided into eight sections: top, sides and bottom, the symmetry plane, inlet, outlet, inlet and outlet walls, turbulence controller, and filter. Tetrahedral meshes were employed for flexibility in meshing the complex geometries. To ensure accurate resolution of flow and particle dynamics, mesh refinement was applied in critical regions, with element sizes of 0.005 m at the inlet and outlet and 0.01 m in the turbulence controller and filter regions. The base element size was set to 0.02 m in bulk flow areas. Boundary layers were resolved using two inflation layers at all solid–fluid interfaces, ensuring precise capture of near-wall velocity gradients.
A grid independence study was performed using three mesh densities: coarse (0.8 million cells), medium (1.5 million cells), and fine (2.3 million cells). Key variables such as velocity distributions and inclusion removal rates showed less than 1% deviation between the medium and fine meshes, confirming that the medium mesh provided a good balance of accuracy and computational efficiency. Therefore, the medium mesh was used for all simulations in this study. Grid division was shown in Fig. 4. (Detailed experiments are presented in section “Mesh sensitivity test”).
Fig. 4.
Grid division diagram (medium).
Result analysis and discussion
Influence of filter elevation angle on removal rate of molten steel impurities in tundish
Figure 5 shows the relationship between the elevation angle of the tundish filter and the average removal rate of inclusions of various sizes, ranging from 20 to 80 μm, in molten steel (with a flow velocity of 1.33 m/s). As can be seen from Fig. 5, when the filter pore elevation angle ranges between 20° and 40°, the removal efficiency exhibits a “wave curve” trend, initially increasing, then decreasing, and subsequently increasing again. At 30°, the inclusion removal efficiency in molten steel exhibits a “relative valley” state. As the elevation angle increases from 30° to 40°, the inclusion removal rate gradually improves. At 40°, the removal rate is the highest, reaching 74.05%. If the molten steel flows directly through the filter, the porous filter adapts to the flow field within the tundish, indicating that the removal rate varies significantly with different angles. Further analysis of the removal rates for various particle sizes reveals that despite the variation in inclusion size, the 40° filter angle consistently achieves the highest removal efficiency.
Fig. 5.
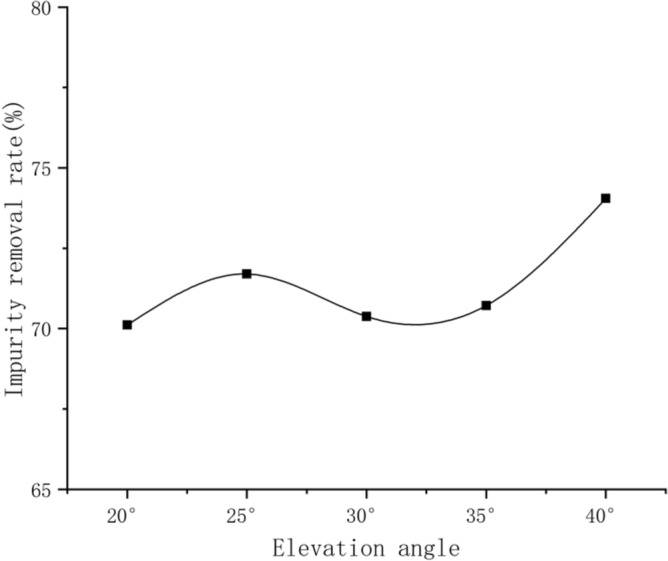
Relationship between elevation angle of filter and removal rate of impurities in molten steel.
As shown in Fig. 6, smaller inclusions, such as 20 μm and 30 μm, though more susceptible to turbulence, exhibit the highest removal efficiency at the larger angle of 40°. This is due to the prolonged contact time between the molten steel and the filter surface, which enhances the interaction between the inclusions and the filter, resulting in more effective removal. Similarly, for medium-sized inclusions of 40 μm, 50 μm, and 60 μm, the removal rate also peaks at 40°. This suggests that at this angle, the fluid flow stability and the inertial motion of the inclusions reach an optimal balance, thereby improving the removal rate.
Fig. 6.
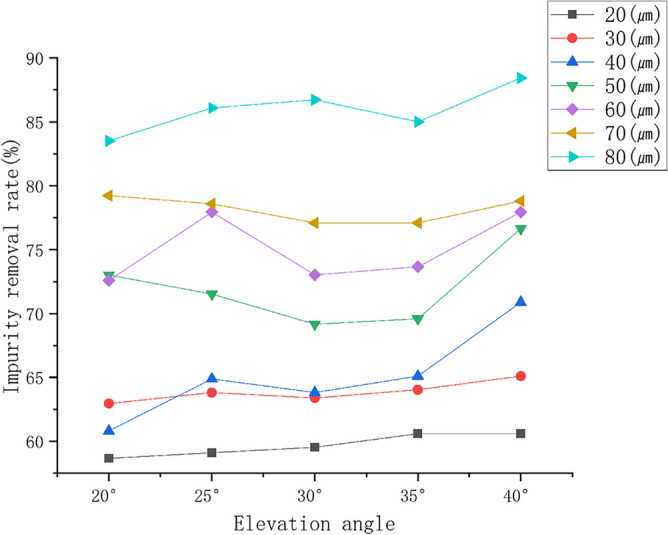
Filter pore elevation angle and impurity sizes on impurity removal rate in molten steel.
For larger inclusions (70–80 μm), although their greater inertia makes them more difficult to stabilize in turbulent flow, the 40° angle still demonstrates the highest removal efficiency. This is attributed to the increased contact area between the inclusions and the filter surface, which significantly enhances the capture efficiency.
Overall, the 40° angle demonstrates the most effective removal performance across all particle sizes. As the angle increases, the removal rate initially follows an upward trend, which is then followed by a pattern of decreasing and subsequently increasing, with distinct troughs appearing at various elevation angles. These troughs shift to higher angles as the inclusion size increases. Specifically, for inclusions ranging from 30 to 60 μm, the removal rate exhibits a trough at 30°, whereas for inclusions of 70 μm and 80 μm, the trough appears at 35°.
In conclusion, these results suggest that optimizing the tundish filter pore angle to 40° is an effective strategy for improving inclusion removal rates across different particle sizes. The 40° angle offers the best removal efficiency for a wide range of inclusion sizes, making it particularly suitable for broad industrial applications.
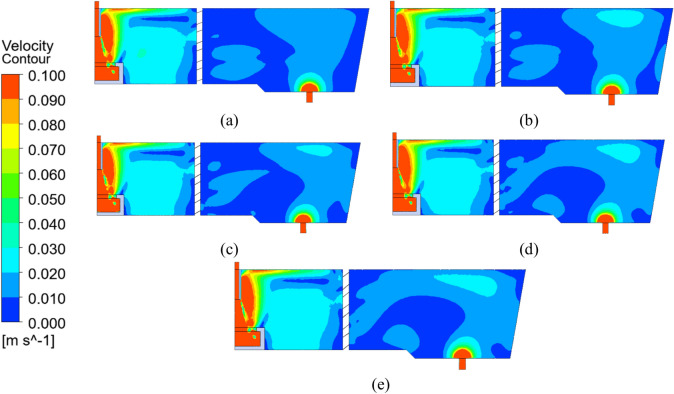
Influence of filter elevation angle on the velocity contour of molten steel in the tundish
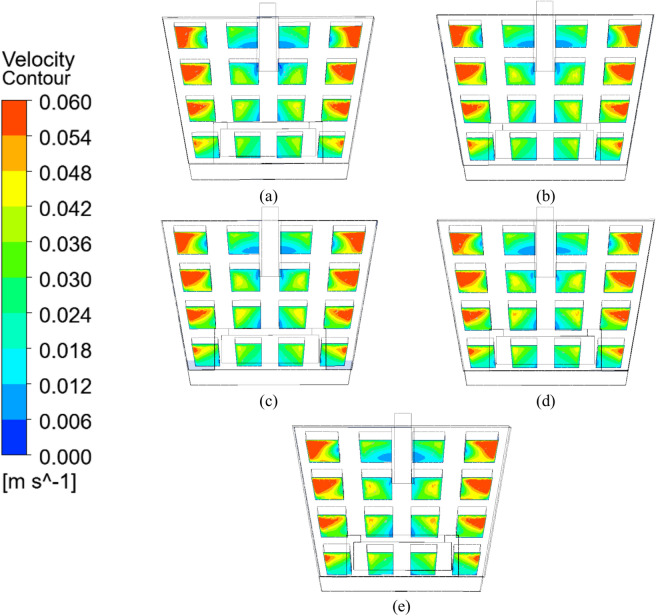
Figure 7 showed the influence of filter elevation Angle on the velocity contour of molten steel in the tundish. It showed that the velocity contour of molten steel in area A and B presented different trends with the filter elevation angles in the tundish. Table 1 showed the relationship between the different area proportion on the area B and the filter elevation angle. As shown in Fig. 7a–e, the velocity of molten steel in area A is greater than that in area B. According to the calculation results in Table 1, the proportions of bright blue, light blue, and dark blue regions in area B indicate high, intermediate, and low velocity flows within the tundish, respectively. At elevation angles of 20° and 25°, a continuous velocity contour is not formed from the filter pores to the tundish exit in area B. As illustrated in Fig. 7a and b, due to the lower elevation angle of the filter, the light blue region in area B does not form a continuous distribution. As the elevation angle increases to 30°, the total proportion of light blue and dark blue regions gradually decreases, with the light blue proportion dropping to its lowest value of 38.96%, resulting in the lowest removal efficiency. Figure 7d and e show the formation of a continuous velocity contour and a high-speed flow field. According to Table 1, as the elevation angle increases from 30° to 40°, the proportion of bright blue, representing high-speed flow, increases from 2.39 to 6.12%. When the elevation angle reaches 40°, the light blue region reaches a maximum of 58.13%, while the dark blue region reaches a minimum of 35.70%, with the largest contact area with the top surface. Therefore, as molten steel passes through the tundish filter, increasing the elevation angle alters the flow velocity of molten steel in various directions, resulting in either continuous or discontinuous velocity contour. In summary, the formation of a continuous velocity contour, the medium-to-high velocity flow of molten steel in area B, and the increased contact area with the top surface collectively contribute to enhancing the removal of inclusions.
Fig. 7.
Influence of elevation Angle on the velocity contour of molten steel in tundish filter. (a) 20°, (b) 25°, (c) 30°, (d) 35°, (e) 40°.
Table 1.
The effect of elevation angle on the area proportion of bright blue, light blue and dark blue on the area B in the tundish.
| Elevation Angle | Bright blue proportion | Light blue proportion | Dark blue proportion |
|---|---|---|---|
| 20° | 0% | 54.87% | 45.01% |
| 25° | 4.89% | 44.91% | 44.04% |
| 30° | 2.39% | 38.96% | 42.33% |
| 35° | 5.05% | 54.35% | 42.19% |
| 40° | 6.12% | 58.13% | 35.70% |
The bold means the best performance. Significant values are in italics.
The analysis of the velocity contour of molten steel suggests that smaller elevation angles result in discontinuous velocity contour and low-velocity flow fields, whereas larger elevation angles produce continuous velocity contour and medium-to-high velocity flow fields. The medium-to-high velocity flow enables inclusions to float rapidly after passing through the filter, promoting extensive contact with the top surface, which facilitates their absorption. This rapid floatation significantly enhances the removal efficiency of inclusions. In contrast, the discontinuous velocity contour and low-velocity flow associated with smaller elevation angles hinder the effective floatation of inclusions.
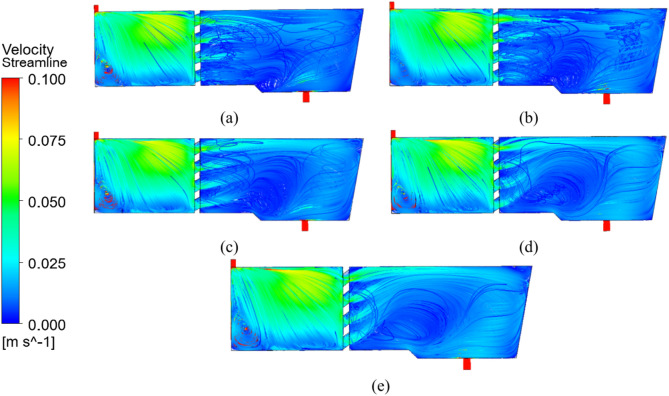
Influence of filter elevation Angle on linear distribution of molten steel track in the intermediate envelope
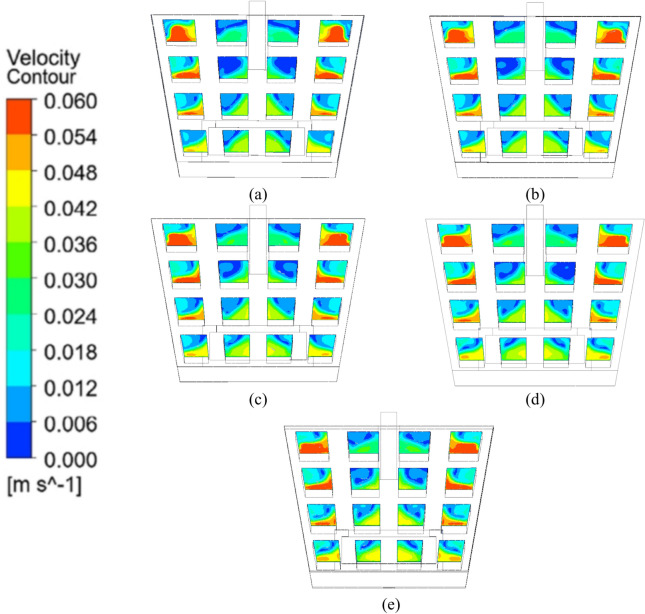
Figure 8 shows the influence of elevation Angle on the molten steel flow diagram in tundish filter. The streamline density(Proportion of molten steel in a specific area) on the area A of the filter was overall greater than that on the area B of the filter. With the different elevation Angle, the flow field density of the molten steel passing through the filter also change. Table 2 shows the streamline density of molten steel after passing through the filter. It could be seen from Table 2 that the flow line density was the highest (17.61%) when the elevation Angle is 40°, the molten steel was stirred rapidly between the turbulence and the filter, which would increase the collision and polymerization of impurities in the molten steel, thus increasing the removal rate.
Fig. 8.
Influence of elevation Angle on flow diagram of molten steel in tundish filter. (a) 20°, (b) 25°, (c) 30°, (d) 35°, (e) 40°.
Table 2.
Streamline density of molten steel after passing through the filter.
| Elevation angle | Streamline density of molten steel after passing through the filter |
|---|---|
| 20° | 11.81% |
| 25° | 14.47% |
| 30° | 14.03% |
| 35° | 15.17% |
| 40° | 17.61% |
The bold means the best performance.Significant values are in italics.
However, when the elevation Angle was 20°, the streamline density was only 11.81%, indicating that the molten steel was not sufficiently stirred between the turbulence and the filter, so the removal rate was the lowest in the 5 groups of experiments. It was also shown in Table 2 that when the elevation Angle was 40°, the flow line density of the molten steel passing through the filter was the highest (17.61%). Although no more stirring phenomenon occurs after the molten steel passing through the filter, the path from the filter to the outlet was the smallest, and it could be seen from Fig. 8 that (a–d) all appear vortex subsidence, which could be seen from Fig. 8e, the flow line with an elevation Angle of 40° was relatively stable, and there was no vortex sinking, indicating that there was no slagging in the experiment with an elevation Angle of 40°. In this way, the molten steel flow state would be stable, which could make the molten steel stay in the tunder for more time. Therefore, the removal rate of impurities in the molten steel was the highest when the elevation Angle of 40°. Streamline density was also an important factor affecting the removal rate of impurities in molten steel by tundish filter.
Filter pore flow field distribution
In order to further verify the experiment, this paper will study the changes in the flow field at the cross section of the filter pore entrance and outlet by comparing them. The influence of elevation Angle on the velocity contour of the molten steel at the pore entrance of the tundish filter was shown in Fig. 9 below.
Fig. 9.
Influence of elevation Angle on molten steel velocity contour at pore entrance of tundish filter (a) 20°; (b) 25°; (c) 30°; (d) 35°; (e) 40°.
The turbulator is a key flow control device that significantly influences the flow field in the inlet region of the tundish. By introducing turbulence into the molten steel, the turbulator disrupts the flow, reduces the risk of stagnant zones, and promotes more uniform flow distribution. As a result of the turbulator’s effect, more molten steel flows through the upper part of the filter, further enhancing the filter’s performance. The increased turbulence helps to improve the interaction between the molten steel and the filter, leading to enhanced inclusion removal efficiency. The swirling motion generated by the turbulator ensures that the steel enters the filter with a more homogeneous flow, which is critical for maximizing the effectiveness of the filtration process.
As could be seen from Fig. 9, the flow field of molten steel at the filter entrance was generally distributed as the left and right side areas mostly pass through the molten steel at high velocity, while the middle area of the filter is mostly the middle and low velocity area. Moreover, since the molten steel didn’t pass through the filter inlet, different elevation angles had less influence on the velocity contour at the filter inlet then. Such a distribution state of molten steel velocity contour field was due to the existence of boundary effect on the left and right sides of the filter, and the contact between the middle-upper molten steel and the tundish covering agent and the envelope wall. There was tension on the surface of the molten steel, pressure at the bottom, and relatively small resistance. Therefore, there was no boundary effect in the middle area of the filter, resulting in a low flow rate.
Figure 10 shows the influence of elevation Angle on the molten steel velocity contour at the pore outlet of tundish filter. When the molten steel passes through the filter, the distribution of molten steel flow field changes obviously. Figure 11 showed a comparison of the velocity of the molten steel flowing through the inlet and outlet of the filter. When the elevation Angle was 20°, the flow field velocity changes the most, and the green and yellow middle and high velocity areas increase in the upper part of the filter. In contrast, at an elevation angle of 40°, the velocity of molten steel is lower at the top and higher in the middle. This is because, at an elevation angle of 20°, the filter resistance is relatively high, causing most of the molten steel to flow out from the upper region of the filter, resulting in the greatest velocity difference. Conversely, at an elevation angle of 40°, the filter resistance is relatively low, leading to the smallest velocity difference before and after the molten steel passes through the filter. This suggests that when molten steel flows out from the middle region, larger inclusions are more likely to come into contact with the tundish covering agent and the envelope wall, allowing them to be absorbed and thereby improving the removal efficiency of inclusions in molten steel. When the velocity difference between the inlet and outlet is small, the flow field of molten steel is more stable, which also promotes adequate contact between the inclusions and the tundish covering agent and envelope wall, further enhancing the removal efficiency. Therefore, the difference in flow velocity of molten steel before and after passing through the filter affects the effectiveness of inclusion removal by the tundish filter.
Fig. 10.
Influence of elevation Angle on molten steel velocity contour at pore outlet of tundish filter (a) 20°; (b) 25°; (c) 30°; (d) 35°; (e) 40°.
Fig. 11.
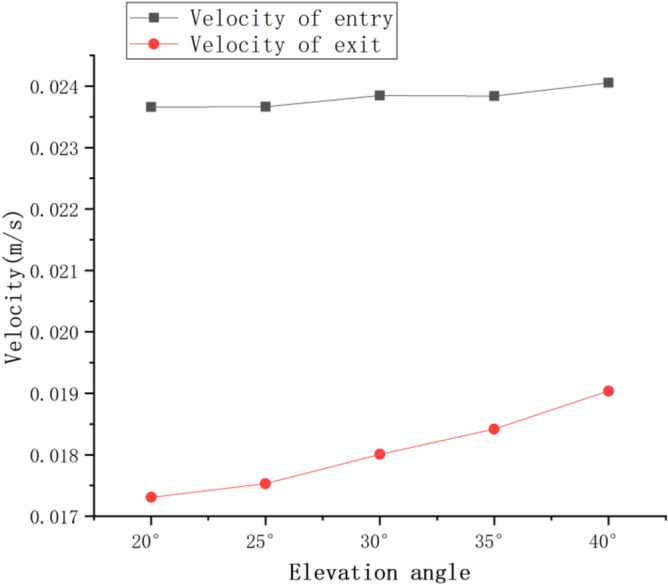
Comparison of entry and exit velocities of molten steel flowing through the filter.
Vector distribution of tundish filters
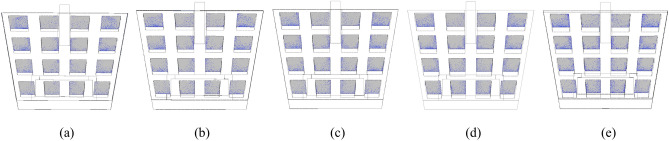
The flow field distribution of molten steel in this study is highlighted, and the regions with higher flow field density at different angles are extracted and converted into their vector distributions, as shown in Table 3.
Table 3.
Vector density of molten steel at the pore outlet of tundish filter.
| Elevation angle | Vector density of molten steel at the pore outlet of tundish filter |
|---|---|
| 20° | 14.11% |
| 25° | 15.62% |
| 30° | 16.26% |
| 35° | 16.91% |
| 40° | 21.60% |
The bold means the best performance. Significant values are in italics.
Figure 12 shows the influence of elevation Angle on the molten steel vector diagram at the pore outlet of tundish filter. Comparing the total groups of experiments, it was found that the filter generally had uniform particle distribution, indicating that the filter itself has the function of removing impurities. The more evenly the filter passed through each filter pore, the better the removal rate of impurities in molten steel. When the filter was designed at an elevation Angle, the molten steel would passed unevenly through the pores of the filter. Different elevation angles would lead to different flows of molten steel contacting the tunder covering agent and the envelope wall, which would also affect the removal effect of impurities in the molten steel. Figure 13 showed the relationship between the elevation Angle and the top vector density at the outlet of the filter. As shown in Fig. 13, the density vectorof the tundish filter exhibits an overall increasing trend. however, when the elevation Angle was 40°, the vector density of the molten steel at the outlet of the tundish significantly increases, reaching the maximum experimental value of 21.60%. Combining Figs. 12 and 13, it can be observed that the number of particles in the middle-to-upper section of the filter outlet gradually increases, and the vector density of molten steel significantly rises, indicating that the molten steel predominantly flows through the middle-to-upper section of the filter. When the elevation angle is 40°, the filter demonstrates the highest impurity removal efficiency for molten steel. Therefore, when the molten steel flow is uneven and primarily passes through the middle-to-upper section of the filter, the impurity removal efficiency of the filter is maximized.
Fig. 12.
Influence of elevation Angle on the molten steel vector diagram at the pore outlet of tundish filter. (a) 20°; (b) 25°; (c) 30°; (d) 35°; (e) 40°.
Fig. 13.
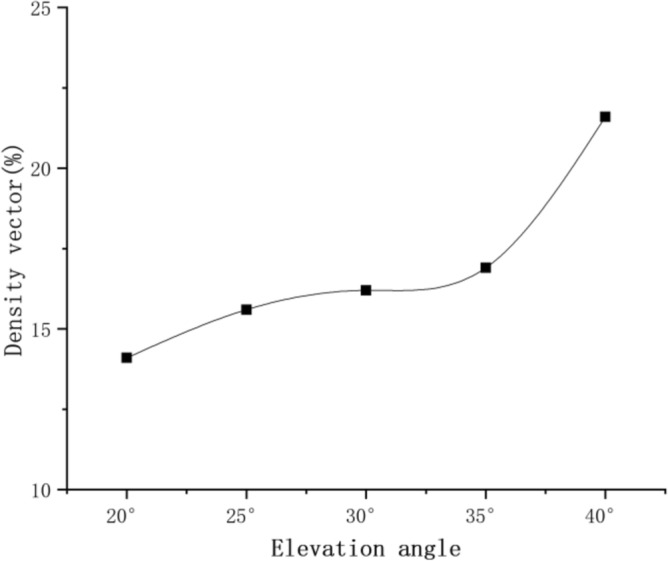
The relation between the elevation angle and the topmost vector density at the filter outlet.
Mesh sensitivity test
From the data provided in the Table 4, it is evident that as the number of mesh elements increases, the computation time grows exponentially, whereas the improvement in inclusion removal efficiency does not exhibit a proportional geometric increase. This highlights a significant decline in computational efficiency with mesh refinement. Specifically, when transitioning from the coarse mesh (0.8 million elements) to the medium mesh (1.5 million elements), the number of mesh elements increases by approximately 1.875 times, and computation time rises from 47.38 to 73.43 s, an increase of about 1.55 times. However, the inclusion removal rate only improves by 3.02 percentage points, from 71.03 to 74.05%. Further refinement from the medium mesh to the fine mesh (2.3 million elements) results in a 1.53-fold increase in the number of elements and a 1.67-fold increase in computation time, reaching 122.76 s, while the inclusion removal rate only marginally increases by 0.77 percentage points, from 74.05 to 74.82%.
Table 4.
Effect of mesh resolution on impurity removal rate and computation time.
| Cells (million) | Impurity removal rate (%) | Times (s) | |
|---|---|---|---|
| Coarse mesh | 0.8 | 71.03 | 47.38 |
| Medium mesh | 1.5 | 74.05 | 73.43 |
| Fine mesh | 2.3 | 74.82 | 122.76 |
This analysis demonstrates that the improvement in inclusion removal efficiency due to mesh refinement gradually approaches convergence. While finer meshes are capable of capturing flow field details with greater accuracy, the incremental gains in inclusion removal efficiency diminish, and the increase in removal rate is disproportionate to the significant rise in computation time. Particularly in the refinement from the medium to the fine mesh, the computation time grows exponentially while the improvement in inclusion removal efficiency becomes negligible. This indicates that further mesh refinement has entered a phase of diminishing returns, where the substantial increase in computational resources does not yield a commensurate improvement in results.
Conclusion
In this study, a tundish filter was designed with different elevation angles to explore the impact on the flow field distribution and impurity removal efficiency. The results indicate that the elevation angle significantly affects both the flow field distribution and streamline density in the tundish. When more molten steel flows at high speed through the upper part of the filter, the impurity removal efficiency is enhanced.
It was observed that higher flow densities after passing through the filter resulted in improved impurity removal. Specifically, the filter achieved the highest removal efficiency (74.05%) at a 40° elevation angle, while the lowest efficiency occurred at 20°. The comparative analysis of inlet and outlet velocities demonstrates that the filter’s elevation angle directly influences the flow velocity of molten steel, with lower velocity differences leading to better impurity removal.
Additionally, the vector distribution analysis revealed that when more molten steel passed through the middle-to-upper section of the filter, the impurity removal effect was enhanced. Therefore, while traditional filters can remove impurities from molten steel, optimizing the filter’s elevation angle, particularly at 40°, can significantly improve the removal efficiency.
Author contributions
Aiwei Lv: conceptualization, methodology, writing—original draft. Guoqiang Ding: conceptualization, investigation. Xudong Luo: supervision, writing—review & editing.
Funding
The research work was supported by the National Natural Science Foundation of China (U1908227 and U20A20239).
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Solorio-Diaz, G., Morales, R., Palafox-Ramos, J. & Ramos-Banderas, A. Modeling the effects of a swirling flow on temperature stratification of liquid steel and flotation of inclusions in a tundish. ISIJ Int.45(8), 1129–1137 (2005). [Google Scholar]
- 2.Sahai, Y. Tundish Technology for Clean Steel Production (World Scientific, 2007).
- 3.Ling, H. & Zhang, L. Numerical simulation of the growth and removal of inclusions in the molten steel of a two-strand tundish. JOM65, 1155–1163 (2013). [Google Scholar]
- 4.Liu, J., Zhou, P., Zuo, X., Wu, D. & Wu, D. Optimization of the liquid steel flow behavior in the tundish through water model experiment, numerical simulation and industrial trial. Metals12(9), 1480 (2022). [Google Scholar]
- 5.Liu, Y., Li, G., Wang, L. & Zhang, Z. Effect of the tundish gunning materials on the steel cleanliness. High Temp. Mater. Process.37(4), 313–323 (2018). [Google Scholar]
- 6.Neumann, S., Asad, A., Kasper, T. & Schwarze, R. Numerical simulation of metal melt flow in a one-strand tundish regarding active filtration and reactive cleaning. Metall. Mater. Trans. B50, 2334–2342 (2019). [Google Scholar]
- 7.Chen, X. et al. Structural optimisation of three-strand asymmetric tundish for super large round bloom continuous casting. Ironmaking Steelmaking51(5), 441–459 (2024). [Google Scholar]
- 8.Chen, X., Wang, H., Xiao, S., Lei, H. T. & Zhang, J. Research on the relative placement angle of the induction heater and the channel in a four-channel induction-heating tundish. Materials17, 12 (2024). [DOI] [PMC free article] [PubMed]
- 9.Dinda, S. K., Li, D., Guerra, F., Cathcart, C. & Barati, M. Continuous casting tundish dead volume study by physical modeling and computational investigation. Steel Res. Int.95, 11 (2024).
- 10.Farhan, M., Gupta, V. K. & Jha, P. K. Effect of inlet position and transverse wall inclination on the behaviour of inclusions in four-strand curved shaped tundish for steelmaking. In 9th International and 49th National Conference on Fluid Mechanics and Fluid Power, FMFP 2022 237–250 (Springer Science and Business Media Deutschland GmbH, 2024).
- 11.Liu, Y. R., Chu, X., Li, N. H., & Wang, W. Simulation of the effect of continuous casting tundish filter on removing inclusions in steel. In 12th Global Conference on Materials Science and Engineering, CMSE 2023, vol. 2680 (Institute of Physics, 2024).
- 12.Lu, J., Luo, Z. & Zou, Z. Numerical simulation of collision-coalescence and removal of inclusion in split swirling flow tundish. Metall. Res. Technol.121, 4 (2024).
- 13.Ocampo Vaca, F. A. et al. Effect of ladle shroud blockage on flow dynamics and cleanliness of steel in coupled ladle–shroud–tundish system. Steel Res. Int.95, 4 (2024).
- 14.Plappally, A. K., Sharif, M. A. R. & Bradt, R. C. Modeling the flow of molten steel in a tundish containing an inclusion filtering trap. Fluid Dyn. Mater. Process.3(2), 115–128 (2007). [Google Scholar]
- 15.Smirnov, A. et al. Numerical investigation and physical modeling for optimisation hydrodynamic processes in continuous casting tundish. Metall. Res. Technol.120, 3 (2023).
- 16.Bao, Y. & Wang, M. Development trend of tundish metallurgical technology. Contin. Cast33, 2–11 (2021). [Google Scholar]
- 17.Janiszewski, K. & Panic, B. Industrial investigations of the liquid steel filtration. Metalurgija53(3), 339–342 (2014). [Google Scholar]
- 18.Janiszewski, K. Influence of steel filtration on reduction of clogging of immersed nozzles in continuous steel casting installations. In 25th International Conference on Metallurgy and Materials, METAL 167–172 (TANGER Ltd, 2016) .
- 19.Isayev, O., Kislitsa, V., Zhang, C., Wu, K. & Hress, A. Metallurgical effects of a novel tundish refining process for high-strength low-alloy hot-rolled plate steels. Metallurgist59(9–10), 980–986 (2016). [Google Scholar]
- 20.Sahai, Y. Tundish technology for casting clean steel: a review. Metall. Mater. Trans. B47, 2095–2106 (2016). [Google Scholar]
- 21.Liu, C. et al. Numerical investigation on motion and removal of inclusions in continuous casting tundish with multiorifice filter. Steel Res. Int.93(12), 2100818 (2022).
- 22.Ding, G. et al. Numerical simulation study on the influence of tundish filter on molten steel flow and inclusions removal. Steel Res. Int.95(5), 2300807 (2024).
- 23.Tan, C. et al. Understanding of baffle effect of inserting a filter within a tundish via a water model experiment and numerical simulation. Metal. Res. Technol.121, 1 (2024).
- 24.Wang, J., Liu, Z., Chen, W., Chen, H. & Zhang, L. Numerical simulation on the multiphase flow and reoxidation of the molten steel in a two-strand tundish during ladle change. Int. J. Miner. Metall. Mater.31(7), 1540–1553 (2024). [Google Scholar]
- 25.Wang, Z. et al. Channel-type induction heating tundish technology for continuous casting: a review. Materials16, 2 (2023). [DOI] [PMC free article] [PubMed]
- 26.Zhang, Y. et al. Hydraulic and numerical simulation of flow field characteristics in induction heating continuous casting tundish. Ironmaking Steelmaking51(3), 236–248 (2024). [Google Scholar]
- 27.Zhang, Z.-X. et al. Numerical investigation on transient flow and inclusion removal behavior in tundish during ladle change process. Steel Res. Int.95, 12 (2024).
- 28.Mazumdar, D. Review, analysis, and modeling of continuous casting tundish systems. Steel Res. Int.90(4), 1800279 (2019).
- 29.Janiszewski, K. Refining of liquid steel in a tundish using the method of filtration during its casting in the CC machine. Arch. Metall. Mater.58(2), 513–521 (2013). [Google Scholar]
- 30.Murata, N., Sonoda, S., Hino, H., Kitada, H. & Kano, M. Sensitivity analysis for controlling molten steel temperature in Tundish. In 2012 IFAC Workshop on Automation in the Mining, Mineral and Metal Industries, MMM, vol. 45 270–271 (IFAC Secretariat, 2012) .
- 31.Hudzieczek, Z., Kurka, V., Bedronova, P., Pindor, J. & Cienciala, J. Design of Tundish for vacuum over-pressure induction melting device. In 22nd International Conference on Metallurgy and Materials, METAL 103–109 (TANGER Ltd, 2013).
- 32.Wang, X.-Y., Zhao, D.-T., Qiu, S.-T. & Zou, Z.-S. Effect of tunnel filters on flow characteristics in an eight-strand tundish. ISIJ Int.57(11), 1990–1999 (2017). [Google Scholar]
- 33.Li, M., Tao, B., Wu, H. & Sun, Y. Effect of ZrO2 filters on inclusions in steel. In Symposium on Materials Processing Fundamentals held at the TMS Annual Meeting and Exhibition 155–164 (Springer Science and Business Media Deutschland GmbH, 2021).
- 34.Zhang, W.-W., Zheng, W., Yan, W. & Li, G.-Q. Formation mechanism of interface reaction layer between microporous magnesia refractories and molten steel and its effect on steel cleanliness. J. Iron Steel Res. Int.30(9), 1743–1754 (2023). [Google Scholar]
- 35.Janiszewski, K., Gajdzik, B., Gryc, K., Socha, L. & Bogdal, A. Industrial experiments filtration of steel. Solid State Phenom.226, 189–192 (2015). [Google Scholar]
- 36.Takahashi, K., Ando, M. & Ishii, T. Numerical investigation of unsteady molten steel flow and inclusion behavior in the tundish in the ladle change period. ISIJ Int.54(2), 304–310 (2014). [Google Scholar]
- 37.Jin, Y. et al. Removal mechanism of microscale non-metallic inclusions in a tundish with multi-hole-double-baffles. Metals8(8), 611 (2018). [Google Scholar]
- 38.Yang, B., Lei, H., Bi, Q., Xiao, Y. & Zhao, Y. Numerical simulation of collision-coalescence and removal of inclusions in a tundish. JOM70, 2950–2957 (2018). [Google Scholar]
- 39.Wang, Q. et al. CFD investigation of effect of multi-hole ceramic filter on inclusion removal in a two-strand tundish. Metall. Mater. Trans. B: Process Metall. Mater. Process. Sci.51(1), 276–292 (2020). [Google Scholar]
- 40.Qin, X., Cheng, C., Chen, H., Li, Y. & Jin, Y. Numerical study on metallurgical effect of filtering weir with multi-stepped orifices in tundish. Metall. Mater. Trans. B: Process Metall. Mater. Process. Sci.55(3), 1910–1924 (2024). [Google Scholar]
- 41.Quan, Q. et al. Physical and numerical investigation on fluid flow and inclusion removal behavior in a single-strand tundish. J. Iron Steel Res. Int.30(6), 1182–1198 (2023). [Google Scholar]
- 42.Huang, W. et al. Removal of inclusions using swirling flow in a single-strand tundish. ISIJ Int.62(7), 1439–1449 (2022). [Google Scholar]
- 43.Chen, S. et al. Collision-coalescence among inclusions with bubble attachment and transport in molten steel of RH. J. Mater. Res. Technol.15, 5141–5150 (2021). [Google Scholar]
- 44.Li, Y. et al. Numerical and experimental studies on the effects of molten steel viscosity on fluid flow, inclusion motion, and temperature distribution in a tundish. Phys. Fluids36, 7 (2024).
- 45.Wang, J. et al. Effect of tundish impact zone optimization on inclusion removal in steel: industrial and simulation studies. Metall. Mater. Trans. B55(2), 808–820 (2024). [Google Scholar]
- 46.Wang, Z. et al. Residence time distribution (RTD) applications in continuous casting Tundish: a review and new perspectives. Metals12(8), 1366 (2022). [Google Scholar]
- 47.Huang, K. et al. Suppression of free-surface vortex in tundish by rotating stopper-rod and its impact on multiphase flow in mold. Metall. Mater. Trans. B,55(4), 2960–2975 (2024).
- 48.Lee, H. C. & Wahab, A. K. A. Performance of different turbulence models in predicting flow kinematics around an open offshore intake. SN Appl. Sci.1(10), 1266 (2019).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.