Unveiling anharmonic scattering in van der Waals semiconductor GaPS₄ through Raman spectroscopy and theoretical calculation

Summary

The van der Waals thiophosphate GaPS₄ presents additional opportunities for gallium-based semiconductors, but limited research on phonon interactions has hindered optimization on thermal properties. This research undertakes a comprehensive investigation into the anharmonic phonon scattering within GaPS₄. The findings reveal pronounced anharmonic scattering, with both cubic and quartic phonon scatterings significantly influencing phonon redshift and broadening. Notably, the scattering strength is markedly higher in Raman peaks with higher wavenumbers, where quartic phonon scattering leads to conspicuous nonlinear broadening. Furthermore, a large amount of cubic and quartic scattering events is found to be Umklapp process. Besides, the molecular dynamics calculation quantitatively confirms the extensive redshift and broadening and suggests stronger anharmonic scattering beyond the Brillouin zone center. This research not only elucidates the anharmonic phonon scattering in GaPS4 but also provides theoretical foundation for further application. Concurrently, it enhances the understanding of anharmonic scattering in semiconductors within the condensed matter physics.

Graphical abstract

Highlights

• •Reveal the temperature-dependent Raman phonon properties in GaPS₄
• •Quantify the contribution from cubic and quartic phonon scattering
• •Temperature-dependent phonon dispersion curves obtained by molecular dynamics

Condensed matter physics; Materials science; Computational materials science

Introduction

Gallium-based and -related semiconductors have made significant progress in various fields, including optoelectronic sensing, optical communication, and power devices.^1,2,3,4,5,6 The van der Waals (vdW) semiconductor gallium thiophosphate GaPS₄ represents a frontier in the realm of gallium-based semiconductors, initially reported by Buck et al. in 1973.⁷ The distinctive layered nature bestows upon it vast potential applications and significant scholarly merit. The anisotropic optical and mechanical properties have been rigorously validated in GaPS₄, and a wide band gap of 4.5 eV can be realized by cross substitution. Furthermore, GaPS₄ is anticipated to play a pivotal role as a catalyst in the photolytic water splitting processes and serves as an efficacious charge trapping medium within high-temperature artificial synapses.^{8,9,10,11,12,13} Nevertheless, the potential of GaPS₄ is tempered by the paucity of research on phonon-phonon interactions or scattering mechanisms, which are crucial determinants of thermal transport within the material.¹⁴ It is widely acknowledged that phonon scattering in crystalline structures is inherently anharmonic, resulting in diminished thermal conductivity, alterations in phase transitions, modulation of optical characteristics, and the augmentation of thermoelectric properties, among other effects.^{15,16,17,18,19} The investigation into anharmonic phonon scattering is imperative for advancing comprehension of the thermal transport phenomena in semiconductors, which not only sheds light on the underlying mechanisms but also opens up an avenue for regulating and controlling the device performance.

For long times, the scientific community has concentrated on investigating third-order (cubic) phonon scattering.^20,21,22 However, increasing literature underscore the significance of fourth-order (quartic) phonon scattering, suggesting its non-negligible contribution to the overall thermal dynamics.^19,23,24,25 Concurrently, the Umklapp process and anharmonic scattering of phonons outside the Brillouin zone center still pose intricate scientific issues. In this investigation, both cubic and quartic phonon scattering processes and anharmonic phonon properties throughout the Brillouin zone are comprehensively studied to unravel the complexities of phonon anharmonic scattering within GaPS₄.

Specifically, Raman spectroscopy is employed to elucidate temperature-dependent Raman phonon characteristics at the Brillouin zone center. Concurrently, first-principles calculations alongside the quasi-harmonic approximation (QHA) and Ab initio molecular dynamics (AIMD) are utilized to determine the thermal expansion coefficient, Grüneisen parameters, and anharmonic phonon properties of GaPS₄. Raman spectroscopy stands as a robust, non-destructive analytical technique, and the intrinsic accuracy of non-empirical parameters of first-principles calculation affords precise determination of phonon-related attributes. Employing both symmetric and asymmetric scattering models, the anharmonic scattering in GaPS₄ has been quantified. The findings reveal pronounced quartic phonon scattering, evidenced by both the nonlinearity of redshift and broadening in high wavenumber Raman peaks, indicative of numerous Umklapp processes, and potential stronger scattering on phonons outside Brillouin zone center.

Results and discussion

Temperature-dependent Raman spectrum and irreducible representation

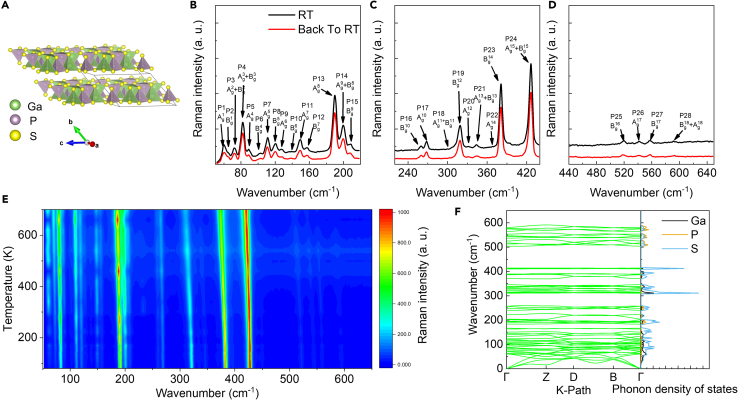
The primitive cell of GaPS₄ comprises 24 atoms, manifesting a quintessential triclinic lattice with the space group P2₁/C, as depicted in Figure 1A. In the side view, each gallium (Ga) and phosphorus (P) atom is tetrahedrally bonded to four sulfur (S) atoms. These alternating tetrahedrons constitute the intricate lattice framework of GaPS₄. Concurrently, a layered nature is discernible along the b-axis, with each layer being connected exclusively by vdW forces.

Figure 1.

Lattice structure, Raman and phonon properties

(A) Schematic diagrams of the GaPS₄ crystal.

(B–D) The Raman spectra of GaPS₄ crystal of (B) 50–220 cm⁻¹, (C) 220–440 cm⁻¹, and (D) 440–650 cm⁻¹, measured at room temperature before and after the heating.

(E) Contour plot of temperature-dependent Raman spectra from 80 to 700 K.

(F) The phonon dispersion curve and density of states of GaPS₄ crystal.

To ascertain the temperature-dependent Raman phonon properties of GaPS₄, the sample was initially cooled to 80 K and subsequently heated to 700 K. During this process, the Raman spectra were measured. Figures 1B–1D illustrate the Raman spectra of GaPS₄ under room temperature before and after heating. The consistency of Raman spectrum observed suggests that the GaPS₄ crystal remained stable, with no discernible phase transitions occurring during the heating. This observation further corroborates the thermal robustness of GaPS₄ up to at least 700 K. Within 50 cm⁻¹ to 600 cm⁻¹, as many as 28 Raman peaks are discernible, as depicted in Figures 1B–1D. The specific peak modes and irreducible representations have been confirmed in previous work.²⁶

The temperature-dependent Raman spectra from 80 to 700 K, as illustrated in Figure 1E, manifest discernible variations in peak positions and linewidths correlating with temperature. The Raman peaks between 500 cm⁻¹ and 600 cm⁻¹ are difficult to intuitively exhibit their change due to their relatively lower intensity. It becomes evident that, as the temperature ascends, a majority of the Raman peak positions undergo a redshift toward lower wavenumbers. This redshift manifests with variable magnitudes across the different peaks. Meanwhile, the broadening of Raman peak can also be clearly observed. Generally, the phonon self-energy, indicative of phonon-phonon interaction, is expressed by

$$\Sigma \left(\omega \right)=\Delta \left(\omega \right)+i\Gamma \left(\omega \right)$$ (Equation 1)

where the real part $\Delta \left(\omega \right)$ and imaginary part $i\Gamma \left(\omega \right)$ signify the peak position shift and linewidth broadening, respectively. The aforementioned observations compellingly demonstrate the pronounced impact of temperature on the phonon self-energy of GaPS₄, thereby confirming the presence of significant anharmonic phonon scattering.

To furnish reference for subsequent calculation and analysis, the phonon dispersion curve and density of states (DOS) of GaPS₄ primitive cell were calculated employing the finite displacement method. As delineated in Figure 1F, the phonon dispersion curve conspicuously shows no imaginary frequency across the entire Brillouin zone path, thereby affirming the reliability of the phonon calculation. In phonon DOS, the contribution of Ga and P atoms is predominantly observed at lower and higher wavenumbers, respectively, whereas the contribution of S atoms is discernible across the entire range. This phenomenon is attributed to the mass disparity among different atoms. Here, in GaPS₄ primitive cell, which encompasses 24 atoms, a total of 72 phonon modes are discerned at the Brillouin zone center, delineated as follows:

$${\Gamma }_{acoustic}=A_u+2B_u$$ (Equation 2)

$${\Gamma }_{optic}=18A_g+17A_u+18B_g+16B_u$$ (Equation 3)

where Ag and Bg represent Raman active modes and Au and Bu denote infrared active modes. Given the lattice structure, the Raman tensor of GaPS₄ is articulated as²⁷:

$$A_g=\left(\begin{array}{ccc}a& d& 0\\ d& b& 0\\ 0& 0& 0\end{array}\right){,B}_g=\left(\begin{array}{ccc}0& 0& e\\ 0& 0& f\\ e& f& 0\end{array}\right)$$ (Equation 4)

The theoretical phonon wavenumbers and Raman peak Lorentz fitting of 7 degenerate peaks and 21 non-degenerate peaks are comprehensively listed in Table S1, and the theoretical and experimental values are relatively close, which corroborates the reliability of the results.

Theoretical foundation and related coefficients

To thoroughly understand the Raman phonon anharmonic scattering GaPS₄, a quantitative framework is indispensable. Here, a phonon scattering model is adopted to fit the redshift and broadening in temperature-dependent Raman spectra.²⁸ The wavenumber of the Raman peak as a function of temperature can be articulated as^29,30:

$$\omega \left(T\right)={\omega }_0+\Delta {\omega }_j{\left(T\right)}_V+\Delta {\omega }_j{\left(T\right)}_p$$ (Equation 5)

where ${\omega }_0$ denotes the Raman phonon wavenumber at absolute zero and $\Delta {\omega }_j{\left(T\right)}_V$ and $\Delta {\omega }_j{\left(T\right)}_p$ represent the contribution to wavenumber shift from thermal expansion and phonon scattering, respectively. The contribution from thermal expansion can be expressed as³¹:

$$\Delta {\omega }_j{\left(T\right)}_V={\omega }_0\left[e^{-\gamma \underset{0}{\overset{T}{\int }}\left(\beta \left(T\right)\right)d{T}^{\prime }}-1\right]$$ (Equation 6)

where $\beta \left(T\right)$ delineates the volume thermal expansion coefficient and γ is the mode Grüneisen parameter, which will be discussed later. Given phonons follow the Bose-Einstein distribution, it signifies³²:

$${\omega }_j{\left(T\right)}_p=A\left[1+\sum _{i=1}^2\frac{1}{e^{\frac{\hslash {\omega }_i}{2k_{B}T}}-1}\right]+B\left[1+\sum _{l=1}^3\frac{1}{e^{\frac{\hslash {\omega }_l}{3k_{B}T}}-1}+\frac{1}{{\left(e^{\frac{\hslash {\omega }_l}{3k_{B}T}}-1\right)}^2}\right]$$ (Equation 7)

Analogously, the scattering’s contribution to phonon broadening is articulated as follows:

$${\Gamma }_j\left(T\right)={\Gamma }_0+C\left[1+\sum _{i=1}^2\frac{1}{e^{\frac{\hslash {\omega }_i}{2k_{B}T}}-1}\right]+D\left[1+\sum _{l=1}^3\frac{1}{e^{\frac{\hslash {\omega }_l}{3k_{B}T}}-1}+\frac{1}{{\left(e^{\frac{\hslash {\omega }_l}{3k_{B}T}}-1\right)}^2}\right]$$ (Equation 8)

where ℏ represents the reduced Planck constant, k_B is the Boltzmann constant, and Γ₀ is the intrinsic linewidth. Here, the coefficients A and C correspond to the cubic anharmonic scattering, whereas B and D pertain to the quartic anharmonic scattering, collectively representing the scattering strength.

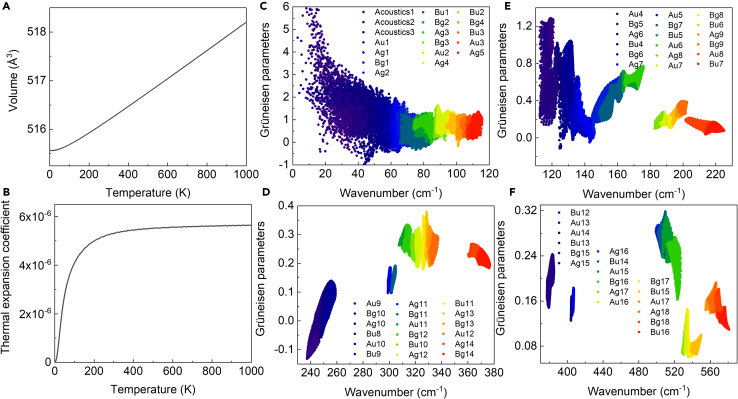
To quantify the anharmonic phonon scattering, the phonon properties of GaPS₄ subjected to a strain range of 98%–102% were calculated via the finite displacement method. Here, the volume thermal expansion coefficient is obtained by fitting the free energy by the QHA method, as represented in Figures 2A and 2B. As the temperature escalates, the GaPS₄ primitive cell demonstrates an initial non-linear thermal expansion, subsequently transitioning to a linear thermal expansion. This phenomenon is aptly characterized by the thermal expansion coefficient, which exhibits a swift augmentation with temperature, ultimately plateauing at approximately 5.5 × 10⁻⁶. To obtain a formulaic representation for later investigation, a logistic formula has been employed to achieve the following expression for the thermal expansion coefficient:

$$\beta \left(T\right)=A_2+\frac{\left(A_1-A_2\right)}{\left(1+{\left(\frac{T}{T_0}\right)}^p\right)}$$ (Equation 9)

where A₁ = −1.64 × 10⁻⁷, A₂ = 5.71 × 10⁻⁶, T₀ = 51.88, and p = 1.49.

Figure 2.

Coefficients predicted by first-principles calculation

(A–B) Temperature-dependent volume and thermal expansion coefficient of GaPS₄ primitive cell.

(C–F) Mode Grüneisen parameters of all phonon modes in GaPS₄.

Additionally, the mode Grüneisen parameters are derived from the phonon wavenumbers of GaPS₄ under a strain range of 99%–101%, formulated as follows:³³

$$\gamma \left(q\nu \right)=-\frac{V}{\omega \left(q\nu \right)}\frac{\partial \omega \left(q\nu \right)}{\partial V}$$ (Equation 10)

where V represents the crystal volume and $\omega \left(q\nu \right)$ denotes the mode phonon wavenumber. All mode Grüneisen parameters of Raman and infrared phonon modes of GaPS₄ in the Brillouin zone are shown in Figures 2C–2F, which exhibit a notable decrement concomitant with the escalation of wavenumber in general. Here, only the mode Grüneisen parameters at the Brillouin zone center will be utilized. Owing to the degenerate Raman peaks, the mode Grüneisen parameters pertinent to these peaks have been averaged, with the results presented in Table 1.

Table 1.

Mode Grüneisen parameters of all Raman peaks in GaPS₄

Peak	Mode	Grüneisen parameters	Peak	Mode	Grüneisen parameters	Peak	Mode	Grüneisen parameters
1	Ag1	0.75	11	Ag7	0.24	21	Ag13	0.28
2	Bg1	0.47	12	Bg7	0.57		Bg13	0.26
3	Ag2	0.38	13	Ag8	0.10	22	Ag14	0.27
	Bg2		14	Bg8	0.27	23	Bg14	0.21
4	Ag3	0.83		Ag9		24	Bg15	0.17
	Bg3		15	Bg9	0.28		Ag15
5	Ag4	1.12	16	Bg10	0.06	\	Ag16	0.28
6	Bg4	0.71	17	Ag10	0.05	25	Bg16	0.27
7	Ag5	1.33	18	Ag11	0.15	26	Ag17	0.07
8	Bg5	0.96		Bg11		27	Bg17	0.08
9	Ag6	0.12	19	Bg12	0.24	28	Ag18	0.18
10	Bg6	0.01	20	Ag12	0.28		Bg18

Symmetric and asymmetric anharmonic scattering fitting

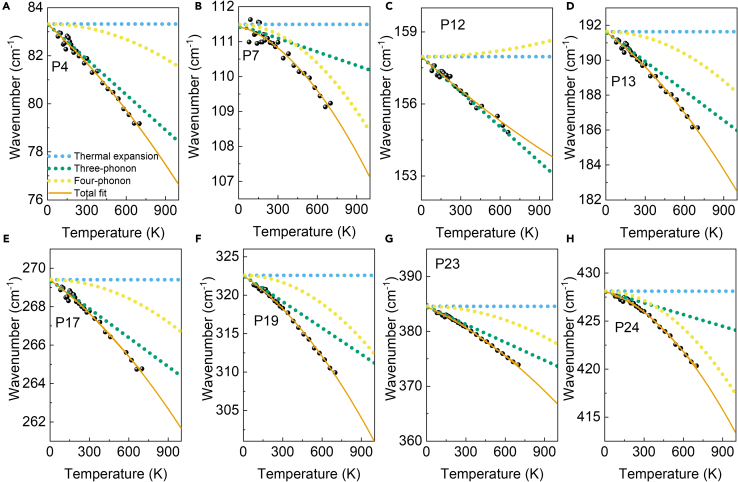
Building upon the previously delineated Equations 5, 6, 7, and 8, the cubic and quartic anharmonic phonon scattering in GaPS₄ can be quantified. Here, a symmetric scattering model is employed, which means ${\omega }_0={\omega }_c+{\omega }_c$ for cubic scattering and ${\omega }_0={\omega }_q+{\omega }_q+{\omega }_q$ for quartic scattering. It is imperative to note that the particle scattering process is governed by the energy conservation. Consequently, only those peaks that exhibit phonon (DOS) at one-third and half of the wavenumber are amenable for fitting symmetrically. Therefore, owing to the non-continuous phonon DOS and the presence of certain Raman peaks exhibiting suboptimal signal-to-noise ratios, only partly Raman peaks have been fitted here. The fitting outcomes, exhibiting the redshift of the Raman peaks, are depicted in Figure 3, while the quantitative data are tabulated in Table 2. It becomes evident that the influence of thermal expansion on the redshift phenomenon is limited, attributable primarily to the diminutive mode Grüneisen parameters of GaPS₄.

Figure 3.

Fitting results of Raman wavenumber

(A–H) Temperature-dependent Raman peak wavenumber and the anharmonic fitting results of P4, P7, P12, P13, P17, P19, P23, and P24.

Table 2.

Numerical fitting results of cubic and quartic phonon scattering from symmetric model

Peak	A	B	C	D	ω0 (cm−1)	Γ0 (cm−1)
4	−0.0234	−0.00002	0.0039	0.0000	83.32	4.18
7	−0.0077	−0.00008	0.0047	0.0000	111.46	4.30
12	−0.0440	0.00003	0.0095	0.0000	157.97	5.34
13	−0.0620	−0.0003	0.0528	0.0000	191.63	3.98
17	−0.0776	−0.0004	0.0652	0.0000	269.41	4.25
19	−0.2109	−0.0015	0.1911	0.0009	322.59	4.10
23	−0.2406	−0.0020	0.0603	0.0013	384.57	4.25
24	−0.0997	−0.0038	0.0504	0.0017	428.12	5.09

The redshift can be mainly ascribed to the anharmonic phonon scattering, Among which both cubic and quartic phonon scattering mechanisms are pivotal. Specifically, cubic phonon scattering predominates at lower temperatures. In contrast, at elevated temperatures, the influence of quartic phonon scattering becomes markedly pronounced. In redshift exhibiting greater linearity, such as those observed in P4 and P17, cubic phonon scattering emerges as the predominant mechanism. Notably, in P12, the redshift is nearly linear but decelerates with increasing temperature, hinting at a potential inhibitory contribution from quartic phonon scattering. Furthermore, quartic phonon scattering is pronounced in nonlinear redshift, exemplified by P7 and P24, where its contribution overtakes that of cubic phonon scattering around a relatively lower temperature of 400 K. Additionally, the scattering strength value presented in Table 2 corroborate that both cubic and quartic scattering intensities manifest more robustly in redshift of Raman peaks with higher wavenumbers.

Relative to the redshift, the contribution of anharmonic scattering to the Raman peak linewidth broadening is markedly more regular. As delineated in Figure 4, in Raman peaks with lower wavenumbers such as P4, P7, and P12, the broadening is only limited to 1–2 cm⁻¹. In these instances, the broadening displays a near-linear trend and is predominantly driven by cubic scattering, with the quartic scattering being virtually inconsequential. Significant broadening is discernible at peaks with higher wavenumbers, notably P19, P23, and P24. In these cases, the broadening exhibits a distinctly non-linear character, with quartic phonon scattering assuming a dominant role, which contributes more to broadening at high temperatures compared to cubic scattering. A case in point is P24, where the influence of quartic scattering surpasses that of cubic scattering at temperatures around at ∼400 K. The results presented in Table 1 also unequivocally demonstrate that in the higher wavenumber Raman peaks, a more enhanced strength of quartic scattering can be observed. It is imperative to note that in Table 1 and some later results, the intensity of certain quartic scattering is denoted as zero. This reflects their limited intensity but should not be misconstrued as an absence of quartic scattering phenomena altogether. Moreover, according to the definition

$${\tau }_{\lambda }=\frac{1}{2{\mathrm{\Gamma }}_{\lambda }\left({\omega }_{\lambda }\right)}$$ (Equation 11)

$$P_{\lambda }=\frac{1}{{\tau }_{\lambda }}$$ (Equation 12)

Figure 4.

Fitting results of Raman linewidth

(A–H) Temperature-dependent Raman peak linewidth and the anharmonic fitting results of P4, P7, P12, P13, P17, P19, P23, P24.

The temperature-dependent phonon lifetime and scattering rate are illustrated in Figure S1. It reveals that the Raman phonon lifetime of GaPS₄ predominantly ranges between 0.1 and 0.6 ps, with corresponding scattering rate from 1.6 to 10 ps⁻¹. The phonon lifetime exhibits a decreasing trend with increasing temperature, which is particularly pronounced in higher wavenumber.

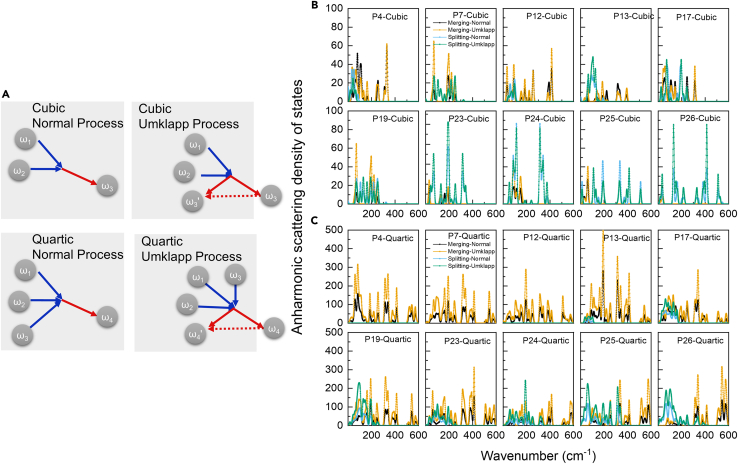
For Raman peaks that defy fitting within the symmetric scattering, the asymmetric scattering model is employed for further analysis. This model is also applied to P12, P23, and P24 for comparative purposes against the symmetric model, as it may be closer to reality. As depicted in Figure 5A, asymmetric cubic and quartic phonon scatterings are discerned as the Merging process, which leads to higher wavenumber phonons ${\omega }_0+{\omega }_1={\omega }_2$ and ${\omega }_0+{\omega }_1+{\omega }_2={\omega }_3$, and the Splitting process of phonon scattering into lower wavenumber phonons ${\omega }_0={\omega }_1+{\omega }_2$ and ${\omega }_0={\omega }_1+{\omega }_2+{\omega }_3$ to obey the energy conservation, respectively. In addition to the intrinsic Raman phonons wavenumber (${\omega }_0$), phonons partaking in scattering are set at the peak of phonon DOS, where phonon occurrence probability is large. Given that higher wavenumber peaks such as P25, P26, and P27 cannot scatter to higher wavenumbers, which will be exhibited later, and the quartic scattering such as ${\omega }_0+{\omega }_1={\omega }_2+{\omega }_3$ is impossible for fitting here, only the Splitting process is considered. All involved phonons and numerical results are listed in Table 3. It is pertinent to highlight that, due to the partial continuity of the phonon DOS, the listed scattering channels represent the most probable, rather than the exclusive ones.

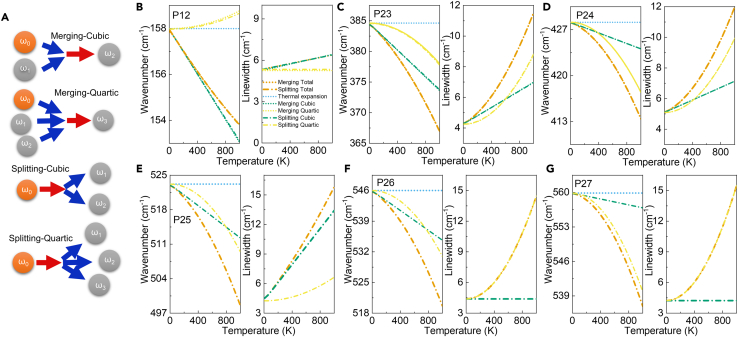
Figure 5.

Fitting results of asymmetric scattering model

(A) Schematic diagram of cubic and quartic phonon anharmonic scattering, with Merging and Splitting scattering, respectively.

(B–G) Asymmetric anharmonic scattering fitting results of (B) P12, (C) P23, (D) P24, (E) P25, (F) P26, and (G) P27 peaks.

Table 3.

Numerical fitting results of asymmetric cubic and quartic phonon scattering from asymmetric model, with Merging and Splitting scattering channel

Peak	Type	Cubic phonon (cm−1)	Quartic phonon (cm−1)	A	B	C	D	ω0 (cm−1)	Γ0 (cm−1)
12	Merging	216.88; 374.88	126.39; 253.07; 537.46	−0.1557	0.0005	0.0368	0.0000	157.99	5.25
	Splitting	82.95; 75.05	57.62; 35.90; 64.48	−0.0439	0.00003	0.0095	0.0000	157.97	5.34
23	Merging	191.54; 574.84	90.14; 72.10; 545.53	−0.3621	−0.0011	0.0905	0.0007	384.62	4.24
	Splitting	216.88; 166.42	90.19; 126.39; 166.72	−0.2334	−0.0016	0.0585	0.0011	384.57	4.25
24	Merging	90.19; 517.09	82.95; 57.62; 567.47	−0.0712	−0.0012	0.0360	0.0006	428.12	5.09
	Splitting	310.98; 115.92	191.54; 82.95; 152.41	−0.0781	−0.0026	0.0395	0.0012	428.12	5.09
25	Splitting	310.98; 211.6	191.54; 90.20; 240.87	−0.3151	−0.0043	0.2644	0.0008	523.19	4.25
26	Splitting	394.23; 150.67	191.54; 253.07; 100.29	−0.2834	−0.0055	0.0000	0.0037	545.99	4.39
27	Splitting	310.98; 248.82	198.78; 111.91; 249.11	−0.0948	−0.0086	0.0000	0.0049	559.87	4.23

The comparative analysis of the fitting outcomes presented in Figures 5B–5D reveals the similar tendency to the symmetric scattering model in contribution to both redshift and linewidth. However, stark contrasts emerge between the Merging and Splitting processes as delineated in Table 3. In the case of P12, which exhibits a lower wavenumber, the intensities of both cubic and quartic scattering of Merging process significantly surpass those of the Splitting process. A similar pattern is observed in P23, where cubic scattering strength is considerably more pronounced in the Merging process, whereas quartic scattering intensity is more substantial in the Splitting process. In contrast, for P24 with a higher wavenumber, both cubic and quartic scattering in Splitting process exceed those of the Merging process.

In the case of Raman peaks with much higher wavenumbers, as illustrated in Figures 5E and 5F, peaks P25 to P27 manifest a linewidth broadening exceeding 10 cm⁻¹ and a redshift greater than 20 cm⁻¹ from 80 to 700 K. This shows that the anharmonic phonons scattering in high wavenumber peaks is extremely strong, and cubic and quartic scattering both play crucial roles here. Notably, in P26 and P27, the broadening is predominantly ascribed to quartic scattering within the Splitting process, leading to a marked nonlinearity in the broadening. Moreover, in alignment with the symmetric scattering model, it is observed that the quartic scattering in higher wavenumber Raman peaks exhibits a general enhancing trend.

The aforementioned quantitative results comprehensively illustrate the anharmonic phonon scattering in GaPS₄. It is evident that both cubic and quartic phonon scatterings contribute significantly to the redshift phenomenon, whereas the contribution of quartic phonon to broadening exists almost exclusively in high wavenumber phonons. In addition, the comparative analysis of Splitting and Merging process indicates that the increase of wavenumber may lead to a stronger splitting process and a weaker Merging process. Additionally, the anharmonic scattering intensity of high wavenumber Raman peaks is significantly stronger than that of low wavenumber peaks. This indicates that at high temperatures, high wavenumber Raman phonons are more likely to scatter to lower wavenumbers, whereas the opposite process of scattering from low to high wavenumbers is considerably more difficult.

Umklapp and normal process from scattering DOS

As previously discussed, it is clear that anharmonic phonon scattering must adhere to the energy conservation. However, the issue of momentum conservation is decidedly more complex. Typically, as depicted in Figure 6A, when the wavevector symbolizing the phonon momentum after scattering remains within the first Brillouin zone, the scattering event is deemed to obey momentum conservation, thus categorizing it as a normal process. Conversely, when the phonon momentum after scattering surpasses the boundaries of the first Brillouin zone, the anharmonic phonons involved in the scattering process deviate from momentum conservation. In such scenarios, it becomes apparent that an additional wavevector intervenes, redirecting the scattered phonon wavevector back into the first Brillouin zone. This mechanism, which is crucial to thermal transport and referred to as the Umklapp process, is recognized as the primary source of thermal resistance and is correlated with reduced thermal conductivity.^34,35

Figure 6.

DOS of phonons involved in different scattering processes

(A) Schematic diagrams illustrating the normal process and Umklapp process.

(B and C) Phonon density of states involved in (B) cubic and (C) quartic scattering of Raman phonons in GaPS₄.

In accordance with the energy conservation formula previously articulated, an exhaustive ergodic analysis of both cubic and quartic phonon anharmonic scattering channels has been undertaken across the entirety of the Brillouin zone of GaPS₄. The ω₀ of each peak is inferred from the fitting results of the Raman spectrum. Moreover, the phonon wavevectors subsequent to cubic and quartic scattering are inferred based on distinct phonon Merging and Splitting process, as depicted in Figures S2 and S3, respectively. Significantly, the wavevectors that exceed the first Brillouin zone suggest the occurrence of the Umklapp process. After the cubic scattering, the wavevectors demonstrate symmetry within the Brillouin zone. Conversely, the wavevectors resulting from quartic scattering display a markedly heightened level of complexity. This complexity highlights the intricate effects engendered by higher-order anharmonic scattering.

Figure 6B delineates the DOS of phonons involved in cubic anharmonic scattering corresponding to select Raman peaks. These depictions can indicate the relative probability of Raman phonons scattering into or from specific phonon wavenumber. It is imperative to note that the numerical magnitude of the DOS should not be misconceived as indicative of the actual strength of anharmonic scattering. It is observable that within the domain of lower wavenumber Raman peaks, the phonon Merging process is heightened and aligns with a low possibility of scattering into high wavenumber phonons, among which the highest phonon is at ∼400 cm⁻¹ in P4. Manifestly, the phonon Splitting process predominates within the ambit of high wavenumber Raman peaks. Notably in P25 and P26, phonons close to 600 cm⁻¹ are distinctly implicated in anharmonic scattering. This outcome echoes the fitting results of the asymmetric scattering model presented in Figure 5. Intriguingly, in the higher wavenumber peaks, such as P23–P26, the phonon DOS at 200–300cm⁻¹ progressively diminishes and approaches zero. This trend intimates the low possibility for high wavenumber phonons to scatter into these specific wavenumbers. Moreover, the Umklapp process constitutes a substantial fraction of phonon Merging and Splitting process. In the higher wavenumber Raman phonons, there is a marked predilection for scattering into particular wavenumbers, engendering notably discrete high peaks in DOS, as opposed to the relatively continuous DOS discerned in low wavenumber peaks.

Owing to more phonons involved, quartic anharmonic scattering engenders increased complexity within GaPS₄, as evidenced in Figure 6C. It is discernible that phonon Merging is the predominant mechanism, whereas phonon Splitting only becomes notably significant within the higher wavenumber Raman peaks, specifically P19–P26, and predominantly scatters into lower wavenumber phonons. This observation is in alignment with the inferences drawn from quartic scattering depicted in Figure 5. Furthermore, in contrast to cubic scattering, the phonon DOS associated with quartic scattering intimates a heightened participation of phonons in the Umklapp process. This suggests a propensity for the Umklapp process to transpire with greater facility in quartic scattering, necessitating more additional wavevectors to return the scattered phonon wavevector back to the first Brillouin zone.

The aforementioned results delineate the anharmonic scattering processes of different Raman peaks from the perspective of DOS of the phonons involved in anharmonic scattering, which show similar tendency as the results from fitting results of Raman spectrum. Assuming equiprobability across all feasible scattering channels, the contributions of diverse channels to the anharmonic phonon scattering in GaPS₄ have been quantitatively depicted in Figure S4. The analysis reveals that more than half of the cubic and quartic scattering events could potentially constitute the Umklapp process. Considering the pronounced non-linear enhancement of the quartic scattering, it is reasonable to conclude that with the increase in temperature, this Umklapp process in quartic scattering will progressively govern the thermal transport mechanisms and cause higher thermal resistance within GaPS₄. This mechanism suggests the potential low thermal conductivity of GaPS₄, which has implications for its thermal management properties.

Anharmonic phonon properties from AIMD

The aforementioned research provides a comprehensive quantification and elucidation of the anharmonic scattering of Raman phonons at the Brillouin zone center in GaPS₄. However, the investigation of anharmonic scattering of phonons away from the Brillouin zone center poses a more complex situation. The introduction of quartic and higher-order anharmonic scattering necessitates the consideration of more intricate many-body problems. To address this, the atomic trajectories of GaPS₄ are simulated at various temperatures using AIMD. Following this, a Fourier transformation allows for the extraction of the wavenumbers and broadenings of all phonons across the whole Brillouin zone under anharmonic scattering. Given that the thermal expansion of GaPS₄ has been previously shown to contribute minimally to the redshift, the results of the QHA have not been incorporated in this analysis. The examination of atomic trajectories and velocities, predicated on the Boltzmann distribution, is presented in Figure S5, thereby attesting to the reliability of the AIMD calculations conducted in this study.

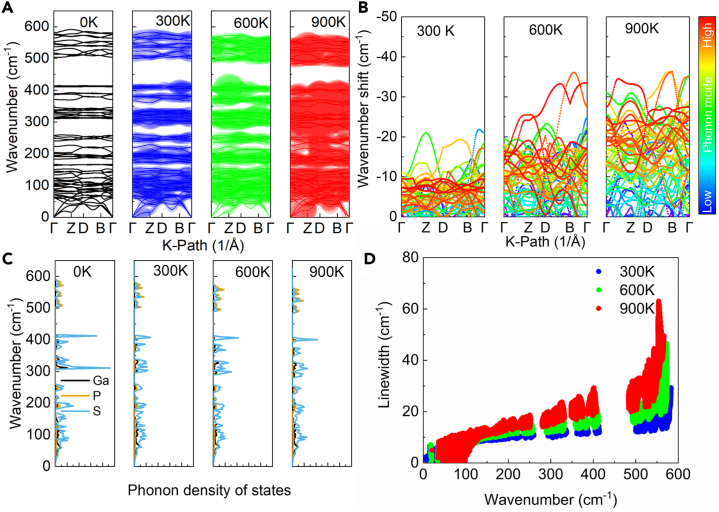
Figure 7A presents the phonon dispersion curves at different temperatures, where the linewidths denote the phonon broadening. For comparison, the dispersion curves without broadening are also depicted in Figure S6. The anharmonic phonon dispersion shows no imaginary wavenumber at the Γ point, with a negligible presence along the Brillouin zone path. This implies that GaPS₄ is poised to retain its structural integrity at 900 K. A discernible trend emerges as temperatures escalate that the phonon broadening intensifies markedly, echoing the phenomenon observed in Raman spectrum. From the harmonic phonon at 0 K, as the temperature elevates to 900 K, there is a progressive infilling of the erstwhile phonon band gaps due to the phonon broadening, especially within the wavenumber range at 166–183 cm⁻¹, 257–311 cm⁻¹, and 413–504 cm⁻¹. By 900 K, the only remaining prominent phonon band gap is between 400 and 483 cm⁻¹. Previous reports confirm that the robust phonon band gap could be an incentive for strong quartic phonon scattering of phonons nearby, which is consistent with the aforementioned fitting results.³⁶ Additionally, the phonon wavenumber redshifts also warrant attention. It is evident that, throughout the Brillouin zone, phonons situated at the higher wavenumber echelons, ranging from 300 to 600 cm⁻¹, manifest a pronounced redshift, whereas the redshift magnitude for phonons at the lower wavenumber is comparatively subdued, as observed in Raman spectrum. To further elucidate the redshift phenomenon of phonons quantitatively across varying temperatures within the Brillouin zone path, the wave number shifts of anharmonic phonons relative to 0 K were calculated, as delineated in Figure 7B. The analysis reveals that pronounced redshifts are predominantly from phonons at the higher wavenumber. The redshifts of low wavenumber phonons remain inconspicuous even until 600 K. Furthermore, a general trend is that the redshifts of the majority of phonons escalate continuously as temperature rises.

Figure 7.

Anharmonic phonon properties

(A)Anharmonic phonon dispersion relations, (B) wavenumber shift, (C) density of states, and (D) linewidth in GaPS₄ at 300, 600, and 900 K.

The anharmonic phonon DOS also manifests an impressive variation as temperatures ascend, as delineated in Figure 7C. Beyond the aforementioned redshift, anharmonic phonon mode frequencies tend to be more diffuse than concentrated. This can be typically observed in the pronounced peaks proximal to 400 cm⁻¹ and 300 cm⁻¹ at 0 K, where the peaks values decrease and become less obviously as temperature increases. The overall broadening of phonons throughout the Brillouin zone can be observed in the relationship between linewidth and wavenumber as depicted in Figure 7D. Similar to Figure 7A, it is evident that phonon broadening escalates substantially with temperature. And the broadening phenomenon is also markedly accentuated for phonons at higher wavenumbers, signifying strong anharmonic phonon scattering, corroborating with the conclusion from Raman spectrum fitting. Moreover, it is noteworthy that at 900 K, the broadening of high wavenumber phonons soars to 20–40 cm⁻¹, surpassing the corresponding broadening of phonons at Brillouin zone center of 12.3 cm⁻¹ (Ag17) and 10.3 cm⁻¹ (Bg17), with Raman spectral fitting results yielding 12.4 cm⁻¹ (P26) and 13.0 cm⁻¹ (P27). Besides, the most pronounced scattering is exhibited by Bu16, where the broadening potentially exceeds 60 cm⁻¹.

Aforementioned findings offer a thorough quantified elucidation of the phonon anharmonic scattering phenomena throughout the Brillouin zone of GaPS₄ and exhibit a preferable consistency to experimental conclusion. It is evident that higher temperatures engender a pervasive broadening and redshift across the phonon spectrum, with phonons at higher wavenumbers experiencing a pronounced alteration. Notably, anharmonic phonon scattering precipitates a greater discrepancy of phonon mode wavenumber relative to harmonic phonons. Furthermore, the phonon broadening expands the energy range, which phonons may transport, and fills in the phonon band gap. This broader energy distribution results in more phonon states and facilitates energy and momentum conservation, rendering various related particle/quasiparticle scattering processes more probable. This could profoundly influence the electron-phonon and photon-phonon interactions within GaPS₄, potentially modifying its electronic transport properties, optical absorption characteristics, and excitonic behaviors. Moreover, phonons situated away from the Brillouin zone center may encounter intensified anharmonic scattering, being characterized by stronger broadening, significantly surpassing the results of Raman spectrum fitting.

Conclusion

In summary, this research presents an exhaustive analysis of anharmonic phonon scattering in GaPS₄ utilizing temperature-dependent Raman spectroscopy and first-principles calculations. The investigation corroborates the occurrence of peak position redshift and linewidth broadening within Raman peaks, signaling significant anharmonic phonon scattering processes in GaPS₄. The thermal expansion coefficient and mode Grüneisen parameters for GaPS₄ are also reported. Quantitative analyses ascertain that thermal expansion marginally influences the redshift, whereas both cubic and quartic phonon scatterings are found to significantly influence redshift and linewidth broadening at lower and higher temperature, respectively. It is observed that the scattering strength for both cubic and quartic interactions at high wavenumber peaks surpasses that of low wavenumber peaks, with pronounced nonlinear broadening attributed to the remarkable quartic scattering. Besides, the DOS of phonons engaged in anharmonic scattering for each peak suggests a significant presence of phonons with momentum beyond the first Brillouin zone, particularly in quartic scattering. Furthermore, AIMD confirms the pervasive phonon redshift and broadening across the entire Brillouin zone and presence of stronger scattering than the Brillouin zone center. This study offers a comprehensive understanding of anharmonic phonon scattering in GaPS₄, enriches the discussion on quasiparticle interactions that limit thermal conductivity, and provides a theoretical foundation for optimizing the thermal properties of GaPS₄-based devices.

Limitations of the study

In this study, the anharmonic phonon scattering properties of bulk GaPS₄ were primarily investigated. However, due to experimental limitations, it was not feasible to conduct more detailed Raman spectroscopy studies at temperatures below that of liquid nitrogen. This restriction prevents a comprehensive quantification of the anharmonic scattering. Additionally, as a typical vdW material, GaPS₄ presents significant challenges in obtaining few-layer samples via mechanical exfoliation, which impedes further investigation into the role of vdW forces in anharmonic scattering. Although these limitations do not undermine the conclusions of this study, they highlight potential avenues for future research and underscore significant unresolved scientific challenges.

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Zeng Liu (zengliu@imu.edu.cn).

Materials availability

This study did not generate new unique material.

Data and code availability

Data: The Raman spectra and first principles data of GaPS₄ have been provided in the paper.

Code: The Python code used for post analysis in this article can be provided upon reasonable request.

All other requests: Any additional information required to reanalyze the data reported will be shared by the lead contact upon request.

Acknowledgments

This work was funded by the National Key Research and Development Program of China (Grant No. 2022YFB3605404), the Young Scientists Fund of the National Natural Science Foundation of China (Grant Nos. 62204125 and 62305171), the Joint Fund of the National Natural Science Foundation of China (Grant No. U23A20349), the Natural Science Foundation of Jiangsu Province (Grant No. BK20230361), the Natural Science Foundation of Jiangsu Higher Education Institutions (Grant No. 23KJB510017), the Natural Science Research Start up Foundation of Recruiting Talents of NJUPT (Grant Nos. XK1180922062 and XK1060921002), the Jiangsu Provincial Team of Innovation and Entrepreneurship (Grant No. JSSCTD202351), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province(Grant No. KYCX24_1235 and SJCX23_0300). In addition, the authors gratefully acknowledge HZWTECH for providing computation facilities and thanks Xiaowen Shi (from HZWTECH) for help and discussions regarding this study.

Author contributions

S.Y. conceived the concept and produced pictures. S.L., Z.L., and W.T. supervised the project. S.Y. and J.Z. contributed to data analysis. S.Y., S.Z., and M.J. prepared the manuscript. S.Y., S.W., C.-K.T., and S.L. performed the first-principles calculation. S.Y. and J.Z. contributed to the temperature-dependent Raman spectrum measurement.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Gallium thiophosphate (GaPS4)	Sixcarbon technology	http://www.2dmaterialshop.com/pr.jsp?keyword=GaPS4&_pp=0_324
Deposited data
GaPS4 structure file	Materials project	https://next-gen.materialsproject.org/materials/mp-30979
Software and algorithms
VASP	Uiversitat wien	https://www.vasp.at/
phonopy	Togo et al.33	https://phonopy.github.io/phonopy/
vaspkit	Wang et al.37	https://github.com/vaspkit/vaspkit.github.io
Dynaphopy	Carreras et al.38	https://github.com/abelcarreras/DynaPhoPy
Python program	Yan et al.	https://github.com/ElvenFireworks/3_4_phonon
Other
Renishaw inVia confocal Raman microscope	Renishaw	https://www.renishaw.com/en/products--32083

Method details

Crystal synthesizing

The GaPS₄ crystal used in this study was synthesized using Chemical Vapor Transport. Specifically, gallium, phosphorus, sulfur, and iodine were encapsulated in a 15mm diameter quartz tube under high vacuum at a molar ratio of 1:1:4:0.05. Then the heating is carried out under dual temperature zone, and the reaction occurs at 750°C in the high temperature zone. Iodine drives other element to deposit crystals at 650°C in the low temperature zone. The reaction lasts for 150 hours before being cooled to room temperature.

Raman spectra

The temperature-dependent Raman spectra were acquired using a Renishaw inVia confocal Raman microscope, operating at laser power of 10 mW to prevent sample damage, excitation wavelength is set as 532 nm, and temperature range is from 80 K to 700 K.

First-principles calculation

The first-principles calculation software package Vienna Ab initio Simulation Package (VASP) was harnessed to obtain the phonon dispersion curves, density of states, and thermal expansion coefficient. Projector Augmented Wave (PAW) method and Perdew-Burke-Ernzerhof (PBE) pseudopotential, with energy and force tolerance of 1×10^-8 eV and 1×10^-2 eV/Å, K-points of 8×8×4, energy cutoff of 600 eV were applied to acquire high precision lattice structure and reaching electronic ground state. AIMD were conducted using a 2×2×2 supercell, totaling 192 atoms, with the NVT ensemble. The simulations were run for 5000 steps with a time step of 0.01 ps. Phonon-related properties were computed via finite displacement, employing 2×2×2 supercell and 3×3×2 K-points. The software package Phonopy and Dynaphopy was employed for phonon and AIMD post-processing with q-points of 30×30×30.^33,38

Quantification and statistical analysis

The fitting of anharmonic scattering was performed using Origin software, with an error standard of R² reaching 95%. This study did not involve testing with a large number of samples, therefore statistical testing, measurement of dispersion and accuracy were not considered.

Published: September 27, 2024