A Deep Learning‐Based Approach to Characterize Skull Physical Properties: A Phantom Study

ABSTRACT

Transcranial ultrasound imaging is a popular method to study cerebral functionality and diagnose brain injuries. However, the detected ultrasound signal is greatly distorted due to the aberration caused by the skull bone. The aberration mechanism mainly depends on thickness and porosity, two important skull physical characteristics. Although skull bone thickness and porosity can be estimated from CT or MRI scans, there is significant value in developing methods for obtaining thickness and porosity information from ultrasound itself. Here, we extracted various features from ultrasound signals using physical skull‐mimicking phantoms of a range of thicknesses with embedded porosity‐mimicking acoustic mismatches and analyzed them using machine learning (ML) and deep learning (DL) models. The performance evaluation demonstrated that both ML‐ and DL‐trained models could predict the physical characteristics of a variety of skull phantoms with reasonable accuracy. The proposed approach could be expanded upon and utilized for the development of effective skull aberration correction methods.

We extracted various features from ultrasound signals using skull‐mimicking phantoms (including variation in thicknesses and porosity) and analyzed them using machine learning and deep learning models. The evaluation demonstrated that ML‐ and DL‐trained models could predict the physical characteristics of skull phantoms with reasonable accuracy for developing skull aberration correction methods.

1. Introduction

Transcranial ultrasound imaging is a potentially valuable noninvasive method to assess cerebral functionality and diagnose possible brain injuries [1]. However, a major limitation in transcranial imaging is the presence of skull bone, which acts as a dispersive barrier and causes distortion to the amplitude and phase of the received acoustic waves [2, 3, 4]. This distortion is evident in terms of acoustic attenuation, dispersion, signal broadening, and temporal shift [5, 6]. The degree of distortion caused by these phenomena depends primarily on the acoustic properties of the cranium (i.e., speed of sound, density, absorption, scattering, and acoustic impedance) [7, 8]. However, these acoustic properties can be determined from the mechanical characteristics of the skull bone (i.e., bone type, density, porosity, and thickness). Among these parameters, thickness and porosity, which vary depending on location, age, and gender, have one of the most significant impacts [5, 9, 10, 11, 12, 13, 14]. Since thicker skull bones force the acoustic pressure wave to propagate longer distances with a high absorption rate, the amplitude is greatly impacted in terms of attenuation. Simultaneously, higher porosity increases the frequency of propagating media interfaces (bone‐fluid), introduces scattering phenomena [9], and affects the phase information in terms of dispersion [8], broadening (widening of the pulse) [15], and temporal shift [8, 15, 16, 17, 18, 19, 20]. Therefore, the estimation of the thickness and porosity of the skull bone is of great interest. Methods to noninvasively estimate these parameters would help recover the original signal and would be a major advancement in brain imaging.

While computed tomography (CT) and magnetic resonance imaging (MRI) using methods such as ultrashort time echo (UTE) and zero time echo (ZTE) imaging can predict skull thickness and porosity [21], they are not widely available and require relatively long scan times [21, 22]. Ultrasound is widely available, and innovative technologies could be harnessed to determine thickness and porosity, but few analytical‐based approaches have been tested to make such predictions [23, 24]. Some that have been tried include porosity prediction from ultrasound backscatter using multivariate analysis [20]; use of axial transmission velocities [12]; and thickness prediction using Sono Pointer [25]. However, these methods predict either porosity or thickness, require user inputs, and demonstrate results that vary significantly between studies. With the ability to train models from image sets, machine learning (ML) and deep learning (DL) techniques have the potential for better interpretation of imaging data across diverse applications [26, 27, 28, 29, 30, 31], offering a solution to challenges that traditional methods encounter [32].

If appropriate features can be extracted from the data, ML models can be trained using a relatively small dataset. Conversely, if no relevant features are known, DL models can explore existing data to identify the most relevant features. Over the years, DL models have shown prominent results in the field of phase recovery and scattering imaging for different modalities including ultrasound imaging [33, 34]. To our knowledge, while there are studies using DL models for extracting skull characteristics from other imaging technologies such as MRI and CT [35], there are few using ultrasound data [36, 37, 38, 39]. In [36], the authors estimated the micro‐architectural parameters of cortical bone such as pore diameter, pore density, and porosity using an artificial neural network. However, the research was limited by only using simulation data for training and testing. Also, the results were limited to predicting the porosity of cortical layers, where the size of the pores is in the micron range. Porosity in this range does not affect the acoustic wavelengths typically used in transcranial imaging.

According to [5], the diploë layer of skull bone consists of a more complex formation of porous and bone structures that dominates the acoustic scattering, and hence distortion of the ultrasound pressure wave. In addition to the variability of porosity, the thickness of the diploë layer varies with age [11]. Therefore, a good model must predict both porosity and thickness of diploë type skull bone in order to compensate for aberrated acoustic signal [17].

In this paper, our objective was to achieve high accuracy for determining skull bone thickness and porosity in order to improve our understanding of the influence of diploë layer characteristics. Such an objective could enable the development of effective skull aberration correction methods. We have utilized both ML and DL approaches to test their capability to determine the “thickness” and “porosity” of solid skull phantoms, where we varied phantom thickness to mimic changes in skull thickness and mixed varying concentrations of poppy seeds into resin to mimic porosity [40, 41] (200 phantoms with varied thickness and porosity were made). After we explain the method of preparing the skull phantoms, we describe the selected ML and DL approaches. The results for determining thickness and porosity are reported separately.

2. Materials And Methods

2.1. Sample Preparation and Experimental Setup

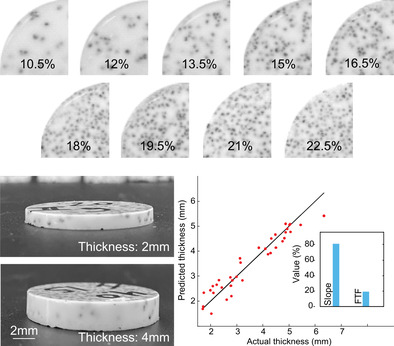
The diploë type skull bone phantom was prepared from a mixture of titanium dioxide (Loudwolf, USA), (1% w/w) and different concentrations of poppy seeds in an epoxy resin solution (Clearcast 7050, The Epoxy Resin Store) (2:1 hardener: epoxy). First, the titanium dioxide is homogenized with the resin hardener with the help of a vortex mixer and a sonicator bath. Then, the resin was added, and the mixture was vortexed and sonicated again before being poured into a Petri dish and placed inside a vacuum chamber for 30 min to eliminate any air bubbles before solidification. A predefined number of poppy seeds are added to the solution inside the Petri dish before placing it in the vacuum chamber. A further detailed explanation of the skull bone phantom preparation method can be found in [42]; top and side views of phantoms showing a range of poppy seed concentrations and thicknesses can be seen in Figure 1a (top view) and Figure 1b (side view).

FIGURE 1.

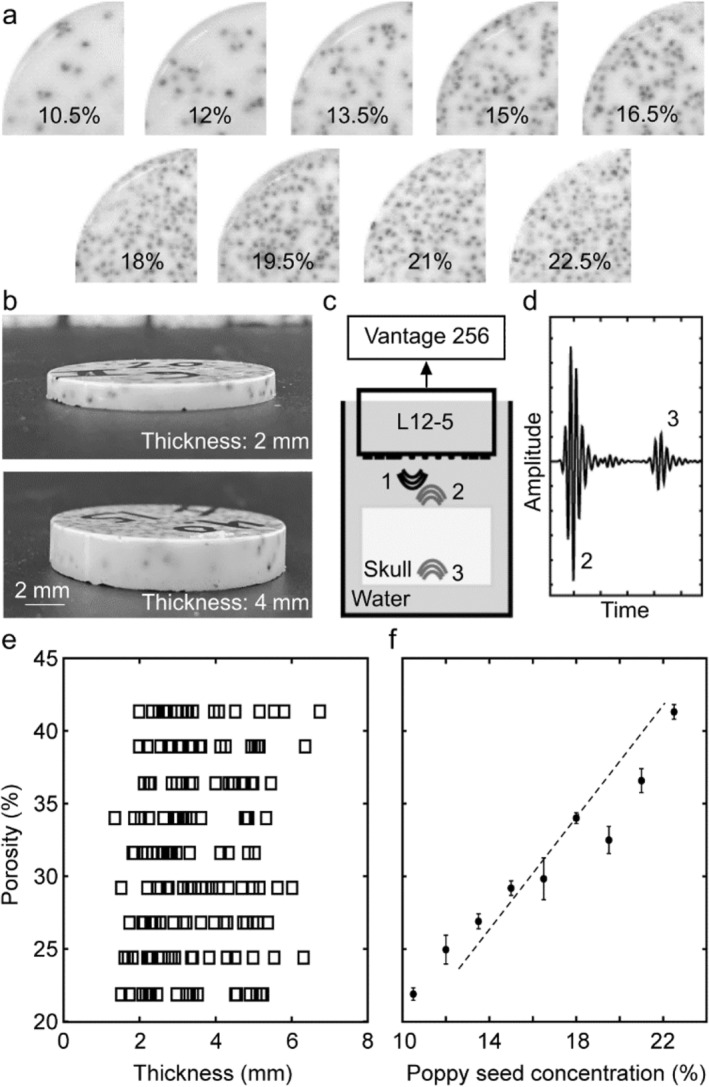
Skull phantoms and signal acquisition from same. (a) Top view of samples with different concentrations of poppy seeds (10%–22.5%). (b) Side view of samples showing samples of different thicknesses. (c) Schematic of the experimental setup used to obtain the signals. (d) An example of the acoustic signal obtained from the samples. (e) Thickness and calculated porosity of 180 phantoms. (f) Relationship between poppy seed concentration and sample porosity as empirically measured.

A total of 180 samples (diameter: 30 mm) were created with different thicknesses ranging between 1 and 7 mm and different concentrations of poppy seeds (range from 10.5% to 22.5% w/w). Addition of poppy seeds (diameter: ~1 mm) was used to represent fluid‐filled pockets within the diploë layer of the skull bone [42]. This range of poppy seed concentrations was selected to mimic a range in porosity of 21%–42% (Figure 1f). We calculate porosity by image segmentation of each sample's cross‐section, using the ratio between the detected seeds in the image and the total surface. The presence of the seed inside the sample generates similar acoustic behavior as is produced in the real skull porous region due to the impedance mismatch (high changes in density and speed of sound between two environments at their interface), creating phenomena such as reflection, mode conversion, refraction, and signal distortion [43]. For each seed mass concentration, 20 samples were made with variable thickness (ranging from 1 to 7 mm).

Skull phantoms were suspended in a water‐filled (coupling medium) bucket that was normal to the ultrasound sensor surface. To detect ultrasound pressure waves generated from acoustic reflection at the phantom‐water interface, we used a linear array transducer (L12‐5, ATL‐Philips, USA). The acquired signals were sampled at 62.5MS/s using a Vantage 256 system (Vera Sonics Inc., USA). We acquired 50 signals from each element of a linear array probe, averaging them to suppress background noise and address the random distribution of seeds in the sample. The width of the probe, with elements spaced 0.2 mm apart and positioned parallel to the sample's center, means each element experiences a slightly different acoustic path through the sample. These signals were averaged to represent the characteristics of the sample (Figure 1c). Each averaged signal was decomposed into two parts: the first echo (#2 in Figure 1d) represents the reflection at the top interface between the water and the sample and the second echo (#3 in Figure 1d) represents the reflection at the bottom interface between the sample and the water. To isolate each echo during the signal processing, the envelope of the entire signal was obtained, locating the maximum of each signal and their starting/ending points.

2.2. Dataset

We utilized the averaged signals from our 180 phantoms of varying thickness and porosity, shown in Figure 1e, to train the system. For the thickness predictions, 144 samples were used for training, which, for DL models, includes 129 samples for training and 15 for validation, and then 36 samples were used for testing. For the porosity predictions, we have the same 180 samples representing 9 different porosity values. Among the 180 samples, 171 were used for training, which, for DL models, includes 153 for training and 18 for validation, and 9 (one from each porosity) were used as a test dataset. The rationale for selecting the size of training/testing/validation datasets can be found in [44].

2.3. Dataset Preprocessing and Feature Extraction

As a first data preprocessing step, we used min–max normalization to the signals to maintain data consistency [45]. This ensures that all signals are scaled to the same range, which is essential for effective model training. Next, we extracted features from the normalized signals. In our previous work [42], we extracted many features from ultrasound signals of skull phantoms and analyzed whether they varied with changes in phantom width and porosity. There, we identified nine features that were the most significant. These features are shown in Table 1. Detailed descriptions of these features can be found in our prior publication [42]. To ensure that features with larger numerical values do not disproportionately influence the results, we normalized them using standard scaling before applying ML and DL techniques.

TABLE 1.

Feature table with corresponding descriptions.

Feature name	Feature description
Delay	Delay between the first and second peak (TD)
Slope	Slope between the first and second peak (TD)
SA‐Total‐T	Surface area of complete signal (TD)
Phase‐Shift‐T	Phase shift of complete signal (TD)
FWHM‐SP‐T	FWHM of second peak (TD)
SA‐Total‐F	Surface area of complete signal (FD)
SA‐SP‐F	Surface area of second peak (FD)
FWHM‐Total‐F	FWHM of complete signal (FD)
FWHM‐SP‐F	FWHM of second peak (FD)

Abbreviations: FD, frequency domain; FWHM, full width half maximum; SA, surface area; SP, second peak; TD, time domain.

For our DL experiments, we used either the same nine features or the envelope of the signal.

2.4. Implementation of Three ML Regression Models

We employed ML techniques, where we used the nine features identified above as inputs. ML regression models use combinations of independent variables (in our case signal features) to map input features to an output value (thickness or porosity). Three algorithms of increasing complexity were tested. The first method is multiple linear regression (MLR), which explores linear relationships between the nine features and the target variables [46]. This method allowed us to quantify the influence of each feature on the target by estimating the regression coefficients. The general form of the MLR equation is

$$Y={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_i{X}_i$$ (1)

where ${\beta }_0$ represents intercept, ${\beta }_i$ represents the learned coefficient of $X_i$, $X_i$ represents the ith feature value, and $Y$ represents the target value. Ridge linear regression (RLR) is an extension of MLR that includes a regularization term to prevent overfitting and enhance model generalization. By adding a penalty proportional to the squared magnitude of the coefficients [47], RLR reduces the impact of less important features, thereby providing more stable and reliable coefficient estimates. While the equation for RLR is the same as for MLR, RLR utilizes a loss function with an additional penalty component, λ, which demonstrates a regularization parameter (controls the amount of shrinkage applied to coefficients).

Loss Function:

$$\underset{\beta }{\min }\left(\sum _{i=1}^n\left(Y_i-{\beta }_0-\sum _{j=1}^i{\beta }_j{X}_j^2\right)\right)+\lambda \sum _{j=1}^i{\beta }_j^2$$ (2)

Polynomial Regression (PNR) is another extension of MLR used to identify nonlinear relationships between the nine features and the dependent variables [48]. The model is defined as

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_2{X}^2\dots +{\beta }_i{X}^i$$ (3)

where $Y$ is the dependent variable, $X$ is one of the features, ${\beta }_0$, ${\beta }_1$, ${\beta }_2$… ${\beta }_i$ are the coefficients, and i is the degree of the polynomial. For this study, we used a polynomial degree of 2, which incorporates all squared features and all pairwise interaction terms. This degree was chosen because it allows for simpler interpretation by limiting the model to linear and quadratic interactions, while also minimizing the risk of overfitting. For our system with nine original features, this translates to a total of 54 features (9 original features, 9 squared features, and 36 paired interactions).

2.5. Implementation of Two DL Models

Additionally, we explored two DL techniques with two different input datasets: One using the same nine features as inputs (see Table 1) and another using the envelope as input. Use of the envelope allows the models to autonomously learn the most relevant features. This approach minimizes the risk of overlooking potentially important features that might be missed with manual feature selection. By using the entire signal, the model is able to learn intricate patterns and complexities within the data, thereby identifying the most significant features without relying on prior assumptions.

To reduce model complexity while still capturing intricate features that might have been overlooked during manual selection, we designed two DL models, the first of which is a feed‐forward neural network (FFN) consisting of an initial dense layer with 8 units, followed by a dense layer with 4 units, and finally, an output layer for prediction (Figure 2a). We modify the FFN by introducing a convolution layer to build our second DL model, a convolution neural network (CNN) [49, 50] to add complexity, as it allows hierarchical decomposition of input, and can extract high‐level features from the input. The CNN design is shown in Figure 2b. The architecture consists of one convolutional hidden layer with a set of filters whose parameters were learned throughout the training process and a feed‐forward network. These parameters are utilized to obtain the unique and hidden learning features which are essential for mapping.

FIGURE 2.

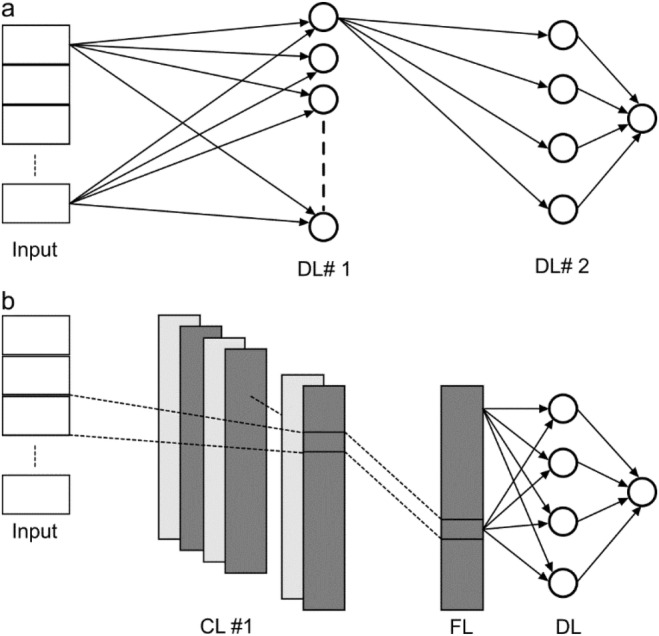
A schematic overview of the FFN and CNN architectures used in this study. (a) FFN architecture; DL#1 (8 units) and DL#2 (4 units) are both dense layers. (b) CNN architecture; CL #1 represents a convolutional layer (8 filters), FL represents a Flatten layer, and DL represents a dense layer (4 units). In (b), the dotted lines illustrate how each part of the input is processed by different filters in the convolutional layers, visually representing the learning process and the interaction of various filters with different regions of the input data.

Given different ultrasound signals acquired from skull phantoms with varied thickness and porosity values, our neural networks learn the distinctive features from the signal and map them to the actual thickness or porosity value. Over the years, FFN and CNN and their variations have been used in biomedical imaging to solve problems such as seizure prediction [31, 51] and EEG data classification [52]. More complex DL architectures such as long short‐term memory (LSTM) and generative adversarial networks (GANs) require large amounts of training datasets, whereas simple neural networks (few layers) have performed well on small datasets [53]. Another reason for selecting simple neural networks is the relatively small size of the inputs: in one set of experiments, we use only nine features, and in another, we employ an envelope of length 200 which is straightforward, lacking complexities such as dips or noise. We aimed to predict continuous values—thickness and porosity—by optimizing filter parameters through the minimization of a loss function using as input either the extracted features (CNN‐F or FFN‐F) or the extracted envelope (CNN‐E or FFN‐E). Hyperparameter tuning led us to utilize the Adam optimizer with 2500 epochs and employ the mean absolute error (MAE) as the loss function for porosity and mean squared error (MSE) as the loss function for thickness.

3. Results And Discussion

3.1. Thickness

Table 2 reports the combined results for all methodologies (ML and DL) predicting thickness. The results of the models are summarized as follows: The MLR model achieved the best performance of all the models, but all the ML models were very similar (and good, average R ² = 0.907 ± 0.004). MLR showed an MAE of 0.29, MSE of 0.13, and RMSE of 0.36. The PNR model yielded an MAE of 0.30, MSE of 0.14, and RMSE of 0.38, while RLR showed an MAE of 0.32, MSE of 0.15, and RMSE of 0.39. Among the DL models, FFN‐F had the best performance, with an MAE of 0.31, MSE of 0.24, RMSE of 0.49, and R ² = 0.85. The CNN‐F model had higher error metrics with an MAE of 0.71, MSE of 0.89, and RMSE of 0.94. When using the envelope as input, the FFN‐E model recorded an MAE of 0.65, MSE of 0.68, and RMSE of 0.82, whereas the CNN‐E model showed an MAE of 0.64, MSE of 0.66, and RMSE of 0.81. Overall, the ML models slightly outperformed the DL models for determining thickness. Among the DL models, those using features as inputs (FFN‐F and CNN‐F) performed better than those using envelopes (FFN‐E and CNN‐E). This suggests that envelope‐based inputs may not be as effective as features for predicting thickness.

TABLE 2.

Performance comparison of models for predicting thickness values (mm): MAE, MSE, and RMSE Metrics (models depicted in bold are graphed in Figure 3).

Model	MAE	MSE	RMSE
MLR	0.29	0.13	0.36
PNR	0.30	0.14	0.38
RLR	0.32	0.15	0.39
FFN‐F	0.31	0.24	0.49
CNN‐F	0.71	0.89	0.94
FFN‐E	0.65	0.68	0.82
CNN‐E	0.64	0.66	0.81

Figure 3 shows the best‐performing models from both ML and DL methodologies for predicting thickness: MLR for ML (Figure 3a) and FFN‐F for DL (Figure 3b). The figure highlights the accuracy of the predicted thickness values. Some outliers are observed: we anticipate that increasing the size of the training dataset would help reduce these discrepancies and improve the overall accuracy of the models.

FIGURE 3.

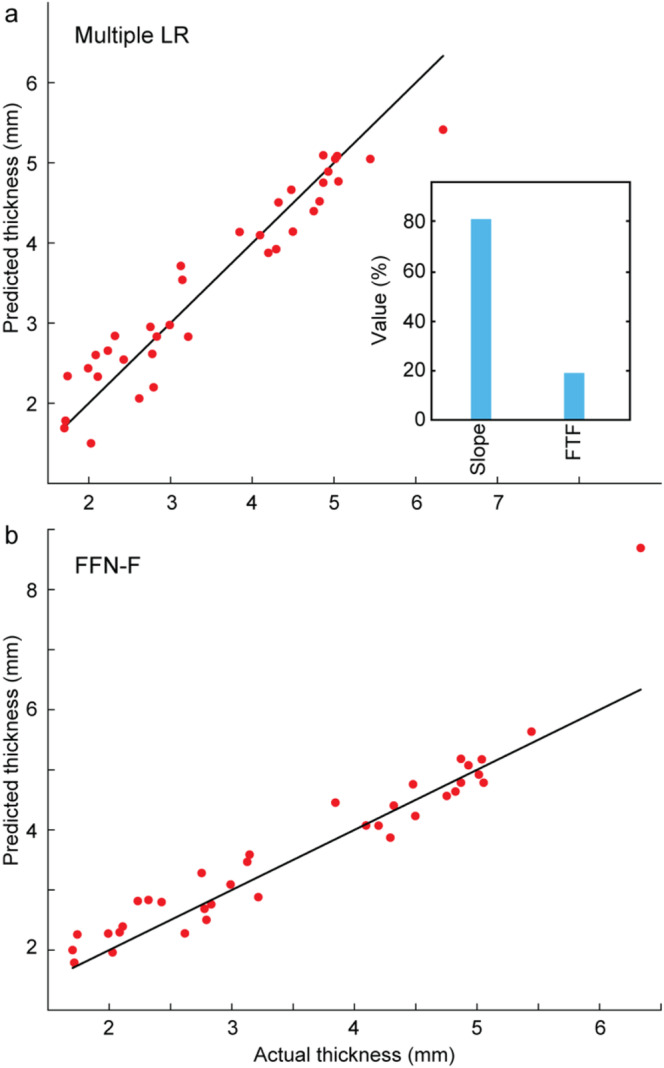
Evaluation of the performance of thickness prediction on the test data. (a) best ML architecture (MLR: multiple LR) and (b) best DL architecture (FFN‐F). Percent contributions of the most significant features are shown for the ML architecture. Multiple LR: multiple linear regression; FFN‐F: feed‐forward network (features as input).

3.2. Feature Contributions to ML Thickness Model

The relative contributions of the features for the MLR model are shown in Figure 3a. Slope contributes the most to the model, with a weight of 80.19%. The second most significant feature is FWHM‐Total‐F, contributing 19.21%. The results indicate that thickness can be reasonably well portrayed by linear combinations of the two identified features.

3.3. Porosity Results

Table 3 contains the combined results for all methodologies predicting porosity using the same performance metrics (MAE, MSE, and RMSE). Among the models, the CNN‐E, DL model achieved the best overall performance, with the lowest MAE of 2.98, MSE of 17.94, and RMSE of 4.23. The RLR model achieved the best performance from the ML category, exhibiting a competitive performance with an MAE of 3.42, MSE of 17.01, and RMSE of 4.13 (R ²  = 0.47). While FFN‐E also performed well, achieving an MAE of 3.21, MSE of 19.04, and RMSE of 4.36, the feature‐based DL models (FFN‐F and CNN‐F) had higher error metrics. FFN‐F recorded an MAE of 4.10, MSE of 23.82, and RMSE of 4.88, while CNN‐F had an MAE of 3.18, MSE of 23.79, and RMSE of 4.87. Among all other ML models, PNR showed relatively higher error rates with an MAE of 3.42, a surprising MSE of 94.54, RMSE of 9.72, and R ² of 0.10. MLR performed nearly as well as RLR, with an MAE of 3.42, MSE of 17.16, RMSE of 4.14 and R ² of 0.46. The superior performances of the FFN‐E and CNN‐E models highlight the advantage of using envelope data for improved porosity prediction accuracy despite potential relationships suggested between features and porosity in [42].

TABLE 3.

Performance comparison of models for predicting porosity values (%): MAE, MSE, and RMSE Metrics (models depicted in bold are graphed in Figure 4).

Model	MAE	MSE	RMSE
MLR	3.42	17.16	4.14
PNR	3.42	94.54	9.72
RLR	3.42	17.01	4.13
FFN‐F	4.10	23.82	4.88
CNN‐F	3.18	23.79	4.87
FFN‐E	3.21	19.04	4.36
CNN‐E	2.98	17.94	4.23

3.4. Feature Contributions to Porosity ML Models

The relative contributions of the RLR features are shown in Figure 4a: SA‐SP‐F contributes the most to the model, with a weight of 43.15%. The second most significant feature is SA‐Total‐F, contributing 23.74%, followed by FWHM‐SP‐T at 12.35%. The other features, FWHM‐SP‐F and SA‐Total‐T, contribute 10.25% and 7.57%, respectively. This distribution suggests that surface area (SA) and FWHM, both in the time and FD, are the most influential features in predicting porosity, with some contributions from other features as well.

FIGURE 4.

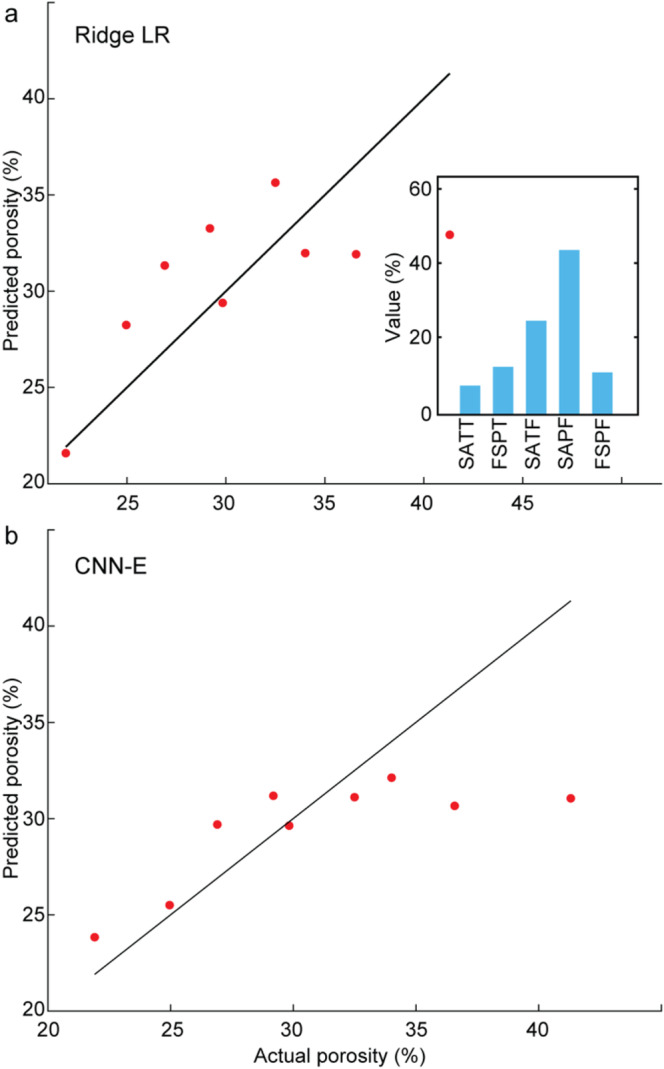
Evaluation of the performance of porosity prediction on the test data. (a) best ML architecture (RLR: Ridge LR), and (b) best DL architecture (CNN‐E). Percent contributions of the most significant features are shown for the ML architecture. Ridge LR: ridge linear regression. CNN‐E: convolutional neural network (envelope as input). SATT: SA‐Total‐T, FSPT: FWHM‐SP‐T, SATF: SA‐Total‐F, SAPF: SA‐SP‐F, FSPF: FWHM‐SP‐F.

Reviewing Figure 4, it is clear that while the general trend is captured, the performance at the extremes, particularly on higher values, suggests a need for improvement. This indicates that the models struggle to predict at the upper end of the range, possibly due to the limited data available for these higher values. Our use of poppy seeds simulated a porosity range of 21%–42%. For comparison, the porosity of the parietal bone varies, with the outer and inner tables typically having porosities between 10% and 30%, while the central diploe layer has a much higher porosity, ranging from 50% to 80% [10]. On average, the entire bone likely exhibits a porosity in the range of 20%–41%, which is consistent with the range simulated by our poppy seed concentrations. While our model successfully captures this average porosity, more complex phantoms with multiple layers exhibiting different porosity values would provide a more accurate representation of bone structure.

Up to this point, we have described our results for independent models generated to predict either thickness or porosity from our phantoms, where a range of models for each variable were trained and tested separately. We also designed a model to predict both thickness and porosity simultaneously. To enhance the simultaneous model's accuracy, we introduced additional complexities to capture more detailed lower‐level features. However, this approach resulted in a high MSE for both predictions (data not shown). We then sought to analyze the variables sequentially by first finding thickness, and then feeding thickness values into the porosity model. However, incorporating thickness values into the porosity model did not improve performance. To understand these results, we generated a correlation matrix encompassing the nine identified features as well as thickness and porosity. Analysis of the matrix indicated that thickness and porosity are driven by distinct signal features, with no significant correlation between them. Based on these findings, we decided to develop two separate models, one for each variable, to optimize accuracy for both thickness and porosity separately.

Analyzing the range of models tested for predicting thickness, it is evident that the ML models performed exceptionally well, demonstrating that they were able to effectively leverage the information contained in the features to extract thickness. This may be because the ML models worked with specific features that had previously been demonstrated to be highly correlated with thickness [42]. Two key features that significantly contributed to thickness prediction in ML models were Slope in the time domain and FWHM of the complete signal in the frequency domain (FWHM‐Total‐F). Slope combines delay and amplitude, which were previously shown to correlate with thickness prediction [42]. FWHM‐Total‐F is expected to be broadened by the length of time the signal takes to pass through the phantom, making it a reasonable key indicator for thickness. The DL models also showed promising results, if not quite as accurate as the ML models. The DL‐F models (CNN‐F and FFN‐F) had the same initial inputs as the ML models, and here, the unstructured learning of neural networks showed, principally, that the sample size was perhaps too small to achieve high accuracy. The DL‐E models (CNN‐E and CNN‐F) also performed reasonably well, likely because the envelope somewhat recapitulates aspects of the broadening extracted by the slope and FWHM‐Total‐F features.

For porosity predictions, the best results were observed using the RLR method in the ML models. We noticed that FWHM and SA features, both in the frequency (FD) and time (TD) domains, made significant contributions. In the FD, acoustic aberrations caused by porosity appear to introduce variations in the frequency components of the signal. Both FWHM and SA effectively capture these changes: FWHM reflects the broadening of the signal in the FD, while SA captures changes in the signal's area. Similarly, in TD, porosity‐induced echoes can lead to a reduction in signal peak amplitude. Both SA and FWHM in TD are sensitive to these changes, allowing them to capture the effects of porosity on the signal. The feature‐based DL and the ML models performed worse than the envelope models, demonstrating the extracted features dataset was insufficient to fully capture porosity values. The envelope‐based methods, particularly the CNN‐E model, were able to extract features that are relevant to porosity, though these features were not fully captured due to the limited sample size as demonstrated by the modest R ² value (0.46).

This limitation suggests that future work in this area, with a larger dataset, could further improve the accuracy of porosity prediction using DL methods. The envelope worked better for porosity prediction because it captures much of the critical information from the ultrasound signal, such as peak position, amplitude, and FWHM. The waveform also simplifies the signal, reducing the complexity compared to the full signal, which contains multiple peaks with amplitude variations. Such variations are often influenced by hardware, making DL applications using full signals as input more challenging than applications using the envelope as input.

Given a larger dataset (>> 180 samples), the DL models might have been able to capture these relationships more effectively. Our sample size was limited by the requirement to fabricate and test each sample manually. Multiple simulation studies have been reported such as [25], but we were dissatisfied with the capability of that or other studies to capture the complex effect of the acoustic mismatch presented by the presence of diploë in skull. Here, we developed physical phantoms that capture this mismatch to some extent (although not perfectly, as they are of approximately uniform porosity throughout). A limitation of our physical phantoms is that there is some estimation required for characterizing porosity (see, e.g., Figure 1f) due to local/internal variations in poppy seed concentrations, which could affect the accuracy of the training and testing data sets.

4. Conclusion

The cranial bone poses a significant barrier to sound waves in ultrasound‐based transcranial imaging techniques, such as focused ultrasound, photoacoustic, thermoacoustic, and x‐ray acustic imaging [3, 4, 34, 54, 55, 56, 57, 58, 59]. Standard reconstruction algorithms used in these procedures typically assume that ultrasound waves travel through a homogenous medium [60]. The assumption often leads to distorted images of the target area due to the heterogeneous nature of the cranial bone [60]. To produce more accurate images, it is crucial to incorporate the physical characteristics of the skull into the reconstruction algorithms. Transcranially acquired ultrasounds have aberrations due to the presence of skull bone largely due to variations in skull thickness and bone porosity. Therefore, it is essential to identify appropriate methods for determining these parameters to correct the aberrations. In this study, we evaluated the performance of seven different models—comprising three ML models and four DL models—for predicting thickness and porosity independently. None of the models used the full signal but instead were based on either the envelope of the signal or extracted features. This reduces the effect of extraneous input caused by system noise while still capturing critical information. Among these models, the MLR method, which is an ML approach, achieved the lowest MAE of 0.29 for thickness prediction. For porosity prediction, the CNN‐E, a DL technique, demonstrated the best performance with the lowest MAE of 2.98. For practical applications to a human adult cranium, a three‐layer model should be considered, including the inner and outer tables of the skull bone around the diploe. Part of our study could be applied to the inner and outer tables, where similar thickness variations occur but with lower porosity levels. Accurate thickness and porosity for each layer should be evaluated within the ranges reported in the literature to examine the impact of these physical characteristics on signal features. This work can help in understanding the influence of the diploe layer on the ultrasound signal and suggests a process for developing an effective skull aberration compensating method.

Conflicts of Interest

The authors declare no conflicts of interest.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.