Abstract
Spin and valley polarizations (Ps and PKK’) and tunneling magnetoresistance (TMR) are demonstrated in the ferromagnetic/barrier/normal/barrier/ferromagnetic WSe2 junction, with the gate voltage and off-resonant circularly polarized light (CPL) applied to the two barrier regions. The minimum incident energy of non-zero spin- and valley-resolved conductance has been derived, which is consistent with numerical calculations and depends on the electric potential U, CPL intensity ΔΩ, exchange field h, and magnetization configuration: parallel (P) or antiparallel (AP). For the P (AP) configuration, the energy region with PKK’ = -1 or Ps = 1 is wider (narrower) and increases with ΔΩ. As h increases, the Ps = 1 (PKK’ = -1 or Ps = 1) plateau becomes wider (narrower) for the P (AP) configuration. As U increases, the energy region with PKK’ = -1 increases first and then moves parallel to the EF-axis, and the energy region with Ps = 1 for the P configuration remains unchanged first and then decreases. The energy region for TMR = 1 increases rapidly with h, remains unchanged first and then decreases as U increases, and has little dependence on ΔΩ. When the helicity of the CPL reverses, the valley polarization will switch. This work sheds light on the design of spin-valley and TMR devices based on ferromagnetic WSe2 double-barrier junctions.
Keywords: Transfer matrix method, WSe2, Spin/valley polarization, Landauer-Büttiker formula, Circularly polarized light, TMR
Subject terms: Applied physics, Condensed-matter physics
Introduction
In recent years, monolayer transition-metal dichalcogenides (TMDCs) have attracted extensive attention for promising applications in future devices1–4. In TMDCs, according to the requirement of time-reversal symmetry6–9, the conduction and valence band extrema occur at the two degenerate valleys (K, K’) located at the corners of the hexagonal Brillouin zone9, which can be broken by the helicity of light10. In monolayer TMDCs, because of the broken inversion symmetry and the strong spin–orbit coupling (SOC)6, the spin and valley degrees of freedom are coupled (spin-valley locking), and the spin splitting of the valence band is opposite at the two valleys due to the time-reversal symmetry11. Therefore, in TMDCs, full spin and valley polarizations can be achieved, which is crucial for spintronics and valleytronics. Significantly, high-quality WSe2 with strong SOC exhibits novel behaviors that differ from other TMDCs and two-dimensional materials. Moreover, a monolayer WSe2 provides a suitable platform for developing novel spintronics and valleytronics devices, as it is a direct band-gap semiconductor (band gap Eg = 0.85 eV)12.
Several methods have been adopted to manipulate spin and valley degrees of freedom in TMDCs. First is the peculiar magnetic field13. The Zeeman effect induced by the magnetic field opens different spin-dependent band gaps at the K and K’ valleys, leading to spin- and valley-polarized transport in normal/ferromagnetic/normal (N/F/N) WSe2 junctions9. Second is the magnetic modulation induced through magnetic doping14 or proximity effect15–20. The magnetic proximity effect in WSe2/EuS can lead to a giant valley splitting in monolayer WSe221. Thirdly, utilizing the optical Stark effect, the pseudomagnetic field induced by the off-resonant CPL is used to select one of the two inequivalent valleys22–27. The influence of the off-resonant CPL on the valley polarization in monolayer TMDCs has attracted widespread attention recently5,12,23–25,28–30. For example, Hao et al. predicted the quantum spin and valley Hall effects in MoS2 irradiated with the off-resonant CPL12, and Qiu et al. demonstrated that the perfect spin and valley polarizations in WSe2 are caused by the off-resonant CPL and the massive SOC28.
Tunneling magnetoresistance (TMR) is another key topic in spintronics, which has been widely applied to storage and magnetic sensor technologies31, magnetic random access memory32, and hard disk drives33. So far, the spin- and valley-dependent transport and TMR have been investigated theoretically and experimentally in many ferromagnetic junctions based on graphene34,35, silicene16,17, and MoS218,19,36,37. Moreover, the spin-valley current in many ferromagnetic junctions based on silicene38, MoS237, and WSe24,39,40 can also be controlled by the off-resonant CPL. Liu et al. demonstrated that the normal/barrier/normal/barrier/normal (N/B/N/B/N) WSe2 junction modulated by the off-resonant CPL and gate voltage can function as a valley filter and valley valve device22. Hajati et al. found highly spin- and valley-polarized current and high TMR in the ferromagnetic/ferromagnetic/normal (F/F/N) WSe2 junction in the presence of gate voltage and off-resonance CPL in the middle ferromagnetic region40. However, by designing appropriate geometric structures, it is possible to further improve or modulate the energy region of full spin and valley polarizations as well as large TMR in WSe2 junctions. As an extension of the system and model studied in Ref.22, here we consider the ferromagnetic/barrier/normal/barrier/ferromagnetic (F/B/N/B/F) WSe2 junction, where the same gate voltage and off-resonance CPL are applied in the two barrier regions. The spin- and valley-resolved effective potential for electrons in each region of the F/B/N/B/F WSe2 junction will depend on the spin and valley degrees of freedom, the helicity of the off-resonance light, and magnetization configuration. This will certainly affect the spin- and valley-resolved conductance, spin and valley polarizations, and TMR in this junction. Furthermore, to my knowledge, existing literature has not considered the tunneling properties of the F/B/N/B/F WSe2 junction, as well as how the spin and valley polarizations and TMR in the junction depend on the exchange field, the electrostatic potential, and the strength of the off-resonance CPL.
This paper discovers full spin and valley polarizations, as well as large TMR in the F/B/N/B/F WSe2 junction, with gate voltage and off-resonance CPL applied to the barrier regions. We demonstrate that the energy regions of full spin and valley polarizations and large TMR can be regulated by the electric potential (U), CPL intensity (ΔΩ), and exchange field (h), and discover the underlying physical mechanisms, which have not been reported in similar ferromagnetic-TMDC junctions18. We derived the minimum incident energy for non-zero spin- and valley-resolved conductance, and verified it through numerical calculations. The energy region for TMR = 1 increases (decreases) with h (U) and has little dependence on ΔΩ. For the P (AP) configuration, the energy region with PKK’ = -1 or Ps = 1 is relatively wider (narrower) and widens as ΔΩ increases. As h increases, the energy region with Ps = 1 (PKK’ = -1 or Ps = 1) widens (narrows) for the P (AP) configuration. As U increases, the energy region with PKK’ = -1 increases first and then moves parallel to the EF-axis, and the energy region with Ps = 1 for the P configuration remains unchanged first and then decreases. When the helicity of the off-resonance light reverses, the valley polarization will switch, while the spin polarization and TMR will not.
The remainder of the paper is organized as follows. In Sec. II, the theoretical model and the schematic structure of the F/B/N/B/F WSe2 junction are presented. Sec. III studies the spin and valley polarizations along with TMR of the WSe2 junction in the presence of off-resonant CPL and gate voltage. Finally, Sec. IV gives a summary.
Theory and model
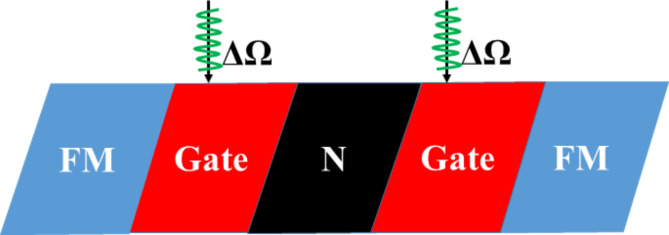
The proposed symmetric F/B/N/B/F WSe2 junction is shown schematically in Fig. 1, where the two barrier regions are formed by the electrostatic potential U induced by the gate voltage and illuminated by the off-resonant CPL with a frequency of Ω. An electromagnetic potential can describe the CPL as A(t) = [E0sin(± Ωt)/Ω, E0cos (± Ωt)/Ω], where + (-) corresponds to the right-handed (left-handed) circular polarization, and E0 is the amplitude of the electric field. Due to broken inversion symmetry, monolayer TMDCs exhibit valley-dependent optical interband excitation, i.e. electrons from different valleys are selectively excited by CPLs with different helicities41. Moreover, the magnetization orientation in the left ferromagnetic region is assumed to be always positive, while that in the right ferromagnetic region can be positive or negative, resulting in two types of magnetization configurations: parallel (P) and antiparallel (AP).
Fig. 1.
Schematic diagram of WSe2-based F/B/N/B/F junction. The two barrier regions are formed by the top gate voltage and illuminated by the off-resonant circularly polarized light.
For eAvf /Ω < < 1 (vf = 5 × 105 m/s is the Fermi velocity in WSe2), the low-energy effective Hamiltonian for the proposed WSe2 junction is given by6,22,28,42:
 |
1 |
Here Eg is the band gap of WSe222,39, ΔΩ = (eAvf)2/hΩ is the effective energy term describing the CPL intensity43. sz = + 1 (-1) denotes the up (down) spin of electrons, τz = + 1 (-1) stands for the K (K’) valley. σx,y,z represents the Pauli matrix in the sublattice space, and σ± = σ0 ± σz, with σ0 being the unit matrix22,39. λc = 7.5 meV (λv = 112.5 meV)22,39 is the spin splitting at the conduction (valence) band edge caused by the intrinsic SOC. The last term in Eq. (1) represents the magnetic modulation in the ferromagnetic region, where h is the exchange field.
The electrostatic gate potential and off-resonance CPL in the two barrier regions can be defined as  and
and  , respectively, with [
, respectively, with [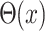 ] being the Heaviside step function. Moreover, the exchange field in the two ferromagnetic regions can be described as
] being the Heaviside step function. Moreover, the exchange field in the two ferromagnetic regions can be described as 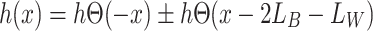 , where + (-) corresponds to the P (AP) magnetization configuration.
, where + (-) corresponds to the P (AP) magnetization configuration.
The energy dispersion relation in the modulated regions is22,39:
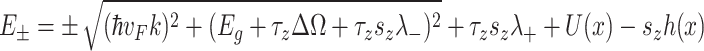 |
2 |
with λ± = λc ± λv. Thus the spin- and valley-resolved conduction band minimum (CBM) energy of the WSe2 junction can be written as:
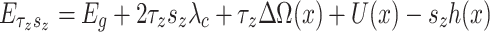 |
3 |
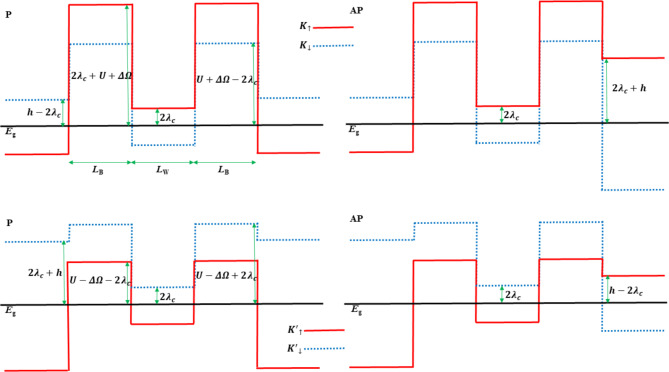
As shown in Eqs. (2) and (3), the exchange field, off-resonance CPL, and SOC collectively lift the spin and valley degeneracy of the energy dispersion relation. Figure 2 shows the spin- and valley-resolved CBM energy (effective potential for electrons) in each region of the F/B/N/B/F WSe2 junction, which depends on the spin and valley degrees of freedom and magnetization configuration, and will affect the spin- and valley-resolved conductance, spin and valley polarizations, as well as TMR of this junction. As shown in Eqs. (2) and (3), 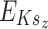 (
(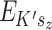 ) for ΔΩ > 0 approximately equals
) for ΔΩ > 0 approximately equals 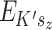 (
(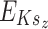 ) for ΔΩ < 0, because the term
) for ΔΩ < 0, because the term 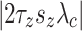 = 15 meV is relatively small. Therefore, when ΔΩ reverses the sign, the valley polarization (PKK’) will reverse the sign synchronously, while the spin polarization (Ps) and TMR will not be deeply affected. Thus, we will only discuss the case where ΔΩ > 0.
= 15 meV is relatively small. Therefore, when ΔΩ reverses the sign, the valley polarization (PKK’) will reverse the sign synchronously, while the spin polarization (Ps) and TMR will not be deeply affected. Thus, we will only discuss the case where ΔΩ > 0.
Fig. 2.
Spin- and valley-resolved conduction band minimum (CBM) energy in each region of the F/B/N/B/F WSe2 junction. The width of the two barrier layers is LB = 5 nm, and the width of the central well layer is Lw = 5 nm. The left (right) column corresponds to the P (AP) configuration. The horizontal line denotes the energy level with E = Eg = 850 meV. ↑ (↓) denotes the up (down) spin of electrons, respectively.
As can be concluded from Eq. (1) and Fig. 2, the critical minimum incident energy of non-zero spin- and valley-resolved conductance (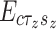 ) equals the highest CBM energy of the F/B/N/B/F WSe2 junction, which can be expressed as follows:
) equals the highest CBM energy of the F/B/N/B/F WSe2 junction, which can be expressed as follows:
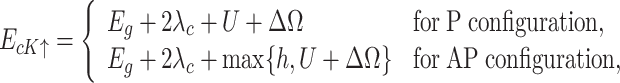 |
4 |
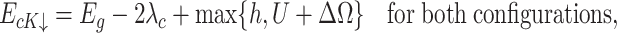 |
5 |
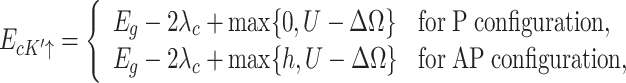 |
6 |
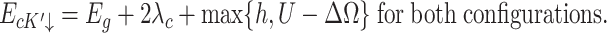 |
7 |
The wave function in each region can be expressed in the following form22:
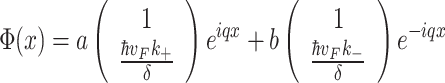 |
8 |
Here 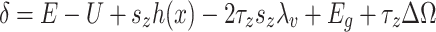 , a and b are the scattering coefficients. The parallel and perpendicular wave vectors in each region are
, a and b are the scattering coefficients. The parallel and perpendicular wave vectors in each region are
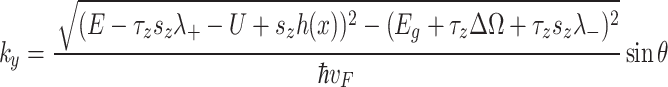 |
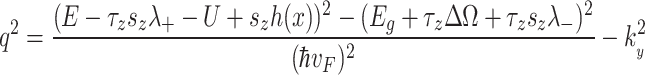 |
9 |
Here θ denotes the incident angle. Using the continuity condition of the wave function at the interfaces and the transfer-matrix method, the spin- and valley-dependent transmission probability (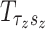 ) can be calculated. Then, the conductance at zero temperature is given by the Landauer-Büttiker formula44:
) can be calculated. Then, the conductance at zero temperature is given by the Landauer-Büttiker formula44:
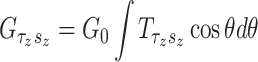 |
10 |
Here G0 = 2e2/h is the quantum conductance.
The spin- and valley-resolved conductance can be written as45,46:
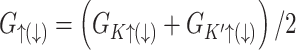 |
11 |
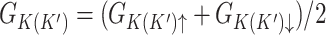 |
12 |
Using the spin- and valley-resolved conductance, the valley and spin polarizations (PKK’ and Ps) are defined as follows4:
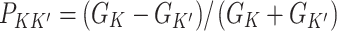 |
13 |
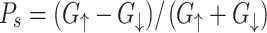 |
14 |
Finally, TMR can be defined as39:
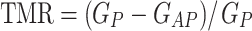 |
15 |
Here GP (GAP) is the total conductance of the F/B/N/B/F WSe2 junction in the P (AP) configuration, with 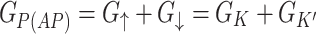 19.
19.
Results and discussion
In this section, we calculate the spin- and valley-dependent conductance and TMR in the F/B/N/B/F WSe2 junction for both parallel and antiparallel magnetization configurations in the presence of off-resonant CPL and gate voltage. Firstly, the cases of electric potential U = 100 meV, exchange field h = 200 meV, and different CPL intensity (ΔΩ) are explored. Secondly, the cases of ΔΩ = 200 meV, h = 200 meV, and different U are studied. Finally, the cases of U = 100 meV, ΔΩ = 200 meV, and various h are examined.
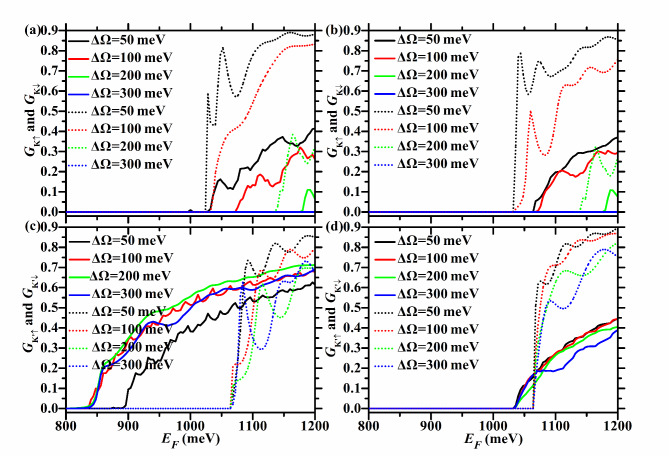
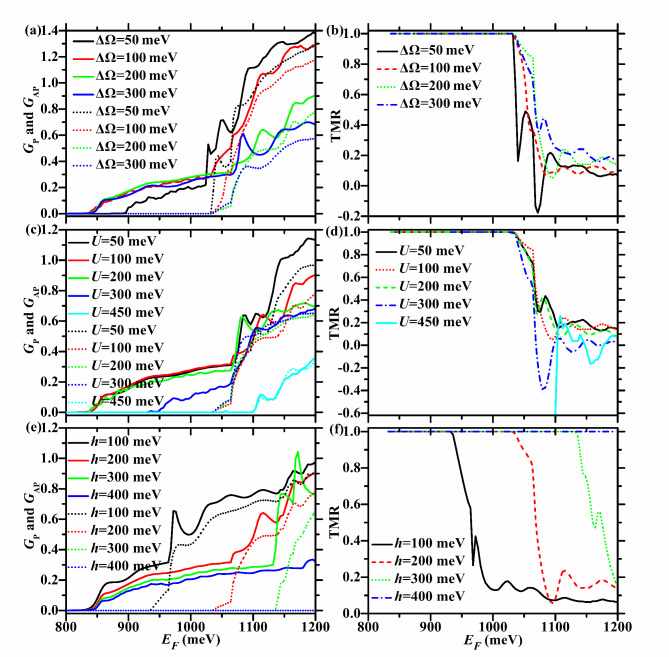
Figures 3 and 4 show the spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in P and AP configurations with U = 100 meV, h = 200 meV, and different ΔΩ. Figure 9 exhibits the corresponding total conductance as well as TMR, and Tables 1 and 2 depict the corresponding critical incident energy for the non-zero spin- and valley-resolved conductance.
Fig. 3.
Spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction with ΔΩ = 50, 100, 200, and 300 meV. Here h = 200 meV and U = 100 meV. In the left (right) column, the junction is in the P (AP) configuration. The solid (dotted) lines correspond to spin-up (-down) electrons.
Fig. 4.
GK (dotted lines), GK’ (solid lines), G↑ (solid lines), G↓ (dotted lines), PKK’, and Ps versus EF for the F/B/N/B/F WSe2 junction with ΔΩ = 50, 100, 200, and 300 meV. Here h = 200 meV and U = 100 meV. In the left (right) column, the junction is in the P (AP) configuration.
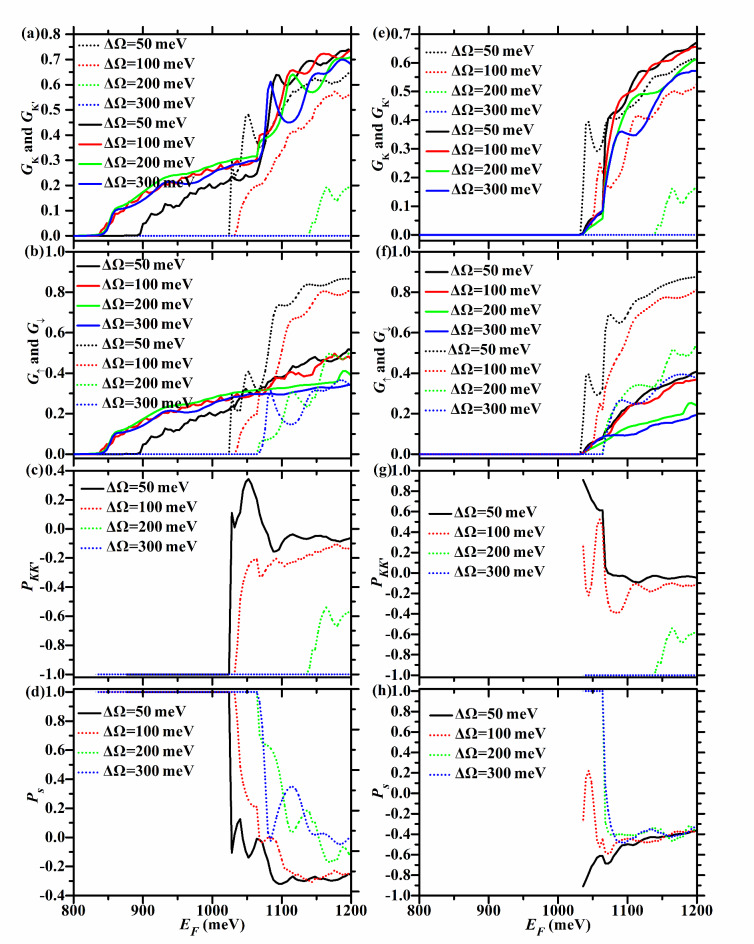
Fig. 9.
The total conductance (left column) of the F/B/N/B/F WSe2 junction in P and AP configurations, as well as the corresponding TMR (right column). The solid (dotted) lines correspond to the P (AP) configuration. Here U = 100 meV and h = 200 meV in the first row, h = 200 meV and ΔΩ = 200 meV in the second row, and U = 100 meV and ΔΩ = 200 meV in the third row.
Table 1.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the P configuration with U = 100 meV, h = 200 meV, and ΔΩ = 50, 100, 200, and 300 meV, respectively.
| ΔΩ |
EcK
|
EcK
|
EcK’
|
EcK’
|
EcK | EcK’ |
Ec
|
Ec
|
|---|---|---|---|---|---|---|---|---|
| 50 | 1028 | 1028 | 876 | 1068 | 1028 | 876 | 876 | 1028 |
| 100 | 1076 | 1036 | 836 | 1068 | 1036 | 836 | 836 | 1036 |
| 200 | 1180 | 1140 | 812 | 1068 | 1140 | 812 | 812 | 1068 |
| 300 | > 1200 | > 1200 | 824 | 1068 | > 1200 | 824 | 824 | 1068 |
Table 2.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the AP configuration with U = 100 meV, h = 200 meV, and ΔΩ = 50, 100, 200, and 300 meV, respectively.
| ΔΩ |
EcK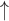
|
EcK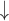
|
EcK’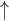
|
EcK’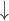
|
EcK | EcK’ |
Ec
|
Ec
|
|---|---|---|---|---|---|---|---|---|
| 50 | 1068 | 1036 | 1036 | 1068 | 1036 | 1036 | 1036 | 1036 |
| 100 | 1068 | 1036 | 1036 | 1068 | 1036 | 1036 | 1036 | 1036 |
| 200 | 1176 | 1140 | 1036 | 1068 | 1140 | 1036 | 1036 | 1068 |
| 300 | > 1200 | > 1200 | 1036 | 1068 | > 1200 | 1036 | 1036 | 1068 |
For U = 100 meV and h = 200 meV, 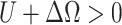 and
and 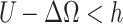 hold. So
hold. So 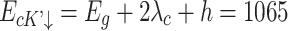 meV, and it is the same for both P and AP configurations and does not change with ΔΩ, as shown in Fig. 3(c) and (d), as well as Tables 1 and 2. For the P case,
meV, and it is the same for both P and AP configurations and does not change with ΔΩ, as shown in Fig. 3(c) and (d), as well as Tables 1 and 2. For the P case, 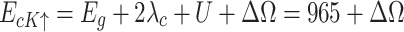 meV, and increases with ΔΩ, as seen in Fig. 3(a) and Table 1. For the AP case,
meV, and increases with ΔΩ, as seen in Fig. 3(a) and Table 1. For the AP case, 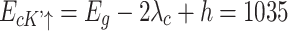 meV, and does not change with ΔΩ, as illustrated in Fig. 3(d) and Table 2.
meV, and does not change with ΔΩ, as illustrated in Fig. 3(d) and Table 2.
When ΔΩ < 100 meV,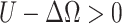 and
and 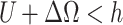 hold. So
hold. So 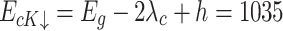 meV, and it is the same for both P and AP configurations and does not vary with ΔΩ, as depicted in Fig. 3(a) and (b), as well as Tables 1 and 2.
meV, and it is the same for both P and AP configurations and does not vary with ΔΩ, as depicted in Fig. 3(a) and (b), as well as Tables 1 and 2.
For the P case, 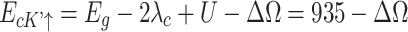 meV, and decreases with ΔΩ, as described in Fig. 3(c) and Table 1. So
meV, and decreases with ΔΩ, as described in Fig. 3(c) and Table 1. So 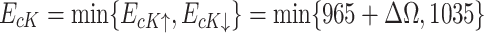 meV,
meV, 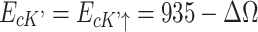 meV,
meV, 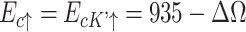 meV, Ec↓ = EcK↓ = 1035 meV, as seen in Fig. 4(a) and (b), and Table 1. Therefore, for the P case, PKK’ = -1 in the energy region [
meV, Ec↓ = EcK↓ = 1035 meV, as seen in Fig. 4(a) and (b), and Table 1. Therefore, for the P case, PKK’ = -1 in the energy region [ ,
,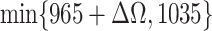 meV], which is relatively wide and increases with ΔΩ, as shown in Fig. 4(c). Ps = 1 in the energy region [
meV], which is relatively wide and increases with ΔΩ, as shown in Fig. 4(c). Ps = 1 in the energy region [ ,1035 meV], which is relatively wide and increases with ΔΩ, as shown in Fig. 4(d).
,1035 meV], which is relatively wide and increases with ΔΩ, as shown in Fig. 4(d).
For the AP case, 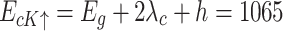 meV, and does not vary with ΔΩ, as seen in Fig. 3(b) and Table 2. So EcK = EcK↓ = 1035 meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, Ec↓ = EcK↓ = 1035 meV, as seen in Fig. 4(e) and (f), and Table 2. Therefore, for the AP case, the energy region with PKK’ = -1 (Ps = 1) does not exist, as shown in Fig. 4(g), (h).
meV, and does not vary with ΔΩ, as seen in Fig. 3(b) and Table 2. So EcK = EcK↓ = 1035 meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, Ec↓ = EcK↓ = 1035 meV, as seen in Fig. 4(e) and (f), and Table 2. Therefore, for the AP case, the energy region with PKK’ = -1 (Ps = 1) does not exist, as shown in Fig. 4(g), (h).
TMR = 1 in the energy region [ ,1035 meV], which is relatively wide and increases with ΔΩ, and its upper limit does not change with ΔΩ, as shown in Fig. 9(a) and (b).
,1035 meV], which is relatively wide and increases with ΔΩ, and its upper limit does not change with ΔΩ, as shown in Fig. 9(a) and (b).
When ΔΩ ≥ 100 meV, 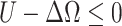 and
and 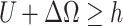 hold. So
hold. So 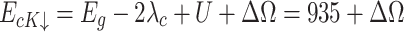 meV, and increases with ΔΩ, regardless of P or AP configuration, as depicted in Fig. 3(a) and (b), as well as Tables 1 and 2.
meV, and increases with ΔΩ, regardless of P or AP configuration, as depicted in Fig. 3(a) and (b), as well as Tables 1 and 2.
For the P case, 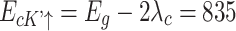 meV, and does not vary with ΔΩ, as seen in Fig. 3(c) and Table 1. So
meV, and does not vary with ΔΩ, as seen in Fig. 3(c) and Table 1. So 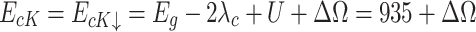 meV,
meV, 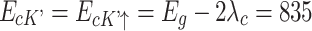 meV,
meV, 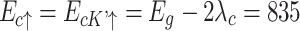 meV,
meV, 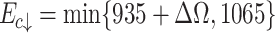 meV, as seen in Fig. 4(a) and (b) and Table 1. For the P case, PKK’ = -1 in the energy region [
meV, as seen in Fig. 4(a) and (b) and Table 1. For the P case, PKK’ = -1 in the energy region [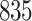 ,
,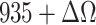 meV], which is relatively wide and increases with ΔΩ, as seen in Fig. 4(c). As shown in Fig. 4(d), Ps = 1 in the energy region [835,
meV], which is relatively wide and increases with ΔΩ, as seen in Fig. 4(c). As shown in Fig. 4(d), Ps = 1 in the energy region [835,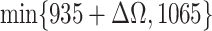 meV]. This increases with ΔΩ when 100 < ΔΩ < 130 meV, and remains at [835,1065 meV] when ΔΩ ≥ 130 meV, with a width of 230 meV.
meV]. This increases with ΔΩ when 100 < ΔΩ < 130 meV, and remains at [835,1065 meV] when ΔΩ ≥ 130 meV, with a width of 230 meV.
For the AP case, 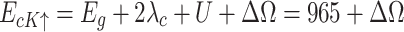 meV, and increases with ΔΩ, as seen in Fig. 3(b) and Table 2. So
meV, and increases with ΔΩ, as seen in Fig. 3(b) and Table 2. So  meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV,
meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, 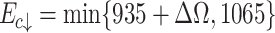 meV, as seen in Fig. 4(e) and (f) and Table 2. For the AP case, PKK’ = -1 in the energy region [1035,
meV, as seen in Fig. 4(e) and (f) and Table 2. For the AP case, PKK’ = -1 in the energy region [1035,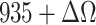 meV], which increases with ΔΩ, as shown in Fig. 4(g). As shown in Fig. 4(h), Ps = 1 in the energy region [1035,
meV], which increases with ΔΩ, as shown in Fig. 4(g). As shown in Fig. 4(h), Ps = 1 in the energy region [1035,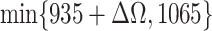 meV]. This region increases with ΔΩ when 100 < ΔΩ < 130 meV, and remains at [1035,1065 meV] when ΔΩ ≥ 130 meV, with a width of 30 meV.
meV]. This region increases with ΔΩ when 100 < ΔΩ < 130 meV, and remains at [1035,1065 meV] when ΔΩ ≥ 130 meV, with a width of 30 meV.
Therefore, when ΔΩ ≥ 100 meV, TMR = 1 in the energy region [835,1035 meV], which is relatively wide and remains at 200 meV, as described in Fig. 9(a) and (b).
Figures 5 and 6 show the spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in P and AP configurations with ΔΩ = 200 meV, h = 200 meV, and different U. Figure 9 exhibits the corresponding total conductance as well as TMR, and Tables 3 and 4 depict the corresponding critical incident energy for the non-zero spin- and valley-resolved conductance.
Fig. 5.
Spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction with ΔΩ = 200 meV, h = 200 meV, and U = 50, 100, 200, 300 and 450 meV. The solid (dotted) lines correspond to spin-up (-down) electrons. In the left (right) column, the junction is in the P (AP) configuration.
Fig. 6.
GK (dotted lines), GK’ (solid lines), G↑ (solid lines), G↓ (dotted lines), PKK’, and Ps versus EF for the F/B/N/B/F WSe2 junction with U = 50, 100, 200, 300, and 450 meV. Here h = 200 meV and ΔΩ = 200 meV. In the left (right) column, the junction is in the P (AP) configuration.
Table 3.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the P configuration with ΔΩ = 200 meV, h = 200 meV, and U = 50, 100, 200, 300 and 450 meV, respectively.
| U |
EcK
|
EcK
|
EcK’
|
EcK’
|
EcK | EcK’ |
Ec
|
Ec
|
|---|---|---|---|---|---|---|---|---|
| 50 | 1128 | 1092 | 820 | 1068 | 1092 | 820 | 820 | 1068 |
| 100 | 1180 | 1140 | 812 | 1068 | 1140 | 812 | 812 | 1068 |
| 200 | > 1200 | > 1200 | 836 | 1068 | > 1200 | 836 | 836 | 1068 |
| 300 | > 1200 | > 1200 | 932 | 1068 | > 1200 | 932 | 932 | 1068 |
| 450 | > 1200 | > 1200 | 1096 | 1100 | > 1200 | 1096 | 1096 | 1100 |
Table 4.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the AP configuration with ΔΩ = 200 meV, h = 200 meV, and U = 50, 100, 200, 300 and 450 meV, respectively.
| U |
EcK
|
EcK
|
EcK’
|
EcK’
|
EcK | EcK’ |
Ec
|
Ec
|
|---|---|---|---|---|---|---|---|---|
| 50 | 1108 | 1092 | 1036 | 1068 | 1092 | 1036 | 1036 | 1068 |
| 100 | 1176 | 1140 | 1036 | 1068 | 1140 | 1036 | 1036 | 1068 |
| 200 | > 1200 | > 1200 | 1036 | 1068 | > 1200 | 1036 | 1036 | 1068 |
| 300 | > 1200 | > 1200 | 1036 | 1068 | > 1200 | 1036 | 1036 | 1068 |
| 450 | > 1200 | > 1200 | 1096 | 1100 | > 1200 | 1096 | 1096 | 1100 |
For ΔΩ = 200 meV and h = 200 meV, 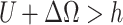 holds. So
holds. So 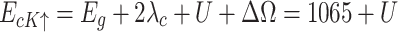 meV,
meV, 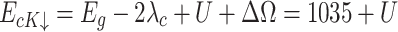 meV, and they are the same for both P and AP configurations and increase with U, as seen in Fig. 5(a) and (b), as well as Tables 3 and 4.
meV, and they are the same for both P and AP configurations and increase with U, as seen in Fig. 5(a) and (b), as well as Tables 3 and 4.
When U < 200 meV, 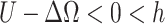 holds. So
holds. So 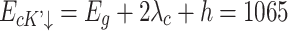 meV, and does not change with U, whether P or AP configuration, as shown in Fig. 5(c) and (d), as well as Tables 3 and 4.
meV, and does not change with U, whether P or AP configuration, as shown in Fig. 5(c) and (d), as well as Tables 3 and 4.
For the P case, 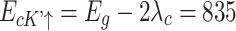 meV, and does not change with ΔΩ, as seen in Fig. 5(c) and Table 3. So
meV, and does not change with ΔΩ, as seen in Fig. 5(c) and Table 3. So 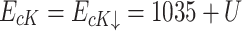 meV, EcK’ = EcK’↑ = 835 meV, Ec↑ = EcK’↑ = 835 meV,
meV, EcK’ = EcK’↑ = 835 meV, Ec↑ = EcK’↑ = 835 meV, 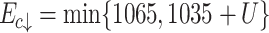 meV, as illustrated in Fig. 6(a) and (b) and Table 3. Therefore, for the P case, PKK’ = -1 in the energy region [835,
meV, as illustrated in Fig. 6(a) and (b) and Table 3. Therefore, for the P case, PKK’ = -1 in the energy region [835,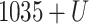 meV], which increases with U, as seen in Fig. 6(c). As shown in Fig. 6(d), Ps = 1 in the energy region [835,
meV], which increases with U, as seen in Fig. 6(c). As shown in Fig. 6(d), Ps = 1 in the energy region [835,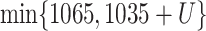 meV]. This region increases with U when 0 < U < 30 meV, and remains at [835,1065 meV] when 30 ≤ U < 200 meV, with a width of 230 meV.
meV]. This region increases with U when 0 < U < 30 meV, and remains at [835,1065 meV] when 30 ≤ U < 200 meV, with a width of 230 meV.
For the AP case, 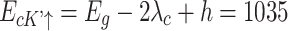 meV, and does not change with U, as seen in Fig. 5(d) and Table 4. So
meV, and does not change with U, as seen in Fig. 5(d) and Table 4. So 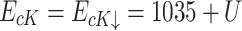 meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV,
meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, 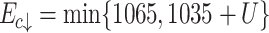 meV, as seen in Fig. 6(e) and (f) and Table 4. For the AP case, PKK’ = -1 in the energy region [1035,
meV, as seen in Fig. 6(e) and (f) and Table 4. For the AP case, PKK’ = -1 in the energy region [1035,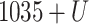 meV], which increases with U, as seen in Fig. 6(g). As shown in Fig. 6(h), Ps = 1 in the energy region [1035,
meV], which increases with U, as seen in Fig. 6(g). As shown in Fig. 6(h), Ps = 1 in the energy region [1035,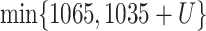 meV]. This region increases with U when 0 < U < 30 meV, and remains at [1035,1065 meV] when 30 ≤ U < 200 meV, with a width of 30 meV.
meV]. This region increases with U when 0 < U < 30 meV, and remains at [1035,1065 meV] when 30 ≤ U < 200 meV, with a width of 30 meV.
Therefore, when U < 200 meV, TMR = 1 in the energy region [835,1035 meV], which is relatively wide and remains at 200 meV, as shown in Fig. 9(c) and (d).
When 200 ≤ U < 400 meV, 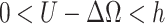 holds. So
holds. So 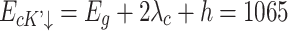 meV, and it is the same for both P and AP configurations and does not vary with U, as seen in Fig. 5(c) and (d), as well as Tables 3 and 4.
meV, and it is the same for both P and AP configurations and does not vary with U, as seen in Fig. 5(c) and (d), as well as Tables 3 and 4.
For the P case, 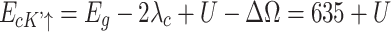 meV, and increases with U, as seen in Fig. 5(c) and Table 3. So
meV, and increases with U, as seen in Fig. 5(c) and Table 3. So 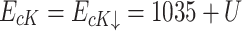 meV,
meV, 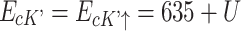 meV,
meV, 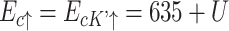 meV, Ec↓ = EcK’↓ = 1065 meV, as seen in Fig. 6(a) and (b) and Table 3. For the P case, PKK’ = -1 in the energy region [
meV, Ec↓ = EcK’↓ = 1065 meV, as seen in Fig. 6(a) and (b) and Table 3. For the P case, PKK’ = -1 in the energy region [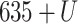 ,
,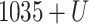 meV], which is relatively wide and remains at 400 meV. As U increases, it moves parallel to the EF-axis as a whole, as seen in Fig. 6(c). Ps = 1 in the energy region [
meV], which is relatively wide and remains at 400 meV. As U increases, it moves parallel to the EF-axis as a whole, as seen in Fig. 6(c). Ps = 1 in the energy region [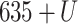 ,1065 meV], which decreases with U, as seen in Fig. 6(d).
,1065 meV], which decreases with U, as seen in Fig. 6(d).
For the AP case, 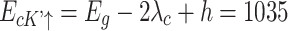 meV, and does not change with U, as seen in Fig. 5(d) and Table 4. So
meV, and does not change with U, as seen in Fig. 5(d) and Table 4. So 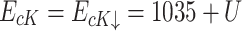 meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, Ec↓ = EcK’↓ = 1065 meV, as seen in Fig. 6(e) and (f) and Table 4. For the AP case, PKK’ = -1 in the energy region [1035,
meV, EcK’ = EcK’↑ = 1035 meV, Ec↑ = EcK’↑ = 1035 meV, Ec↓ = EcK’↓ = 1065 meV, as seen in Fig. 6(e) and (f) and Table 4. For the AP case, PKK’ = -1 in the energy region [1035,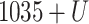 meV], which increases with U, as seen in Fig. 6(g). As seen in Fig. 6(h), Ps = 1 in the energy region [1035,1065 meV], which is relatively narrow and remains at 30 meV as U increases.
meV], which increases with U, as seen in Fig. 6(g). As seen in Fig. 6(h), Ps = 1 in the energy region [1035,1065 meV], which is relatively narrow and remains at 30 meV as U increases.
Therefore, when 200 ≤ U < 400 meV, TMR = 1 in the energy region [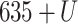 ,1035 meV], which decreases evidently with U, as shown in Fig. 9(c) and (d).
,1035 meV], which decreases evidently with U, as shown in Fig. 9(c) and (d).
When U ≥ 400 meV, 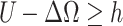 holds.
holds. 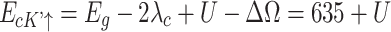 meV,
meV, 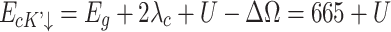 meV, and they are the same for both P and AP configurations and increase with U, as seen in Fig. 5(c) and (d), as well as Tables 3 and 4. So
meV, and they are the same for both P and AP configurations and increase with U, as seen in Fig. 5(c) and (d), as well as Tables 3 and 4. So 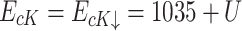 meV,
meV, 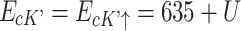 meV,
meV, 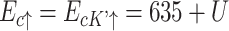 meV,
meV, 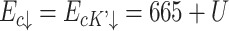 meV, as seen in Fig. 6(a), (b), (e), and (f) and Tables 3 and 4. Thus PKK’ = -1 in the energy region [
meV, as seen in Fig. 6(a), (b), (e), and (f) and Tables 3 and 4. Thus PKK’ = -1 in the energy region [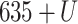 ,
,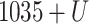 meV], which is relatively wide and remains at 400 meV. As U increases, it moves parallel to the EF-axis as a whole, as shown in Fig. 6(c) and (g). In theory, Ps = 1 in the energy region [
meV], which is relatively wide and remains at 400 meV. As U increases, it moves parallel to the EF-axis as a whole, as shown in Fig. 6(c) and (g). In theory, Ps = 1 in the energy region [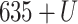 ,
,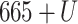 meV], which is relatively narrow and moves parallel to the EF-axis as U increases. However, when U = 450 meV, as seen in Fig. 6(b) and (f) and Tables 3 and 4, Ec↑ (1096 meV) and Ec↓ (1100 meV) are very close, making it difficult to see the energy region with Ps = 1 in Fig. 6(d) and (h).
meV], which is relatively narrow and moves parallel to the EF-axis as U increases. However, when U = 450 meV, as seen in Fig. 6(b) and (f) and Tables 3 and 4, Ec↑ (1096 meV) and Ec↓ (1100 meV) are very close, making it difficult to see the energy region with Ps = 1 in Fig. 6(d) and (h).
Therefore, the energy region with TMR = 1 does not exist when U ≥ 400 meV, as described in Fig. 9(c) and (d).
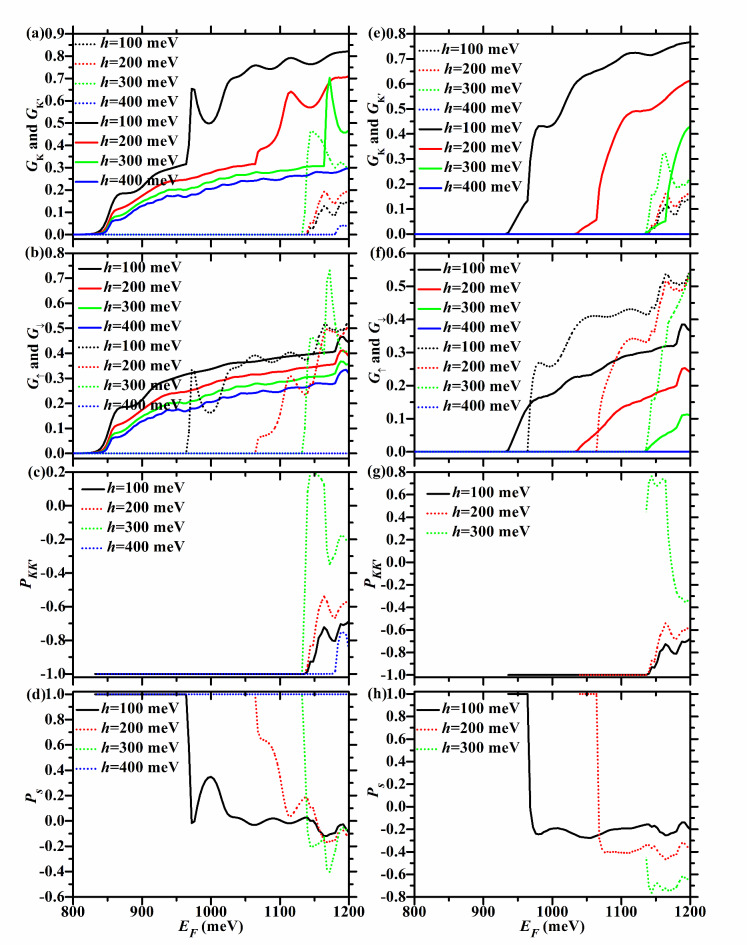
Figures 7 and 8 show the spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in P and AP configurations with U = 100 meV, ΔΩ = 200 meV, and different h. Figure 9 exhibits the corresponding total conductance as well as TMR, and Tables 5 and 6 depict the corresponding critical incident energy for the non-zero spin- and valley-resolved conductance.
Fig. 7.
Spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction under different h and fixed U (100 meV) and ΔΩ (200 meV). The solid (dotted) lines correspond to spin-up (-down) electrons. In the left (right) column, the junction is in the P (AP) configuration.
Fig. 8.
GK (dotted lines), GK’ (solid lines), G↑ (solid lines), G↓ (dotted lines), PKK’, and Ps versus EF for the F/B/N/B/F WSe2 junction with U = 100 meV and ΔΩ = 200 meV, h = 100, 200, 300, and 400 meV, respectively. In the left (right) column, the junction is in the P (AP) configuration.
Table 5.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the P configuration with U = 100 meV, ΔΩ = 200 meV, and h = 100, 200, 300, and 400 meV, respectively.
| h |
EcK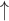
|
EcK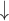
|
EcK’
|
EcK’
|
EcK | EcK’ |
Ec
|
Ec
|
|---|---|---|---|---|---|---|---|---|
| 100 | 1180 | 1140 | 812 | 968 | 1140 | 812 | 812 | 968 |
| 200 | 1180 | 1140 | 812 | 1068 | 1140 | 812 | 812 | 1068 |
| 300 | 1180 | 1140 | 808 | 1168 | 1136 | 808 | 808 | 1136 |
| 400 | 1180 | > 1200 | 808 | > 1200 | 1180 | 808 | 808 | > 1200 |
Table 6.
The critical incident energy (in units of meV) of non-zero spin- and valley-resolved conductance of the F/B/N/B/F WSe2 junction in the AP configuration with U = 100 meV, ΔΩ = 200 meV, and h = 100, 200, 300, and 400 meV, respectively.
| h |
EcK
|
EcK
|
EcK’
|
EcK’
|
EcK | EcK’ |
Ec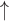
|
Ec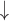
|
|---|---|---|---|---|---|---|---|---|
| 100 | 1180 | 1140 | 936 | 968 | 1140 | 936 | 936 | 968 |
| 200 | 1176 | 1136 | 1036 | 1068 | 1140 | 1036 | 1036 | 1068 |
| 300 | 1176 | 1136 | 1136 | 1168 | 1136 | 1136 | 1136 | 1136 |
| 400 | > 1200 | > 1200 | > 1200 | > 1200 | > 1200 | > 1200 | > 1200 | > 1200 |
For U = 100 meV and ΔΩ = 200 meV, 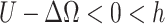 holds. So
holds. So 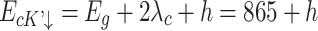 meV, and it is the same for both P and AP configurations and increases with h, as described in Fig. 7(c) and (d), as well as Tables 5 and 6. For the P case,
meV, and it is the same for both P and AP configurations and increases with h, as described in Fig. 7(c) and (d), as well as Tables 5 and 6. For the P case, 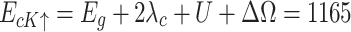 meV,
meV, 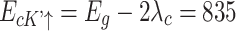 meV, and they do not change with h, as seen in Fig. 7(a) and (c) and Table 5. For the AP case,
meV, and they do not change with h, as seen in Fig. 7(a) and (c) and Table 5. For the AP case, 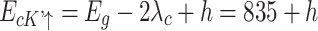 meV, and increases with h, as shown in Fig. 7(d) and Table 6.
meV, and increases with h, as shown in Fig. 7(d) and Table 6.
When h < 300 meV, 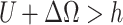 holds.
holds. 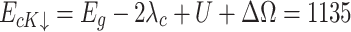 meV and does not change with h, whether P or AP configuration, as depicted in Fig. 7(a) and (b), as well as Tables 5 and 6.
meV and does not change with h, whether P or AP configuration, as depicted in Fig. 7(a) and (b), as well as Tables 5 and 6.
For the P case, EcK = EcK↓ = 1135 meV, EcK’ = EcK’↑ = 835 meV, Ec↑ = EcK’↑ = 835 meV, 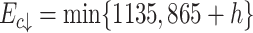 meV, as seen in Fig. 7(a) and (b) and Table 5. Therefore, for the P case, as h increases, the energy region with PKK’ = -1 remains at [835,1135 meV], which is relatively wide and remains at 300 meV, as shown in Fig. 8(c). As shown in Fig. 8(d), Ps = 1 in the energy region [835,
meV, as seen in Fig. 7(a) and (b) and Table 5. Therefore, for the P case, as h increases, the energy region with PKK’ = -1 remains at [835,1135 meV], which is relatively wide and remains at 300 meV, as shown in Fig. 8(c). As shown in Fig. 8(d), Ps = 1 in the energy region [835,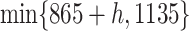 meV]. This region increases evidently with h when 0 < h < 270 meV, and remains at [835,1135 meV] when 270 ≤ h < 300 meV.
meV]. This region increases evidently with h when 0 < h < 270 meV, and remains at [835,1135 meV] when 270 ≤ h < 300 meV.
For the AP case, 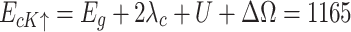 meV, and does not change with h, as shown in Fig. 7(b) and Table 6, just like in the P case. So EcK = EcK↓ = 1135 meV,
meV, and does not change with h, as shown in Fig. 7(b) and Table 6, just like in the P case. So EcK = EcK↓ = 1135 meV, 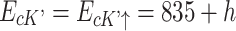 meV,
meV, 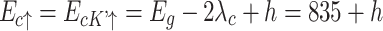 meV,
meV, 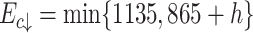 meV, as seen in Fig. 8(e) and (f) and Table 6. For the AP case, PKK’ = -1 in the energy region [
meV, as seen in Fig. 8(e) and (f) and Table 6. For the AP case, PKK’ = -1 in the energy region [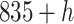 ,1135 meV], which decreases evidently with h, as seen in Fig. 8(g). When h = 300 meV, the energy region with PKK’ = -1 disappears completely. As shown in Fig. 8(h), Ps = 1 in the energy region [
,1135 meV], which decreases evidently with h, as seen in Fig. 8(g). When h = 300 meV, the energy region with PKK’ = -1 disappears completely. As shown in Fig. 8(h), Ps = 1 in the energy region [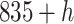 ,
,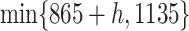 meV]. When 0 < h < 270 meV, this region remains at [
meV]. When 0 < h < 270 meV, this region remains at [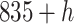 ,
,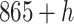 meV], with a width of 30 meV. When 270 < h < 300 meV, it decreases evidently with h. When h = 300 meV, it disappears completely.
meV], with a width of 30 meV. When 270 < h < 300 meV, it decreases evidently with h. When h = 300 meV, it disappears completely.
Therefore, when h < 300 meV, TMR = 1 in the energy region [835,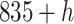 meV], which is relatively wide and increases rapidly with h, as shown in Fig. 9(e) and (f).
meV], which is relatively wide and increases rapidly with h, as shown in Fig. 9(e) and (f).
When h ≥ 300 meV, 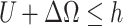 holds. So
holds. So 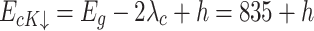 meV, and increases with h, regardless of P or AP configuration, as seen in Fig. 7(a) and (b), as well as Tables 5 and 6.
meV, and increases with h, regardless of P or AP configuration, as seen in Fig. 7(a) and (b), as well as Tables 5 and 6.
For the P case,  meV, EcK’ = EcK’↑ = 835 meV, Ec↑ = EcK’↑ = 835 meV,
meV, EcK’ = EcK’↑ = 835 meV, Ec↑ = EcK’↑ = 835 meV, 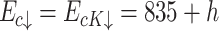 meV, as seen in Fig. 8(a) and (b) and Table 5. For the P case, PKK’ = -1 in the energy region [
meV, as seen in Fig. 8(a) and (b) and Table 5. For the P case, PKK’ = -1 in the energy region [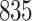 ,
,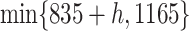 meV], as shown in Fig. 8(c). When 300 < h < 330 meV, it increases with h. When h ≥ 330 meV, it remains at [835,1165 meV], with a width of 330 meV. Ps = 1 in the energy region [835,
meV], as shown in Fig. 8(c). When 300 < h < 330 meV, it increases with h. When h ≥ 330 meV, it remains at [835,1165 meV], with a width of 330 meV. Ps = 1 in the energy region [835,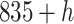 meV], which increases with h, as seen in Fig. 8(d).
meV], which increases with h, as seen in Fig. 8(d).
For the AP case, 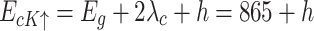 meV, and increases with h, as seen in Fig. 7(b) and Table 6. So
meV, and increases with h, as seen in Fig. 7(b) and Table 6. So 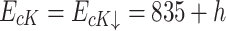 meV,
meV, 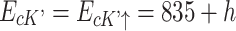 meV,
meV, 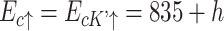 meV,
meV, 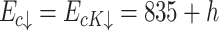 meV, as seen in Fig. 8(e) and (f) and Table 6. For the AP case, the energy region with PKK’ = -1 (Ps = 1) does not exist, as seen in Fig. 8(g), (h).
meV, as seen in Fig. 8(e) and (f) and Table 6. For the AP case, the energy region with PKK’ = -1 (Ps = 1) does not exist, as seen in Fig. 8(g), (h).
Therefore, when h ≥ 300 meV, TMR = 1 in the energy region [835,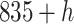 meV], which increases with h, as seen in Fig. 9(e) and (f).
meV], which increases with h, as seen in Fig. 9(e) and (f).
Conclusion
In conclusion, by tuning the exchange field h in the FM region, the electrostatic potential U and CPL intensity ΔΩ in the barrier region, the energy region of full spin and valley polarizations as well as large TMR in the F/B/N/B/F WSe2 junction can be modulated, and the underlying physical mechanisms have been unveiled. We have derived the minimum incident energy of non-zero spin- and valley-resolved conductance, which is demonstrated by numerical calculations. The sign of the valley polarization PKK’ depends on the helicity of the CPL, which does not happen to TMR and Ps. The energy region with TMR = 1 increases with h rapidly, remains unchanged first and then decreases as U increases, and has little dependence on ΔΩ. The energy region with PKK’ = -1 or Ps = 1 for the P case is much wider than that of the AP case, and they both increase evidently with ΔΩ. With increasing h, the Ps = 1 plateau widens for the P configuration, while the PKK’ = -1 or Ps = 1 plateau narrows for the AP configuration. For the P configuration, as U increases, the energy region with PKK’ = -1 (Ps = 1) increases (decreases) and that of Ps = 1 (PKK’ = -1) remains unchanged when U is relatively small (large). When U increases to a certain degree, the plateaus with PKK’ = -1 or Ps = 1 move parallel to the EF-axis, regardless of P or AP configuration. Our research helps the practical application of ferromagnetic WSe2 double-barrier junctions in fabricating spin-valleytronic and TMR devices.
Acknowledgements
This work was supported by the “316” Project Plan of Xuchang University.
Author contributions
Ming Li: Conceptualization, Funding acquisition, Writing-review & editing. Zheng-Yin Zhao: Methodology, Writing-review & editing. Jia-Yi Sheng: Investigation, Writing-original draft.
Data availability
Data will be made available on request.
Declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA102, 10451 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee, C. K. S. et al. Frictional characteristics of atomically thin sheets. Science328, 76 (2010). [DOI] [PubMed] [Google Scholar]
- 3.Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett.105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
- 4.Luo, L., Wang, S., Zheng, J. & Guo, Y. Spin- and valley-resolved tunneling magnetoresistance in a ferromagnetic transition metal dichalcogenide planar heterojunction modulated by polarized light. Phys. Rev. B108, 075434 (2023). [Google Scholar]
- 5.Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys.10, 343 (2014). [Google Scholar]
- 6.Xiao, D., Liu, G. B., Feng, W., Xu, X. & Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett.108, 196802 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Lu, H. Z., Yao, W., Xiao, D. & Shen, S. Q. Intervalley scattering and localization behaviors of spin-valley coupled Dirac fermions. Phys. Rev. Lett.110, 016806 (2013). [DOI] [PubMed] [Google Scholar]
- 8.Bertoni, R. et al. Generation and evolution of spin-, valley-, and layer-polarized excited carriers in inversion-symmetric WSe2. Phys. Rev. Lett.117, 277201 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Tahir, M., Krstaji’c, P. M. & Vasilopoulos, P. Magnetic and electric control of spin- and valley-polarized transport across tunnel junctions on monolayer WSe2. Phys. Rev. B95, 235402 (2017). [Google Scholar]
- 10.Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol.8, 634 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transitionmetal dichalcogenide semiconductors. Phys. Rev. B84, 153402 (2011). [Google Scholar]
- 12.Hao, X. J., Yuan, R. Y., Ji, T. & Guo, Y. Switch effect for spin-valley electrons in monolayer WSe2 structures subjected to optical field and Fermi velocity barrier. J. Appl. Phys.128, 154303 (2020). [Google Scholar]
- 13.MacNeill, D. et al. Breaking of valley degeneracy by magnetic field in monolayer MoSe2. Phys. Rev. Lett.114, 037401 (2015). [DOI] [PubMed] [Google Scholar]
- 14.Scharf, B., Xu, G., Matos-Abiague, A. & Žuti’c, I. Magnetic proximity effects in transition-metal dichalcogenides: Converting excitons. Phys. Rev. Lett.119, 127403 (2017). [DOI] [PubMed] [Google Scholar]
- 15.Wang, Z., Tang, C., Sachs, R., Barlas, Y. & Shi, J. Proximity-induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys. Rev. Lett.114, 016603 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Saxena, R., Saha, A. & Rao, S. Conductance, valley and spin polarizations, and tunneling magnetoresistance in ferromagnetic-normal-ferromagnetic junctions of silicene. Phys. Rev. B92, 245412 (2015). [Google Scholar]
- 17.Wang, D., Huang, Z., Zhang, Y. & Jin, G. Spin-valley filter and tunnel magnetoresistance in asymmetrical silicene magnetic tunnel junctions. Phys. Rev. B93, 195425 (2016). [Google Scholar]
- 18.Qiu, X. J., Cao, Z. Z., Hou, J. & Yang, C. Y. Controlled giant magnetoresistance and spin–valley transport in an asymmetrical MoS2 tunnel junction. Appl. Phys. Lett.117, 102401 (2020). [Google Scholar]
- 19.Lu, W. T., Tian, H. Y., Liu, H. M., Li, Y. F. & Li, W. Spin- and valley-dependent negative magnetoresistance in a ferromagnetic MoS2 junction with a quantum well. Phys. Rev. B98, 075405 (2018). [Google Scholar]
- 20.Lazi’c, P., Belashchenko, K. D. & Žuti’c, I. Effective gating and tunable magnetic proximity effects in two-dimensional heterostructures. Phys. Rev. B93, 241401(R) (2016). [Google Scholar]
- 21.Zhao, C. et al. Enhanced valley splitting in monolayer WSe2 due to magnetic exchange field. Nat. Nanotechnol.12, 757 (2017). [DOI] [PubMed] [Google Scholar]
- 22.Liu, D., Liu, B., Yuan, R., Zheng, J. & Guo, Y. Valley filter and valley valve based on WSe2 double-barrier junctions modulated by polarized light. Phys. Rev. B103, 245432 (2021). [Google Scholar]
- 23.Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Commun.3, 887 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol.7, 494 (2012). [DOI] [PubMed] [Google Scholar]
- 25.Zeng, H. L., Dai, J. F., Yao, W., Xiao, D. & Cui, X. D. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol.7, 490 (2012). [DOI] [PubMed] [Google Scholar]
- 26.Qi, F. H., Cao, J. & Jin, G. J. Valley-controlled nonlocal transistor based on irradiated and biased bilayer graphene. Phys. Rev. B98, 045422 (2018). [Google Scholar]
- 27.Qiu, X. J., Cao, Z. Z., Lei, J. M., Shen, J. & Qin, C. C. Optical and electric control of charge and spin-valley transport in ferromagnetic silicene junction. Superlatt. Microstruct.109, 735 (2017). [Google Scholar]
- 28.Qiu, X., Lv, Q. & Cao, Z. Optical, electric and magnetic controlled ballistic conductance in monolayer WSe2: the perfect valley and spin polarizations. J. Phys. D: Appl. Phys.50, 455106 (2017). [Google Scholar]
- 29.Yang, Q., Yuan, R. & Guo, Y. Valley switch effect based on monolayer WSe2 modulated by circularly polarized light and valley Zeeman field. J. Phys. D: Appl. Phys.52, 335301 (2019). [Google Scholar]
- 30.Tahir, M., Manchon, A. & Schwingenschlögl, U. Photoinduced quantum spin and valley Hall effects, and orbital magnetization in monolayer MoS2. Phys. Rev. B90, 125438 (2014). [Google Scholar]
- 31.Moodera, J. S., Kinder, L. R., Wong, T. M. & Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett.74, 3273 (1995). [DOI] [PubMed] [Google Scholar]
- 32.Butler, W. H. Tunneling magnetoresistance from a symmetry filtering effect. Sci. Technol. Adv. Mater.9, 014106 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Maehara, H. et al. Tunnel magnetoresistance above 170% and resistance–area product of 1 (μm) 2 attained by in situ annealing of ultra-thin MgO tunnel barrier. Appl. Phys. Express4, 033002 (2011). [Google Scholar]
- 34.Zou, J., Jin, G. & Ma, Y. Q. Negative tunnel magnetoresistance and spin transport in ferromagnetic graphene junctions. J. Phys.: Condens. Matter21, 126001 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Bai, C. & Zhang, X. Large oscillating tunnel magnetoresistance in ferromagnetic graphene single tunnel junction. Phys. Lett. A372, 725 (2008). [Google Scholar]
- 36.Khezerlou, M. & Goudarzi, H. Valley permitted Klein tunneling and magnetoresistance in ferromagnetic monolayer MoS2. Superlatt. Microstruct.86, 243 (2015). [Google Scholar]
- 37.Hajati, Y., Amini, Z. & Sabaeian, M. Controllable photoenhanced spin- and valley-polarized transport in ferromagnetic MoS2 junction. J. Magn. Magn. Mater.503, 166580 (2020). [Google Scholar]
- 38.Chantngarm, P., Yamada, K. & Soodchomshom, B. Polarized-photon frequency filter in double-ferromagnetic barrier silicene junction. J. Magn. Magn. Mater.429, 16–22 (2017). [Google Scholar]
- 39.Hajati, Y. & Alipourzadeh, M. Spin- and valley-polarized transport and magnetoresistance in asymmetric ferromagnetic WSe2 tunnel junctions. Phys. Rev. B103, 245435 (2021). [Google Scholar]
- 40.Hajati, Y., Alipourzadeh, M. & Makhfudz, I. Spin-valley dependent Klein tunneling and perfect spin- and valley-polarized transport in a magnetic WSe2 superlattice. Phys. Rev. B104, 205402 (2021). [Google Scholar]
- 41.Hao, K. et al. Direct measurement of exciton valley coherence in monolayer WSe2. Nat. Phys.12, 677 (2016). [Google Scholar]
- 42.Tahir, M. Electrical and optical transport properties of single layer WSe2. Physica E97, 184–190 (2018). [Google Scholar]
- 43.Luo, L., Wang, S., Zheng, J. & Guo, Y. Optically controlled valley filter and transistor based on transition-metal Dichalcogenide planar heterojunctions. Phys. Rev. APPL.18, 044020 (2022). [Google Scholar]
- 44.Büttiker, M. Four-terminal phase-coherent conductance. Phys. Rev. Lett.57, 1761 (1986). [DOI] [PubMed] [Google Scholar]
- 45.Fujita, T., Jalil, M. & Tan, S. Valley filter in strain engineered graphene. Appl. Phys. Lett.97, 043508 (2010). [Google Scholar]
- 46.Nguyen, V. H., Bournel, A. & Dollfus, P. Spin-polarized current and tunneling magnetoresistance in ferromagnetic gate bilayer graphene structures. J. Appl. Phys.109, 073717 (2011). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.