Abstract
Theoretical predictions of NMR chemical shifts from first principles can greatly facilitate experimental interpretation and structure identification of molecules in gas, solution, and solid-state phases. However, accurate prediction of chemical shifts using the gold-standard coupled cluster with a full treatment of singles and doubles and triplet perturbation (CCSD(T)) method with a complete basis set (CBS) can be prohibitively expensive. By contrast, machine learning (ML) methods offer inexpensive alternatives for chemical shift predictions but are hampered by generalization to molecules outside the original training set. Here we propose several new ideas in machine learning of chemical shift prediction for H, C, N, and O that first introduces a novel feature representation, based on the atomic chemical shielding tensors within a molecular environment using an inexpensive quantum mechanics (QM) method, and training it to predict NMR chemical shieldings of a high-level composite theory that approaches the accuracy of CCSD(T)/CBS. In addition we train the ML model through a new progressive active learning workflow that reduces the total number of expensive high-level composite calculations required while allowing the model to continuously improve on unseen data. Furthermore, the algorithm provides an error estimation, signaling potential unreliability in predictions if the error is large. Finally we introduce a novel approach to keep the rotational invariance of the features using tensor environment vectors (TEVs) that yields a ML model with highest accuracy compared to a similar model using data augmentation. We illustrate the predictive capacity of the resulting inexpensive shift machine learning (iShiftML) models across several benchmarks including unseen molecules in the NS372 data set, gas-phase experimental chemical shifts for small organic molecules, and much larger and more complex natural products in which we can accurately differentiate between subtle diastereomers based on chemical shift assignments.
Graphical Abstract

1. Introduction
Nuclear magnetic resonance (NMR) spectroscopy is a highly accurate experimental technique to probe chemical bonding and subtle environmental differences of atoms in various molecular systems, ranging from small molecules,1-3 natural products,1,4 biopolymers,5,6 to materials.7-9 The NMR chemical shift (CS), which describes the shielding effect offset of a nucleus of interest relative to a defined standard molecule, is one of the most informative data obtained from an NMR measurement, especially for molecular structure,10 identifying the crystal morphology from a selection of candidates,9 distinguishing among synthetic outcomes for natural products,4 and building and refining atomic level models for proteins.11,12 Therefore, accurate CS back-calculators which connect structure to shift perturbations are an indispensable tool in trying to help scientists understand and make good use of NMR chemical shift measurements.
Chemical shifts arise from the electron shielding of a nucleus under an external magnetic field. The shift values can be calculated from first principles13-15 using the second-order magnetic shielding tensor , which describes the response of the induced magnetic field in all directions, but usually only the isotropic component is mapped to an experimental observable.16 Calculation of chemical shifts can be done with exceptional accuracy using coupled-cluster theory with single and double excitation and perturbative-approximated triple excitations [CCSD(T)] together with a complete basis set (CBS) or one that is sufficiently large for convergence.17-19 However, with present-day algorithms and computing resources, such calculations are essentially impractical for any complex systems that contain more than ten heavy atoms (non-hydrogen atoms), due to their large computational scaling. Efforts continue to reduce the cost by approaches such as composite methods,20,21 and nucleus-optimized electronic structure models.22
Alternatively, data-driven approaches have also been quite successful in predicting experimental or calculated chemical shifts at greatly reduced cost. For aqueous proteins, chemical shifts can be predicted from carefully curated features extracted from 3-dimensional geometries of the peptides using machine learning (ML) methods including neural networks and random forests, such as implemented in SPARTA+,23 SHIFTX224 and UCBShift.25 For organic small molecules in crystalline form, kernel ridge regression (KRR)9,26and 3D convolutional networks (CNN)27 have been employed to predict chemical shieldings calculated using gauge-including projector-augmented waves (GIPAW) density functional theory (DFT) methods from merely the molecular structure inputs. Recent work by Guan et al. has trained a 3D graph neural network to predict H and C chemical shifts for neutral organic molecules found in NMRShiftDB28 using quantum mechanics (QM) optimized geometries and DFT calculated chemical shifts, and then transfer learning to predict experimental chemical shifts from force-field optimized geometries.29 These ML models that directly predict chemical shifts from input geometries are orders of magnitude faster than QM calculations, and can usually achieve comparable accuracy to the quantum mechanical method they have been trained on. However, this has typically relied upon DFT that can calculate chemical shieldings at a much more acceptable cost, but also can often suffer from insufficient accuracy.30-32 In addition, machine learning methods are not expected to generalize to a different molecular system, unlike QM methods that are still much more generalizable and rigorous in terms of predicting chemical shieldings for a specific input geometry.
The question arises whether a machine learning method can be used to “amend” a low-level QM prediction to high accuracy, hence achieving generalizability and speed at the same time. An intuitive way is to use machine learning to predict the difference between a high-level and low-level calculation, using molecular geometries as input. Such -machine learning idea are exemplified in the work of Unzueta, et al. that predicts a correction to a cheap DFT calculation using small basis set and arrives at the target accuracy of the same DFT method with a large basis set.33 Very recently, Büning and Grimme have shown that a similar approach can correct DFT predictions of chemical shieldings to CCSD(T) quality, signifying an important step in predicting CS at the highest level of theory achievable from theoretical calculations.34
But what is true about many such ML approaches is that they can be poor in predicting out-of-distribution cases, i.e. outside the specifics of the training data.35 Ideally, through effective feature engineering, one can achieve an enriched chemical representation that extends beyond mere molecular configurations.25,35 Such information, preferably sourced from cheap calculations, becomes invaluable not just for achieving high-level accuracy but also for ensuring model transferability. This concept has been effectively demonstrated in predicting correlation energies at MP2 and CCSD levels using molecular orbital features derived from the mean-field Hartree-Fock (HF) level.36
In this work, we present an innovative feature representation obtained from a low-level DFT chemical shielding calculation of the diamagnetic (DIA) and paramagnetic (PARA) shielding tensor elements, and combine it with geometric-dependent features that are used as input into a neural network (NN) model to predict chemical shieldings with training data generated with a composite QM method with nearly equivalent CCSD(T)/CBS accuracy.21 In addition we introduce a novel active learning (AL) training procedure that selects out-of-distribution training data with an increasing number of heavy atoms (HA) from a full set of off-equilibrium geometries obtained from the ANI-1 dataset.37 The resulting model achieves similar level of accuracy as a high-level CCSD(T) calculation with large basis set, but requires computational cost at only a low-level DFT calculation with a tiny basis set. Given that the feature generation and NN model inference almost comes free when compared with the QM calculations, our inexpensive shift machine learning (iShiftML) model can achieve 35 times speedup for 2HA systems and 700 times speedup for 8HA systems when compared with the high level CCSD(T) method according to Ref. 21 To analyze the transferability of our physics-informed ML model to other systems, we find that error estimations in terms of the standard deviation among a committee of ML models are a good indicator for the actual error without knowing the target values, signaling when the model is not trustworthy for applications outside the original training set. We also compare an invariant multi-layer perceptron (MLP) architecture that maintains rotational invariance of the features through data augmentation with an equivariant architecture based on tensor environment vectors (TEVs).
The physically motivated tensor features of the resulting iShiftML model trained with data up to 7 heavy atoms (7HA) from the ANI-1 data set37 achieves both higher accuracy and better transferability across a range of benchmarks that are independent of the training set. We find exceptional predictive performance when evaluated on the 8HA test data, achieving prediction errors of 0.11 ppm for H, 1.34 ppm for C, 3.05 ppm for N, and 6.03 for O between predicted chemical shieldings and the target CCSD(T) composite method values. A similar level of accuracy was also achieved when the model is evaluated on the extended theoretical benchmark nuclear shielding NS372 dataset, and surpasses the performance of the recent -machine learning model.34 The iShiftML model when compared against experimental gas phase CS measurements for molecules that are not included in the training set reduces the error of the low-level DFT calculation by at least two-thirds. Finally, we have used our method to predict experimental CSs for natural products that are vastly larger and more chemically complex than any molecule from our training set, illustrated with strychnine and vannusal, in which we show that diastereomers of the vannusal B molecule can be easily differentiated by inspecting the errors between predicted CS and experimental measurements.
2. Methods and Models
2.1. Feature Selection for Machine Learning of Chemical Shifts
The magnetic shielding tensor is defined as the total second derivative of the energy with respect to nuclear spin at nucleus and the external magnetic field , with components defined as
| (1) |
Here “d” means total derivative and , correspond to Cartesian indices. For a variationally optimized wavefunction with parameters, (even the exact wavefunction), the total derivative has two partial derivative contributions:
| (2) |
Given that the chemical shielding tensor and each of its components, , can also be decomposed into diamagnetic (DIA) and paramagnetic (PARA) components within the DFT gauge-including atomic orbitals (GIAO) approach,38,39
| (3) |
It comes naturally that the isotropic chemical shieldings at the same level of theory can be calculated as
| (4) |
in which the off-diagonal elements have a contribution of zero to the final isotropic chemical shielding formula. However, the full tensor still encodes useful information about the local atomic environments for each nucleus and might be helpful with predicting chemical shieldings at a higher level of accuracy. Hence we formulate the NMR shielding DIA and PARA tensors as a feature set for the machine learning approach described further below.
In addition, we use Atomic Environment Vectors (AEVs) as geometric descriptors that are used to describe the atomic environments at each nucleus, following previous studies.33,37 AEVs are reformulations of the atomic symmetry functions used by Behler and Parinello in their neural networks for predicting molecular energies,40 which contain orientation-independent angular and radius terms that are determined by local geometries of nearby atoms categorized by atom type within a cutoff. The 384-dimensional AEV for an atom constitutes a radial part (the first 64 elements) and an angular part (the remaining 320 elements). The radial elements for atom are calculated as
| (5) |
where denotes a specific atom type of H, C, N, O for the second atom, and is a distance index that defines the different reference distances from the center atom. The summation is done over all neighbor atoms with type near the central atom within a cutoff, and is the distance between atoms and . The reference distances are defined as where is the Bohr radius and ranges from 0 to 15. was used to adjust the width of each Gaussian so that it matches with the separation between two consecutive reference distances. Finally, is a cutoff function that smoothly modulates the Gaussian term around the cutoff radius, with the following formula and cutoff radius :
| (6) |
We have used 16 distance indices for each atom type and hence 64 radial AEV values.
Similarly, the angular components of an AEV vector are defined as
| (7) |
| (8) |
with , defining the two different atom types for nearby atoms, and thus 4+3+2+1 = 10 different atom type combinations are possible. and are the angle and distance indices that define the reference angles and positions by with from 0~7, , and denotes the angle centered at atom , and . We used the same mathematical form of the distance cutoff function, but with a radial cutoff value of . The 10 atom type combinations, 8 reference angles, and 4 reference distances altogether defines 320 different angular components of the AEV vector. The calculated AEVs were obtained from precompiled C++ code from Ref. 33.
2.2. NMR Shielding Calculations and Stability Analysis
Recently Liang et al. presented a systematic investigation on using locally dense basis sets (LDBS) and composite QM methods for chemical shielding calculations, which have been categorized into low-level, middle-level and high-level effectiveness based on a balance of accuracy and computational cost.21 We selected the B97X-V functional41 in conjunction with the pcSseg-1 basis set42 as our low-level method. The B97X-V functional offers robust and transferable performance for various properties prediction,43-50 particularly the dipole moment,45 a simple but effective measure of electron density in polar molecules. We opted for this functional over the low-level methods recommended in Ref. 21, which provide more accurate shielding predictions, due to error cancellation. Thus, we believe it is more advantageous to use B97X-V as input for predicting high-level results. The advantage of using B97X-V for the low-level input was also validated by its better in-distribution and out-of-distribution prediction error when comparing models trained with different low-level methods as input, which are described in Supplementary Table S1. The ORCA 5.0.3 software51 was utilized for these calculations, and local exchange-correlation integrals were computed over DefGrid3, a default ORCA grid, for all atoms. GIAOs39 were used in all shielding calculations, including subsequent high-level computations.
We directly adopted the high-level method suggested in Ref. 21, namely CCSD(T)/pcSseg-1 with a basis set correction between pcSseg-1 and pcsSeg-3 calculated from the resolution of identity Møller-Plesset second-order perturbation theory (RIMP2), abbreviated with CCSD(T)(1)RIMP2(3). This high-level method can achieve impressively low root mean square errors (RMSEs) (0.048 ppm for H, 0.47 ppm for C, 3.58 ppm for N, and 4.68 ppm for O) in comparison to the theoretical best estimates, CCSD(T)/pcSseg-3, on the NS372 dataset. The CFOUR program package, version 2.1, was utilized for CCSD(T) computations,52-54 while ORCA was used for RIMP2 calculations. In RIMP2 calculations, the def2-JK55 auxiliary basis set was employed for the Coulomb and exchange part, whereas the cw5C56 auxiliary basis set was used for auxiliary correlation fitting to expedite the computation.
As our training set encompasses many conformations far from equilibrium and quantum mechanical (QM) calculations are likely to fail, we employed the stability analysis57 at HF/pcSseg-1 level to exclude all conformations that might exhibit any instabilities.
2.3. Dataset Preparation
The ANI-1 dataset,37 which contains over 20 million off-equilibrium geometries of small organic molecules up to 8HA obtained through normal mode sampling, together with the equilibrium structures of these 57,462 molecules, was used to define the most inclusive dataset (DS-ANI-1) used in this work. However, it is very challenging to perform chemical shielding calculations for all the data in DS-ANI-1, even at a low-level DFT, and is not accessible for the CCSD(T) calculations that are orders of magnitude more time-consuming than DFT calculations.
To reduce the size of the dataset while keeping the diversity of the conformations of the molecules, a “farthest sampling” algorithm was developed that down-samples off-equilibrium geometries for each molecule in the ANI-1 dataset. The root-mean-square-deviations (RMSDs) for molecules after the optimal alignment using the Quarternions method58 was used to evaluate conformation dis-similarities between geometries of the same molecule. A conformation collection pool was defined with the first conformation of a molecule being the first element. In each iteration, the aligned RMSDs for all geometries in ANI-1 dataset but not in the collected pool were calculated towards all conformations in the collected pool, and the geometry with the highest RMSD was added to the collected pool.
The total number of collected conformations depends on the number of heavy atoms (HA) in the molecule. For molecules up to 4HA, 200 most dissimilar conformations were collected into the pool. For molecules with 5, 6, and 7 heavy atoms, the number of non-equilibrium conformations collected for each molecule were 100, 50, and 5 respectively. The equilibrium geometries for molecules with 5-7HA were always included in the dataset. A stability analysis was performed to further exclude systems for which the NMR shielding calculations are likely to fail or be erroneous. This collection of a sub-sampled dataset (DS-SS) is our primary data for model training and development of the active learning workflow of the iShiftML model, which contains 12,677 geometries for molecules up to 4HA, 13,313 geometries for molecules with 5HA, 31,462 geometries for molecules with 6HA and 37,105 geometries with 7HA.
Using the geometries of all these data, we calculated the DIA and PARA matrix elements under the low-level composite DFT method B97X-V/pcSseg-1 DFT.21 For the dataset with 5-7HA, 1500 geometries were selected from active learning to perform the high-level composite method.21 The active learning dataset covering all data using the high-level target values are subsequently labeled DS-AL-N, where N ranges from 4-7, which represents the maximum number of heavy atoms included in the dataset. Finally, 40 randomly selected molecules with 8HA were collected from DS-ANI-1. The equilibrium geometries and a random non-equilibrium geometry for each of the 40 molecules were used to define our test set. Our full training and testing dataset is provided in the Supplementary Information.
2.4. iShiftML Ensemble Model and Training Details
We have employed an ensemble machine learning approach by randomly splitting the training and validation data into 5 even portions, and 5 separate ML models were trained, each model using a different portion as validation data and the rest as training data. In addition, the network parameters for these five models were also initialized with different random numbers. After all models have been trained, they are combined into an ensemble model. When making predictions, each model in the ensemble predicts a value, and the final prediction is given by their average.
Because outliers resulting from failed predictions may contaminate the average, any outliers should be identified and excluded from the calculation. To estimate outliers, we used the local outlier factor (LOF) algorithm implemented in the scikit-learn package to detect outliers.59 The algorithm relies on a local neighbor density estimation to identify outliers as data points that have a significantly lower density of neigbors than the rest of the data points. Finally, the average and standard deviation among the non-outlier predictions were calculated.
All five ML models are trained by minimizing the mean squared error between the predicted isotropic chemical shieldings and the calculated high-level targets, under the following loss function:
| (9) |
where represents the networks parameterized by , are the input features, and are the target values. Weight decay of 3 × 10−5 and dropout with probability 0.160 were used after each linear layer to reduce overfitting to the training data. Starting from a learning rate of 1×10−3, a stepwise learning rate decay schedule was used that monitors evaluation performance on the validation dataset, and reduces learning rate by 30% if the validation error did not decrease after 20 epoch since last error reduction on the validation dataset, unless the learning rate is already smaller than 1×10−6. The neural network was implemented in pytorch61 and optimized using the Adam optimizer62 with a batch size of 128 and was trained for 750 epochs.
3. Results
3.1. Interpretability and transferability
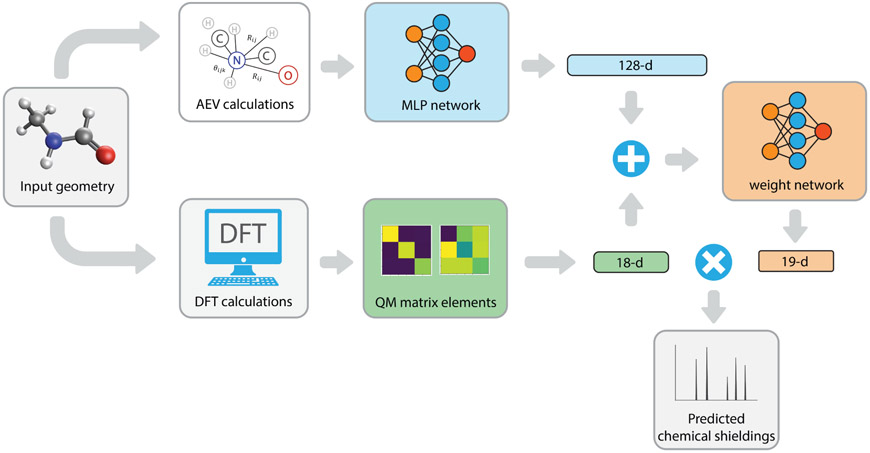
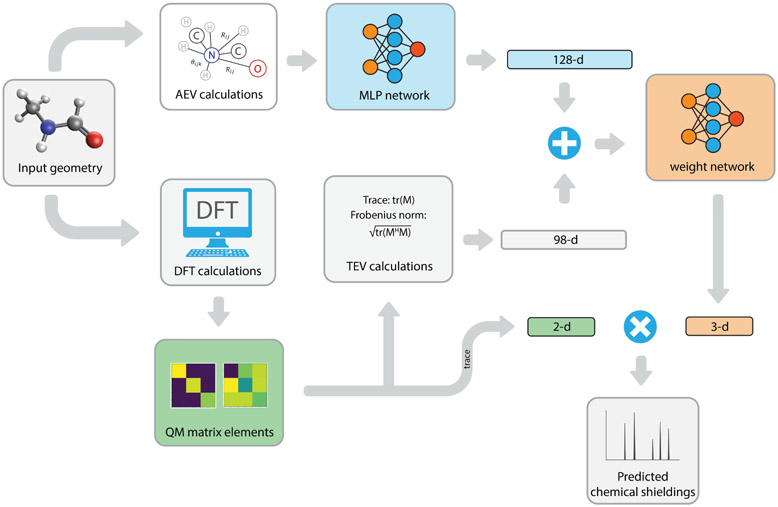
We begin with the overall layout and the analysis of the MLP version of the iShiftML model, with an emphasis on the connection between the model architecture and the chemical shielding formula. We then explain the benefits of ensemble training, and a new active learning protocol and emphasize the ability of the model to generalize, predict error confidence, and to construct affordable datasets for chemical shift prediction. A schematic of the original MLP iShiftML model architecture is depicted in Figure 1. For a given input geometry, the atomic environment vectors together with the paramagnetic and diamagnetic elements of the shielding tensor are calculated with the lower-level B97X-V/pcSseg-1 method and are used as neural network inputs that are trained to predict chemical shieldings of the high-level CCSD(T)(1)RIMP2(3) composite method for the four atom types: hydrogen, carbon, nitrogen, and oxygen.
Figure 1: The iShiftML ensemble learning model that uses low-level QM calculations of the shielding tensor and AEVs to predict high-level chemical shieldings.
Given a molecular geometry, the AEV around each nucleus is prepared and sent into a MLP network with two layers, each of which contains 128 neurons, in which the ReLU activation function63 is used for the first layer to encode the AEVs into a 128-dimension internal representation. On the second branch, we perform low-level composite QM calculations to obtain the 18 DIA and PARA chemical shielding values that are concatenated with the AEVs from the first branch to provide input for the second MLP weight network. The weight MLP is composed of a first layer containing 64 neurons and uses ReLU activation, followed by a second layer of 19 neurons (including a bias term) without an activation function.
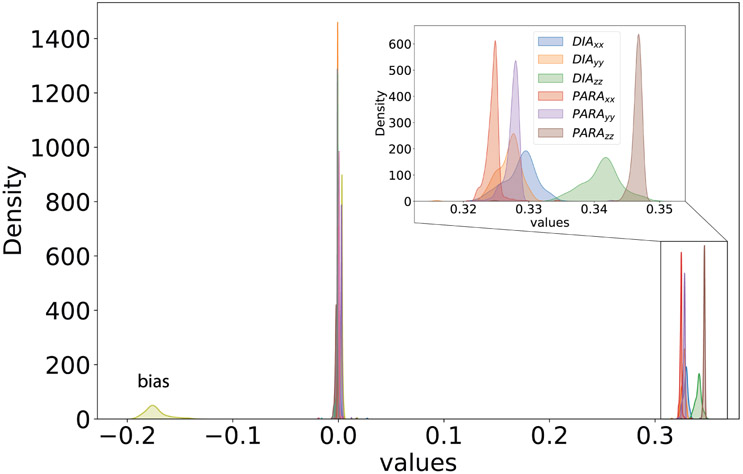
Figure 2 illustrates the distribution of the learnable weights of the 18 DIA and PARA values from the network in the MLP model. This distribution is based on the hydrogen atom of the test set, obtained after the training process converges. Intriguingly, even without explicit enforcement, the diagonal elements from the DIA and PARA matrices exhibit weights close to , while the off-diagonal elements are distributed around 0. This behavior aligns well with Eq. 4. The model also incorporates a bias term of −0.17 to rectify the systematic error found in low-level chemical shieldings. This result proves that the model captures the physical connection between the isotropic chemical shieldings and the intermediate matrix elements, and should be generalizable to new predictions even outside of the training set, as long as the low-level QM matrix elements are reasonably accurate.
Figure 2: Distributions of weights of the original model without considering rotational invariance for hydrogen atom evaluated on test data.
Distributions of the weights for diagonal elements in the DIA and PARA matrices are centered close to 1/3, off-diagonal elements are centered around 0, and the bias term is distributed around −0.17.
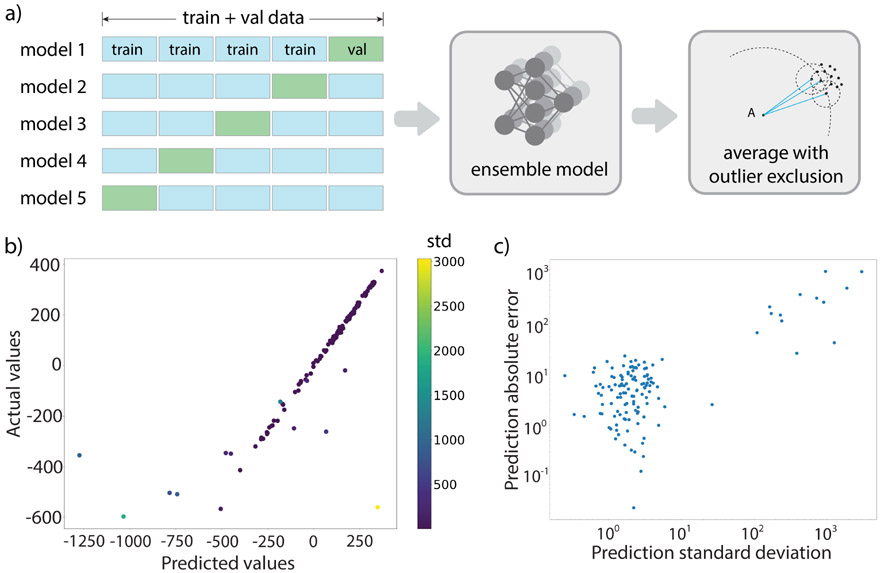
We have also employed an ensemble prediction technique to improve the accuracy compared to any individual training of the iShiftML model (Figure 3a). Table 1 shows the performance comparisons for individual models and the ensemble average for the original model trained on DS-AL-4 for oxygen. We see that while an individual model may make large errors, such as in models 3 and 5, the ensemble average model can mitigate these erroneous predictions, and still reach a consensus prediction that has a lower RMSE and standard deviation than any individual model.
Figure 3: Ensemble prediction and correlation with actual prediction error.
(a) An ensemble learning approach using 5-fold cross-validation to train individual models in the ensemble. The final prediction is the average prediction from the models after excluding outliers recognized by the Local Outlier Factor algorithm.59 (b) An undertrained model for oxygen tested on the 8-heavy-atom test set, showing the correlation between predicted and actual values. Data points are colored according to their standard deviation (STD), with warm colors representing high STDs and cool colors representing low STDs. (c) Prediction errors compared to reference values are found to be well correlated with standard deviations of the predictions in the ensemble on a log-log plot. See Methods for further details.
Table 1:
Root mean square errors (RMSE) and standard deviations of prediction errors from individual models and from the ensemble model for oxygen prediction when trained using DS-AL-4. Data with high standard deviations among ensemble models (std>30) has been excluded to make the trend more concise. All units in ppm. See Methods for further detail.
| RMSE | standard deviation | |
|---|---|---|
| Model 1 | 8.30 | 5.23 |
| Model 2 | 8.65 | 6.18 |
| Model 3 | 16.76 | 15.01 |
| Model 4 | 8.86 | 5.73 |
| Model 5 | 23.34 | 21.72 |
| Ensemble model | 7.60 | 4.82 |
But just as importantly the ensemble model can provide standard deviations that can be used to estimate actual prediction errors even without knowing the actual ground truth for the chemical shift value. Figure 3b shows an undertrained model using DS-AL-4 evaluated on 8HA test data, and compares the predicted and target chemical shielding values with data points colored by the standard deviations from the ensemble. We find that all data points with large standard deviations correlate with high predicted errors. Figure 3c further illustrates the correlation between the prediction standard deviation and the absolute error from the ensemble prediction, showing that large standard deviations can signal when the model is not trustworthy.
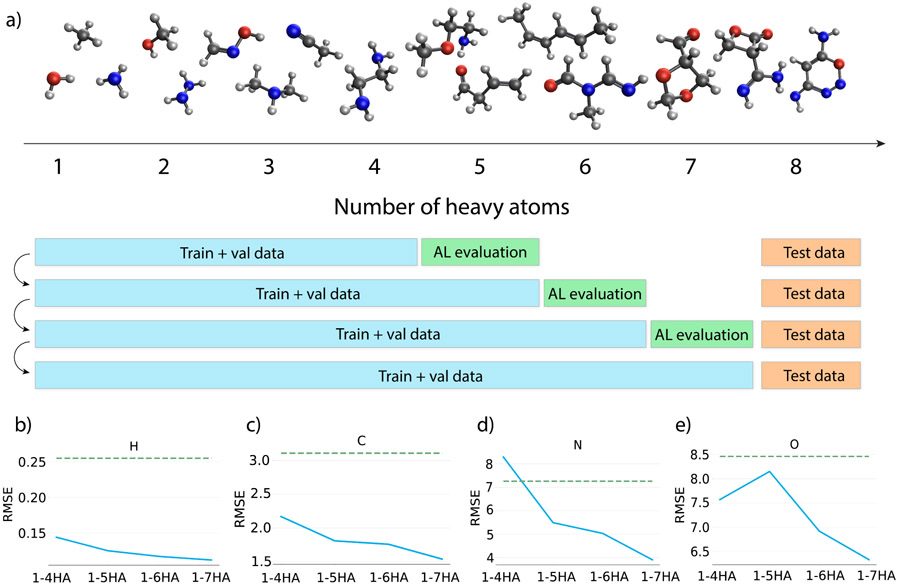
Finally, the ability to identify out-of-distribution data not effectively covered by existing training data through ensemble learning has inspired a novel active learning technique to select only the most important training data to calculate time-consuming high-level chemical shieldings while still improving model performance. In particular, given that the high-level QM calculation scales as with system size, it is best to generate as much training data with a smaller number of heavy atoms as possible in order to reduce the number of calculations needed for molecules with more heavy atoms (Figure 4a).
Figure 4: Procedure and results of the active learning workflow.
a) The active learning (AL) workflow. Starting from a model trained with data up to 4 heavy atoms (HA), data with 5HA are evaluated using the trained model, and 1500 structures with the largest predicted standard deviations from the 5HA dataset were included to define the training set for the next iteration until the training set contains molecules up to 7HA. The 8HA dataset was always used as the test set. b-e) RMSE on the 8HA test set for models trained with AL on training sets containing molecules with different sizes (blue curve), and also a baseline model that is trained using linear regression (green dotted line). Figures are for hydrogens (b), carbons (c), nitrogens (d) and oxygens (e). (b-e) are also provided in tabular form in Supplementary Table S2. Note that the RMSEs are calculated with uncertain predictions excluded, which removes any prediction with an ensemble standard deviation larger than 0.5 ppm for H, 2.5 ppm for C, 5 ppm for N, or 10 ppm for O.
In this case, we start by training a model with all subsampled data with up to 4HA (DS-AL-4) to allow sufficient initial coverage of the chemical space, which provides a good starting point for the AL workflow. For simplicity, the “original” model was used. After training converges with DS-AL-4, the model was used to predict chemical shieldings on the 5HA data using the low-level QM features. Large standard deviations from the ensemble prediction were utilized to select 1500 structures to generate the next batch of high-level target chemical shieldings which are then added to the training set to define the next DS-AL-5 dataset. This process continues until we have included high-level calculations for molecules up to 7HA in the training set.
After each AL iteration, the model performance was evaluated on the test set composed of randomly selected molecules with 8HA to show the effectiveness of the AL approach. Test errors in terms of RMSE for the four atom types are visualized in Figure 4b-e, showing that the errors decrease as larger molecules are added to the training set. To make the trend clearer, predictions with large standard deviations (STD) predicted from the ensemble are excluded. Retained data has STD for hydrogen less than 0.5 ppm, STD for carbon less than 2.5 ppm, STD for nitrogen less than 5 ppm, and STD for oxygen less than 10 ppm. As a reference, a linear regression (LR) model that uses QM features in DS-AL-7 was also trained, which acts as a baseline equivalent to a model that has fixed coefficients on the DIA and PARA terms instead of atomic environment dependent weights.
Figure 4b-e shows that even the model trained with DS-AL-4 surpasses the LR reference performance in all atom types other than nitrogen. With more training data included, even though every new training set only has ~10% more data (1500 more molecules) than the dataset with one less heavy atom, the model performance continues to systematically improve on the 8HA test set. After the model has been trained with DS-AL-7, the RMSE between predicted and actual high-level QM chemical shieldings are 0.11 ppm for hydrogen, 1.60 ppm for carbon, 4.02 ppm for nitrogen, and 6.32 ppm for oxygen.
3.2. Increasing accuracy through equivariance
One drawback of directly using the shielding tensor matrix elements as model features is their reliance on the external frame. The isotropic chemical shieldings are invariant under a rotation of the molecular geometry, but the DIA () and PARA () matrix elements will change after rotation. Consider a rotation characterized by the rotation matrix , in which the diamagnetic and paramagnetic tensors of atom ( and ) transform as
| (10) |
where and denote the transformed tensors. This transformation implies that the and matrices lack rotational invariance. To address this issue, one strategy is to utilize data augmentation by rotating the molecule by a random angle for each input batch. When rotational invariance is applied through data augmentation, the weights become more closely centered around the values of and 0, as seen in Supplementary Figure S1. As expected, the diagonal elements in the DIA matrix (and similarly PARA matrix), which theoretically should bear the same weight of , do exhibit highly similar weight distributions in the converged model. The closer weight distributions around the theoretical values indicate the augmented data model is able to better capture underlying physics.
An alternative approach is to embed and into a rotationally invariant vector, like an AEV, that we refer to as the tensor environment vector (TEV). Inspired by the radius and angular terms of AEV, we design the magnitude and direction terms of the TEVs. The magnitude elements for atom are calculated as
| (11) |
where represents the isotropic diamagnetic value (i.e., one-third of trace ), the isotropic paramagnetic value (i.e., one-third of trace), or the final isotropic value (i.e., the sum of the former two values). We concatenate the embedded vectors of these three values together to form the magnitude part of TEV. is a magnitude index that defines the different reference magnitudes to equally cover all the possible values (shown in Supplementary Table S3). The corresponding is calculated by and , where , , and are the maximum, minimum, and number of reference magnitude values. This magnitude part is rotationally invariant since is a rotationally invariant scalar.
The direction elements for atom are defined as
| (12) |
where represents the and matrices normalized by their Frobenius norms. Because these tensors are not symmetric, and define the two different atom types for nearby atoms, leading to 4 × 4 = 16 different atom type combinations. Here and represent the unit vectors along the direction from atom to atom and , respectively. The rotational invariance of this part can be shown as
| (13) |
due to the orthogonality of rotation matrix . Figure 5 shows the equivariant model. As shown in Supplementary Figure S2, the TEV model variant displays a slightly different behavior than that of the invariant model with and without data augmentation (Figures 2 and S1). With a bias term that optimizes to near 0, the TEV model corrects the systematic overestimation of low-level shieldings by employing weights smaller than 1, especially for the PARA tensor. While it’s challenging to definitively state which ML model behavior aligns better with physical reality, we next consider which model is more accurate.
Figure 5: Architecture of the TEV variant of the iShift ML model.
As an alternative to the model in Figure 1, in the second branch the DIA and PARA chemical shielding tensors are embedded into a 98-dimension TEV vector that is concatenated with the AEVs from the first branch to provide input for the second MLP weight network. The weight MLP is composed of a first layer containing 64 neurons and uses ReLU activation, followed by a second layer of 3 neurons (including a bias term) without an activation function. In total, the TEV of one atom comprises 98 elements, including 16 reference magnitude indices each for isotropic diamagnetic and paramagnetic values, 32 indices for the final isotropic value, and 16 direction elements each for the diamagnetic and paramagnetic tensors. This combination ensures both magnitude and direction while maintaining rotational invariance.
After the DS-AL dataset is fully prepared using the active learning obtained from the original model, both the data augmentation model and the TEV model ensembles are retrained using DS-AL-7, and their evaluation performance on the 8-heavy-atom test set is compared with the original models in Table 2. The number of excluded uncertain predictions is less than 1%, and is listed in Supplementary Table S4. We see the TEV model achieves the best performance among all models, with an RMSE of 0.11 ppm for H, 1.34 ppm for C, 3.05 ppm for N, and 6.03 ppm for O. Based on the retrained model performances, the TEV model is selected for further studies due to its higher accuracy.
Table 2:
Root mean square errors (RMSE) for the original model, model trained with data augmentation by rotating input geometries, and the rotational invariant tensor environment vector (TEV) model trained with DS-AL-7 and evaluated on the 8-heavy-atom test set. Uncertain predictions with standard deviations (STD) greater than 0.5 ppm for H, 2.5 ppm for C, 5 ppm for N, and 10 ppm for O were excluded.
| H | C | N | O | |
|---|---|---|---|---|
| Original model | 0.11 | 1.60 | 4.02 | 6.32 |
| Data augmentation model | 0.11 | 1.39 | 4.06 | 6.77 |
| TEV model | 0.11 | 1.34 | 3.05 | 6.03 |
3.3. Predicting chemical shieldings for molecules in the NS372 dataset
The NS372 benchmark dataset was developed by Schattenberg et al. which contains in total 372 chemical shieldings from 117 small molecules with light main group elements, calculated at the CCSD(T)/pcSseg-3 level of theory.19 The NS372 dataset provides a standardized evaluation for theoretical chemical shielding predictions using different methods. We have taken a subset of the NS372 that is composed of only H, C, N, and O atoms and without atomic charges, which results in 34 molecules containing 49 shieldings for hydrogens, 44 shieldings for carbons, 16 shieldings for nitrogens, and 16 shieldings for oxygen, respectively. To prevent data leakage, molecules in this NS372 subset were excluded from DS-AL-7 and the models were retrained with the same hyperparameters.
Table 3 compares the RMSE between the low-level DFT method, our iShiftML method, and the recent work by Büning and Grimme.34 The exact prediction values for each nucleus are provided in Supplementary Table S5. Even though the NS372 benchmark includes some molecular configurations not present in our training set, such as carbon monoxide (CO) and allene (CH2CCH2), the overall performance of the iShiftML method on the NS372 dataset is similar to its performance on the 8HA test set, with slightly higher RMSE on carbons and lower RMSE on nitrogens. Compared to the low-level DFT method used for the ML input, the error reduction ranges from 72% to 87% depending on the atom type. The result indicates our iShiftML method can generalize to different types of molecules than what the model has been trained on with reasonable accuracy. Furthermore, by comparing to the same set of molecules that were also predicted by the -machine learning method in Ref. 34, our method also demonstrates around 10% improvement on both hydrogen and carbon nuclei even though our low-level method employs a smaller basis set than that of Ref. 34.
Table 3:
Performance comparison in terms of RMSE for the low-level DFT method, iShiftML model and Ref. 34 evaluated on the NS372 subset19 containing H, C, N, O atoms and no atomic charges.
3.4. Application to predicting experimental gas phase chemical shifts
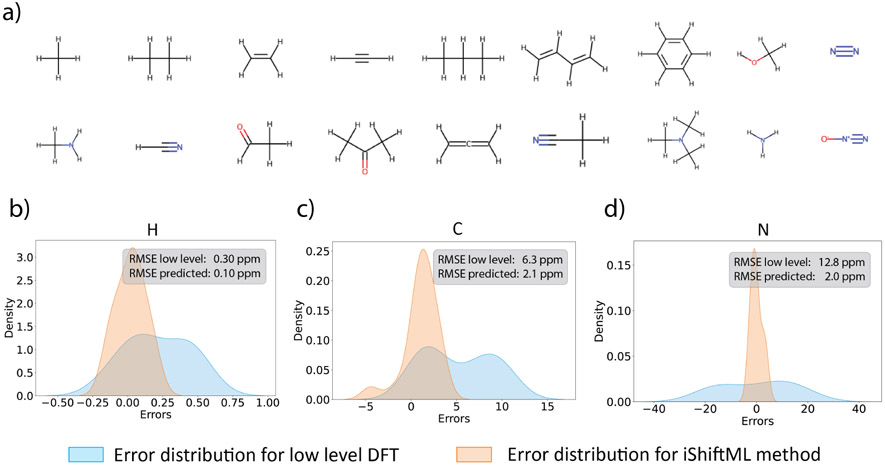
The iShiftML model can predict NMR chemical shieldings at a high-level CCSD(T) composite method accuracy using only a tiny fraction of the calculation time of a low-level DFT calculation, which enables us to explore new possibilities of experimental CS prediction as well. We first show that experimental gas phase CS for molecules not included in the training set can be accurately predicted and error is significantly reduced compared to the low-level DFT that provides the QM matrix elements. Gas phase chemical shifts were used to minimize the effect of environmental complexities, including any influence of solvent and perturbations to chemical shifts due to other molecules nearby.
Figure 6a shows a set of 18 molecules that were collected from the literature for their experimental gas phase CS values,66-68 and the geometries of the molecules were taken from NS37264 and NIST database.65 Because some of these molecules were already in the DS-AL-7 data set, the iShiftML models were retrained after excluding all molecules in Figure 6a that are to be tested. Chemical shifts were calculated with two techniques. For H and C, the reference chemical shieldings for the respective nuclei in the standard substance tetramethylsilane (TMS) were calculated at the low-level B97X-V/pcSseg-1 and high-level CCSD(T)(1)RIMP2(3), and chemical shifts were calculated using , where is the isotropic chemical shielding for TMS, and is the isotropic chemical shielding for the target nucleus. Reference chemical shieldings are 31.766 ppm and 189.588 ppm using the low-level theory for hydrogen and carbon, respectively, while the references were 31.522 ppm and 193.972 ppm using the high-level theory. Due to the lack of a standard substance for nitrogen, a linear model was fit between the predicted chemical shieldings and experimental chemical shifts using a fixed slope of −1 such that only the intercept was fitted. The resulting intercept is −146.224 ppm and −130.297 ppm for the low-level and high-level theories, respectively. Oxygen nuclei were not assessed due to the lack of experimental gas phase chemical shifts for this test set. We note that by comparing to CS instead of chemical shieldings, error cancellation might be possible. However it is not a concern for users that need predictions on CS instead of chemical shieldings.
Figure 6: Predicting experimental gas phase chemical shifts for small organic molecules.
(a) the small molecules under investigation. 3D geometries of these molecules are taken from NS37264 and NIST database.65 (b-d) Distributions of errors between predicted and experimental gas phase NMR chemical shifts for low-level DFT calculations (B97X-V/pcSseg-1, blue distributions) and iShiftML predictions for the high-level CCSD(T) composite method (orange distributions) for hydrogens (b), carbons (c), and nitrogens (d). Also see Figure S3 and Table S6.
When compared directly to experimental measurements, we find that iShiftML can predict CS for hydrogen nuclei with RMSE of 0.10 ppm, 2.1 ppm for carbon, and 2.0 ppm for nitrogen. By comparison, the low-level DFT calculations give an RMSE of 0.30 ppm for hydrogen, 6.3 ppm for carbon, and 12.8 ppm for nitrogen indicating that with an inexpensive method, we have significantly reduced error by 3-6 fold. Figures 6b-d show the error distributions for the low-level calculated chemical shifts and high-level predicted chemical shifts, both compared with experimental CS for different nuclei. We see that the low-level CS has a systematic offset for the hydrogen and carbon nuclei, resulting in error distributions shifting towards positive values. This systematic trend was corrected in the predicted high-level CS, whose errors are centered around zero with a much sharper distribution, in line with its overall superior performance compared to the low-level DFT calculations. The standard deviations from the predictions are also small, indicating the model can confidently predict the chemical shifts for this set of molecules not included in the training set.
3.5. Application to natural product chemical shifts prediction
Finally, we consider a more challenging application of iShiftML to highlight the transferability of the model. Synthetic chemists often rely on NMR CS as an essential tool to validate the structural correctness of synthesized molecules, especially for natural products.15 In turn, automated methods such as DP469 and DP4+70 and corresponding ML advances such as DP4-AI71 for computing NMR spectra reliably enough to confirm the chemical composition and stereochemistry of natural products are a critically important counterpart to the experimental data.70,72-74 Here we demonstrate that iShiftML can also improve the accuracy of predicted CS for a given molecular structure when compared with experimental measurements.
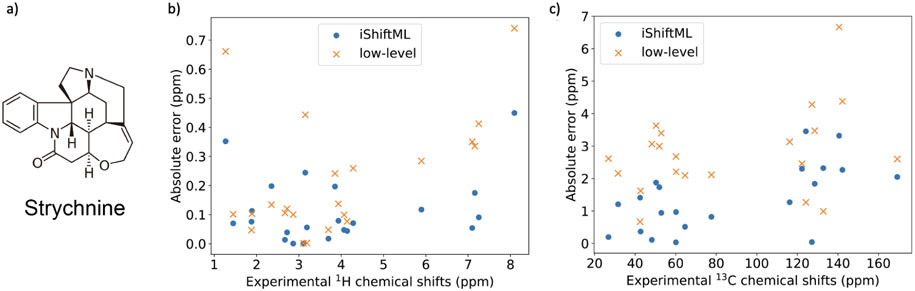
We have used strychnine73,75-78 as a starting example since it is a relatively rigid molecule (Figure 7a) so that conformational averaging will not play a major role in predicting its chemical shifts accurately. Figure 7b and c shows the absolute errors between experimental and calculated CSs using both the low-level DFT and high-level predictions from the iShiftML model for hydrogens and carbons, and the correlation plots are provided in Figure S4. Due to potential limitations from theory, referencing issues, or discrepancies in solvents and experimental conditions,79 former comparisons were typically made with predictions of CS that were fit to experiment measurements through linear regression.77 To minimize scaling compensation of systematic error from theory, we have only fit the intercept while keeping the slope at 1 when comparing with experimental CS of natural products. All iShiftML predictions were made with small standard deviations and hence no outliers were found.
Figure 7: Results on predicting and comparing CS for strychnine.
a) Molecular structure of strychnine. b) Absolute prediction error for the low-level DFT method and iShiftML across the experimental CS range for hydrogens. c) Absolute prediction error for the low-level DFT method and iShiftML across the experimental CS range for carbons. All predicted CS are re-referenced to have the same mean values as experimental measurements.
The RMSEs between the experiment and calculated CS of low-level DFT and high-level iShiftML predictions, along with four other DFT methods reported in Ref. 77 after re-referencing are also provided in Table 4. We find that iShiftML has significantly improved over the low-level B97X-V/pcsSeg-1 DFT calculation that provides input for our model, and is as good or better than other DFT methods that use a much larger basis set. Hence even though strychnine is significantly larger and its fused ring system is not covered by our training set, we still realize significant improvements over much more expensive methods, with errors that remain commensurate with the errors of the 8HA test set for high-level CCSD(T) calculations. This demonstrates the reliability and generalizability of the iShiftML model.
Table 4:
RMSEs between predicted and measured CS in strychnine using different methods. The 3-dimensional geometry of the strychnine molecule and the experimental measurements of CS are taken from Ref. 77. Predicted CS are re-referenced to have the same mean values as experimental measurements. However, the slopes are fixed at unity.
Finally, we consider a more challenging natural product synthesis application to identify the correct molecular structure of vannusal B (5-2 in Figure 8a), whose structural assignment had been uncertain due to the errors in back-calculations and comparison to the experiment of a set of highly similar diastereomers of the natural product itself (Figure 8a).80,81 Here we have uses iShiftML to investigate the match between experimental and calculated CS for carbon atoms and compare our results with the M06/pcS-2 DFT method reported in Ref.82. However, we did not rescale predicted CS values as was done in Ref. 82, so that our reported errors reflect true prediction errors on various atoms in the molecule. Additionally, hybridized carbons (C1, C2, C11, C12, C21, C31) were retained in our analysis, unlike the original study, as the iShiftML model should provide accurate predictions (or indicate if it is an outlier) without any prior system knowledge.
Figure 8: Predictive analysis and comparison of chemical shifts for the 8 diastereomers of vannusal B.
a) Molecular structures of the 8 diastereomers of vannusal B. Reproduced from reference [ 82] Copyright 2011 American Chemical Society. b) The prediction RMSE margins for various vannusal B isomers. The bottom position in each bar represents comparison with the true experimental CS, while the top indicates a comparison to vannusal B CS in its native form, 5-2. Predictions were made using iShiftML, low-level DFT, and M06/pcS-2 (the latter from Ref. 82). Large bars with a low bottom therefore indicate good discrimination between predicted CS for the true structure against potential misidentification with CS of the native structure. All predicted CS are re-referenced to have the same mean values as experimental measurements. Also see Figure S5.
Figure 8b provides the RMSEs between predicted and experimental CSs for vannusal B (5-2) and the same for the structures of the other diastereomers (2-1, 2-2, 3-1, 3-2, 4-1, 4-2, and 5-1). We find that iShiftML consistently predicts lower RMSE across all molecules compared with the low-level DFT method or M06/pcS-2 from Ref. 82 (i.e. the bottom of the blue bars for iShiftML are well below the bottom of the orange and green bars). Furthermore, in Figure 8b the bottom of each bar provides the RMSE between the experimental chemical shifts that match the true structure of each diastereomer, while the top position of the RMSE bar shows the error made if the experimental CS for natural product structure 5-2 involved an (erroneous) assignment to the diastereomer structure of interest. On average, iShiftML has a larger RMSE margin (longer bars) between the correct structure assignment of the given diastereomer and the erroneous matching (to 5-2) based on the two sets of experimental CS. Therefore iShiftML can identify the correct structure from other candidates with higher confidence, as well as recognize the true vannusal B molecule with ease.
4. Conclusion
Methods for ab initio calculation of chemical shieldings lie on a spectrum, with one end being DFT calculations that are cheap but less accurate, and the other end being CCSD(T)/CBS methods that are highly accurate but prohibitively expensive for large systems. We have now created a tool to bridge the two ends using machine learning, so that with input features coming from a relatively fast DFT calculation, the predictions can approach the highest level of accuracy achievable through quantum mechanics calculations, without incurring extra cost. By utilizing a feature set that relies on chemical shielding DIA and PARA tensor components, together with features that describe molecular geometry, we demonstrated that iShiftML can achieve not only excellent accuracy compared to the high-level target chemical shieldings, but greater transferability to test molecules larger than any molecule contained in our training set, approaching the intrinsic errors for the high-level targets when compared to CCSD(T)/CBS calculations.
There are also some limitations of the current method. It is trained with equilibrium and non-equilibrium geometries of closed-shell small organic molecules that contain only H, C, N and O atoms. Also, only single molecule data were included in our training set. Therefore it is not expected to work for open-shell molecules, molecules containing other elements, or for molecular systems in which intermolecular interactions play a major role in the chemical shifts. However, we are planning to improve the method in the future to make it even more transferable and widely applicable. For example, adding support for more atom types will be our first step to allow this method to work for a broader range of organic compounds. Nevertheless, we believe in its current form iShiftML can already benefit those in need of a fast and reliable chemical shift predictor.
While iShiftML is readily helpful for those who study the chemical shieldings of small organic molecules using coupled cluster methods, its broader applicability is exemplified with predicting experimental chemical shifts with higher accuracy for larger and variable organic systems. Our trained model without any fine-tuning can predict the ab initio generated chemical shifts for the NS372 dataset with modest improvement over the delta-learning model.34 Greater transferability and accuracy of iShiftML was also demonstrated for gas phase experimental chemical shifts of small organic molecules, reducing error by more than 50% compared to the direct calculation using the same level of QM theory as our input features. When applying this method to synthesized natural products, we illustrated it could achieve better agreement between predicted and measured chemical shifts when the structures match and provide better differentiation capability between matched and mismatched diastereomer structures given the CS experimental data. We believe there are many more application possibilities for our method, including predicting chemical shifts for proteins, correcting assignment errors in databases, and aiding drug discovery in determining structure-activity relationships.
Supplementary Material
Acknowledgement
This work was supported by funding from the National Institute of General Medical Sciences under grant number 5U01GM121667. This research used computational resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. A. L. Ptaszek was funded by the Christian Doppler Laboratory for High-Content Structural Biology and Biotechnology, Austria and received further support from the DosChem doctoral school program faculty of Chemistry, University of Vienna. We thank Yi Xie (UC Berkeley) for contributing his substantial knowledge on the subject of natural products. Some of the material was previously included in a dissertation submitted to UC Berkeley.
Footnotes
DATA AND CODE AVAILABILITY
The code package is provided through GitHub repository link: https://github.com/THGLab/iShiftML
DS-SS (subsampled dataset from ANI-1 with unstable molecules excluded): https://github.com/THGLab/iShiftML/blob/master/dataset/DS-SS.txt
DS-AL (active learning dataset): https://github.com/THGLab/iShiftML/blob/master/dataset/DS-AL.txt
Removed chemical shielding: 8_atom/mol_34274/99.xyz/atom_6 (calculated low-level chemical shielding: −2.066, calculated high-level chemical shielding: 197.792)
SUPPORTING INFORMATION
Scatter plots and tabulated values of experimental chemical shifts versus the predicted or calculated chemical shieldings under the low-level DFT calculation and high-level neural network prediction with ensemble standard deviation.
DECLARATION OF INTERESTS
M.H.G. is a part-owner of Q-Chem Inc, whose software was used for many of the calculations reported here.
References
- (1).Jacobsen NE NMR data interpretation explained: understanding 1D and 2D NMR spectra of organic compounds and natural products; John Wiley & Sons, 2016. [Google Scholar]
- (2).Hore PJ Nuclear magnetic resonance; Oxford University Press, USA, 2015. [Google Scholar]
- (3).Derome AE Modern NMR techniques for chemistry research; Elsevier, 2013. [Google Scholar]
- (4).Saielli G; Nicolaou K; Ortiz A; Zhang H; Bagno A Addressing the stereochemistry of complex organic molecules by density functional theory-NMR: Vannusal B in retrospective. J. Am. Chem. Soc 2011, 133, 6072–6077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Wüthrich K. Protein structure determination in solution by NMR spectroscopy. J. Biol. Chem 1990, 265, 22059–22062. [PubMed] [Google Scholar]
- (6).Marion D. An introduction to biological NMR spectroscopy. Mol. Struct. Proteom 2013, 12, 3006–3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Brown SP Applications of high-resolution 1H solid-state NMR. Solid State NMR 2012, 41, 1–27. [DOI] [PubMed] [Google Scholar]
- (8).MacKenzie KJ; Smith ME Multinuclear solid-state nuclear magnetic resonance of inorganic materials; Elsevier, 2002. [Google Scholar]
- (9).Paruzzo FM; Hofstetter A; Musil F; De S; Ceriotti M; Emsley L Chemical shifts in molecular solids by machine learning. Nature Comm. 2018, 9, 4501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Barone G; Gomez-Paloma L; Duca D; Silvestri A; Riccio R; Bifulco G Structure validation of natural products by quantum-mechanical GIAO calculations of 13C NMR chemical shifts. Chem. Eur. J 2002, 8, 3233–3239. [DOI] [PubMed] [Google Scholar]
- (11).Bratholm LA; Jensen JH Protein structure refinement using a quantum mechanics-based chemical shielding predictor. Chem. Sci 2017, 8, 2061–2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Shen Y; Lange O; Delaglio F; Rossi P; Aramini JM; Liu G; Eletsky A; Wu Y; Singarapu KK; Lemak A; Ignatchenko A; Arrowsmith CH; Szyperski T; Montelione GT; Baker D; Bax A Consistent blind protein structure generation from NMR chemical shift data. Proc. Natl. Acad. Sci 2008, 105, 4685–4690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Helgaker T; Jaszunski M; Ruud K Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev 1999, 99, 293–352. [DOI] [PubMed] [Google Scholar]
- (14).Gauss J; Stanton JF Electron-correlated approaches for the calculation of NMR chemical shifts. Adv. Chem. Phys 2002, 123, 355–422. [Google Scholar]
- (15).Lodewyk MW; Siebert MR; Tantillo DJ Computational prediction of 1H and 13C chemical shifts: a useful tool for natural product, mechanistic, and synthetic organic chemistry. Chem. Rev 2012, 112, 1839–1862. [DOI] [PubMed] [Google Scholar]
- (16).Webb GA Modern magnetic resonance: Part 1: Applications in chemistry, biological and marine sciences, Part 2: Applications in medical and pharmaceutical sciences, Part 3: Applications in materials science and food science; Springer Science & Business Media, 2007. [Google Scholar]
- (17).Gauss J. Analytic second derivatives for the full coupled-cluster singles, doubles, and triples model: Nuclear magnetic shielding constants for BH, HF, CO, N 2, N 2 O, and O 3. J. Chem. Phys 2002, 116, 4773–4776. [Google Scholar]
- (18).Teale AM; Lutnæs OB; Helgaker T; Tozer DJ; Gauss J Benchmarking density-functional theory calculations of NMR shielding constants and spin–rotation constants using accurate coupled-cluster calculations. J. Chem. Phys 2013, 138, 024111. [DOI] [PubMed] [Google Scholar]
- (19).Schattenberg CJ; Kaupp M Extended benchmark set of main-group nuclear shielding constants and NMR chemical shifts and its use to evaluate modern DFT methods. J. Chem. Theory Comput 2021, 17, 7602–7621. [DOI] [PubMed] [Google Scholar]
- (20).Reid DM; Collins MA Approximating CCSD (T) nuclear magnetic shielding calculations using composite methods. J. Chem. Theory Comput 2015, 11, 5177–5181. [DOI] [PubMed] [Google Scholar]
- (21).Liang J; Wang Z; Li J; Wong J; Liu X; Ganoe B; Head-Gordon T; Head-Gordon M Efficient Calculation of NMR Shielding Constants Using Composite Method Approximations and Locally Dense Basis Sets. J. Chem. Theory Comput 2023, 19, 514–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Wong J; Ganoe B; Liu X; Neudecker T; Lee J; Liang J; Wang Z; Li J; Rettig A; Head-Gordon T, et al. An in-silico NMR laboratory for nuclear magnetic shieldings computed via finite fields: Exploring nucleus-specific renormalizations of MP2 and MP3. J. Chem. Phys 2023, 158, 164116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Shen Y; Bax A SPARTA+: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network. J. Biomol. NMR 2010, 48, 13–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Han B; Liu Y; Ginzinger SW; Wishart DS SHIFTX2: significantly improved protein chemical shift prediction. J. Biomol. NMR 2011, 50, 43–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Li J; Bennett KC; Liu Y; Martin MV; Head-Gordon T Accurate prediction of chemical shifts for aqueous protein structure on “Real World” data. Chem. Sci 2020, 11, 3180–3191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Cordova M; Engel EA; Stefaniuk A; Paruzzo F; Hofstetter A; Ceriotti M; Emsley L A machine learning model of chemical shifts for chemically and structurally diverse molecular solids. J. Phys. Chem. C 2022, 126, 16710–16720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Liu S; Li J; Bennett KC; Ganoe B; Stauch T; Head-Gordon M; Hexemer A; Ushizima D; Head-Gordon T Multiresolution 3D-DenseNet for chemical shift prediction in NMR crystallography. J. Phys. Chem. Lett 2019, 10, 4558–4565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Kuhn S; Schlörer NE Facilitating quality control for spectra assignments of small organic molecules: nmrshiftdb2 – a free in-house NMR database with integrated LIMS for academic service laboratories. Mag. Res. Chem 2015, 53, 582–589. [DOI] [PubMed] [Google Scholar]
- (29).Guan Y; Sowndarya SS; Gallegos LC; John PCS; Paton RS Real-time prediction of 1 H and 13 C chemical shifts with DFT accuracy using a 3D graph neural network. Chem. Sci 2021, 12, 12012–12026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Helgaker T; Jaszunski M; Ruud K Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev 1999, 99, 293–352. [DOI] [PubMed] [Google Scholar]
- (31).Cheeseman JR; Trucks GW; Keith TA; Frisch MJ A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys 1996, 104, 5497–5509. [Google Scholar]
- (32).Flaig D; Maurer M; Hanni M; Braunger K; Kick L; Thubauville M; Ochsenfeld C Benchmarking hydrogen and carbon NMR chemical shifts at HF, DFT, and MP2 levels. J. Chem. Theory Comput 2014, 10, 572–578. [DOI] [PubMed] [Google Scholar]
- (33).Unzueta PA; Greenwell CS; Beran GJ Predicting density functional theory-quality nuclear magnetic resonance chemical shifts via -machine learning. J. Chem. Theory Comput 2021, 17, 826–840. [DOI] [PubMed] [Google Scholar]
- (34).Kleine Büning JB; Grimme S Computation of CCSD(T)-Quality NMR Chemical Shifts via -Machine Learning from DFT. J. Chem. Theory Comput 2023, 19, 3601–3615. [DOI] [PubMed] [Google Scholar]
- (35).Haghighatlari M; Li J; Heidar-Zadeh F; Liu Y; Guan X; Head-Gordon T Learning to Make Chemical Predictions: The Interplay of Feature Representation, Data, and Machine Learning Methods. Chem 2020, 6, 1527–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Welborn M; Cheng L; Miller III TF Transferability in machine learning for electronic structure via the molecular orbital basis. J. Chem. Theory Comput 2018, 14, 4772–4779. [DOI] [PubMed] [Google Scholar]
- (37).Smith JS; Isayev O; Roitberg AE ANI-1, A data set of 20 million calculated off-equilibrium conformations for organic molecules. Scientific data 2017, 4, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Wolinski K; Hinton JF; Pulay P Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc 1990, 112, 8251–8260. [Google Scholar]
- (39).Schreckenbach G; Ziegler T Calculation of NMR shielding tensors using gauge-including atomic orbitals and modern density functional theory. J. Phys. Chem 1995, 99, 606–611. [Google Scholar]
- (40).Behler J; Parrinello M Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett 2007, 98, 146401. [DOI] [PubMed] [Google Scholar]
- (41).Mardirossian N; Head-Gordon M B97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Phys. Chem. Chem. Phys 2014, 16, 9904–9924. [DOI] [PubMed] [Google Scholar]
- (42).Jensen F. Segmented contracted basis sets optimized for nuclear magnetic shielding. J. Chem. Theory Comput 2015, 11, 132–138. [DOI] [PubMed] [Google Scholar]
- (43).Mardirossian N; Head-Gordon M Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys 2017, 115, 2315–2372. [Google Scholar]
- (44).Goerigk L; Hansen A; Bauer C; Ehrlich S; Najibi A; Grimme S A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys 2017, 19, 32184–32215. [DOI] [PubMed] [Google Scholar]
- (45).Hait D; Head-Gordon M How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values. J. Chem. Theory Comput 2018, 14, 1969–1981. [DOI] [PubMed] [Google Scholar]
- (46).Dohm S; Hansen A; Steinmetz M; Grimme S; Checinski MP Comprehensive thermochemical benchmark set of realistic closed-shell metal organic reactions. J. Chem. Theory Comput 2018, 14, 2596–2608. [DOI] [PubMed] [Google Scholar]
- (47).Veccham SP; Head-Gordon M Density functionals for hydrogen storage: Defining the H2Bind275 test set with ab initio benchmarks and assessment of 55 functionals. J. Chem. Theory Comput 2020, 16, 4963–4982. [DOI] [PubMed] [Google Scholar]
- (48).Kim M; Gould T; Izgorodina EI; Rocca D; Lebègue S Establishing the accuracy of density functional approaches for the description of noncovalent interactions in ionic liquids. Phys. Chem. Chem. Phys 2021, 23, 25558–25564. [DOI] [PubMed] [Google Scholar]
- (49).Hait D; Liang YH; Head-Gordon M Too big, too small, or just right? A benchmark assessment of density functional theory for predicting the spatial extent of the electron density of small chemical systems. J. Chem. Phys 2021, 154, 074109. [DOI] [PubMed] [Google Scholar]
- (50).Liang J; Feng X; Hait D; Head-Gordon M Revisiting the Performance of Time-Dependent Density Functional Theory for Electronic Excitations: Assessment of 43 Popular and Recently Developed Functionals from Rungs One to Four. J. Chem. Theory Comput 2022, 18, 3460–3473. [DOI] [PubMed] [Google Scholar]
- (51).Neese F; Wennmohs F; Becker U; Riplinger C The ORCA quantum chemistry program package. J. Chem. Phys 2020, 152, 224108. [DOI] [PubMed] [Google Scholar]
- (52).Matthews DA; Cheng L; Harding ME; Lipparini F; Stopkowicz S; Jagau T-C; Szalay PG; Gauss J; Stanton JF Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys 2020, 152, 214108. [DOI] [PubMed] [Google Scholar]
- (53).CFOUR, a quantum chemical program package written by Stanton JF; Gauss J; Cheng L; Harding ME; Matthews DA; Szalay PG with contributions from Auer AA, Bartlett RJ, Benedikt U, Berger C, Bernholdt DE, Bomble YJ, Christiansen O, Engel F, Faber R, Heckert M, Heun O, Hilgenberg M, Huber C, Jagau T-C, Jonsson D, Jusólius J, Kirsch T, Klein K, Lauderdale WJ, Lipparini F, Metzroth T, Mück LA, O’Neill DP, Price DR, Prochnow E, Puzzarini C, Ruud K, Schiffmann F, Schwalbach W, Simmons C, Stopkowicz S, Tajti A, Vázquez J, Wang F, Watts JD and the integral packages MOLECULE (Almlöf J and Taylor PR), PROPS (Taylor PR), ABACUS (Helgaker T, Jensen H.J. Aa., Jørgensen P, and Olsen J), and ECP routines by Mitin AV and van Wüllen C. http://www.cfour.de (accessed Sep 1, 2022). [Google Scholar]
- (54).Harding ME; Metzroth T; Gauss J; Auer AA Parallel calculation of CCSD and CCSD (T) analytic first and second derivatives. J. Chem. Theory Comput 2008, 4, 64–74. [DOI] [PubMed] [Google Scholar]
- (55).Weigend F. Hartree–Fock exchange fitting basis sets for H to Rn. J. Comput. Chem 2008, 29, 167–175. [DOI] [PubMed] [Google Scholar]
- (56).Hättig C Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple- basis sets for H to Ar and QZVPP basis sets for Li to Kr. Phys. Chem. Chem. Phys 2005, 7, 59–66. [Google Scholar]
- (57).Seeger R; Pople JA Self-consistent molecular orbital methods. XVIII. Constraints and stability in Hartree–Fock theory. J. Chem. Phys 1977, 66, 3045–3050. [Google Scholar]
- (58).Melander M; Laasonen K; Jonsson H Removing external degrees of freedom from transition-state search methods using quaternions. J. Chem. Theory Comput 2015, 11, 1055–1062. [DOI] [PubMed] [Google Scholar]
- (59).Breunig MM; Kriegel H-P; Ng RT; Sander J LOF: identifying density-based local outliers. Proceedings of the 2000 ACM SIGMOD international conference on Management of data. 2000; pp 93–104. [Google Scholar]
- (60).Srivastava N; Hinton G; Krizhevsky A; Sutskever I; Salakhutdinov R Dropout: a simple way to prevent neural networks from overfitting. J. ML Res. 2014, 15, 1929–1958. [Google Scholar]
- (61).Paszke A; Gross S; Massa F; Lerer A; Bradbury J; Chanan G; Killeen T; Lin Z; Gimelshein N; Antiga L, et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst 2019, 32. [Google Scholar]
- (62).Kingma DP; Ba J Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 2014, [Google Scholar]
- (63).Agarap AF Deep learning using rectified linear units (relu). arXiv preprint arXiv:1803.08375 2018, [Google Scholar]
- (64).Schattenberg CJ; Kaupp M Extended Benchmark Set of Main-Group Nuclear Shielding Constants and NMR Chemical Shifts and Its Use to Evaluate Modern DFT Methods. J. Chem. Theory Comput 2021, 17, 7602–7621. [DOI] [PubMed] [Google Scholar]
- (65).Johnson RD, et al. NIST computational chemistry comparison and benchmark database. http://srdata.nist.gov/cccbdb 2006, [Google Scholar]
- (66).Zuschneid T; Fischer H; Handel T; Albert K; Häfelinger G Experimental Gas Phase 1H NMR Spectra and Basis Set Dependence of ab initio GIAOMO Calculations of 1H and 13C NMR Absolute Shieldings and Chemical Shifts of Small Hydrocarbons. Z. Naturforsch. B 2004, 59, 1153–1176. [Google Scholar]
- (67).Cheeseman JR; Trucks GW; Keith TA; Frisch MJ A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys 1996, 104, 5497–5509. [Google Scholar]
- (68).Gregušová A; Perera SA; Bartlett RJ Accuracy of computed 15N nuclear magnetic resonance chemical shifts. J. Chem. Theory Comput 2010, 6, 1228–1239. [Google Scholar]
- (69).Smith SG; Goodman JM Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: The DP4 probability. J. Am. Chem. Soc 2010, 132, 12946–12959. [DOI] [PubMed] [Google Scholar]
- (70).Marcarino MO; Cicetti S; Zanardi MM; Sarotti AM A critical review on the use of DP4+ in the structural elucidation of natural products: the good, the bad and the ugly. A practical guide. Nat. Prod. Rep 2022, 39, 58–76. [DOI] [PubMed] [Google Scholar]
- (71).Howarth A; Ermanis K; Goodman JM DP4-AI automated NMR data analysis: straight from spectrometer to structure. Chem. Sci 2020, 11, 4351–4359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Bagno A; Saielli G Addressing the stereochemistry of complex organic molecules by density functional theory-NMR. WIREs Comput. Mol. Sci 2015, 5, 228–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Semenov VA; Krivdin LB DFT computational schemes for 1H and 13C NMR chemical shifts of natural products, exemplified by strychnine. Magn. Reson. Chem 2020, 58, 56–64. [DOI] [PubMed] [Google Scholar]
- (74).MacGregor CI; Han BY; Goodman JM; Paterson I Toward the stereochemical assignment and synthesis of hemicalide: DP4f GIAO-NMR analysis and synthesis of a reassigned C16–C28 subunit. Chem. Comm 2016, 52, 4632–4635. [DOI] [PubMed] [Google Scholar]
- (75).Carter JC; Luther III GW; Long TC Proton magnetic resonance spectra and assignments of strychnine and selectively deuterated strychnine. J. Magn. Res 1974, 15, 122–131. [Google Scholar]
- (76).Martin GE; Hadden CE; Crouch RC; Krishnamurthy V ACCORD-HMBC: advantages and disadvantages of static versus accordion excitation. Magn. Reson. Chem 1999, 37, 517–528. [Google Scholar]
- (77).Bagno A; Rastrelli F; Saielli G Toward the complete prediction of the 1H and 13C NMR spectra of complex organic molecules by DFT methods: application to natural substances. Chem. Eur. J 2006, 12, 5514–5525. [DOI] [PubMed] [Google Scholar]
- (78).Seeman JI; Tantillo DJ From decades to minutes: steps toward the structure of strychnine 1910–1948 and the application of today’s technology. Ang. Chem. Int. Ed 2020, 59, 10702–10721. [DOI] [PubMed] [Google Scholar]
- (79).Robien W. A critical evaluation of the quality of published 13 C NMR data in natural product chemistry. Progress in the Chemistry of Organic Natural Products 105 2017, 137–215. [DOI] [PubMed] [Google Scholar]
- (80).Nicolaou K; Ortiz A; Zhang H; Dagneau P; Lanver A; Jennings MP; Arseniyadis S; Faraoni R; Lizos DE Total synthesis and structural revision of vannusals A and B: Synthesis of the originally assigned structure of vannusal B. J. Am. Chem. Soc 2010, 132, 7138–7152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Nicolaou K; Ortiz A; Zhang H; Guella G Total synthesis and structural revision of vannusals A and B: synthesis of the true structures of vannusals A and B. J. Am. Chem. Soc 2010, 132, 7153–7176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Saielli G; Nicolaou K; Ortiz A; Zhang H; Bagno A Addressing the stereochemistry of complex organic molecules by density functional theory-NMR: Vannusal B in retrospective. J. Am. Chem. Soc 2011, 133, 6072–6077. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.