Prediction of ECG signals from ballistocardiography using deep learning for the unconstrained measurement of heartbeat intervals

Abstract

We developed a deep learning–based extraction of electrocardiographic (ECG) waves from ballistocardiographic (BCG) signals and explored their use in R–R interval (RRI) estimation. Preprocessed BCG and reference ECG signals were inputted into the bidirectional long short-term memory network to train the model to minimize the loss function of the mean squared error between the predicted ECG (pECG) and genuine ECG signals. Using a dataset acquired with polyvinylidene fluoride and ECG sensors in different recumbent positions from 18 participants, we generated pECG signals from preprocessed BCG signals using the learned model and evaluated the RRI estimation performance by comparing the predicted RRI with the reference RRI obtained from the ECG signal using a leave-one-subject-out cross-validation scheme. A mean absolute error (MAE) of 0.034 s was achieved for the beat-to-beat interval accuracy. To further test the generalization ability of the learned model trained with a short-term-recorded dataset, we collected long-term overnight recordings of BCG signals from 12 different participants and performed validation. The beat-to-beat interval correlation between BCG and ECG signals was 0.82 ± 0.06 with an average MAE of 0.046 s, showing practical performance for long-term measurement of RRIs. These results suggest that the proposed approach can be used for continuous heart rate monitoring in a home environment.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-84049-0.

Introduction

With an increase in the aging population, the incidence of cardiovascular disease is increasing, and it is more important than ever to understand the risk factors associated with the disease and its prevention. To provide the essential information necessary for the diagnosis and treatment, particularly for the elderly and patients with cardiovascular diseases, ongoing and long-term assessment of cardiac activity is effective as it allows detection of changes in physical conditions and improvement of health outcomes¹. However, accessing a hospital when required is not feasible for all individuals, especially for older patients with limited mobility. Therefore, the development of devices that allow individuals to easily monitor vital signs in their home environment without being restrained by their daily lives is awaited. When monitoring biological signals outside a hospital, the measurement and recording are performed automatically, unconsciously, and unrestrainedly to eliminate the physical and mental burden on individuals. In daily life, individuals who are not experts cannot be expected to consciously attach electrodes or sensors to their bodies daily.

The heart rate (HR) is the most commonly measured vital sign and is routinely monitored in clinical practice using an electrocardiogram (ECG); however, wearing ECG electrodes can cause discomfort and skin inflammation, especially for long-term monitoring. Furthermore, the ECG-measuring device is inaccessible to the public. Therefore, the current research is primarily focused on the realization of noncontact and unobtrusive HR monitoring, wherein the researchers are seeking alternatives to ECG-based HR monitoring in the wellness domain. Various noninvasive methods for monitoring the HR have been proposed. Most of them involve unrestrained sensing using environment-embedded sensors such as conductive fibers for bed sheets², load cells under the bed leg^3,4, pressure sensors embedded in the pillow or air mattress^5,6, piezoelectric sensors placed on the mattress^7–9, microwave Doppler shift on the body surface^10,11, and fiber Bragg grating sensors placed on the bed mattress^12,13. Most of these methods detect heartbeats based on body vibrations due to the cardiac physiological signature. This technique, known as ballistocardiography (BCG), measures the ballistic force generated by cardiac contractions and blood circulation in the body¹⁴. Similar to the QRS complex in the ECG, the waveform of the BCG for each heartbeat is characterized by an “IJK” complex at the extremes of signal, which is related to the ventricular ejection and aortic pulse pressure^15,16. The morphology of BCG waveforms varies depending on the position and lying posture of the individual, with diversity across individuals^17,18. Moreover, BCG is susceptible to noise and body movement interference during the acquisition process. This poses a significant challenge in identifying heartbeats from BCG signals. Thus far, several studies have attempted to analyze the BCG signal for the accurate extraction of heartbeats from BCG signals using a variety of approaches.

Related works

Most of the previous studies on extraction of heartbeats from BCG signal are based on the J-peak detection using waveform characteristics, spectral-based methods, and the clustering technique. Mora et al.¹⁹. proposed a precise J-peak annotation algorithm that identifies candidate intervals containing J-waves using a subject-specific search window. Their proposed method achieved a mean absolute error (MAE) metric of 4.7 ms for estimating the heartbeat interval. Similarly, Shin et al.²⁰. implemented a template matching approach to detect the J-peaks of the BCG waveform, where the BCG template was constructed using ensemble averaging of valid BCG cycles centered at J-peak points; subsequently, matching was performed using the correlation coefficient function, which improved the detection accuracy with a sensitivity of 95%. The template matching approach is based on the correlation between a fixed individual heartbeat template and the obtained signal; it has relatively low robustness to the beat-to-beat variation in the waveform morphology. Alvarado-Serrano et al.²¹. introduced a wavelet transform–based algorithm to detect J-waves, in which an optimal wavelet scale was selected by implementing a continuous wavelet transform with splines to reduce noise and mechanical interference. Although this method is intuitive, it requires extensive complicated preprocessing. Brüser et al.²². proposed an unsupervised machine learning technique to identify the shape of a single heartbeat in the BCG, in which features describing the BCG waveform are extracted using a modified k-means algorithm. Paalasmaa et al.⁹. introduced an adapted heartbeat model in which the heartbeat shape was adaptively deduced from the BCG signal using a hierarchical clustering approach, and the inter-beat intervals (IBI) were identified by detecting the positions where the heartbeat shape best matched the signal. Although the authors acknowledged the large variation in the coverage rate across the participants, an MAE of 13 ms was achieved for the heartbeat interval. However, if the wave peak of the BCG signal is not distinct, then the probability of clustering errors increases, leading to misidentification of J-peaks, which is a major shortcoming of the clustering technique. Such a situation can occur because significant peak distortion is observed when even slight movements of a body parts occur. Moreover, the shapes of BCG waveforms vary depending on the lying posture in the same individual. To address these challenges, deep learning approaches have been implemented for measuring heartbeats. Deep learning methods can effectively capture BCG-signal variability via data-driven supervised learning. Pröll et al.²³ demonstrated a deep learning model based on a stacked convolutional and recurrent neural network, whose accuracy of estimating the mean HR was higher than that of the traditional digital signal processing approach. Zhang et al.²⁴ proposed a deep neural network-based auto-labeling technique that identifies the “IJK” complex of the BCG wave automatically by making the model learn the association between the continuous BCG waves and the labeled sequence with an ECG reference. Recently, Schranz et al.²⁵. proposed a model of discrete reference heartbeat events with a kernel function. The learned deep neural network model approximates the kernel shape that encodes discrete heartbeat events, thereby allowing a more precise J-peak extraction. In most of these approaches, the deep learning models process the input BCG signal to represent as a time-series of discrete J-peak events.

In this study, we introduced a novel approach based on deep neural networks under a regression framework that enables the prediction of ECG waves directly from BCG signals for the accurate measurement of IBI. The possibility of extracting the corresponding ECG signal from the piezoelectric BCG signal has been previously suggested by identifying an inverse transfer function between the ECG and the BCG^26,27; however, to the best of our knowledge, a deep learning–based regression model that generates continuous ECG waves from BCG signals has not been reported. We considered that a deep learning model that can learn the association between the temporal patterns of BCG and ECG and can generate an ECG corresponding signal directly from a BCG signal has the ability to detect heartbeats easily with a high accuracy. The primary goal of this study was to evaluate the correlation of the IBI analyzed from the predicted ECG (pECG) from BCG signals with those analyzed from a genuine ECG in various lying postures and overnight long-term recordings.

Materials and methods

Study design and participants

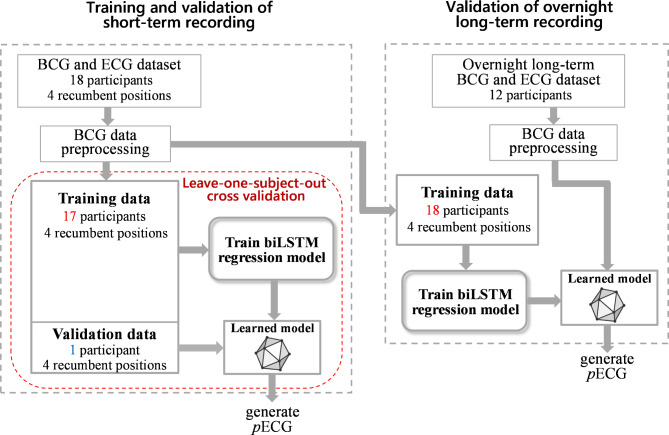
In this study, a bidirectional long short-term memory network (biLSTM), with a regression framework, was used to generate an ECG corresponding signal from BCG for the measurement of heartbeat interval. The biLSTM architecture can capture the temporal dependencies between the local features of ECG and BCG signals in forward and backward sequences. The workflow of this study is illustrated in Fig. 1. First, we investigated whether biLSTM models can accurately generate pECG from a BCG signal and validated the performance of the developed models on the calculated R–R interval (RRI) data acquired from short-term recording using the leave-one-subject-out cross-validation scheme. Subsequently, we examined whether the learned model achieves good prediction accuracies for RRI calculation in different participants recruited for overnight long-term recording.

Fig. 1.

Study design for the development and validation of a deep learning model to generate pECG from BCG signals. Training and validation were performed with a leave-one-subject-out cross-validation approach for the short-term recording. Validation for the overnight long-term recording was performed using the learned model based on the training data from all participants recruited for the short-term recording.

For short-term recording, a total of 18 young healthy volunteers (15 males and 3 females) were recruited from the Yamagata University student body to gather training data and build a deep learning model designed to predict ECG waves from BCG signals. The mean age, weight, and body mass index (BMI) of the participants were 22.7 ± 1.7 (standard deviation [SD]) years, 66.1 ± 7.4 kg, and 22.8 ± 2.1 kg/m², respectively. To validate the overnight long-term recordings, 12 male participants were recruited separately from the same institution. The mean age, weight, and BMI of these participants were 22.7 ± 1.0 years, 67.2 ± 6.5 kg, and 22.6 ± 1.9 kg/m², respectively. All the participants were normotensive nonsmokers, were not taking any medications, and were self-described “normal sleepers.” Each participant provided informed consent to participate in the study after receiving a complete written and oral explanation of the procedures. The experimental protocol was approved by the Yamagata University Institutional Human Subjects Ethics Committee (approval no.: H30-240). The study was performed in accordance with the guidelines established by the Declaration of Helsinki.

Piezoelectric sensor

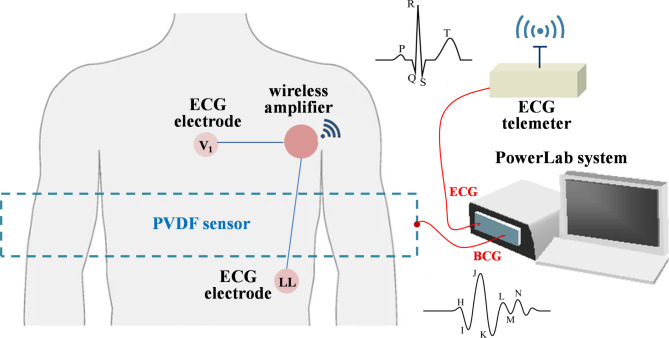
A sheet-type piezoelectric element made of polyvinylidene fluoride (PVDF), a fluorine-based organic ferroelectric material, was used to measure the BCG signal. In the PVDF material, electric polarization occurs when the displacement of the ions arranged in the crystal lattice increases owing to pressure and deformation. The PVDF sensor was sandwiched between positive and negative electrodes in the thickness direction, and the accumulated charge was converted from current to voltage to extract the electric signal. The sheet-type PVDF sensor is commercially available as Suijin delta® (Health Sensing Co. Ltd, Tokyo, Japan). The width and height of the sensor sheet were 70 and 10 cm, respectively, and the thickness was approximately 1 mm, including a protective cover. This sensor was placed beneath the bedsheets without direct contact with the body surface. The sensor was sufficiently thin to prevent the participant from consciously being aware of its presence. BCG captures the ballistic forces of the heart caused by the ejection of blood into the great vessels with each heartbeat. The BCG waveform varies depending on the direction of propagation of the ballistic forces and the position of the participant on the bed with respect to the sensor. In this study, the PVDF sensor was positioned at the location of the thorax perpendicular to the axis along the great blood vessels such that the measurement was performed in the dorsoventricular axis (see Fig. 2).

Fig. 2.

Schematic of a recording system for simultaneous acquisition of ECG and BCG signals. The PVDF sensor was installed beneath the bedsheets without direct contact with the body surface. PVDF polyvinylidenefluoride film, ECG electrocardiogram, BCG ballistocardiogram.

ECG and BCG data acquisition

Short-term recordings for preparing the deep learning dataset

Simultaneous measurement of the ECG and BCG signals was performed to enable the model to learn the relationship between the ECG and BCG waveforms obtained from 18 participants. The schematic of the data acquisition system is presented in Fig. 2. The ECG data used for the comparative analysis were acquired using a wireless ECG (ZM-940P; Nihon Kohden, Tokyo, Japan) with unipolar thoracic leads by placing the Ag–AgCl electrodes on the 4th intercostal space and left lower abdomen (Fig. 2). The participants were comfortably lying on a bed in the supine, prone, left lateral, or right lateral decubitus positions. After achieving stable BCG and ECG waveforms, the ECG and BCG signals were recorded simultaneously at a sampling frequency of 200 Hz using a PowerLab device with a resolution of 16 bits (Bio Research Center Co. Ltd, Nagoya, Japan). During the BCG and ECG collections, participants were asked to remain silent and stationary as much as possible. After the recording, participants were asked to change their positions, and the recording was repeated at different positions. The order of the positions tested was counterbalanced among participants. The recording period for each position was 2 min. For subsequent analyses, the recorded signals were exported to text files.

Overnight long-term recording

A total of 12 participants voluntarily participated in the long-term overnight recording study. After familiarization with the laboratory environment and equipment, each participant was required to attend the laboratory at approximately 22:00 on the night of the recording. All participants were asked to abstain from exercise and caffeine for 6 h before the experimental session. The participant was placed in a relaxed supine position on the bed, with the PVDF sensor placed at the location of the participant’s thorax under the bedsheet. Similar to the case of the short-term recordings, participants wore wireless ECG electrodes on their chests. After confirming that the ECG and BCG signals were stable, the room light was turned off and signals were continuously recorded throughout the night using the PowerLab device at a sampling frequency of 200 Hz. To maintain the sleep environment as similar as possible to their home sleep, experiments were performed in a quiet room with the temperature maintained at 22–24 °C and the recordings were started when the participants went to bed according to their sleep habits and ended when they woke up the next morning. Following the overnight study, participants were allowed to leave the laboratory.

Preprocessing of the BCG signal

To explore the appropriate filter preprocessing of the BCG signal, the auto- and cross-power spectral density estimates (PSD and cPSD, respectively) of the ECG and BCG signals were obtained using Welch’s periodogram. As a preprocessing step, a bandpass filter followed by full rectification were used to emphasize the power of the fundamental frequency of heartbeats and remove the respiratory influence on the BCG signal. The fourth-order Butterworth bandpass filter with a variable lower cutoff frequency was designed with the higher cutoff frequency remaining fixed at 50 Hz. The PSD and cPSD estimations were conducted using 2-min data with fixed segment lengths of 4096 points (approximately 20 s) for a fast Fourier transform with 50% overlap. For each segment, we subtracted the linear trend and applied the Hanning window. In addition, the magnitude of the squared coherence function (MSC) between the ECG and preprocessed BCG signals was estimated using the following equation to quantify the degree of similarity in the frequency domain:

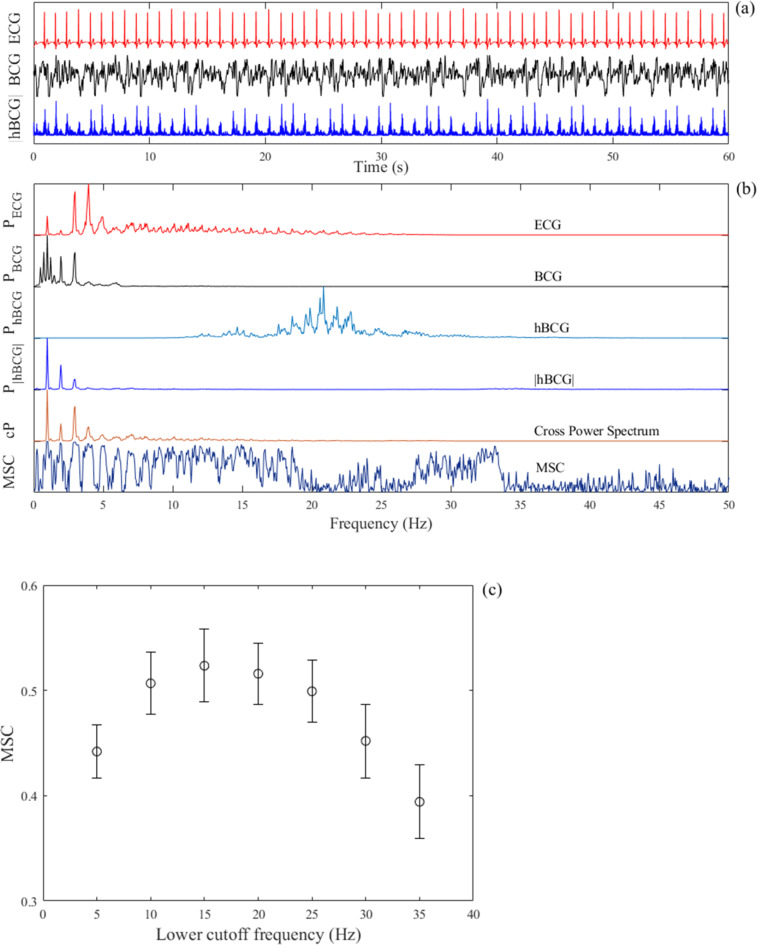
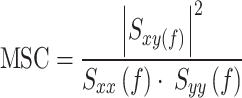, where S_xy(f) is the cross-power spectrum between the ECG and preprocessed BCG signals and S_xx(f) and S_yy(f) are the auto-power spectra of each signal. The mean value determined by averaging the MSC over the frequency range between 0.5 and 35 Hz was used as a quantitative measure of similarity between the preprocessed BCG and ECG signals because the fundamental frequency of the ECG signal and its harmonics energy ranges in this frequency band. To determine a suitable lower cutoff frequency for the bandpass filter, the average MSC values were compared by varying the lower cutoff frequency from 5 to 35 Hz. An example of the analysis is illustrated in Fig. 3, which shows parts of the raw ECG and BCG signals measured in the supine position, together with the preprocessed BCG signal (Fig. 3a), that is, the fully rectified bandpass filter BCG signal (hereafter denoted as |hBCG|). In this example, the lower cut-off frequency of the bandpass filter was set to 15 Hz. Spectral analyses of these signals provided PSD, cPSD, and MSC profiles. As shown in Fig. 3b, the PSD of the rectified bandpass filter BCG signal (PSD_|hBCG|) and the cPSD between the ECG and |hBCG| signals had distinct peaks in the fundamental frequency of heartbeats at approximately 1 Hz and its harmonics. The MSC exhibited peaks at frequencies where the cPSD increased and almost disappeared above 35 Hz. Figure 3c shows the effect of the lower cutoff frequency of the bandpass filter on the average MSC values. Based on the observation that MSC showed a higher value in the frequency range of 10–25 Hz, we set the lower cutoff frequency of the bandpass filter to 15 Hz in the present study.

Fig. 3.

(a) Example of the tracings of the ECG signal (red), BCG signal (black) in the supine position, and bandpass-filtered BCG signals followed by full-wave rectification (blue) within a frequency range of 15–50 Hz. (b) Auto-power spectral densities of ECG (P_ECG), BCG (P_BCG), bandpass-filtered BCG (P_hBCG), and bandpass-filtered BCG signals followed by full-wave rectification (P_|hBCG|) together with the cross-power spectral density (cP) and magnitude squared coherence function (MSC) between the ECG and |hBCG| signals. The auto- and cross-power spectral densities are normalized by the respective maximum value. The fundamental frequency of heartbeats and its first and second harmonics are clearly visualized in the power spectral density of the bandpass-filtered BCG signal after full-wave rectification. (c) The mean and SD of the average MSC values plotted as a function of the lower cutoff frequency of the bandpass filter over a frequency range of 5–35 Hz. ECG electrocardiography, BCG ballistocardiography, |hBCG| full-wave rectified bandpass-filtered BCG signal, pECG predicted ECG signal, pBCG predicted BCG signal, SD standard deviation.

Deep learning model

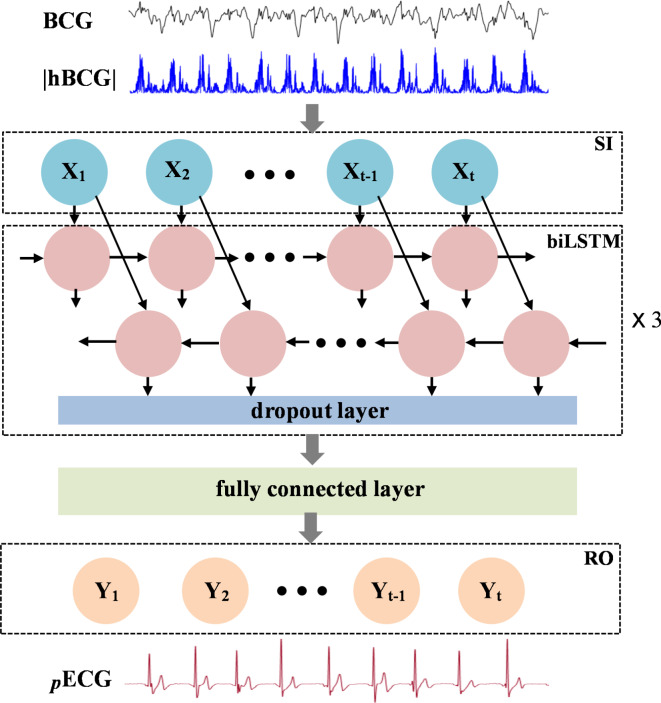
The ECG signal from the BCG was predicted by training a biLSTM deep neural network to learn the association between the preprocessed BCG signals (|hBCG|) and the reference ECG. The biLSTM architecture learns to generate ECG waves under the regression framework of machine learning in the backward and forward directions. An overview of the model structure is presented in Fig. 4. The model is composed of a sequential input layer, three biLSTM layers, a fully connected layer, and a regression layer. Each bi-LSTM layer consists of 128 hidden cells. A dropout layer (rate of 0.2) was applied after each biLSTM layer during the training phase to reduce overfitting. The fully connected layer integrates the features extracted from the previous biLSTM layer and outputs a single value at each time step. The last layer of the neural network is the regression layer, which computes the mean squared error (MSE) between the pECG and reference ECG signals. During the training process, the weights and biases of the biLSTM network layers were adjusted to minimize the MSE.

Fig. 4.

Architecture of the bidirectional long short-term memory (biLSTM) deep learning neural network model for predicting the ECG wave from BCG signals. The model is composed of a sequential input layer (SI), three biLSTM layers, a fully connected layer, and a regression output layer (RO). Each biLSTM layer consists of 128 hidden cells. A dropout layer (rate of 0.2) is added after each biLSTM layer to reduce overfitting. For simplicity, only a single biLSTM with the dropout layer is shown. BCG ballistocardiography signal, |hBCG| full-wave rectified bandpass filter BCG signal, pECG predicted ECG signal.

Training and validation of short-term recording

The training dataset, D, included N paired preprocessed BCG signals and the reference ECG, 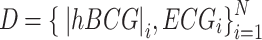. For each participant and recumbent position, four segments of 10-s paired data were randomly selected, yielding 288 segments (18 participants × 4 positions × 4 segments) that were prepared for the training data. We aimed to train the biLSTM neural network to learn a functional mapping (f) parameterized by a set of weights (w) of hidden layers in the network such that the input signal |hBCG| matched the genuine ECG signal, solving the following optimization problem through a set of weight vectors (w), 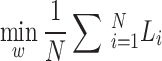(w), where L_i(w) describes a loss function, 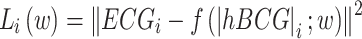. The model was trained and validated using a leave-one-subject-out cross-validation scheme (a block surrounded by the red dotted lines in Fig. 1). This implies that if we want to evaluate the performance of a model on the data of participant “A,” then we must train the model using the data of the remaining participants. The learned model was used to generate pECG for participant “A” and to validate the model performance by comparing the RRI estimated from pECG to that derived from genuine ECG. This process was repeated for all participants in the validation set. The network was trained using a mini-batch of 2000 sequences (10 s). The Adam training optimizer was used to minimize the MSE between the output pECG and the genuine ECG signals. The initial learning rate was set to 0.005, which was reduced to 1/100th of the previous rate every 50 epochs. The L2 norm-based gradient threshold method was employed to clip the gradient values that exceeded the gradient threshold of 1. The training process was terminated when there was no improvement in the test data over 100 consecutive epochs. The validation accuracy and loss function were used as the stopping criteria to avoid overfitting. The hyperparameters used in this study are listed in Table 1. Hyperparameter values were selected based on several trial-and-error trials. The model was trained on a machine with an NVIDIA GeForce RTX4090 GPU and 40GB VRAM.

Table 1.

Ranges and selected values of hyperparameters for deep learning.

Hyperparameters	Range searched	Selected values
Number of biLSTM layers	[2, 3, 4]	3
Hidden units in an individual biLSTM cell	[32, 64, 128]	128
Dropout rate	[0.1, 0.2, 0.3]	0.2
Initial learn rate	[0.001–0.01]	0.005
Dropping of the learning rate	[0.01–0.1]/50 epochs	0.01/50 epochs
L2 regularization	[0.01–1]	0.1
Gradient threshold	[0.1–3]	1
Maximum epochs	[1000–5000]	3000

biLSTM bidirectional long short-term memory.

Validation of overnight long-term recording

To validate the model performance for overnight long-term recordings, a deep learning regression model was constructed by feeding the entire training dataset, obtained from all the participants in the short-term recording study, to the biLSTM model (see the right side of Fig. 1). The training conditions for deep learning were the same as those for the short-term recording. The resultant learned model was applied to generate pECG using a preprocessed BCG signal, which was measured in the night from each participant of the overnight long-term study, as the input.

Data analysis

Beat-to-beat interval calculation

The identification of the R-peaks in the ECG and pECG signals was performed using the built-in “findpeaks” function in MATLAB software (R2022b, MathWorks Inc., MA, USA). The ECG and pECG signals were differentiated and normalized before identifying the R-peaks. The minimum peak height was defined as the amplitude threshold of unity, and the minimum peak distance was set to 0.4 s. The beat-to-beat RRI was calculated as the duration between successive R peaks. Following this, automatic artifact rejection was performed by excluding those beats with an RRI of greater than 1.8 s (HR: <33 beats/min). The RRI estimated from the pECG signal is referred to as predicted RRI (pRRI).

Because the PVDF sensor has a high sensitivity, the physical motion of the participant during measurements causes an excessive amplitude voltage signal, which prevents the accurate evaluation of heartbeats. Therefore, for the overnight long-term recording, during which body movement may occur owing to changes in the sleeping position, the BCG signal was analyzed every 10 s; if a body movement was detected, analysis was skipped in this segment. Body movement was considered to have occurred if the amplitude of the raw BCG signal exceeded five times the SD of the raw BCG signal in a time window of 10 s.

Evaluation of performance and statistical analyses

The accuracy of the pRRI estimated using the pECG signal was assessed by beat-by-beat comparison with the RRI measured using the reference ECG signal. The timing accuracy of the pECG signal generated by the model was evaluated on the basis of the time difference in the onset of the R-wave (Δt_R) between the ECG and pECG signals. To gauge the difference between the RRI and pRRI, the MAE for all pRRI and RRI values was computed as 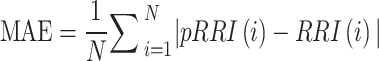, where N represents the number of heartbeats. For overnight long-term recording, the number of detected pRRIs differed from that of detected RRIs because BCG signals were occasionally hampered by body movement during data collection. If consecutive missing datapoints are present, then the reliability of the interpolated data becomes questionable. Therefore, the MAE was computed as 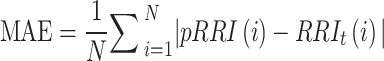, where RRI_t is the linearly interpolated RRI value aligned with the onset of the R wave of the pECG signal.

Linear regression analysis and Bland–Altman plots were used to describe the relationship and agreement between the beat-to-beat RRI and pRRI. The level of agreement (LoA) and mean bias were calculated. Spearman rank correlation analysis was performed between the difference (pRRI–RRI) and the average RRI calculated using ECG and pECG signals to test for the constant or proportional bias in Bland–Altman plots. Data are presented as means ± SD. All statistical tests were 2-sided, and a P value of less than 0.05 was judged to be statistically significant. Data processing and analyses were performed using customized scripts programmed in MATLAB with machine learning and signal processing toolboxes.

Results

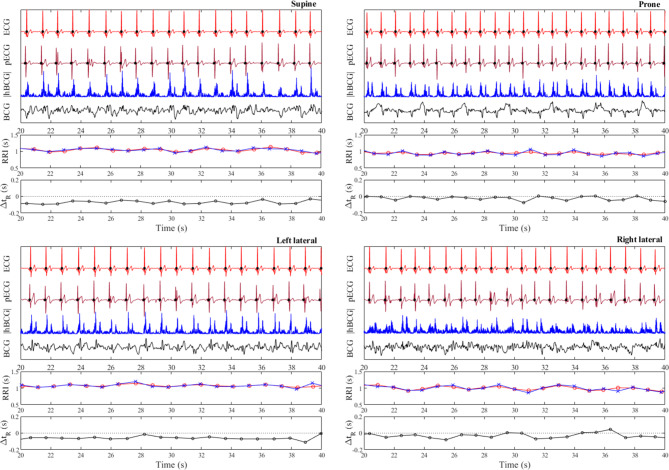
Examples of pECG profiles generated by the learned model for all body positions in a single participant are shown in Fig. 5. The pECG and reference ECG profiles showed high similarity. The R-wave peaks (closed black circles) on both the ECG and pECG signals were well aligned; however, a small time difference existed between the onset of the R-wave on the ECG and that on the pECG (Δt_R). The estimated pRRI from the pECG and the calculated RRI from the ECG matched well, where respiratory modulation of the RRI was clearly observed, especially in the prone position. The pECG profiles generated by the deep learning model using the leave-one-subject-out cross-validation strategy in the supine, prone, left-lateral, and right-lateral positions per participant are shown in Supplementary Fig. S1.

Fig. 5.

Typical examples of predicted ECG (pECG) profiles generated by the deep learning model using the leave-one-subject-out cross-validation strategy in each of four different recumbent positions (supine, prone, left lateral, and right lateral) for a single participant. For visual clarity, only 20 s of the analyzed data are shown. The raw BCG signal (black) and the preprocessed BCG signal (blue) are labeled as “BCG” and “|hBCG|,” respectively. Closed black circles on the ECG and pECG signals represent the location of the R wave determined by the peak detection algorithm. Calculated R–R interval (RRI) from the ECG (red open circles) and pECG (blue crosses) signals and the time difference of the onset of the R wave between the ECG and pECG signals (Δt_R) are also presented. ECG electrocardiogram, BCG ballistocardiogram, |hBCG| full-wave rectified bandpass-filtered BCG signal, RRI R-to-R interval, pECG predicted ECG signal, Δt_R time difference of the onset of the R wave between the ECG and pECG signals (a positive value indicates that the onset of the R wave on the pECG signal appeared later than that on the ECG signal).

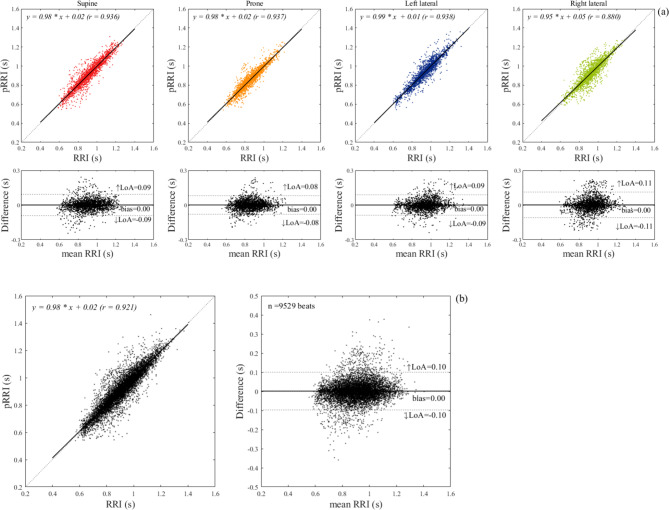
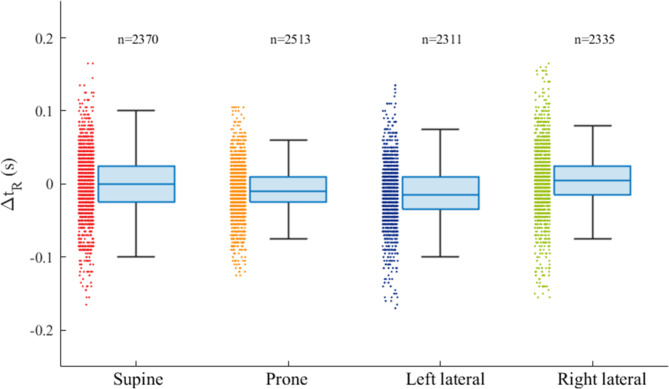
Figure 6a shows the results of linear regression and Bland–Altman analyses for the comparison between the RRI and pRRI in each body posture. The slope of the linear regression was close to unity and the association was highly significant for all body postures. Pearson’s correlation coefficients ranged from 0.87 for the right-lateral position to 0.92–0.94 for the supine, prone, and left-lateral positions. The biases for all body postures were zero, indicating a good mean agreement. However, Spearman’s rank correlation analysis between the differences (pRRI–RRI) and means of the Bland–Altman plots demonstrated that a small positive proportional bias was present for all body postures (supine: regression coefficient (β) = 0.043, r = 0.112, p < 0.001; prone: β = 0.044, r = 0.084, p < 0.001; left lateral: β = 0.058, r = 0.140, p < 0.001; and right lateral: β = 0.086, r = 0.160, p < 0.001). The LoA ranged from ± 0.08 and ± 0.11 s. The linear regression and Bland–Altman analyses for the comparison of between the pRRI and RRI obtained in all body postures are presented in Fig. 6b. The correlation between the estimated pRRI and the simultaneously obtained reference RRI was highly significant (r = 0.92), and the slope of the regression line was nearly identical. Out of the 9529 heartbeats analyzed, 94.6% were accurately estimated within ± 5% error. Table 2 summarizes the mean values and SDs for the RRI, pRRI, and MAE together with the Δt_R. The MAE between the pRRI and RRI was approximately 0.03–004 s regardless of body postures (approximately 3.5% of the mean RRI). The mean Δt_R was almost zero for each body posture; however, a variation was observed when individual heartbeats were considered, as demonstrated in Fig. 7, which shows the box plot distributions of Δt_R for each body posture. The Δt_R varied with SD between 0.035 and 0.055 s regardless of the body posture. Enlarged cutouts of the signal timing measured from different participants in the supine position are displayed in Fig. 8, which shows the typical cases of positive (a), almost zero (b), and negative Δt_R (c). By comparing the timing of the signals, we found that an R-wave on the pECG occurred near the foot point of the preprocessed BCG signal (|hBCG|) in all the cases, suggesting that the model appeared to be learning to generate an R-wave at this time.

Fig. 6.

(a) Linear regression and Bland–Altman analyses for a comparison between ECG- and pECG-derived R–R intervals in each of four recumbent positions on the bed. The linear regression plot illustrates the fitted linear model (solid line) and the identity line (dotted line) with the regression equation and correlation coefficient (r). In Bland–Altman plots, 95% limits of agreement (LoA) and bias are displayed with dashed and solid lines, respectively, along with their numerical values. The upper (↑LoA) and lower (↓LoA) LoA are presented with a ± 1.96 standard deviation. (b) Linear regression and Bland–Altman analyses for a total of 9529 heartbeats obtained in the four body positions for all participants. ECG electrocardiogram; BCG: ballistocardiogram, pECG predicted ECG signal, pRRI predicted R–R interval calculated from the pECG signal generated by the deep learning model.

Table 2.

Comparison of the RRI and pRRI and time differences in the onset of the R-wave between the ECG and pECG signals in the four recumbent positions from short-term recordings.

	Supine (n = 2370)	Prone (n = 2513)	Left lateral (n = 2311)	Right Lateral (n = 2335)	All (n = 9529)
RRI (s)	0.911 ± 0.127	0.860 ± 0.112	0.934 ± 0.123	0.925 ± 0.111	0.906 ± 0.122
pRRI (s)	0.912 ± 0.134	0.861 ± 0.120	0.935 ± 0.132	0.927 ± 0.125	0.907 ± 0.131
MAE (s)	0.032 ± 0.013	0.032 ± 0.011	0.033 ± 0.011	0.040 ± 0.020	0.034 ± 0.006
ΔtR (s)	− 0.003 ± 0.029	− 0.010 ± 0.011	− 0.012 ± 0.018	0.006 ± 0.020	− 0.004 ± 0.015

Values are expressed as means ± standard deviations. RRI: R–R interval calculated from the ECG signal; pRRI: predicted RRI calculated from the pECG signal; MAE: mean absolute error; Δt_R: time difference of the onset of the R-wave between ECG and pECG signals (a negative value indicates that the onset of R-wave on the pECG signal appeared earlier than that on the ECG signal).

Fig. 7.

Box and whisker plots showing the distribution of ΔtR in the four recumbent positions. The box plot displays the 25th percentile, median, and 75th percentile and the whiskers extend to the minimum and maximum values without outliers. The number of heartbeats (n) is indicated over each box plot. Δt_R: time difference of the onset of the R wave between the ECG and pECG signals (positive value indicates that the onset of the R wave on the pECG signal appeared later than that on the ECG signal).

Fig. 8.

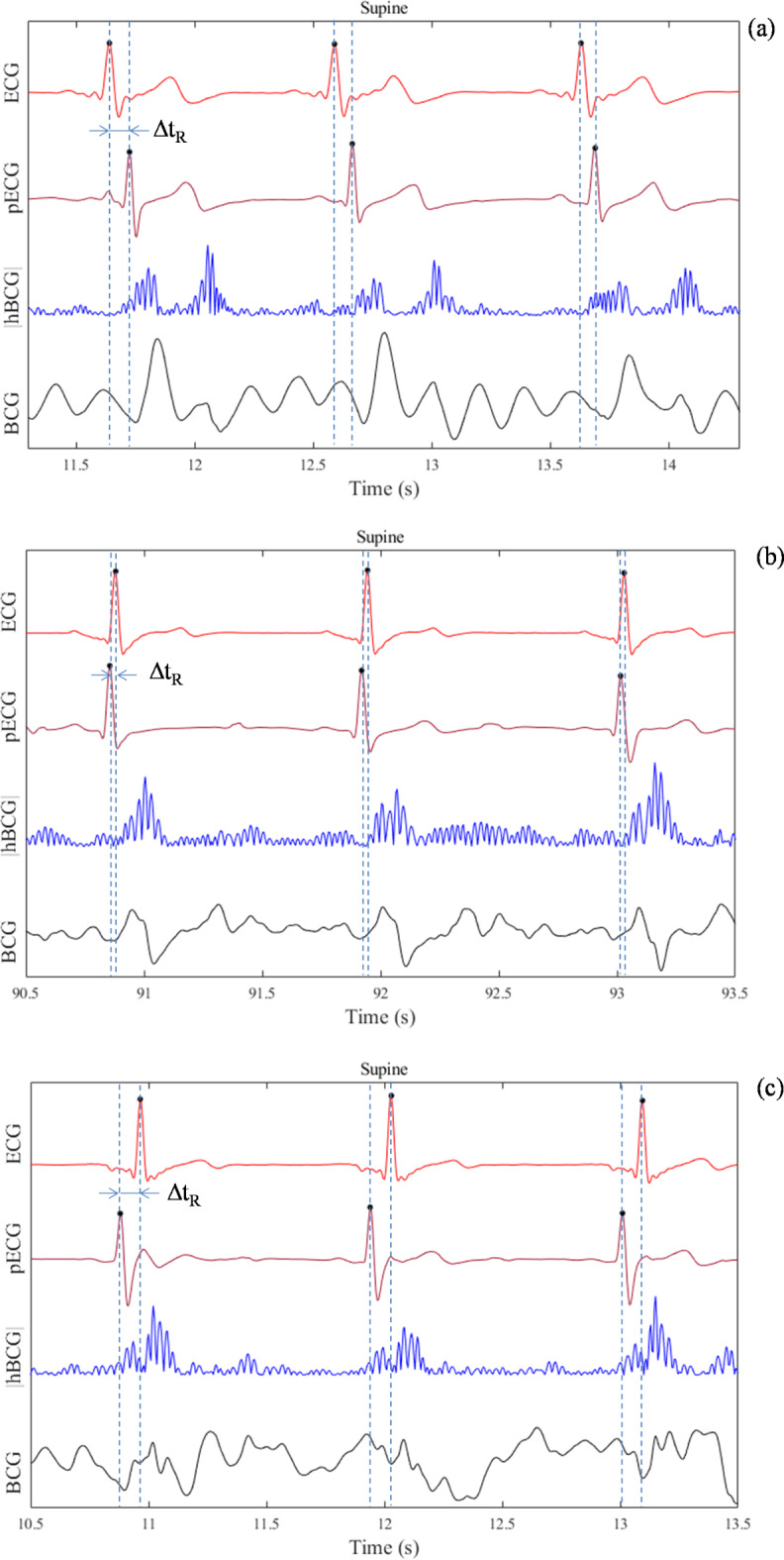
Enlarged cutouts of the signal timing showing positive (a), almost zero (b), and negative Δt_R (c) measured in the supine position for different participants. Average Δt_R values of the three heartbeats in each condition are 0.09 (a), − 0.02 (b), and − 0.07 s (c), respectively. Δt_R: time difference of the onset of the R wave between the ECG and pECG signals (positive value indicates that the onset of the R wave on the pECG signal appeared later than that on the ECG signal).

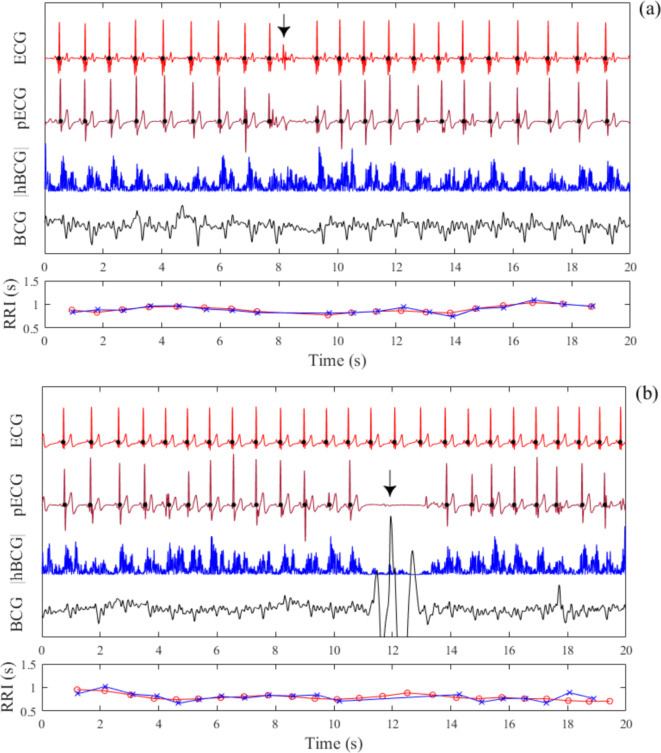
We then examined whether the generation of pECG signals was affected when an extrasystole occurred and when the BCG signal was contaminated by motion artifacts. Figure 9a shows an example of the pECG profile when an extrasystole occurred. Extrasystoles are caused by the abnormal function of the cardiac conduction system, which does not result in mechanical activity of the heart. Thus, a pECG signal was not generated because of the lack of heartbeat-induced vibrations in the BCG signal. In addition, Fig. 9b shows an example in which the BCG signal was contaminated by motion artifacts caused by brief physical movements of the body parts of the participant. In this case, a pECG signal was not generated because the amplitude of the |hBCG| signal was significantly decreased. In both cases, the resulting longer periods of the RRI and pRRI during the extrasystole and a longer period of the pRRI during the contamination of motion artifacts were considered outliers if the automatic artifact rejection criterion was satisfied.

Fig. 9.

Predicted ECG (pECG) profiles during the occurrence of an extrasystole (a) and temporary body movement (b) during measurements in the supine position. The pECG profile is predicted using the leave-one-subject-out cross-validation scheme. Closed black circles on the ECG and pECG signals represent the locations of the R wave detected using the finding peak algorithm. The calculated R–R interval (RRI) from the ECG (red open circles) and pECG (blue crosses) signals are presented. The BCG signal was temporarily silent owing to the lack of a ventricular contraction during an extrasystolic beat (arrow); thus, a pECG signal was not generated during this period (a). Furthermore, the generation of the pECG signal is hampered by the superposition of a body movement artifact (arrow) onto the BCG signal (b). ECG electrocardiogram, BCG ballistocardiogram, |hBCG| full-wave rectified bandpass-filtered BCG signal.

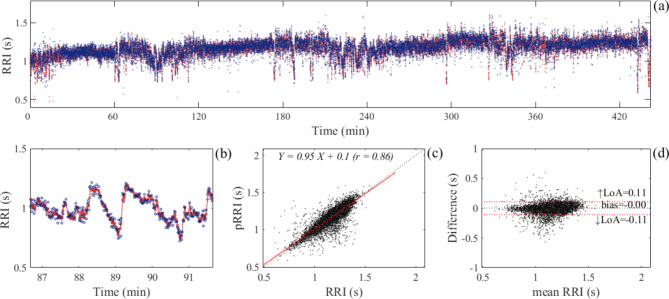
A representative example of the heartbeats analyzed from the overnight long-term recordings is shown in Fig. 10. For this participant, the total recorded time was 442 min, and 19,212 pECG heartbeats (coverage: 84.4%) were analyzed. Linear regression analysis demonstrated that the pRRI estimated from pECG signals correlated well with the reference RRI calculated from simultaneously recorded ECG signals, with a correlation coefficient of 0.86. Bland–Altman plot of the analyzed heartbeats demonstrated that the bias was zero and that the LoA was ± 0.11 s. The results of all participants are summarized in Table 3, and the heartbeats analyzed for each overnight long-term recording per participant are shown in Supplementary Fig. S2. None of the participants reported leaving bed at night or complaining about not being able to sleep. Because BCG signals can be interfered with and distorted by the motion artifacts owing to postural changes during sleep, analyzable heartbeats were reduced to 78.3% on average (Table 3). The MAE value varied from 0.028 to 0.060 s among the participants and the average value was 0.046 ± 0.010 s, which corresponds to 4.0% of the overall mean RRI (1.087 s). The correlation coefficients between the estimated pRRI and reference RRI ranged from 0.74 to 0.91. Bland–Altman analysis demonstrated that the mean bias was zero with upper and lower LoAs ranging between 0.14 ± 0.03 and − 0.14 ± 0.03 s, respectively, indicating a good mean agreement with a modest accuracy.

Fig. 10.

(a) An example of the analyzed heartbeats from the overnight long-term recording in a single participant. Red and blue dots represent the beat-to-beat interval of the heart analyzed from ECG and pECG signals, respectively. (a) Enlarged view of the part where the RRI shows high fluctuations during the period between 86 and 92 min. (c) Scatter plot and linear regression line (red line) for the RRI and pRRI calculated from the ECG and pECG signal, respectively. The regression equation and correlation coefficient of regression (r) are shown. (d) Bland–Altman plot of the analyzed heartbeats. The limits of agreement (LoA) and bias are displayed with dashed red lines and dashed black lines, respectively, along with their numerical values. The upper (↑LoA) and lower (↓LoA) LoA are presented with a ± 1.96 standard deviation (SD). ECG electrocardiogram, pECG predicted ECG signal, RRI R-to-R interval, pRRI predicted RRI calculated using the pECG signal generated by the deep learning model.

Table 3.

Comparison of the RRI and pRRI and the limits of agreements and bias derived from the bland–Altman plot analysis of overnight long-term recordings.

Participant ID	Record time (min)	Heartbeats (n)	Coverage (%)	RRI (s)	pRRI (s)	R	MAE (s)	Bias (s)	↑LoA (s)	↓LoA (s)
19	450	24,701	80.5	1.107 ± 0.174	1.097 ± 0.178	0.91	0.046	− 0.01	0.14	− 0.15
20	442	22,768	84.4	1.167 ± 0.099	1.166 ± 0.109	0.86	0.037	0.00	0.11	− 0.11
21	484	20,386	84.8	1.252 ± 0.179	1.258 ± 0.167	0.91	0.055	0.01	0.23	− 0.22
22	502	31,650	67.2	0.979 ± 0.090	0.979 ± 0.101	0.81	0.036	0.00	0.12	− 0.12
23	415	21,686	80.9	1.170 ± 0.092	1.167 ± 0.112	0.74	0.052	0.00	0.14	− 0.15
24	458	25,628	72.2	1.096 ± 0.116	1.094 ± 0.126	0.88	0.038	0.00	0.12	− 0.12
25	419	23,857	74.9	1.064 ± 0.097	1.063 ± 0.106	0.89	0.028	0.00	0.09	− 0.10
26	436	21,523	80.7	1.193 ± 0.100	1.193 ± 0.106	0.74	0.050	0.00	0.15	− 0.15
27	397	20,129	82.7	1.147 ± 0.097	1.144 ± 0.110	0.80	0.044	0.00	0.13	− 0.13
28	436	31,606	69.0	0.827 ± 0.081	0.827 ± 0.092	0.76	0.044	0.00	0.12	− 0.12
29	371	21,721	78.2	1.018 ± 0.119	1.015 ± 0.132	0.80	0.060	0.00	0.16	− 0.16
30	429	19,899	83.9	1.266 ± 0.102	1.263 ± 0.119	0.78	0.056	0.00	0.15	− 0.15
Mean ± SD	437 ± 36	23,795 ± 4069	78.3 ± 6.1	1.112 ± 0.121	1.106 ± 0.124	0.82 ± 0.06	0.046 ± 0.010	0.00 ± 0.00	0.14 ± 0.03	− 0.14 ± 0.03

Values are presented as means ± standard deviations (SD). RRI: R–R interval calculated from the ECG signal; pRRI: predicted RRI calculated from the pECG signal generated by the deep learning model; R: linear regression coefficient; MAE: mean absolute error; ↑LoA: upper limit of agreement; ↓LoA: lower limit of agreement.

Discussion

The present study aimed to evaluate the performance of heartbeat interval measurement using a pECG signal generated by the deep learning model learned from the BCG signals acquired from a PVDF sensor and simultaneously recorded reference ECG signals. By entering the preprocessed BCG (i.e., |hBCG|) and reference ECG signals as training data into the biLSTM neural network, the deep neural network generalizes the implicit mapping function between |hBCG| and genuine ECG signals by adjusting the connection weights in the stacked hidden layers containing neurons. The learned model generates a realistic ECG wave similar to a genuine ECG wave. However, the shape of the pECG waveform does not need to be exactly the same as that of the genuine ECG waveform; it is sufficient that the intervals between successive R-waves of the pECG are the same as those of the genuine ECG signals for the measurement of heartbeat intervals.

The estimated pRRI from the pECG signal via leave-one-subject-out cross-validation in the short-term recording showed a good agreement with the reference RRI irrespective of body postures, with an average MAE of 0.034 s, which corresponds to 3.7% of the average RRI observed (0.906 s). Moreover, the average SD of the MAE across participants for each recumbent position was low (0.006 s), indicating low inter-participant variability in the MAE. The Bland–Altman analysis indicated the presence of a small but significant proportional bias regardless of the body posture, whereas these biases were sufficiently small that they were unlikely to have a practical significance. As indicated in Table 4, Mora et al.¹⁹. achieved a smaller MAE than that reported using the current approach. This superior performance (IBI MAE: 4.7 ms) may be attributed to individual calibration procedures, which deal with inter-subject differences in the BCG signal morphology. The method based on the parameterization of local maxima in the BCG as well as on a modified k-means clustering algorithm achieved an MAE of less than 20 ms for IBI²². However, the requirement of repeating the training step whenever subjects change their posture in bed is a major limitation of this method. A previous study utilizing a wavelet-transform-based peak detection algorithm²¹ reported an LoA of 29 ms. Other studies^23,24 using a deep learning approach have also shown good results in terms of HR MAE or root mean squared error (RMSE). Pröll’s deep learning model, which was designed using stacked convolutional and recurrent deep network layers, achieved an MAE of ~ 2 beats/min (bpm) across 14 patients in a held-out testing set²³. However, the HR measurements were performed every 8 s patches, not on a beat-by-beat basis. Zhang et al.²⁴ proposed an auto-labeling technique using the biLSTM network to identify the IJK complex, and the model improved the accuracy of heartbeat detection with an HR RMSE of 1.4 bpm.

Table 4.

Comparison of parameters reported in previous studies on the measurement of heartbeats from BCG.

Paper	Study population (size)	Sensor type & location	Algorithm	Acquisition time	Coverage	Performance
Short-term recording
Mora et al. 19	Healthy (16)	MEMS accelerometer attached to a bed slat	J-peak annotation guided by subject-specific search windows	5 min	N/A	IBI MAE: 4.7 ms
Alvarado-Serrano et al.21	Healthy (7)	Piezoelectric sensor on a chair	Wavelet transform based J-wave detection	100 s	N/A	IBI LoA: 29 ms
Brüser et al.22	Healthy (16)	MEMS accelerometer on a bed	J-peak detection by feature vector & k-means clustering	26 min	95.9%	IBI MAE: 17 ms
Pröll et al.23	Hospital patients (14)	Pneumatic pressure sensor embedded in a bed	IJK complex detection by CNN + GRU DL	calculated each 8 s patch	100%	HR RMSE: 2.1 ± 1.1 bpm
Zhang et al.24	Healthy (8)	fiber-optics sensor attached to an arm-chair	IJK labeling by biLSTM DL	200–500 s	98.9%	HR RMSE: 1.4 bpm
Present study	Healthy (18)	Piezoelectric sensor placed under a bed sheets	ECG wave extraction by biLSTM DL	2 min	100%	IBI MAE: 34 ms
Overnight recording
Paalasmaaet al.9	Healthy (46)	Piezoelectric sensor installed under a bed sheet	Adaptive heartbeat shape modeling	N/A	54.1%	IBI MAE: 13 ms
Siyahjani et al.30	Healthy (45)	Pressure sensor embedded in a bed	Peak detection of bandpass filtered signal	459 min	N/A	30 s epoch HR LoA: 6 bpm
Zink et al.31	suspected SDB patients (21)	charged polymer foil placed under a bed sheet	Amplitude pattern tracking with quality index	TMT for all subjects: 93 h	65%	IBI MAE: 4 ± 72 ms
Schranz et al.25	Healthy (11)	3D-accelerometer embedded in a bed	J-peak detection by CNN + ResNet DL	TMT for all subjects: 134 h	N/A	IBI MAE: 27.9 ± 7 ms
Present study	Healthy (12)	Piezoelectric sensor placed under a bed sheet	ECG wave extraction by biLSTM DL	437 ± 36 min	78.3%	IBI MAE: 46 ± 10 ms

SDB: Sleep disordered breathing; MEMS: Micro Electro Mechanical Systems; HR: heart rate; IBI: inter-beat interval; bpm: beats/min; DL: deep learning; CNN: convolutional neural network; GRU: gate recurrent unit; biLSTM: bidirectional long short-term memory; ResNet: residual neural network; TMT: total measurement time; LoA: limit of agreement; MAE: mean absolute error; RMSE: root mean squared error; N/A: not available.

Methodological differences and variations in performance metrics preclude definitive comparisons across the studies; however, variations in Δt_R should be considered in relation to the MAE in the present study. As shown in Fig. 7; Table 2, even though the mean Δt_R was close to zero, variations were observed in the beat-to-beat Δt_R regardless of the body posture. More specifically, Fig. 8 provides an intuitive visualization of the variation in Δt_R, where the R-wave of the pECG appears to occur at the foot point of the |hBCG| signal. Assuming that the foot point of |hBCG| indicates the mechanical start of blood ejection, Δt_R variations would reflect inter-individual changes in the pre-ejection period (PEP). Previous study has suggested that the PEP shows high inter-individual variability and is prone to large changes under the influence of sympathetic and parasympathetic activities²⁸. However, in the case of the negative Δt_R shown in Fig. 8c, the foot point of |hBCG| preceded the onset of the R-wave of the genuine ECG signal, which cannot be explained by the change in the PEP. We assumed that, in some individuals, atrial contraction might have been captured with a significant oscillatory amplitude owing to the preprocessing of the BCG signal. Although the physiological interpretation of the origin of BCG waves is complicated, presystolic waves called “F” and “G” waves are found in the BCG signal¹⁵. These waves appear between the P and Q waves of the ECG or immediately before the QRS complex and are considered to be associated with atrial contraction or an atrial systole²⁹. Presumably, the first chunk of the bimodal-shaped oscillatory |hBCG| signal appearing at every heartbeat shown in Fig. 8c reflects atrial contraction that must have been the timing to generate the R-wave in the model. This may partially explain the extent of the MAE. The pRRI could be accurately estimated to yield the RRI as long as the |hBCG| signal is consistent across the heartbeats; however, if the |hBCG| signal fluctuates across the heartbeats, for example, if the first chunk of the bimodal-shaped signal shown in Fig. 8c becomes obscure or even absent, it may shift the time at which the R-wave occurs in the model, thereby causing an error in the pRRI estimation.

In this study, the feasibility of overnight long-term heartbeat interval detection was demonstrated with a good mean agreement and modest accuracy. The correlation of the estimated pRRI from pECG signals with the reference RRI ranged between 0.74 and 0.91 and the average MAE value was 0.046 ± 0.010 s. Bland–Altman analysis indicated that the zero bias resulted in an LoA of ± 0.140 s on average for 12 participants. These performances were lower than those for short-time recordings, which may be related to the increased number of heartbeats and the distortion of BCG deflection caused by slight body movements below the movement threshold or the ambiguous character of the BCG signal with interpersonal variability that does not conform to the sequence characteristic rule learned by the model. Further investigation is required to determine whether the performance improves with the expansion of the training dataset.

Siyahjani et al.³⁰ compared a BCG-derived HR using a pressure sensor embedded in a bed with polysomnography on an epoch-by-epoch basis. They achieved an LoA of approximately ± 6 bpm (Table 4). This is comparable with our finding of the beat-by-beat LoA of ± 0.14 s, which is equivalent to ± 7 bpm in terms of the HR. When evaluating the performance on the same epoch-by-epoch basis with a duration of 30 s, the LoA was reduced to ± 2 bpm. Zink et al.³¹. used an electromechanical film sensor to measure the length of the heartbeat cycle in patients with sleep-disordered breathing using polysomnography. They introduced a quality index that allowed the identification of segments with artifacts in the BCG signal and automatically excluded them from the analysis. Their proposed algorithm provided a good correlation of beat-to-beat cycle length detection with simultaneously recorded ECG signals with a correlation coefficient of 0.95 and an IBI MAE value of 4 ± 72 ms, indicating a higher accuracy than that reported in the present study. However, the number of analyzable heartbeats is significantly reduced (coverage of approximately 65%) when analyzing quality metrics. The algorithm based on adaptive heartbeat shape modeling combined with hierarchical clustering produced good results with an IBI MAE of 13 ms⁹. However, it showed large variability in the coverage rate (8.2–94%; average: 54.1%) possibly owing to the different clarity of the heartbeat shapes across the subjects. Recently, Schranz et al.²⁵. proposed a deep learning architecture consisting of convolutional and ResNet neural networks for modeling discrete reference heartbeat events with a symmetric kernel function. The results obtained using their model were in good agreement with the reference ECG, showing an IBI MAE of 28 ms.

It is worth mentioning that, for preprocessing the BCG signal, we employed a bandpass filter followed by a full-rectification technique and estimated the optimum lower cutoff frequency that would provide the highest coherence value between the preprocessed BCG and reference ECG signals. To predict a waveform similar to a genuine ECG signal from a BCG signal using a deep learning regression framework the deep neural network must be inputted with a dataset containing common frequency components present in both signals. As shown in Fig. 3b, applying a full-wave rectification process to the bandpass-filtered BCG signal yielded several clear spectral peaks at the dominant frequency of heartbeats and extra signal components from the raw BCG signal were removed through harmonics. We considered that this preprocessing helps ensure that the most relevant frequency components related to the heartbeat are selected as training data; therefore, the model is constructed appropriately.

According to previous reports, without using deep learning, a pseudo-ECG waveform can be estimated from a BCG signal. Al Ahmad et al.^26,27 demonstrated the feasibility of extracting an ECG corresponding signal using a chest-worn piezoelectric sensor by identifying an inverse transfer function between piezoelectric output voltages and ECG signals in the frequency domain; however, the quantitative accuracy of the IBI measurements was not reported.

Methodological limitations remain to be addressed before implementing this approach in the healthcare domain. The present study was compromised by the small sample size of the training dataset and was conducted only on young healthy participants to understand inter-subject variability in a reasonably uniform study population. However, there is substantial variation in the shape and amplitude of BCG waveforms among the individuals¹⁴. Previous studies have suggested that the BMI is positively correlated with the performance metrics of the MAE for beat-to-beat interval estimation⁹. Hence, future studies should include a larger sample size with wider age and BMI ranges to increase the generalizability of the pECG model. Furthermore, validation should be performed with more diverse participants, including elderly people and patients with pathologies, particularly when applied to those with irregular heartbeats. If the current pECG model is applied to patients with frequent arrhythmia, a similar performance may not be achieved. Further testing is required to clarify the accuracy of the proposed approach for extremely short or long heartbeat intervals. For application in an at-home setting, it may be worth considering collecting an individual’s data and tailoring the pECG model to that individual because the variability of the BCG waveform within the same individual is comparatively low³².

In summary, a deep learning approach for the extraction of ECG signals from a BCG was proposed for accurate heartbeat interval measurements. We demonstrated the feasibility of using BCG signals to provide an unobtrusive method to estimate the RRI with practical performance when the participant is asleep. Deep learning with a regression framework used in the present study does not require complex feature extraction of heartbeats in BCG, like previously reported signal processing approaches. In addition, we have shown that an ECG corresponding signal can be estimated by feeding the BCG signal, preprocessed through a simple bandpass filter followed by full rectification, into a deep biLSTM network. The proposed method simplifies peak detection and requires a low computational load once the model is built. Although our model does not necessarily outperform the previously reported best performing models, it shows consistent results across different participants and different lying postures.

One of the prominent features of the BCG is the ready accessibility and reusability of the sensors, which allows us to deploy the sensor in the home environment of the individual and perform measurements without affecting user comfort and the presence of medical staff. We expect that the proposed approach will be a viable alternative to conventional methods of HR monitoring in settings outside hospitals, provided that the above issues are satisfactorily addressed.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

K.N. contributed to study conceptualization. T.S. and K. N. performed the experiments and collected the data. K. N., S.I. and S. M. drafted the original manuscript. N.M. and M.K. contributed to the critical revision of the manuscript for intellectual content. All authors have approved the final version of the manuscript for publication. K.N. takes responsibility for the integrity of the data and accuracy of the data analysis.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.