Temporal and spatial variations of urban surface temperature and correlation study of influencing factors

Abstract

Urban overheating significantly affects thermal comfort and livability, making it essential to understand the relationship between urban form and land surface temperature (LST). While the horizontal dimensions of urban form have been widely studied, the vertical structures and their impact on LST remain underexplored. This study investigates the influence of three-dimensional urban form characteristics on LST, using ECOSTRESS sensor data and four machine learning models. Six urban morphology variables—building density (BD), mean building height (MH), building volume (BVD), gross floor area (GFA), floor area ratio (FAR), and sky view factor (SVF)—are analyzed across different seasons and times of day. The results reveal that MH, BD, and FAR are season-stable factors, with higher MH correlated with lower LST ((e.g., an observed reduction of approximately 3 °C in spring), while higher BD is associated with higher LST (e.g., an increase of about 3.5 °C in autumn). In contrast, BVD, GFA, and SVF are season-varying factors with variable impacts depending on the time of year. Higher BVD is generally associated with elevated LST, while GFA and SVF are linked to lower LST. These associations reflect absolute changes in LST, measured directly from ECOSTRESS data. These findings offer valuable insights into the complex interactions between urban morphology and LST, helping to inform strategies for urban heat mitigation and sustainable planning.

Introduction

The intensifying impacts of urban heat islands (UHI) and heat waves are exacerbated by climate change and increasing urbanization^1–3. According to the United Nations, 70% of the world’s population will live in cities by 2050, which is an increase from 54% in 2016⁴. The IPCC’s Sixth Assessment Report states that global surface temperatures have risen by 0.99 °C since 1850–1900, with irreversible impacts once warming exceeds 1.5 °C⁵. UHI effect is a key factor in characterizing the impact of urbanization on the microclimate and an important factor of urban ecological effects. UHI effect has a global impact, with increasingly dramatic effects on regional climate change, urban atmospheric patterns, energy consumption, and population health. The increasing importance of the urban thermal environments to human well-being has become a matter of public concern.

Urban thermal environments can be measured using either air temperature (AT) or land surface temperature (LST)⁶. Measured mainly by fixed weather stations, AT has high spatial and temporal resolution, allowing for long-term historical data recording⁷. It also correlates well with human perception, making it widely used for exploring temporal temperature variations in different climates⁸. However, the limited and sparse network of weather stations can only provide localised temperature variations in cities⁹. In addition, satellite remote sensing LST is directly correlated with surface features and has the advantages of clear spatial information, wide coverage, and providing extensive spatial coverage and addressing the high variability of surface conditions^10,11.

Surface temperature is closely related to urban thermal environment factors from both two-dimensional (2D) and three-dimensional (3D) perspectives. The 2D factors of the urban thermal environment include landscape composition (e.g., proportion of impervious surfaces, vegetation cover, and water distribution) and landscape pattern (e.g., patch density, edge density, patch cohesion, and maximum patch index), as well as socio-economic factors (e.g., artificial heat emissions, nighttime lighting, population size, and road density)^12–14. However, 3D factors also play a key role in regulating the urban thermal environment. These 3D factors mainly include building height, sky view factor and building frontage area index^15,16, as well as 3D tree features and topographic elements (e.g., elevation, slope, and slope direction)^17,18. Landscape composition significantly impacts the urban thermal environment by determining solar radiation absorption efficiency and heat dissipation via evapotranspiration, thereby affecting energy transfer and heat balance^19,20. However, 3D factors further regulate the urban thermal environment by influencing the distribution of solar radiation, air flow patterns, and evapotranspiration within urban canyons²¹. Building height and sky view can significantly alter the angle of incidence and coverage of solar radiation while affecting the distribution of heat in urban canyons²². Topographic factors, such as elevation and slope, also profoundly affect surface temperatures by altering radiation reception and heat accumulation patterns²³. The combined effects of 3D factors cannot be ignored in the regulation of urban thermal environments, and their importance increases with the complexity of the urban spatial structure.

Despite extensive research on the effects of urban 2D and 3D factors on LST, several aspects warrant further exploration. First, as the Earth rotates and revolves, the solar intensity and seasonal climate in the same region also change. Therefore, the effect of urban thermal environment factors on LST will be different in the 24-hour cycle versus the four seasons. ASTER (90 m)²⁴and Landsat 5–9 (60–120 m)²⁵have fixed observation times, leading to limitations: ASTER provides fewer images for each city, while Landsat cannot acquire nighttime images, resulting in temporal continuity issues²⁶. On 29 June 2018, the LST survey conducted by the National Aeronautics and Space Administration (NASA)-built Ecosystems Onboard Experimental Calorimeter for Thermal Emission on Satellites (ECOSTRESS) was launched to the International Space Station (ISS). ECOSTRESS is capable of fine imaging of urban temperatures at different times of the day and night with a resolution of 70 m²⁷. Its good diurnal acquisition capability and spatial temporal resolution give it great potential for the observation of daily changes in urban surface temperature. Secondly, scale control is a core issue in urban climatology research strategies, modelling and applications²⁸. Existing analyses of the effect of 2D, 3D factors on LST have focused on grid, city and region scales, however, less attention has been paid to the scale of city blocks^29–31and the drawback of this method is that if the resulting grid is too large, the samples are too small, which is prone to overfitting in the nonlinear model, and vice versa, if the grid is too small, it will lead to a large error³². In general, cities consist of many urban neighbourhoods including many landscapes, especially buildings with different heights and layouts, which significantly affect the thermal environment³³. Neighbourhoods, as a kind of mesoscale spatial unit, can to some extent compensate for the lack of precision in large-scale geographic studies of administrative districts and the lack of macroscopic effects at small scales of buildings³⁴.

Our goal is to comprehensively explore how 3D building form factors affect LST during the day-night and seasonal cycles in the central Shijiazhuang city area. Machine learning models were applied to conduct regression analyses between these factors and ECOSTRESS LST. By doing this, we quantify the patterns and correlations of the effects of 3D building morphology on surface temperature during day, night and season. These results will provide theoretical basis and scientific guidance for future urban renewal, building site optimization and mitigation of urban heat island effect in Shijiazhuang

Study area and data

Study area

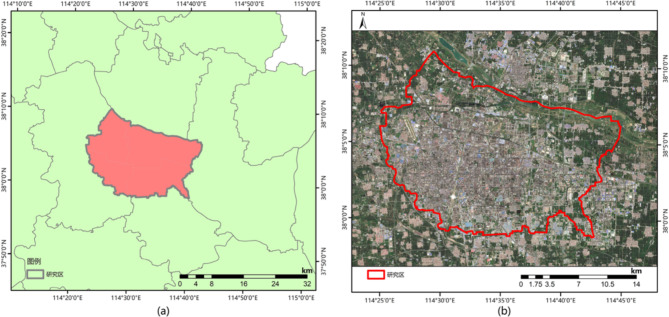
Shijiazhuang, located in Hebei Province, China, has a temperate monsoon climate with an average annual temperature of 13.5 °C and annual precipitation ranging from 401.1 to 752.0 mm. The city covers approximately 14,530 km² and has a population of 11,204,700 people at the end of 2021. This paper focuses on the city center of Shijiazhuang, as shown in Fig. 1. The study area includes Qiaoxi District, Xinhua District, Yuhua District, and Chang’an District, which are all part of the Third Ring Road of Shijiazhuang. This area is densely built up and contains various types of buildings. In this paper, we will study the influence of three-dimensional building parameters on urban land surface temperature.

Fig. 1.

(a) Location of the study area in Shijiazhuang (b) Landsat8 live image of the study area.

Land surface temperature

The research utilizes surface temperature data from the atmospherically corrected surface temperature and emissivity secondary product of the International Space Station’s Experimental Characterizations of Thermal Emission from Ecosystems (ECOSTRESS). The data product employs a temperature and emissivity separation method based on physical principles to provide a high-resolution 70-meter image product in mown format^35,36. A comparison between cloud-free ECOSTRESS situations and measurements derived from sensors with aerial calibration revealed a significant level of data concurrence³⁷. The average root mean square error (RMSE) was 1.07 K, the mean absolute error (MAE) was 0.40 K, and the r2>0.988 for all sites³⁸.

Images were selected under optimal weather conditions, specifically with less than 5% cloud cover, to ensure data accuracy. Surface temperature readings were collected at various dates and times due to the orbit restrictions of the ISS. After the screening, five-time points (as indicated in Table 1) were chosen to accurately measure variations in surface temperature over a day. Data was gathered from July to October, spanning the years 2018 to 2022. The research area encompasses the urban region of Shijiazhuang, characterized by a consistent and unchanging pattern of construction development. The buildings in the central region of Shijiazhuang have remained the same from 2018 to 2022. Consequently, the influence of temporal variations on the study findings is deemed negligible.

Table 1.

Weather conditions at different observation times.

Date	Time(China Beijing time)	maximum temperature /℃	Minimum temperature /℃
September 21, 2022	00:31	26.33	7.07
September 13, 2022	03:45	34.27	12.61
October 25th, 2022	04:20	16.69	−4.29
July 7, 2020	07:20	34.21	20.53
September 1, 2022	08:37	35.81	17.75
August 8, 2022	11:51	60.79	−4.10
October 9, 2022	17:14	26.79	0.95
July 10, 2022	22:23	29.07	12.37

For the study of 3D building morphology and seasonality, Landsat 8 collection 2 level 2 data were selected for inversion in this paper. The cloudless thermal images of the four seasons of 2022, obtained on 21 February, 10 April, 7 July, and 25 September, were gathered.

Data on building morphology.

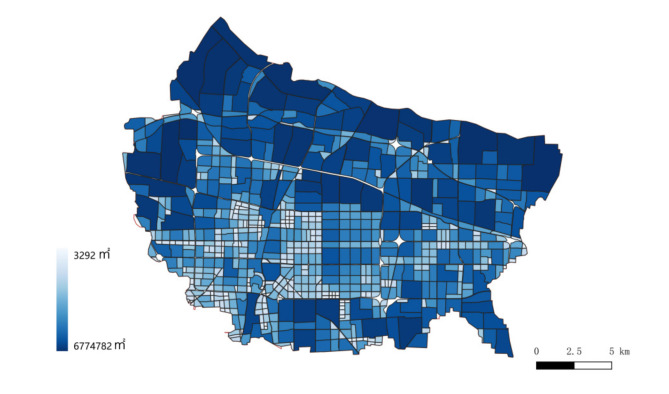
The building data used in this investigation was acquired from OpenStreetMap (OSM) in November 2022. The dataset provides details regarding the geographical coordinates, architectural structure, and elevation of buildings in Shijiazhuang, and includes corresponding road infrastructure details. The QGIS software is used for format conversion and partitioning of blocks. OSM road data is used to divide the blocks. This study, after running multiple tests and taking into account the block scale, chooses six categories of data to build the road network: highways, main roads, subsidiary roads, third-class roads, residential roads, and some unclassified roads. Ultimately, a total of 706 blocks are acquired through the process of division (Fig. 2).

Fig. 2.

Shijiazhuang block division map.

Methods

Calculation of 3D building form factors

To depict the shape of buildings, we have chosen six common three-dimensional building form factors: building density (BD), mean height (MH), mean volume of buildings (BVD), gross floor area (GFA), floor area ratio (FAR), and sky view factor (SVF). These characteristics are explicitly described and are calculated in terms of blocks. BD refers to the percentage of area occupied by the planar projection of buildings in a unit area. A high building density implies a high intensity of land use and development within the blocks. MH refers to the ratio of the total height of buildings to the number of buildings in the blocks. BV is the ratio of the total volume of buildings to the number of buildings in the blocks. GFA refers to the total floor area of buildings in the blocks. The FAR is the ratio of the total above-ground floor area of the block to the area of the block. SVF is a value that describes the 3D urban form and ranges from 0 (no sky visible) to 1 (no horizon obstacles visible). This factor measures the degree of 3D open space and can be expressed as:

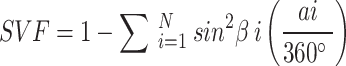1

where N is the total number of sky hemisphere obstacle-obscuring sectors, and αi and βi are the azimuth and maximum building height angles for each sector³⁹.

Multi-collinearity check

The Variance Inflation Factor (VIF) and Tolerance are commonly used metrics for evaluating the level of multicollinearity between the i-th independent variable and other independent variables in a regression model. Multicollinearity can lead to inflated standard errors and unreliable coefficient estimates in the model, potentially distorting the observed relationships between LST and its explanatory factors, thus complicating interpretation^40–42. In this study, six independent variables were employed, and though some exhibited moderate correlations, as shown in Table 2, multicollinearity diagnostics were conducted to assess the severity of the issue. The VIF was used in this study to detect multicollinearity, which can be calculated using the following formula:

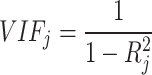2

Table 2.

Variance inflation factor of different indexes.

Data	BD	MH	BVD	GFA	FAR	SVF
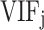
	3.44	4.71	8.26	1.18	5.42	1.66

In this context, 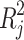denotes the coefficient of determination of the auxiliary regression that includes several explanatory variables. A greater value of 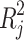suggests a stronger multicollinearity between the variables and a higher 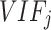. Empirical evidence demonstrates that when 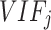≥ 10, it indicates that there is serious multicollinearity between the explanatory variables and the rest of the explanatory variables and should be removed from the model⁴³. After calculation, all variable VIF values were restricted to less than 10.

Machine learning model

Four regression models were built, with the six parameters as independent variables and LST as the dependent variable. The models consist of Gradient Boosting Machine (GBM), Multivariate Adaptive Regression Splines (MARS), Multivariate Linear Regression (MLR), and Random Forest (RF). GBM is a widely used machine learning algorithm that has achieved notable success in diverse domains, including biology and medicine. The algorithm constructs a series of shallow trees in a sequential manner, where each tree acquires knowledge and enhances its performance based on the preceding one^44,45. MARS is an algorithm that adaptively builds piecewise linear models by identifying optimal points (knots) in the data, allowing it to effectively capture nonlinear relationships. MARS exhibits a high level of adaptability and precision in its model predictions⁴⁶. This method facilitates the straightforward assessment of the combined impact of individual variables and the interplay of several variables⁴⁷. MLR employs a divide-and-conquer approach by partitioning the feature space into multiple localised regions and constructing a linear model in each region⁴⁸. The outcome is generated via a weighted aggregation of linear forecasts. The suggested method utilises a novel approach to acquire knowledge about non-linear interactions between features in the original space. It also has the capability to automatically identify patterns that may be applied to other datasets. This leads to a significant enhancement in both efficiency and accuracy when compared to manual techniques. RF is a non-linear, non-parametric machine learning technique that was initially introduced for prediction and regression tasks in several domains. The learning process relies on a decision tree, and the selection of samples is entirely random, making it insensitive to multivariate covariance. Additionally, RF assigns an importance value to each element, enabling the quantification of the impact of each variable⁴⁹. It requires relatively little parameter tuning to achieve good predictive performance. We selected four regression models—GBM, MARS, MLR, and RF—based on their ability to handle complex, non-linear relationships between urban morphology and LST. GBM and RF are ensemble methods known for their robustness in modeling non-linear interactions, while MARS offers flexibility through segmented linear regression⁵⁰. MLR was included as a benchmark linear model to compare the performance of parametric vs. non-parametric approaches⁵¹. Each model was chosen to explore different aspects of how urban form influences LST, with non-parametric models generally expected to perform better due to the complex nature of the urban environment⁵².

With the exception of MLR, all models used in this study are non-parametric, meaning they do not rely on predefined assumptions about the functional form of the relationships between the variables. While non-parametric models offer flexibility, they can still suffer from overfitting, which occurs when a model performs well on the training data but fails to generalize to unseen data (test set)⁵³. To detect and mitigate the risk of overfitting, we employed repeated k-fold cross-validation (CV), a robust evaluation technique that divides the data into multiple subsets⁵⁴. Cross-validation does not directly prevent overfitting; instead, it helps assess a model’s generalization ability by ensuring every data point is included in both training and validation phases across different trials⁵⁵. Specifically, in each fold, one segment of the data is used as the validation set, allowing for performance evaluation on unseen data, while the remaining segments serve as the training set. This iterative validation approach provides a more reliable estimate of the model’s performance on genuinely unseen data, which also aids in hyperparameter tuning⁵⁶.

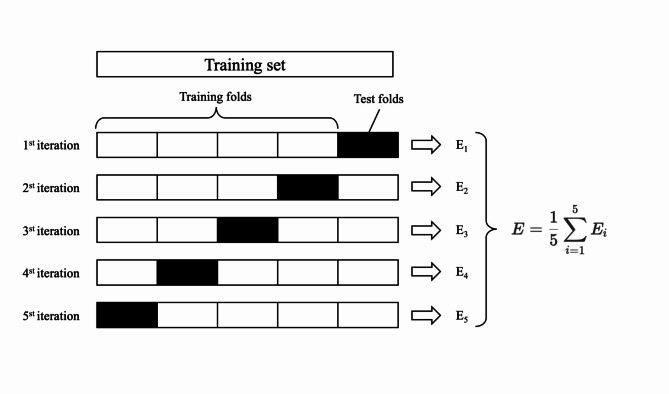
Generally, values of k range from 5 to 10, but it can vary significantly based on the dataset size and characteristic. A smaller k (like 2–4) might lead to high bias in the model evaluation, while a larger k leads to lower bias but potentially higher variance⁵⁷. In cases of larger datasets, a smaller value, such as 5, is often used to reduce computational cost without significantly impacting the reliability of the performance estimates⁵⁸. In our study, the validation set is considered by repeated 5-fold cross-validation method. This method divides the data into 5 folds, where in each iteration, 1 fold is used as validation set while the remaining 4 folds are used for training. Each fold is used as a validation set once and the process is repeated several times to ensure reliable performance estimates. The final model performance is the average of all these iterations, which provides a more reliable measure of the model’s ability to generalize to unseen data. This technique does not rely on a single test set, but rather utilizes multiple validations of different data slices to fine-tune the model. Figure 3 illustrates the steps used in calculating the performance of the model through 5-fold cross-validation.

Fig. 3.

The steps for calculating the performance of the model trained using 5-fold.

By averaging the accuracy across the five trials, we estimated the model’s overall performance. To further quantify performance, the Root Mean Square Error (RMSE) was computed for each model, with the most optimal model identified based on this metric.

Partial dependence plot, PDP

The global approach characterises the overall tendencies of a machine learning model, whereas the local approach characterises its individual tendencies. Global approaches are commonly formulated as anticipated values derived from the distribution of data. The Partial Dependence Plot (PDP or PD) displays the predicted outcome when all other factors are marginalized. It illustrates the marginal impact of one or two features on the prediction of a machine-learning model⁵⁹. The partial correlation plot can provide insights into the nature of the relationship between the target variable and the attributes, revealing whether it is linear, monotonic, or exhibits a more intricate pattern. The partial dependence plot (PDP) is a frequently employed tool in machine learning models for examining the individual influence of each factor on the LST. It demonstrates the impact of individual variables (such as BD, MH, and BV) on the model’s predictions, while keeping all other element constant.

Results and analysis

Model performance

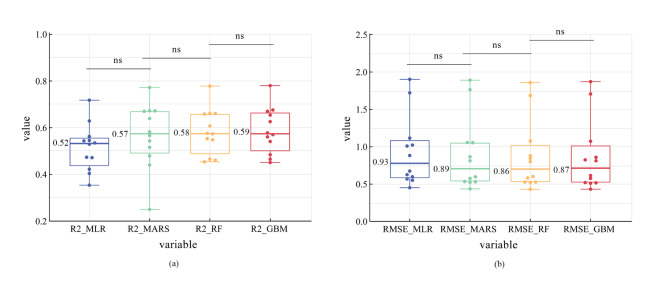
The study aims to examine how urban design affects the seasonal and daily patterns of LST at a detailed spatial level, while also conducting a relative relevance analysis. In order to accomplish this, multiple statistical models were trained with LST as the dependent variable (y-variable) and urban form as the independent variable (x-variable). The precision of each regression model was assessed using R² and RMSE as metrics (refer to Fig. 4). The findings demonstrate that all models had strong performance, as evidenced by average RMSE values ranging from 0.860 to 0.927 and average R² values ranging from 0.516 to 0.588. A decreased RMSE value and an increased R² value imply a model with improved accuracy. Non-parametric models, such as GBM, MARS, and RF, shown superior accuracy in comparison to the parametric model MLR. GBM outperformed the others. Hence, the GBM model was chosen for subsequent investigation.

Fig. 4.

(a) R2 values for four regression models. (b) RMSE values of four regression models.

Importance analysis

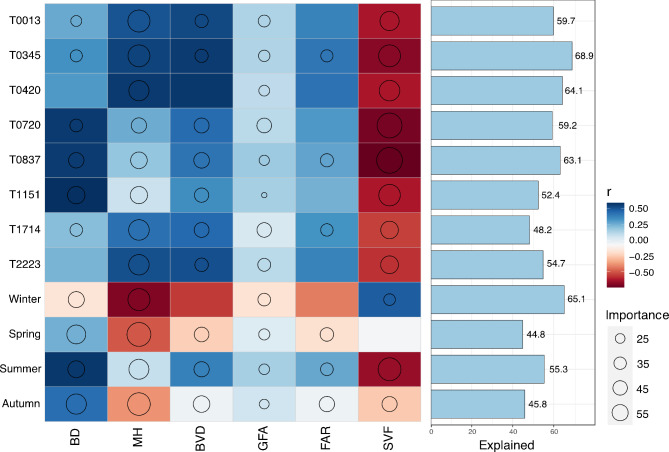
Figure 5 displays the correlation ranking of the impacts of the six measures on LST. The study examines the impact of three-dimensional architectural elements on day-night LST from July to October. Table 1 displays the specific information of the chosen data. The eight data points obtained by ECOSTRESS are categorized into three distinct time intervals: (1) 07:20 to 08:37 (morning), (2) 11:51 to 17:14 (afternoon), (3) 22:23 to 04:20 (night). During the morning, there was an inverse relationship between SVF and LST, but BD exhibited a positive connection. During the afternoon, BD, MH, and SVF were the primary determinants, with BD exerting the most significant impact at 11:51, MH having a greater influence at 17:14. During nighttime, MH exerts the most significant impact on SVF, whereas BV has the second most substantial influence. The influence of six elements on LST in all seasons is evident. BD has the most pronounced impact on LST during the summer, autumn, and winter seasons, highlighting its importance compared to the other six element. MH exhibits a negative correlation in spring, autumn, and winter, but a positive correlation in summer. This indicates that shadows play a role in decreasing LST as the solar altitude angle decreases and building shadows increase during seasonal changes. Among the many parameters, GFA and FAR exert the least influence on LST.

Fig. 5.

Explanatory rates between different indicators. The color change of the heat map indicates the magnitude of the correlation between the 3D building form factor and the longitudinal axis at different times; the circle in the map indicates importance(%), and the bar on the right side is the degree of Explained variation(%) of the effect of the 3D building form on the LST at different times.

Analysis of factors affecting urban surface temperature under different seasons

This research employs Partial Dependence Plot (PDP) analysis to assess the influence of six correlation factors on LST. The PDPs demonstrate the impact of the correlation factors on LST at various time points, providing a more thorough comprehension of the intricate connection between them. This approach is more advantageous than traditional multiple linear regression, as it is capable of elucidating not just the linear correlation between factors and LST. The partial correlation plot in Fig. 5 displays the relationships between the six three-dimensional architectural variables and the four seasons. The X-axis represents the distribution of data, where denser data corresponds to a greater quantity of data. If the data distribution is characterized by a low density of data points, the trend line may not be provide an accurate representation and should be disregarded. The graphic demonstrates that certain elements display consistent trends across different seasons, whilst others do not. The six elements were categorized into two categories: season-stable factors (MH, BD, FAR) and season-varying factors (BV, GFA, SVF). We analyzed and summarized the different correlations between the various factors.

In relation to the seasonal stability factors, it was observed that as the MH increased, the LST tended to decrease (Fig. 6). Additionally, it was discovered that the BD exhibited a positive correlation with LST. Similarly, the FAR showed a positive correlation when the ratio was below 1, but a negative correlation afterwards. The largest changes in LST caused by MH were − 3.0 °C, −2.0 °C, −1.4 °C, and − 2.0 °C, respectively, with an average of −2.1°C across all four seasons. This demonstrates the cooling effect of MH on LST. Based on the regulation mechanism of LST, the influence of building height on LST is complex and context-dependent. In autumn, the LST exhibited an initial increase followed by a decrease with increasing MH, with a node occurring at 12.5 m. This occurs due to more heat is trapped in the building canyons. Conversely, higher structures experience cooler temperatures due to the creation of additional shaded regions. This reduces the amount of direct solar radiation received by non-building surfaces and thus reduces warming caused by solar radiation⁶⁰. The most significant building density (BD) warming impact occurs in fall, with a temperature increase of 3.5 °C. This indicates that a higher concentration of buildings in the vicinity results in reduced wind speed, hence decreasing ventilation efficiency and further raising the local temperature. The influence of FAR on LST is extremely slight, with an inflection point at a ratio of 1. The rationale behind this is analogous to that of MH.

Fig. 6.

Partial Dependence Plot of seasonal LST with input variables.

With respect to the seasonal variation factor, BV exhibited two distinct patterns. During the summer, autumn, and winter seasons, BV exhibited a progressive rise followed by a decline, reaching a turning point when BV reached a value of 4. During the spring season, there was a negative correlation between BV and LST. Among the factors considered, GFA had the smallest influence on LST and had distinct patterns in each of the four seasons. In contrast, SVF exhibits a positive correlation with LST in spring, while showing a negative correlation in autumn and winter. This reflects the variable impact of SVF on temperature regulation depending on seasonal weather patterns. The maximum cooling effect in Shijiazhuang is −3°C, which is attributed to the sunny and less rainy weather during this season. This indicates that when the size of the SVF increases, the efficiency of airflow and heat transmission also increases⁶¹. In summer, SVF and LST exhibit a complex correlation. Initially negative. The correlation becomes positive when SVF is in the range of 0.4–0.5, before returning to a negative correlation. It is hypothesized that the positive correlation between SVF and LST is due to the increased incident sunlight resulting from a larger SVF. Conversely, the subsequent negative correlation attributed to the facilitation of air movement in the street canyon through convection, which is supported by a larger amount of open space, resulting in a decrease in LST. The study illustrates that SVF plays an important measure of 3D cities, but its impact on LST is intricate and contingent on the specific environment⁹.

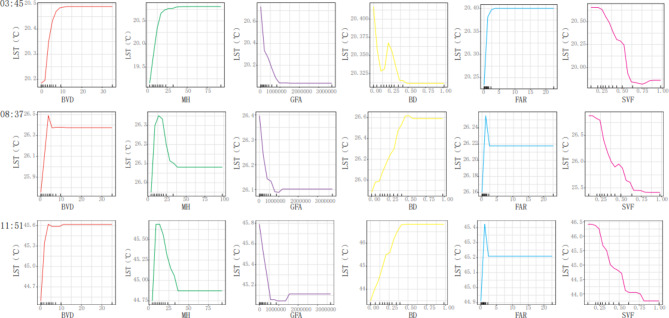
Analysis of factors affecting urban surface temperature under diurnal conditions

In the study on the diurnal effect factor, three specific time points were chosen based on their high explanation rate. These time points are 03:45, 08:37, and 11:51. The explanation rate for each of these time periods is presented and examined in Table 3. Figure 7 illustrates a one-way PDP analysis that examines the impact of the 3D building form factor on LST at three-time points. The BV in Shijiazhuang shows a positive association with the summer LST at various time points. The correlation between them is nearly linear, with a sharp reduction of 0.1 °C in LST in the afternoon when the BV approaches 4. The second variable of the study, LST, exhibits a progressive increase as MH increases throughout the night. However, during the daytime when MH exceeds 12.5 m, the surface temperature of Shijiazhuang experiences a significant fall as building height increases. The factor GFA exhibits a minimal impact on LST and demonstrates a negative correlation throughout. However, once it is above a threshold of 10⁷, there is a brief period of plateauing followed by a slight increase after stabilizing. The variable BD exhibited significant fluctuations during the night, with a decrease in LST corresponding to an increase in BD ranging from 0 to 12%. This relationship indicated a positive connection between BD values of 12.3% and 19.5%. Subsequently, the correlation became negative before gradually stabilizing. BD and LST were positively correlated in the morning and at noon, and the slope was more stable at noon than in the morning. The variables FAR and LST exhibited a linear correlation. Specifically, LST showed a positive correlation with FAR when the FAR ratio was below 1 throughout the morning and midday. Conversely, LST steadily declined when the FAR ratio exceeded 1. During nighttime, there was a consistent positive correlation between FAR and LST, and their rates of change decreased and reached a stable level. The impact of SVF on LST was not consistently linear. The curves demonstrated that LST declined rapidly with a steeper slope after SVF beyond around 0.25. Before that point, there was no notable alteration in LST as SVF increased.

Table 3.

Explanation rate at different time points.

Time	00:13	03:45	04:20	07:20	08:37	11:51	17:14	22:23
Explanation	59.743	68.931	64.119	59.202	63.105	52.436	48.157	54.741

Fig. 7.

Partial Dependence Plot of diurnal LST with input variables.

Discussion

Selection of analysis scales, machine learning algorithms

A large number of studies have explored the effects of 2D/3D urban landscapes and buildings on LST, and the scales of analyses have mainly focused on the grid scale. For example, Han et al. investigated the scale effect of urban morphology on LST, selected 13 scales from 30 to 600 m, and pointed out that 270 m was the optimal scale to study the effect⁶². Chen et al. explored the effect of urban spatial morphology on LST in 10 sizes (60 to 600 m) indeed, and identified 60 m as the most suitable scale¹⁰. Although these effects have been extensively studied at the grid scale, fewer studies have been conducted at the urban scale. Unlike conventional grids, urban neighbourhoods are demarcated by roads or rivers and have been shown to be independent thermal zones^63,64. The effect of 2D/3D urban factors on LST vs. at different times remains uncertain, especially at the neighbourhood scale, and therefore neighbourhoods were chosen as the unit of analysis to explore the effects at different times.

Many statistical methods, such as ordinary least squares regression and multiple linear regression, have been widely used to explore the effects of urban factors on LST^65,66. In recent years, scholars intensity impacts are complex and nonlinear⁸, and the above methods cannot meet the needs of exploring the impacts due to the simple assumption of linearity¹⁸. Machine learning algorithms, such as MARS, RF, and GBM, have an advantage in capturing nonlinear relationships to obtain relative importance and marginal effects, and this method has been used to explore the replicated nonlinear relationships of urban factor effects on LST⁶². In this study, four machine learning algorithms, including three nonlinear models and one linear model, were selected to explore the influence of urban 3D morphological factors on LST. The performance of the algorithms is first evaluated. Referring to existing studies, R² and RMSE are selected as the indicators to evaluate the model performance fitting performance, and the dependent variable is estimated using the test data set¹¹. The results show that the nonlinear regression model still outperforms linear regression in this study, which is consistent with previous scholarly studies, and the GBM performs optimally. Although there are errors in the fitted models determined by the four machine learning algorithms, this is tolerable because other factors, such as meteorological parameters, were not considered in this study⁶³. Therefore GBM is best suited for research at the urban neighbourhood scale.

Day and Seasonal effects of 3D urban factors on LST

Using the GBM model, in comparing the data in the morning and at noon, it is found that the slope at noon is always greater than that in the morning, regardless of the warming or cooling effect of the 3D building factor on LST. This may be due to the slower warming of the urban surface in the morning when the sun angle is lower, so we can conclude that the effect of urban characteristics on LST is mainly determined by the intensity of sunlight, rather than a single day/night division. We find that the average height of buildings in a neighbourhood has a significant effect on LST during daytime and nighttime, with taller buildings providing more shading, which is beneficial in reducing LST, although the opposite effect occurs when the average height of buildings is lower than 12.5 m. This can be attributed to 2 reasons: firstly, taller buildings block out more solar radiation, creating a larger shaded area to cool the surface temperature. Secondly, the roughness of the surfaces of high-rise buildings promotes mechanical turbulence, thus increasing convective heat dissipation. This is similar to the results of previous scholars studying Wuhan, Shanghai and Beijing, albeit with turning points of 10, 30 and 60 m respectively^67–69, which may be due to climatic and seasonal wind directions. It is also worth noting that it is wrong to arbitrarily assume that taller buildings reduce LST, as this conclusion only considers LST during the daytime. On the contrary, our study found that higher MHs consistently increased LST at night due to the fact that the shadow of the buildings disappears with the sun as the evening progresses, when heat emitted by impervious surfaces is trapped in urban canyons leading to an increase in temperature²¹. Higher BD means more heat storage between buildings, less heat evaporation, and poorer ventilation. In our study, the heating effect of BD on LST is stable, which is consistent with previous studies^67,70. The effect of SVF on LST is complex, and the results of our study show that SVF is mainly negatively correlated with LST, which mainly affects the ventilation and incoming solar radiation in a way that affects urban surface temperature. A larger SVF means better air circulation in a dense built environment, which will take away some heat and lower the temperature, while more solar radiation enters and increases the temperature, and the effect of SVF on the surface temperature is ultimately determined by the trade-off between these two aspects. Therefore, the effect of SVF on LST shows complex variations in summer⁷⁰.

In terms of urban planning, according to our study, different urban characteristics affect LST to different degrees, which suggests that urban planning efforts should be ordered accordingly. Overall, the most important thing to improve the thermal environment is to reduce the urban density, on the other hand taller buildings can provide extensive shading and some researchers have suggested that building heights can be increased to reduce the LST. however, from the night time data we measured, the average building heights show a positive correlation with the LST, at night time people are mainly at home and higher temperatures increase the use of air conditioning, leading to higher energy consumption in buildings, which in turn increasing greenhouse gas emissions and affecting sustainability. Therefore, it is important to be conservative when attempting to increase building heights.

Limitations

There are still some limitations in our study. Firstly, the LST data comes from satellite observations on top of the city, which may ignore vertical surfaces and cause bias in understanding the real thermal environment, especially in densely built-up areas. Secondly, the satellite image data is a mixture of multiple surface types, from which it is difficult to extract the roof temperature of a specific building, while other structures such as roof framing and planting are also non-excludable elements that can affect the data. Thirdly, in future studies, it is possible to fuse data from multiple sources at more sophisticated scales, such as surface temperatures captured by drones, or even to combine some microclimates with simulation models and observational data to gain a deeper understanding of the urban thermal environment. Fourth, the analyses were conducted in one city, and since seasonal climates and diurnal temperature differences vary in different geographic regions, similar studies should be conducted in other climates.

Conclusions.

In this paper, we use ECOSTRESS high-resolution imagery to quantify the effect of three-dimensional building factors on surface temperature at different spatial and temporal scales using machine learning at the neighbourhood scale. The results show that (1) GMB has the best accuracy in the comparison of four regression models. (2) The effects of urban 3D factors on surface temperature are nonlinear, and the bias correlation plot curves can reveal important ranges of values and key inflection points of the factors affecting surface temperature. (3) MH, BVD, and SVF have significant effects on surface temperature, while GFA has the least effect on LST. (4) MH, BD, and FAR are seasonal stability factors, which show decreasing, increasing, and first increasing then decreasing effects on LST in all seasons. MH has the strongest cooling effect in spring, 3 °C, and BD has the strongest warming effect in autumn, 3.5 °C. BVD, GFA, and SVF are seasonal variability factors, which show warming, cooling, and descending effects, respectively, and GFA and SVF have a cooling effect except in spring. BVD has a slight cooling effect in autumn. (5) When using day and night as time variables, BVD, GFA, and SVF show a single trend in all-weather, exhibiting warming, cooling, and descending effects, respectively. MH and FAR show a warming effect at night, and a warming and then cooling effect in the morning and midday, while BD shows a warming effect in the morning and midday, and has a cooling effect at night. These findings will provide a better understanding of the urban heat island effect and provide a reference for the formulation of mitigation policies.

Author contributions

L. X. and H. wrote the main manuscript text and X. and W. prepared all figures.

Data availability

The datasets used and analysed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.