Abstract
An ancient and counterintuitive phenomenon known as the Mpemba effect (water can cool faster when initially heated up) showcases the critical role of initial conditions in relaxation processes. How to realize and utilize this effect for speeding up relaxation is an important but challenging task in purely quantum system till now. Here, we experimentally study the strong Mpemba effect in a single trapped ion system in which an exponentially accelerated relaxation in time is observed by preparing an optimal quantum initial state with no excitation of the slowest decaying mode. Also, we demonstrate that the condition of realizing such effect coincides with the Liouvillian exceptional point, featuring the coalescence of both the eigenvalues and the eigenmodes of the systems. Our work provides an efficient strategy to engineer the dynamics of open quantum system, and suggests a link unexplored yet between the Mpemba effect and the non-Hermitian physics.
Subject terms: Quantum simulation, Quantum information, Single photons and quantum effects
The Mpemba effect is an archetype for various anomalous relaxation phenomena. Here, the authors experimentally study a quantum version of the Mpemba effect in a single trapped ion system, where relaxation is exponentially accelerated by removing the excitation of the slowest decaying mode. This phenomenon, seen in Markovian open quantum systems containing Liouvillian exceptional points, indicates a link between the Mpemba effect and non-Hermitian physics.
introduction
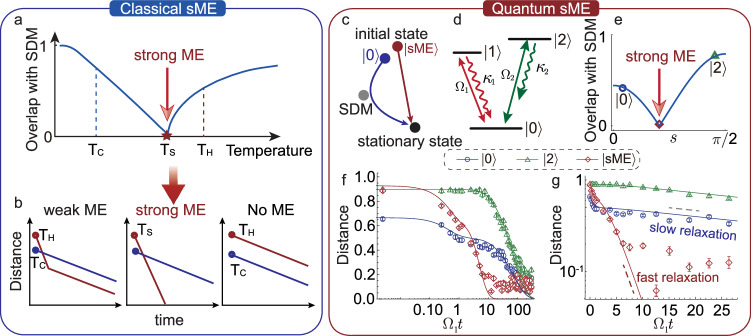
Relaxations or dissipative evolutions from initial states to a stationary state, widely existing in nature, are vital for fundamental studies of nonequilibrium phenomena and practical control of dynamical devices1,2. In quantum realm, rapid relaxations are highly desirable for efficient quantum state preparation and qubit engineering3–8. As a possible strategy to achieve this goal, the Mpemba effect (ME)9, well-known in the counterintuitive example that water can cool faster when initially heated up, has attracted growing interests both in classical10–17 and quantum systems in recent years18–30. Often, this and related phenomena admits a general explanation10–12,31: the state of the hotter system overlaps less with the slowest decaying mode (SDM) of the dissipative or cooling dynamics, implying the critical role of initial conditions in relaxations (see Fig. 1(a, b)).
Fig. 1. Comparison for classic and quantum Mpemba effect.
a The ME can be understood in an intuitive way: the amplitude of the overlap of the initial state with the slowest decaying mode (SDM) depends on the initial temperature in a nonmonotonic way. The sME appears when the overlap with the SDM vanishes. b Weak ME: If an initial high temperature state has a smaller SDM amplitude than that of the lower temperature state, it can reach the thermal equilibrium faster. Strong ME: the system reaches equilibrium at an exponentially faster rate. No ME: the initial high temperature state has a larger overlap with the SDM and thus reaches the equilibrium slower. c By applying a unitary operation, one can realize an initial sME state and approaches the stationary state with a faster rate. d The energy levels for observing the sME (with κ2 ≪ κ1). e The overlap ∣c1∣ of a rotated initial random state with the SDM as a function of the rotation angle s. f The distance between the time-relaxed state ρ(t) and the stationary state ρss for different initial states: (blue), (green) and (red), respectively. The initial sME state starts with a longer distance from ρss than the initial state but reaches ρss faster. g The logarithmic scale of the distance evolves with time for different initial states. An exponential speed-up of relaxation is clearly observed for the sME initial state. The experimental parameters for (e–g) are Ω1 = 2π × 20 kHz, Ω2 = 0.06Ω1, κ1 = 2Ω1, κ2 = 0.0015Ω1, and the solid lines here are the theoretical predictions based on the experimental parameters.
For purely quantum systems at zero temperature, the main challenge is to identify ME-induced rapid relaxations that are not smeared out by quantum superposition18. Very recently, Carollo et al.18 proposed that strong ME (sME) or exponential speed-up of relaxation can emerge in Markovian open quantum systems by devising an optimal initial state (i.e., sME state) to prohibit excitation of the slowest decaying mode (SDM, see Fig. 1(c)). This prediction of quantum sME, however, has not been experimentally realized till now, hindering its possible applications in e.g., ‘engineered’ relaxation dynamics of the open quantum system14.
Here, we report the observation of the sME in a truly quantum system, which is a genuine quantum effect and cannot be captured by semi-classical methods. As an essential step towards this target, we construct the sME state via efficient gate operations on a single trapped ion and show that with such special pure state, featuring zero overlap with the SDM, exponential speeding-up of relaxations can be observed (see Fig. 1(d–g)). Also we find that a critical point can appear in our system, separating the regimes with or without exponential acceleration of relaxations, which coincides well with the Liouvillian exceptional point (LEP)32–39. Furthermore, we observe both eigenvalues and eigenmodes coalesce at the LEP in the experiment by measuring the overlaps with the decaying modes. Our findings indicate a possible link unexplored yet between quantum ME and non-Hermitian physics7,38–44, which may stimulate more exciting efforts on e.g., engineering quantum sME with higher-order or topological LEPs38,39,44.
Results
Theory of quantum strong Mpemba effect
To understand the quantum sME, we consider a Lindblad master equation , where is the Liouvillian superoperator18,36,45
| 1 |
Here H is the Hamiltonian of the system and Jα are the quantum jump operators. The density operator ρ(t) can be expanded as the sum of all eigenmodes (Ri) of
| 2 |
Here Ri(Li) are the right (left) eigenmatrices of the Liouvillian superoperator , with the corresponding eigenvalues , and λ0 = 0. λ0 or its eigenmatrix R0 denotes the stationary state ρss, which is independent of any initial state ρin, while the real parts of other eigenvalues λi≥1 indicate the relaxation rates of the eigenmodes Ri. Coefficients give the overlap of Li with ρin, and d2 denotes the number of the decay modes.
Generally, an initial state can overlap with all decaying modes of Lindblad dynamics, but at long times the relaxation is dominated by the slowest one R113,15,45,46. The decay rate of the eigenmode R1 sets an exponential timescale of the relaxation 45–47, which is normally independent of the initial state. But for the ME case, anomalous fast relaxations can be achieved by designing a special form of the overlap c1 featuring smaller or even zero overlap with the SDM11,13,18,20.
The quantum sME can be realized by designing such an initial state satisfying18,
| 3 |
This optimal state is prepared by applying a well devised unitary transformation to an initially pure quantum state of the system18. Therefore the sME state is normally a quantum superposition state, which represents a fundamental difference from classic sME, and thus the resulting dynamical behaviour cannot be captured by semi-classical approaches (see Supplementary note 1). Since this sME initial state has zero overlap with the SDM, the relaxation rate of the system is thus , with the timescale , instead of . This implies an exponentially faster convergence to the stationary state by a factor .
Experimental approach
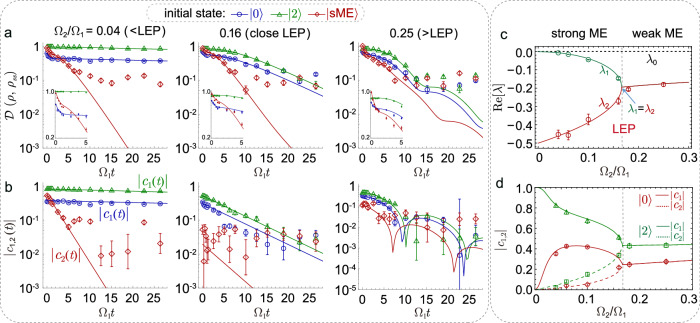
The experimental setup and relevant energy levels for the quantum sME are shown in Fig. 2(a, b). The ground state is resonantly coupled to state and by one 729 nm laser beam with two frequency components and the corresponding Rabi frequencies are Ω1 and Ω2, respectively. Another laser at 854 nm with right circular polarization induces a tunable decay channel between state and with decay rate κ1, by coupling to a short-life level , which will decay quickly back to the state (see Supplementary note 2). The imperfect polarization of 854 nm will cause slow decay from state to with decay rate κ2 ≪ κ1 and also the leakage of population to the other Zeeman ground state. Fortunately, the leakage problem can be fixed by introducing a weak optical pumping beam at 397 nm during the data acquisition process. Then for the effective three-level system, we have the Hamiltonian and two jump operators (j = 1, 2).
Fig. 2. Experimental setup and relaxation dynamics for different initial states.
a Experimental setup of quantum sME. The coherent driving between the S state and D state is realized by using a 729 nm laser beam with linewidth about 100 Hz. Two transitions required (as shown in b) are simultaneously driven by injecting two RF frequencies to an acoustic-optic modulator (AOM1) via an arbitrary waveform generator (AWG). The decay rate of the D state is controlled by the power of 854 nm laser. b The relevant energy levels of a single 40Ca+ ion involved in the experiment, with state are encoded in the energy levels , and , respectively. The energy gap of state and can minimize detrimental effect from the polarization impurity of the 854 nm laser beam. c Protocol to generate the sME initial state and tomography of the density matrix ρ(t). After generating the initially sME state by applying two rotation gates on the state , the system evolves with the Liouvillian superoperator of interest. After a time t, projective measurements are performed for the tomography of the state ρ(t). d–f Left: The dynamics of the state population for initial states (d), (e) and (f) on a logarithmic timescale. Right: The evolving overlap for three time stamps at 0, τ2, τ1. The solid lines indicate the theoretical results based on the experimental parameters same with Fig. 1(e–g) and the error bars are generated by using Monte Carlo simulation.
To observe quantum sME, we initialize the ion in the ground state and subsequently rotate it by applying a unitary operation U18 (see Fig. 2(c)). Although this transformation can be exactly constructed through the decomposition method48, it is still challenging to realize it with high fidelity in the experiment since at least six gate operations are required for our case. To overcome this obstacle, here we optimize the operations to two qubit-rotations (see “Methods” for technical details). The rotated state then relaxes with the desired Liouvillian superoperator . The final step is quantum state tomography, i.e., performing the projective measurements on the time-relaxed state ρ(t) as it relaxes from the initial state ρin to the final stationary ρss. We remark that both the dynamical process and the state readout need to be carefully regulated, accompanying with the optimization procedure (see “Methods”).
Quantum strong ME
With the aid of tomography of ρ(t), we can characterize the relaxation process by using the Hilbert-Schmidt distance18
| 4 |
with the notation . As presented in Fig. 1(f), the sME initial state generated by our method is farther from the stationary state than normal initial states . This is due to the fact that while U removes the SDM excitation, it also modifies the excitation of the remaining ones18. Nonetheless, the approach to stationarity for sME initial state is still faster since the SDM (R1) is cut off by U18. Figure 1(g) gives the Logarithmic scale of distance . Compared with the normal initial states, an exponential speeding-up of the relaxation is reached for the sME initial state, a clear evidence of quantum sME. It can also be observed by other distance measures, for instance, the trace distance48 or Bures distance49,50 (see Supplementary note 1).
Figure 2(d–f) illustrates the relaxation dynamics of initial states , , and , respectively, under same experimental parameters. We find that they all reach the same steady state after a sufficiently long time, but the relaxation time of the sME initial state is significantly shorter. For the normal initial states (see Fig. 2(d, e)), when t ≫ τ2 the system relaxes into a state in the metastable manifold till 45. Differently, as seen in Fig. 2(f), the application of U, cutting of the excitation of the SDM, leads to striking faster approach to the steady state with the time scale τ2 ≪ τ1. In order to visualise their overlaps on each decaying mode, we give all coefficients ci(t) of ρ(t) decomposition into all the decaying modes at time t = 0, t = τ2, and t = τ1, respectively. As depicted in Fig. 2(d, e), when time t = 0, a generic initial state will normally overlap with the slowest one, i.e., c1(0) ≠ 0. When time t > τ2, the overlap of initial state with the short-life excitation modes (Ri>1) becomes very small, while the SDM (R1) is still relevant and keeps the system away from stationarity for a long time till t ≫ τ1. However, for the sME initial state, c1 = 0, therefore, the relaxation time scale is reduced to τ2 with a faster decay rate (see Fig. 2(f)). Note that the coefficient on R0 (i.e., the stationary state) has the form and consistently remains at 1 for all the time, while the coefficients on other decay modes decrease with time for the reason .
From strong ME to weak ME
Can this exponential acceleration always happen for the sME initial state? To check this, we measure the distance and the overlaps c1,2(t) for different parameters of the system. As shown in Fig. 3(a-b), for the normal initial state , the distance has similar dynamical behavior with the overlap c1(t) at the final stage of the relaxation, i.e., . While for sME intial state, it becomes to . When Ω2/Ω1 ≪ 1, the accelerated relaxation achieved for sME initial state is very significant, since in this regime , as shown in Fig. 3(c). While as Ω2 increases, this exponential gain decreases and even disappears when Ω2 passes across the LEP, where λ1 = λ2 and R1 = R2. The reason is that when Ω2/Ω1 > LEP, the eigenvalue of the SDM of the forms a complex conjugate pair, i.e., (see Fig. 3(c)), which means that the decaying modes R1 and R2 have the same decay rate. Meanwhile, the imaginary parts of eigenvalues λ1,2 result in the oscillating during the relaxation process7,43 (Supplementary note 1). Even though, comparing with normal initial states which have two SDMs, the sME initial state here just has one so that it may still be faster to the stationary state. Different with sME featuring a faster decay rate, this acceleration here corresponds to the weak ME which is associated with a smaller overlap with the SDM11. As a consequence, LEP is the boundary between the quantum strong ME and weak ME, showing that an existence of the quantum strong ME is limited to the regime in which λ1 is real. It is helpful for deepening the understanding of the relaxation speed limit from both LEPs and quantum ME perspectives.
Fig. 3. From strong ME to weak ME.
a Logarithmic scale of distance evolves with time for different initial state: (blue), (green) and (red), respectively. b The corresponding coefficients c1(t) (of initial state ) and c2(t) (of initial state ). The sME that exits exponential acceleration is observed for Ω2/Ω1 = 0.04, 0.16( < LEP). When Ω2/Ω1 = 0.25( > LEP), has the same decay rate with the normal initial states , meaning the strong ME disappears but weak ME is allowed. c Real parts of the eigenvalues of the Liouvillian operator as a function of Ω2/Ω1. d Overlaps ∣c1∣ (solid) and ∣c2∣ (dashed) for different initial states (red) and (green), respectively. The parameters are Ω1 = 2π × 20 kHz, κ1 = 2Ω1, κ2 = 0.0015Ω1. All error bars in this figure are calculated by using Monte Carlo simulation.
Based on the measurements of the overlaps, we further demonstrate both eigenvalues (Fig. 3(c)) and eigenmodes (Fig. 3(d)) coalesce at LEP in the experiment. Whereas the impact of the decaying modes is often limited to transient dynamics, it presents a practical challenge for experimental observation of more than one eigenvalue of . Normally, LEP happens at the point that an eigenvalue changes from real to complex38,39. However, this change just can show where LEP happens, but does not demonstrate the coalesce of the LEP, because the coalesce of LEPs typically occur in two or more eigenvalues. This challenge could be solved by fitting the measurement of using a single exponential function of time. Based on this, theoretically, one can get the full spectrum of . For our system here, considering the overlap c2 is very small for initial state ), we choose to get λ2 by measuring c2(t) of initial sME state and λ1 by measuring c1(t) of initial state . The results, as depicted in Fig. 3(c), match well with the theoretical results and show that LEP is signaled by the degenerated of λ1,2.
As shown in Fig. 3(d), the coalesce of the eigenmodes R1(L1) and R2(L2) at LEP is indicated by c1 = c2 for a fixed initial state, because at LEP . This means the coalesce the coefficients is a detectable way to show the eigenmodes coalesce of LEP. Note that, as we observed in Fig. 3(c-d), the bifurcation singularity of the spectrum and the overlaps c1,2 is not detectable in the steady state but rather in the relaxation process36. In fact, for the dynamics at long times, , thus LEP corresponds the final direction change of the dynamics from R1 to . This direction change occurring at LEP is the further evidence of a direct link with anomalous phenomena arising in the relaxation process such as sME and the dynamical phase transition15,51.
Discussion
In summary, we have observed the quantum sME in a single trapped-ion system by preparing an optimal pure state that has zero overlap with the SDM. For the quantum sME initial state, we propose an efficient quantum control technique for state preparation, dynamical engineering and state tomography. In addition, we reveal that quantum sME only happens within a certain parameter range, which is determined by LEP. Together with well-developed techniques of engineering quantum states, our work not only provides a powerful tool for exploring and utilizing the quantum sME as examples of engineered relaxation dynamics14 but also bridges the LEP and quantum ME, two previously independent effects. Besides, the experimentally accessible methods discussed in the present manuscript, such as the the efficient unitary transformation and the overlaps measurement, will be valuable tools to assess the quality of the state preparation and the control of the system relaxation.
Note added: While submitting our manuscript, we became aware of another two experimental studies of the Mpemba effect performed with trapped ion systems appeared on arXiv, and currently they have been published on Phys. Rev. Lett29,30.
Methods
We explain here how to devise the unitary transformation U to generate the quantum sME initial (pure) state . We firstly use the method performed in ref. 18 to get , then we explicitly construct feasible operation U based on our experimental setting (see Fig. 4).
Fig. 4. Protocol to prepare arbitrary pure qutrit (three-level) states and to get the density matrix ρ(t) in the experiment.
First, we construct the quantum state by engineering an 'virtual' but efficient unitary transformation U = R02R01. Then in the dynamical process, the parameters of the lasers Ω1,2 are adjusted accordingly to Ω1eiϕ and . Finally, the state tomography operations are changed accordingly to .
As discussed in ref. 18, the formula of this unitary can be expressed as
| 5 |
where are the eigenstates of the left-hand eigenmatrix L1 with the corresponding negative (positive) eigenvalues α1(2), . This qutrit (three-level) U operations can be decomposed into several qubit (two-level) rotations48. Compared with qubit operations, a notable challenge in qutrit operations is that the elementary qubit operations lose their ‘global-phase’ gauge freedom because any phase shift is measured relative to the spectator level52.
Now we discuss how to overcome this technical challenge by applying a more efficient and practical way of decomposition, which requires only 2 two-level rotation operations in the experiment (see Fig. 4). Suppose an arbitrary qutrit pure state and ∣a∣2 + ∣b∣2 + ∣c∣2 = 1, then U can be decomposed into a product of 2 two-level unitary matrices U = AB48, where
| 6 |
with . The unitary A and B can be written in the form
| 7 |
where
and
Here we have translated the phase gates P and Z backwards which implement appropriate phase-shifts between the qutrit states52,53. Then the final decomposed unitary operation for U can be written as
| 8 |
with .
We can further simplify the unitary operation U in a more efficient way by translating phase gates P and Z to the operation backwards till the detection due to the fact that the detection does not need phase information53. By calculating the translated phase in software, we just need two rotation operations R01R02 to generate arbitrary qutrit pure state experimentally, which can not only greatly simplify operations, but also improve the fidelity of sME state.
As shown in Fig. 4, our careful analysis shows that the corresponding dynamical operator and state tomography operations need to be modulated accordingly,
| 9 |
The state tomography for the qutrit system here requires 9 measurement basis, which are , , , ,, , , , . However, only S or D state can be detected in the trapped ion system, therefore we need to rotate the basis to state before applying the detection beam since we have encoded state and in D state manifold. The rotation operation in the state tomography can be realized by simply combining the π or π/2 pulses with translating phase on the transition and on the transition respectively. After we get the projective measurement results of these basis, we can reconstruct density matrix by using maximum-likelihood method, and the error bars for the density matrix are obtained by using numerical simulations54,55.
Supplementary information
Source data
Acknowledgements
This work was supported by the Cornerstone fundation of NUDT (Y.L.Z.), Natural Science Foundation of Hunan Province of China under grant Nos. 2023JJ30626 (Y.L.Z.), 2022RC1194 (J.Z.), 2023JJ10052 (J.Z.), National Natural Science Foundation of China under grant Nos. 12004430 (J.Z.), 12174448 (C.W.W.), 12074433 (P.X.C.), 12174447 (W.W.) and 12204543 (T.C.). H.J. is supported by the NSFC (grant No.11935006), the Science and Technology Innovation Program of Hunan Province (grant No. 2020RC4047), National Key R&D Program of China (No. 2024YFE0102400) and Hunan provincial major sci-tech program (No. 2023ZJ1010), and P.X.C. acknowledges the support from Innovation Program for Quantum Science and Technology under grant No. 2021ZD0301605.
Author contributions
Y.L.Z. conceived and designed the research with helpful discussions with H.J.,W.L. and P.X.C.; J.Z. and G.X. were responsible for the experimental implementation, the data acquisition and its evaluation; J.Z., Y.L.Z. and C.W.W. designed the experiment with the help of T.C., Y.X., W.W. and P.X.C.; Y.L.Z. performed the simulations; Y.L.Z., J.Z. and G.X. analyzed the data; Y.L.Z., J.Z, H.J., W.L. and C.W.Q. wrote the paper with inputs from G.X., T.C., Q.Z. and W.B.S. ; H.J., W.L. and P.X.C. supervised this project. All authors discussed the results and contributed to the manuscript.
Peer review
Peer review information
Nature Communications thanks Antonio Lasanta, Pengfei Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data that supports the findings are presented in the article and Supplementary Information. Source data are provided with this paper.
Code availability
The code used for data analysis and simulation is available from the corresponding author upon request. Source data are provided with this paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Jie Zhang, Gang Xia.
Contributor Information
Weibin Li, Email: weibin.li@nottingham.ac.uk.
Hui Jing, Email: jinghui73@foxmail.com.
Yan-Li Zhou, Email: ylzhou@nudt.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-54303-0.
References
- 1.Breuer, H.-P. & Petruccione, F. The Theory Of Open Quantum Systems. (Oxford University Press, 2007).
- 2.Mohseni, M. et al. Quantum Effects In Biology. (Cambridge University Press, 2014).
- 3.Verstraete, F., Wolf, M. M. & Cirac, J. I. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys.5, 633 (2009). [Google Scholar]
- 4.Harrington, P. M., Mueller, E. J. & Murch, K. W. Engineered dissipation for quantum information science. Nat. Rev. Phys.4, 660 (2022). [Google Scholar]
- 5.Dann, R., Tobalina, A. & Kosloff, R. Shortcut to equilibration of an open quantum system. Phys. Rev. Lett.122, 250402 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Wu, S. L., Ma, W., Huang, X. L. & Yi, X. Shortcuts to adiabaticity for open quantum systems and a mixed-state inverse engineering scheme. Phys. Rev. Appl.16, 044028 (2021). [Google Scholar]
- 7.Khandelwal, S., Brunner, N. & Haack, G. Signatures of liouvillian exceptional points in a quantum thermal machine. PRX Quantum2, 040346 (2021). [Google Scholar]
- 8.Kumar, P., Snizhko, K., Gefen, Y. & Rosenow, B. Optimized steering: quantum state engineering and exceptional points. Phys. Rev. A105, L010203 (2022). [Google Scholar]
- 9.Mpemba, E. B. & Osborne, D. G. Cool? Phys. Educ.4, 172 (1969). [Google Scholar]
- 10.Lu, Z. & Raz, O. Nonequilibrium thermodynamics of the Markovian Mpemba effect and its inverse. Proc. Natl Acad. Sci. USA114, 5083 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Klich, I., Raz, O., Hirschberg, O. & Vucelja, M. Mpemba index and anomalous relaxation. Phys. Rev. X9, 021060 (2019). [Google Scholar]
- 12.Gal, A. & Raz, O. Precooling strategy allows exponentially faster heating. Phys. Rev. Lett.124, 060602 (2020). [DOI] [PubMed] [Google Scholar]
- 13.Kumar, A. & Bechhoefer, J. Exponentially faster cooling in a colloidal system. Nature584, 64 (2020). [DOI] [PubMed] [Google Scholar]
- 14.Bechhoefer, J., Kumar, A. & Chétrite, R. A fresh understanding of the mpemba effect. Nat. Rev. Phys.3, 534 (2021). [Google Scholar]
- 15.Teza, G., Yaacoby, R. & Raz, O. Eigenvalue crossing as a phase transition in relaxation dynamics. Phys. Rev. Lett.130, 207103 (2023). [DOI] [PubMed] [Google Scholar]
- 16.Pemartín, I. G.-A., Mompó, E., Lasanta, A., Martín-Mayor, V. & Salas, J. Shortcuts of freely relaxing systems using equilibrium physical observables. Phys. Rev. Lett.132, 117102 (2024). [DOI] [PubMed] [Google Scholar]
- 17.Ibáñez, M., Dieball, C., Lasanta, A., Godec, A. & Rica, R. A. Heating and cooling are fundamentally asymmetric and evolve along distinct pathways. Nat. Phys.20, 135–141 (2024). [Google Scholar]
- 18.Carollo, F., Lasanta, A. & Lesanovsky, I. Exponentially accelerated approach to stationarity in markovian open quantum systems through the mpemba effect. Phys. Rev. Lett.127, 060401 (2021). [DOI] [PubMed] [Google Scholar]
- 19.Nava, A. & Fabrizio, M. Lindblad dissipative dynamics in the presence of phase coexistence. Phys. Rev. B100, 125102 (2019). [Google Scholar]
- 20.Kochsiek, S., Carollo, F. & Lesanovsky, I. Accelerating the approach of dissipative quantum spin systems towards stationarity through global spin rotations. Phys. Rev. A106, 012207 (2022). [Google Scholar]
- 21.Manikandan, S. K. Equidistant quenches in few-level quantum systems. Phys. Rev. Res.3, 043108 (2021). [Google Scholar]
- 22.Ares, F., Murciano, S. & Calabrese, P. Entanglement asymmetry as a probe of symmetry breaking. Nat. Commun.14, 2036 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rylands, C. et al. Microscopic origin of the quantum mpemba effect in integrable systems. Phys. Rev. Lett.133, 010401 (2024). [DOI] [PubMed] [Google Scholar]
- 24.Ivander, F., Anto-Sztrikacs, N. & Segal, D. Hyperacceleration of quantum thermalization dynamics by bypassing long-lived coherences: An analytical treatment. Phys. Rev. E108, 014130 (2023). [DOI] [PubMed] [Google Scholar]
- 25.Chatterjee, A. K., Takada, S. & Hayakawa, H. Quantum mpemba effect in a quantum dot with reservoirs. Phys. Rev. Lett.131, 080402 (2023). [DOI] [PubMed] [Google Scholar]
- 26.Chatterjee, A. K., Takada, S. & Hayakawa, H. Multiple quantum mpemba effect: exceptional points and oscillations. Phys. Rev. A110, 022213 (2024). [Google Scholar]
- 27.Moroder, M., Culhane, O., Zawadzki, K. & Goold, J. Thermodynamics of the quantum mpemba effect. Phys. Rev. Lett.133, 140404 (2024). [DOI] [PubMed] [Google Scholar]
- 28.Boubakour, M., Endo, S., Fogarty, T. & Busch, T. Dynamical invariant based shortcut to equilibration in open quantum systems. arXiv:2401.11659 (2024).
- 29.Joshi, L. K. et al. Observing the quantum mpemba effect in quantum simulations. Phys. Rev. Lett.133, 010402 (2024). [DOI] [PubMed] [Google Scholar]
- 30.Aharony Shapira, S. et al. Inverse mpemba effect demonstrated on a single trapped ion qubit. Phys. Rev. Lett.133, 010403 (2024). [DOI] [PubMed] [Google Scholar]
- 31.Lasanta, A., Vega Reyes, F., Prados, A. & Santos, A. When the hotter cools more quickly: Mpemba effect in granular fluids. Phys. Rev. Lett.119, 148001 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Bender, C. M., Brody, D. C., Jones, H. F. & Meister, B. K. Faster than hermitian quantum mechanics. Phys. Rev. Lett.98, 040403 (2007). [DOI] [PubMed] [Google Scholar]
- 33.Chen, W., Özdemir, Ş. K., Zhao, G., Wiersig, J. & Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature548, 192 (2017). [DOI] [PubMed] [Google Scholar]
- 34.Hodaei, H. et al. Enhanced sensitivity at higher-order exceptional points. Nature548, 187 (2017). [DOI] [PubMed] [Google Scholar]
- 35.Miri, M. A. & Alù, A. Exceptional points in optics and photonics. Science363, eaar7709 (2019). [DOI] [PubMed] [Google Scholar]
- 36.Minganti, F., Miranowicz, A., Chhajlany, R. W. & Nori, F. Quantum exceptional points of non-hermitian hamiltonians and liouvillians: the effects of quantum jumps. Phys. Rev. A100, 062131 (2019). [Google Scholar]
- 37.Naghiloo, M., Abbasi, M., Joglekar, Y. N. & Murch, K. W. Quantum state tomography across the exceptional point in a single dissipative qubit. Nat. Phys.15, 1232–1236 (2019). [Google Scholar]
- 38.Chen, W., Abbasi, M., Joglekar, Y. N. & Murch, K. W. Quantum jumps in the non-hermitian dynamics of a superconducting qubit. Phys. Rev. Lett.127, 140504 (2021). [DOI] [PubMed] [Google Scholar]
- 39.Chen, W. et al. Decoherence induced exceptional points in a dissipative superconducting qubit. Phys. Rev. Lett.128, 110402 (2022). [DOI] [PubMed] [Google Scholar]
- 40.Ding, K., Ma, G., Xiao, M., Zhang, Z. Q. & Chan, C. T. Emergence, coalescence, and topological properties of multiple exceptional points and their experimental realization. Phys. Rev. X6, 021007 (2016). [Google Scholar]
- 41.Zhou, Y.-L. et al. Accelerating relaxation through liouvillian exceptional point. Phys. Rev. Res.5, 043036 (2023). [Google Scholar]
-
42.Purkayastha, A., Kulkarni, M. & Joglekar, Y. N. Emergent
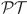 symmetry in a double-quantum-dot circuit qed setup. Phys. Rev. Res.2, 043075 (2020). [Google Scholar]
symmetry in a double-quantum-dot circuit qed setup. Phys. Rev. Res.2, 043075 (2020). [Google Scholar] - 43.Zhang, J. W. et al. Dynamical control of quantum heat engines using exceptional points. Nat. Commun.13, 6225 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bu, J.-T. et al. Enhancement of quantum heat engine by encircling a liouvillian exceptional point. Phys. Rev. Lett.130, 110402 (2023). [DOI] [PubMed] [Google Scholar]
- 45.Macieszczak, K., Guţă, M., Lesanovsky, I. & Garrahan, J. P. Towards a theory of metastability in open quantum dynamics. Phys. Rev. Lett.116, 240404 (2016). [DOI] [PubMed] [Google Scholar]
- 46.Minganti, F., Biella, A., Bartolo, N. & Ciuti, C. Spectral theory of Liouvillians for dissipative phase transitions. Phys. Rev. A98, 042118 (2018). [Google Scholar]
- 47.Žnidarič, M. Relaxation times of dissipative many-body quantum systems. Phys. Rev. E92, 042143 (2015). [DOI] [PubMed] [Google Scholar]
- 48.Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (10th anniversary edition) (Oxford University Press, 2011).
- 49.Van Vu, T. & Hasegawa, Y. Geometrical bounds of the irreversibility in markovian systems. Phys. Rev. Lett.126, 010601 (2021). [DOI] [PubMed] [Google Scholar]
- 50.García-Pintos, L. P., Nicholson, S. B., Green, J. R., del Campo, A. & Gorshkov, A. V. Unifying quantum and classical speed limits on observables. Phys. Rev. X12, 011038 (2022). [Google Scholar]
- 51.Orgad, D., Oganesyan, V. & Gopalakrishnan, S. Dynamical transitions from slow to fast relaxation in random open quantum systems. Phys. Rev. Lett.132, 040403 (2024). [DOI] [PubMed] [Google Scholar]
- 52.Ringbauer, M. et al. A universal qudit quantum processor with trapped ions. Nat. Phys.18, 1053–1057 (2022). [Google Scholar]
- 53.McKay, D. C., Wood, C. J., Sheldon, S., Chow, J. M. & Gambetta, J. M. Efficient Z gates for quantum computing. Phys. Rev. A96, 022330 (2017). [Google Scholar]
- 54.Thew, R. T., Nemoto, K., White, A. G. & Munro, W. J. Qudit quantum-state tomography. Phys. Rev. A66, 012303 (2002). [Google Scholar]
- 55.Hu, X.-M. et al. Self-testing of a single quantum system from theory to experiment. npj Quantum Inf.9, 103 (2023). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that supports the findings are presented in the article and Supplementary Information. Source data are provided with this paper.
The code used for data analysis and simulation is available from the corresponding author upon request. Source data are provided with this paper.