Hierarchical representations of relative numerical magnitudes in the human frontoparietal cortex

Abstract

The ability to estimate numerical magnitude is essential for decision-making and is thought to underlie arithmetic skills. In humans, neural populations in the frontoparietal regions are tuned to represent numerosity. However, it remains unclear whether their response properties are fixed to a specific numerosity (i.e., absolute code) or dynamically scaled according to the range of numerosities relevant to the context (i.e., relative code). Here, using functional magnetic resonance imaging combined with multivariate pattern analysis, we uncover evidence that representations of relative numerosity coding emerge gradually as visual information processing advances in the frontoparietal regions. In contrast, the early sensory areas predominantly exhibit absolute coding. These findings indicate a hierarchical organization of relative numerosity representations that adapt their response properties according to the context. Our results highlight the existence of a context-dependent optimization mechanism in numerosity representation, enabling the efficient processing of infinite magnitude information with finite neural resources.

Are neural representations of magnitude adaptable to changes in the environment? Here, the authors provide evidence that numerical magnitude is represented in a flexible, relative manner and is hierarchically organized in the human brain.

Introduction

The processing of magnitude information, such as quantity, length, or size of objects, is essential for decision-making and behavior guidance. The ability to estimate numerical quantities, known as numerosity, has been widely reported across species¹ (e.g., monkeys^2,3, crows⁴, humans⁵), indicating its adaptive value that helps an organism to survive and reproduce⁶. In humans, the ability to estimate numerosity is evident throughout different developmental stages⁷ and among both numerate and innumerate adults⁸, suggesting that the numerosity estimation may serve as a fundamental skill, underpinning arithmetic ability¹.

In recent decades, extensive research has explored the neural basis of numerosity processing in both animals and humans. Electrophysiological studies in non-human primates have provided substantial evidence indicating that the frontoparietal regions, including the intraparietal sulcus (IPS) and the lateral prefrontal cortex (PFC), play a pivotal role in representing numerosity information. In these regions, numerical magnitudes are represented by populations of numerosity-tuned neurons that fire most frequently at their preferred numerosity^2,3, forming a labeled line code⁹. Importantly, the firing patterns of these numerosity-tuned neurons align closely with behavioral response, adhering to Weber-Fechner’s law^10,11. These findings are also consistent with human functional magnetic resonance imaging (fMRI) studies, which demonstrate reduced fMRI responses to the repeated presentation of similar numerosities^5,12 and the ability to decode numerosity from the multivariate activity patterns^13–15. In addition, meta-analyses of neuroimaging studies^16,17 highlight the supplementary motor area (SMA) as another key region frequently engaged in numerosity processing.

While existing studies strongly support the notion that numerosity is represented in the frontoparietal regions, the impact of context, such as the range or distribution of numerical magnitudes in the given environment, on neural responses remains an open question. More specifically, it remains unknown whether the response properties of the numerosity representations are static, adhering to a specific numerical magnitude (an absolute code), or whether they dynamically adjust according to the contextual factors (a relative code). This distinction is crucial, considering the brain’s neuronal capacity is finite (e.g., limited number of neurons), whereas spatial magnitudes such as quantity, length, or size are boundless, unlike circular attributes such as orientation or direction of motion. One possible neural strategy to handle such infinite magnitudes may involve gathering statistical data of magnitudes (e.g., range or distribution) of the environment and subsequently modulating neural response properties accordingly. In this way, the brain could potentially optimize the allocation of neural resources, ensuring accurate representation of numerosity.

To investigate this, we conducted an fMRI study where participants performed a numerosity discrimination task. The task involved different contexts with numerosities derived from three partially overlapping sets, presented as visual dot arrays. Our hypothesis was twofold: firstly, that numerosity representations would scale according to the range of numerical magnitudes in each set; secondly, that this relative representation of numerosity would emerge progressively along the numerical processing hierarchy¹⁸. Specifically, we predicted non-scaled, absolute numerosity encoding in lower sensory areas (such as the visual cortex), while higher-level association cortices (including IPS and PFC) and areas beyond (e.g., SMA) would represent relative numerosity.

Our results, derived from classification analysis of multivariate activity patterns, reveal that relative representation of numerosity is distributed across both the visual cortex and frontoparietal regions. The relative representation of numerosity was emphasized from the parietal region through the lateral PFC to the SMA. Additionally, using linear mixed-effect modeling combined with representational similarity analysis, we found that while the visual cortex predominantly exhibits absolute coding, the frontoparietal regions are more inclined towards relative coding. These findings suggest that the brain constructs a relative representation of numerosity through hierarchical processing.

Results

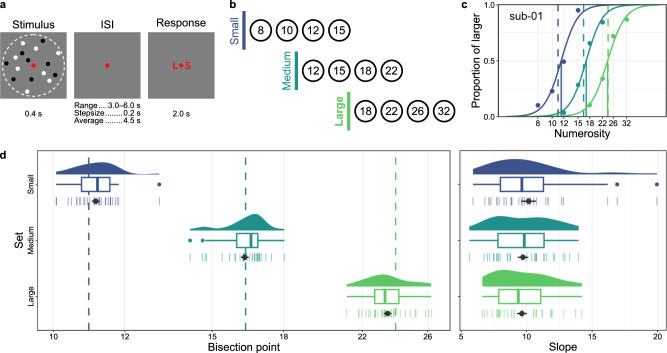
Participants completed three separate sessions of our fMRI experiments, which were performed on different days. In each session, participants performed a numerosity bisection task (Fig. 1a). During each trial, a visual dot array was presented at the center of the screen for 0.4 s, and participants judged whether the number of dots was smaller or larger than the average numerosity of preceding trials. Following an inter-stimulus interval (ISI; jittered between 3.0 and 6.0 s), a response cue appeared, indicating the spatial correspondence between the judgments (S for smaller, L for larger) and the position of the response key (left or right button). This design helped to isolate fMRI responses associated with numerosity processing, distinct from motor planning and execution which were not the focus of the present study. The numerosity of the visual dot arrays was sampled from one of the three sets of partially overlapping, logarithmically spaced, four numerosities (Fig. 1b): small (8, 10, 12, 15), medium (12, 15, 18, 22), and large (18, 22, 26, 32). Each set was assigned to a different fMRI session in a counter-balanced manner across participants.

Fig. 1. Overview of stimulus sequence, numerosity sets, and behavioral data.

a Schematic illustration of the stimulus sequence used in each trial. A single dot array was presented within an implied virtual circle (dotted line, not visible during the experiment), followed by a jittered inter-stimulus interval (ISI) and a response cue indicating which of the two response buttons corresponded to larger (L) or smaller (S). b Three partially overlapping numerosity sets used in the study. c The psychometric functions fitted to the individual data of a representative participant. The vertical lines represent the average numerosity (dashed lines) and estimated bisection points (solid lines) for each stimulus set, with the colors matching those used in b. Source data are provided as Source Data file. d Distributions of the bisection points (left panel) and slopes (right panel) of all participants (n = 30). The density plots illustrate the distribution of the estimated parameters among participants. In the boxplots, the thick vertical lines indicate the median of the estimated parameters, the box bounds represent the first (Q1) and third (Q3) quartiles, and the whiskers extend to Q1-1.5×IQR (interquartile range) and Q3+1.5×IQR. Outliers are represented by colored dots. The average values across participants (n = 30), along with the standard error of the mean, are indicated by black points and horizontal solid lines. Individual participant data are denoted by small vertical lines. The dashed lines in the left panel indicate the mean numerosity for each stimulus set, as detailed in c. Source data are provided as Source Data file.

Comparable task performance across numerosity ranges

Task performance was in line with our expectations. First, for each of the three numerosity ranges, the bisection points derived from individually fitted psychometric functions (Fig. 1c and Supplementary Fig. 1), closely matched the mean of each range (Fig. 1d) (small: MSE = 0.017 ± 0.010, 95% CI = [−0.003, 0.037], t(29) = 1.771, p = 0.087, BF₁₀ = 0.777; medium: MSE = −0.002 ± 0.010, 95% CI = [−0.023, 0.018], t(29) = −0.212, p = 0.833, BF₁₀ = 0.199; large: MSE = −0.020 ± 0.010, 95% CI = [−0.041, 7.416e-5], t(29) = −2.038, p = 0.051, BF₁₀ = 1.182), confirming minimal systematic bias in task performance. Secondly, the estimated slopes of the psychometric curves (Fig. 1d), which reflect the precision of numerosity judgments, were comparable across all three sets (F(1.591, 46.136) = 0.731, p = 0.458 with Greenhouse-Geisser correction, BF₁₀ = 0.176). This consistency supports Weber-Fechner’s law in numerosity perception^10,11. Consequently, these results suggest that the subsequent fMRI results are not likely influenced by any biases or precisions in task performance specific to certain numerosity sets (see Supplementary Fig. 2 for reaction time data).

Relative coding of numerosity distributed across visual and frontoparietal cortices

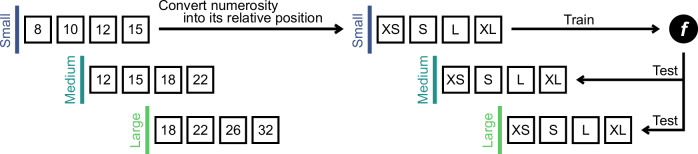
We identified the neural locus of the relative numerosity coding through a region-of-interest (ROI) based multivariate pattern analysis (MVPA). The ROIs were predetermined based on cortical parcellation methods^19,20 (Table 1, Supplementary Fig. 3). First, we employed a general linear model (GLM) to obtain event-related multivariate activity patterns for each numerosity with each stimulus set. We then trained a four-class classifier (linear support vector machine; linear SVM) using the multivariate activity patterns of selected 500 voxels per ROI on one numerosity set. The primary objective was to identify the ROI that exhibited relative coding. To achieve this, we tested the classifier’s ability to accurately decode the relative position of numerosity in the other two numerosity sets (Fig. 2).

Table 1.

The ROIs for the ROI-based MVPAs

ROI Label	Functional Network	Laterality	Anatomical Location
Vis	Visual	–
SomMot	Somatomotor	–
DA lFEF+lPrCv	Dorsal Attention	left	Frontal eye fields + Precentral ventral
DA rFEF+rPrCv	Dorsal Attention	right	Frontal eye fields + Precentral ventral
DA Post	Dorsal Attention	–	Posterior
VA lPFCl	Ventral Attention	left	Lateral prefrontal cortex
VA lParOper	Ventral Attention	left	Parietal operculum
VA rTempOcc+rPar	Ventral Attention	right	Temporal occipital + Parietal
VA lFrOper+lIns	Ventral Attention	left	Frontal operculum + Insula
VA rFrOper+rIns	Ventral Attention	right	Frontal operculum + Insula
VA Med	Ventral Attention	–	Medial
Fp lTemp	Frontoparietal	left	Temporal
Fp rTemp	Frontoparietal	right	Temporal
Fp pCun	Frontoparietal	–	Precuneus
Fp lPar	Frontoparietal	left	Parietal
Fp rPar	Frontoparietal	right	Parietal
Fp PFCmp+Cing	Frontoparietal	–	Medial posterior prefrontal cortex + Cingulate
Fp lPFCl	Frontoparietal	left	Lateral prefrontal cortex
Fp rPFCl	Frontoparietal	right	Lateral prefrontal cortex
Df rPFCv	Default	right	Ventral prefrontal cortex
Df rPar	Default	right	Parietal
Df rTemp	Default	right	Temporal
Df pCun+PCC	Default	–	Precuneus + Posterior cingulate cortex
Df lPar+lTemp	Default	left	Parietal + Temporal
Df PFC	Default	–	Prefrontal cortex

All the ROI labels stem from those in a preceding study that utilized the same cortical parcellation²⁰. In general, all the labels were in the form of “<Functional Network > <Laterality > <Anatomical Location > .” “<Functional Network > ” was one of the abbreviated labels of functional networks: Vis (Visual), SomMot (Somatomotor), DA (Dorsal Attention), VA (Ventral Attention), Fp (Frontoparietal), and Df (Default). When an ROI spanned both hemispheres, “<Laterality > ” information was omitted from the ROI label and indicated as “–“ in the table. Otherwise, “<Laterality > ” was either “l” or “r,” indicating the left or right hemisphere. “<Anatomical Location > ” was an abbreviated anatomical label.

Fig. 2. Procedure for classification analysis on relative numerosity coding.

We trained a four-class classifier using one of the three numerosity sets and then tested its ability to decode the relative position of numerosity in the other two numerosity sets. This procedure was repeated for each possible combination of stimulus sets. Note that only one fold of this procedure is illustrated here for clarity. XS, extra small; S, small; L, large; XL, extra large.

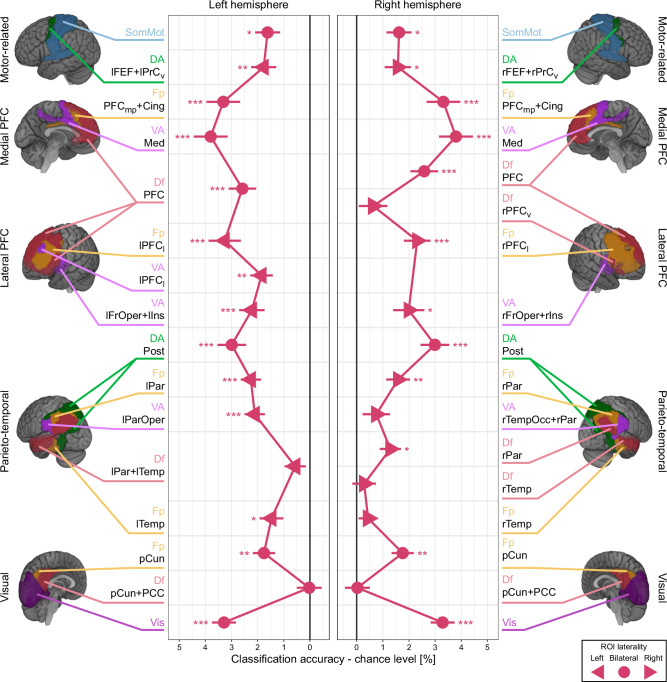
Classification performance above-chance level was notably present across various ROIs, including the parietal, lateral prefrontal, medial prefrontal areas, and the early visual cortex (Fig. 3 and Supplementary Table 1; Supplementary Fig. 4 for confusion matrices). Within the frontoparietal regions, we observed a progressive increase in classification performance, starting from the parietal areas (VA lParOper, Df rPar, Fp lPar, Fp rPar, and DA Post) and moving towards the lateral prefrontal areas (VA lFrOper+lIns, VA rFrOper+rIns, VA lPFC_l, Fp lPFC_l, Fp rPFC_l, and Df PFC). The performance reached its peak in the medial prefrontal areas (VA Med and Fp PFC_mp+Cing). This trend suggests that the neural representation of the relative magnitudes of numerosity was emphasized along these frontoparietal regions. In contrast, classification performance in the temporal areas was comparatively lower and generally lacked statistical significance (Df lPar+lTemp, Fp rTemp, Df rTemp, and VA rTempOcc+rPar).

Fig. 3. ROI-based MVPA classification performance on relative numerosity coding.

The figure illustrates classification performance (x-axis) across all ROIs (y-axis). The classification results in the left and right hemisphere ROIs, indicated by left- and right-headed triangles, are depicted in the left and right panels, respectively. For the bilateral ROIs (circles), which span across both hemispheres, identical data are displayed in both panels to aid interpretation. The data points represent the mean classification performance across all participants (n = 30), with error bars indicating the standard error of the mean. *p < 0.05, **p < 0.01, ***p < 0.001 (one-sided t-tests against zero, Holm corrected for multiple comparisons). The suffix of ROI labels indicates the functional network each ROI belongs to. Vis, visual; SomMot, somatomotor; DA, dorsal attention; VA, ventral attention; Fp, frontoparietal; Df, default. The remainder of ROI labels indicates the anatomical location. pCun, precuneus; PCC, posterior cingulate cortex; Temp, temporal; TempOcc, temporal-occipital; ParOper, parietal operculum; Par, parietal; Post, posterior; FrOper, frontal operculum; Ins, insula; PFC, prefrontal cortex; PFC_l, lateral prefrontal cortex; PFC_v, ventral prefrontal cortex; PFC_mp, medial posterior prefrontal cortex; Med, medial; Cing, cingulate; FEF, frontal eye field; PrC_v, precentral ventral. See Table 1 for a detailed description of ROI labeling. See Supplementary Table 1 for the statistical test results. Source data are provided as Source Data file.

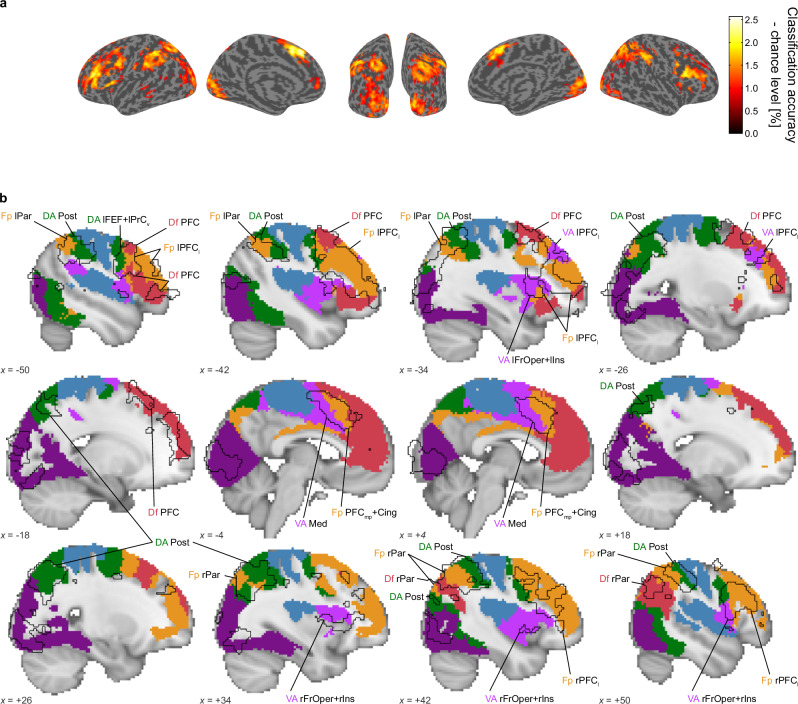
While our ROI-based classification approach effectively revealed the hierarchical emergence of relative numerosity coding across cortical areas, it had a limitation in spatial specificity due to the feature selection procedure, which could select any distant voxels in the relatively large ROIs. To address this issue, we conducted a supplementary searchlight-based classification analysis using a small, moving sphere. The results were largely aligned with those of the ROI-based analysis; Clusters where classification performance exceeded chance level were predominantly found around the visual cortex and frontoparietal regions (Fig. 4a). Notably, the statistically significant clusters identified in the searchlight-based analysis largely overlapped with the ROIs that showed statistically significant classification performance in the ROI-based analysis (Fig. 4b). This overlap suggests that the results of our ROI-based classification were not unduly influenced by the way we defined the ROIs.

Fig. 4. Searchlight-based MVPA classification performance.

a Blobs represent brain regions where the searchlight-based MVPA identified performances above chance levels (one-sided t-test (n = 30), cluster-wise p_FWE < 0.05 with voxel-wise threshold p < 0.001 (uncorrected) to define clusters). b Sagittal views of the statistically significant clusters (black solid outlines) identified in (a). The filled and colored areas indicate statistically significant ROIs in the ROI-based MVPA; the colors correspond to each functional network associated with these ROIs, as detailed in Supplementary Fig. 3. See the legend for Fig. 3 and Table 1 for a detailed description of ROI labeling. The MNI coordinates, located at the bottom left corner of each panel, indicate the specific location of each sagittal slice.

Relative versus absolute coding of numerosity

Our ROI- and searchlight-based classification analyses demonstrated the existence of a relative coding of numerosity within the visual and the frontoparietal regions. Crucially, the results revealed that the relative coding evolves along the numerosity processing hierarchy. This raises a question: Is the absolute coding of numerosity similarly distributed across cortices, and which form of coding, relative or absolute, predominates in each ROI?

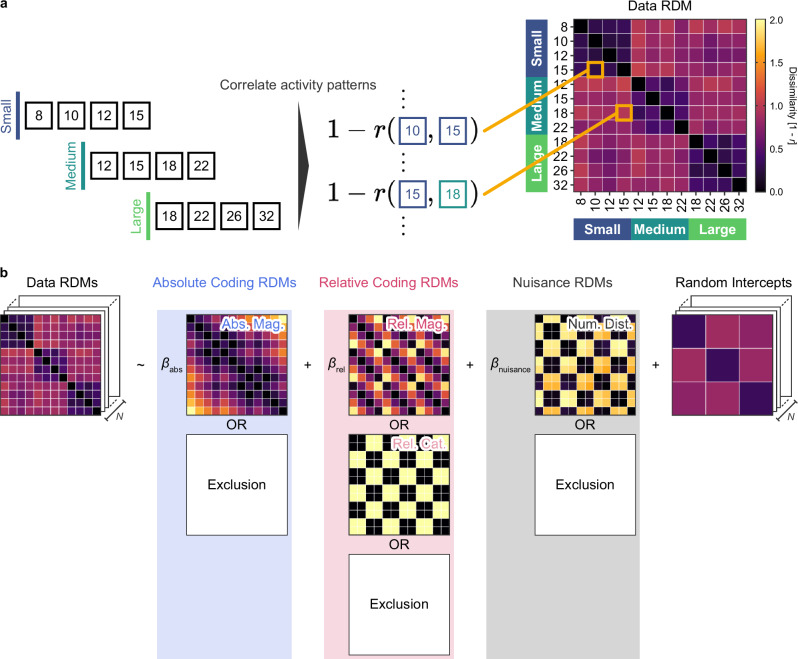
To address these questions, we examined whether the activity patterns in each brain region better represent absolute numerosity, relative numerosity, or a combination of both using our representational similarity analysis with linear mixed-effect modeling. This involved measuring the dissimilarity in the brain activity patterns between pairs of numerosities and constructing a representational dissimilarity matrix (data RDM) for each ROI (Fig. 5a). These data RDMs were then subjected to regression analysis against a combination of hypothetical dissimilarity matrices, employing linear mixed-effect modeling (Fig. 5b). A model selection approach was adopted to determine the most parsimonious and best fitting model for each ROI, considering all possible combinations of regressors.

Fig. 5. Schematic illustration of representational similarity analysis.

a Dissimilarity in neural activity patterns was determined by calculating Pearson’s correlation between each pair of recorded patterns. For every participant, we generated one data representational dissimilarity matrix (RDM) for each ROI. b Within each ROI, the data RDMs were subjected to regression analysis against a set of hypothetical dissimilarity matrices. Abs Mag, absolute magnitude-based RDM; Rel Mat, relative magnitude-based RDM; Rel Cat, relative category-based RDM; Num Dist, numerical distance-based RDM. These hypothetical RDMs were derived based on the numerical magnitudes of the stimuli.

Our key regressors included three hypothetical RDMs, treated as fixed-effects: absolute magnitude-, relative magnitude-, and relative category-based RDMs. The absolute magnitude-based RDM represented differences in the absolute numerosity magnitude. In contrast, the relative magnitude-based RDM anchored on deviation from the mean numerosity in each set, reflecting differences in relative numerosity magnitude. Additionally, to account for the task-related dichotomic categories of numerosity (i.e., smaller and larger), the relative category-based RDM was defined as the difference in numerosity categories, namely, whether numerosities were smaller or larger than the set’s mean. Note that, due to their collinearity, the relative magnitude- and category-based RDMs were mutually exclusive in every candidate model (Supplementary Fig. 5). To further control for the potential influences of task difficulty and experimental sessions, another hypothetical RDM based on the numerical distance between numerosity pairs was included, along with random intercepts for session pairs (see the Methods for details). Note that all dissimilarity measures in the hypothetical RDMs were defined on the logarithm of numerosity, in accordance with Weber-Fechner’s law in numerosity discrimination^10,11.

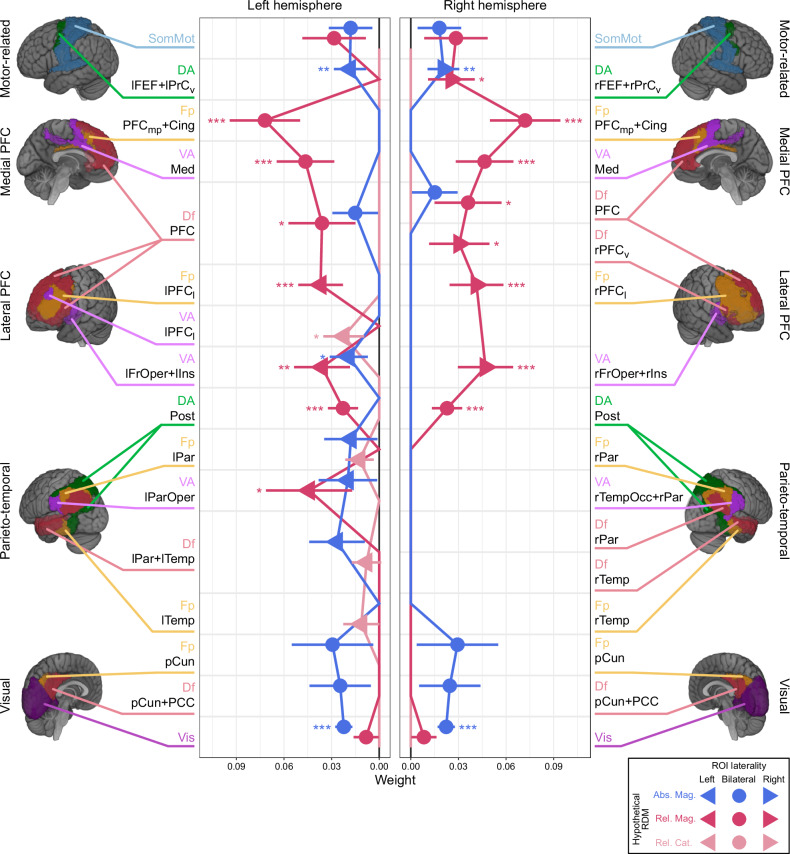
Significant regression coefficients, indicating non-zero weights for the relative magnitude, were found in the frontoparietal cortex. This includes the parietal regions (VA lParOper and DA Post), lateral PFC (VA lFrOper+lIns, VA rFrOper+rIns, Fp lPFC_l, Fp rPFC_l, Df rPFC_v, and Df PFC), medial PFC (VA Med and Fp PFC_mp+Cing), and a motor-related region (DA rFEF+rPrC_v). The upward trend in these regression coefficients was noted, beginning in the parietal regions and reaching a peak in the medial PFC (Fig. 6 and Supplementary Table 2). These results align well with the findings from our earlier classification analysis (Fig. 3). The relative category-based RDM showed a non-zero coefficient exclusively in a lateral prefrontal region (VA lPFC_l), suggesting a focal representation of the relative category of numerosity. In contrast to the relative representations, absolute coding was significant only in a limited number of ROIs: visual and prefrontal ROIs (Vis, VA lFrOper+lIns, DA lFEF+lPrC_v, and DA rFEF+rPrC_v). We did not observe any clear increasing or decreasing trends in the regression coefficients along the information processing hierarchy for the absolute coding. Finally, the numerical distance-based RDM showed a non-zero coefficient in a few ROIs, alongside other coefficients (VA lPFC_l, VA Med, and DA lFEF+lPrC_v, Supplementary Table 2).

Fig. 6. Regression coefficients in ROI-based representational similarity analysis.

Displayed are the regression coefficients for fixed-effects (x-axis) across all ROIs (y-axis). The results for the left and right hemisphere ROIs, indicated by left- and right-headed triangles, are shown in the left and right panels, respectively. For the bilateral ROIs (circles), which span across both hemispheres, identical data are displayed in both panels to aid interpretation. The data points represent three different types of fixed effects: absolute magnitude-based (blue), relative magnitude-based (magenta), and relative category-based (light magenta) RDMs. The data points represent the regression coefficient, with error bars indicating the standard error of the coefficient, derived from the best model fitted to data RDMs from all participants (n = 30). In ROIs where a data point is absent, the corresponding fixed-effect was excluded in the selected model. *p < 0.05, **p < 0.01, ***p < 0.001 (one-sided t-tests against zero, Holm corrected for multiple comparisons). See the legend for Fig. 3 and Table 1 for a detailed description of ROI labeling. See Supplementary Table 2 for the statistical test results. Source data are provided as Source Data file.

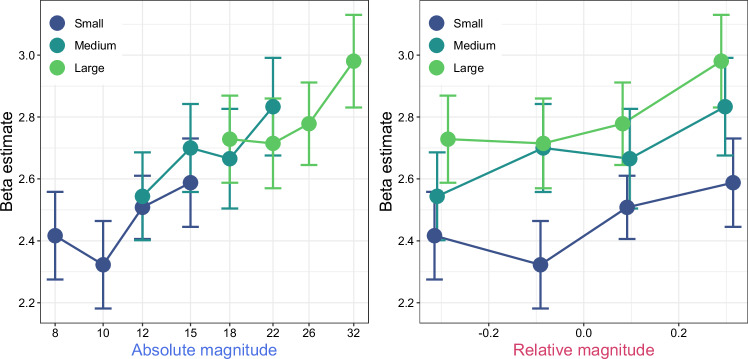
While our multivariate approach revealed brain regions exhibiting distinct multivariate activity patterns for varying numerical magnitudes, it does not completely discount the possibility that these regions might encode numerical magnitudes through a simpler mechanism, such as monotonic increase or decrease in activity corresponding to the rise in numerosity. To explore this further, we assessed whether changes in average activity within each ROI were linked to either the absolute or relative magnitude of numerosity (Supplementary Figs. 6–7). Employing this additional univariate method, we found a significant Spearman’s rank correlation exclusively in the visual cortex ROI (Fig. 7); the mean activities positively correlated with the absolute magnitude of numerosity (two-sided Wilcoxon signed-rank test: median $\rho$ = 0.377, 95% CI = [0.095, 0.528], W = 393.5, p = 0.024). There was also a weaker correlation with the relative magnitude of numerosity (two-sided Wilcoxon signed-rank test: median $\rho$ = 0.203, 95% CI = [0.038, 0.311], W = 362.5, p = 0.044); however, the difference in these correlations was not statistically significant (two-sided Wilcoxon signed-rank test: median $\mathrm{\Delta }\rho$ = 0.119, 95% CI = [−0.015, 0.266], W = 321, p = 0.070). This result supports the notion that the visual cortex may represent numerosity through monotonic neural responses, and it reinforces our multivariate findings that highlight the dominance of absolute numerosity coding in the visual cortex.

Fig. 7. Correlation between the average activity in the visual cortex and stimuli.

The figure presents scatter plots showing the correlation of the average activity in the visual cortex ROI (y-axis) with stimulus magnitudes (x-axis), categorized into either absolute magnitude (left panel) or relative magnitude (right panel). Each data point represents the average activity across participants, with error bars depicting the standard error of the mean (n = 30). The colors correspond to the numerosity set, as detailed in Fig. 1b. Source data are provided as Source Data file.

Discussions

The present study investigated whether the neural representation of numerosity encodes the absolute or relative magnitude of non-symbolic numbers. Through ROI- and searchlight-based classification analysis, we first demonstrated that relative magnitude representations were distributed in the visual cortex and the frontoparietal regions. The classification performance improved progressively along the frontoparietal network, indicating a hierarchical development of relative numerosity coding.

Next, by employing representational similarity analysis with linear mixed-effect modeling, which accounted for the influence of relative category and task difficulty, we observed a transition from absolute to relative magnitude representation along the information processing hierarchy; the absolute coding was predominant in the early visual cortex, while the relative coding of numerical magnitude was more pronounced in the frontoparietal regions. In line with the classification analysis, the weight of the relative coding increased along the frontoparietal areas, supporting the idea that relative numerosity plays a crucial role in guiding magnitude-based decisions and actions.

Neural representations of relative numerosity

Our study revealed that the frontoparietal regions encode the relative magnitude of numerosity. This finding might seem contradictory to a recent fMRI study with a population receptive field (pRF) analysis suggesting that numerosity preference is fixed irrespective of the numerical context²¹. In their experiment, Cai and colleagues used two sets of dot arrays, one ranging narrowly from 1 to 7 and the other widely from 1 to 64, to present numerosity. Although their analyses indicated a slight shift in preferred numerosity at each recording site depending on the range presented, it did not strongly support the existence of relative coding of numerosity.

The discrepancies between Cai’s findings and ours could be attributed to difference in task design. While Cai’s study engaged participants in a color detection task unrelated to numerosity, our study explicitly required participants to judge whether the presented numerosity was larger or smaller than the average of preceding trials. Our task inherently involved making judgments about relative magnitude differences, potentially compelling our participants to internally scale numerical magnitude. This requirement might have enhanced the representation of relative numerosity in the frontoparietal regions.

Another potential explanation for the differing conclusions could be the difference in the analysis method. While Cai’s pRF analysis focused on the magnitude of brain activity for each voxel (i.e., univariate approach), our MVPA examined the spatial pattern across a group of voxels (i.e., multivariate approach). Although not directly compared, our MVPA approach might be better suited to address our research question than the pRF approach. This is because MVPA, without assuming any specific format of representation a priori, can detect numerosity-sensitive activity with greater sensitivity than the univariate method²², whereas pRF analysis is specialized in identifying voxels tuned to specific numerosities. An example that MVPA could uniquely identify, but not pRF, is when numerosity information is embedded in the populations of neurons without a distinct preference for a specific numerosity. In a previous electrophysiological study²³, Tudusciuc and Nieder suggested that the temporal structure of spike trains in numerosity-untuned neurons may convey numerosity information. Although such temporal dynamics may be blurred in fMRI data, they could still be reflected in the estimated multi-voxel activity patterns. Hence, we speculate that, if these neural populations contribute to the relative coding of numerosity, they are more likely to be detected by MVPA than by pRF analysis.

Collectively, the differences in the task or the fMRI data analyses methods, or possibly a combination of both, could have led to the varied findings between Cai and colleagues and our study. Future research, employing comparable task designs and analytical techniques, is necessary to bridge the gap between these studies and provides a better understanding of the neural mechanisms underlying the scaling of response properties in different contexts.

Contributions of predictive processing to the relative numerosity representation

The underlying mental process that shapes relative numerosity representation remains an open question. Beyond the influence of task demands discussed earlier, we propose that predictive processing²⁴ might play a role. This concept suggests that deviations from prior expectations, constructed based on past experiences, could lead to the formation of relative numerosity representations. Supporting this idea, a recent electrophysiological study in non-human primates reported such relative representation driven by predictive processing in the temporal domain. In this study, Meirhaeghe and colleagues manipulated expectations of time intervals using two different stimulus ranges (short vs. long) and found that neural dynamics in the dorsomedial frontal cortex were modulated according to these expectations, reflecting deviations from the expected intervals²⁵.

We speculate that the relative representations driven by predictive processing may be linked to numerosity adaptation, given the potential connection between predictive processing and perceptual adaptation^26–28. A large body of psychophysical research has shown that numerosity perception is susceptible to adaptation^29–31 where participants are repeatedly exposed to a specific numerosity. Several neuroimaging studies indicated that adaptation alters neural responses to numerosity stimuli in the parietal cortex^5,32,33, which is where we observed relative numerosity representations. Since the experimental manipulations are comparable in that both adaptation and our study involve altering the external statistical structure (i.e., repeated exposure to a particular numerosity in adaptation and shifting the range of numerosity distribution in our study), we speculate that the neural consequences may be similar. Specifically, adaptation may also reorganize neural responses in a relative manner, centered around the adapted numerosity.

Our study, however, could not conclusively determine whether relative representation of numerosity was driven by specific task demands (such as comparison with an internal reference) or by predictive processing. This limitation arises because, in our experimental design, the numerical distance from a reference numerosity (i.e., the internal average numerosity of preceding trials) and the deviation from the expected numerosity (i.e., the mean of the uniform stimulus distribution) were nearly identical (Fig. 1d), making them not dissociable. A potential avenue for future research is to investigate whether the neural representation for a comparison stimulus is more related to a reference stimulus or to prior expectations. This could be achieved by independently manipulating these variables and examining if the relative representations observed in the present study are affected accordingly.

Hierarchical processing of numerosity in the frontoparietal regions

The involvement of the frontoparietal regions in numerosity processing aligns with previous human fMRI studies employing diverse analytical methods, including conventional univariate analysis^5,12,34,35, MVPA^{13–15,33,36–41}, pRF analysis^{21,32,42–45}, and meta-analysis^16,17, as well as insights from brain-lesion⁴⁶ and -stimulation^47,48 studies. Most importantly, our study showed that numerosity processing is hierarchically organized in the frontoparietal regions. This finding agrees with a neurophysiological study in monkeys showing a longer response latency of the lateral PFC than the IPS during numerosity processing⁴⁹.

We speculate that the relative representations of numerosity in the occipital, parietal, and frontal cortices may contribute to different stages of numerosity processing. While relative numerosity representations in the occipital and parietal cortices likely contribute to perceptual processes, those in the frontal cortices may be more involved in decision-making processes. This notion is supported by previous neuroimaging studies that have shown a dissociation between active and passive (or numerosity-irrelevant) tasks. For instance, studies using decision-free, passive viewing paradigms, such as pRF^21,43,44 and numerosity adaptation studies^5,32,33, consistently reported perceptual-level numerosity representations in the occipital and parietal regions (see also a meta-analysis¹⁷). In contrast, studies requiring explicit numerosity judgments reported involvement of the lateral PFC^{2,9,11,16–18,49}, where we observed relative representations, suggesting a role in decision-making process. Indeed, the lateral PFC is well-known for its involvement in decision-related cognitive processes, such as executive control⁵⁰. Importantly, in addition to the lateral PFC, we also found relative representations in the medial PFC, which is anatomically connected to the lateral PFC⁵¹ and has been implicated in decision-making processes, such as conflict monitoring and behavior controll⁵². Based on these findings, we speculate that relative numerosity representations are first established at a perceptual level in the occipital and parietal regions, then transferred to the frontal association cortices (i.e., lateral and medial PFC) to incorporate task-dependent components, such as relative categorization and decision-making. This idea is consistent with a neurophysiological study that proposed a flow of numerosity information from the IPS to the lateral PFC⁴⁹ and a recent fMRI study that identified the parietal and prefrontal cortices as key regions for representing internally generated numerical magnitudes during approximate calculation, with the parietal cortex specifically implicated in transforming external inputs to internal numerical magnitudes⁵³.

This notion is also in line with the two-stage model of numerosity-time interaction, which posits that numerosity information may be more abstractly represented in the prefrontal than in the parietal cortex⁴⁸. By illustrating that the representation of relative numerosity emerges through this hierarchical process, our study goes beyond these previous studies and introduces an additional dimension of abstraction: the transition from absolute to relative numerical magnitude. We speculate that this abstraction process might be a fundamental principle in magnitude coding, potentially offering more efficiency and robustness, and might even be applicable across other domains⁵⁴.

Mixed representations of absolute and relative numerosity in the visual cortex

The classification analysis showed the presence of relative numerosity representation in the visual cortex, albeit with a smaller weight on relative coding compared to absolute magnitude in the representational similarity analysis. We interpret these results as indicating a mixture of absolute and relative magnitude representations, with a relatively smaller proportion of information dedicated to relative magnitude. This interpretation aligns with our observations that the average activity in the visual cortex showed a positive correlation with absolute magnitude, and to a lesser extent, with relative magnitude (Fig. 7).

The question of whether the visual cortex encodes numerosity directly or low-level visual features that construct numerosity in the later processing stages is a topic of ongoing debate. A recent fMRI study by Paul and colleagues found that while BOLD responses in the early visual cortex (V1–3) exhibited monotonic increases with numerosity, this was likely a reflection of increased local image contrast (or aggregated Fourier power), rather than numerosity itself ⁴⁵. This finding was supported by another study indicating that multivariate activity patterns before V3 mainly reflect non-numerical visual features¹⁵. In contrast, another line of research suggests that the monotonic response to numerosity observed in a visual-system-inspired convolutional neural network cannot be attributed to lower-level visual features of the stimuli, but rather to the concept of numerosity itself ⁵⁵.

Although we do not rule out the potential contributions of non-numerical stimulus features, the present study, demonstrating successful classification performance of numerical magnitudes, offers further support to the notion that the visual cortex is involved in representing numerosity information. Considering our findings of mixed absolute and relative numerosity representations in the visual cortex, it would be intriguing to investigate how these two coding strategies are related to the transitions across different sub-regions of the visual cortex. While this remains speculative, it is possible that there is a transition point around V3, where neural populations in the earlier stages are more sensitive to lower-level visual features, and those in later stages are more sensitive to numerosity information.

The absolute magnitude coding observed in the visual cortex ROI in our representational similarity analysis may also align with the findings from pRF studies that reported numerosity tuning in the occipito-temporal regions^{21,32,42–45}. Although none of our ROIs exclusively covered the occipito-temporal regions, the ROI designated for the visual cortex was, in fact, relatively large and likely included portions of these regions (Vis in Supplementary Fig. 3). Interestingly, the representational similarity analysis also revealed relative coding in the same Vis ROI, and the searchlight-based classification analysis further highlighted the occipito-temporal regions as areas where relative coding exists. Collectively, these findings suggest that the occipito-temporal regions may encode both the absolute and relative magnitude of numerosity. In contrast, the involvement of other temporal regions in numerosity representation has been rarely reported in pRF studies^{21,32,42–45}, meta-analyses^16,17, or in the present study. Although we can only speculate, this consistent lack of observations might suggest that these temporal regions do not play a significant role in numerosity representation.

In the present study, we observed that relative coding of numerosity was distributed across the frontoparietal regions whereas absolute coding co-exists with relative coding in the early sensory cortex. Notably, we found that the representation of relative magnitude is hierarchically organized along the numerosity processing pathway within these frontoparietal regions. These findings offer insights into the plasticity of numerosity representations, suggesting a potential for optimizing these representations in a context-dependent manner. We believe that our findings inspire a range of subsequent studies aimed at exploring the computational mechanisms underlying the emergence of such relative coding of numerosity through the information processing stream and its role in guiding magnitude-based decisions and actions.

Methods

Participants

To obtain complete fMRI data sets from 30 participants, which we planned a priori, we recruited 45 volunteers. Of these, nine were unable to complete the three experimental sessions. Additionally, six participants were excluded due to exceptionally accurate or inaccurate behavioral responses (n = 3; see Behavioral data analysis) or excessive head motions (n = 3; see Preprocessing in fMRI data analysis). Consequently, data from the remaining 30 participants (20 males and 10 females, M_age = 22.467, SD_age = 1.383) were analyzed to finalize the results. All participants had normal or corrected-to-normal vision and had no history of psychiatric and neurological disorders. Participants received monetary compensation for their participation. They provided written informed consent prior to participation. The study’s protocol was approved by the institutional ethics and safety committees of the National Institute of Information and Communications Technology.

Sex and/or gender were not considered in the study design. Participants self-reported their sex prior to the experiment. Since sex differences were beyond the scope of our study, no analyses based on sex were performed.

Experimental design

The experiment consisted of three sessions, conducted on three different days. To reduce the potential for carryover or learning effects from previous sessions, we scheduled the interval between sessions to range from 3 to 21 days. Participants were instructed to disregard any experiences from the earlier sessions.

Task and stimuli

Participants were asked to maintain their gaze at the red fixation cross (0.219 × 0.219 deg) presented at the center of the monitor throughout experimental runs (Fig. 1a). In each trial, a dot array was presented for 0.4 s within a virtual circle located at the monitor’s center. Following an inter-stimulus interval (jittered between 3.0 and 6.0 s with 0.2 s step size), the red response cues indicating the spatial position of the response buttons for smaller (S) or larger (L) responses were presented for 2 s. Participants responded whether the numerosity was smaller or larger than the running average of the preceding trials (i.e., bisection task) by pressing one of the two response buttons. Following this, the dot array for the subsequent trial appeared after an inter-trial interval (jittered between 3.1 and 5.9 s with 0.2 s step size). To record the blood-oxygen-level-dependent (BOLD) signal baseline, a rest period of 16 s with a fixation cross was included at the beginning and end of each run.

The participants were instructed to pay attention to the numerosity of the dot array while ignoring the task-irrelevant stimulus features such as the color of dots or the dot positions. Also, participants were explicitly instructed not to count the dots. The spatial positions of the response cues (S for smaller and L for larger), corresponding to the two response buttons (the left cue for the right index and the right cue for the right middle finger), were randomized across trials. This randomization was expected to help distinguish the BOLD responses reflecting the numerosity encoding process from those involved in preparing, selecting, and executing a response. This distinction was possible because participants were not able to decide which button to press until the response cue was shown. The participants were encouraged to prioritize response accuracy. In the first trial of the first run of each session, participants were asked to press one of the two buttons at random, as there was no previous trial to use as a reference for numerosity.

Since previous studies suggested that different mechanisms may be involved depending on the range of numerical magnitude^56–59, our study focused on the approximate number system (ANS) range. We created the three sets of numerosity, each containing four values that were approximately equidistant on a logarithmic scale. These sets were categorized as small (8, 10, 12, or 15), medium (12, 15, 18, or 22), and large (18, 22, 26, or 32) as shown in Fig. 1b. In each session, only one set was used, with the order of sets being counterbalanced across participants. Participants were not informed about the number of numerical magnitudes in each set, the number of sets, and the order in which they would be presented.

By referencing a preceding study¹⁵, other irrelevant stimulus parameters, such as item surface area (the dot size), and total field area (the size of the virtual circle) of the dot arrays, were manipulated independently from numerical magnitudes. The range of numerosities varied across sessions, but the item surface area remained constant at either 0.2²π deg² or 0.237²π deg², and the total field area was fixed at either 5.92²π deg² or 7²π deg², regardless of the session. Thus, in each session, the dot arrays were defined by 4 (numerical magnitude) × 2 (item surface area) × 2 (total field area) combinations, resulting in 16 unique combinations. These combinations were presented in a random order in each run. Dot positions were also randomized across trials. To prevent the texture-density mechanism from becoming predominant, we ensure that minimum edge-to-edge distance between elements, including the fixation cross, was no less than 0.219 deg. This constraint yielded an average edge-to-edge distance of at least 0.665 deg (mean = 1.173, max = 1.955) and an average center-to-center distance of at least 1.108 deg (mean = 1.610, max = 2.373), facilitating the processing of numerosity primarily through the ANS⁵⁹. Furthermore, to prevent the luminance of the dot array from being a proxy to estimate numerosity, half of the dots within an array were presented in black, and the rest were presented in white⁶⁰: for arrays with an odd number of dots (2 N + 1), half the trials featured N white dots and N + 1 black dots, while the other half had N + 1 white dots and N black dots.

All stimuli were generated and presented with MATLAB 2020a (Mathworks, Natick, MA, USA) and Psychophysics Toolbox Version 3^61–63. The stimuli were presented on the gamma-corrected MRI-compatible LCD monitor (32 inches, resolution = 1920 × 1080, refresh rate = 60 Hz, width = 69.84 cm; BOLDscreen 32”, Cambridge Research Systems, Rochester, UK). The participants viewed the monitor through a mirror mounted on the head coil (viewing distance 153.0 cm). The participants’ responses were recorded using an MRI-compatible button box (4 Button Bimanual, Current Designs, Philadelphia, PA, USA).

Procedure

To ensure the task and experimental procedure, the participants performed practice trials outside and inside the scanner before each experimental session. The numerosity set in the practice blocks was the same as in the subsequent fMRI runs. The practice blocks outside and inside the scanner consisted of four trials, where each of the four numerical magnitudes in a set was presented only once.

In the subsequent 16 fMRI runs with 16 trials per run, BOLD signals were recorded while we monitored behavioral performances. The first run was considered as a practice run to establish the bisection point while the following 15 runs were considered as the real experimental runs. When they did not make a button press during the response phase, that trial was recorded as a miss. If responses were missed more than two times in a run, that run was repeated with the same stimulus parameters. The data of participants whose experimental session was aborted due to such repetition more than three times were excluded from the data analyses.

MRI data acquisition

A 3 T MRI scanner (MAGNETOM Prismafit, Siemens, Erlangen, Germany) equipped with a 64-channel head coil (Head/Neck 64, Siemens, Erlangen, Germany) was used for the image acquisitions. A field-map image was acquired with the double-echo spoiled gradient-echo sequence (78 axial slices, phase encoding direction A ≫ P, FOV = 216 × 216 mm, voxel size = 2 × 2 × 2 mm, phase partial Fourier = 7/8, bandwidth = 827 Hz/pixel, flip angle = 50˚, TR = 763.0 ms, TE₁/TE₂ = 4.95/7.41 ms). In the fMRI runs BOLD signals were acquired with a multi-band accelerated echo planar imaging (EPI) (version R016b, multi-band factor = 6, 78 axial slices, phase encoding direction = A ≫ P, FOV = 216 × 216 mm, voxel size = 2 × 2 × 2 mm, phase partial Fourier = 7/8, bandwidth = 2436 Hz/pixel, flip angle = 60˚, TR = 1000 ms, TE = 30 ms, echo spacing = 0.57 ms). The leak-block kernel⁶⁴ was applied to minimize slice leakages. An anatomical image was also acquired using the magnetization prepared rapid acquisition with gradient echo (MPRAGE; phase encoding direction = A ≫ P, FOV = 256 × 256 mm², voxel size = 0.8 × 0.8 × 0.8 mm³, bandwidth = 220 Hz/pixel, flip angle = 8˚, TR = 2400 ms, TE = 2.22 ms, TI = 1000 ms, GRAPPA reduction factor = 2).

Behavioral data analysis

The proportion of larger responses in the actual experimental runs was calculated at each numerical magnitude within each set. For each individual’s data, a psychometric function (logistic function) was fitted on the log scale for each set (Fig. 1c and Supplementary Fig. 1). We estimated two key parameters: the numerical value at which the proportion of larger responses is 0.5, representing the subjective bisection point, and the slope, indicating the precision of the participants’ responses. Participants whose bisection point and slope values deviated by more than 3 SDs from the group average were considered outliers and excluded from the subsequent data analyses. We conducted two-sided t-tests to examine whether the subjective bisection points were under- or overestimated and whether they significantly differed from the mathematical average of each set. Additionally, we used a one-way repeated-measures ANOVA with numerosity set as the factor to assess whether the slopes differed across the numerosity sets, potentially contradicting Weber-Fechner’s law. The significance level was set at α = 0.05. When Mauchly’s test indicated a violation of sphericity, the degrees of freedom were adjusted using the Greenhouse-Geisser correction. Bayesian t-tests and Bayesian repeated-measures ANOVA were also applied to test the null hypotheses. In the Bayesian hypothesis testing, we used the Jeffreys-Zellner-Siow prior, which is the default option in JASP^65–67. The prior on effect size was specified as a Cauchy distribution with scale $r$: $r=\sqrt{2}/2$ for the Bayesian t-test, $r=0.5$ for the fixed effect, and $r=1$ for the random effect in the Bayesian repeated-measures ANOVA, while the prior on variance was set as a Jeffreys prior $p\left({\sigma }^2\right)=1/{\sigma }^2$. The statistical analyses were performed with R⁶⁸, JASP⁶⁹, MATLAB 2020a (Mathworks, Natick, MA, USA), and Palamedes toolbox⁷⁰.

fMRI data analysis

Preprocessing

The fMRI data of the real experimental runs were preprocessed using SPM12 (v7771) software implemented on MATLAB 2017a (Mathworks, Natick, MA, USA). First, geometrical distortions and head movements were corrected. The anatomical image was registered onto the average functional image for each session. All the coregistered images were then normalized onto the MNI (Montreal Neurological Institute) space. The functional images were smoothed with the three-dimensional Gaussian kernel with an FWHM of 2 mm in light of the possibility of performance improvement in multivariate pattern analyses (MVPA)⁷¹. Participants who showed translations greater than 2 mm or rotations greater than 0.05 radians were excluded from the following fMRI data analyses.

General linear model analysis

To estimate brain activity during numerosity processing, a general linear model was applied to each numerosity set using SPM12. The model included four regressors of interest, one for each numerical magnitude. To regress out nuisance variables, we incorporated parametric modulation terms for both the item surface area and the total field area into the numerosity regressors. Additionally, regressors accounting for button presses, the six head movement parameters, and constant terms were included in the design matrix. The regressors on numerosity, their modulation terms, and participant responses were all set at the onset of each event, with a duration of zero. Each regressor was convolved with a canonical hemodynamic response function. The model for each participant was high-pass filtered (cutoff period = 128 s). Since TR was relatively short (1 s), temporal autocorrelation in the BOLD signal was accounted for by the FAST model⁷² in the SPM12. As a result, beta images for the 15 real experimental runs were estimated for each numerical magnitude.

Region of interest

To define network-constrained regions of interests, we employed a cortical parcellation based on functional connectivity¹⁹. The parcellation consists of seven functional networks: visual (Vis), somatomotor (SomMot), dorsal attention (DA), ventral attention (VA), limbic, frontoparietal (Fp), and default (Df) network. The limbic network was excluded from our ROIs as it contains brain regions susceptible to geometrical distortion and signal loss in the EPI sequence, such as the orbitofrontal cortex⁷³. Consequently, including the limbic network could lead to controversial interpretations of the results.

The ROIs were formed from the liberal masks of the cortical parcellation on the MNI space distributed with FreeSurfer⁷⁴. To define network-constrained but spatially local ROIs, each network mask was divided into sub-regions based on geometrical continuity (voxel connectivity parameter was 26) using FSL v5.0⁷⁵. The ROIs with less than 500 voxels were excluded in the following analyses for the subsequent feature extraction. Eventually, 25 ROIs were constructed (Table 1 and Supplementary Fig. 3), and unique ROI labels were assigned for identification²⁰.

Classification analysis

To decode the relative positions of numerosity from multivariate patterns (Fig. 2), we employed a four-class classifier. This classifier was a linear SVM with a regularization parameter C set at 1. It was trained using the fMRI data (beta images, without any feature scaling) on one numerosity set and then tested on the other two sets. This procedure was repeated across all possible combinations of the three numerosity sets, effectively implementing a 3-fold cross-validation approach. The average classification performance was then assessed based on these cross-validation results.

For the ROI-based classification analysis, 500 voxels were extracted within each ROI to make the ROIs comparable in their size. Before conducting the classification analyses, we performed feature selection for each ROI and each participant, using a leave-one-participant-out approach. Initially, a first-level analysis was conducted within each set for each participant, where a contrast image against zero was defined for each numerical magnitude. Following this, a second-level analysis was applied to the contrast images from the remaining 29 participants for each participant. This process produced a t-value map for the 12 numerical magnitudes (4 stimuli × 3 set). The 12 t-value maps were aggregated by taking the minimum value at each voxel. The top 500 voxels were then selected within each ROI mask based on these aggregated t-value maps. The classification performance was derived for each ROI and participant. To determine whether the classifications was successful, we tested if the performance exceeded the theoretical chance level of 25% for each ROI using a one-sided t-test. The p-values were Holm corrected for multiple comparisons across ROIs⁷⁶. The significance level was set to $\alpha$ = 0.05.

To evaluate the robustness of the results, we conducted a whole-brain searchlight-based classification analysis. For this analysis, we used a searchlight sphere with a radius of four voxels (8 mm). The classification performance map was derived for each participant and smoothed with a three-dimensional Gaussian kernel with an FWHM of 4 mm. The performance maps were then subjected to one-sided t-tests to determine if they exceeded the chance level. The statistical significance was defined by cluster-wise family-wise error (FWE) corrected p < 0.05: clusters were defined by voxel level threshold p < 0.001 (uncorrected).

Both ROI- and searchlight-based classification analyses were performed using The Decoding Toolbox (3.999E)⁷⁷ implemented on MATLAB 2017a (Mathworks, Natick, MA, USA).

Representational similarity analysis

In the representational similarity analysis (RSA)⁷⁸, we focused on the same 500 voxels that were selected for the ROI-based classification. For each ROI, we constructed a representational dissimilarity matrix (data RDM) where the dissimilarity in brain activity patterns between each pair of numerosities was represented as 1 minus Pearson’s correlation, $1-r$ (Fig. 5a). To examine whether the data RDMs could be explained by the absolute and relative coding, we regressed the data RDMs onto a combination of hypothetical dissimilarity matrices using a linear mixed-effect modeling approach (Fig. 5b).

We modeled the hypothetical dissimilarity matrices as fixed slopes. The dissimilarity matrices were defined in the stimulus space, with numerosity log-transformed in advance, in accordance with Weber-Fechner’s law in numerosity discrimination^10,11. The dissimilarity between numerosities was based on different aspects: absolute magnitude (numerical magnitude), relative magnitude (deviation of the presented numerosity from the mathematical bisection point), or relative category (smaller or larger than the mathematical bisection point, binarized as 0 for smaller and 1 for larger). To regress out the effect of task difficulty, we included a numerical distance-based dissimilarity matrix as another fixed slope. This dissimilarity matrix resembled the relative magnitude-based matrix, but with a key distinction: we used the absolute value of the deviation of presented numerosity from the mathematical bisection point. Finally, to account for any possible nuisance effects by comparing activity patterns across experimental sessions, such as spatial displacements that may persist after preprocessing and impair the dissimilarity measure across the sessions, we added a random intercept as a nuisance regressor. This random intercept was defined for each combination of participant and session pairs, reflecting the fact that the effect depends on which pair of sessions was compared for each participant. The session pairs (i.e., numerosity sets) included within-set comparisons (small-set vs. small-set, medium-set vs. medium-set, and large-set vs. large-set), and cross-set comparisons (small-set vs. medium-set, medium-set vs. large-set, and large-set vs. small-set). Notably, within-set comparisons did not distinguish between small-, medium-, or large-set pairings. This approach aimed to control for intra-individual and/or intra-session nuisance factors that could influence the comparisons of brain activity patterns.

We applied a model selection framework to determine the most parsimonious and predictive model for each ROI. This involved constructing various candidate models based on possible combinations of the regressors. There was a total of 12 candidate models, derived from: 2 (include or exclude absolute magnitude-based regressor) × 3 (include relative magnitude-based regressor, include relative category-based regressor, or exclude them) × 2 (include or exclude numerical distance-based regressor). Due to the high correlation between the relative magnitude-based regressor and the relative category-based regressor (Supplementary Fig. 5), these regressors were not included together in the model, but rather mutually exclusively. The random intercept was always contained in the model. The selection of the top models was based on the Akaike information criterion (AIC). We considered the top models, rather than solely the model with the minimum AIC, because models with a small AIC difference relative to the minimum AIC (ΔAIC < 2) are also considered to have substantial support⁷⁹. Among these top models, the best model was defined as the one that was most parsimonious in terms of the number of free parameters. In case where there was a tie in the number of free parameters, the model with the lower AIC value was selected as the best. This approach insured a balanced consideration of model fit and complexity.

In the best model, we assumed that the weights on each regressor reflected the amount of evidence of the corresponding hypothesis. We anticipated positive weights for each regressor, indicating a positive linear association between dissimilarities in the stimulus space and those in the brain activity patterns. However, negative weights could be also informative, potentially revealing unexpected insights. To assess this, we tested whether the weight on each regressor deviated from 0 with a two-sided t-test via the Satterthwaite approximation^80,81. The p-values were Holm corrected for multiple comparisons across ROIs for each regressor⁷⁶. The significance level was set to $\alpha$ = 0.05. When a regressor was excluded, the weight on that regressor was replaced by 0.

The data RDMs were calculated using rsatoolbox implemented in Python⁸².

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

Conceptualization: M.J.H.; Methodology: T.K. and M.J.H.; Software: T.K.: Formal analysis: T.K.; Investigation: T.K., Data curation: T.K.; Writing–Original draft: T.K.; Writing–Review and Editing: M.J.H. and Y.Y.; Visualization: T.K.; Supervision: M.J.H. and Y.Y.; Project administration: M.J.H; Funding acquisition: M.J.H., T.K., and Y.Y.

Peer review

Peer review information

Nature Communications thanks David Burr and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The fundamental data generated in this study (ROI- and searchlight-based classification performance for each participant, data RDM for each ROI and participant, and average activity level for each ROI and participant) have been deposited in the Zenodo repository (10.5281/zenodo.14262987). Source data of presented figures are provided with this paper. Source data are provided with this paper.

Code availability

The code that supports the findings of this study is available from the Zenodo repository (10.5281/zenodo.14262995).

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55599-8.