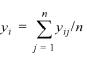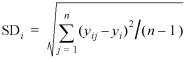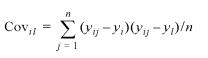Abstract
The prediction of operons, the smallest unit of transcription in prokaryotes, is the first step towards reconstruction of a regulatory network at the whole genome level. Sequence information, in particular the distance between open reading frames, has been used to predict if adjacent Escherichia coli genes are in an operon. While appreciably successful, these predictions need to be validated and refined experimentally. As a growing number of gene expression array experiments on E.coli became available, we investigated to what extent they could be used to improve and validate these predictions. To this end, we examined a large collection of published microarry data. The correlation between expression ratios of adjacent genes was used in a Bayesian classification scheme to predict whether the genes are in an operon or not. We found that for the genes whose expression levels change significantly across the experiments in the data set, the currently available gene expression data allowed a significant refinement of the sequenced-based predictions. We report these co-expression correlations in an E.coli genomic map. For a significant portion of gene pairs, however, the set of array experiments considered did not contain sufficient information to determine whether they are in the same transcriptional unit. This is not due to unreliability of the array data per se, but to the design of the experiments analyzed. In general, experiments that perturb a large number of genes offer more information for operon prediction than confined perturbations. These results provide a rationale for conducting expression studies comparing conditions that cause global changes in gene expression.
INTRODUCTION
DNA microarray has generated great enthusiasm and a large amount of gene expression data in both eukaryotic and prokaryotic systems. One ultimate goal of such expression analysis is the deduction of transcriptional regulation in the entire genome. So far, however, the main focus of the microarray experiments has been more specific: rather than attempting to reconstruct the global regulatory network, researchers have focused on studying the patterns of expression changes under a series of very specific conditions. While less ambitious, this is certainly a better defined problem. Indeed, the transcriptional regulation is a complex and condition-dependent network, which we can only probe with snapshots that capture a small portion of the overall picture. Studying the changes in expression induced by variation in a particular environmental condition or gene knockouts has produced a series of such informative snapshots (1–11).
Because of the unique operon structure, prokaryotes, such as Escherichia coli, offer an additional feature for the snapshots of the global regulatory network that hold across different environmental conditions and genetic backgrounds. In operons, multiple open reading frames (ORFs) are transcribed from the same promoter to a single mRNA transcript. Therefore, while an operon can be induced or repressed by a combination of different regulatory proteins under a variety of conditions, the genes in an operon are largely transcribed at the same level. This implies that, in the absence of measurement error, secondary promoters, or differential mRNA degradation, the correlation between expression levels across a series of different array experiments should be equal to 1 for genes that are in an operon. Therefore, using the empirical correlation between gene pairs in a series of array experiments we should be able to deduce the operon status of each gene.
There are quite a number of well-studied operons, which conveniently serve as a training set. Previous work has shown that genes in an operon tend to be separated by a smaller number of bases than genes not in an operon. Indeed, on the basis of this information, for every pair of adjacent genes that are transcribed in the same direction, it has been predicted if they are in an operon or not (12–14). While reasonably accurate, these predictions are purely based on sequence information and lack experimental validation. In this article, we use empirical correlation between the expression values of these genes as a validation of the sequence-based prediction. We then present a series of examples of the features identified by expression correlation and also discuss the design of experiments that are best suited for this type of analysis.
MATERIALS AND METHODS
Microarray data sets
To carry out the analysis, we compiled data from 72 DNA microarray experiments performed on E.coli: nine from our laboratory and 63 publicly available. The details of each of these experiments, their literature references and the location of the data set are listed in Table 1. Some of these experiments induced changes in genes regulated directly or indirectly by a specific regulator, whereas others affect genes regulated by multiple, and often unknown, regulators. The experiments carried out in our laboratory include comparison of growth in glucose versus acetate minimal media in the log phase and time course of the transition from growth in glucose to acetate (4,5). The set of 63 publicly available data was produced from seven laboratories [Tao et al. (3), Arfin et al. (6), Richmond et al. (7), Khodursky et al. (8), Zimmer et al. (9), Tao et al. (10), Pomposiello et al. (11) Courcelle et al. (15)] and comprises a total of 13 different sets of experimental conditions. We provide a brief description of these experiments in the Supplementary Material.
Table 1. DNA microarray data sets used in this work.
| Experiment number | Condition | Number of measurements | Reference |
|---|---|---|---|
| 2 | Ihf– versus ihf+ | 1 | 6 |
| 1 | Minimal versus rich media | 1 | 3 |
| 24–46 | Tryptophan regulation | 23 | 8 |
| 5–15 | NtrC regulation | 11 | 9 |
| 16 | Heat shock | 1 | 7 |
| 61–66 | Xylose fermentation | 6 | 10 |
| 47–60 | LexA regulation | 14 | 15 |
| 67–69 | SoxRS regulation | 3 | 11 |
| 70–72 | MarRAB regulation | 3 | 11 |
| 17–23 | Transition from glucose to acetate | 7 | This laboratorya |
| 3–4 | Balanced growth in acetate versus glucose minimal medium | 2 | This laboratorya |
aData available from http://www.seas.ucla.edu/~liaoj/
Operon training set
The operon status of selected genes was derived from Regulon DB (16) (http://www.cifn.unam.mx/regulondb/) with the following revisions: (i) leader peptides were removed from the operon set because of transcriptional attenuation within the operon, which may disrupt the co-expression pattern within the operon; (ii) operons with significant secondary promoters were deleted; (iii) new operons were added based on literature data. The 257 known operons we used are listed in Table S1 of the Supplementary Material. Additionally, 102 genes were identified as single transcriptional units and are listed in Table S2.
Sequence information and definition of potential operon pairs (POPs)
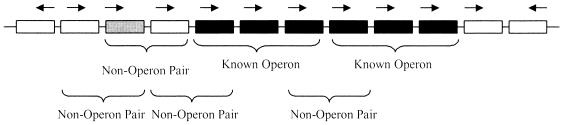
The sequence for the whole E.coli K12 genome (17) and the annotation files were downloaded from the NCBI ftp site (ftp://ncbi.nlm.nih.gov/genbank/genomes/Bacteria/Escherichia_coli_K12/). The files were obtained in July 2001, corresponding to version M54, accession no. U00096, and contained 4289 ORFs. We scanned the whole E.coli K12 genome to identify pairs of adjacent ORFs transcribed in the same direction. We call these POPs and we identified 3024 of them. Among the POPs, we can distinguish three types: (i) known operon pairs (OPs); (ii) known non-operon pairs (NOPs); and (iii) pairs of unknown operon status. The OPs are subunits of operons, as defined in Table S1; we identified 604 OPs. Known NOPs are genes that are (i) adjacent, (ii) transcribed in the same direction and (iii) either containing one gene that is known to be a single transcript (as defined in Table S2) or genes in front of known promoters. We opted not to include among the NOPs the gene pairs formed by the last element of an known operon and the following gene whose transcriptional unit was of unknown status (that is we neither could establish that it is transcribed by itself nor part of the existing operon). These criteria are illustrated in Figure 1 and led to the identification of 151 NOPs.
Figure 1.
Illustration of the NOPs definition. Gray boxes indicate genes that are single transcriptional units. Black boxes indicate genes that are part of a known operon, and the white boxes indicate genes that are of unknown status. NOPs are classified as the gene pairs that contain either (i) a known single transcript or (ii) the first element of an operon and the gene that precedes it. The last gene in a known operon and the following gene, if this is of unknown status, are not classified to be a NOP, due to uncertainty on the terminal boundary of an operon.
The intergenic distance between the stop codon and the start codon for a POP was also determined from the annotation file, which was subsequently used in the prediction of operons.
Expression data statistics
All the analysis here is based on the use of the log10-ratio of expression values obtained with cDNA experiments. A log-ratio value close to zero indicates that the gene in question is expressed at similar levels in the two conditions compared in the experiment. Let yij be the log-ratio of expression intensities for gene i in experiment j. Looking at the specific behavior of a gene, we indicate with yi, the sample average of expression values for the gene i where n is the number of experiments, in this case n = 72:
1
The sample standard deviation (SD) of the expression ratio of a particular gene across all data sets is
In each experiment j, we can consider the difference of the log-ratios of two adjacent genes i and l that are in the same operon pair k:
DOPkj = yij – ylj 3
If there was no unexplained biological variability and measurement error, each of these differences should be equal to zero. Thus, if we calculate ![]() we obtain a variance-type measure of the overall noise level. In order to have a measurement that is less sensitive to outliers, we considered a more robust estimator of the population SD that is proportional to the median absolute deviation and is known as mad. This noise measure can be defined for each experiment j:
we obtain a variance-type measure of the overall noise level. In order to have a measurement that is less sensitive to outliers, we considered a more robust estimator of the population SD that is proportional to the median absolute deviation and is known as mad. This noise measure can be defined for each experiment j:
Experiment noise SDj = madk(│DOPkj│)/![]() 4
4
Here madk represents the mad value across all OPs in the same experiment.
We also define an overall noise considering all DOPkj across all experiments:
where madkj is the mad value across all OPs in all experiments. For each gene i, the total variance is the sum of signal variance and noise variance. Thus, we can define a quantity, total-to-noise standard deviation (TTNSD) ratio for each gene i across all experiment, as:
TTNSDi = SDi/noise SD 6
The sample covariance of the expression values of two genes i and l across all data sets is:
The sample correlation (that in the text and figures will be indicated with r) is the sample covariance divided by the product of the SDs of the two genes:
Corril = Covil/(SDiSDl) 8
Statistical methods
Aside from the summary measurements that we have defined above whose meaning we will discuss in more detail in the following, our analysis required the use of two statistical methodologies. We used the bootstrap to assess the variability of some sample quantities of interest and a Bayesian classification technique to investigate how correlation of expression across experiments can be used to predict the operon status of genes. The bootstrap is a general technique to reconstruct the effect of sample variability on the base of the observed data (18). Briefly, a series of hypothetical alternative data sets (bootstrap samples) is created by re-sampling with replacement from the current set of observations. For each of these data sets the statistics of interest are calculated and the distribution of the statistics across the bootstrap samples is taken as representative of the distribution of the statistics across experiments. In particular, we used the bootstrap methodology to obtain the SD of the average correlation of a pair of genes in different groups.
To construct a Bayesian classifier, two ingredients are needed: a prior probability for each POP of being an operon and a distribution for the correlation of expression values given the operon status. The posterior probability of being an operon, then, will have the following form:
Post(OP/corr) = [(Prior(OP)f(Corr│OP)]/
{(Prior(OP)f(Corr│OP) + [1 – (Prior(OP)]f(Corr│NOP)} 9
where Prior(OP) is the prior probability for each POP of being an operon and f(Corr│OP) and f(Corr│NOP) are the probability density of the correlation given that the considered POP is in an operon or not, respectively. We considered two possible genome-wide definitions of prior probability: constant prior for each POP and prior dependent on the gene distance in the POP. The second type of prior is really the one of interest, as our main goal is to validate or question the operon predictions based on distance. We also considered the first prior, however, so as to have a measure of the indication coming from array data alone. The specific values of these are described in the Supplementary Material. Notice that the prior obtained by the second case is equivalent to the posterior used by Salgado et al. (12) in their operon-prediction rule. The posterior probabilities of operons can be used to classify each POP. We treat as equal the costs of misclassifying a POP as an operon or as a NOP and hence we classify as an operon each POP whose posterior probability of operon is higher than 0.5. Such a threshold could be altered to control the false positive and false negative rates.
RESULTS AND DISCUSSION
Known OPs exhibit higher expression correlation
As described above, we expected the correlation between expression levels of genes in the same operon to be higher than the correlation between genes that are not in the same operon. To investigate to what extent the available data reproduced this expected pattern, we identified three types of gene pairs with different levels of co-regulation: (i) 200 randomly selected pairs; (ii) 151 adjacent genes, transcribed in the same direction but each pair is known to be in different operons (NOPs); and (iii) 604 pairs of adjacent genes that are part of the known operons (OPs).
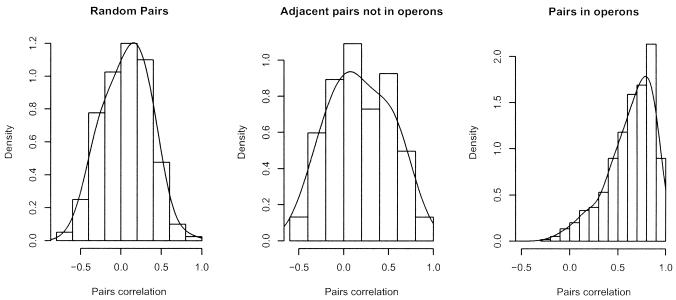
The empirical expression correlations obtained from the ensemble of DNA microarray data sets are displayed in Figure 2. A smooth density estimate is superimposed on the histogram of correlations in the three different pairs. Figure 2 has two messages: (i) there is a clear trend of increasing correlation from random pairs to adjacent pairs and OPs; (ii) the distinction between OPs and NOPs is not as clear-cut as one might expect. In detail, genes in OPs tend to have a higher correlation (mean value of 0.632, which has a bootstrap SD 0.01) than NOPs (mean 0.177 with bootstrap SD 0.027), which in turn have a higher correlation than random gene pairs (not significantly different from 0). Adjacent genes in NOPs may be slightly correlated because of transcriptional read-through, as only adjacent non-operon genes that are transcribed in the same direction are considered as NOPs. As for ‘perfect’ operons, if expression levels could be measured exactly, one would expect a correlation of 1. There are various reasons that explain the observed departure from this value. (i) Biologically, it is known that there exist secondary promoters within operons that are active in specific conditions. Additionally, regulation such as transcriptional attenuation or differential degradation of mRNA from the termini would also reduce the expression correlation between gene pairs in an operon. (ii) To the biological variability one has to add the variation due to measurement errors, which in expression array experiments is considerable. (iii) The effect of measurement errors depends on the experimental design. We explore this in detail below.
Figure 2.
Histogram of the correlation between expression values across experiments of genes in random pair, adjacent and transcribed in the same direction, but not in an operon adjacent and in an operon. A smooth estimate of the density is superimposed on the histograms.
Determining operon structures requires perturbing a large number of genes
If the expression level of one gene is not changed in an experiment, the recorded log-ratio represents purely a measurement error. If we consider two genes in the same operon whose expression is not perturbed by the experiments, the correlation between their log-ratios will be close to zero. Hence, it is more difficult to separate operons from non-operons, the smaller the percentage of genes perturbed in each experiment. Since this remark may influence an experimental design decision, we illustrate it in some detail.
Consider the following simple model for the expression values of two genes in an operon:
G1t = St + e1t, G2t = St + e2t 10
In any experiment t, the expression level for gene i (Git) is equal to the true expression level of that operon St plus a random noise eit. Assume that e1 and e2 have the same distribution and are independent. Then, the covariance between the expressions of the two genes, in this case, is equal to the variance of the signal Var(S) and the correlation is:
Cor(G1,G2) = 1/[1 + Var(e)/Var(S)] 11
It is clear, then, that the covariance will be 1 in the absence of noise [Var(e) = 0]. The higher the noise, the lower the covariance. It is also clear that a crucial parameter is the ratio Var(S)/Var(e): if the variance of the signal is significantly greater than the variance of the noise we will have a strong correlation and vice versa. If the value St is constant across all the experiments, so that Var(S) = 0, the expected value of the correlation that we measure for this pair of genes is zero. Therefore, it is important that the experimental conditions under study should cause differential regulation of the operon. This has important implications in terms of experimental design. If each array experiment is studying a condition that will affect only a small number of genes, the signal for most of the genes will be zero in most of the experiments. This will translate in a low correlation between genes regardless of whether they are in an operon or not. If the goal is to collect information about operon status, it is then preferable to conduct experiments using conditions that affect a large number of genes—even if they induce the same kind of variation in numerous transcriptional units. A collection of such experiments will be more informative than a collection of the same size of experiments that induce highly specific perturbations. This point is illustrated with a simulation in the Supplementary Material. Note that this type of experimental design is at odds with the conventional reductionist approach, which advocates changes of one regulator at a time.
Empirical measures of information content: gene-wide and experiment-wide
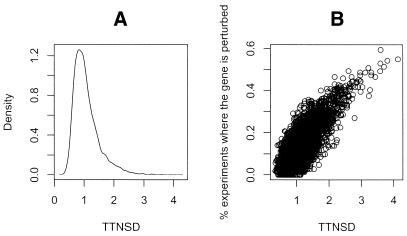
The analysis above points to the fact that for some operons, we may have no information in the existing data set for prediction of operons. We then needed a measure of the information available in the whole data set for each gene. We considered two such measures: (i) frequency of induction (and repression) of the gene i among all experiments and (ii) the TTNSD ratio for gene i across all experiments. Both of these measures offer a first screening guideline. We considered the absolute log expression ratio of a given gene >0.3 as an indication of gene induction (or repression) under the experimental conditions. Therefore, the frequency of induction (and repression) is calculated as the percentage of experiments in which │yij│ is >0.3. The second measure (TTNSD) estimates the total signal to noise ratio. The noise SD is based on the known operon status to obtain the equivalent of replicate spots for the same gene. This value is a useful estimator of overall noise level without duplicate spots. The total signal is the extent to which the gene is perturbed across all experiments. Figure 3A shows that the majority of genes have a TTNSD value around or below 1, suggesting that the genes are not sufficiently perturbed beyond the noise level. Figure 3B shows how TTNSD values correlate with the frequency of perturbation for all the genes. For a given gene, the percentage of experiments that perturb the particular gene correlate well with the TTNSD ratio.
Figure 3.
Measure of the amount of change in expression in our data set. (A) Distribution of TTNSD values for genes in the whole genome based on the entire data set. (B) Scatter plot of the TTNSD ratio for each gene against fraction of experiments in which the absolute log expression ratio of that gene is >0.3.
Based on these measurements, it is possible to evaluate the amount of information we have on each gene pair to discriminate their operon status on the basis of the correlation of their expression levels across experiments. For example, the data set does not have sufficient information on genes such as b0322, b1672 and lysR to determine their operon status, because they are only induced (or repressed) in a small fraction of experiments and the TTNSD ratio is too low (all ∼0.5). If we restrict our attention to the OPs with a SD greater than twice the noise level (TTNSD > 2), for example, the median correlation increases from 0.68 to 0.85. However, this leaves us with a small number of OPs and NOPs in the training set. We decided, then, to use all OPs and NOPs to construct a classifier based on the simple correlation (the use of more robust definitions of correlation were explored, but did not substantially change the results). In a second stage, we evaluate the significance of the prediction based on the actual information content.
We can also evaluate the information content of each experiment for our goal. Based on the known operon status of genes in the training set, we can calculate the experiment noise SD using the equation shown in Materials and Methods. In turn, this quantity can be used to define the fraction of induced genes per experiment as the relative count of how many genes have an absolute log-ratio >1.5 * Experiment noise SDk. A detail report of this analysis can be found in the Supplementary Material. Here we simply note that some experiments in our collection—such as heat shock, tryptophan starvation and glucose to acetate transition—induced a large number of genes and thus contain more information for operon prediction. On the negative side, the data set we considered lacks experiments for anaerobic gene regulation, which will limit the information we can gather on such genes.
Operon prediction based on Bayesian classification
We now proceed to examine to what extent the microarray data set contributes to the prediction of operons beyond the prediction based on gene distance. To achieve this goal we used the Bayesian framework, which makes it particularly easy to update the current knowledge on a pair of genes on the base of novel information.
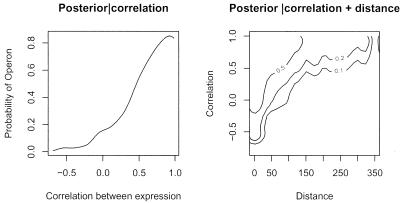
As mentioned before, the ingredients of the Bayesian classification procedure are the prior distributions and the likelihood f(r│OP) and f(r│NOP) (distribution of correlation given the operon status). The specification of the priors is described in the Supplementary Material. For the classifier based on correlation in expression only, we used equation 9 with Prior(OP) = 0.5 for all POPs. Alternatively, we used gene distance to calculate the POP-specific prior (see Supplementary Material). We estimated the functions f(r│OP) and f(r│NOP) with the smooth densities represented in Figure 2, based on the previously described collection of 604 OPs and 151 NOPs. As we considered two different specifications of the prior distribution, we have two sets of posterior probabilities. Figure 4A shows the posterior probability of an operon based only on expression correlation, Post(OP│r). The posterior probability obtained from the second prior is based on both distance and expression correlation and it is shown in Figure 4B.
Figure 4.
Posterior probability for a pair of genes of being in an operon—as a function of correlation alone (left) and correlation and distance (right).
We evaluate the correct classification rates for the 604 known OPs and 151 NOPs obtained when classifying as OPs all the POPs for which (i) Post(OP│r) > 0.5, (ii) Post(OP│d) > 0.5 or (iii) Post(OP│r,d) > 0.5. To avoid underestimating the error rate, we used a leave-one-out cross-validation procedure, so that each POP is, in turn, excluded from the training set, the likelihoods are re-estimated and the status of the POP is predicted on the basis of the newly evaluated decision boundary. We calculated the percentage of correctly classified operons (sensitivity of the operon prediction rule) and correctly classified non-operons (specificity of the operon prediction rule). The results are in Table 2.
Table 2. Comparison of sensitivity and specificity of the different operon prediction methods.
| Method | Sensitivity | Specificity |
|---|---|---|
| Correlation |
0.82 |
0.70 |
| Distance |
0.84 |
0.82 |
| Distance and correlation | 0.88 | 0.88 |
As a benchmark, recall that the sensitivity and specificity of a uniform random classification of operon and non-operon are equal to 0.5. Hence, using the correlation of expression values across microarray experiments produces a 64% increase in sensitivity and 40% increase in specificity. Notice that a comparable sensitivity is obtained, with an increased specificity, by the classifier based on distance alone. This classifier represents one of the current standards for operon prediction: the fact that comparable performance can be obtained with array data is an indication that indeed correlation between expression levels contains a considerable amount of information. The most interesting result, however, is the increase in sensitivity when both distance and array information are used at the same time. Not only array data contain a considerable amount of information but this is, at least in part, independent from the one carried by distance between genes, so that even if distance is included in a model, correlation in array experiments should be added to improve the prediction (the error rate of operon decreases by 25%).
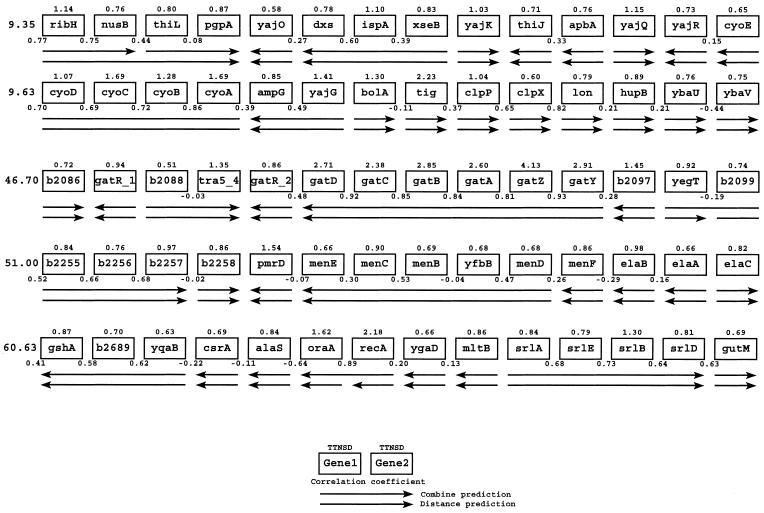
We then applied the above prediction based on both microarray data and distance to the whole POP set. The POPs in the E.coli genome (total 3024) comprise the collection of all the pairs of adjacent genes that are transcribed in the same direction (including OPs, NOPs and POPs of unknown status). The results of these predictions are presented graphically in an expression correlation map of the entire E.coli genome, which is available on the internet (www.seas.ucla.edu/~liaoj). The structure of the map is illustrated in Figure 5. The map is organized in minutes. For each gene we report the TTNSD as an indication of the amount of information available in our data set to predict its operon status. For each gene pair we report the expression correlation value and the result of the operon prediction based on distance and correlation in the expression. By simply looking up the genes of interest in this map, the researcher can quickly gather information about the extent to which currently available microarray results (which are experimental data) confirm or shed suspicion on the prediction of operon status based on distance (which is purely sequence based). We illustrate how to best interpret the information in the map by analyzing one example in detail—further cases are documented in the Supplementary Material.
Figure 5.
Example of gene map. Each box represents a gene. Above each is the TTNSD value given for that gene. Between the genes transcribed in the same direction is the correlation coefficient given. The first arrow represents the predicted operon structure when both distance and microarray data are taken into account. The second arrow represents the operon structure as it is predicted by distance alone. On the left an approximate minute count is given.
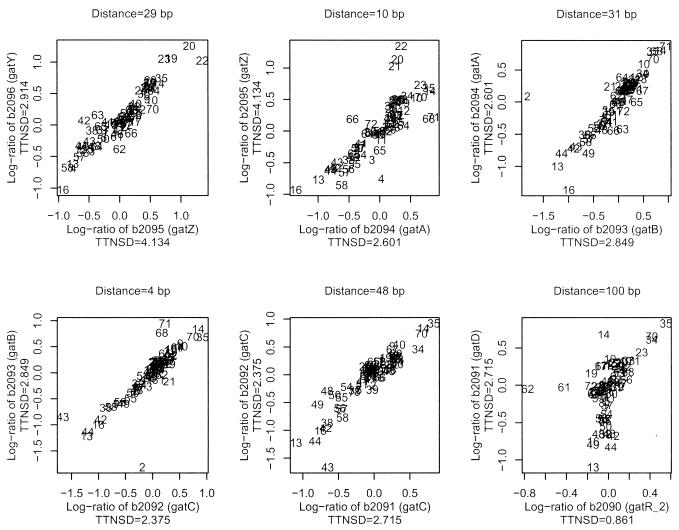
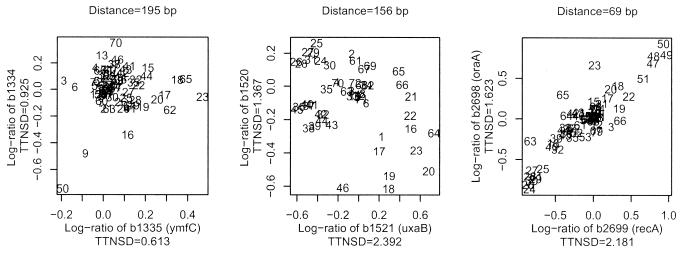
Figures 6 and 7 offer a more detailed version of the information condensed in the genome map. We analyze three operons and three NOPs from our training set. For each gene pair, we present the scatter plot of the expression values of each of the two genes across all the experiments. Each pair of log-ratios is indicated with a number representing the experiment that generates it. These scatter plots visualize both the correlation in expression between the genes in the pair and the amount of variation that the expression of each of the genes experience across experiments.
Figure 6.
Scatter plot of expression values for the adjacent genes in the gatYZABCDR operon.
Figure 7.
Scatter plot of expression values for the adjacent genes in three NOPs (from left to right): b1334, b1335; b1520, b1521; and b2698, b2699.
Figure 6 presents the scatter plot of the log-ratio in the 72 considered experiments for the genes b2096 (gatY) to b2090 (gatR) (in order of transcription). This is the gatYZABCDR operon, which is involved in galactitol metabolism. Nobelmann and Lengeler (19) reported two transcriptional initiation sites upstream of gatY and gatR. A quick look at Figure 5 minute 46.70 shows how the information in Figure 6 is condensed in the map. The prediction based both on distance and array information validates the (correct) prediction based on distance. Both the scatter plots in Figure 6 and the correlation values in Figure 5 indicate that the array experiments support the hypothesis of an operon involving these genes. The high TTNSD values and the range of expression values indicate that the expression levels of this operon were perturbated a number of times in the array experiments, so that the prediction based on correlation can be considered relevant. It is interesting to note that the last gene in the operon (gatR) is not often activated and does not exhibit the same correlation, suggesting the presence of a more important promoter between this and the previous gene. Notice that there is indeed space for such a regulatory element, with 100 bp separating the two genes. Indeed, it has been documented that in E.coli K-12 there is a potential IS3E insert that might interrupt the gatR gene (19).
Figure 7 illustrates three cases of NOPs (only the last one of these is illustrated in Fig. 5). In Figure 7A there is no correlation between the points, but also not much signal, so that we cannot infer any real conclusions from the data. In Figure 7B, we have relatively high signal and no correlation, making a strong case in favor of the non-operon prediction and hence confirming the distance-based prediction. Indeed, a potential Rho-dependent terminator hairpin loop has been documented between b1520 and b1521, suggesting that this is really a NOP (20). In Figure 7C we have a significant amount of signal and significant amount of correlation suggesting that actually this pair of genes (recA and oraA) may be in an operon. This contradicts the information on which our non-operon training set was constructed and also the prediction based on distance. The literature with regard to these two genes is inconclusive (15,21). They may either be in an operon or are regulated by the same regulator (LexA) but transcribed from different promoters. It is notable that the array data would have difficulties distinguishing between the two cases.
CONCLUSION
The empirical nature of expression array measurements offers an important complement to the information that can be obtained by the analysis of genome sequences. Multiple research groups are trying to use array information to validate and improve binding motifs prediction, for example. In E.coli, one of the simplest uses of sequence information is the prediction of operons based on the distance in base pairs between two adjacent genes transcribed in the same direction. The results of gene expression array experiments are an important source of data to verify such predictions. We used a set of 72 experiments for this purpose and proposed a measure of information content of each gene in the data set in terms of the TTNSD value. We also describe the design of the experiment that is more useful to carry out operon validation on the base of expression data. The results of our work are numerous. On the one hand, we provide one of the first large-scale validations of the information content of array experiments. On the other hand, we offer an up-to-date and easy to consult database of how currently available array experiments validate, question or complement current knowledge on the operon status of adjacent genes. Additionally, we point the experimenters towards novel types of array experiments in E.coli. In particular, we highlight the importance and the value of employing conditions that affect a large number of genes, when trying to reconstruct global regulatory patterns. Another conclusion of our study is the necessity of using a large number of experiments to reconstruct a global regulatory network. We found that our collection of 72 arrays represented a bare minimum, given the amount of missing data and the fact that a majority of the genes is not perturbed in each experiment.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENT
This work was supported in part by NSF grant BES-0120359.
REFERENCES
- 1.DeRisi J.L., Iyer,V.R. and Brown,P.O. (1997) Exploring the metabolic and genetic control of gene expression on a genomic scale. Science, 278, 680–686. [DOI] [PubMed] [Google Scholar]
- 2.Chu S., DeRisi,J., Eisen,M., Mulholland,J., Botstein,D., Brown,P.O. and Herskowitz,I. (1998) The transcriptional program of sporulation in budding yeast. Science, 282, 699–705. [DOI] [PubMed] [Google Scholar]
- 3.Tao H., Bausch,C., Richmond,C., Blattner,F.R. and Conway,T. (1999) Functional genomics: expression analysis of Escherichia coli growing on minimal and rich media. J. Bacteriol., 181, 6425–6440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Oh M.K. and Liao,J.C. (2000) DNA microarray detection of metabolic responses to protein overproduction in Escherichia coli. Metabol. Eng., 2, 201–209. [DOI] [PubMed] [Google Scholar]
- 5.Oh M.K. and Liao,J.C. (2000) Gene expression profiling by DNA microarrays and metabolic fluxes in Escherichia coli. Biotechnol. Prog., 16, 278–286. [DOI] [PubMed] [Google Scholar]
- 6.Arfin S.M., Long,A.D., Ito,E.T., Tolleri,L., Riehle,M.M., Paegle,E.S. and Hatfield,G.W. (2000) Global gene expression profiling in Escherichia coli K12. The effects of integration host factor. J. Biol. Chem., 275, 29672–29684. [DOI] [PubMed] [Google Scholar]
- 7.Richmond C.S., Glasner,J.D., Mau,R., Jin,H. and Blattner,F.R. (1999) Genome-wide expression profiling in Escherichia coli K-12. Nucleic Acids Res., 27, 3821–3835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khodursky A.B., Peter,B.J., Cozzarelli,N.R., Botstein,D., Brown,P.O. and Yanofsky,C. (2000) DNA microarray analysis of gene expression in response to physiological and genetic changes that affect tryptophan metabolism in Escherichia coli. Proc. Natl Acad. Sci. USA, 97, 12170–12175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zimmer D.P., Soupene,E., Lee,H.L., Wendisch,V.F., Khodursky,A.B., Peter,B.J., Bender,R.A. and Kustu,S. (2000) Nitrogen regulatory protein C-controlled genes of Escherichia coli: scavenging as a defense against nitrogen limitation. Proc. Natl Acad. Sci. USA, 97, 14674–14679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tao H., Gonzalez,R., Martinez,A., Rodriguez,M., Ingram,L.O., Preston,J.F. and Shanmugam,K.T. (2001) Engineering a homo-ethanol pathway in Escherichia coli: increased glycolytic flux and levels of expression of glycolytic genes during xylose fermentation. J. Bacteriol., 183, 2979–2988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pomposiello P.J., Bennik,M.H. and Demple,B. (2001) Genome-wide transcriptional profiling of the Escherichia coli responses to superoxide stress and sodium salicylate. J. Bacteriol., 183, 3890–3902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Salgado H., Moreno-Hagelsieb,G., Smith,T.F. and Collado-Vides,J. (2000) Operons in Escherichia coli: genomic analyses and predictions. Proc. Natl Acad. Sci. USA, 97, 6652–6657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ermolaeva M.D., White,O. and Salzberg,S.L. (2001) Prediction of operons in microbial genomes. Nucleic Acids Res., 29, 1216–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Craven M., Page,D., Shavlik,J., Bockhorst,J. and Glasner,J. (2000) A probabilistic learning approach to whole-genome operon prediction. Proc. Int. Conf. Intell. Syst. Mol. Biol., 8, 116–127. [PubMed] [Google Scholar]
- 15.Courcelle J., Khodursky,A., Peter,B., Brown,P.O. and Hanawalt,P.C. (2001) Comparative gene expression profiles following UV exposure in wild-type and SOS-deficient Escherichia coli. Genetics, 158, 41–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Salgado H., Santos-Zavaleta,A., Gama-Castro,S., Millan-Zarate,D., Blattner,F.R. and Collado-Vides,J. (2000) RegulonDB (version 3.0): transcriptional regulation and operon organization in Escherichia coli K-12. Nucleic Acids Res., 28, 65–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blattner F.R., Plunkett,G., Bloch,C.A., Perna,N.T., Burland,V., Riley,M., Collado-Vides,J., Glasner,J.D., Rode,C.K., Mayhew,G.F. et al. (1997) The complete genome sequence of Escherichia coli K-12. Science, 277, 1453–1474. [DOI] [PubMed] [Google Scholar]
- 18.Efron B. and Tibshirani,R. (1993) An Introduction to the Bootstrap. Chapman Hall, New York.
- 19.Nobelmann B. and Lengeler,J.W. (1996) Molecular analysis of the gat genes from Escherichia coli and of their roles in galactitol transport and metabolism. J. Bacteriol., 178, 6790–6795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ermolaeva M.D., Khalak,H.G., White,O., Smith,H.O. and Salzberg,S.L. (2000) Prediction of transcription terminators in bacterial genomes. J. Mol. Biol., 301, 27–33. [DOI] [PubMed] [Google Scholar]
- 21.Van Dyk T.K., DeRose,E.J. and Gonye,G.E. (2001) LuxArray, a high-density, genomewide transcription analysis of Escherichia coli using bioluminescent reporter strains. J. Bacteriol., 183, 5496–5505. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.