Abstract
Objective
It takes significant time and energy to collect data on explicit networks. This study used graph machine learning to identify hidden networks and predict mental health conditions in the middle-aged and old.
Methods
Data came from the Korean Longitudinal Study of Ageing (2016–2018), with 2,000 participants aged 56 or more. The dependent variable was mental disease (no vs. yes) in 2018. Twenty-eight predictors in 2016 were included. Graph machine learning with systematic hyper-parameter selection was conducted.
Results
The area under the curve was similar across different models in different scenarios. However, sensitivity (93%) was highest for the graph random forest in the scenario of 2,000 participants and the centrality requirement of life satisfaction 90. Based on the graph random forest, top-10 determinants of mental disease were mental disease in previous period (2016), age, income, life satisfaction–health, life satisfaction–overall, subjective health, body mass index, life satisfaction–economic, children alive and health insurance. Especially, life satisfaction–overall was a top-5 determinant in the graph random forest, which considers life satisfaction as an emotional connection and a group interaction.
Conclusion
Improving an individual’s life satisfaction as a personal condition is expected to strengthen the individual’s emotional connection as a group interaction, which would reduce the risk of the individual’s mental disease in the end. This would bring an important clinical implication for highlighting the importance of a patient’s life satisfaction and emotional connection regarding the diagnosis and management of the patient’s mental disease.
Keywords: Graph machine learning, Systematic hyper-parameter selection, Life satisfaction, Subjective class, Mental health
INTRODUCTION
Mental disease is a significant part of disease burden on the globe. For example, depressive disorder is a major contributor for disability on a global level, influencing more than 350 million in the world [1]. Together with cancer, diabetes and ischemic heart disease, it formed top-4 contributors for death or disability on the globe for 2017–2018 [2]. This worldwide movement is consistent with its Korean counterpart. Unipolar depression (1508) was Korea’s second cause of disability-adjusted life years per 100,000 for the year 2010 [3]. Suicide was the fifth cause of death in the nation for the year 2018, i.e., 26.6 per 100,000 [4]. Research on mental disease would have global implications in this context. Specifically, the fields of graph learning and machine learning are garnering great attention for the prediction of mental disease at this point. A recent review used 72 references to review recent progress in the examination of mental disorders as network issues [5]. This study suggests that network analysis would serve as an effective approach of personized psychiatry investigating complex variations across different individuals and groups alike. Specifically, this study focused on two research topics of network problems for clinical purposes, i.e., comorbid states as dependent variables and group interactions as predictor variables [5].
Likewise, a recent study reviewed the current status and future prospect of machine learning for the early diagnosis of major depressive disorder (depression) [6]. Data came from 32 original studies with search terms “depression” (title) and “random forest” (abstract) in the Web of Science. These original studies were deemed eligible with the following criteria: the publication journal of SCIE/SSCI; the publication language of English; and the publication year of 2000; the dependent variable of depression; the interventions of machine learning (artificial neural network, support vector machine, random forest, naïve Bayesian, and/or decision tree); and the outcomes of the area under the curve and/or accuracy. It was found that different machine learning approaches would be optimal for different modes of data for the early diagnosis of depression, e.g., the random forest for genomic data, the artificial neural network, the support vector machine, the random forest and/or logistic regression for numeric data. Their performance outcomes registered variations within 64.0–96.0 in the case of the area under the curve and within 60.1-100.0 in the case of accuracy. It was concluded that machine learning provides an effective, non-invasive decision support system for early diagnosis of depression [6].
However, it takes significant time and energy to collect data on explicit networks, whereas hidden networks can serve as major predictors of mental disease. But current studies based on graph machine learning center on explicit networks including bio-chemical, citation, social and traffic networks [7-10]. No analysis has been done on graph machine learning to identify hidden networks and predict mental health conditions. Moreover, systematic hyper-parameter selection on network characteristics such as the number and strength of group interactions can improve the performance of graph machine learning. Here, systematic hyper-parameter selection is called “graph neural architecture search” or “graph reinforcement learning” in a professional term [10]. In this type of graph machine learning, the agent (the network) takes a series of actions (systematic hyper-parameter selection) to maximize the cumulative award (the performance of the network) [10]. Unfortunately, no examination in this direction has been done to identify hidden networks and predict mental health conditions. In this context, this study used graph machine learning with systematic hyper-parameter selection to identify hidden networks and predict mental health conditions in the middle-aged and old.
METHODS
Participants and variables
The data source of this study was the Korean Longitudinal Study of Ageing (KLoSA) (2016–2018) [11]. This study did not require the approval of the ethics committee given that data were publicly available (https://survey.keis.or.kr/eng/klosa/klosa01.jsp) and de-identified. The final sample of this study included 2,000 participants aged 56 or more, who were randomly selected out of 5,527 participants with full information. The final sample had no missing value. The KLoSA question on mental disease in 2016 and 2018 was “Since the last survey, have you ever been diagnosed by a doctor mental disease? 1. Yes. 5. No.” [C043]. The dependent variable was mental disease in 2018 with the binary category of no vs. yes. The independent variables were the following 28 predictors in 2016 listed in Tables 1 and 2 [12,13]: (health-related information) drinker, smoker, body mass index, subjective health; (social activity [monthly frequency]) political, voluntary, family, leisure, friendship, religious; (socioeconomic conditions) economic activity, health insurance, income, educational level; (family support) marital status, parents alive, brothers/sisters cohabiting, children alive; (demographic information) gender, age; mental disease; (other determinants) life satisfaction–overall, life satisfaction–economic, life satisfaction–health, subjective class, residential type, religion, region.
Table 1.
Descriptive statistics for participants’ categorical variables for year 2018/2016
| Variable | Value |
|---|---|
| Mental disease (in 2018) | |
| No | 1,870 (93.5) |
| Yes | 130 (6.5) |
| Education (in 2016 Hereafter) | |
| Elementary or below | 785 (39.3) |
| Junior high | 375 (18.8) |
| Senior high | 639 (32.0) |
| College or above | 201 (10.1) |
| Gender | |
| Male | 1,166 (58.3) |
| Female | 834 (41.7) |
| Marriage | |
| Married | 1,498 (74.9) |
| Separated | 420 (21.0) |
| Divorced | 52 (2.6) |
| Widowed | 15 (0.8) |
| Unmarried | 15 (0.8) |
| Religion | |
| Non | 1,027 (51.4) |
| Protestant | 409 (20.5) |
| Catholic | 383 (19.2) |
| Buddhist | 170 (8.5) |
| Won-Buddhist | 1 (0.1) |
| Other | 10 (0.5) |
| Residential type | |
| Apartment | 1,091 (54.6) |
| Other | 909 (45.5) |
| Region | |
| Urban, big | 1,845 (92.3) |
| Urban, small | 53 (2.7) |
| Rural | 102 (5.1) |
| Parents alive | |
| Father & mother | 63 (3.2) |
| Father | 30 (1.5) |
| Mother | 277 (13.9) |
| None | 1,630 (81.5) |
| Health insurance | |
| Medicare | 1,854 (92.7) |
| Medicaid | 146 (7.3) |
| Economic activity | |
| Employed | 643 (32.2) |
| Unemployed | 1,357 (67.9) |
| Subjective health | |
| Very good | 12 (0.6) |
| Good | 491 (24.6) |
| Middle (neither good nor poor) | 919 (46.0) |
| Poor | 472 (23.6) |
| Very poor | 106 (5.3) |
| Smoker | |
| Non | 1,378 (68.9) |
| Former | 427 (21.4) |
| Current | 195 (9.8) |
| Drinker | |
| Non | 682 (34.1) |
| Former | 348 (17.4) |
| Current | 970 (48.5) |
| Subjective class | |
| High-A | 10 (0.5) |
| High-B | 37 (1.9) |
| Middle-A | 343 (17.2) |
| Middle-B | 681 (34.1) |
| Low-A | 511 (25.6) |
| Low-B | 418 (20.9) |
| Mental disease | |
| Yes | 120 (6.0) |
| No | 1,880 (94.0) |
Data are presented as number (%)
Table 2.
Descriptive statistics for participants’ continuous variables for year 2016
| Variable | IQR | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|
| Age | 14 | 56 | 63 | 70 | 77 | 101 |
| Activity–religious | 0 | 0 | 0 | 0 | 0 | 10 |
| Activity–friendship | 4 | 0 | 0 | 2 | 4 | 10 |
| Activity–leisure | 0 | 0 | 0 | 0 | 0 | 9 |
| Activity–family | 0 | 0 | 0 | 0 | 0 | 9 |
| Activity–voluntary | 0 | 0 | 0 | 0 | 0 | 8 |
| Activity–political | 0 | 0 | 0 | 0 | 0 | 1 |
| #Children alive | 1 | 0 | 2 | 2 | 3 | 9 |
| #Brothers/sisters cohabiting | 0 | 0 | 0 | 0 | 0 | 3 |
| Income (monthly, $) | 1,290 | 5 | 260 | 600 | 1,550 | 40,580 |
| Body mass index | 3 | 3 | 22 | 23 | 25 | 93 |
| Life satisfaction–health | 20 | 0 | 50 | 60 | 70 | 100 |
| Life satisfaction–economic | 30 | 0 | 40 | 50 | 70 | 100 |
| Life satisfaction–overall | 20 | 0 | 50 | 60 | 70 | 100 |
IQR, interquartile range Q3 (75%)–Q1(25%)
Graph learning analysis
Figure 1 shows a flow chart of this study. Graph machine learning with hyper-parameter selection was conducted in the following manner for the optimal “centrality requirement” (the minimum requirement of life satisfaction for a central node in a graph network). A graph network consists of nodes (or participants) and edges (or their explicit or implicit connections) [7-10]. A node has the 29 characteristics described above, i.e., mental disease in 2018 (dependent variable) as well as mental disease in 2016 and other determinants of mental disease in 2018 (independent variables). Here, the mental disease of a node depends on its own characteristics as well as those of other nodes connected with edges. In a simple graph network, the mental disease of a node is determined by weighted averages for its own characteristics and those of other nodes connected. In this network, there are two types of nodes, so called, central and peripheral according to the following “centrality requirement” of life satisfaction: 1) a central node satisfies the minimum requirement of life satisfaction (70, 80 or 90) and 2) it has higher life satisfaction and a higher or equal subjective class compared to its peripheries. For example, let’s assume that the minimum requirement of life satisfaction for each central node is 90. Then, the life satisfaction of a central node is 100 and that of a peripheral node is 90 or lower. Indeed, the subjective class of a central node is higher or equal compared to those of peripherals connected with it. In this network, the mental disease of a node is determined by weighted averages for its own characteristics and those of other nodes connected.
Figure 1.
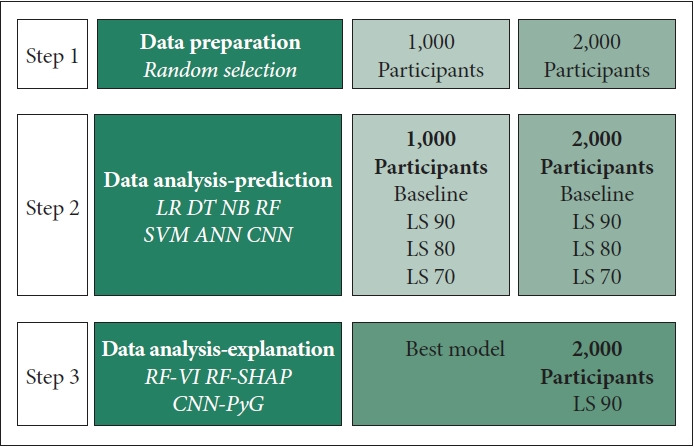
Flowchart. In Step 1, two data sets were prepared based on random selection, i.e., 1,000 and 2,000 participants (see the section of participants and variables). In Step 2, two baseline scenarios of basic machine learning were compared to the following six scenarios of graph machine learning: 1) 1,000 vs. 2,000 participants, 2) the centrality requirement of 70 vs. 80 vs. 90. The best model in the best scenario (graph random forest with 2,000 participants and the centrality requirement of 90) was chosen in terms of accuracy, the area under the curve, specificity and sensitivity (see the sections of graph learning analysis and machine learning analysis). In Step 3, graph random forest permutation importance and SHAP values were utilized to evaluate the strengths and directions of associations between the predictors and the dependent variable (see the section of machine learning analysis). Finally, explainable graph convolutional neural networks were derived based on PyG regarding which peripheral nodes connect with which central nodes (see the section of results). LS Minimum Requirement of Life Satisfaction for Central Nodes (e.g., 70, 80, 90). LR, logistic regression; DT, decision tree; NB, naïve bayes, RF, random forest; SVM, support vector machine; ANN, artificial neural network; CNN, convolutional neural network; VI, variable importance; SHAP, Shapley Additive Explanation; PyG, PyTorch Geometric.
In this study, graph machine learning is defined as “machine learning applied for the prediction of mental disease within a graph network”. Likewise, basic machine learning is denoted as “machine learning applied for the prediction of mental disease without a graph network.” With these notions, two baseline scenarios of basic machine learning were compared to the following six scenarios of graph machine learning in this study: 1) 1,000 vs. 2,000 participants, 2) the centrality requirement of 70 vs. 80 vs. 90. The best model in the best scenario was chosen in terms of accuracy, the area under the curve, specificity and sensitivity. The explanation of machine learning in this study is presented below.
Machine learning analysis
Seven machine learning models were employed to predict mental disease: (graph) convolutional neural network, artificial neural network, support vector machine, random forest, naïve Bayes, decision tree and logistic regression [7-10,12-15]. These models were chosen for their popularity in existing literature [9,16]. The 1,000 or 2,000 cases were split into training and validation sets with a 75:25 ratio (750 cases vs. 250 cases or 1,500 cases vs. 500 cases). Evaluation criteria were accuracy (a ratio of correct predictions among 250 cases or 500 cases), the area under the curve, specificity and sensitivity. Then, random forest permutation importance was used to derive the variable importance rankings and values of all predictors for the prediction of the dependent variable. Also, random forest Shapley Additive Explanation (SHAP) values were utilized to evaluate the directions of associations between the predictors and the dependent variable. Here, the permutation importance of a predictor calculates an overall accuracy decline from the permutation of the predictor’s data. The SHAP value of a predictor for a participant calculates a gap between what machine learning predicts for the probability of mental disease with and without the predictor [16]. Finally, it can be noted that Python 3.8.8 [17] and PyTorch 2.1.0 [18] were employed for the analysis during January 1, 2024–June 30, 2024.
RESULTS
Descriptive statistics for participants’ categorical and continuous variables are shown in Table 1 and 2, respectively. Among the 2,000 participants in 2018, 130 (6.5%) were diagnosed as mental disease. On average, the body mass index, monthly income and age of the participant were 24, $1170 and 71, correspondingly. Model performance was given in Table 3. The area under the curve was similar across different models in different scenarios. However, sensitivity (93%) was highest for the graph random forest in the scenario of 2,000 participants and the centrality requirement of 90 (the best model in the best scenario based on graph machine learning with systematic hyper-parameter selection). Sensitivity was 91% for the basic random forest in the scenario of 2,000 participants (baseline scenario). Indeed, graph convolutional learning was found to have the best performance in the scenario of 2,000 participants with the centrality requirement of 70. Based on graph random forest variable importance in the scenario of 2,000 participants and the centrality requirement of 90, top-10 determinants of mental disease were mental disease in previous period (2016), age, income, life satisfaction–health, life satisfaction–overall, subjective health, body mass index, life satisfaction–economic, children alive and health insurance (Table 4).
Table 3.
Model performance
| 1,000 participants |
2,000 participants |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc | AUC | Spe | Sen | Acc | AUC | Spe | Sen | ||
| Baseline | Baseline | ||||||||
| LR | 0.99 | 0.96 | 1.00 | 0.90 | LR | 0.99 | 0.97 | 1.00 | 0.90 |
| DT | 0.99 | 0.95 | 0.99 | 0.90 | DT | 0.99 | 0.95 | 0.99 | 0.91 |
| NB | 0.94 | 0.96 | 0.94 | 0.94 | NB | 0.97 | 0.97 | 0.97 | 0.93 |
| RF | 0.99 | 0.97 | 1.00 | 0.90 | RF | 0.99 | 0.97 | 1.00 | 0.91 |
| SVM | 0.93 | 0.89 | 1.00 | 0.00 | SVM | 0.93 | 0.93 | 1.00 | 0.00 |
| ANN | 0.97 | 0.92 | 1.00 | 0.60 | ANN | 0.96 | 0.92 | 1.00 | 0.37 |
| LS_90 | LS_90 | ||||||||
| LR | 0.99 | 0.96 | 1.00 | 0.88 | LR | 0.99 | 0.97 | 1.00 | 0.90 |
| DT | 0.98 | 0.94 | 0.99 | 0.88 | DT | 0.99 | 0.96 | 0.99 | 0.92 |
| NB | 0.33 | 0.81 | 0.29 | 0.92 | NB | 0.17 | 0.83 | 0.11 | 0.97 |
| RF | 0.99 | 0.97 | 1.00 | 0.88 | RF | 0.99 | 0.97 | 1.00 | 0.93 |
| SVM | 0.93 | 0.86 | 1.00 | 0.00 | SVM | 0.94 | 0.87 | 1.00 | 0.00 |
| ANN | 0.97 | 0.93 | 1.00 | 0.59 | ANN | 0.96 | 0.93 | 1.00 | 0.45 |
| CNN | 0.94 | 0.93 | 1.00 | 0.87 | |||||
| LS_80 | LS_80 | ||||||||
| LR | 0.99 | 0.97 | 1.00 | 0.91 | LR | 0.99 | 0.96 | 1.00 | 0.92 |
| DT | 0.99 | 0.95 | 0.99 | 0.92 | DT | 0.99 | 0.96 | 0.99 | 0.92 |
| NB | 0.11 | 0.67 | 0.06 | 0.96 | NB | 0.10 | 0.61 | 0.04 | 0.97 |
| RF | 0.99 | 0.97 | 1.00 | 0.91 | RF | 0.99 | 0.96 | 1.00 | 0.92 |
| SVM | 0.94 | 0.67 | 1.00 | 0.00 | SVM | 0.94 | 0.62 | 1.00 | 0.00 |
| ANN | 0.97 | 0.93 | 0.99 | 0.58 | ANN | 0.88 | 0.61 | 0.93 | 0.15 |
| CNN | 0.94 | 0.94 | 1.00 | 0.87 | |||||
| LS_70 | LS_70 | ||||||||
| LR | 0.97 | 0.91 | 0.98 | 0.84 | LR | 0.97 | 0.89 | 0.98 | 0.81 |
| DT | 0.98 | 0.91 | 0.99 | 0.84 | DT | 0.98 | 0.92 | 1.00 | 0.83 |
| NB | 0.22 | 0.64 | 0.17 | 0.95 | NB | 0.26 | 0.65 | 0.22 | 0.88 |
| RF | 0.99 | 0.93 | 1.00 | 0.84 | RF | 0.99 | 0.90 | 1.00 | 0.83 |
| SVM | 0.93 | 0.55 | 1.00 | 0.00 | SVM | 0.94 | 0.48 | 1.00 | 0.00 |
| ANN | 0.81 | 0.59 | 0.86 | 0.18 | ANN | 0.72 | 0.58 | 0.75 | 0.34 |
| CNN | 0.95 | 0.93 | 1.00 | 0.87 | |||||
Sensitivity (93%) was highest for the graph random forest in the scenario of 2,000 participants and the centrality requirement of 90 (the best model in the best scenario based on graph machine learning with systematic hyper-parameter selection). Indeed, graph convolutional learning was found to have the best performance in the scenario of 2,000 participants with the centrality requirement of 70. LS Minimum Requirement of Life Satisfaction for Central Nodes (e.g., 70, 80, 90). Acc, accuracy; AUC, area under the curve; Spe, specificity; Sen, sensitivity; LR, logistic regression; DT, decision tree; NB, naïve bayes; RF, random forest; SVM, support vector machine; ANN, artificial neural network; CNN, convolutional neural network
Table 4.
Random forest variable importance & shapley additive explanations min-max results
| Variable | Importance |
SHAP |
||
|---|---|---|---|---|
| Value | Rank | Min | Max | |
| Education | 0.009 | 15 | -0.015 | 0.055 |
| Gender | 0.005 | 21 | -0.006 | 0.024 |
| Age | 0.031 | 2 | -0.016 | 0.180 |
| Marriage | 0.008 | 16 | -0.004 | 0.099 |
| Religion | 0.012 | 11 | -0.011 | 0.066 |
| Activity–religious | 0.007 | 18 | -0.013 | 0.071 |
| Activity–friend | 0.011 | 12 | -0.011 | 0.041 |
| Activity–culture leisure sports | 0.003 | 25 | -0.002 | 0.026 |
| Activity–family | 0.004 | 22 | -0.004 | 0.053 |
| Activity–voluntary | 0.001 | 27 | -0.001 | 0.000 |
| Activity–political | 0.000 | 28 | 0.000 | 0.000 |
| Residential type | 0.007 | 19 | -0.008 | 0.026 |
| Region | 0.002 | 26 | -0.005 | 0.006 |
| #Children alive | 0.015 | 9 | -0.008 | 0.079 |
| #Brothers/sisters cohabiting | 0.004 | 24 | -0.003 | 0.120 |
| Parents alive | 0.006 | 20 | -0.003 | 0.027 |
| Health insurance | 0.013 | 10 | -0.010 | 0.138 |
| Economic activity | 0.004 | 23 | -0.012 | 0.020 |
| Income | 0.031 | 3 | -0.011 | 0.069 |
| Subjective health | 0.018 | 6 | -0.012 | 0.107 |
| Body mass index | 0.018 | 7 | -0.009 | 0.131 |
| Smoking | 0.009 | 14 | -0.007 | 0.061 |
| Drinking | 0.007 | 17 | -0.007 | 0.023 |
| Life satisfaction–health | 0.023 | 4 | -0.011 | 0.115 |
| Life satisfaction–economic | 0.018 | 8 | -0.007 | 0.078 |
| Life satisfaction–overall | 0.021 | 5 | -0.015 | 0.116 |
| Subjective class | 0.010 | 13 | -0.006 | 0.050 |
| Mental disease | 0.703 | 1 | -0.081 | 0.786 |
Based on graph random forest variable importance in the scenario of 2,000 participants and the centrality requirement of 90, top-10 determinants of mental disease were mental disease in previous period (2016), age, income, life satisfaction–health, life satisfaction–overall, subjective health, body mass index, life satisfaction–economic, children alive and health insurance. SHAP, Shapley Additive Explanation
Figure 2 is called the SHAP summary plot. In the case of a positive association, blue points of low values are located in the left and red points of high values are located in the right, e.g., mental disease in the previous period, age, negative subjective health and body mass index. Here, the SHAP max value in Table 4 is taken for final interpretation, e.g., mental disease in the previous period (0.79), age (0.18), negative subjective health (0.11) and body mass index (0.13). The inclusion of mental disease in the previous period, age, negative subjective health or body mass index into the graph random forest will increase the probability of mental disease by 0.79, 0.18, 0.11, or 0.13. The opposite is true for a negative association. Blue points of low values are located in the right and red points of high values are located in the left, e.g., income and children alive. Here, the SHAP min value in Table 2 is taken for final interpretation, i.e., income (-0.01) and children alive (-0.01). The inclusion of income or children alive into the graph random forest will decrease the probability of mental disease by 0.01. Finally, Figure 3 shows explainable graph convolutional neural networks based on PyTorch Geometric regarding which peripheral nodes connect with which central nodes (https://pytorch-geometric.readthedocs.io/en/latest/tutorial/explain.html). For example, a peripheral node 643, which belongs to the second highest subjective class, has a connection to one central node only (410). Another peripheral node 1,243, which belongs to the lowest subjective class, has connections to all four central nodes (410, 1,477, 1,693, and 1,890).
Figure 2.
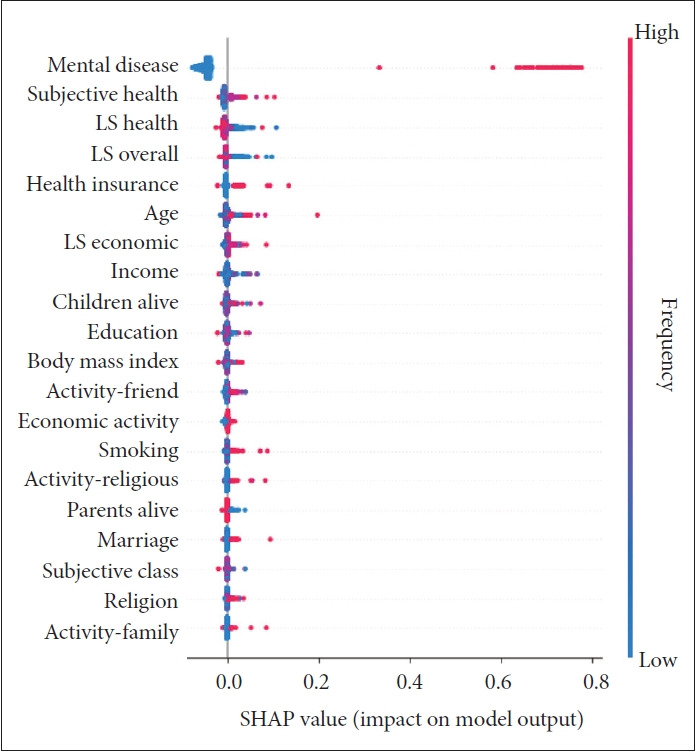
Random forest SHAP summary plot. In the case of a positive association, blue points of low values are located in the left and red points of high values are located in the right, e.g., mental disease in the previous period, age, negative subjective health and body mass index. Here, the SHAP max value in Table 4 is taken for final interpretation. The opposite is true for a negative association. Blue points of low values are located in the right and red points of high values are located in the left, e.g., income and children alive. Here, the SHAP min value in Table 2 is taken for final interpretation. LS, life satisfaction; SHAP, Shapley Additive Explanation.
Figure 3.
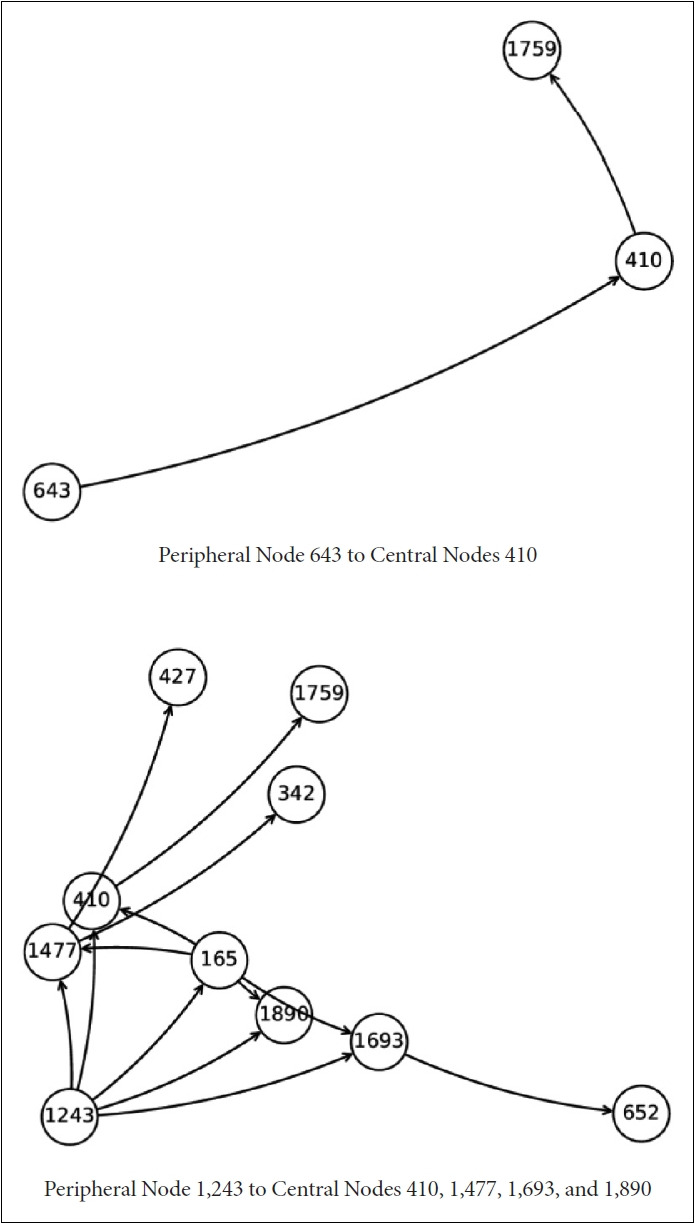
Explainable graph convolutional neural networks. This figure shows explainable graph convolutional neural networks regarding which peripheral nodes connect with which central nodes. For example, a peripheral node 643, which belongs to the second highest subjective class, has a connection to one central node only (410). Another peripheral node 1,243, which belongs to the lowest subjective class, has connections to all four central nodes (410, 1,477, 1,693 and 1,890).
DISCUSSION
Summary
This study used graph machine learning with systematic hyper-parameter selection to analyze hidden networks and mental health conditions in the middle-aged and old. Based on the results, the area under the curve was similar across different models in different scenarios. However, sensitivity (93%) was highest for the graph random forest in the scenario of 2,000 participants and the centrality requirement of 90 (the best model in the best scenario based on graph machine learning with systematic hyper-parameter selection). Based on graph random forest variable importance in the scenario of 2,000 participants and the centrality requirement of 90, top-10 determinants of mental disease were mental disease in previous period, age, income, life satisfaction–health, life satisfaction– overall, subjective health, body mass index, life satisfaction– economic, children alive and health insurance. Based on the Shapley Additive Explanations summary plot, some associations were positive, e.g., mental disease in the previous period, age, negative subjective health and body mass index, whereas the opposite was true for income and children alive.
Contributions
This study makes the following contributions. Firstly, this study introduces cutting-edge approaches of graph machine learning with systematic hyper-parameter selection and explainable graph learning in the area of mental health for the first time [19,20]. A recent review used 72 references to review recent progress in the examination of mental disorders as network issues [5]. This study suggests that network analysis would serve as an effective approach of personized psychiatry investigating complex variations across different individuals and groups alike [5]. Specifically, this study focused on two research topics of network problems for clinical purposes, i.e., comorbid states as dependent variables and group interactions as predictor variables. For example, comorbid mental disorders, which are considered to be independent or separate conditions in conventional analysis, become dependent or networked states in network analysis, which share common symptoms and predictors [21]. Likewise, emotional connections as group interactions are major predictors of major depressive disorder [22]. More recent research extended this approach in various spectrums [23-29]. It covered depressive symptoms [23-29], anxiety 23,25,28,29], affective symptoms [27] and loneliness [28]. Its data size varied within 579–5,797 from Qatar [23], China [24-26], Spain [27], and the United Kingdom [28,29]. These previous studies requested due attention to COVID-19 as an influential risk factor for mental disorders besides individuals’ characteristics and group interactions. However, graph machine learning and graph deep learning were beyond the scope of the existing literature above. This study brings most advanced approaches of graph machine learning with systematic hyper-parameter selection and explainable graph learning in the field of mental health for the first time.
Secondly, this study confirms existing literature based on basic machine learning, denoted above as “machine learning applied for the prediction of mental disease without a graph network.” According to basic random forest variable importance for a previous study on diabetes mellitus and its comorbid condition [13], top-10 determinants of diabetes-mental disease comorbidity in 2018 were the following predictors in 2016: diabetes, mental disease, body mass index, income, age, life satisfaction–health, subjective health, life satisfaction–economic, children alive and life satisfaction–overall. These top-10 predictors were very similar with those of mental disease from graph random forest variable importance in the scenario of 2000 participants and the centrality requirement of 90 for this study: mental disease, age, income, life satisfaction–health, life satisfaction–overall, subjective health, body mass index, life satisfaction–economic, children alive and health insurance. These two studies affirm a diverse scope of major predictors for the prediction of mental health, which includes mental disease in a previous period, demographic information (age), family support (children alive), socioeconomic conditions (income, health insurance), health-related information (subjective health, body mass index) and life satisfaction– health, economic and overall. However, some changes can be noted, i.e., the ranking of body mass index moved down from the second to the seventh and the opposite is true for life satisfaction–overall, which moved up from the ninth to the fifth. One possible explanation is that life satisfaction–overall is an emotional connection, which is considered to be a major predictor of major depressive disorder as a group interaction [22].
In other words, improving an individual’s life satisfaction as a personal condition is expected to strengthen the individual’s emotional connection as a group interaction, which would reduce the risk of the individual’s mental disease in the end. This would be one plausible argument on the higher importance of life satisfaction compared to other predictors. This would bring an important clinical implication for highlighting the importance of a patient’s life satisfaction and emotional connection regarding the diagnosis and management of the patient’s mental disease [30].
Limitations
This study had the following limitations. Firstly, the number of participants was limited to 2,000 because of memory capacity and time constraint. Expanding the sample size is expected to improve the performance of graph machine learning. Secondly, attention mechanisms were not considered for graph machine learning. Some nodes (participants) and edges (interactions) would make more contributions hence giving more weights on these nodes and edges (attention mechanisms) would strengthen the performance of graph machine learning. Thirdly, more advanced reinforcement learning approaches than systematic hyper-parameter selection were beyond the scope of this study. For example, systematic hyperparameter selection in this study considered the performance of graph machine learning only, whereas actor-critic approaches consider other variables under various scenarios as well [10]. Rigorous comparison of different graph reinforcement learning methods to investigate hidden networks and mental health conditions in the middle-aged and old is expected to further the boundary of knowledge on this topic. Finally, extending this study to anxiety disorder, major depressive disorder and other mental disorders would bring significant contributions for this line of research.
Conclusion
This study demonstrates the usefulness of graph machine learning with systematic hyper-parameter selection to analyze hidden networks and mental health conditions in the middleaged and old. Improving an individual’s life satisfaction as a personal condition is expected to strengthen the individual’s emotional connection as a group interaction, which would reduce the risk of the individual’s mental disease in the end. This would bring an important clinical implication for highlighting the importance of a patient’s life satisfaction and emotional connection regarding the diagnosis and management of the patient’s mental disease.
Acknowledgments
None
Footnotes
Availability of Data and Material
The original data is available in https://survey.keis.or.kr/eng/klosa/ klosa01.jsp. The code and final data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors have no potential conflicts of interest to disclose.
Author Contributions
Conceptualization: Kwang-Sig Lee, Byung-Joo Ham. Data curation: Kwang-Sig Lee, Byung-Joo Ham. Formal analysis: Kwang-Sig Lee, Byung-Joo Ham. Funding acquisition: Kwang-Sig Lee, Byung-Joo Ham. Investigation: Kwang-Sig Lee, Byung-Joo Ham. Methodology: Kwang-Sig Lee, Byung-Joo Ham. Project administration: Kwang-Sig Lee, Byung-Joo Ham. Resources: Kwang-Sig Lee, Byung-Joo Ham. Software: Kwang-Sig Lee, Byung-Joo Ham. Supervision: Kwang-Sig Lee, Byung-Joo Ham. Validation: Kwang-Sig Lee, Byung-Joo Ham. Visualization: Kwang-Sig Lee, Byung-Joo Ham. Writing—original draft: Kwang-Sig Lee, Byung-Joo Ham. Writing—review & editing: Kwang-Sig Lee, Byung-Joo Ham.
Funding Statement
This work was supported by (1) National Research Foundation of Korea (NRF) grant funded by the Ministry of Education, Science and Technology of South Korea (No.NRF-2020M3E5D9080792) and (2) Korea Health Industry Development Institute grant funded by the Ministry of Health and Welfare of South Korea (No.HI23C1234; No.HI22C1302 [Korea Health Technology R&D Project]).
REFERENCES
- 1.World Federation for Mental Health . Depression: a global crisis. Occoquan: World Federation for Mental Health; 2012. [Google Scholar]
- 2.Institute for Health Metrics and Evaluation . Findings from the global burden of disease study 2017. Seattle: IHME; 2018. [Google Scholar]
- 3.Lee KS, Park JH. Burden of disease in Korea during 2000-10. J Public Health (Oxf) 2014;36:225–234. doi: 10.1093/pubmed/fdt056. [DOI] [PubMed] [Google Scholar]
- 4. Statistics Korea. [Year 2018 statistics on causes of death in Korea]. Daejeon: Statistics Korea; 2019. Korean. [Google Scholar]
- 5.Fried EI, van Borkulo CD, Cramer AO, Boschloo L, Schoevers RA, Borsboom D. Mental disorders as networks of problems: a review of recent insights. Soc Psychiatry Psychiatr Epidemiol. 2017;52:1–10. doi: 10.1007/s00127-016-1319-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lee KS, Ham BJ. Machine learning on early diagnosis of depression. Psychiatry Investig. 2022;19:597–605. doi: 10.30773/pi.2022.0075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv [Preprint] 2016 doi: 10.48550/arXiv.1609.02907. Available at: . Accessed July 1, 2024. [DOI] [Google Scholar]
- 8.Chen M, Wei Z, Huang Z, Ding B, Li Y. Simple and deep graph convolutional networks. arXiv [Preprint] 2020 doi: 10.48550/arXiv.2007.02133. Available at: . Accessed July 1, 2024. [DOI] [Google Scholar]
- 9.Wu Z, Pan S, Chen F, Long G, Zhang C, Yu PS. A comprehensive survey on graph neural networks. IEEE Trans Neural Netw Learn Syst. 2021;32:4–24. doi: 10.1109/TNNLS.2020.2978386. [DOI] [PubMed] [Google Scholar]
- 10.Nie M, Chen D, Wang D. Reinforcement learning on graphs: a survey. IEEE Trans Emerg Top Comput Intell. 2023;7:1065–1082. [Google Scholar]
- 11.Korea Employment Information Service About KLoSA [Internet] Available at: https://survey.keis.or.kr/eng/klosa/klosa01.jsp. Accessed June 1, 2024.
- 12.Lee KS, Park KW. Social determinants of the association among cerebrovascular disease, hearing loss and cognitive impairment in a middle-aged or older population: recurrent neural network analysis of the Korean longitudinal study of aging (2014-2016) Geriatr Gerontol Int. 2019;19:711–716. doi: 10.1111/ggi.13716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim R, Kim CW, Park H, Lee KS. Explainable artificial intelligence on life satisfaction, diabetes mellitus and its comorbid condition. Sci Rep. 2023;13:11651. doi: 10.1038/s41598-023-36285-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cho H, Lee EH, Lee KS, Heo JS. Machine learning-based risk factor analysis of necrotizing enterocolitis in very low birth weight infants. Sci Rep. 2022;12:21407. doi: 10.1038/s41598-022-25746-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cho H, Lee EH, Lee KS, Heo JS. Machine learning-based risk factor analysis of adverse birth outcomes in very low birth weight infants. Sci Rep. 2022;12:12119. doi: 10.1038/s41598-022-16234-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee KS, Kim ES. Explainable artificial intelligence in the early diagnosis of gastrointestinal disease. Diagnostics (Basel) 2022;12:2740. doi: 10.3390/diagnostics12112740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Van Rossum G, Drake Jr FL. Python reference manual. Amsterdam: Centrum voor Wiskunde en Informatica; 1995. [Google Scholar]
- 18.Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, et al. Py-Torch: an imperative style, high-performance deep learning library. arXiv [Preprint] 2019 doi: 10.48550/arXiv.1912.01703. Available at: . Accessed July 1, 2024. [DOI] [Google Scholar]
- 19.Li Y, Zhou J, Verma S, Chen F. A survey of explainable graph neural networks: taxonomy and evaluation metrics. arXiv [Preprint] 2022 doi: 10.48550/arXiv.2207.12599. Available at: . Accessed July 1, 2024. [DOI] [Google Scholar]
- 20.Kakkad J, Jannu J, Sharma K, Aggarwal C, Medya S. A survey on explainability of graph neural networks. arXiv [Preprint] 2023 doi: 10.48550/arXiv.2306.01958. Available at: . Accessed July 1, 2024. [DOI] [Google Scholar]
- 21.Cramer AO, Waldorp LJ, van der Maas HL, Borsboom D. Comorbidity: a network perspective. Behav Brain Sci. 2010;33:137–150. doi: 10.1017/S0140525X09991567. [DOI] [PubMed] [Google Scholar]
- 22.Lee Pe M, Kircanski K, Thompson RJ, Bringmann LF, Tuerlinckx F, Mestdagh M, et al. Emotion-network density in major depressive disorder. Clin Psychol Sci. 2015;3:292–300. doi: 10.1177/2167702614540645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Abdul Karim M, Ouanes S, Reagu SM, Alabdulla M. Network analysis of anxiety and depressive symptoms among quarantined individuals: cross-sectional study. BJPsych Open. 2021;7:e222. doi: 10.1192/bjo.2021.1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao N, Li W, Zhang SF, Yang BX, Sha S, Cheung T, et al. Network analysis of depressive symptoms among residents of Wuhan in the later stage of the COVID-19 pandemic. Front Psychiatry. 2021;12:735973. doi: 10.3389/fpsyt.2021.735973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cai H, Bai W, Liu H, Chen X, Qi H, Liu R, et al. Network analysis of depressive and anxiety symptoms in adolescents during the later stage of the COVID-19 pandemic. Transl Psychiatry. 2022;12:98. doi: 10.1038/s41398-022-01838-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jin Y, Sun HL, Lam SC, Su Z, Hall BJ, Cheung T, et al. Depressive symptoms and gender differences in older adults in Hong Kong during the COVID-19 pandemic: a network analysis approach. Int J Biol Sci. 2022;18:3934–3941. doi: 10.7150/ijbs.69460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cecchini JA, Carriedo A, Méndez-Giménez A, Fernández-Río J. Network analysis of physical activity and depressive and affective symptoms during COVID-19 home confinement. Glob Ment Health (Camb) 2023;10:e63. doi: 10.1017/gmh.2023.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ramos-Vera C, García O’Diana A, Basauri MD, Calle DH, Saintila J. Psychological impact of COVID-19: a cross-lagged network analysis from the English longitudinal study of aging COVID-19 database. Front Psychiatry. 2023;14:1124257. doi: 10.3389/fpsyt.2023.1124257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ramos-Vera C, García O’Diana A, Basauri-Delgado M, Calizaya-Milla YE, Saintila J. Network analysis of anxiety and depressive symptoms during the COVID-19 pandemic in older adults in the United Kingdom. Sci Rep. 2024;14:7741. doi: 10.1038/s41598-024-58256-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hoffner CA, Bond BJ. Parasocial relationships, social media, & wellbeing. Curr Opin Psychol. 2022;45:101306. doi: 10.1016/j.copsyc.2022.101306. [DOI] [PubMed] [Google Scholar]


