A Low-power Impedance-to-frequency Converter for Frequency-Multiplexed Wearable Sensors

Abstract

We propose a low-power impedance-to-frequency (I-to-F) converter for wearable transducers that change both its resistance and capacitance in response to mechanical deformation or a change in ambient pressure. At the core of the proposed I-to-F converter is a fixed-point circuit comprising of a voltage-controlled relaxation oscillator and a proportional-to-temperature (PTAT) current reference that locks the oscillation frequency according to the impedance of the transducer. Using both analytical and measurement results we show that the operation of the proposed I-to-F converter is well matched to a specific class of sponge mechanical transducer where the system can achieve higher sensitivity when compared to a simple resistance measurement techniques. Furthermore, the oscillation frequency of the converter can be programmed which ensures that multiple transducer and I-to-F can communicate simultaneously over a common channel (physical wire or virtual wireless channel) using frequency-division multiplexing. Measured results from proof-of-concept prototypes show an impedance sensitivity of $19.66\text{Hz}/\text{Ω}$ at $1.1\text{kΩ}$ load impedance magnitude and a current consumption of $128\text{μA}$. As a demonstration we show the application of the I-to-F converter for human gesture recognition for radial pulse sensing.

I. Introduction

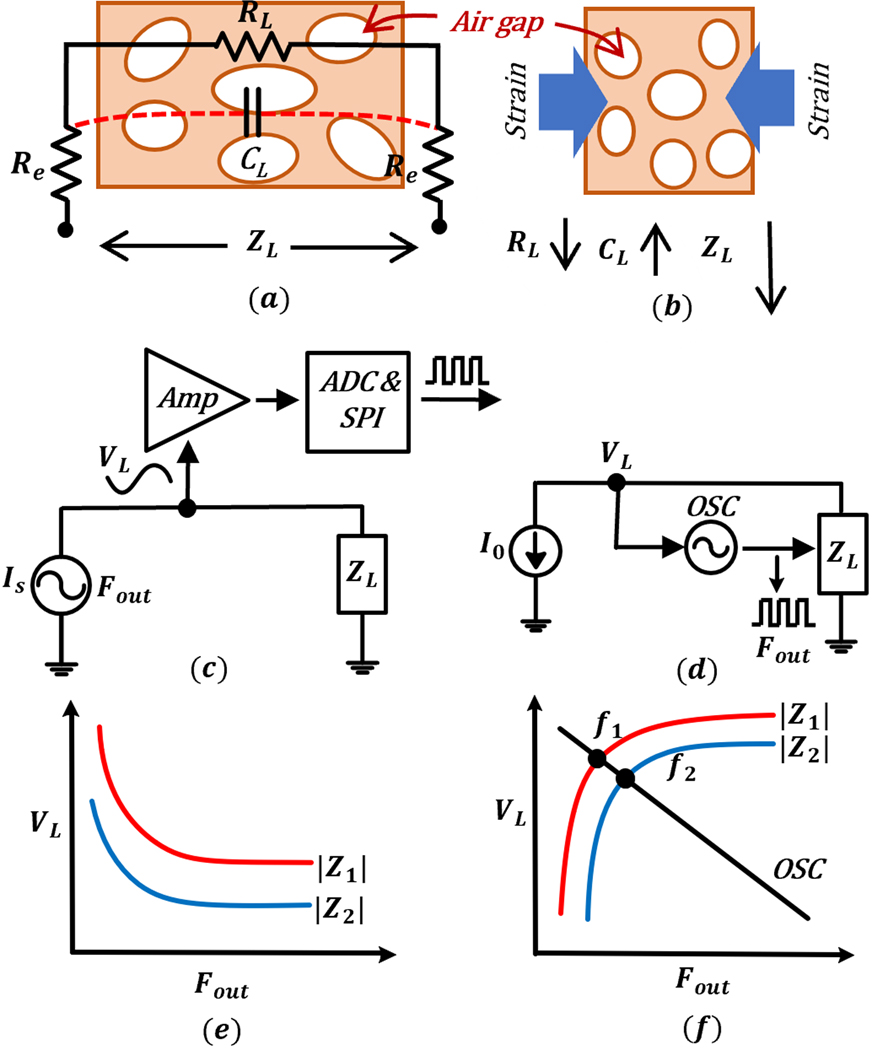
Smart wearable sensors have gained considerable attention in various fields, including human health monitoring, human-machine interface, and motion detection [3]–[11]. The next generation of soft and flexible sensors can be comfortably and securely attached to the human body surface while converting physical signals into electrical signals. However, the transduction mechanism in traditional wearable sensors, such as strain or pressure involves a change in only one of their electrical properties, its resistance or its capacitance, in response to an external mechanical stimulus [12]–[17]. Recently we reported a wearable sponge transducer [1], [2] that can produce changes in both resistance and capacitance in response to the external mechanical stimulus. Fig. 1(a) illustrates the cross-sectional view of the poly(3,4-ethylene dioxythiophene) polystyrene sulfonate (PEDOT:PSS) sponge transducer reported in [1] where the air gaps within the transducer contribute towards the total capacitance $C_L$ measured across the transducer. The resistance across the transducer $R_L$ on the other hand is determined by the density of the conductive polymer PEDOT:PSS. When the transducer is subjected to a mechanical strain, as shown in Fig. 1(b) both the resistance and capacitance change but in opposite directions respectively. This implies that an impedance measurement method that weighs the change in $R_L$ and $C_L$ appropriately (opposite sensitivity) can achieve significantly higher sensitivity than just measuring the resistance or the capacitance alone. Another challenge in scaling the number of wearable/flexible sensors is that each of the sensor units needs to be ultra-low-power and each sensor can be individually addressed so that the information can be retrieved. In a conventional implementation, the information is multiplexed on a physical (wire or body) channel [18]–[21] or a virtual (packet-switched) channel [22]–[24]. This requires the integration of batteries on the sensor or the use of remote powering, both of which require ultra-low-power impedance sensing and communication circuits.

Fig. 1.

(a) Cross-sectional illustration of a sponge transducer [1], [2] comprising of several air-gaps which contribute to the transducer capacitance; (b) mechanical deformation of the transducer leads to change in resistance and capacitance; (c)-(e) A conventional approach for measuring changes in impedance; and (d)-(f) proposed approach using a fixed-point frequency locking technique

In literature, the most common approach for measuring impedance follows a topology shown in Figure 1(c) [25]–[29]. A voltage controlled current source $G_m$, drives the sensor impedance $Z_L$ resulting in a voltage $V_L$ across the sensor. $V_L$ is then demodulated using the source signal $V_S$ as a reference. Using both coherent and non-coherent approaches the impedance can be measured at different frequencies $F_{out}$ as shown in Figure 1(e). Generally, the frequency at which the impedance is measured $F_{out}$ is chosen a-priori or swept over a pre-determined range; however, the optimal operating frequency could vary based on the sensor dimensions and the environmental conditions (sweat and dry conditions). Also, to minimize the power dissipation and for safety considerations, the impedance $Z_L$ is driven using small currents, hence an amplifier is required to amplify the change in voltage $V_L$. An Analog-to-digital converter (ADC) and serial peripheral interface (SPI) interfaces are used for extracting the impedance changes and for signal transmission and post-processing. However, if the objective is to measure the change in the magnitude of the impedance $\left|Z_L\right|$ rather than its resistive or reactive components, then the number of modules (and hence power) can be significantly reduced. Also, note that the conventional approach shown 1(e) uses an open-loop configuration, implying that any noise injected into the internal nodes has to compensated using post-processing techniques.

In this paper, we explore a compact, low-power impedance-to-frequency (I-to-F) converter shown in Fig. 1(d) and alleviates some of the disadvantages of the topology shown in Fig. 1(c). It uses a current reference source and a voltage-controlled oscillator (VCO) in a feedback configuration to modulate the sensor’s impedance (due to its resistive & capacitive elements). The configuration thus locks the frequency $F_{out}$ such that the average current $I_0$ driven through the sensor impedance remains constant. This is equivalent to a transfer characteristic shown in Fig 1(f) where the fixed-point ($V_L,F_{out}$) is determined by the sensor impedance $Z_L$. The key advantages of the this topology which has been verified using analytical and measured results are summarized below:

1. The measurement or the operating frequency is a stable fixed-point of the circuit and hence is robust to small perturbation and noise when compared to the open-loop configuration in Fig. 1(c).

2. The lock-in frequency is determined by the transducer impedance, hence, the measurement frequency need not be determined a-priori and the dynamic range of the converter is determined by the dynamic range of the relaxation oscillator.

3. The output of the proposed I-to-F converter is encoded as the frequency of a square-wave which can be viewed as a pulse-density digital code. Thus, the I-to-F converter does not need an additional analog-to-digital (ADC) converter. Even though this type of encoding is not minimal, simply implying a counter or digital low-pass filter can estimate a binary encoding of the frequency measurement. The energy footprint for such a counter could be less than $1\mu \text{W}$ for a counter operating at 100 kHz (assuming $1\mathit{\text{pJ}}/$ bit operation).

4. The pulse-density digital code produced by the I-to-F converter can be used for direct frequency modulation which then be backscattered, similar to our previous approach [30]. This not only reduces the overall form-factor of the system but can significantly reduce the overall power-dissipation.

5. The fixed-point frequency $F_{out}$ can be tuned such that when multiple sensors are used, the frequency output could be directly multiplexed over a single communication channel (wireless or wired). Combining the impedance sensing with the information multiplexing feature reduces the form factor, improves the energy-efficiency, and makes the proposed topology scalable across a large number of wearable sensors.

The paper is organized as follows: In Section II we first present a system-level analysis of the proposed impedance-to-frequency converter and highlight different design tradeoffs. In Section III we present a circuit-level and system-level implementation of the converter, and in Section IV we present measurement results using an assembled prototype. Section V concludes the paper with a summary and comparison of system performance and a brief discussion of future directions.

II. I-to-F Converter Principle and Analysis

In this section, we describe the system-level architecture of the proposed I-to-F converter and analyze its system response. The architecture is shown in Fig. 2(a) where we have assumed that the transducer A is placed between two metallic junctions B and C. One junction B is connected to a an external DC voltage source $V_0$ and the other junction C is used for sensing the load current $I_L$. To simplify the analysis we have assumed that the transducer equivalent circuit is a parallel combination of $R_L$ and $C_L$. A combination of the bias current $I_{ref}$ and a biasing resistor $R_1$ generates a change in the voltage $V_x$ in response to the change in the load current $I_L$. A low-pass filter $H\left(s\right)$ tracks ${\bar{V}}_x$ which is the average of $V_x.{\overline{V}}_x$ then modulates the frequency $F_{out}$ of the clock signal $V_{CLK}$ generated by a voltage-controlled oscillator (VCO). $V_{CLK}$ drives the switch $M$ through an enable switch $S$. Note that the switch $S$ is used to disable the feedback loop in which case the frequency $F_{out}$ (in its steady state) is determined only by $R_L$. For the sake of completeness, in Fig. 2(a) we have also shown the parasitic capacitances $C_{p1}$ and $C_{p2}$ which will be ignored for the analysis below. We will assume a linear DC model for the VCO where $F_{out}$, is related to its input voltage $V_{in}$ according to

$$F_{out}=-\alpha V_{in}+\beta$$ (1)

where $\alpha$ and $\beta$ are constant parameters. These coefficients will be determined experimentally as will be shown in Section III.

Fig. 2.

(a) Equivalent circuit describing the operation of the proposed impedance-to-frequency converter; and (b) timing diagram showing the evolution of the voltage ${\mathit{V}}_{\mathit{x}}$ when the switch S is ON and the VCO output drives the NMOS switch $\mathit{M}$. ${\overline{\mathit{V}}}_{\mathit{x}}$ shows an average of the voltage ${\mathit{V}}_{\mathit{x}}$ and the red line represents a linear approximation to the Vx discharging curve.

When the switch $M$ is ON, the transducer is effectively short-circuited, hence the voltage $V_x=V_0$. When the switch $M$ is OFF, the load current $I_L$ is determined by both the current flowing through $R_L$ and the discharge current through $C_L$. Applying Kirchhoff’s current law (KCL) at node $V_x$ leads to

$$I_{ref}+\frac{V_0-V_x}{R_L}+C_L\frac{d(V_0-V_x)}{dt}=\frac{V_x}{R_1}$$ (2)

which under steady-state (equilibrium) condition would let $V_x$ converge to a potential $V_e$

$$V_e=\frac{V_0{R}_1+I_{ref}{R}_1{R}_L}{R_1+R_L}.$$ (3)

This is depicted in Fig. 2(b) which shows a timing diagram corresponding to the switch $M$ which is periodically turned ON and OFF by $V_{CLK}$ according to a frequency $F_{out}$. However, if $F_{out}\gg 1/R_L{C}_L$, then we can linearize the differential equation 2 such that $V_x$ discharges only to a non-equilibrium potential $V_d$, as shown in Fig 2. We have previously used non-equilibrium-based analysis for designing multi-channel data acquisition systems [21]. After linearization, as shown in Fig. 2, the equation 2 can be approximated as

$$I_{ref}{R}_L+V_0(1+\frac{1}{{\omega }_{1}T})=V_d(1+\frac{R_L}{R_1}+\frac{1}{{\omega }_{1}T})$$ (4)

where ${\omega }_1$ & the sampling period $T$ is given by

$${\omega }_1=\frac{1}{R_L{C}_L},T=\frac{1}{2F_{out}}$$ (5)

A low-pass filter modeled as $H\left(s\right)$ in Fig.2(a) tracks the average voltage of $V_x$. Using the linearized equation 4 and assuming a 50% duty-cycle, we can estimate the average voltage $\overline{V_x}$ as

$$\overline{V_x}=\frac{3V_0+V_d}{4}=\frac{V_0}{4}(3+\frac{A}{B})+\frac{I_{ref}{R}_L}{4B}$$ (6)

where,

$$A=1+\frac{1}{{\omega }_{1}T}$$ (7)

$$B=1+\frac{R_L}{R_1}+\frac{1}{{\omega }_{1}T}.$$ (8)

Fig. 2(b) shows the average voltage $\overline{V_x}$ which determines the VCO frequency $F_{out}$ according to equation 1 as

$$\begin{gathered} F_{out}=-\alpha \overline{V_x}+\beta \\ =-(\frac{3}{4}+\frac{A}{4B})\alpha V_0+\frac{\alpha }{4B}{I}_{ref}{R}_L+\beta \end{gathered}$$ (9)

Solving the equation 9 yields a quadratic problem in terms of locking frequency $F_{out}$ of which only one is practically realizable and is given by the equation in table I. The equation shows that $F_{out}$ and the dynamic range of the I-to-F converter can be adjusted by changing the current reference $I_{ref}$ and $V_0$. Figure 3(a) and (b) plot the value of $F_{out}$ as the load resistance $R_L$ and load capacitance $C_L$ is varied. For each of these plots, the value of the external voltage source $V_0$ and $I_{ref}$ are kept constant. The results show that $F_{out}$ increases when $R_L$ increases where as $F_{out}$ decreases when $C_L$ increases. This shows that the sensitivity of the I-to-F converter would match the physics of the sponge-transducer shown in Fig. 1 where the resistance and capacitance change in opposite direction in response to a mechanical stimulus [1]. The sensitivity of the I-to-F converter and the resulting signal-power can be estimated through a perturbation analysis of $F_{out}$ as

$$\begin{gathered} \text{Δ}{F}_{out}=\frac{\partial F_{out}}{\partial R_L}\text{Δ}{R}_L+\frac{\partial F_{out}}{\partial C_L}\text{Δ}{C}_L \\ \text{Δ}{F}_{out}^2={\left(\frac{\partial F_{out}}{\partial R_L}\right)}^2\text{Δ}{R}_L^2+\left(\frac{\partial F_{out}}{\partial C_L}\right)\text{Δ}{C}_L^2 \\ +2\left(\frac{\partial F_{out}}{\partial R_L}\right)\left(\frac{\partial F_{out}}{\partial C_L}\right)\text{Δ}{R}_L\text{Δ}{C}_L \end{gathered}$$ (11)

where $\text{Δ}{R}_L$ and $\text{Δ}{C}_L$ denote incremental change in resistance and capacitance in response to mechanical deformation. The term $\text{Δ}{F}_{out}^2$ denotes the total signal-power and comprises of $\text{Δ}{R}_L\text{Δ}{C}_L$ which is the correlation between the resistance and capacitance change. Since $\text{Δ}{R}_L\text{Δ}{C}_L\le 0$ for the sponge-transducer and from Fig. 1 and $\left(\frac{\partial F_{out}}{\partial R_L}\right)\left(\frac{\partial F_{out}}{\partial C_L}\right)\le 0$ from Fig. 3, equation 11 indicate that the signal measured by the proposed I-to-F converter would be higher compared to measuring changes in $R_L$ or $C_L$ independently. This has been validated later in the measured results in section III. Note that the variance/noise in measuring $\text{Δ}{F}_{out}$ can be estimated as

$${\sigma }^2\left(\text{Δ}{F}_{out}\right)={\left(\frac{\partial F_{out}}{\partial R_L}\right)}^2{\sigma }^2\left(\text{Δ}{R}_L\right)+{\left(\frac{\partial F_{out}}{\partial C_L}\right)}^2{\sigma }^2\left(\text{Δ}{C}_L\right)$$ (12)

where ${\sigma }^2(\text{Δ}{R}_L)$ and ${\sigma }^2(\text{Δ}{C}_L)$ denote the respective noise-power in measuring change in resistance and capacitance and are assumed to be independent.

TABLE I.

$$F_{out}=\frac{2R_1(V_0\alpha -\beta )+\sqrt{{(R_1+R_L)}^2{\omega }_1^2+{\omega }_1(R_1^2(2I_{ref}{R}_L\alpha -4V_0\alpha +4\beta )+2R_1{R}_L(V_0\alpha -2\beta ))+{(2R_1{V}_0\alpha -2\beta R_1)}^2}-(R_1+R_L){\omega }_1}{4R_1}$$ (10)

Fig. 3.

Analytically calculated ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ for an RC parallel load with different ${\mathit{R}}_{\mathit{L}}$ and ${\mathit{C}}_{\mathit{L}}$ under 4 different ${\mathit{V}}_0$ external voltage sources and $\mathit{S}$ ON modality: (a) For this transfer characteristics, ${\mathit{R}}_{\mathit{L}}$ is varied, the capacitance ${\mathit{C}}_{\mathit{L}}$ was chosen to be 1.5 nF. (b) For this transfer characteristics, ${\mathit{C}}_{\mathit{L}}$ is varied, the resistance ${\mathit{R}}_{\mathit{L}}$ was chosen to $14.67\text{kΩ}$.

To visualize the analysis based on equation 11, we consider the solution for $F_{out}$ by restricting the operating regime to $1/{\omega }_{1}T\gg R_L/R_1$ where the ratio $A/B\approx 1$ in equation 9. Note that this regime is achieved for large values of $R_L$ or $C_L$. In this case $F_{out}$ can be approximated as

$$F_{out}=\frac{\beta -\alpha V_0+\sqrt{{\left(\alpha V_0-\beta \right)}^2+\frac{\alpha I_{ref}}{2C_L}}}{2}$$ (13)

which leads to

$$\frac{\partial F_{out}}{\partial R_L}=0$$ (14)

$$\frac{\partial F_{out}}{\partial C_L}=-\frac{\alpha I_{ref}}{8{C_L}^2\sqrt{{(\alpha V_0-\beta )}^2+\frac{\alpha I_{ref}}{2C_L}}}$$ (15)

Equation 14 shows that in this restricted regime the I-to-F converter is not sensitive to changes in resistance $\text{Δ}{R}_L$, however, the change in $F_{out}$ is inversely proportional to change in $\text{Δ}{C}_L$. This operating regime highlights a key advantage of joint measurement of resistance and capacitance changes, compared to measuring just changes in resistance which might saturate at larger values.

Using equation 13 we can also derive the expression for input-referred noise in this restricted regime. We assume that the source of the external noise and variation is due to the parameters $\beta$ and $I_{ref}$ in equation 13 and the gain of the I-to-F is determined by gain $\alpha$ of the VCO. The input-referred noise (in-terms of voltage) is thus given by

$$\overline{V_{in}^2}=\frac{{(\frac{\partial F_{out}}{\partial \beta })}^2{\sigma }^2(\beta )+{(\frac{\partial F_{out}}{\partial I_{ref}})}^2{\sigma }^2(I_{ref})}{{\alpha }^2}$$ (16)

where,

$$\frac{\partial F_{out}}{\partial \beta }=\frac{1}{2}(1-\frac{\alpha V_0-\beta }{\sqrt{{(\alpha V_0-\beta )}^2+\frac{\alpha I_{ref}}{2C_L}}})$$ (17)

$$\frac{\partial F_{out}}{\partial I_{ref}}=\frac{\alpha }{8C_L\sqrt{{(\alpha V_0-\beta )}^2+\frac{\alpha I_{ref}}{2C_L}}}.$$ (18)

The parameters ${\sigma }^2\left(\beta \right),{\sigma }^2\left(I_{ref}\right)$ denote the respective variance of $\beta$ and $I_{ref}$ and are determined by the circuit topology and the specific implementation of the I-to-F converter. In section III-A, we experimentally determine the magnitude of the input-referred noise.

A. I-to-F Circuit implementation

The system architecture shown in Fig. 2(a) has been implemented using the circuit shown in Figure 4(a). While each of the functional modules in Fig. 2(a) uses commercial-off-the-shelf (COTS) circuits the novelty lies in interfacing these circuits and exploiting the coupling between the circuits to optimize for energy-efficiency. For instance the current reference $I_{Ref}$ implemented using a standard bipolar transistor-based PTAT circuit shown in Fig. 4(b) also implements the low-pass filter $H\left(s\right)$ in 4(a). $I_{ref}$ is then determined by the resistor $R_{ref}$ which sets the constant potential difference between the voltages $V_c$ and ${\bar{V}}_x$. The VCO has been implemented using a standard relaxation oscillator, shown in Fig. 4(c) where the output frequency $F_{out}$ is determined by the resistor $R_{osc}$ and the voltage $V_c$. The switching circuit in the converter has been implemented using a combination of a bipolar and an nMOS transistor shown in Fig. 4(d). The circuit also includes an active shield module comprising of a buffer, as shown in Fig. 4(e), and is used to cancel out the parasitic capacitances $C_{p1}$ and $C_{p2}$ in Fig. 4(a). This ensures that the output frequency $F_{out}$ is determined only by the load impedance $Z_L$. Fig. 4(f) shows an assembled impedance-to-frequency converter board that integrates different commercial-off-the-shelf (COTS) chipsets implementing each of the circuit modules in Fig. 4(b)–(e). While an integrated circuits approach would have led to significant miniaturization of the system, We chose a COTS approach because the form-factor of the overall system is limited by the size of the transducer and the battery. Furthermore, the COTS implementation of the PTAT, relaxation oscillator and the active shield are highly optimized for energy efficiency while achieving high reliability. In the prototype implementation, the PTAT current reference has been implemented using the LM234 chipset from Texas Instruments [31], the relaxation oscillator has been implemented using the TS3006 chipset from Silicon Lab [32]. Even though a COTS implementation was chosen to demonstrate the proof-of-concept, we note that a further improvement in energy-efficiency can be achieved using an integrated circuits implementation.

Fig. 4.

(a) Circuit implementation of the proposed impedance-to-frequency converter comprising of (b) a current reference circuit, (c) a relaxation oscillator circuit, (d) a control switch, and (e) a circuit for active shielding. (f) Assembled printed circuit board(PCB) prototype of the converter using COTS chipsets.

III. Measured Results

In this section we characterize the performance of the I-to-F converter circuit shown in Fig. 2 and verify the analysis presented in section II. In all experiments, the biasing current $I_{ref}$ was chosen to be $9.4\mu A$ which sets an upper limit on the current flowing through the transducer impedance $Z_L$.

A. Model Characterization

Our initial measurements were designed to determine the VCO coefficients $\alpha$ and $\beta$ in the equation 1 and to create a SPICE simulation model that could be used for parametric studies. Note that the VCO coefficients could have been estimated using an open-loop input-output measurement based on equation 1. However, equation 1 models the DC response of the VCO, whereas the circuit in Fig. 2 comprises of switching circuits and reactive elements in a feedback configuration. Therefore, a more accurate approach to estimate the coefficients $\alpha$ and $\beta$ would be based on equation 9. Furthermore, the parameters of the low-pass filter $H\left(s\right)$ also needs to be estimated in the feedback configuration. In this experiment $Z_L$ was fixed by choosing different values of $R_L$ and $C_L$, and the voltage $V_0$ was swept. Estimation of $F_{out}$ was achieved by counting the number of digital cycles over a measurement window of 20 ms. Even though for this experiment a Keithley DAQ6510 data acquisition system [33] was used for frequency counting, any digital decimation filter implemented on a microcontroller or an FPGA could have been used. $V_0$ was varied between 0.01 V to 0.21 V at an increment of 0.02 V. Fig. 5 shows the measured results obtained for three different parallel RC combinations. The results conform to the linear model described by equation 9 and the VCO parameters are estimated to be $\alpha =3.43\times {10}^{5}Hz/V$ and $\beta =8.2\times {10}^{4}Hz$. These parameters have been used to validate the measured response in the subsequent experiments. Instead of directly estimating the parameters of the $H\left(s\right)$ in Fig.2(a), for the I-to-F SPICE model, we directly estimated the relationship between $F_{out}$ and $V_x$ using a fifth-order polynomial. An VerilogA model was used to implement the polynomial mapping in the SPICE simulations.

Fig. 5.

(a) Measured transfer characteristic between the output frequency ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ and the tunable voltage ${\mathit{V}}_{\mathbf{0}}$ for different values of ${\mathit{R}}_{\mathit{L}}$ and ${\mathit{C}}_{\mathit{L}}$ in Fig. 2. (b) A zoom-in of an arbitrary region to better visualize the output frequency difference.

The next set of experiments used a parallel RC impedance to validate the analysis in section II. For the first experiment, $R_L$ was varied from $130\text{Ω}$ to $80\text{kΩ}$, whereas the capacitance $C_L$ was held constant at 1.5 nF. Both the simulation and measured results are shown in Figure 6(a) which verifies the monotonic relationship between $F_{out}$ and $R_L$ consistent with the analysis in section II. Note that at higher value of $R_L$ the sensitivity of $F_{out}$ with respect to $R_L$ decreases which confirms the model in equation 14. Higher sensitivity in $F_{out}$ is achieved at lower values of $R_L$.

Fig. 6.

Simulated and Measured ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ for an RC parallel load with different ${\mathit{R}}_{\mathit{L}}$ and ${\mathit{C}}_{\mathit{L}}$ when $\mathit{S}$ is ON: (a) & (c) For this transfer characteristics ${\mathit{R}}_{\mathit{L}}$ is varied, the capacitance ${\mathit{C}}_{\mathit{L}}$ was chosen to be 1.5 nF. (b) For this transfer characteristics, ${\mathit{C}}_{\mathit{L}}$ is varied, the resistance ${\mathit{R}}_{\mathit{L}}$ was chosen to $14.67\text{kΩ}$.

In the next set of experiments, $R_L=14.67\text{kΩ}$ was kept constant, whereas the capacitance $C_L$ was varied from 1.5 nF to 22 nF. The simulation and measured results are shown in Figure 6(b), which shows the frequency $F_{out}$ monotonically decreases with increase in $C_L$ as described by the analysis in section II. Furthermore, the change in $F_{out}$ is lower at higher values of $C_L$ which is also consistent with the equation 15. The results in Figure 6 show that the SPICE model our modeled I-to-F converter simulation results match the measured results with the prototyped device.

The next set of experiments verified the functionality of the I-to-F converter for different R-C impedance. One of the impedance corresponds to the equivalent circuit of the sponge transducer and comprises of the electrode resistance $R_S$ in series with a parallel combination of $R_L$ and $C_L$ [1], shown in the inset of Fig.7(a). We first varied the series resistance $R_s$ from $130\text{Ω}$ to $80\text{kΩ}$, whereas $R_L=14.67\text{kΩ}$ and $C_L=1.5\text{nF}$ were kept constant. Then we kept the series resistance $R_s=5\text{kΩ}$ and $C_L=1.5\text{nF}$ and varied $R_L$ from $130\text{Ω}$ to $80\text{kΩ}$. Both the simulation and measured results are shown in Fig.7(a). Next we verified the I-to-F converter response for an impedance comprising of a capacitance $C_s$ in series with a parallel combination of $R_L$ and $C_L$. We first varied the series capacitance $C_s$ from $C_L=1.5\text{nF}$ to $C_L=22\text{nF}$, while $R_L=14.67\text{kΩ}$ and $C_L=1.5\text{nF}$ were kept constant. Then we varied $C_L$ from $C_L=1.5\text{nF}$ to $C_L=22\text{nF}$, while keeping $C_s=1.5\text{nF}$ and $R_L=14.67\text{kΩ}$ constant. Fig.7(b) shows both the measurement and simulation results, as well as the circuit model.

Fig. 7.

Simulated and Measured ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ when $\mathit{S}$ is ON and for different RC impedance shown in the inset: (a) ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ when series resistance ${\mathit{R}}_{\mathit{s}}$ is varied, the capacitance ${\mathit{C}}_{\mathit{L}}$ was chosen to be 1.5 nF and ${\mathit{R}}_{\mathit{L}}$ was chosen to be $14.67\text{kΩ}$; (b) $F_{out}$ when parallel resistance ${\mathit{R}}_L$ is varied, the capacitance ${\mathit{C}}_{\mathit{L}}$ was chosen to be 1.5 nF and ${\mathit{R}}_{\mathit{s}}$ was chosen to be $5\text{kΩ}$; (c) ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ when series capacitance ${\mathit{C}}_{\mathit{s}}$ is varied, the capacitance ${\mathit{C}}_{\mathit{L}}$ was chosen to be 1.5 nF and ${\mathit{R}}_{\mathit{L}}$ was chosen to be $14.67\text{kΩ}$; (d) ${\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ when capacitance ${\mathit{C}}_{\mathit{L}}$ is varied, the capacitance ${\mathit{C}}_{\mathit{s}}$ was chosen to be 1.5 nF and ${\mathit{R}}_{\mathit{s}}$ was chosen to be $14.67\text{kΩ}$.

For estimating the input-referred noise of the I-to-F converter we followed the procedure described in [34]. A $3.5\text{kΩ}$ and 1.5 nF parallel RC impedance was applied, and $V_0$ was set at 0.11 V. The frequency output of the voltage-controlled oscillator (VCO) was recorded using a Keithley DAQ6510, with a measurement window of 20 ms. The frequency output signal, with embedded noise, is depicted in Figure 8(a). To analyze the noise spectrum, we applied a Fast Fourier Transform (FFT) on the frequency output signal. In the previous experiment, we derived the VCO parameter $\alpha$, which allows the conversion of frequency output signal noise into input-referred voltage noise. The input-referred noise power is calculated and displayed in Figure 8(b) within a 15 Hz bandwidth. From this data, an estimated noise power of $0.5\times {10}^{-16}{V}^2/Hz$ can be inferred. Using the calculated noise power, the average input-referred noise is estimated to be approximately $7.07\text{nV}/\sqrt{\text{Hz}}$.

Fig. 8.

(a) Measured frequency output under a $3.5\text{kΩ}$ and 1.5 nF parallel RC impedance over a moving window of 20ms. (b) Power analysis plot of the measured frequency signal.

Table II summarizes the measured specifications of the I-to-F converter circuit shown in Figure 4. The Table includes a breakdown of the current consumed by each of the modules and the overall power dissipation (without the active shield circuit) of the converter. Note that the response of the I-to-F converter with respect to the magnitude of the impedance is non-linear. Therefore, the output sensitivity of the I-to-F converter is a function of its operating/biasing condition, and hence sensitivity is only defined for a small-signal operation. For the sensitivity measurements a parallel RC impedance was chosen with $C=1.5\text{nF}$ and $R$ was varied from $3\text{kΩ}$ to $4\text{kΩ}$. The frequency output changes from 58.32 kHz to 60.13 kHz, resulting in a calculated parallel RC impedance magnitude $\left|Z\right|$ varies from $1.13\text{kΩ}$ to $1.224\text{kΩ}$. The sensitivity $\text{Δ}{F}_{out}/\text{Δ}\left|Z\right|$ is approximated as $19.66\text{Hz}/\text{Ω}$ at $\left|Z\right|=1.1\text{kΩ}$. The I-to-F converter has a measured noise of approximately 5 Hz at the same operating point as shown in Figure 8(a). If we assume a system signal-to-noise ratio (SNR) of 1, the impedance resolution is approximated as $0.254\text{Ω}$.

TABLE II.

Measured System Specification

Parameter	Value
Supply Voltage	3.3 V
Current Consumption (Feedback off)	$28\text{μA}$
Current Consumption (Feedback on)	$128\text{μA}$
Voltage Controlled Oscillator	$2.4\text{μA}$
Current Reference	$9.8\text{μA}$
Switching Circuit	$100\text{μA}$
Other Components	$15.8\text{μA}$
Impedance Measurement Range	$1-47\text{kΩ}$
Impedance Sensitivity @ $\left|Z\right|=1.1\text{kΩ}$	$19.66\text{Hz}/\text{Ω}$
Impedance Sensitivity @ $\left|Z\right|=47\text{kΩ}$	$0.05\text{Hz}/\text{Ω}$
Impedance Resolution @ $\left|Z\right|=1.1\text{kΩ}$	$0.254\text{Ω}$

The I-to-F converter’s measurement range is defined as the range of the impedance magnitude $\left|Z\right|$ over which the measured sensitivity is at least $0.05\text{Hz}/\text{Ω}$. To estimate the measurement range, we biased the parallel RC load at $C=15\text{pF}$ and $R$ was varied from $99\text{kΩ}$ to $100\text{kΩ}$. The frequency output varies from 118.26 kHz to 118.27 kHz, corresponding to a impedance magnitude $\left|Z\right|$ change from $47.1\text{kΩ}$ to $47.3\text{kΩ}$.

B. Radial Pulse Sensing

The objective of this experiment was to verify the higher sensitivity of the proposed I-to-F converter for monitoring the radial artery pulse. We recreated the experimental setup that was reported in [12] and shown in Fig. 9(a) where the I-to-F converter was interfaced with a sponge transducer. The transducer was fabricated using porous polydimethylsiloxane (PDMS) cubes coated with a conductive polymer PEDOT:PSS. Details regarding the fabrication of the transducer and its electrical characterization can be found in our previous work [1] and has been omitted here for the sake of brevity. To ensure stable recording, a wristband was wrapped over the sensor, providing secure and consistent contact. The mechanical changes induced by arterial pulses was sensed by the sponge transducer as a change in impedance which was then measured by the I-to-F converter. Each experiment was repeated twice where the I-to-F converter was set to $S$-ON and $S$-OFF modes. Figure 9(b) shows the measured results for both the modes, where we have plotted only the change in $\text{Δ}{F}_{out}$ from the baseline frequency. The measured results clearly show the arterial pulse signal corresponding to a heart rate of 108 beats per minute (bpm). However, the higher sensitivity of I-to-F converter in $S$-ON mode can be clearly seen when compared to the I-to-F converter output in $S$-OFF mode. This improvement in sensitivity allows for more accurate and reliable detection of the radial pulse signals.

Fig. 9.

Measured radial pulse sensing results using a prototype sponge transducer: (a) experimental setup where the transducer is clamped to the wrist; and (b) measured normalized temporal changes in the converter frequency $\mathbf{\text{Δ}}{\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}/{\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ for $\mathit{S}$-ON mode and $\mathit{S}$-OFF mode respectively.

C. Gesture Tracking Application

The next set of experiments explored the use of the sponge-transducer and the I-to-F converter for gesture-tracking application. The specific gesture that was chosen was the mechanical motion of the human finger. In Figure 10(a) we show the placement of the sponge transducer on a human finger joint in a straight and a bent position respectively. In the straight position, the sponge sensor maintains its original shape, whereas bending the finger causes the transducer to stretch, resulting in a change in the transducer’s impedance. These impedance changes are measured by the I-to-F converter. The states of the finger (bent and unbent) was maintained for a duration of 5 -seconds and the measured responses are shown in Figure 10(b). For comparison, the response of the I-to-F converter is measured for the modes $S$-ON and $S$-OFF. The measured results clearly show higher sensitivity in the $S$-ON mode when both $R_L$ and $C_L$ are being sensed. Note that in Figure 10(b) the waveforms corresponding to $S$-ON and $S$-OFF are not time-aligned as the experiments were conducted independently. Figure 10(b) shows more than 10 times higher sensitivity when compared to measuring changes in resistance.

Fig. 10.

Experiment to validate the application of the converter for gesture tracking and the multi-access capability of the impedance-to-frequency converter: (a) measurement setup showing the sponge transducer attached to a human finger joint when the finger is straight (state 1) and when the finger is bent at 90 degrees (state 2); (b) measured the normalized $\mathbf{\text{Δ}}{\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$ dynamics ($\mathbf{\text{Δ}}{\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}/{\mathit{F}}_{\mathit{o}\mathit{u}\mathit{t}}$) when switching between state 1 and state 2, shown here for resistance only sensing mode and impedance sensing mode; (c) experimental setup comprising of two sponge transducers/converters (sensor 1 and 2) in two different states (state1 and state2); (d) Measured output after signal demultiplexing which clearly shows the dynamic states of both sensors.

D. Multi-sensor experiment & Frequency-multiplexing

Since the baseline frequency of the converter can be set using the voltage $V_0$, it is possible to set the baseline operating frequency $F_{out}$ of many I-to-F converters to be different. This enables frequency-multiplexing of the sensed information (encoded by $\text{Δ}{F}_{out}$) over a common physical channel (Wireless, wired or using the body-channel) [35]–[38]. In the next set of experiments we have verified the frequency multiplexing measurement using an experimental setup shown in Fig 10(c). Two sponge-transducers and I-to-F converters were attached to different fingers and their outputs $F_{out}$ were physically connected to each other using a piece of wire. The transmission bandwidth is set by the VCO output frequency range, which is determined by resistor $R_{osc}$, as explained in II-A. We chose $R_{osc}$ to be $1\text{MΩ}$, achieving a bandwidth of 108 kHz.

The external voltage sources $V_0$ were set to 0.11 V and 0.24 V to bias the output frequency baseline at 85 kHz and 60 kHz, respectively. The measured results are shown in Fig 10(d), which shows that different hand-motions corresponding to different finger movements (clicking the mouse).

Fig 10(d), shows the time-frequency measurement where one can clearly distinguish the two types of motions, shown in Fig 10(c). The multiplexed time-frequency waves were then separated into two sections based on a 70 kHz cutoff frequency. Note that previous work [1] has shown that for the sponge transducer, the resistance and capacitance change differently in response to compressive strain, tensile strain, and pressure. This attribute in conjunction with the proposed impedance-to-frequency conversion could therefore be used for designing multi-modal and frequency multiplexed sensors.

IV. Conclusions and Discussions

This paper presents a compact, impedance-to-frequency (I-to-F) converter that is suitable for integration with a multimodal transducer that changes its impedance in response to mechanical deformation. By simultaneously monitoring the changes in resistance and capacitance across a sponge-based multi-modal transducer, the proposed I-to-F converter was shown to exhibit significantly higher sensitivity compared to monitoring just the change in resistance. Even though the functionality of the proposed I-to-F converter has been demonstrated for the sponge-sensor, the converter can be used for other types of transducers. For specific impedance configuration combination, as shown in Fig.7(a), the functionality of the I-to-F converter can be augmented to determine the resistive and the capacitive components of the impedance. This is achieved by enabling and disabling the feedback using the external switch S in Fig. 2. When S is turned ON, the I-to-F measures the magnitude of the impedance, whereas when the S is turned OFF, the I-to-F measures only the resistance. Using the two-point measurements (in the ON and OFF states) the I-to-F could therefore be used to estimate both the resistive and reactive components.

The proposed I-to-F converter uses a fixed-point approach for measuring impedances and in the process eliminates the need for sinusoidal current source generation, signal amplification and analog-to-digital conversion stages. This makes the architecture simple and amenable for a ultra-low-power implementation. Even though a COTS approach have been used for proof-of-concept, the architecture can be easily mapped onto an integrated circuits solution. This will lead to further miniaturization and improvements in energy-efficiency. However, even with a COTS implementation, the proposed I-to-F converter achieve better performance metrics when compared to other impedance measurement solutions reported in literature as shown in the Table III. Notably, most of the solutions examined utilize a conventional topology, as depicted in Figure 1(c). In contrast, our approach, based on commercial off-the-shelf (COTS) components, leverages a novel topology as proposed in Figure 1(d). It’s important to highlight that the solutions discussed in [39]–[42] primarily encompass analog front-ends, typically requiring a separate analog-to-digital converter (ADC) for integration into a complete system. Our prototype uniquely integrates the ADC functionality. The custom integrated circuit solutions highlighted in [39]–[41] are reported in academic literature and while these solutions exhibit lower current consumption, they often compromise important performance factors such as dynamic range and input-referred noise. In comparison, our COTS-based solution is more directly comparable to the widely used commercial product, the Texas Instruments AFE4300. Notably, our system outperforms the AFE4300 in various key performance metrics, as evident from the comparison table. The commercial-off-the-shelf (COTS) chipsets are generally trimmed to be robust to mismatch. However, the converter architecture will exhibit sensitivity to ambient temperature. The oscillator’s temperature dependency coefficient is reported as 0.02%/°C [32], which shows a minimal effect on the parameter $\beta$ in equation1. The highest sensitivity to temperature variation arises due to the PTAT current reference. For LM234 reference, the reported temperature dependence is 0.33%/°C [31] which results in a 0.195% change in the output frequency for a 1 °C variation in temperature.

TABLE III.

Performance Comparision

Parameter	This work	Zamani [39]	Yan [40]	Kim [41]	AFE4300 [42]
Supply Voltage	3.3	1	1.8	0.5	3
Modulation	Square	Semi-ramp	Square	Pseudo-sine	Pseudo-sine
Injection Current	$<10\text{μA}$	$0.5-1\text{μA}$	$10-40\text{μA}$	$8.4\text{μA}$	NA
Injection frequency	NA	2 kHz	2 kHz	$20/50\text{Hz}$	$8/16/3264\text{Hz}$
Measurement Range	1 to $47\text{kΩ}$	0.1 to $3.3\text{kΩ}$	0.1 to $4.4\text{kΩ}$	NA	NA
Input-referred noise	$7.07\text{nV}/\sqrt{H}z$	$221.36\text{nV}/\sqrt{H}z$	$146.46\text{nV}/\sqrt{H}z$	$45\text{nV}/\sqrt{H}z$	$48\text{nV}/\sqrt{H}z$
Supply Current	$128\text{μA}$	$1.55\text{μA}$	$28\text{μA}$	$18.5\text{μA}$	$970\text{μA}$

In addition to measuring changes in impedance, we also demonstrated that the I-to-F converter can support frequency multiplexing of the measured output where many converters can be connected to the same physical communication channel. This feature makes the design scalable to a large number of transducers. We can configure system parameters to ensure that different I-to-F converters operate within different frequency bands. The frequency range of the impedance to frequency converter can be adjusted by tuning the current reference $I_{ref}$ and the center frequency can be adjusted by changing the external voltage source $V_0$.