Development of a single port dual arm robotically steerable endoscope for neurosurgical applications

Abstract

Single-port surgical robots have gained popularity due to less patient trauma and quicker post-surgery recovery. However, due to limited access provided by a single incision, the miniaturization and maneuverability of these robots still needs to be improved. In this paper, we propose the design of a single-port, dual-arm robotically steerable endoscope containing one steerable major cannula and two steerable minor cannulas. By integrating the proposed nine degrees-of-freedom (DoFs) robotically steerable endoscope with an industrial robotic arm and a joystick controller, this robotic system can potentially achieve intuitive, and remote multi-arm manipulation capability. We present the design of the robotically steerable endoscope consisting of tendon-driven joints controlled by a compact actuation system and derive the kinematic and static models. We validate the derived models using different kinematic trajectories with an average RMSE value of 0.98 mm and 0.66 mm for the distal tip position errors of the two steerable minor cannulas.

Introduction

Robot-assisted minimally invasive surgery (RAMIS) has become increasingly common since the FDA approved the da Vinci® robotic surgical system (Intuitive Surgical Inc., Sunnyvale, CA) in 2000¹. RAMIS provides better vision and instrumentation, can potentially cause lesser tissue trauma², and has shown improved patient outcomes³. During RAMIS, surgical tools are inserted through the working channels of an endoscopic device. We broadly describe the term “endoscope” to encompass scope(s) with or without working channel(s). While several small incisions can be created to use multiple tools simultaneously during surgical procedures (multi-port systems), single-port systems have multiple working channels and allow surgeries to be performed with a single incision, potentially resulting in lesser tissue damage.

Single-port (SP) systems can provide several benefits including lower invasiveness, better cosmetic results, and lower postoperative pain^4–7. An existing SP system that has been developed includes the da Vinci® Single-Port (SP) system (Intuitive Surgical Inc., Sunnyvale, CA), an FDA-approved robotic surgical system used in minimally invasive surgery (MIS). This system features a stereoscopic binocular camera and three flexible instruments, all housed in a 25 mm diameter cannula^8,9. It is intended for single-port urological and transoral otolaryngology surgical procedures⁸. In a review presented by Dobbs et al.¹⁰, the clinical data and the initial clinical experience using the SP system are reported. The data showed that most major robotic urologic procedures appear technically feasible using this system. However, one of the key limitations of this SP system reported by Park et al.⁹ included the overall large diameter of the cannula (25 mm). This makes the system difficult to be used for other particularly constrained minimally invasive procedures such as endoscopic cranial procedures (ECPs).

For ECPs, several unique challenges and requirements exist. The fixed volumes of the skull hinder endoscopes from expanding their workspace^11–14. Any gross movement of the endoscope may result in adjacent brain parenchymal injury. Also, the sensitive brain regions that have functional tissue require that instruments or endoscopes entering the brain are to be kept as small as possible to avoid permanent neurologic deficit. The working channel is therefore constrained regarding the tools that can be introduced, leading to the use of tools that are typically rigid, unwieldy, and have limited functionality and range of motion by surgeons’ standards. Consequently, this restricts the complexity of cranial diseases that can be treated using minimally invasive endoscopy.

Recently, dual-arm SP endoscopic systems have been developed to overcome some of the aforementioned challenges. Rox et al.¹⁵ designed a two-arm concentric tube robot system for rigid neuroendoscopy. While the two tools decreased the tilting required for the endoscope, which would reduce tissue trauma at the incision site, the endoscope used in the design was not steerable, thereby limiting the systems reachability to the intracranial structures. Manjila et al.¹⁶ designed a prototype of an MR-compatible multi-port neuroendoscope with two imaging ports, allowing tissue resection at the tip port and electrocautery at the lateral port. However, the tools necessary for this neuroendoscope were not developed in their work. Lim et al.¹⁷ developed three magnetically actuated robotic forceps for neuroendoscopy using laser welding manufacturing techniques. These devices can pass through a 3D-printed rigid trocar (3.2 mm working channel). However, the devices rely on a large external magnetic actuation system. Price et al.¹⁸ created a two-armed, joystick-controlled endoscopic robot for brain surgeries with an outer diameter of 10 mm. In most of the designs presented in the literature, the robotic steering of the endoscope with channels for multiple tools is not shown. For the designs where the endoscope can be robotically steered, the diameter of the overall system is larger than 8 mm^19–21. Steering the endoscope can facilitate a larger workspace and minimize the tilting of the endoscope at the site of the incision, which can potentially reduce tissue trauma.

Endoscopic neurosurgery is unique in the way that the brain ventricles offer a small but viable cavity for steerable manipulation and current intervention is hampered by linear instruments or trajectories. Unfortunately, the ventricle has complex anatomy (see Fig. 1) and is surrounded by important functional brain parenchyma that should not be damaged. Some of the common ECPs include treatment of hydrocephalus and tumor resection procedures (biopsy or resection)²². In hydrocephalus, cerebrospinal fluid (CSF) accumulates deep in the ventricles of the brain and causes pressure buildup in the brain and skull. The condition can be treated by inserting a shunt or by endoscopic third ventriculostomy (ETV). In an ETV procedure, an opening is made in the floor of the brain ventricle. ETV is usually preferred over shunt treatment due to lesser complications²³. In tumor resection procedures, particularly deep-seated tumors adjacent to the ventricle, linear paths through the brain parenchyma are not feasible given the overlying functional areas of brain. Utilizing the ventricular system as a highway to the tumor is challenging, given the complex ventricular anatomy, and is currently hampered by available linear tools and limited visualization. This results in suboptimal tumor resection or non-diagnostic biopsies.

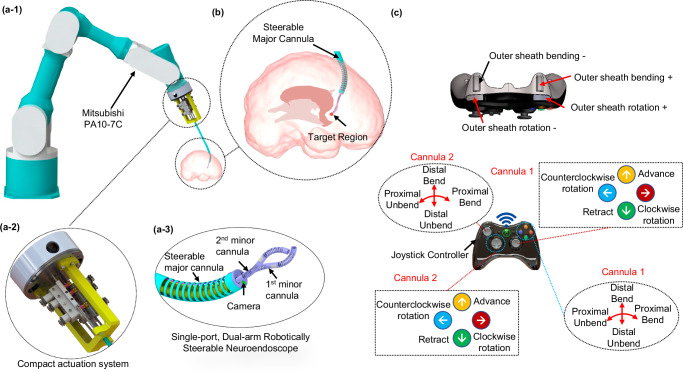
Fig. 1. Schematic of the single-port dual-arm robotically steerable endoscope system.

a-1 The robotically steerable endoscope mounted onto a Mitsubishi PA10-7C robot arm, (a-2) the compact actuation system, (a-3) the steerable major cannula and two steerable minor cannulas, (b) illustration of the robotically steerable endoscope for a neurosurgical procedure, and (c) the controller layout for teleoperation.

This paper introduces the novel design of a single-port, dual-arm steerable major cannula (outer diameter (OD): 6.9 mm and inner diameter (ID): 6.3 mm) and two steerable minor cannulas (OD: 1.93 mm and ID: 1.49 mm). Compared to the existing systems mentioned above, our proposed device has the ability to enter the body through a smaller single incision with a larger reachable workspace compared to the state-of-the-art. The primary contributions of this work are summarized as follows:

• Design and fabrication of a single-port, dual-arm robotically steerable endoscope that consists of a steerable major cannula that houses two minor cannulas comprising of two active bending joints and one passive compliant joint.

• The development of a modular and compact actuation system for the translation, rotation, and bending of each steerable minor cannula.

• Derivation and validation of the mechanics of the individual steerable cannulas and the kinematics of the entire robotic system.

In the design presented in this paper, the steerable major cannula is the trocar (Fig. 1) and the goal of the robotically steerable cannulas is to operate within the constrained regions of the brain and have the capability to do bimanual manipulation tasks within the complex cavities of the ventricles. This is currently very challenging for neurosurgeons to accomplish, especially for combined indications, such as ETV and biopsy or complex tumor resection. The steerable major cannula can enable precise placement of the minor cannulas close to the target region. This can reduce any tilting typically required of rigid trocars, potentially reducing parenchymal injury¹⁵ through the superficial brain via the cannulas, as well as spare the functional parenchyma adjacent to the ventricles, such as the fornices (related to memory), the thalami (related to movement and a variety of functions), etc.

The paper is organized as follows: In the ‘Results’ section, we first present the subsection ‘System Design’ which includes the design of the robotically steerable endoscope (steerable major cannula and the steerable minor cannulas) and the design of the compact actuation system used to actuate the robotically steerable endoscope. We further present the ‘Joint Model Verification’ subsection, validating the joint models derived for the minor cannula, the ‘Major Cannula Joint Model’ subsection, describing the data-driven model for the bending of the major cannula, and the ‘Verification of Robot Kinematics’ subsection, where the kinematic trajectory verification for the robotically steerable cannulas is presented. We next present the ‘Discussion’ section. Lastly, in the ‘Methods’ section, we present the ‘Joint Kinematics and Statics Models’ subsection which details joint models of the minor cannula followed by the ‘Kinematic Modeling’ subsection where the kinematics of the entire robotic system is presented.

Results

System Design

The proposed single-port, dual-arm robotically steerable endoscope, shown in Fig. 1 consists of a steerable major cannula with two channels for steerable minor cannulas, a channel for an endoscope camera, and a compact actuation system. The mechanism can be integrated onto a 7-DoF robotic arm (PA10-7C, Mitsubishi Heavy Industries, Ltd., Japan), both controlled by a wireless joystick (Xbox 360 Controller, Microsoft, WA) for intuitive and remote multi-arm manipulation capabilities.

The robotically steerable endoscope consists of a steerable major cannula (6.7 mm OD and 6.3 mm ID nitinol (NiTi) tube) and two steerable minor cannulas (1.93 mm OD and 1.49 mm ID NiTi tubes).

Steerable Major Cannula

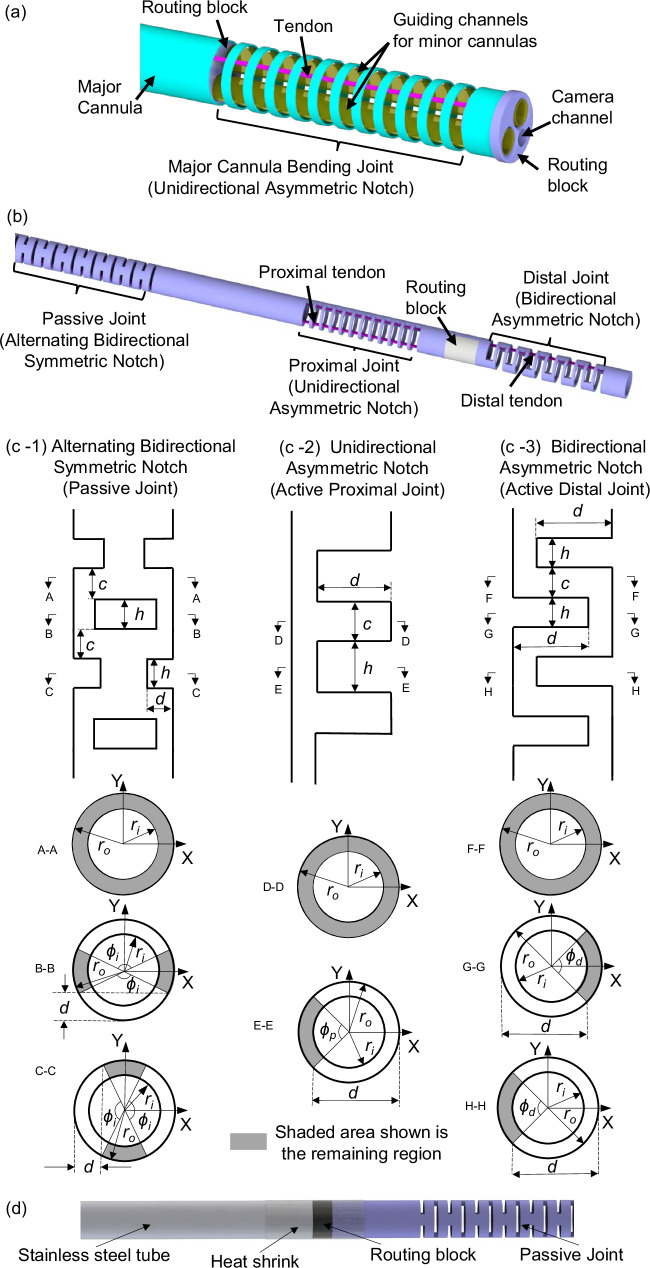
The major cannula has a bending joint at the distal end. The bending joint is created by laser micromachining a unidirectional asymmetric notch (UAN) pattern using a femtosecond laser (Optec Laser S.A., Frameries, Belgium). Several prior works have also utilized laser micromachining for developing flexible joints for continuum robots^24–28. Two guiding channels are located inside the major cannula to guide the minor cannulas as shown in Fig. 2(a). The guiding channels are fabricated using two polyether block amide (Pebax®) tubes (2.67 mm OD and 2.41 mm ID) and two 3D-printed (Projet 5600, 3D Systems, USA) routing blocks that are attached at the base and distal end of the bending joint. An additional channel is placed inside the routing blocks for an endoscope camera. A NiTi tendon (0.2 mm OD) is soldered on the inner wall of the major cannula at the tip of the bending joint. Application of tension to the tendon causes the major cannula and the components housed within it to bend. The compliance of the major cannula can be adjusted through the notch parameters {d, c, h, n} where d is the depth of cut, h is the notch width, c is the notch spacing, and n is the number of notches. For the UAN pattern, the depth of cut is constrained to be d ∈ (r_o, r_o + r_i) to ensure sufficient compliance without cutting through the tube. The datum for measuring the depth of cut, d, is shown in Fig. 2. The machining parameters used for the major cannula are shown in Table 1.

Fig. 2. Schematic of the robotically steerable cannulas.

a The steerable major cannula with two guiding channels for minor cannulas, (b) the steerable minor cannula comprising a passive (alternating BSN), proximal (UAN), and distal (BAN) joint, (c-1) the bidirectional symmetric notch (BSN) pattern, (c-2) the unidirectional asymmetric notch (UAN) pattern, and (c-3) the bidirectional asymmetric notch (BAN) pattern, and (d) NiTi tube section of the steerable minor cannula attached to a stainless steel tube section.

Table 1.

Specifications of the robotically steerable cannulas

Items	Major cannula	Minor cannula	Tendon
Total length (mm)	180	230	300/260/240a
Outer diameter, 2ro, (mm)	6.70	1.93	0.203/0.152/0.076a
Inner diameter, 2ri, (mm)	6.30	1.49	–
d (mm)	6.30	–	–
h (mm)	1.5	–	–
c (mm)	1.0	–	–
n	12	–	–
Passive joint, d (mm)	–	0.67	–
Passive joint, h (mm)	–	0.20	–
Passive joint, c (mm)	–	0.50	–
Passive joint, n	–	73	–
Proximal joint, d (mm)	–	1.68	–
Proximal joint, h (mm)	–	0.50	–
Proximal joint, c (mm)	–	0.20	–
Proximal joint, n	–	12	–
Proximal joint, lp (mm)	–	8.4	–
Distal joint, d (mm)	–	1.60	–
Distal joint, h (mm)	–	0.50	–
Distal joint, c (mm)	–	0.20	–
Distal joint, n	–	12	–
Distal joint, ld (mm)	–	8.4	–
Young’s modulus (GPa)	40–45	40–45	30–35

^aMajor cannula/minor cannula proximal joint/minor cannula distal joint.

Steerable Minor Cannula

Each of the minor cannulas has three joints: two active bending joints at the steerable section of the minor cannula and one passive joint at the base of the steerable section (Fig. 2(b)). The steerable section comprises proximal and distal joints that provides two DoFs in the same plane, allowing for S-shape trajectories for bimanual triangulation capabilities^29,30. The minor cannulas are capable of being advanced out and retracted in the major cannula. The passive joint ensures compliance within the actuated major cannula while the minor cannulas are advanced out.

The bending joints, as shown in Fig. 2(b), are achieved by laser micromachining different notch patterns on the minor cannula. The micromachined notch patterns on the minor cannulas are as follows: 1) an alternating bidirectional symmetric notch (BSN) pattern for the minor cannula passive joint (see Fig. 2(c-1)), 2) a unidirectional asymmetric notch (UAN) pattern for the minor cannula proximal joint (see Fig. 2(c-2)), and 3) a bidirectional asymmetric notch (BAN) pattern for the minor cannula distal joint (see Fig. 2(c-3)). The alternating BSN pattern of the passive joint ensures that the overall system is compliant in the bending plane of the major cannula even when the minor cannula is rotated. Similar to the UAN pattern, the BAN pattern, and the alternating BSN pattern, are characterized by the depth of cut, d, the notch spacing, c, and the notch width, h. For the BAN pattern, the depth of cut is constrained to be d ∈ (r_o, r_o + r_i) to ensure sufficient compliance without cutting through the tube, and for the BSN pattern d ∈ (r_o − r_i, r_o) to avoid cutting through the tube. The machining parameters {d, c, h, n} for each rectangular notch pattern are given in Table 1.

The notch patterns of the steerable major cannula and the minor cannulas, and the datum each machining parameter is measured from, are shown in Fig. 2(c-1)–(c-3). Each cross-section is defined by the angle subtended by the remaining material of the notched segment, ϕ_p, for a UAN joint, and ϕ_d, for a BAN joint, and is given by:

$${\varphi }_p={\varphi }_d=\left\{\begin{array}{c}2\arccos \left(\frac{d-r_o}{r_o}\right)\mathrm{if}d>r_o\hfill \\ 2\pi -2\arccos \left(\frac{r_o-d}{r_o}\right)\mathrm{if}d<r_o\hfill \\ \pi \mathrm{if}d=r_o\hfill \end{array}\right)$$ 1

while, ϕ_i, is the angle subtended from the removed region for a BSN joint and is given by:

$${\varphi }_i=2\arccos \left(\frac{r_o-d}{r_o}\right),\mathrm{where}:d\in \left(r_o-r_i,r_o\right)$$ 2

where r_o is the outer radius of the NiTi tube being considered. The proximal and distal joints have a 0.152 mm OD and 0.076 mm OD NiTi tendon soldered at the tip of the joint, respectively. A 3D-printed routing block ensures the distal tendon is approximately routed along the neutral axis of the proximal joint such that the motion of the two joints is primarily decoupled³¹. Another 3D-printed routing block is placed at the base to route each of the tendons and to join the NiTi tube section with a stainless steel tube (1.97 mm OD and 1.4 mm ID) connected to the actuation system (shown in Fig. 2(d)).

Compact Actuation System

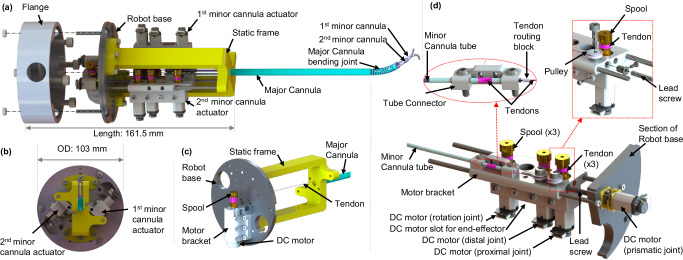
The compact actuation system (CAS) as shown in Fig. 3(a), has a base of diameter 103 mm and is 161.5 mm long. The mechanism comprises 9 joint actuators, where the major cannula bending is controlled by pulling a NiTi tendon. The NiTi tendon is soldered to the end tip of the major cannula joint on one end while the other end is wrapped around a spool (6.86 mm OD) attached to a DC motor (1.2 W, 16 mm OD, Maxon Precision Motors, MA) with a 141:1 gear ratio (see Fig. 3(b)). The motor is attached to the robot base by the motor bracket with six M3 screws. Also, the static frame, as shown in Fig. 3(c), is attached to the robot base by six screws, and the major cannula is mounted on the static frame.

Fig. 3. Schematic of the compact actuation system (CAS).

a Exploded view of the CAS with the steerable cannulas, (b) top view of the CAS, (c) major cannula bending joint actuator, and (d) section and exploded views of the 1^st minor cannula actuator.

The CAS has two modular minor cannula actuators as shown in Fig. 3(a). Each of the minor cannula actuator modules can be used for actuating the proximal and the distal joints of the minor cannula (see Fig. 3(d)). Further, the rotation and the prismatic motion of the minor cannulas can also be achieved. Hence, the 9 DoFs of the overall system can be summarized as follows:

• One DoF major cannula (UAN joint)

• Two DoFs (active) of each minor cannula bending joints that include a proximal UAN joint and distal BAN joint

• One DoF of each minor cannula prismatic joint

• One DoF of each minor cannula rotation joint

The DC gearmotor (HPCB 6V dual-shaft, gear ratio 986.41:1, Pololu Corp., NV) pulls a tendon that wraps around a spool attached to the motor’s shaft through a pulley mechanism, thereby bending the proximal joint of the minor cannula. The gearmotor and pulley are attached to the moving motor bracket using two M2 screws and a shoulder screw, respectively. The distal joint is actuated using the same actuation mechanism as the proximal joint, except the DC motor controlling the distal joint has a gear ratio of 380:1.

The rotational motion of the minor cannula is achieved through the use of two slots in the tube connector (see Fig. 3(d)). The minor cannula is held in the slots using six stainless steel washers (1.94 mm ID, 2.80 mm OD, and 0.25 mm thickness) micromachined with the Optec Femtosecond laser and two sections of polyethylene terephthalate (PET) heat shrink (0.2 mm wall thickness, Zeus, Orangeburg, SC) that are 14 mm and 156 mm long, respectively. The tube connector is attached to the moving motor bracket by two M3 screws. An ultra-high molecular weight polyethylene (UHMWPE) tendon, wrapping around the shorter heat shrink and spool, is used for force transmission. The rotational motion of the minor cannula is achieved when the spool, attached to a DC motor (Pololu Corp., NV) with a gear ratio 380:1, rotates.

For the prismatic joint motion of the minor cannula, the actuator module can slide along two parallel rods attached to the robot base and the static frame using four M2 screws. An M3 lead screw nut is affixed to the moving motor bracket and the DC gearmotor (HPCB 6V dual-shaft, gear ratio 100:1, Pololu Corp., NV) attached to the robot base actuates the lead screw (M3 × 50 mm, 0.5 mm pitch), thereby advancing and retracting the minor cannula.

Additionally, each minor cannula actuator module has one more slot to install a tendon actuator (same as the proximal or distal joint actuator) to operate an end-effector, e.g., a grasper or a scissor tool (not integrated in this paper). The working prototype of the robotically steerable endoscope is shown in the video attached in the supplementary materials. Also, in this paper, the CAS has two modular cannula actuators, but the number of actuators can be extended if necessary. Compared to the actuation mechanism in³², the proposed CAS offers several advantages: 1) simultaneously actuates the end-effector, proximal, distal, rotation, and prismatic joints, 2) results in a smaller OD (1.93 mm), whereas EndoWrist® instruments (Intuitive Surgical Inc., Sunnyvale, CA) are available with 5 mm and 8 mm ODs, and 3) embeds miniature DC motors. In comparison to magnetically actuated systems used for similar endoscopic robotic systems³³, tendon-driven actuation mechanisms can be made significantly more compact³⁴. Furthermore, the tendon-driven rotation joint mechanism presented in this work can allow the placement of the robotically steerable minor cannulas to be closer to each other, thereby decreasing the dimensions of the overall endoscope and the actuation mechanism.

Joint Model Verification

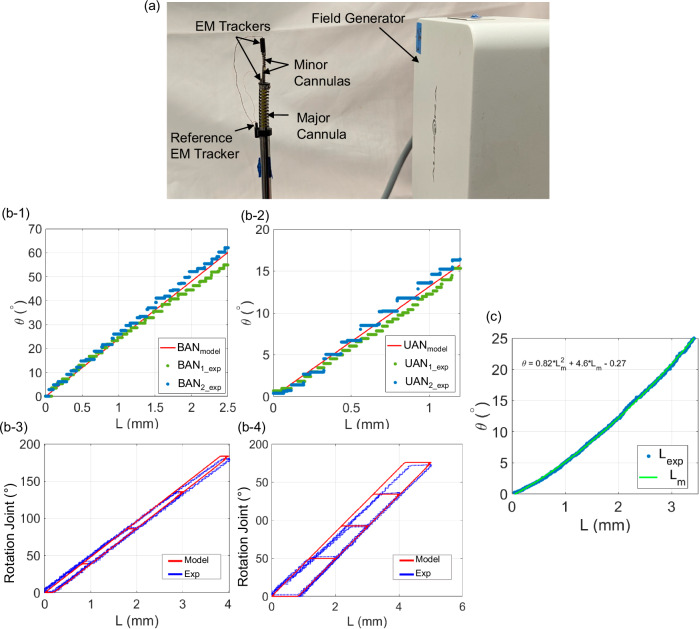
The joint kinematics and statics models for the proximal joint, distal joint, and rotation joint of the minor cannula are derived in the subsection ‘Joint Kinematics and Statics Models’. To experimentally validate the derived models, a 6-DoF EM tracker (Aurora, Northern Digital Inc., Waterloo, Ontario, Canada) is attached at the tip of each minor cannula to collect bending angle and rotation angle data (Fig. 4(a)). All of the joints are actuated individually by pulling the corresponding tendons. Sinusoidal input signals are applied to the DC motors to actuate the joints. The quaternion data generated by the EM trackers is converted to the joint deflection using:

$$Q=Q_t{Q}_{t_0}^{†}$$ 3

$$Q=q_0+q_1\widehat{i}+q_2\widehat{j}+q_3\widehat{k}$$ 4

$$\theta =2\arccos \left(q_0\right)$$ 5

where ${\mathbf{Q}}_{t_0}\in {\mathbb{R}}^4$ and ${\mathbf{Q}}_t\in {\mathbb{R}}^4$ are obtained from the EM tracker and are the unit quaternions at time t₀ and t, respectively. $Q_{t_0}^{†}$ represents the conjugate of $Q_{t_0}$, and θ is the joint deflection with respect to the initial joint configuration at t₀ = 0.

Fig. 4. Joint statics models experimental setup and results.

a Experimental setup for evaluation of the proximal, distal, and rotation joint statics models along the minor cannula, (b) modeling verification for minor cannula joints: (b-1) BAN joint model and experimental data for minor cannula 1 and minor cannula 2, (b-2) UAN joint model and experimental data for minor cannula 1 and minor cannula 2, (b-3) rotation joint model and experimental data for minor cannula 1, and (b-4) rotation joint model and experimental data for minor cannula 2, and (c) bending angle vs. tendon stroke relationship for the major cannula.

Using the joint models developed in the ‘Joint Kinematics and Statics Models’ section we estimate the joint angle for a given tendon stroke. The experimental and modeled deflection of the BAN joints and UAN joints for both the minor cannulas is shown in Fig. 4(b-1)-(b-2), respectively. The values of the parameters utilized in the models are given in Table 1. The, Young’s modulus, E of the NiTi tendon used was 34.6 GPa³⁵. For the NiTi tubes, E was iteratively adjusted in the range provided by the manufacturer (40–45 GPa), and the value of 40 GPa was chosen since it gave the least error between the model and the collected data. For the rotation joint, the tendon is loaded and unloaded at a speed of 1 mm/s for four different tendon stroke values as shown in Fig. 4(b-3)-(b-4) for minor cannula 1 and minor cannula 2, respectively. The joints follow the derived models with the root-mean-square error (RMSE) values given in Table 2. The joint statics model verification error in Table 2 for the UAN and BAN joints is based on data collected over two loading cycles. For the rotation joints, the RMSE value is computed using a single loading and unloading cycle for the four different tendon stroke values.

Table 2.

Joint statics modeling verification error

Joint	RMSE
Minor Cannula 1, UAN	1.4°
Minor Cannula 1, BAN	3.4°
Minor Cannula 1, Rotation	3.9°
Minor Cannula 2, UAN	1.2°
Minor Cannula 2, BAN	2.1°
Minor Cannula 2, Rotation	3.8°

Major Cannula Joint Model

The relationship between the tendon stroke and the bending angle of the major cannula is experimentally determined. The modeling method utilized in the previous works^34,36,37 cannot be applied because the minor cannulas and the major cannula are not constrained to follow the same curvatures. The experimental data collected is observed to behave quadratically with respect to the tendon stroke. As a result, a quadratic model is fit to the experimental data collected for the joint deflection vs. tendon stroke with an RMSE of 0.17° and is shown in Fig. 4(c).

Verification of Robot Kinematics

To verify the kinematic models of the robot derived in the ‘Kinematic Modeling’ subsection, we attached an EM tracker at the tip of the robot. Different tendon strokes are applied to the joints and the maximum joint deflection for a given trajectory is indicated in Table 3. Based on the models derived in the ‘Joint Kinematics and Statics Models’ section, the joint angles are computed from the applied tendon strokes. The computed joint angles are used to compute the position of the tip using the model presented in the ‘Kinematic Modeling’ section. The position change is estimated using the kinematic model and the actual position change is measured using the data from the EM trackers. All of the measured and estimated tip position values are with respect to the base frame of the robot.

Table 3.

Trajectories for kinematics verification with RMSE-values

Joints Actuated	x (mm)	y (mm)	z (mm)	Tip position error (mm)	Fig. No.
Minor cannula 1, BAN 83°	0.19	0.46	0.30	0.58	Fig. 5(a-1)
Minor cannula 1, UAN 23°	0.01	0.54	0.17	0.57	Fig. 5(a-2)
Minor cannula 1, BAN 55°, UAN 20°	1.55	0.70	0.49	1.77	Fig. 5(a-3)
Minor cannula 2, BAN 76°	0.23	0.70	0.40	0.84	Fig. 5(a-4)
Minor cannula 2, UAN 28°	0.04	0.55	0.36	0.67	Fig. 5(a-5)
Minor cannula 2, BAN 48°, UAN 18°	0.07	0.19	0.12	0.24	Fig. 5(a-6)
Minor cannula 1, BAN 34°	0.07	0.76	0.07	0.77	Fig. 5(b-1)
Minor cannula 1, UAN 16°	0.06	0.40	0.34	0.53	Fig. 5(b-2)
Minor cannula 1, BAN 48°, UAN 21°	0.17	0.87	1.4	1.66	Fig. 5(b-3)
Minor cannula 2, BAN 57°	0.15	0.61	0.25	0.68	Fig. 5(b-4)
Minor cannula 2, UAN 13°	0.05	0.51	0.66	0.84	Fig. 5(b-5)
Minor cannula 2, BAN 47°, UAN 10°	0.19	0.50	0.41	0.67	Fig. 5(b-6)

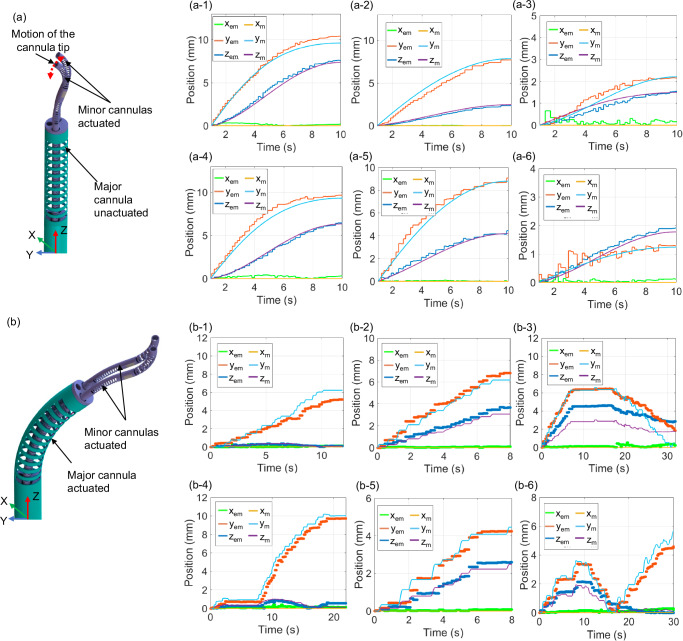
For the first six trajectories, as shown in Fig. 5(a-1)–(a-6), the major cannula is held in its home configuration, while the prismatic joints of the minor cannula are actuated to expose the minor cannulas. This is followed by the bending of the proximal and distal joints of each minor cannula. For these trajectories, the tendon stroke is applied as a sinusoidal signal. Also, the major cannula is not perfectly straight in its home configuration due to a pre-curvature induced in its UAN joint during micromachining. A pre-curvature of 3.5° is considered in the kinematic model and is measured using images of the UAN joint.

Fig. 5. Kinematic modeling verification.

a Kinematic trajectories when major cannula bending joint is unactuated: (a-1) minor cannula 1 BAN actuated, (a-2) minor cannula 1 UAN actuated, (a-3) minor cannula 1 UAN and BAN actuated, (a-4) minor cannula 2 BAN actuated, (a-5) minor cannula 2 UAN actuated, and (a-6) minor cannula 2 UAN and BAN actuated, and (b) kinematic trajectories when major cannula bending joint is actuated to 23.4°: (b-1) minor cannula 1 BAN actuated, (b-2) minor cannula 1 UAN actuated, (b-3) minor cannula 1 UAN and BAN actuated, (b-4) minor cannula 2 BAN actuated, (b-5) minor cannula 2 UAN actuated, and (b-6) minor cannula 2 UAN and BAN actuated. The x, y, and z positions shown in the plot are absolute value change in the position of the tip from its initial configuration in the respective directions. Subscripts “m” and “em” for x, y, and z represent the modeled and experimental tip position, respectively.

For the next six trajectories, as shown in Fig. 5(b-1)–(b-6), the major cannula is actuated to a desired angle. The minor cannulas are then advanced out using the prismatic motion of the joints. The minor cannula proximal and distal joints are then actuated using a joystick controller.

The sequence of all the twelve trajectories and the RMSE value from the desired and actual position measurements in the x, y, and z directions are given in Table 3. Figure 5 show the experimental (x_em, y_em, and z_em), and the modeled (x_m, y_m, and z_m) tip position changes from its initial configuration in the x, y, and z directions. For the errors in Table 3, the kinematic trajectory errors are for a single trial, but we performed six trajectories for each cannula and the average RMSE reported for each cannula is based on the average error in the six trajectories. We observe that the minor cannula position can be controlled with an average RMSE of 0.66 mm for minor cannula 1 and 0.98 mm for minor cannula 2. The errors in the actual measurements are hypothesized to be caused by machining and assembly inaccuracies within the mechanism and unmodeled coupling between the flexible joints.

The error presented in the trajectories wherein the major cannula is bent is the position error from the base frame of the robot. The model used to bend the major cannula was a data-driven model as shown in Fig. 4(c) and has an RMSE of 0.17° and thus, contributes minimally to the overall error. Furthermore, the major cannula is locked in position for the trajectories since in a clinical setting the major cannula would be first steered to a desired configuration and then locked in place, followed by advancing the minor cannulas. The initial steering of the major cannula helps to position the minor cannulas at the desired location, prior to manipulation.

Finally, the developed prototype was further tested with an OV6946 (Omnivision, Inc., USA) endoscope camera. The OD and length of the camera is 1.6 mm and 6 mm, respectively. The camera has 160000 pixels (400 pixels × 400 pixels), 30-Hz frame rate, and a 120° diagonal field of view (FOV)³⁸. We have added a video in the supplementary materials showing the operator’s viewpoint using this endoscopic camera when the steerable minor cannulas are actuated.

Discussion

The design of the robotically steerable endoscope presented in this work is a specific embodiment and the length of the joints of the cannulas can be varied based on the requirement of the procedure. The steerable minor cannula design in this work was chosen based on the requirements of an ETV procedure wherein the surgeon typically advances the tools 24.5 mm to 38.1 mm from the distal end of the trocar³⁰. Often ETV procedures are coupled with tumor biopsy or resection via endoscopic methods, particularly within the brain ventricles. Depending on the location of these deep-seated tumors (e.g., posterior thalamus, pineal region), surgeons may be forced to have two trajectories/incisions/burr holes to achieve both objectives in one surgery, or struggle with one suboptimal trajectory limited by the linear instruments and visualization of the endoscope. Nonlinear trajectories within the lateral and third ventricular space will increase the operative efficacy of endoscopic surgery with less damage to critical structures such as bilateral thalami, fornices, and other sensitive regions. The ability of the major cannula to be steered, helps in the precise placement of the steerable minor cannulas, provides an increased workspace, and can achieve nonlinear trajectories to avoid sensitive regions in the brain. Moreover, in a case where a minor change in the position of the cannulas is required, instead of retracting and inserting the device again, the steering of the major cannula can be utilized to reposition. This also reduces any titling of the major cannula at the insertion point which could potentially reduce tissue injury at the site of incision as stated by previous researchers¹⁵. Furthermore, with modifications in the length of the flexible joints, the developed robotically steerable endoscope can be adopted for other neurosurgical procedures as well. The distal joint in the minor cannula design is chosen to be compliant compared to the proximal joint, which helps to reduce the coupling in the system²⁹. For more than 70% of the neurosurgical tasks, a pilot study quantified the required distal forces for the procedure to be less than 0.3 N³⁹. Thus, we believe that the compliant distal joint can provide sufficient forces for most of the neurosurgical tasks although some tools might require a larger force for which the joint and the tendon would have to be modified to have higher stiffness. A higher stiffness joint can be achieved by changing the notch parameters (d, c, h, n) during the laser micromachining process.

The choice of the joints utilized in the design can also be modified based on the design requirements and the anatomical constraints that exist during a neurosurgical procedure. In this work, the whole-body rotation of the joints is chosen to orient the minor cannula in the required plane of bending while the in-plane bending joints allow for the cannula to form “S”-shaped curves. The combination of these joints can allow the cannula tip to be manipulated orthogonally or at an angle to the tissue³⁰. The “S”-shaped curves can help to avoid obstacles while being steered to the target location and help to ensure that the distal tip of the minor cannula is in the field of view of the camera³⁰. While the modeling presented in the work shows a method to accurately position the tips of the robotically steerable cannulas, further analysis with path planning to avoid singular configurations is beyond the scope of this study and will be considered in our future work.

In the prototype presented in this work, we have demonstrated that the robotically steerable endoscope can be remotely controlled by a Xbox 360 controller. While the control may be intuitive for some users, a learning curve may exist for a different set of users. For the device to be adopted by the medical community, further research is required to assess the ease of use of the tool and the advantages it has over the existing technology. Some prior work has been done to develop an intuitive interface for the users for such medical robotic devices⁴⁰. In our prior work⁴¹, we evaluated a joystick controlled handheld steerable neuroendoscope tool with a similar design to the steerable minor cannula in this work, against a standard rigid tool within a realistic phantom model of the brain. This was tested with a group of neurosurgery residents and fellows as well as non-clinical personnel. A decrease in the overall endoscope movement volume was observed while using the robotic tool compared to the standard rigid tool. This result suggested that using a robotically steerable tool has the potential to reduce parenchyma injuries during the procedure. Moreover, another research study also discussed the potential of this technology in the neurosurgical community with significant enthusiasm². Similar to our prior work, in our future work, we will evaluate the proposed device in a preclinical setting with a group of neurosurgery residents and fellows to test the advantages and limitations of the robotically steerable cannulas in comparison to the current standard procedures.

Furthermore, we aim to attach surgical tools at the ends of the steerable minor cannulas in future. Some of our prior works have shown successful integration of end-effectors on similarly designed prototypes as the steerable minor cannula presented in this work. For example, a tendon-driven grasper tool has been attached to a steerable joint³⁵, in⁴² we show a bipolar cauterization tool integrated at the tip of the steerable joint for applications in a pediatric hydrocephalus procedure, and a MEMS-based force sensor has also been integrated on a steerable probe for tumor margin identification⁴³. The steerable minor cannula presented in this work has a hollow lumen to pass a tendon or electrical wiring, which may be required for the end-effector tools. Also, the current actuation system has the capacity for another motor for each minor cannula, which can be used to accommodate different steerable cannula designs or control tendon-driven tooling.

However, some limitations exist in the work presented in this paper. Upon integration of end-effector tools at the distal tips of the robotically steerable minor cannulas, the models presented in the current work would need to be modified. We do not anticipate the kinematic models presented in the current work to be affected by the integration of the tools. However, the joint static models would be impacted in two ways: 1) the tendon elongation term would be affected by the increased stiffness due to the tool’s presence, and 2) the effects from actuating the tools. The effect of the former can be incorporated by using the combined stiffness of the tube and the tools body (wiring, tubing, additional tendon). The latter can be compensated for by selecting notch parameters that result in sufficiently stiff joints to reduce the impact of tool actuation or by routing tendons along the neutral axis of the joints. Finally, the prototype would also require a quick connect mechanism to replace the steerable minor cannulas if required in the neurosurgical procedure.

Methods

Joint Kinematics and Statics Models

In this subsection, we derive the relationship between the tendon stroke and the desired joint angle for the proximal bending, distal bending, and rotation joints of the minor cannulas. The derived joint static models relating the deflection to tendon stroke, L^t, consist of a kinematic term, L^kin, and tendon elongation term, L^el,^29,34,36,37 and the tendon stroke is given by:

$${\underbrace{L^t\left(\theta \right)}}_{\mathrm{Tendon}\mathrm{Stroke}}={\underbrace{L^{kin}\left(\theta \right)}}_{\mathrm{Kinematic}\mathrm{Term}}+{\underbrace{L^{el}\left(\theta \right)}}_{\mathrm{Elongation}\mathrm{Term}}$$ 6

The kinematic and tendon elongation relationships are derived below assuming the deformation occurs in a constant curvature arc for each segment.

Minor Cannula Proximal Joint

The proximal joint of the minor cannula comprises a UAN pattern and the kinematic term, L^kin(θ_p), for the deflection of the proximal joint, θ_p, and is given by:

$$L^{kin}\left({\theta }_p\right)=y_{p,t}{\theta }_p$$ 7

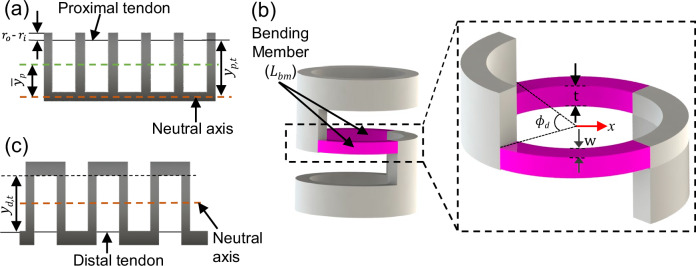
where y_p,t is the moment arm of the proximal tendon shown in Fig. 6(a) and is given by:

$$y_{p,t}={ȳ}_p+r_i-r_t={\underbrace{\frac{4\sin \left(\frac{{\varphi }_p}{2}\right)\left(r_o^3-r_i^3\right)}{3{\varphi }_p\left(r_o^2-r_i^2\right)}}}_{\mathrm{Neutral}\mathrm{Axis}\mathrm{Location}}+r_i-r_t$$ 8

where ${ȳ}_p$ is the neutral axis location for a UAN joint. Furthermore, since significant tendon tension is required to deflect the joint, tendon elongation must be considered. The tendon elongation term for the proximal joint is given by:

$$L^{el}\left({\theta }_p\right)=\frac{E{I}_p{L}_{p,0}}{y_{p,t}{E}_{p,t}\pi r_{p,t}^2{l}_p}{\theta }_p$$ 9

where E is Young’s modulus of the NiTi tube, I_p is the second moment of area of the notched cross-section of the proximal joint, E_p,t is Young’s modulus of the proximal tendon, r_p,t is the radius of the proximal tendon, l_p is the length of the proximal joint, and L_p,0 is the length of the proximal tendon when unloaded. The second moment of area of the notched cross-section of the proximal joint about the neutral axis is given by:

$$I_p=\frac{\left(r_o^4-r_i^4\right)\left({\varphi }_p+\sin \left({\varphi }_p\right)\right)}{8}-\frac{8\sin {\left(\frac{{\varphi }_p}{2}\right)}^2{\left(r_o^3-r_i^3\right)}^2}{9{\varphi }_p\left(r_o^2-r_i^2\right)}$$ 10

Fig. 6. Schematic of the steerable minor cannula notch patterns.

a UAN pattern, (b) bending member of the BAN joint, and (c) BAN pattern.

This model is experimentally validated in the ‘Joint Model Verification’ subsection in the ‘Results’ section.

Minor Cannula Distal Joint

For the distal joint comprising a BAN pattern, the bending member is primarily the member between the two consecutive notches as shown in Fig. 6(b). The distal joint comprises of n notches resulting in (n − 1) bending members. The second moment of area along the length of the bending member is given by⁴²:

$$I_d=\frac{t^{3}w\left(x\right)}{12}$$ 11

where, t, is the thickness of the bending member and w(x) is the width of the bending member given by:

$$w\left(x\right)=\sqrt{r_o^2-x^2}-\sqrt{r_i^2-x^2}$$ 12

where, x, is the length along the beam from the center of the bending member. The kinematic component of bending for the distal joint, L^kin(θ_d), as derived in²⁹ is given by:

$$L^{kin}\left({\theta }_d\right)=n{y}_{d,t}\sin \left(\frac{{\theta }_d}{n}\right),y_{d,t}=d-r_o+r_i-r_t$$ 13

where y_d,t is the moment arm of the tendon as shown in Fig. 6(c) and θ_d is the deflection of the distal joint. The deflection of a single bending member is related to the total deflection of the joint by⁴²:

$${\theta }_d=\left(\frac{n-1}{2}\right){\theta }_{bm}$$ 14

where θ_bm is the deflection of a single bending member. Assuming small deflections of the individual bending members, the deflection of a single member is given by:

$${\theta }_{bm}=\frac{2{\theta }_d}{n-1}=\frac{F_d{y}_{d,t}}{E}{\int }_{-\frac{L_{bm}}{2}}^{\frac{L_{bm}}{2}}\frac{dx}{I_d\left(x\right)}$$ 15

where F_d is the tension of the distal joint tendon and L_bm is the length of the bending member given by:

$$L_{bm}=2\left(d-r_0\right)$$ 16

As a result, the tendon elongation that occurs when achieving a desired bending angle is given by:

$$L^{el}\left({\theta }_d\right)=\frac{L_{d,0}E{\theta }_d}{y_{d,t}\left(\frac{n-1}{2}\right){\int }_{-\frac{L_{bm}}{2}}^{\frac{L_{bm}}{2}}\frac{dx}{I_d\left(x\right)}{E}_{d,t}\pi r_{d,t}^2}$$ 17

where L_d,0 is the length of the distal tendon when unloaded, r_d,t is the radius of the distal tendon, and E_d,t is the Young’s modulus of the distal tendon. This model is experimentally validated in the ‘Joint Model Verification’ subsection in the ‘Results’ section.

Minor Cannula Rotation Joint

For the rotation motion of the minor cannula, we omit the tendon elongation term. This is because the UHMPWE tendon employed in this joint exhibits minimal elongation at lower tendon tension. The kinematic term can be derived as follows:

$$L^{kin}\left({\theta }_r\right)=r{\theta }_r$$ 18

where, r, is the combined radius of the steel tube with the PET heat shrink and the diameter of the UHMWPE tendon and θ_r is the rotation angle of the joint. The tendon slack causes a deadband in the system. Thus, a backlash model is necessary to relate the tendon stroke to the rotation angle of the joint. The backlash model has the deadband term that equals the tendon slack (determined experimentally) and the slope term equal to the kinematic term given in Eq. (18).

Kinematic Modeling

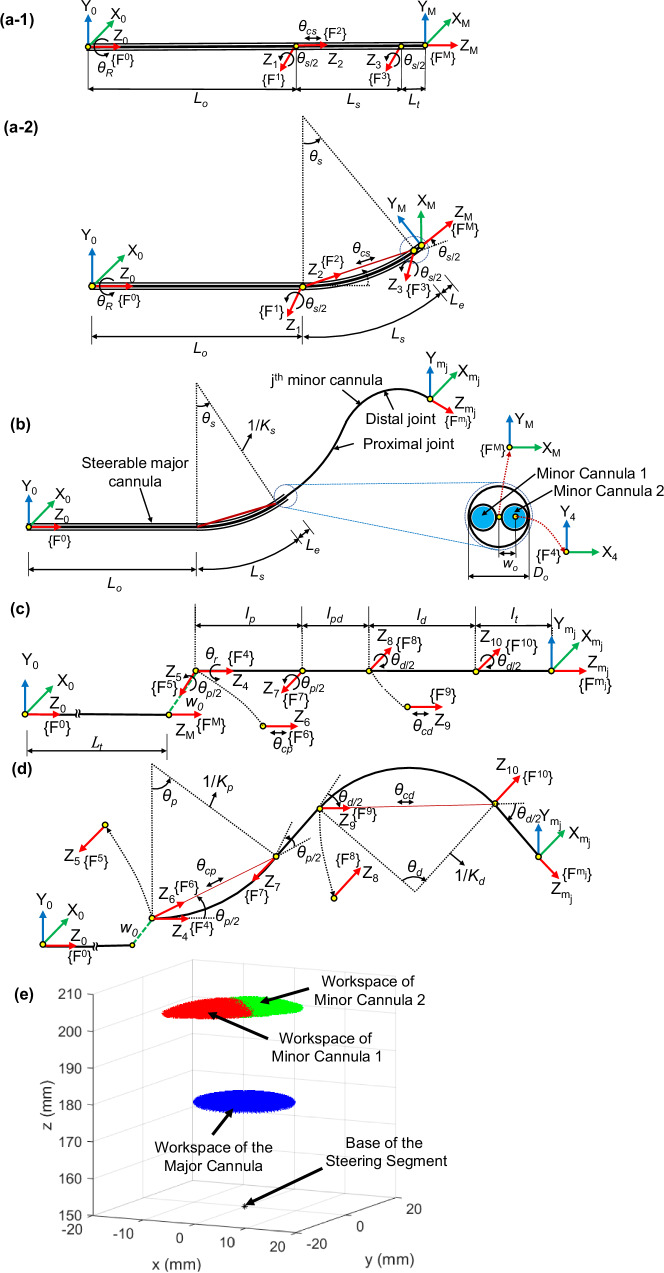
We develop the joint kinematics model to map the joint space coordinates to the Cartesian space position and orientation of the end tip of the robotic system. The kinematics of the system are derived in two states: (A) when the minor cannulas are fully retracted and (B) when the minor cannulas are advanced to expose the steerable minor cannulas. All the frames are defined with respect to the base frame, {F⁰}, of the robot, located at the base of the major cannula, as shown in Fig. 7.

Fig. 7. Schematic of the steerable major and minor cannulas with coordinate frames attached to the joints.

a-1 Schematic of the steerable major cannula in unactuated state, (a-2) schematic of steerable major cannula in actuated state, (b) schematic of the steerable major cannula with the j^th minor cannula and cross-sectional view of the major cannula’s end tip showing the two minor cannulas, (c) schematic of the j^th unactuated minor cannula showing the coordinate frames $\left\{{\mathrm{F}}^4\right\}-\left\{{\mathrm{F}}^{m_j}\right\}$, (d) each bending joint modeled as a revolute-prismatic-revolute (RPR) joint (frames {F⁵}, {F⁶}, and {F⁷} correspond to the proximal bending joint and frames {F⁸}, {F⁹}, and {F¹⁰} correspond to the distal bending joint), and (e) the workspace of the steerable major cannula (shown in blue). The workspace of the minor cannulas for 45° rotation and 10° bending of the major cannula is shown in red and green regions.

Minor Cannulas Fully Retracted

When the minor cannulas are fully retracted, the major cannula can be steered and the origin of the tool-frame of the robot, {F^M}, coincides with the center of the tip of the distal end of the major cannula. The major cannula has two joints: a rotation joint (θ_R) and a bending joint (θ_s), modeled as a revolute-prismatic-revolute (RPR) joint³⁶ with parameters θ_s/2, θ_cs, and θ_s/2. The coordinate frames attached to the robotic system are shown in Fig. 7(a-1)-(a-2), when unactuated and actuated, respectively. The joints of the robotically steerable major cannula, and their respective coordinate frames are defined as follows:

• Joint 1: Revolute joint with rotation θ_R about the Z₀-axis in the {F⁰} frame

• Joint 2: Revolute joint with rotation θ_s/2 about the Z₁-axis in the {F¹} frame

• Joint 3: Prismatic joint with translation θ_cs along the Z₂-axis in the {F²} frame

• Joint 4: Revolute joint with rotation θ_s/2 about the Z₃-axis in the {F³} frame

The length of the non-steerable segment of the major cannula is L₀, followed by a steerable segment of length, L_s, and a short segment at the distal end of length, L_e. The total length of the major cannula is given by L_t, where L_t = L₀ + L_s + L_e. The prismatic joint actuation of the bending joint, θ_cs, is determined by the chord length connecting the ends of the curve and is given by:

$${\theta }_{cs}=\frac{2L_s}{{\theta }_s}\sin \left({\theta }_{s/2}\right)-L_s$$ 19

The twist coordinate, $\xi \in {\mathbb{R}}^6$, for a revolute joint is given by ξ = [−ω × q, ω]^T and for a prismatic joint is given by ξ = [ν, 0]^T, where ν is the velocity of a point attached to the prismatic joint moving with unit velocity. The unit angular velocity, ω, for each revolute joint and the unit velocity, ν, for each prismatic joint, with respect to the base frame, {F⁰}, is given by:

$${\omega }_1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\omega }_2=\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\nu }_3=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\omega }_4=\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\in {\mathbb{R}}^3$$ 20

where the subscript in ω_i or ν_i corresponds to Joint i. The position vector, q, of a point on the axis of rotation relative to the base frame, {F⁰}, for each revolute joint is given by:

$$q_1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];q_2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill L_o\hfill \end{array}\right];q_4=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill L_o+L_s\hfill \end{array}\right]\in {\mathbb{R}}^3$$ 21

The resultant twist coordinates are given by⁴⁴:

$${\xi }_1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\xi }_2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -L_o\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_3=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_4=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -L_o-L_s\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\in {\mathbb{R}}^6$$ 22

The twist of the i^th joint, ${\widehat{\xi }}_i\in se\left(3\right)$, is given by:

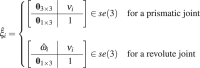23

where ${\widehat{\omega }}_i\in so\left(3\right)$ is the skew-symmetric representation of ${\omega }_i\in {\mathbb{R}}^3$. Through the twists, the forward kinematics of the major cannula can be determined through the product of exponentials⁴⁴ and is given by:

24

where ${\mathbf{R}}_M^0$ and ${\left[{\tilde{p}}_x,{\tilde{p}}_y,{\tilde{p}}_z\right]}^T$ are the orientation and position of the tool-frame, given in the base frame, {F⁰}, respectively. The homogeneous transformation matrix relating the tool-frame, {F^M}, to the base frame, {F⁰}, when the major cannula is unactuated, ${\mathbf{g}}_M^0\left(0\right)$, is given by:

$${\mathbf{g}}_M^0\left(0\right)=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill L_t\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\in SE\left(3\right)$$ 25

Minor Cannulas Fully Advanced

The major cannula has two inner channels for the minor cannulas to bend along with the major cannula. When the major cannula is steered to its desired configuration, the prismatic joints at the base of the minor cannulas can be advanced to expose the steerable section of the minor cannulas. When the minor cannulas are fully advanced, the origin of the tool-frame, {${\mathrm{F}}^{m_1}$}, is located at the tip of minor cannula 1, and the origin of the tool-frame, {${\mathrm{F}}^{m_2}$}, is located at the tip of minor cannula 2. Figure 7(b) shows the schematic of the steerable major cannula with the j^th (j = 1, 2) minor cannula advanced out. For conciseness, we will present the general analysis for a minor cannula without the j^th minor cannula labeling in this subsection.

The individual minor cannula has four joints: prismatic (θ_pris), rotation (θ_r), proximal bending (modeled as an RPR joint: θ_p/2, θ_cp, θ_p/2), and distal bending (modeled as an RPR joint: θ_d/2, θ_cd, θ_d/2) joints. The prismatic joint is only used to advance and retract the minor cannula and hence is omitted from the kinematic modeling. The base of the j^th minor cannula is at an offset ± w₀ in the x-direction from the center of the base frame, {F⁰}. The remaining joints and the coordinate frames {F⁴}–{${\mathrm{F}}^{m_j}$}, attached to the minor cannula as shown in Fig. 7(c), are defined as follows:

• Joint 5: Revolute joint with rotation θ_r about the Z₄-axis in the {F⁴} frame

• Joint 6: Revolute joint with rotation θ_p/2 about the Z₅-axis in the {F⁵} frame

• Joint 7: Prismatic joint with translation θ_cp along the Z₆-axis in the {F⁶} frame

• Joint 8: Revolute joint with rotation θ_p/2 about the Z₇-axis in the {F⁷} frame

• Joint 9: Revolute joint with rotation θ_d/2 about the Z₈-axis in the {F⁸} frame

• Joint 10: Prismatic joint with translation θ_cd along the Z₉-axis in the {F⁹} frame

• Joint 11: Revolute joint with rotation θ_d/2 about the Z₁₀-axis in the {F¹⁰} frame

The link lengths of the minor cannula are shown in Fig. 7(c), and we assume that the proximal and distal bending joints bend with constant curvatures, respectively, and θ_cp and θ_cd are given by:

$${\theta }_{cp}=\frac{2l_p}{{\theta }_p}\sin \left({\theta }_{p/2}\right)-l_p$$ 26

$${\theta }_{cd}=\frac{2l_d}{{\theta }_d}\sin \left({\theta }_{d/2}\right)-l_d$$ 27

The joint parameters for the steerable section on the minor cannulas can be defined as Θ_minor ≜ (θ_r, θ_p/2, θ_cp, θ_p/2, θ_d/2, θ_cd, θ_d/2). The unit angular velocity, ω, for each revolute joint and the unit velocity, ν, for each prismatic joint, with respect to the base frame, {F⁰}, is given by:

$$\begin{array}{c}{\omega }_5=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\omega }_6=\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\nu }_7=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\omega }_8=\left[\begin{array}{c}\hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\omega }_9=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];\hfill \\ {\nu }_{10}=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\omega }_{11}=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\in {\mathbb{R}}^3\hfill \end{array}$$ 28

where the subscript in ω_i or ν_i corresponds to Joint i. The position vector, q, of a point on the axis of rotation relative to the base frame, {F⁰}, for each revolute joint is given by:

$$\begin{array}{c}{q}_5=\left[\begin{array}{c}\hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill L_t\hfill \end{array}\right];q_6=\left[\begin{array}{c}\hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill L_t\hfill \end{array}\right];q_8=\left[\begin{array}{c}\hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill L_t+l_p\hfill \end{array}\right];q_9=\left[\begin{array}{c}\hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill L_t+l_p+l_{pd}\hfill \end{array}\right];\hfill \\ q_{11}=\left[\begin{array}{c}\hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill L_t+l_p+l_{pd}+l_d\hfill \end{array}\right]\in {\mathbb{R}}^3\hfill \end{array}$$ 29

where w₀ denotes the offset of the j^th minor cannula from the center of the base frame, {F⁰}, and can be negative (if the j^th minor cannula is along the negative X₀ axis in its home configuration) or positive (if the j^th minor cannula is along the positive X₀ axis in its home configuration). Similar to Eq. (22), the resultant twist coordinates are given by:

$${\xi }_5^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill w_0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\xi }_6^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -L_t\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_7^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_8^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -l_p-L_t\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_9^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill l_p+l_{pd}+L_t\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_{10}^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_{11}^1=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill l_p+l_{pd}+l_d+L_t\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\in {\mathbb{R}}^6$$ 30

$${\xi }_5^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -w_0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right];{\xi }_6^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -L_t\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_7^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_8^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -l_p-L_t\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_9^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill l_p+l_{pd}+L_t\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_{10}^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right];{\xi }_{11}^2=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill l_p+l_{pd}+l_d+L_t\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\in {\mathbb{R}}^6$$ 31

where the superscript in ξ^j refers to the j^th minor cannula. The homogeneous transformation matrix relating {${\mathrm{F}}^{m_j}$} to {F⁰} for each minor cannula is given by:

$${\mathbf{g}}_{m_1}^0\left(0\right)=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -w_0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill L_t+l_p+l_{pd}+l_d+l_t\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\in SE\left(3\right)$$ 32

$${\mathbf{g}}_{m_2}^0\left(0\right)=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill w_0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill L_t+l_p+l_{pd}+l_d+l_t\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\in SE\left(3\right)$$ 33

where {${\mathrm{F}}^{m_j}$} refers to the end-effector frame of the j^th minor cannula. The forward kinematics of the j^th (j = 1, 2) minor cannula with respect to the base frame, {F⁰}, is given by:

34

where ${\mathbf{R}}_{m_j}^0$ and ${\left[p_{x_j},p_{y_j},p_{z_j}\right]}^T$ are the orientation and position of the tip of the j^th minor cannula with respect to the base frame, {F⁰}, respectively.

The developed prototype has been tested to approximately bend up to the following angles: 30° bending of the steerable major cannula, 30° bending of the proximal joints of the steerable minor cannula, and 90° bending of the distal joints of the steerable minor cannula. Furthermore, approximately ±180° rotation motion of the steerable minor cannulas can be achieved. We believe that this range of motion for the steerable major cannula is sufficient for neurosurgical procedures wherein a confined workspace in the brain exists. The purpose of the steerable major cannula is to allow for minor repositioning, if necessary, during the procedure. For a range of ±180° rotation of the major cannula and up to 30° bending of the major cannula, the simulated workspace of the major cannula is shown in blue in Fig. 7(e). Furthermore, for a 45° rotation angle and 10° bending angle of the major cannula, the workspace of the two minor cannulas with the proximal joints bending up to 30°, distal joints bending up to 90°, and rotation of the minor cannulas in the range of ±180° are shown. The workspace of the two minor cannulas (red and green regions) overlap, which shows the capability to achieve bimanual triangulation, a desired feature for several endoscopic surgeries^45,46.

Author contributions

Conceptualization: R.Q., N.M., J.P.D. Methodology: R.Q., N.M., T.A.B., J.P.D. Experiments: N.M., R.Q., T.A.B. Visualization: N.M., R.Q., T.A.B., J.P.D. Funding acquisition: K.H., J.P.D. Supervision: J.P.D. Writing – original draft: N.M., R.Q., T.A.B. Writing – review and editing: N.M., R.Q., T.A.B., K.H., J.P.D.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Competing interests

Georgia Tech Research Corporation and Emory University have submitted a U.S. Provisional Application for Patent titled ‘Systems and Methods for Teleoperated Control of a Robotic Endoscopic System’. J.P.D., R.Q., N.M., and K.H. are inventors on the provisional patent application (Application No. 63/674,030).

Supplementary information

The online version contains supplementary material available at 10.1038/s44182-024-00017-w.