Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2025 Jan 7;15:1081. doi: 10.1038/s41598-024-82962-y

Hotspot analysis of COVID-19 infection in Tokyo based on influx patterns

Yu Kimura 1,✉, Tatsunori Seki 1, Keisuke Chujo 1, Toshiki Murata 1,✉, Tomoaki Sakurai 1, Satoshi Miyata 1, Hiroyasu Inoue 2,3, Nobuyasu Ito 3
PMCID: PMC11707207  PMID: 39774000

Abstract

We analyse the relationship between population influx and the effective reproduction number in the 23 wards of Tokyo during the COVID-19 pandemic to estimate hotspots of infection. We identify some patterns of population influx via factor analysis and estimate specific areas as infection-related hotspots by focusing on influx patterns that are highly correlated with the effective reproduction number. As a result, several influx patterns are assumed to be directly related to the subsequent spread of the infection. This analytical method has the potential to detect unknown hotspots related to pandemics in the future.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-82962-y.

Subject terms: Diseases, Engineering, Psychology and behaviour

Introduction

Several years have passed since Coronavirus disease 2019, hereafter referred to as COVID-19, spread worldwide in 2019. Each country has taken measures to prevent the spread of infection, such as travel and commercial restrictions, which have been studied from the viewpoint of their effectiveness1–4. According to a paper by Tian et al.5, the travel ban in Wuhan in January 2020 delayed the arrival of the disease in other cities in China. According to a paper by Yabe et al.6, the state of emergency declared in April 2020 in Tokyo decreased people’s movement by approximately 50%, which was correlated with a decrease in the effective reproduction number. These measures have effectively slowed the spread of the infection and caused it to subside, but they have also had a considerable impact on people’s lives by broadly restricting population movement. It is said that there should have been a better way to restrict only relevant population movement to the infection spread and keep irrelevant ones. Therefore, we study methods to decompose population movement into patterns and identify which patterns of population movement are correlated with the spread of infection.

Various studies have attempted to elucidate the relationship between population movement and the spread of infectious diseases by identifying movement patterns via transportation data7,8 or people’s location data9–11. In the case of COVID-19, some studies reported that visiting specific places was associated with a high risk of infection12–17. In fact, data on population movement are assumed to be useful in preventing COVID-19 infection18. Some studies have used individual-level movement data via GPS19–24; thus, Ito25 developed a disease spread simulation model and a GPS data miner, and others have used aggregated location data obtained from mobile cell tower logs26–28. Although datasets for specific places or individual movements are useful to evaluate individual infection risk, aggregated location data have advantages regarding the number of people covered and preserving user’s privacy, as well as providing information about social communities18,19. Nakanishi et al.29 observed night-time population data from Tokyo metropolitan areas and reported an increase in the effective reproduction number three weeks after the night-time population increased. The relationship between the increase or decrease in the number of people and the risk of infection may differ between residential and downtown areas; thus, the effectiveness in downtown areas may not be equally applicable to other areas. In our previous study30, we used the population influx instead of the night-time population to assess the correlations between the populations in residential areas, downtown areas and business districts and the effective reproduction number several weeks later. As a result, a correlation was identified in downtown and business districts, whereas no correlation was identified in residential areas.

There may be specific places that are associated with COVID-19 infection risks, other than wide areas such as downtown areas and business districts, as reported in previous studies12–17. However, previous studies that used aggregated location data26–30 have targeted only some of the areas; thus, they may have missed other areas with a high risk of infection. Furthermore, owing to the disadvantage of the aggregated location data, it is unclear whether the increase or decrease in the aggregated number of the data means that more or less people are visiting the high-risk places that are reported by previous studies, such as closed workplaces15 or karaoke shops17, or other places within the aggregated area. Therefore, the aim of this study was to identify what kind of places would be hotspots for COVID-19 and to determine the areas containing those places at a narrower level than that in our previous study30.

To achieve this purpose, it is not sufficient to simply look at the aggregated macro population movement data, for the part of the population movement for visiting a specific kind of place is merely a part of the population movement similar to any other movement for visiting other places in that area. In other words, it is necessary to estimate the hidden amount of the specific part of the population movement from the aggregated data, which can be obtained and utilized. To estimate the unobserved background variables from the data observed, factor analysis is the commonly used method. Thus, we suggest an analysis method to decompose the complex population movement into patterns (i.e., population movements that seem to occur for similar purposes) by factor analysis and investigate the risk of infection in associated areas, aiming to identify unknown areas as hotspots. We also report the results of applying the proposed method to all 23 wards of Tokyo for several periods of infection spread. The details are explained in the Results and Discussion.

Results and discussion

Cases in the 3rd wave

Details of each factor

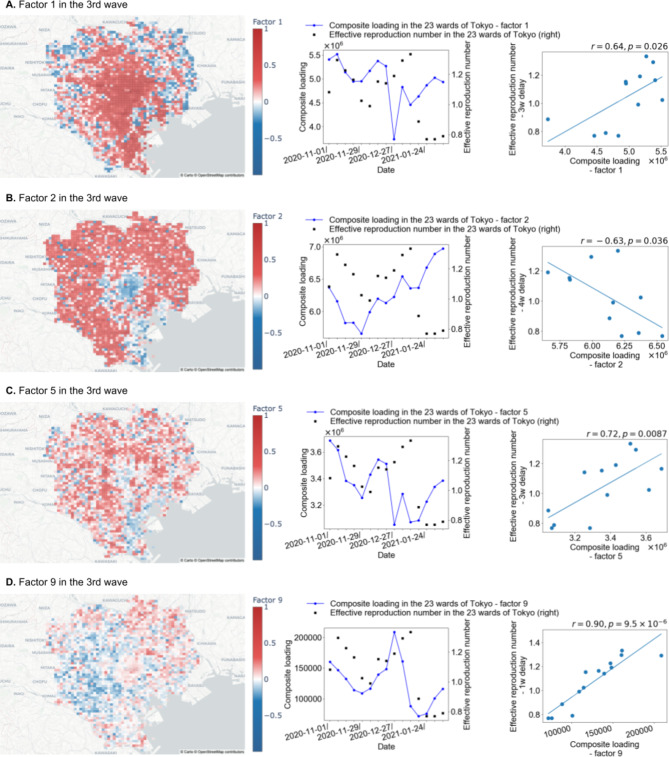
In this section, we show some of the factors, which describe the patterns as normalized vectors, acquired by decomposing the population movement data. The population movement is described by the combination of these factors and the weighting coefficient, which are referred to as “composite loading” hereafter. For the 3rd wave, the factor with extremely high absolute values of correlation coefficients to the effective reproduction number, which is a metric calculated by the ratio of the latest number of new cases and the previous one31, is Factor 9, and the factors that are presumed to represent typical outing activities in the 23 wards of Tokyo, which are Factors 1, 2 and 5, are explained in detail.

Figure 1a displays a map of the loadings of Factor 1, which are values in a vector of Factor 1, for each mesh squared area. The meshes with a factor loading of high absolute value are strongly related to the pattern of population movement corresponding to Factor 1. The meshes with high factor loadings are concentrated near the business districts, indicating that Factor 1 primarily represents people moving towards business districts. In terms of the correlation coefficient with the composite loading, a value of 0.64 is observed for Factor 1 with a 3-week delay, which is the highest absolute value among the different delays. This means that the increase in a pattern of population movement corresponding to Factor 1 has a relatively strong relationship with the spread of infection 3 weeks later. The correlation coefficient between the composite loading and the effective reproduction number, including the time delay for Factors 1 to 10, is shown in Table 1.

Fig. 1.

Fig. 1

Open in a new tab

Maps, graphs, and scatter plots for Factors 1, 2, 5, and 9 for the 3rd wave of infection. The left figures in items A, B, C and D are maps plotting the factor loadings for each mesh for Factors 1, 2, 5, and 9 in the 3rd wave. For each factor, the factor loadings represent the strength of involvement in the incoming population. In other words, the influx to meshes with high positive factor loadings is suggested to be greater than that to other meshes. The middle figures in items A, B, C and D are graphs that show the time series fluctuations of the effective reproduction number in the 23 wards of Tokyo over the period of the 3rd wave and the composite loading for Factors 1, 2, 5, and 9 in the 3rd wave. The right figures in items A, B, C and D are scatter diagrams plotting the effective reproduction number of the 23 wards of Tokyo in the 3rd wave and the composite loading for Factors 1, 2, 5, and 9 in the 3rd wave. r and p are the correlation coefficient and p value, respectively, between the effective reproduction number and the composite loading. Each value of p is less than 0.05; thus, their correlations are assumed to be significant. These maps are created using the Python library ‘Plotly’ version 5.9.0 (https://plotly.com/). The base map is from OpenStreetMap (https://www.openstreetmap.org/), which is available under the Open Data Commons Open Database Licence. The map style is from CARTO (https://carto.com/), which is available under the Creative Commons Attribution 4.0 Licence.

Table 1.

Correlation coefficient table of the composite loading and the effective reproduction number (without a time lag and with a 1- to 4-week lag) in the 3rd wave. p is the p value.

Factor Delay
No delay 1 week 2 weeks 3 weeks 4 weeks
1

-0.027

(p = 0.92)

0.15

(p = 0.60)

0.19

(p = 0.52)

0.64

(p = 0.026)

0.57

(p = 0.067)
2

-0.53

(p = 0.044)

-0.32

(p = 0.26)

-0.42

(p = 0.15)

-0.49

(p = 0.11)

-0.63

(p = 0.036)
3

-0.36

(p = 0.19)

-0.079

(p = 0.79)

-0.37

(p = 0.22)

-0.20

(p = 0.54)

-0.21

(p = 0.54)
4

0.18

(p = 0.53)

0.39

(p = 0.17)

0.36

(p = 0.22)

0.46

(p = 0.14)

0.43

(p = 0.19)
5

0.095

(p = 0.74)

0.49

(p = 0.077)

0.53

(p = 0.063)

0.72

(p = 0.0087)

0.45

(p = 0.16)
6

0.092

(p = 0.75)

0.33

(p = 0.24)

0.15

(p = 0.63)

-0.25

(p = 0.43)

-0.28

(p = 0.40)
7

0.57

(p = 0.025)

0.30

(p = 0.30)

-0.24

(p = 0.42)

-0.70

(p = 0.011)

-0.80

(p = 0.0032)
8

0.057

(p = 0.84)

-0.020

(p = 0.95)

-0.30

(p = 0.32)

-0.64

(p = 0.024)

-0.72

(p = 0.013)
9

0.53

(p = 0.043)

0.90

(p = 9.5 × 10–6)

0.76

(p = 0.0025)

0.13

(p = 0.68)

-0.41

(p = 0.21)
10

-0.60

(p = 0.018)

-0.65

(p = 0.012)

-0.32

(p = 0.28)

-0.18

(p = 0.58)

0.057

(p = 0.87)
Open in a new tab

Figure 1b presents the map plotting the loadings of Factor 2 for each mesh. The meshes with high factor loadings are distributed close to residential areas, suggesting that Factor 2 represents movement towards residential areas. Factor 2 has a correlation coefficient of -0.63 with the composite loading for a 4-week delay, the highest absolute value among the different delays. If the correlation is negative, the effective reproduction number tends to decrease as population movement increases.

Figure 1c shows the map plotting the loadings of Factor 5 for each mesh. The meshes with high factor loadings are centred on the downtown areas, indicating that Factor 5 represents movement towards downtown areas. Factor 5 has a correlation coefficient of 0.72 with the composite loading for a 3-week delay, which is the highest absolute value among the different delays.

The map plotting the loadings of Factor 9 for each mesh is shown in Fig. 1d. For Factor 9, the correlation coefficient with the composite loading is 0.90 for a 1-week delay, which is an extremely high value. The contribution rate of Factor 9 is 0.016, which means that Factor 9 represents a minor pattern of movement to specific meshes with high factor loading values.

Discussion of the case for the 3rd wave

The composite loading value for Factor 1 represents moving to business districts, whereas the value for Factor 5 represents moving to downtown areas. Slightly high correlations are observed between the composite loadings for these factors and the effective reproduction number, which is delayed by 3 weeks. This result is consistent with the data from previous research29,30. As discussed in the Hotspot Estimation section in the Data and Methods, 3 weeks is assumed to be a long time compared with the incubation period of COVID-19, as reported in some studies32–34, even considering the number of days for a positive test after the onset of symptoms. Thus, moving to areas with high factor loadings on Factors 1 and 5 is assumed to have an indirect effect on the subsequent spread of the infection.

In addition, Factor 2 represents moving to residential areas, and the composite loading value for Factor 2 showed a negative correlation with the effective reproduction number. The absolute value of the correlation with the effective reproduction number is lower in residential areas than in downtown areas and business districts. Because the correlation is negative, a greater transfer volume to residential areas corresponds to a lower effective reproduction number for this factor. Therefore, moving to residential areas may not spread COVID-19 infection.

Finally, the composite loading value for Factor 9 represents movement to specific areas, and an extremely high correlation is observed with the effective reproduction number delayed by 1 week. Moving to meshes with high loadings for Factor 9 is assumed to be strongly associated with COVID-19 infection. In other words, the meshes are presumed to be hotspots. Because the time delay is shorter than the 3-week delays in the cases of downtown areas and business districts and is similar to the incubation period for COVID-19 infection, as estimated by previous studies32–34, areas with high factor loadings on Factor 9 are assumed to be more directly related to the subsequent spread of the infection.

Cases for the 4th to 7th waves

Details of each key factor

As described in the “hotspot estimation” section, hotspots in this paper are defined by the factor with the correlation coefficient with the highest absolute value among the factors for which the maximum correlation coefficient is observed in the case of a delay of 2 or fewer weeks. Therefore, we discuss only that factor for each wave of infection.

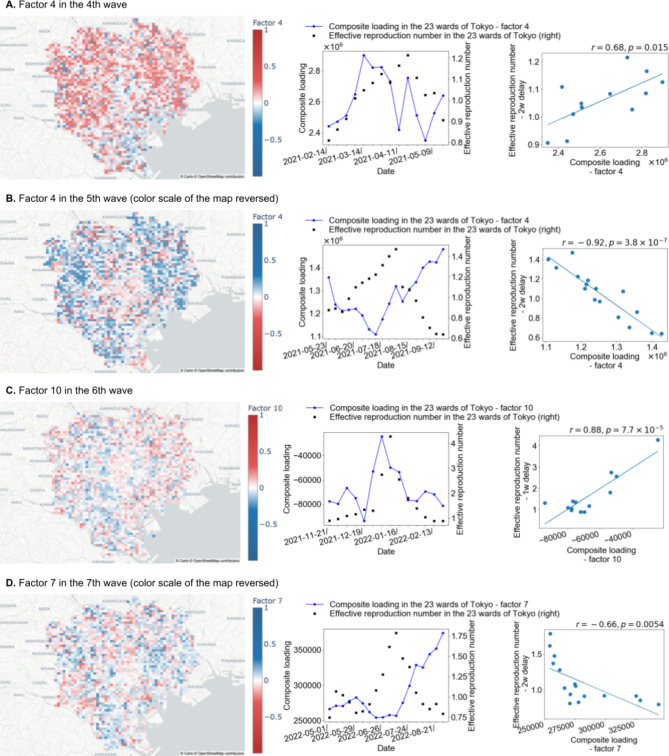
In the 4th wave, the correlation coefficient with the composite loading for Factor 4 is 0.68 when the effective reproduction number is delayed by 2 weeks (Fig. 2a). Additionally, the factor contribution rate of Factor 4 in the 4th wave is 0.050.

Fig. 2.

Fig. 2

Open in a new tab

Maps, graphs, and scatter plots for Factor 4 in the 4th wave, Factor 4 in the 5th wave, Factor 10 in the 6th wave, and Factor 7 in the 7th wave. The left figures in items A, B, C and D are maps plotting the factor loadings for each mesh for Factor 4 in the 4th wave, Factor 4 in the 5th wave, Factor 10 in the 6th wave, and Factor 7 in the 7th wave. For each factor, the factor loadings represent the strength of involvement in the incoming population. In other words, the influx to meshes with high positive factor loadings is suggested to be greater than that to other meshes. Note that the colour bars are reversed for Factor 4 in the 4th wave and Factor 10 in the 6th wave. The middle figures in items A, B, C and D are graphs that show the time series fluctuations of the effective reproduction number in the 23 wards of Tokyo over the periods of the 4th, 5th, 6th and 7th waves and the composite loading for Factor 4 in the 4th wave, Factor 4 in the 5th wave, Factor 10 in the 6th wave, and Factor 7 in the 7th wave. The right figures in items A, B, C and D are scatter diagrams plotting the effective reproduction number of the 23 wards of Tokyo in the 4th, 5th, 6th and 7th waves and the composite loading for Factor 4 in the 4th wave, Factor 4 in the 5th wave, Factor 10 in the 6th wave, and Factor 7 in the 7th wave. r and p are the correlation coefficient and p value, respectively, between the effective reproduction number and the composite loading. Each value of p is less than 0.05; thus, their correlations are assumed to be significant. These maps are created using the Python library ‘Plotly’ version 5.9.0 (https://plotly.com/). The base map is from OpenStreetMap (https://www.openstreetmap.org/), which is available under the Open Data Commons Open Database Licence. The map style is from CARTO (https://carto.com/), which is available under the Creative Commons Attribution 4.0 Licence.

In the 5th wave, Factor 4 has a correlation coefficient of -0.92 with the composite loading when the effective reproduction number is delayed by 2 weeks (Fig. 2b). As discussed in the Hotspot Estimation section in the Data and Methods, since the correlation coefficient of Factor 4 is negative, the meshes with negative and high absolute values of factor loading are considered hotspots. The factor contribution rate of Factor 4 in the 5th wave is 0.048.

In the 6th wave, Factor 10 has a correlation coefficient of 0.88 with the composite loading when the effective reproduction number is delayed by 1 week (Fig. 2c). Additionally, the factor contribution rate of Factor 10 in the 6th wave is 0.013.

For the 7th wave, a correlation coefficient of -0.66 with the composite loading for Factor 7 is observed when the effective reproduction number is delayed by 2 weeks (Fig. 2d). Because the correlation is negative, the map is shown with the colour scale of factor loading reversed. Furthermore, the factor contribution rate of Factor 7 in the 7th wave is 0.019.

Discussion of cases for the 4th to 7th waves

A high level of correlation is observed between the composite loading and the effective reproduction number for some factors in each of the 4th to 7th waves. The meshes with high values of absolute factor loadings are presumed to be hotspots. In particular, each of the factors noted in the detail section of each key factor displays the highest absolute value of the correlation coefficient with the effective reproduction number in the case of a short time delay; therefore, the corresponding meshes are assumed to represent the key areas for the spread of COVID-19 infection. Because the factor contribution rates of these factors are no more than 0.050, all of the key factors found in this research, including that of the 3rd wave, are rare patterns of movement to specific meshes with high factor loading.

To determine whether these specific meshes are consistent across the multiple waves of the infection, a correlation analysis is performed on the value of the factor loading for each hotspot mesh during each wave (values are reversed (positive/negative) for Factor 7 in the 5th wave and Factor 7 in the 7th wave, for which the correlation coefficients are negative for these factors) and on the value of loading for Factor 9 in each mesh in the 3rd wave. The correlation coefficients between all the factor pairs are less than 0.25. Therefore, the hotspots varied in each wave of infection.

These hotspots are estimated based solely on correlations, and the causality35 may not be clear. However, the results of this study reveal some relationships between population influx and COVID-19 infection. Further study is needed to investigate the types of features in these hotspots by identifying similar characteristics in these areas.

Conclusion and perspectives

We analyse the relationship between COVID-19 infection and population influx on the basis of mobile phone location information in the entire area of the 23 wards of Tokyo. The population influx data used in this study are considered closer to reflecting actual data because the usage rate of mobile phones is high in Japan.

In this study, we propose an analysis method to detect influx patterns and estimate hotspots of COVID-19 infections via factor analysis. This analysis revealed a correlation between the population influx and the effective reproduction number. These findings suggest that population influx data can be effectively used to analyse infectious diseases. In fact, we detect hotspots that are assumed to be directly related to infections. This analysis also reveals that these hotspots do not necessarily correspond to the overall influx trend because their factor contributions are low. Not all influxes are assumed to lead to infections, which is an important finding because it highlights the importance of using factor analysis to decompose the population influx. In addition, we do not identify hotspots that are common to each wave but instead identify unique hotspots for each wave. This finding suggests that hotspots that are unknown and unique to a given pandemic may be detected when COVID-19 infections resurge in the future.

In particular, the relationship between infection and population influx for Factor 9 in the 3rd wave, which is estimated to be most directly related to the spread of infection, warrants further verification from an epidemiological point of view. Other conditions, such as vaccination status and weather conditions, may be considered.

The hotspot analysis method can generally be used to analyse the relationship between population movements and social events. Thus, it may be applicable not only to cases involving the spread of other infectious diseases in the future, such as influenza virus but also to studies of business sales, traffic control, and similar processes.

Data and methods

Datasets

Population influx data

The location information used in this study to estimate the population influx in 500 m2 meshes is extracted from the system logs of the mobile cell towers of SoftBank, which is one of the lines of Zenkoku-Ugoki-Tokei36. A 500 m2 mesh refers to an area from which a region is divided into 500 m long square mesh grid cells. It is based on the creation method established by the Japanese Ministry of Internal Affairs and Communications37.

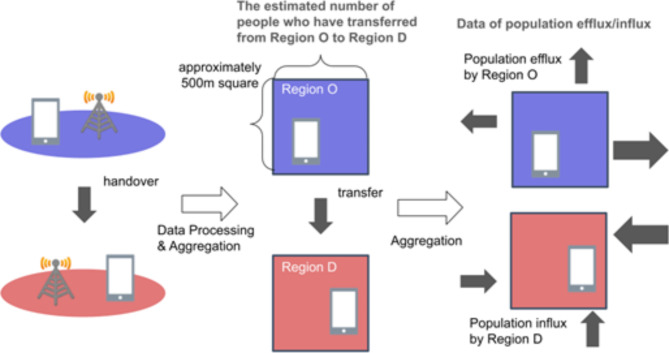
Origin–destination data (OD data) are obtained via the process shown in Fig. 3. Because these data are anonymized and statistical, individual customers could not be identified. Because seeing whether a user has communicated from locations registered in the data records is prohibited, the data processed for this system log do not violate communication privacy. The SoftBank Corporation website38 provides more information about the policies for the use and application of customer data.

Fig. 3.

Fig. 3

Open in a new tab

Data processing scheme used to obtain the population influx data. Each mobile phone in service registers its current location (left) regardless of whether the user communicates (e.g., makes or receives phone calls). Because the system logs the users of SoftBank whose consent is acquired, origin–destination data (OD data) are obtained. These data reflect the estimated number of people who moved from a specific region (O) to another specific region (D) (middle). The values in the OD dataset are the expected numbers of people, including non-SoftBank users, in a given area. By simply calculating the sum of the OD values without grouping them based on the O region, we obtain the population influx data (right).

The destination regions (D) and the period of the population influx data used in this study are based on 500 m2 meshes in the entire area of the 23 wards of Tokyo; the duration considered in this study is from November 1st, 2020, to September 3rd, 2022. The population influxes in this study are the estimated values of the resident flows in the 23 wards of Tokyo.

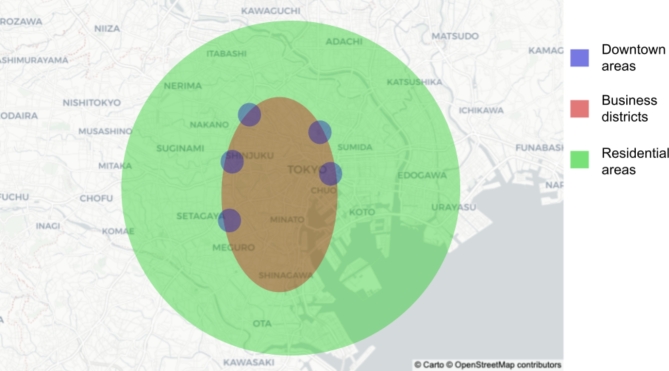
The population influx data include resident city information. Thus, we use the data only for people living in the 23 wards of Tokyo for comparison with new COVID-19 cases reported in the same regions. The distributions of the downtown areas, business districts and residential areas in the 23 wards of Tokyo are shown in Fig. 4.

Fig. 4.

Fig. 4

Open in a new tab

Streetscapes of the 23 wards of Tokyo. It is assumed that each region in the 23 wards of Tokyo can be divided into regional characteristics based on its positional relationship with the train network since Tokyo has well-developed train transportation systems. The Japan Railways (JRs) Yamanote line, which is a circular train network, serves the 23 wards of Tokyo. In general, the business area is distributed inside the JR Yamanote line, and the residential area is distributed outside the JR Yamanote line. In addition, the downtown areas are scattered around the main stations on the JR Yamanote line, such as Shibuya, Shinjuku, Ikebukuro, Ueno, and Ginza. The base map is from OpenStreetMap (https://www.openstreetmap.org/), which is available under the Open Data Commons Open Database Licence. The map style is from CARTO (https://carto.com/), which is available under the Creative Commons Attribution 4.0 Licence.

Data for new COVID-19 cases

The data regarding the number of new COVID-19 cases are obtained from the portal site of the Bureau of Social Welfare and Public Health39. In this study, we use the number of new COVID-19 cases identified in the 23 wards of Tokyo; the duration considered in this study is from October 19, 2020, to September 3, 2022. Some observations are excluded from this study because they are outliers due to counting errors.

Analysis method

Calculation of the effective reproduction number

We convert the data for the new COVID-19 cases into daily series of effective reproduction numbers via the simplified formula suggested by Nishiura et al.31:

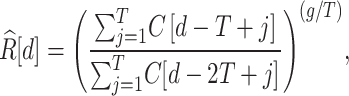graphic file with name M1.gif 1

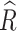where Inline graphic[d] and C[d] are the effective reproduction number and the number of cases reported on day d, respectively. The parameters g and T denote the mean generation time and length of the reporting interval, respectively. The mean generation time is almost equal to the serial interval time, which Nishiura et al.40 estimated as 4.7 ± 2.9 days. The reporting time, T, was set to approximately 7 days because Pavlicek et al.41 reported that the number of new cases in Japan oscillates within a cycle of 7 days. In this study, we set g = 5 and T = 7 to obtain significant figures to one digit. Note that this calculation method was introduced by the National Institute of Infectious Diseases42 and is used in various reports on COVID-19 infection in Japan. The calculated values obtained in this study are approximate to those obtained by another method43; details are provided in the Supplementary Information.

Because the population influx data oscillate with a 7-day cycle (from Monday to Sunday), in the analysis, the population influx is averaged at the weekly scale. Therefore, the effective reproduction number is averaged at the same scale.

Decomposing population influx via factor analysis

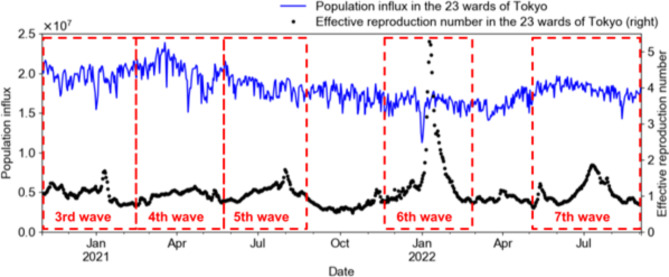
In total, seven COVID-19 pandemics occurred intermittently throughout Japan by September 2022. Data concerning population influx and the effective reproduction number from the 3rd to 7th waves of the pandemic in the 23 wards of Tokyo are used in this study. These data are divided by each period of the COVID-19 pandemic in Japan, as shown in Fig. 5 and Table 2.

Fig. 5.

Fig. 5

Open in a new tab

Population influx and effective reproduction number in the 23 regions of Tokyo from the 3rd wave to the 7th wave of the COVID-19 pandemic. Because the periods of the waves of the COVID-19 pandemic lack a clear boundary, the period boundaries are set in this study based on when the effective reproduction number is less than 1 before and after each peak.

Table 2.

Each period of the COVID-19 pandemic in the 23 regions of Tokyo from the 3rd wave to the 7th wave.

The period of the COVID-19 pandemic
The 3rd wave From November 1, 2020, to February 13, 2021
The 4th wave From February 14, 2021, to May 22, 2021
The 5th wave From May 23, 2021, to September 25, 2021
The 6th wave From November 21, 2021, to February 26, 2022
The 7th wave The 7th wave: from May 1, 2022, to September 3, 2022
Open in a new tab

The patterns of movement of individuals vary (for example, commuting to the office/school, shopping, and walking around in a neighbourhood); thus, multiple patterns of movement coexist within the same region. Because COVID-19 is transmitted through contact with infected people, common movement patterns related to opportunities for interaction with infected people among various visiting behaviours are assumed to underlie the spread of new COVID-19 cases. Therefore, we identify factors of population influx via factor analysis.

The following is a summary of the configurations of factor analysis. The principal factor method is selected for factor extraction. Varimax rotation is selected as the rotation method to calculate the factor loadings for each factor. The number of factors for effective hotspot determination is found to be 10 (therefore, the population influx is decomposed into 10 factors from Factors 1 to 10) as a result of searching. The index of the factors is assigned in descending order of the factor contribution rate among the common factors (in other words, in order of major influx patterns). The cumulative factor contribution rate explained by Factors 1 to 10 is at least 68% in each period. We implemented it in Python using a library called FactorAnalyzer.

Calculation of the sum of the product of the population influx and factor loadings

For each of the factors from 1 to 10, the sum of the product of the population influx and the factor loadings for each mesh in the entire area of the 23 wards of Tokyo, hereafter referred to as composite loading, is calculated.

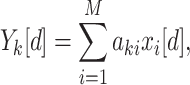graphic file with name M3.gif 2

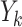where Inline graphic is the composite loading for factor k, 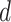Inline graphic is the date of the 7-day cycle, 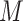Inline graphic is the number of 500 m2 meshes in the 23 wards of Tokyo, 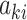Inline graphic is the factor loading value for factor k in mesh i, and 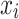Inline graphic is the population influx in mesh i. Inline graphic, the composite loading for factor k, represents the strength of the k-th factor (influx pattern). Note that the total number of meshes in the 23 wards of Tokyo in this research is 2,426, and the meshes for which statistical values are obtained are counted (approximately 2,400 meshes in each period).

Hotspot estimation

To measure the relationship between the influx pattern and the spread of COVID-19 infection, the correlation coefficients of the composite loading and the effective reproduction number are calculated for Factors 1 to 10 in each period. Note that this coefficient is also calculated for all cases when the timing of the effective reproduction number is delayed by 1 to 4 weeks because COVID-19 spreads by infecting others over several stages.

The steps to estimate the hotspot are as follows:

  1. Determine the time lag of the effect on COVID-19 spread for each factor

  2. The factor with the highest absolute value of the correlation coefficient affects in a short term

  3. If the correlation coefficient in step 2 is positive (negative), the meshes with high positive (negative) factor loading are hotspot

The details are explained below.

First, we consider factors that have an effect on the spread of COVID-19 several weeks later on the basis of the weeks of delay with the strongest correlation. For example, if a factor has the strongest correlation with a 1-week delay, then the factor affects the spread of COVID-19 reported next week. If there is a factor of population movement to specific meshes where many people become infected, which are considered hotspots, the delay with the strongest correlation should be the sum of the incubation period, the number of days after symptoms appear to show a positive test and the number of days to report the infection. On the other hand, for a factor that affects COVID-19 spread in more indirect ways, i.e., a factor of population movement to areas where a small number of people trigger many subsequent infections (e.g., the first infected person in a family who triggers subsequent household infections), the delay with the strongest correlation should be the sum of the multiple generation time (4.7 ± 2.9 days40), the time taken to obtain a positive test and the time required to report the infection. Likewise, the delay with the strongest correlation is important information as well as the level of correlation.

Second, to find hotspots, the factors for which the delay with the strongest correlation is 1 or 2 weeks are subjected to further investigation. Because the incubation period for COVID-19 infection is estimated to be approximately 5 days32–34 and additional days are required before a positive test can be obtained and the infection can be reported, the expected delay with the strongest correlation for the factors associated with visits to hotspots is 1 week to 2 weeks. We select the factor with the highest absolute value of the correlation coefficient among the subject factors.

Finally, if the correlation coefficient of the composite loadings with the effective reproduction number for a given factor in the previous step is high and positive, when the influx pattern of the factor is high, i.e., more people move to the meshes with positive factor loading instead of those with negative factor loading for that factor, the effective reproduction number tends to increase. Therefore, the meshes with high factor loading values based on composite loading are presumed to be hotspots of COVID-19 infection. Similarly, visits to meshes with a negative and high absolute value of factor loading may reduce the effective reproduction number, and vice versa, if the correlation coefficient is negative. Therefore, meshes with negative and high absolute values of factor loading are presumed to be hotspots of COVID-19 infection when the correlation coefficient is negative.

In summary, the definitions of hotspots in this paper are as follows.

  1. If the correlation coefficient of the highest absolute value in the factors for which the maximum correlation coefficient is observed with assumptions of delays of 1 and 2 weeks is positive, the meshes with high and positive factor loadings for the factor with the highest correlation coefficient are considered hotspots.

  2. If the correlation coefficient of the highest absolute value in the factors for which the maximum correlation coefficient is observed with an assumption of a delay of 1 or 2 weeks is negative, the meshes with negative and high absolute values of factor loading for the factor with the correlation coefficient with the highest absolute value are hotspots.

We search for areas presumed to be hotspots in each period of the COVID-19 pandemic in the 23 wards of Tokyo.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1 (146.1KB, pdf)

Acknowledgments

This study was financially supported by the COVID-19 AI and Simulation Project of the Cabinet Secretariat of the Japanese Government.

Author contributions

Y.K. performed the data analysis; Y.K., K.C. and T.M. wrote the manuscript; T.S. (Seki), K.C., T.M., H.I. and N.I. provided advice on the analysis and the manuscript; T.M. prepared the population influx data; T.S. (Sakurai) and S.M. managed the project; H.I. reviewed the manuscript; and N.I. established the analysis method. All the authors have read and approved the final manuscript.

Data availability

The population influx data analysed in this study are not publicly available and are commercial products provided through the Zenkoku-Ugoki-Tokei service of the SoftBank Corporation. Please contact the corresponding author for details. The data for the new COVID-19 cases analysed in this study were obtained from the portal site of the Bureau of Social Welfare and Public Health, Tokyo Metropolitan Government. This data source is freely accessible through the web. To view these data sources, visit https://catalog.data.metro.tokyo.lg.jp/dataset/t000055d0000000381.

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Yu Kimura, Email: yu.kimura@g.softbank.co.jp.

Toshiki Murata, Email: toshiki.murata@g.softbank.co.jp.

References

  • 1.Kraemer, M. U. G. et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science368, 493–497 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Greenstone, M. & Nigam, V. Does Social Distancing Matter? Becker Friedman Institute for Economics Working Paper, 2020–2026 (University of Chicago, 2020).
  • 3.Badr, H. S. et al. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. Lancet Infect. Dis.20, 1247–1254 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Jeffrey, B. et al. Anonymised and aggregated crowd level mobility data from mobile phones suggests that initial compliance with COVID-19 social distancing interventions was high and geographically consistent across the UK. Wellcome Open Res.5, 170 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Tian, H. et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science368, 638–642 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Yabe, T. et al. Non-compulsory measures sufficiently reduced human mobility in Tokyo during the COVID-19 epidemic. Sci. Rep.10, 18053 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Colizza, V., Barrat, A., Barthélemy, M. & Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. P. Natl. Acad. Sci. U.S.A.103, 2015–2020 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Balcan, D. et al. Multiscale mobility networks and the spatial spreading of infectious diseases. P. Natl. Acad. Sci. U.S.A.106, 21484–21489 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Tizzoni, M. et al. On the use of human mobility proxies for modeling epidemics. PLoS Comput. Biol.10, e1003716 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Bengtsson, L. et al. Using mobile phone data to predict the spatial spread of cholera. Sci. Rep.5, 8923 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Mazzoli, M., Gallotti, R., Privitera, F., Colet, P. & Ramasco, J. J. Spatial immunization to abate disease spreading in transportation hubs. Nat. Commun.14, 1448 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Fisher, K. A. et al. Community and close contact exposures associated with COVID-19 among symptomatic adults ≥18 years in 11 outpatient health care facilities—United States, July 2020. Morbid. Mortal. W.69, 1258–1264 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Liu, T. et al. Cluster infections play important roles in the rapid evolution of COVID-19 transmission: A systematic review. Int. J. Infect. Dis.99, 374–380 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Furuse, Y. et al. Clusters of coronavirus disease in communities, Japan, January–April 2020. Emerg. Infect. Dis.26, 9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Aizawa, Y. et al. Coronavirus disease 2019 cluster originating in a primary school teachers’ room in Japan. Pediatr. Infect. Dis. J.40, 11 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Ando, H. et al. Effect of commuting on the risk of COVID-19 and COVID-19-induced anxiety in Japan, December 2020. Arch. Public Health79, 222 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Nakashita, M. et al. Singing is a risk factor for severe acute respiratory syndrome coronavirus 2 infection: A case-control study of karaoke-related coronavirus disease 2019 outbreaks in 2 cities in Hokkaido, Japan, Linked by Whole Genome Analysis. Open Forum. Infect. Dis.9, 5 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Buckee, C. O. et al. Aggregated mobility data could help fight COVID-19. Science368, 145–146 (2020). [DOI] [PubMed] [Google Scholar]
  • 19.Alessandretti, L. What human mobility data tell us about COVID-19 spread. Nat. Rev. Phys.4, 12–13 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Hu, T. et al. Human mobility data in the COVID-19 pandemic: Characteristics, applications, and challenges. Int. J. Digit. Earth14, 1126–1147 (2021). [Google Scholar]
  • 21.Yabe, T., Jones, N. K. W., Rao, P. S. C., Gonzalez, M. C. & Ukkusuri, S. V. Mobile phone location data for disasters: A review from natural hazards and epidemics. Comput. Environ. Urban Syst.94, 101777 (2022). [Google Scholar]
  • 22.Molloy, J. et al. Observed impacts of the COVID-19 first wave on travel behaviour in Switzerland based on a large GPS panel. Transp. Policy104, 43–51 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.DePhillipo, N. N., Chahla, J., Busler, M. & LaPrade, R. F. Mobile phone GPS data and prevalence of COVID-19 infections: Quantifying parameters of social distancing in the U.S. Arch. Bone Jt. Surg.9, 217–223 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Kato, H. Development of a spatio-temporal analysis method to support the prevention of COVID-19 infection: Space-time kernel density estimation using GPS location history data. In Urban Informatics and Future Cities (eds Geertman, S. C. M. et al.) 51–67 (Springer, 2021). [Google Scholar]
  • 25.Ito, N. Covid-19 disease and social simulation with the Fugaku supercomputer in Proceedings of the international symposium on artificial life and robotics (AROB 26th) (2021).
  • 26.Heiler, G. et al. Country-wide mobility changes observed using mobile phone data during COVID-19 pandemic. In 2020 IEEE International Conference on Big Data (Big Data) 3123–3132 (IEEE, 2020).
  • 27.Mizuno, T., Ohnishi, T. & Watanabe, T. Visualizing social and behavior change due to the outbreak of COVID-19 using mobile phone location data. New Gener. Comput.39, 453–468 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Ye, Y. et al. Spatiotemporal analysis of COVID-19 risk in guangdong province based on population migration. J. Geogr. Sci.30, 1985–2001 (2020). [Google Scholar]
  • 29.Nakanishi, M. et al. On-site dining in tokyo during the COVID-19 pandemic: Time series analysis using mobile phone location data. JMIR Mhealth Uhealth9, e27342 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Kimura, Y. et al. Hotspot analysis of COVID-19 infection using mobile-phone location data. Artif. Life Robot.28, 43–49 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Nishiura, H., Chowell, G., Heesterbeek, H. & Wallinga, J. The ideal reporting interval for an epidemic to objectively interpret the epidemiological time course. J. R. Soc. Interface7, 297–307 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Ferretti, L. et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science368, 6491 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Linton, N. M. et al. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: A statistical analysis of publicly available case data. J. Clin. Med.9, 2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Lehtinen, S., Ashcroft, P. & Bonhoeffer, S. On the relationship between serial interval, infectiousness profile and generation time. J. R. Soc. Interface18, 174 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Gao, B., Wang, J., Stein, A. & Chen, Z. Causal inference in spatial statistics. Spat. Stat-neth.50, 100621 (2022). [Google Scholar]
  • 36.SoftBank Corporation Website. Zenkoku-Ugoki-Tokeihttps://www.softbank.jp/biz/services/analytics/ugoki/. Online. Accessed 14 November 2023.
  • 37.Website of the Statistics Bureau of Japan. https://www.stat.go.jp/data/mesh/pdf/gaiyo1.pdf. Online. Accessed 5 April 2024.
  • 38.SoftBank Corporation Website. Our response and policy regarding the customers’ privacyhttps://www.softbank.jp/en/privacy/personaldata/. Online. Accessed 14 November 2023.
  • 39.Website of Bureau of Social Welfare and Public Health. https://www.hokeniryo.metro.tokyo.lg.jp/kansen/corona_portal/index.html. Online. Accessed 14 November 2023.
  • 40.Nishiura, H., Linton, N. M. & Akhmetzhanov, A. R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis.93, 284–286 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Pavlíček, T., Rehak, P. & Král, P. Oscillatory dynamics in infectivity and death rates of COVID-19. Clin. Sci. Epidemiol.5, e00700-e720 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Website of National Institute of Infectious Diseases. https://www.niid.go.jp/niid/ja/diseases/ka/corona-virus/2019-ncov/2502-idsc/iasr-in/10465-496d04.html. Online. Accessed 10 April 2024
  • 43.Cori, A., Ferguson, N. M., Fraser, C. & Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol.178, 9 (2013). [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material 1 (146.1KB, pdf)

Data Availability Statement

The population influx data analysed in this study are not publicly available and are commercial products provided through the Zenkoku-Ugoki-Tokei service of the SoftBank Corporation. Please contact the corresponding author for details. The data for the new COVID-19 cases analysed in this study were obtained from the portal site of the Bureau of Social Welfare and Public Health, Tokyo Metropolitan Government. This data source is freely accessible through the web. To view these data sources, visit https://catalog.data.metro.tokyo.lg.jp/dataset/t000055d0000000381.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES