The need for better metrics for floor-tile topography: Conventional metrics correlate only modestly with shoe-floor friction

Abstract

Roughness metrics measured with stylus profilometry are commonly used to explain a floor’s friction performance, yet these metrics inconsistently predict shoe-floor friction. While strong correlations have been shown for systematically modified flooring, the goal of this study is to address a gap regarding the predictive ability of these metrics across heterogeneous porcelain flooring products. The predictive ability of four roughness metrics on oily friction performance was assessed using 23 floors and 4 shoe designs. Roughness was moderately correlated with friction (r ranged from 0.374 to 0.760). These results are a reference point for future studies that aim to improve predictions using novel surface characterization approaches that include multiple scales.

1. Introduction

Slips and falls are a common source of injury and expense [1, 2]. Slips are caused by insufficient friction between the shoe and the floor surface. A common and successful approach to reduce slips is to increase the friction by selecting shoes and flooring with improved friction performance [3–6]. Higher values of coefficient of friction (COF) have been consistently shown to reduce slips in controlled studies of walking [7–9].

Multiple factors influence the friction between the shoe and floor during walking, including characteristics of the shoe outsole (tread geometry and material properties) and characteristics of the floor (material, coatings, and surface topography) and the presence or absence of a contaminant [10–13]. A mechanistic framework has emerged where shoe-floor friction is caused by a combination of adhesive friction and hysteresis friction, primarily associated with viscoelasticity [14–16]. In this framework, adhesive friction can be disrupted by boundary lubrication [11, 17] and both adhesive and hysteresis friction can be reduced by hydrodynamic effects [9, 18]. Solutions that target the shoes or flooring to improve friction are likely to reduce slip-and-fall events.

Previous research has repeatedly aimed to quantify the relationship between surface topography and friction. However, prior reports are inconsistent. Most of the previous investigations into flooring roughness and COF have used stylus profilometers to measure surface roughness [13, 16, 19–21]. Some studies have found that roughness is strongly and linearly associated with COF performance under certain conditions when contaminants have a high viscosity and when a single type of flooring tile is used with systematic modifications to topography (i.e., through sandblasting) [13, 16, 19]. However, other studies were less conclusive, with weaker relationships between friction and roughness [11, 22] or described by a complex nonlinear relationship [20, 21]. Thus, evidence suggests that surface topography contributes to friction but that the relationship between current topography metrics and COF have an unclear level of generalizability.

One potential cause of this lack of correlation is the sensitivity of roughness metrics to the method used for their measurement (measuring device and settings) and analysis (filtering and calculation of parameters) of surface data [23]. While stylus profilometry is an indispensable tool for characterizing surface topography, the comparatively large tip radius (1–10 μm) introduces some artifacts and limits the resolution of the technique [24, 25]. Recent research has identified cross-sectional imaging of floor surfaces via scanning electron microscopy as a supplementary characterization method capable of measuring features that cannot be captured by stylus profilometry [26]. As a step towards understanding the potential need for these supplementary methods, the present study aimed to identify the predictive ability of stylus profilometry on friction performance across porcelain products.

While we acknowledge that much research has been conducted connecting stylus profilometry to friction performance, the present investigation is different and necessary because it focuses on a selection of “real” (commercially available) porcelain tile products and their friction performance against real footwear. Utilizing real products introduces variation into the material formulation and manufacturing processes. This study deviates from prior research that systematically modified the surface properties by sandblasting the surfaces [16, 19], which likely altered certain scales targeted by the abrasive particles but had unknown effects on the topography at other scales. Thus, the present research seeks to investigate the generalizability of relationships between friction and roughness across flooring products.

The purpose of this research was to determine the relationship between common roughness and waviness metrics of flooring, as measured with stylus profilometry, and shoe-floor COF across a sample of commercially available floor products.

2. Methods

2.1. Materials

In this study, 26 porcelain tiles were originally evaluated to determine their surface roughness and shoe-floor COF. During the study, three of the tiles were identified as exterior (outdoor) tiles, which were determined to have a fundamentally different surface than indoor tiles and were excluded from the analyses leaving 23 remaining indoor tiles (26 – 3 excluded tiles). The tiles were sourced across 3 manufacturers and within manufacturers, the tiles had different finishing processes and/or different product lines. Four of the included tiles were known to be made of an unglazed porcelain, 9 tiles were glazed, and the glaze status of the remaining 10 tiles was not disclosed by the tile manufacturer (Table 1). Four shoes were used in the friction measurements, differing in style, material, tread pattern, and advertised slip resistance. These shoes included Rockport K71224 (Shoe A, Hardness: 53), Vans Off the Wall Old Skool Skate Shoes 721278 (Shoe B, Hardness: 52), the SRMax Atlanta Men’s Soft Toe SRM 3700 (Shoe C, Hardness: 52), and the DS Work Service 6671 (Shoe D, Hardness: 59). Prior studies have reported viscoelastic material properties for three of the four shoes in this study ([27], Shoes A, C, and D in the present study correspond with Shoes B, C, and A, respectively, in the cited study). All shoes were approximately Men’s Size 9 or Women’s size 10. The shoes were selected based on prior COF results. These shoes spanned friction performance (high and low values of the measured COF) and two categories of labeling (“slip resistant” as labeled by their manufacturer and not labeled slip resistant). The basis for selecting a high- and low-COF shoe was made from experimental results of our past research [28, 29].

Table 1:

List of tile products included in the study. The tile manufacturer is listed along with the product line and the described finish type. The code is used to identify the product throughout the manuscript.

Manufacturer	Tile Product	Finish	Tile Code
Crossville	Graphite	Polished	BPOL
Crossville	Graphite	Unpolished Sheen	BUPS
Fired Earth	Piemonte	Matte	PPM
Fired Earth	Piemonte	Polished	PPP
Fired Earth	Piemonte	Satin-Bone	PBS
Fired Earth	Piemonte	Satin-Pearl	PPS
Crossville	Roasted Chestnut	Polished	APOL
Crossville	Roasted Chestnut	Unpolished Sheen	AUPS
Crossville	Venho Verde	Unpolished Sheen	CUPS
Fired Earth	Umbria	Polished	UMBP
Fired Earth	Umbria	Matte	UMBM
Fired Earth	Umbria	Satin	UMBS
Fired Earth	Lombardia	Polished	LMBP
Fired Earth	Lombardia	Matte	LMBM
Fired Earth	Lombardia	Satin	LMBS
Crossville	State of Grace	Unpolished Sheen	FUPS
Crossville	State of Grace	Satin	FSAT
Crossville	Juno	Unpolished Sheen	EUPS
Crossville	Juno	Honed	EHON
American Wonder	Asher Haze	Finish 1	AH1
American Wonder	Asher Haze	Finish 2	AH2
American Wonder	Venato	Polished	VPOL
American Wonder	Polar Style	White	PSW

2.2. Measurements of coefficient of friction

The COF was measured using the STEPS machine (XRDS Systems, LLC, Andover, MA) [11], which applies horizontal and vertical forces, to slide the shoe across a flooring sample and apply a normal force, respectively (Figure 1). A force plate under the flooring sample measures reaction forces, and the sliding speed of the shoe is measured by feedback from the horizontal motor. The tests were conducted using a shoe-floor angle of 17° (+/− 2) and a sliding speed of 0.5 m/s with a vertical applied force of 250 N (temperature: mean of 23°C with a standard deviation of 1.9°C; relative humidity: mean of 37% with a standard deviation of 13%). The force and speed parameters were held within 10% over a 50 ms test duration. Prior research has found that the under-shoe conditions at the moment of slip onset are approximately a shoe-floor angle of 15–24 degrees, a slipping speed of about 0.1 to 0.3 m/s that rapidly increases in speed during the slip, and a vertical force of approximately 130–320 N [7, 30]. Validation studies determined that testing conditions of 17° shoe-floor angle, 0.5 m/s, 250 N vertical force, and an averaging time of 50 ms produced the best predictions of human slips [7, 31] and repeatable results [31]. All tests were performed with a contaminant of canola oil (61.2 cP [11]) to reduce adhesion and isolate hysteresis friction [15, 17]. Prior research has found that canola oil leads to consistently low COF relative to other common contaminants [16, 22, 29, 32]. This finding is true even for shoes with tread [11, 22] that have minimal hydrodynamic effects [18, 33, 34] suggesting that these low COF results are due to a reduction in the adhesion component of friction. Furthermore, modeling studies have found that hysteresis friction predictions correlate well with oily friction [15, 35] suggesting that hysteresis friction is the dominant mechanism in oily conditions.

Figure 1:

STEPS device used to measure shoe-floor COF. The vertical and horizontal motors create the motion profile, the shoe-floor angle adjustment is used to adjust the shoe to the specified angle and then locked during trials, and the force plate measures the ground reaction forces.

Three trial replicates were repeated over three different days (nine trials total) for each shoe/floor combination. The tiles and shoes were cleaned after each day of testing. The canola oil was poured onto the floor surface beneath the landing area of the shoe and was sufficiently thick that adding additional fluid did not increase the surface thickness. The canola oil was spread and reapplied as needed between tests to ensure consistent coverage.

The COF was calculated by averaging the ratio of the horizontal force to the normal force over the 50 ms testing period (Figure 2). COF values were averaged across all 9 trial replicates and sessions. The COF values were averaged over these nine trials. Preliminary review of the data revealed that COF values scaled to the performance of the four different shoes leading to highly variable COF values across shoes (Figure 3A). The relative performance between flooring surfaces was consistent across all of the shoes (i.e., a high-COF floor as measured with one shoe also tended to have relatively higher COF with other shoes). To remove the variation caused by the shoes, the COF values for tiles were scaled (Scaled COF (F_i, S_j), Eq. (1)) the scaled COF value (for flooring F_i and shoe S_j) relative to the average COF value across all tiles for a single shoe (mean(COF(S_j)): the mean COF value for shoe S_j, horizontal lines on Figure 3A); a process that was repeated for each shoe (i.e., each shoe-floor COF value was divided by the average COF value across all tiles for that particular shoe) (Figure 3B). By using scaled COF to remove the variation across shoes, we were able to reduce the coefficient of variation (across shoes, within each flooring) from a mean of 93% (based on raw COF values, Figure 3A) to a mean of 10.0% (based on scaled COF values, Figure 3B). This enabled us to accomplish the stated purpose of establishing the relationship between floor roughness and shoe-floor COF while reducing variation caused by the shoe design.

Figure 2:

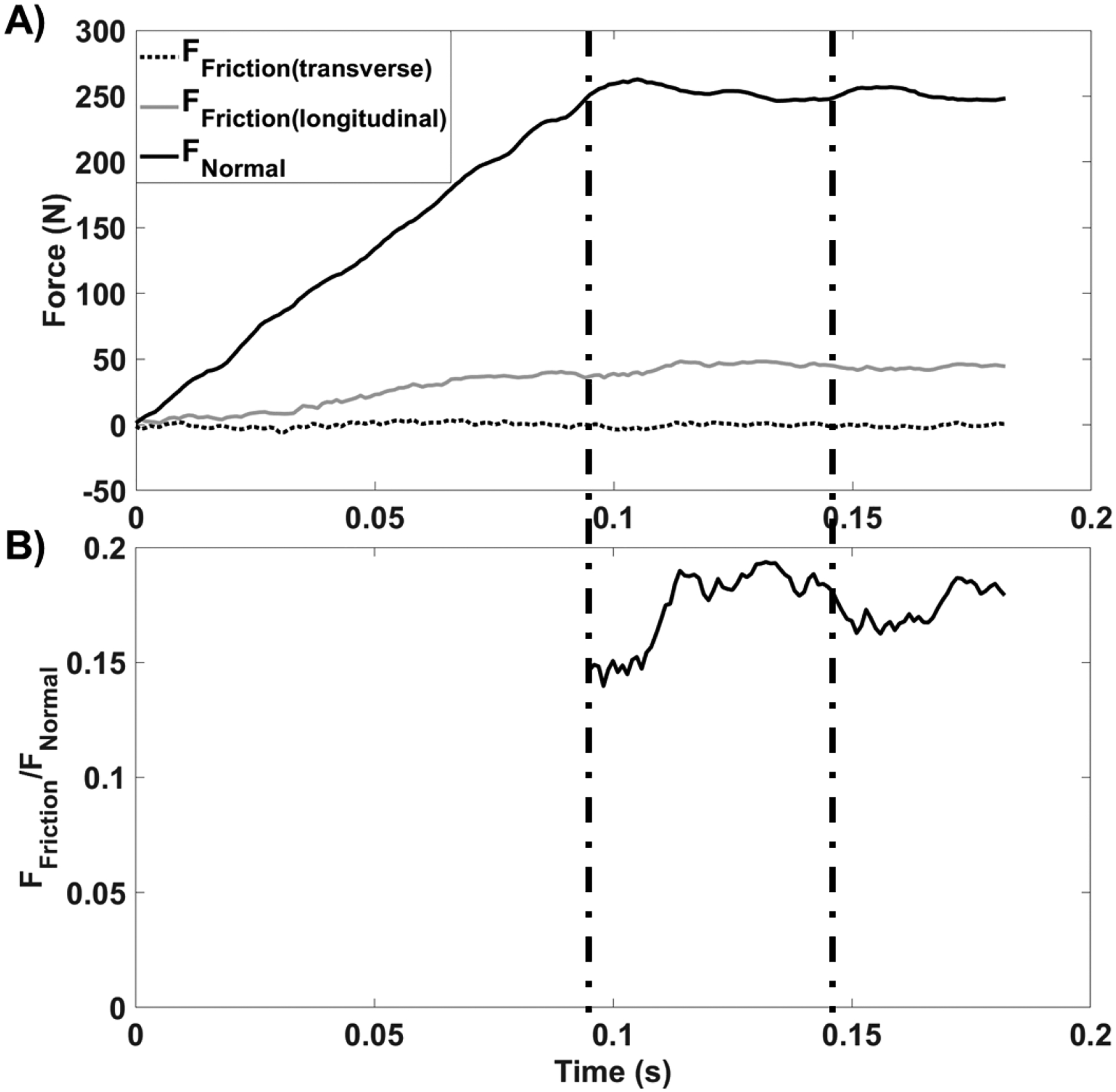
Representative kinetic data from a shoe-floor friction trial. A) The time-series data for ground reaction force, where 0 s represents shoe contact with the floor surface. Both the longitudinal friction (in the direction of sliding) and the transverse friction (perpendicular to the direction of sliding) were measured. B) The time-series of the ratio of the resultant friction force to the normal force. The COF was calculated as the average of this time-series data over a 50 ms period (between the two vertical lines).

Figure 3:

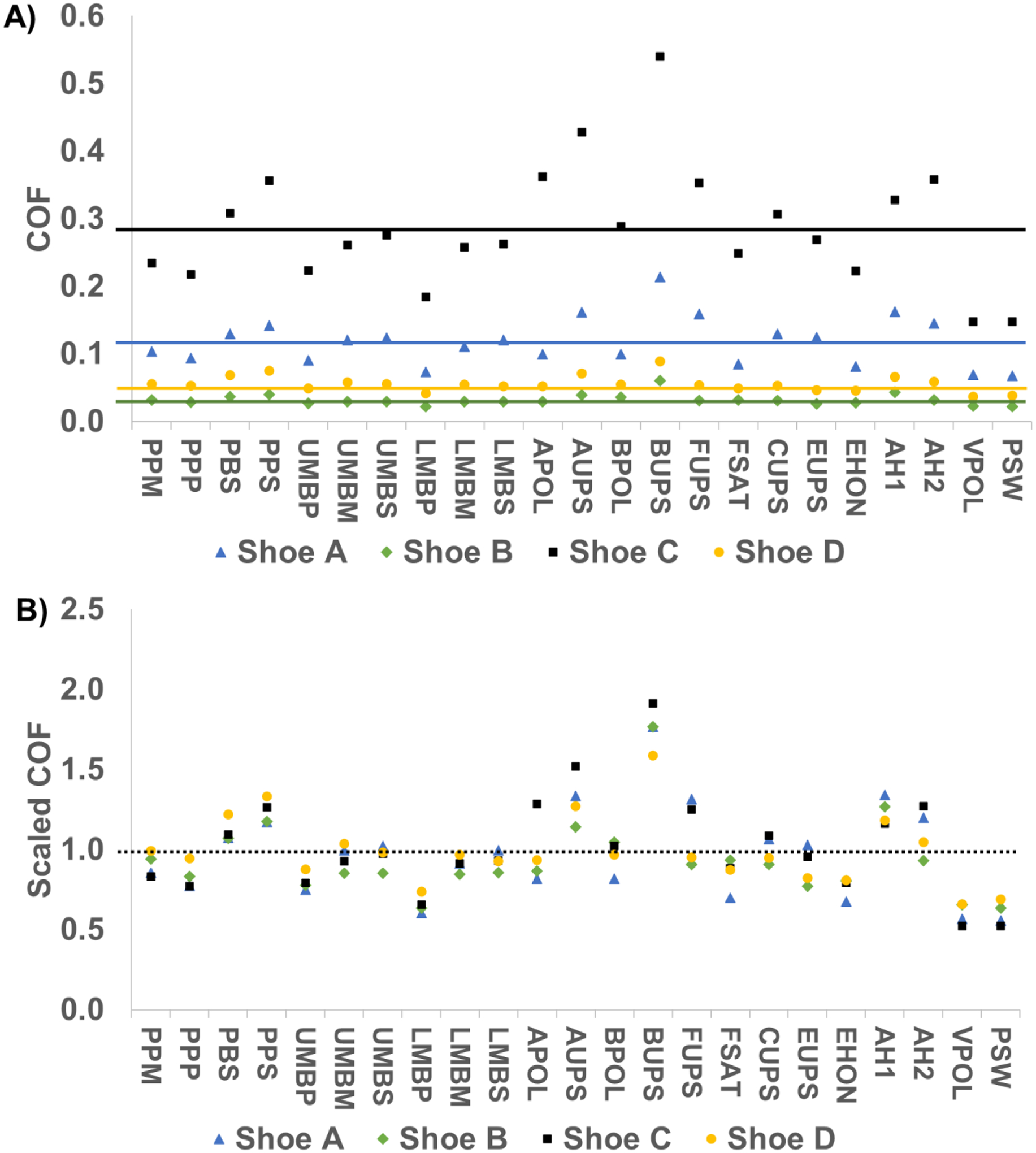
Friction performance between floors (along x-axis) and across shoes (different markers). A) In this graph, the y-axis represents the measured COF values and the horizontal lines represent the mean COF for a particular shoe (top to bottom: Shoe C, Shoe A, Shoe D, Shoe B). B: In this graph, the y-axis is the scaled COF (Eq. 1), such that the mean value for all shoes must be equal to one (horizontal dashed line).

$$\mathit{\text{Scaled}}\mathit{\text{COF}}\left(F_i,S_j\right)=\frac{COF\left(F_i,S_j\right)}{\mathit{\text{mean}}\left(COF\left(S_j\right)\right)}$$ Eq. (1)

2.3. Measurements of surface topography

Surface topography data for the porcelain were collected on a stylus profilometer (DektakXT, Bruker, Billerica, Massachusetts, USA). One-dimensional line scans were taken at different scanning speeds ranging from 1 μm/s to 60 μm/s (Figure 4a–g). A total of 18 measurements were taken for each flooring surface at 6 different scan lengths, 0.05, 0.15, 0.3, 1.5, 3, 10 mm with three repetitions each. The lateral spacing of data points ranged from 40 nm to 2 μm. The radius of the stylus profiler was measured using scanning electron microscopy (Fig. 4h) and determined to be 1.46 μm. The stylus measurements were collected with random orientations with respect to the tile edges, and did not show any significant variation with direction. To remove the tilt of the sample and the bowing artifact from the tool, a parabolic correction was applied to all the measurements. The corrected height measurements are shown in Figure 4a–g; additional details and plots of the power spectral densities are included in the Supplemental Information. All surface measurements have been made publicly available via DOI (see Data Availability), to enable others to examine and reuse the topography data, following FAIR data practices [36].

Figure 4:

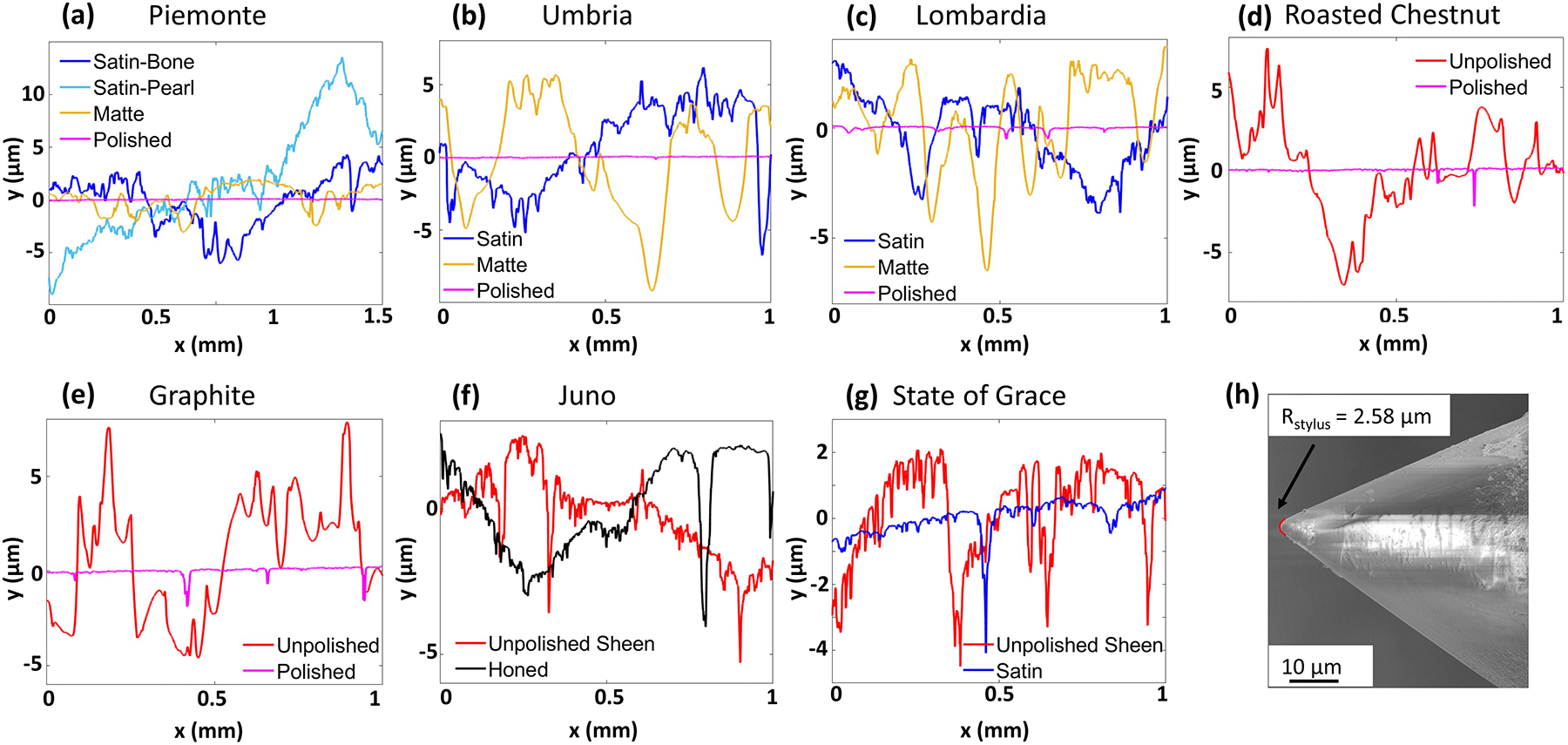
Surface topography was measured using a stylus profilometer. Representative images are shown here comparing different products and polishing conditions. The end-radius of the stylus tool was measured using a scanning electron microscope (Sigma 500VP, Zeiss, Oberkochen, Germany) at 1000X magnification with the secondary-electron detector.

Common roughness parameters were computed according to ISO 21920 [37]. According to this standard, the raw measured profile is filtered such that small-wavelength “noise” is removed, resulting in the “primary profile,” which is used to compute P parameters such as P_a, P_q, etc. This profile can further be filtered into the smaller-scale “roughness,” which is used to compute R parameters, and the larger-scale “waviness,” which is used to compute W parameters. In the present investigation, four parameters were reported, R_a, R_q, R_p, and W_a, where the subscript a designates the arithmetic average deviation from the mean line, and the subscript q designates the root-mean-square deviation from the mean line, each for the respective profile (R or W). R_p designates the maximum height of the profile above its mean line as measured in the analyzed region. These four parameters were chosen because they have previously been suggested to correlate with friction performance [19]. Bruker’s Vision64 mapping and analysis software was used to compute these parameters, with cutoff wavelengths chosen per ISO 4287. For a stylus measurement of a surface with an R_a of approximately 0.02<R_a<10 μm, the “noise” cutoff is set to 8 μm, and the roughness-waviness cutoff is set at 2.5 μm. The evaluation length was set at half of the scan length.

2.4. Statistical analyses

Bivariate correlation analyses (Pearson) were performed comparing the roughness parameters R_a, R_q, W_a, and R_p to the scaled COF for each tile (i.e., averaged across the four shoes). Nonparametric correlation analyses were used to supplement the Pearson analyses since the roughness parameters were slightly positively skewed. The r-values and p-values for each correlation were assessed to determine significance of the correlation. Pearson correlation analyses were performed across the roughness parameters to determine the degree of covariation across these parameters. The significance level was set at 0.05 (i.e., 95% confidence).

3. Results

The average COF observed across the porcelain tiles was 0.123 and ranged from 0.022 to 0.540. The COF values across all shoe-floor conditions had a standard deviation of 0.111. The average scaled COF across these tiles was 1 (by definition), with a minimum of 0.515, a maximum of 1.89, and a standard deviation of 0.272 across tiles. The average roughness value for R_a was 1.9 μm (range of 0.0 to 7.3 μm, standard deviation of 1.7 μm), for R_q was 2.4 μm (range of 0.0 to 8.6 μm, standard deviation of 2.0 μm), for R_p was 4.7 μm (range of 0.1 to 15.0 μm, standard deviation of 4.4 μm), and for W_a was 1.6 μm (range of 0.1 to 5.7 μm, standard deviation of 1.5 μm). The dataset is available as Open Access [38].

Positive but weak correlations were observed between each roughness parameter and the COF, with r-values between 0.374 and 0.760 (Figure 5). The r value (t-value, p-value, RMS error of scaled mean COF) between COF and each roughness parameter were as follows: R_a was 0.546 (t₂₁=2.99; p=0.007; RMSE=0.224), R_q was 0.535 (t₂₁=2.90; p=0.009, RMSE=0.226), R_p was 0.760 (t₂₁=5.36, p<0.001, RMSE=0.174), and W_a was 0.374 (t₂₁=1.85, p=0.078, RMSE=0.248). Similar results were observed using nonparametric analyses (see Supplemental Document). Each of the parameters were correlated with each other, with r-values ranging from 0.649 (between R_p and W_a) to 0.991 (between R_q and R_a) (Figure 6). The correlation between all roughness and waviness parameters had a p-value of less than 0.001.

Figure 5:

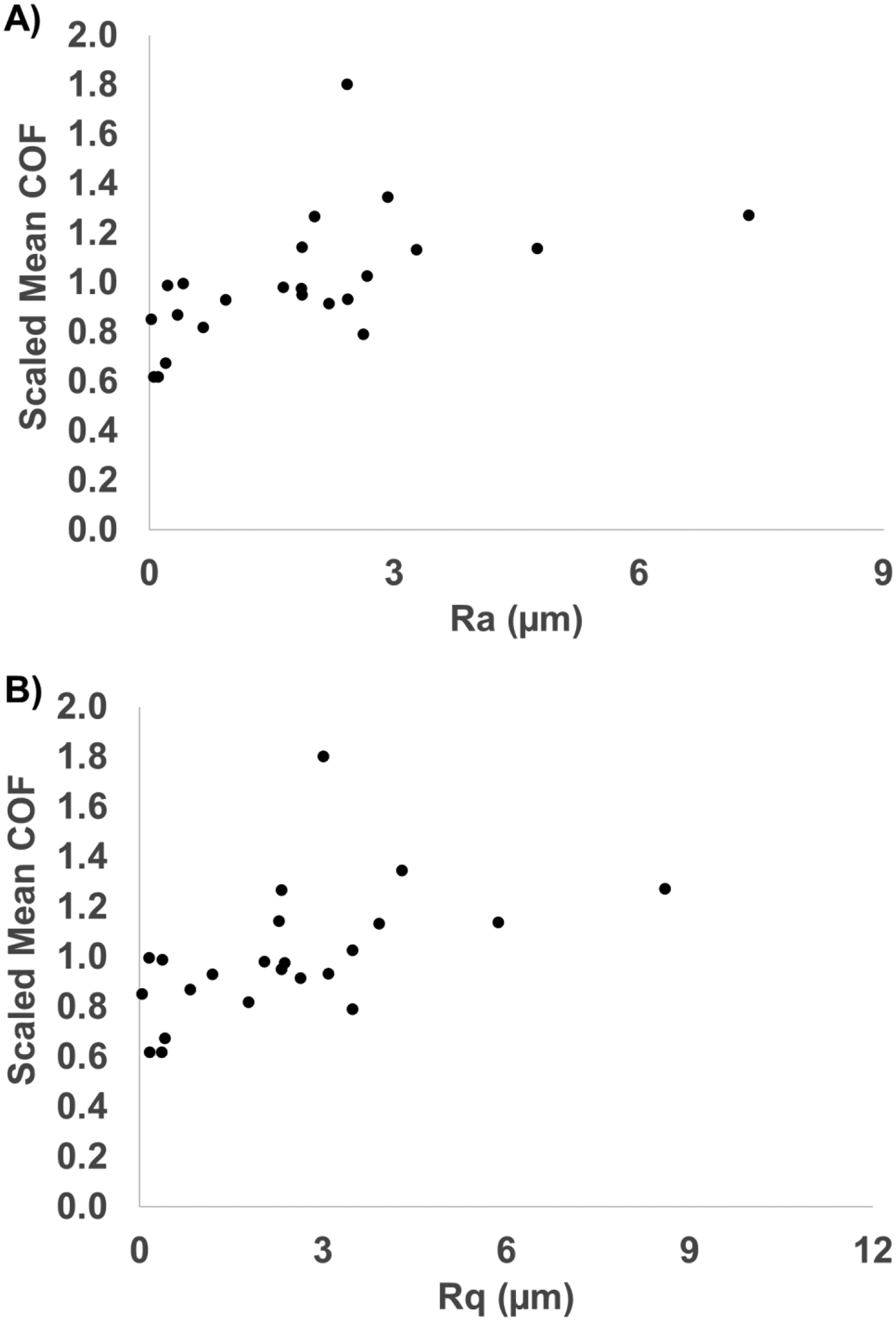
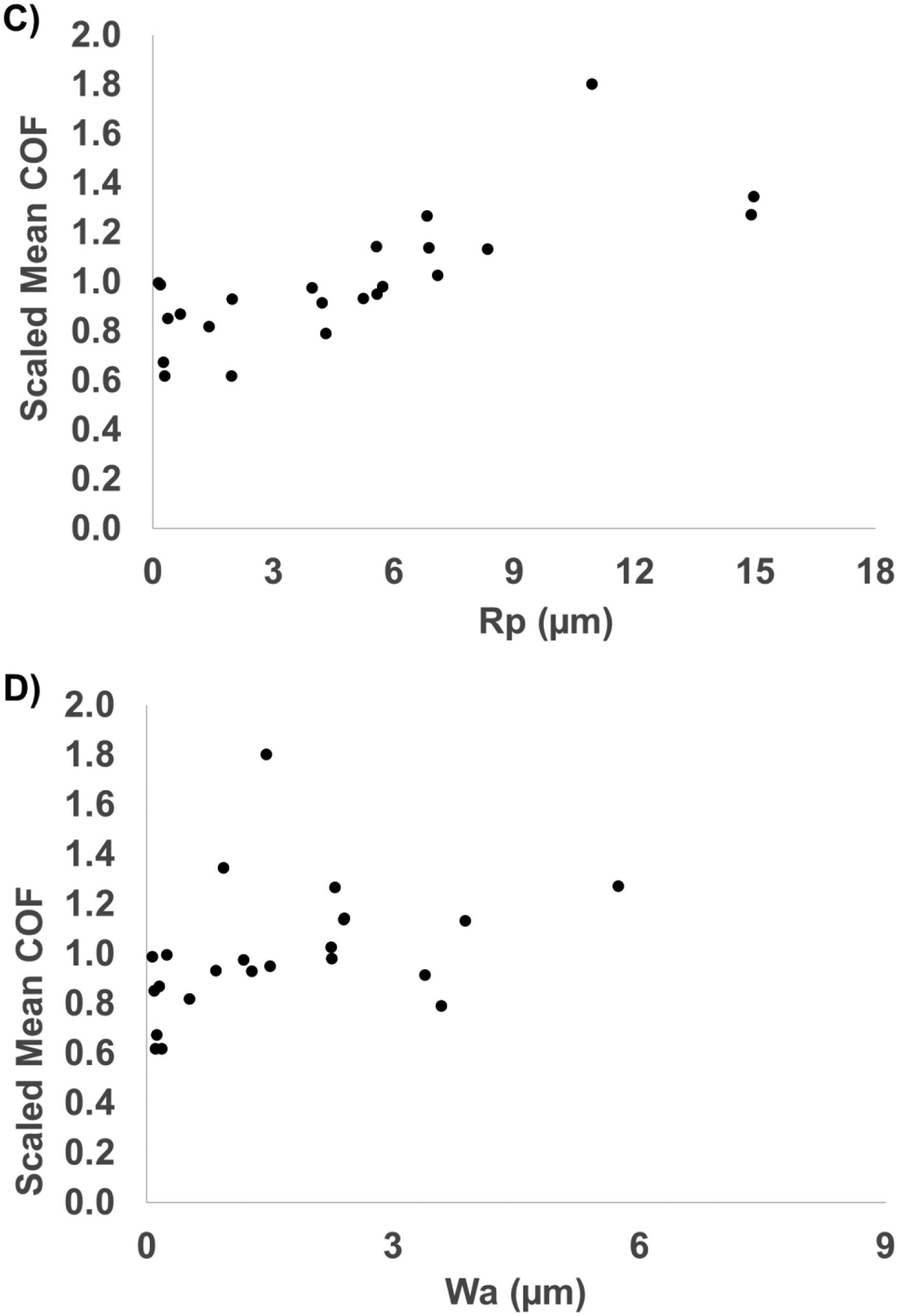
Correlations between roughness parameters (x-axis) and the scaled mean COF values (y-axis). The scaled mean COF values were the scaled values (Figure 3B) averaged across the four shoe conditions. Different panels represent different roughness parameters: A) R_a, B) R_q, C) R_p, D) W_a.

Figure 6:

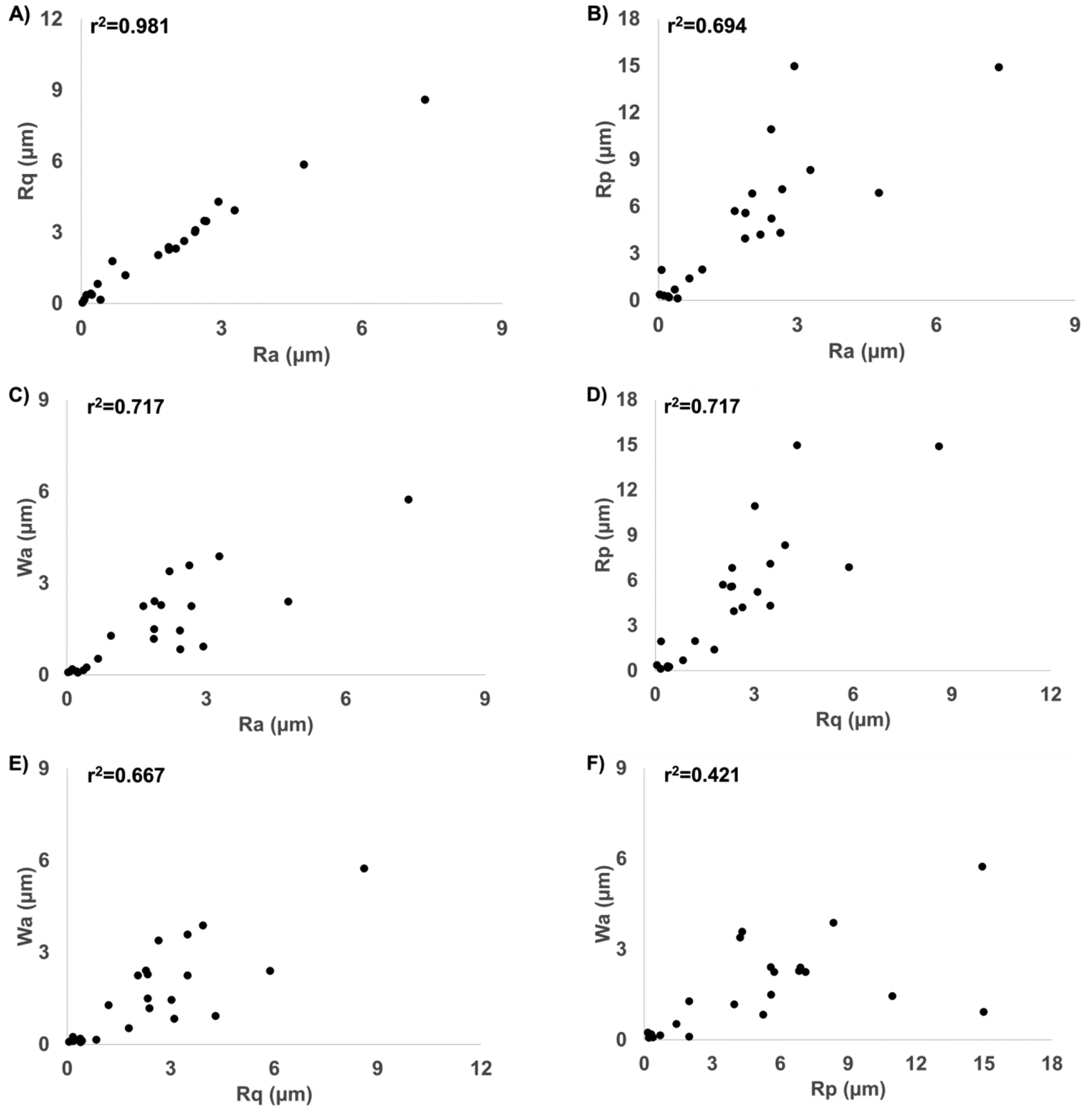
Correlations across roughness (R) and waviness (W) metrics. A) Correlation between R_q and R_a; B) correlation between R_p and R_a; C) correlation between W_a and R_a; D) correlation between R_p and R_q; E) correlation between W_a and R_q; F) correlation between W_a and R_p.

4. Discussion

Positive yet modest correlations were observed between COF performance and roughness values. These results indicate that the scale of roughness that can be measured by a profilometer and parameterized are correlated with the friction results but lack critical information needed for accurate predictions. Notably, the best-fit lines were associated with an RMS error of between 17% and 25% of the mean COF. The correlations across roughness parameters were also strong, indicating redundant information across the roughness parameters. As such, the strength of the correlations was similar across the roughness parameters.

The results from this study were consistent with results from previous research indicating weak correlation between large-scale roughness and shoe-floor friction. The correlations found here were weaker than those of the research discussed earlier on systematically modified (e.g., sandblasted) surfaces [13, 16, 19, 39], but are consistent with research that examined a cross-section of flooring products [20]. Moreover, these weak correlations may explain why Verma et. al. did not find a significant correlation between floor roughness and actual slip rate in real-world restaurants where flooring product heterogeneity is likely [5].

The positive correlations between roughness parameters and coefficient of friction are typically explained by hydrodynamic or viscoelastic mechanisms, and this investigation sheds further light on this mechanism. First, prior flooring roughness research has suggested that a primary mechanism connecting roughness to friction performance is a hydrodynamic effect where larger void volumes (associated with higher peaks) permit greater drainage capacity during the squeeze-film effect and reduce the impact of hydrodynamic pressures [13, 19]. Second, prior modeling studies [15, 35, 40, 41] have demonstrated that higher peaks generate greater deformation. This greater deformation is associated with increased energy loss and friction due to viscoelastic hysteresis. For the present results, if the first (hydrodynamic) mechanism were dominant, then the impact of roughness would be expected to be greater for shoes where hydrodynamic effects were large and lesser for shoes where hydrodynamic effects were small. However, an increase in friction performance was observed in the present study despite the use of slip-resistant shoes, which are known to be associated with minimal hydrodynamic effects [18, 42, 43]. Therefore, we propose that the critical mechanism connecting roughness to oily friction performance is the deformation caused by the floor asperities into the shoe material.

Furthermore, this material deformation mechanism provides a logical basis for why Rp had the strongest correlation. The conforming of the shoe material to the floor surface would indicate that the shoe must deform around the contour of the asperity peaks whereas the shoe material may fail to fill in the valleys of the flooring. Thus, peaks (well captured by Rp) may contribute to friction more than valleys. On the other hands, parameters like Ra, Rq, and Wa that give equal weight to valleys as peaks, may be capturing topographical information that is less relevant to friction. Additional modeling of viscoelastic hysteresis and its ability to predict experimentally measured coefficient of friction may provide increased evidence for this proposed mechanism.

Multiple sources may account for unexplained variance in our study. First, the roughness or waviness parameters captured by a stylus profilometer provide statistical descriptions of the surface that may not fully capture all relevant features. Specifically, stylus profilometry captures larger-scale features and is missing the smaller-scale features, which likely contribute to friction [41]. Prior models of friction integrate across length scales [40, 41] indicating that smaller-scale features should add friction to the larger-scale features. Interestingly, the measured friction level was still >60% of the mean friction even at roughness levels approaching 0 (Figure 5). This surprisingly high friction even in the apparent absence of roughness indicates a source of unexplained friction that could arise from small-scale features of flooring that are undetectable by stylus profilometry and/or not captured by the metrics used in this study. Furthermore, research by Ding et al. identified that information about roughness at one scale is not predictive of roughness at smaller scales, so it cannot be assumed that the unmeasured smaller scales will vary systematically with the measured larger scales [26]. Shoes have a frequency-dependent viscoelastic response, which adds further weight to the suggestion of the important contribution of a variety of size scales to viscoelastic hysteresis friction [40, 41].

Other potential, though likely smaller, sources of unexplained variance may be the role of hydrodynamic pressures, other topographical features that could be captured with stylus profilometry but are not included in the roughness parameters used in this study, adhesion, and differences across shoe designs. Previous researchers have hypothesized that topography may create channels for fluid to disperse and may be relevant in the presence of hydrodynamic effects [14, 19]. As mentioned previously, hydrodynamic effects are unlikely to be present for the slip-resistant shoes [9, 33], which have consistent tread channels (Shoes C and D) and likely only impacted the shoes with fewer tread features (Shoes A and B). Thus, these pressures may contribute to some unexplained variance. Unexplained friction variation may also occur because the roughness metrics do not consider the number of asperities. The number of floor asperities may affect the contact pressure at each asperity [44] (fewer asperities would increase the contact pressure) and therefore may influence friction [35, 45]. Adhesion that is not blocked by the fluid lubricant is expected to be small [16, 17] but is another potential source of unexplained variance. Lastly, features of the shoe (tread geometry and material) may also contribute to unexplained variance although the consistency in floor performance across shoes indicates that this contribution is small.

This study adds to the body of evidence suggesting that care should be taken when attempting to make design recommendations for slip-resistant floors based solely on the common surface metrics that are calculated from stylus profilometry measurements. The correlation between roughness parameters measured by stylus with COF performance, although positive, is not strong enough to warrant using these measurements in place of friction measurements. Documents have been released by SlipSTD, making classification groups for surfaces depending on their roughness Pk value and surface profile; they also make some suggestions for where these different floor groups are appropriate for installation [46]. This group also suggested that the Rz roughness parameter of floors in pedestrian areas should be monitored for maintenance notification purposes. While the present study found correlations between Rp (similar to Rz) and friction performance, further work is necessary to achieve better prediction of flooring to keep workers safe. New methods and/or new metrics may be required to more accurately predict shoe-floor friction and to keep people safe from slip-and-fall accidents.

This study has limitations that should be considered. While the study used more widely varying floor products than many previous studies, the only materials included were porcelain. The correlations may be even poorer when considering a more heterogenous set of materials including polymer-based tiles or natural stone tiles. Canola oil was the only contaminant used in this study. When considering less-viscous fluids, where adhesion would have a stronger contribution to friction, other phenomena would become relevant including the spreading coefficient of the surface-fluid combinations [47, 48] and the material- and topography-dependent real-area of contact [15, 49, 50]. Lastly, validation of the COF results using human slip responses would provide additional validation on the role of roughness on human safety.

5. Conclusion

This study demonstrates that commonly used roughness parameters from stylus profilometry are only somewhat correlated to friction and do not represent a reliable method of predicting the shoe-floor coefficient of friction. It is anticipated that considering additional scales of topography could enhance predictions and be useful for designing and developing new flooring surfaces. This study indicates that, in the development of slip-resistant flooring or the monitoring of existing floor surfaces, direct measurements of COF will have more utility than utilizing common roughness parameters as a proxy measure for COF performance.