Machine learning‐enhanced multi‐trait genomic prediction for optimizing cannabinoid profiles in cannabis

SUMMARY

Cannabis sativa L., known for its medicinal and psychoactive properties, has recently experienced rapid market expansion but remains understudied in terms of its fundamental biology due to historical prohibitions. This pioneering study implements GS and ML to optimize cannabinoid profiles in cannabis breeding. We analyzed a representative population of drug‐type cannabis accessions, quantifying major cannabinoids and utilizing high‐density genotyping with 250K SNPs for GS. Our evaluations of various models—including ML algorithms, statistical methods, and Bayesian approaches—highlighted Random Forest's superior predictive accuracy for single and multi‐trait genomic predictions, particularly for THC, CBD, and their precursors. Multi‐trait analyses elucidated complex genetic interdependencies and identified key loci crucial to cannabinoid biosynthesis. These results demonstrate the efficacy of integrating GS and ML in developing cannabis varieties with tailored cannabinoid profiles.

Significance Statement

This study pioneers the integration of genomic selection and machine learning to optimize cannabinoid profiles in Cannabis sativa L., demonstrating that Random Forest models effectively predict genetic traits critical for cannabinoid biosynthesis. These findings provide a foundation for breeding cannabis varieties with customized medicinal and psychoactive properties, facilitating advancements in cannabis research and cultivation.

INTRODUCTION

Cannabis sativa L., commonly known as marijuana, hemp, or simply cannabis, is one of the earliest crops cultivated by humans and is a member of the Cannabaceae family (Lapierre, Monthony, & Torkamaneh, 2023). This predominantly dioecious diploid species (2n = 20) has been historically cultivated for its fibers, oils, seeds, and notably for its medicinal and psychoactive properties (Hillig, 2005). The pharmacologically active compounds, cannabinoids, are synthesized mainly in the plant's capitate stalked glandular trichomes, primarily on female floral tissues (van Bakel et al., 2011). To date, around 177 cannabinoids have been identified, with D9THC and CBD being the most abundant and extensively studied due to their significant therapeutic potential (Hanuš & Hod, 2020; Hurgobin et al., 2021). Despite the rapid expansion of the global legal cannabis market—projected to reach $102 billion by 2028—the fundamental biology of cannabis remains underexplored, largely due to historical prohibitions (https://www.statista.com/outlook/hmo/cannabis/worldwide).

Cannabinoid biosynthesis involves complex pathways beginning with olivetolic acid, which is converted into CBGA, the precursor to major cannabinoids such as THC, CBD, and CBC (Taura et al., 2007). Understanding these pathways is crucial for genetic selection aimed at enhancing specific cannabinoid profiles. The medicinal utility of cannabis is influenced by the relative concentrations of these secondary metabolites, categorized into three types based on their THC/CBD ratio: Type I (high THC), Type II (balanced THC and CBD), and Type III (high CBD) (Hurgobin et al., 2021). However, it should be noted that this is an oversimplification and that each cannabis plant has a unique chemical fingerprint that may impact its biological activity.

Historically, cannabis breeding was conducted within clandestine operations, focusing on high‐THC plants using undocumented methods and a limited genetic pool (Torkamaneh & Jones, 2022). This approach often neglected the potential of modern technologies in stabilizing desired traits through conventional breeding. Cannabis's dioecious nature presents unique challenges, as unfertilized female plants, which produce the most cannabinoids, are preferred. This has led to a reliance on clonal propagation from elite seedlings to maintain genetic consistency, bypassing conventional breeding programs (Jones & Monthony, 2022).

The introduction of GS—a method using molecular marker data to predict the genetic potential of breeding stock—represents a transformative advancement in plant breeding. This technique enables the prediction of phenotypic performance based solely on genomic data (Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022), circumventing the labor‐intensive phenotypic evaluations typically required (Montesinos‐López et al., 2021; Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022). Traditional methods for analyzing genomic data in plant breeding are limited in their ability to fully capture and interpret the vast amount of information contained in molecular markers (i.e., SNPs) and most of the methods suffer from “large p small n” problems specifically in genomics datasets (Yoosefzadeh‐Najafabadi, Eskandari, et al., 2022). Therefore, in order to harness the full potential of GS and predict breeding stock's genetic potential accurately, the use of ML algorithms has become a necessity (Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022). The integration of ML algorithms with GS has significantly enhanced the precision of these predictions, enabling the analysis of complex interactions within the genome that influence trait heritability (Montesinos‐López et al., 2021; Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022). The recent implementation of multi‐trait genomic prediction, which leverages genetic correlations between various traits, has enhanced prediction accuracy (Sandhu et al., 2022). This method is particularly relevant for cannabis, where the interaction between different cannabinoid profiles crucially impacts plant value and efficacy. However, the efficiency of GS for multi‐trait analysis heavily depends on the ability to effectively select, filter, and analyze genomic data (Wang et al., 2020). Traditional methods used in GS are often challenged by computational inefficiencies and significant efforts to remove redundant SNPs and prepare them for multi‐trait GS analysis (Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022).

As the first study to apply genomic selection to cannabis, this work not only fills a critical gap in genetic research but also lays the groundwork for future studies. By harnessing the potential of genomic tools and machine learning, we can develop cannabis varieties with qualities optimized for specific medical needs and environmental conditions. The implications of this research extend beyond academia, offering actionable insights that can drive innovation in cultivation practices and product development, thereby contributing to the sustainability and profitability of the rapidly evolving cannabis industry.

RESULTS

Cannabinoid diversity and interrelationships

The analysis of different major cannabinoids, namely CBGA, THCA, CBDA, 9THC, CBG, CBC, and CBD, revealed a wide range of variations. The CBGA exhibited values ranging from 0.02 to 11.6% D.W., with an average value of 0.843% D.W. The THCA showed a range of 36.64% D.W., with values spanning from 0.33 to 36.97% D.W. and an average of 20.20% (Figure 1a). The CBDA showcased a range of 0.02–20.42%, with an average value of 1.34% D.W. The D9THC demonstrated a 0.78% D.W., with values varying from 0 to 0.78% D.W. and an average value of 0.21% D.W. The CBG recorded maximum, minimum, and average values of 0.24, 0, and 0.07% D.W., respectively. The CBC showed a maximum value of 0.31% D.W., a minimum value was 0% D.W., and an average value of 0.04% D.W. Finally, CBD recorded maximum, minimum, and average values of 0.20, 0, and 0.01% D.W., respectively (Figure 1a).

Figure 1.

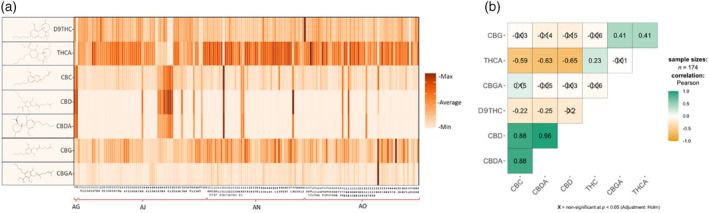
(a) Variations of cannabinoid profiles, and (b) the correlations between different cannabinoids in the tested population.

As illustrated in Figure 1(b), a strong positive correlation was observed between CBD and CBDA (r = 0.96, P < 0.001), while a moderate correlation was found between THCA and D9THC (r = 0.23, P < 0.01). Furthermore, a negative correlation was observed between THCA and CBDA (r = −0.63, P < 0.001). Although D9THC demonstrated a positive correlation with CBGA (r = 0.06), this relationship was not statistically significant. However, D9THC showed negative correlations with both CBD (r = −0.65, P < 0.001) and CBDA (r = −0.20, P < 0.01). Additionally, CBC displayed strong positive correlations with CBDA and CBD (r = 0.88, P < 0.001) and negative correlations with THCA (r = −0.59, P < 0.001) and CBG (r = −0.15, P < 0.05). We observed negative correlations between CBGA and THCA (r = −0.01) and D9THC (r = −0.06), while it showed a non‐significant positive correlation with CBDA (r = 0.05). Finally, CBGA also showed a positive correlation with CBG (r = 0.41, P < 0.001) and a negative correlation with CBC (r = −0.03).

Single cannabinoid genomic prediction

To assess the breeding potential of cannabis lines accurately, based on their cannabinoid profiles, various learning algorithms were employed using full SNP input variables. The effectiveness of these algorithms was evaluated by examining the linear Pearson correlation coefficient (r), coefficient of determination [R (Hillig, 2005)], mean squared error (MSE), and root mean squared error (RMSE) between training and testing prediction results for each dataset (Table 1). Overall, RF exhibited the highest performance for the majority of tested cannabinoids, while, SVR consistently demonstrated the lowest efficacy, except for CBGA (Figure 2). In CBGA, SVR achieved the highest r‐value (0.15), followed by EN (0.10), BA (0.09), BB, and GBLUP (0.09), indicating that all tested algorithms performed less effectively for CBGA compared to other cannabinoids. In terms of R (Hillig, 2005), the highest R ² (0.02) in CBGA was also found in SVM with the lowest MSE (0.011) and RMSE (0.00012), accordingly (Table 1).

Table 1.

Performance metrics of machine learning algorithms for predicting cannabinoid compounds

ML algorithm	CBGA	CBDA	THCA	CBG	CBD	D9THC	CBC
Coefficient of correlation (r)
BA	0.09	0.4	0.54	0.62	0.51	0.48	0.55
BB	0.05	0.38	0.56	0.62	0.47	0.47	0.56
BC	0.05	0.39	0.57	0.63	0.48	0.49	0.55
RF	0.04	0.34	0.69	0.73	0.59	0.58	0.64
GBLUP	0.09	0.4	0.57	0.66	0.5	0.49	0.59
EN	0.1	0.21	0.38	0.44	0.36	0.33	0.39
SVM	0.15	0.13	0.13	0.18	0.15	0.13	0.13
Coefficient of determination (R 2)
BA	0.008	0.160	0.292	0.384	0.260	0.230	0.303
BB	0.003	0.144	0.314	0.384	0.221	0.221	0.314
BC	0.003	0.152	0.325	0.397	0.230	0.240	0.303
RF	0.002	0.116	0.476	0.533	0.348	0.336	0.410
GBLUP	0.008	0.160	0.325	0.436	0.250	0.240	0.348
EN	0.010	0.044	0.144	0.194	0.130	0.109	0.152
SVM	0.023	0.017	0.017	0.032	0.023	0.017	0.017
Mean squared error (MSE)
BA	0.021	0.013	0.593	0.003	0.001	0.672	0.002
BB	0.022	0.064	0.635	0.003	0.001	0.623	0.001
BC	0.011	0.076	0.731	0.003	0.001	0.796	0.002
RF	0.019	0.180	0.699	0.004	0.002	0.608	0.002
GBLUP	0.013	0.035	0.538	0.004	0.001	0.638	0.001
EN	0.013	0.065	0.869	0.004	0.002	0.861	0.001
SVM	0.011	0.096	0.666	0.003	0.002	0.582	0.003
Root mean squared error (RMSE)
BA	0.00044	0.00017	0.35165	0.00001	0.00000	0.45158	0.00000
BB	0.00048	0.00410	0.40323	0.00001	0.00000	0.38813	0.00000
BC	0.00012	0.00578	0.53436	0.00001	0.00000	0.63362	0.00000
RF	0.00036	0.03240	0.48860	0.00002	0.00000	0.36966	0.00000
GBLUP	0.00017	0.00123	0.28944	0.00002	0.00000	0.40704	0.00000
EN	0.00017	0.00423	0.75516	0.00002	0.00000	0.74132	0.00000
SVM	0.00012	0.00922	0.44356	0.00001	0.00000	0.33872	0.00001

BA, Bayesian Algorithm; BB, Bayesian Bootstrapping; BC, Bayesian Classification; CBC, Cannabichromene; CBD, Cannabidiol; CBDA, Cannabidiolic Acid; CBG, Cannabigerol; CBGA, Cannabigerolic Acid; D9THC, Delta‐9‐Tetrahydrocannabinol; EN, Elastic Net; GBLUP, Genomic Best Linear Unbiased Prediction; ML Algorithm, Machine Learning Algorithm; RF, Random Forest; SVM, Support Vector Machine; THCA, Tetrahydrocannabinolic Acid.

Figure 2.

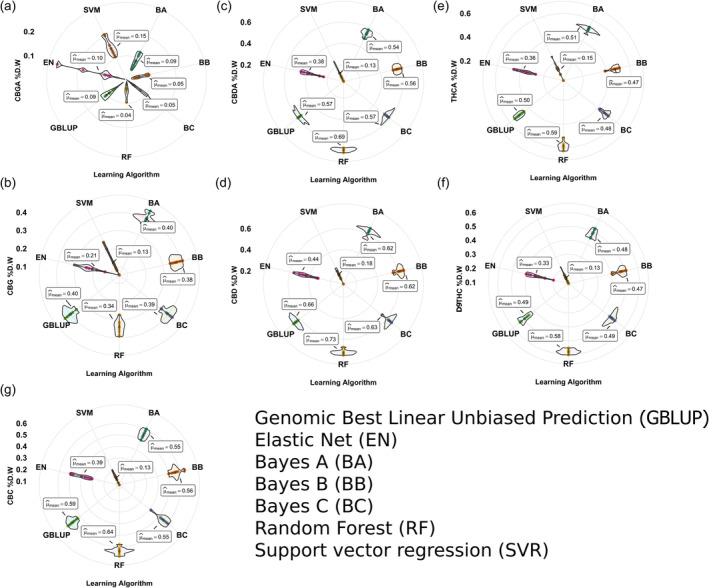
Performance comparison of different methods for predicting breeding values of the tested cannabis panel for different cannabinoids including CBGA (a), CBDA (b), THCA (c), CBG (d), CBD (e), D9THC (f), and CBC (g).

For THCA, RF recorded the highest r‐value (0.69), closely followed by BC (0.57) and GBLUP (0.57). In contrast, SVR had the lowest r‐value (0.13). Similarly, in CBDA, RF outperformed other algorithms with the highest accuracy (0.68), while SVR remained the least effective (0.12) (Figure 2). Regarding the R (Hillig, 2005), MSE, and RMSE values, RF had the highest R ² with a value of 0.47 while BA had the lowest MSE (0.59) and RMSE (0.35) value among all other tested methods (Table 1). In the case of CBG, Bayesian algorithms (BA, BB, and BC) had the same performance, each achieving an r‐value of approximately 0.62 while SVR recorded the lowest at 0.18. The highest r and R ² were obtained in RF with the values of 0.73 and 0.53, respectively. Similarly, the highest MSE and RMSE value was found in RF with the values of 0.004 and 0.00002.

For CBC, RF outperformed the other algorithms, achieving the highest r‐value at 0.64 and R ² of 0.410, indicating a strong predictive capability and a significant portion of explained variance (Table 1). GBLUP followed with an r‐value of 0.59 and an R ² of 0.348, providing solid performance as well. The MSE and RMSE values were minimal across these best‐performing algorithms ranging from 0.001 to 0.003 for MSE and almost 0.00001 for RMSE (Table 1). In terms of evaluating different algorithms for predicting D9THC, RF demonstrated the highest accuracy with a r‐value of 0.58 and an R ² of 0.336 (Table 1). Close contenders included GBLUP with an r‐value of 0.49 and an R ² of 0.240, and BC with an r of 0.49 and an R ² of 0.240. MSE was minimized across algorithms, with BB achieving the lowest MSE at 0.623. RF maintained competitive performance with a low MSE of 0.608. The RMSE was also minimal across all the tested algorithms (Table 1). Overall, RF led in correlation and variance explanation, making it a dependable algorithm for D9THC prediction.

In CBD prediction, the RF algorithm obtained the highest r‐value at 0.59 and an impressive R ² of 0.348, signifying strong capability in capturing variance (Table 1). Following RF, the BA algorithm demonstrated an r‐value of 0.51 and an R ² of 0.260, while BB and BC showed r‐values of 0.47 and R ² values of 0.221 and 0.230, respectively. BB demonstrated the lowest MSE at 0.001, matched by other top algorithms, including RF, which also showed an MSE of 0.002 (Table 1). In CBG prediction, the RF algorithm was the top performer, showcasing the highest r‐value of 0.73 and an R ² of 0.533. GBLUP followed with an r‐value of 0.66 and an R ² of 0.436. BA and BB also showed r‐values at 0.62, with R ² values of 0.384 each. In terms of MSE, all these algorithms, including RF, recorded a low MSE of 0.003 or 0.004, demonstrating consistency in prediction accuracy across different datasets (Table 1). The RMSE for RF was recorded at 0.00002, and BA, BB, and BC algorithms similarly achieved RMSE values near zero (Table 1).

For THCA predictions, RF led with a high r‐value of 0.58 and an R ² of 0.336, followed by GBLUP and BC, each with an r‐value of 0.49, and an R ² of 0.240 (Table 1). In terms of MSE, RF had an MSE value of 0.608, whereas the lowest MSE value was found in GBLUP algorithms with a value of 0.538 (Table 1). In summary, RF proved to be the most effective algorithm for accurately predicting breeding values of cannabis lines for the tested cannabinoids, followed by GBLUP and BA (Table 1). Conversely, SVR consistently showed the lowest efficacy among all tested algorithms. Given these results, RF and GBLUP were primarily used in subsequent analyses (Figure 2).

Multi‐trait optimized genomic prediction analyses

The performance of multi‐trait genomic selection using RF is presented in Figure 3(a,b) and the tunning parameters of each selected traits are shown in Figure 3(c–f). To further understand variables significant in predicting different levels of selected cannabinoids, a variable importance analysis was conducted post‐RF algorithm fitting for each pathway (Figure 4). For this aim, MCFS‐ID was able to reduce the initial 250k input variables (SNPs) into 16.5k variables which significantly increased the computational efficiency.

Figure 3.

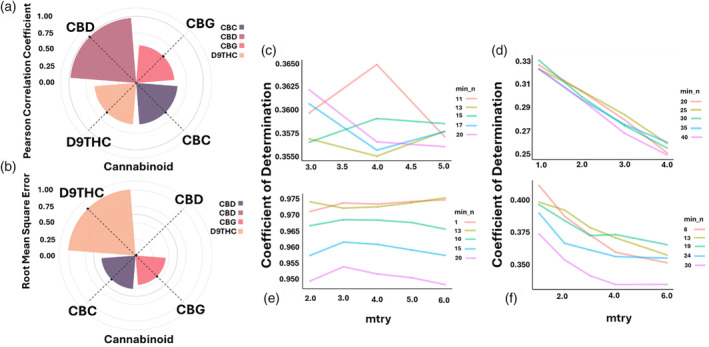
Multi‐trait optimized genomic prediction analyses using RF algorithm for predicting selected cannabinoids. (a) Pearson correlation coefficient. (b) Root mean square error. Tunning RF parameters for (c) D9THC, (d) CBG, (e) CBD, and (f) CBC pathways.

Figure 4.

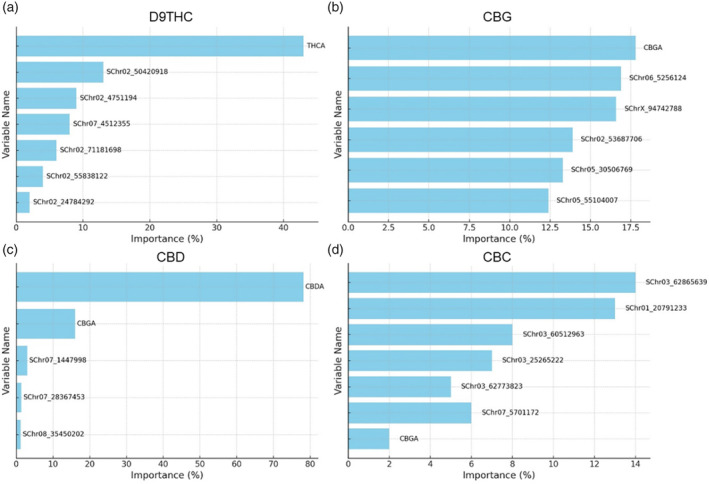
Importance of top input variables in predicting different levels of selected cannabinoids; (a) D9THC, (b) CBG, (c) CBD, and (d) CBC.

D9THC pathway

The THCA and CBGA, as two of the most important components in the D9THC pathway, were used along with SNP data as input variables. The algorithm showed a good fit to the data, evidenced by a coefficient of correlation of 0.62 and a RMSE of 0.081 (Figure 3a,b). THCA emerged as the most influential factor, accounting for 43% of the D9THC level variance (Figure 4a). Among the other variables, the locus SChr02_50420918 was found to have the second‐highest importance in explaining D9THC levels, with a contribution of 13%. Additional significant loci included SChr02_4751194, SChr07_4512355, SChr02_71181698, SChr02_55838122 and SChr02_24784292. Collectively, these seven variables (THCA level and six genetic loci) accounted for 85% of the variation in D9THC levels (Figure 4a).

CBG pathway

The CBGA and SNPs were used as input variables. After tuning the RF parameters to their optimum, the algorithm achieved a correlation coefficient of 0.57 and a RMSE of 0.036 (Figure 3a,b). Further analysis focused on the importance of variables in explaining CBG levels. The top five variables—CBGA, SChr06_5256124, SChrX_94742788, SChr02_53687706, and SChr05_30506769—accounted for 90.9% of the variation in CBG (Figure 4b). CBGA was the most influential variable, contributing to 17.8% of the variation. Similarly, SChr06_5256124, located on chromosome 6, accounted for 16.9% of the variation. SChrX_94742788, located on the X chromosome, was also significant, explaining 16.6% of the variation. The loci SChr02_53687706 and SChr05_30506769, were also key contributors to the variation in CBG levels (Figure 4b).

CBD pathway

The prediction of CBD levels was performed using SNP data, CBDA, and CBGA profiles as input variables. RF with the optimal tunning parameters yielded a high correlation coefficient of 0.98 and a low RMSE of 0.001, demonstrating excellent algorithm fit using CBD pathways variables (Figure 3a,b). Furthermore, variable importance analysis revealed that CBDA and CBGA have the highest importance in explaining the CBD levels, contributing 78.2% and 16% to the variation, respectively (Figure 4c). Together, these variables accounted for 94.2% of the variation in CBD levels. Additionally, loci such as SChr07_1447998, SChr07_28367453, and SChr08_35450202, also played roles, though less significant, contributing 3, 1.4, and 1.2% to the variation, respectively (Figure 4c).

CBC pathway

The performance of RF algorithm for predicting CBC levels was assessed using a dataset consisting of CBGA and SNPs as input variables. Optimal tuning of RF parameters resulted in a high correlation coefficient of 0.98 and a low RMSE of 0.001 (Figure 3a,b). Variable importance analysis indicated that the alleles at loci SChr03_62865639 and SChr01_20791233 were the most significant, each explaining 14 and 13% of the CBC variation, respectively (Figure 4d). This was followed by contributions from SChr03_60512963 and SChr03_25265222, which accounted for 8 and 7% of the variation, respectively. Lesser, yet notable contributions were observed from SChr03_62773823, SChr07_5701172, and CBGA contributing 5, 6, and 2% to the CBC prediction, respectively. Collectively, these variables explained 55% of the variation in CBC levels (Figure 4d).

Extracting candidate genes underlying detected SNPs

The flanking regions of the SNPs were analyzed 20‐kbp upstream and downstream of each significant SNP to identify potential candidate genes associated with the target traits (Table S1). Our analysis highlights significant overlaps in genetic components across cannabinoid biosynthesis pathways. Notably, loci such as SChr02_4751194 and SChr02_71181698 are involved in multiple pathways, linked to genes Phosphoglycolate phosphatase 2 (LOC115707244) and Enolase (LOC115707804), which play crucial roles in metabolic processes and are associated with D9THC. Additionally, the recurrent appearance of loci on chromosome 6, such as SChr06_5256124, associated with genes Glutamyl‐tRNA(Gln) amidotransferase subunit C (LOC115718643), suggests their broad impact on influencing traits across CBG and potentially other cannabinoids. These overlaps highlight critical genetic intersections that are paramount for breeding strategies aimed at optimizing cannabinoid profiles, reflecting the genes' widespread influence on cannabis plant development and stress response mechanisms.

DISCUSSION

The variations observed in cannabinoid content across different samples highlight the significant diversity in cannabinoid profiles among cannabis genotypes. The wide range of CBGA percentages (0.02–11.6% D.W.) suggests diverse metabolic pathways leading to the synthesis of other cannabinoids, given that CBGA is a common precursor (Romero et al., 2020). Particularly noteworthy is the high maximum value of THCA (36.97% D.W.), indicating that the current cannabis panel is heavily selected for high THC content, which aligns with the preferential selection of genotypes for different purposes (Lapierre, de Ronne, et al., 2023).

The correlations among cannabinoids reveal complex biochemical relationships and competitive biosynthetic pathways (Hesami, Pepe, de Ronne, et al., 2023). For example, the robust positive correlation between CBD and CBDA (r = 0.96) confirms the direct biosynthetic conversion from CBDA to CBD, signifying that genotypes high in CBDA are likely also rich in CBD. Conversely, the moderate positive correlation between THCA and D9THC (r = 0.23) might indicate a partial conversion of THCA to D9THC, although the moderate strength of this correlation suggests that other factors, potentially including genetic, environmental, or post‐harvest handling, may also influence this conversion process (Hesami, Pepe, Baiton, & Jones, 2023). The negative correlation between THCA and CBDA (r = −0.63) suggests a competitive biosynthesis pathway where the metabolic energy is directed toward either THCA or CBDA production, rather than both simultaneously. Moreover, the non‐significant positive correlation between D9THC and CBGA (r = 0.06) implies that variations in CBGA do not directly impact D9THC levels, possibly pointing to the multi‐step and multiple enzyme‐involved process converting CBGA to other cannabinoids (Wang et al., 2023), including THCA and ultimately D9THC. The negative correlations of D9THC with both CBD (r = −0.65) and CBDA (r = −0.20) highlight the polar biosynthetic orientation toward THC production at the cost of CBD and its acidic precursor, suggesting distinct genotype development goals depending on intended use (Wang et al., 2023).

The accurate prediction of breeding values using genetic information holds significant potential for the optimization of cannabinoid profiles in cannabis breeding programs (Naim‐Feil et al., 2021). The implementation of both single and multi‐trait genomic prediction strategies in this study aimed at estimating cannabinoid levels in the tested population has revealed significant variability in algorithmic performance. RF emerged as the most effective overall, showing superior performance across the majority of tested cannabinoids with high correlation coefficients for THCA (0.58), CBDA (0.68), CBC (0.64), CBD (0.73), and D9THC (0.58). The strong predictive capability of RF could be attributed to its ability to algorithm complex interactions and non‐linear relationships within genetic data, which are likely prevalent in the expression of cannabinoid biosynthesis pathways (Yoosefzadeh Najafabadi et al., 2023).

On the contrary, SVR consistently underperformed, except in the case of CBGA, where it recorded the highest r‐value (0.14). The poorer performance of SVR might be due to its limitations in handling the high dimensionality and complexity of the genomic data, which can hinder its effectiveness in capturing the complex genetic architectures underlying cannabinoid biosynthesis (Lawson et al., 2021). Other algorithms such as BA, GBLUP, and BC exhibited intermediate performance, with r‐values ranging from 0.55 to 0.65 for CBC and CBD, balancing between linear and non‐linear modeling capabilities.

Multi‐trait predictions, by incorporating additional related traits and SNPs, significantly outperformed single‐trait predictions, especially in the CBD and CBC pathways. This approach benefits from the interconnectedness of cannabinoid biosynthesis pathways, leading to higher accuracy and explanatory power. For instance, integrating CBDA and CBGA into the CBD pathway model highlighted their substantial roles, which might be overlooked by single‐trait models. Moreover, significant loci identified in multi‐trait models offer deeper genetic insights and potential targets for the identification of high‐impact genetic markers and potentially key candidate genes (Raj & Nadarajah, 2022). By analyzing the genetic correlations and interactions across multiple traits, this approach enhances the likelihood of detecting markers that have significant impacts on multiple cannabinoid pathways. This capability is crucial for pinpointing candidate genes that are central to cannabinoid biosynthesis and regulation and can lead to more precise breeding strategies that are tailored to enhance specific desirable traits in cannabis.

Despite the promising findings, this study has several limitations that must be acknowledged. The genetic diversity within the cannabis panel used was relatively low, potentially limiting the generalizability of the results to other cannabis populations with greater genetic variability. Additionally, the study was conducted under controlled greenhouse conditions, which, while beneficial for minimizing environmental variability, also restricts the ability to understand how these traits might express under natural, variable environmental conditions.

CONCLUSION

The findings of this study significantly advance the understanding and application of genomic selection for optimizing cannabinoid profiles in C. sativa. By leveraging advanced machine learning algorithms such as RF and SVR, we demonstrated that multi‐trait genomic prediction models markedly enhance the accuracy and efficiency of breeding programs aiming to enhance cannabinoid content. RF consistently outperformed other algorithms, demonstrating superior predictive capability by effectively modeling complex genetic interactions and non‐linear relationships inherent in cannabinoid biosynthetic pathways. Moreover, multi‐trait analysis provided deeper insights into genetic interrelations, underscoring the importance of incorporating multiple related traits to capture the holistic biological context of cannabinoid biosynthesis. Significant loci identified through this study present novel targets for breeding programs, offering the potential for developing cannabis strains optimized for specific therapeutic and commercial needs. In conclusion, this pioneering work bridges critical gaps in cannabis genetic research, providing a foundation for more sophisticated breeding strategies and promising pathways for creating cannabis varieties with enhanced, specific cannabinoid profiles. The integration of genomic tools and ML in cannabis breeding holds substantial promise for the future, enabling precise genetic selection that could revolutionize the industry by aligning cultivation practices with targeted product development, ultimately contributing to the sustainability and profitability of the burgeoning global cannabis market.

MATERIALS AND METHODS

Metabolomic data collection

All research activities, including the procurement and cultivation of cannabis plants, were conducted in accordance with our cannabis research license (LIC‐QX0ZJC7SIP‐2021) and full compliance with Health Canada's regulations. In this study, we utilized 176 drug‐type accessions, which were previously extensively phenotyped by Lapierre, de Ronne, et al. (2023). This population has been developed from diverse genetic background cannabis varieties to ensure representation of the broad spectrum of drug‐type cannabis varieties available in the legal Canadian market.

Biochemical analysis of trimmed and dried flowers was conducted at the Metabolomics Platform in the Institute of Nutrition and Functional Foods (INAF), Université Laval, Québec, QC, Canada, following procedures outlined by Lapierre, de Ronne, et al. (2023). This analysis facilitated the quantification of 11 distinct cannabinoids, with seven cannabinoids selected for this study based on the availability of quantitative data across all samples. These include THCA, D9THC, CBDA, CBD, CBGA, CBG, and CBC.

Genotyping

Prior to the genomics selection, all samples underwent genotyping by de Ronne et al. (2024) using the HD‐GBS method (Torkamaneh et al., 2021). 486 M paired‐end sequencing reads were processed with Fast‐GBS v2.0 (Torkamaneh et al., 2020) and mapped against the C. sativa cs10 v2 reference genome (GenBank acc. no. GCA_900626175.2). Quality control procedures, including multiple filters, were applied, and missing data were imputed using methods described by Torkamaneh and Belzile (Torkamaneh & Belzile, 2021), resulting in 800K SNPs uniformly distributed across the genome. Additionally, a further filtration step was conducted to retain biallelic variants with heterozygosity lower than 50% and a Minor Allele Frequency (MAF) >0.06 located on assembled chromosomes. Subsequently, a final catalog of approximately 250K SNPs was retained for genomic selection analysis.

Statistical analyses

To address potential errors in the phenotypic data, a wide range of pre‐processing procedures was implemented using the AllInOne preprocessing R package version 1.9.5 (Najafabadi et al., 2023). All assessed traits were centered and standardized to ensure data accuracy. The average value of each trait was estimated using a BLUP method, which accounted for multiple sources of variables as random (Bauer et al., 2006). This analysis was done using the following statistical equation (Equation 1):

$$Y=Z_g+X_a+\epsilon$$ (1)

where Y denotes the observed phenotypic trait, g is a vector of random genotype effects which are normally distributed N(0, ${\mathit{\sigma }}_{\mathit{g}}^{\mathbf{2}}$ ). The vector a , consisting of block effects, is also incorporated in the overall mean. This is followed by ε , which is a vector of residuals with a normal distribution when estimated as N(0, ${\mathit{\sigma }}_{\mathit{\epsilon }}^{\mathbf{2}}$ ). Matrices Z and X are used to represent the incidence of the g and a effects.

Genomic prediction algorithms

Genomic best linear unbiased prediction (GBLUP)

GBLUP is founded on the premise of discerning genetic relationship to estimate the genetic breeding value of genotypes. It conceptualizes the population as a stochastic process driven by a set of underlying random effects (Clark & van der Werf, 2013). Subsequently, GBLUP uses mixed model analysis to estimate these random effects, which are then used to predict trait values according to the following equation (Equation 2):

$$y=X\beta +\mathit{Za}+\epsilon$$ (2)

where y is the observed outcome, β is the vector of fixed genetic effects, X is a design matrix of fixed effects, Za is a design matrix of random additive genetic effects, and $\mathit{\epsilon }$ is the vector of errors. The estimation of breeding values is then derived from the predictions of Z _a .

Elastic net (EN)

Elastic net regression constitutes a regularized regression method that combines both L1 and L2 regularization techniques, with greater emphasis on L2 regularization (Giglio & Brown, 2018). Its primary purpose is to shrink or reduce the β ‐coefficients toward zero, while avoiding the risk of overfitting the data. The overall goal is to select a subset of features that maximizes model accuracy (Zou & Hastie, 2005). The EN algorithm attempts to solve the following optimization objective (Equation 3):

$${\min }_{\beta }\left[\frac{1}{2n}\sum _{i=1}^n{\left(y_i-x_i\beta \right)}^2+\lambda p_{\alpha }\left(\beta \right)\right]$$ (3)

where β is the vector of model coefficients, x _i is a row of the feature matrix, y _i is the corresponding target value, p is the EN penalty where $p_{\mathrm{\alpha }}\left(\beta \right)=\left(1-\alpha \right)\frac{1}{2}{\beta }_{{\lambda }_2}^2+\alpha {\beta }_{{\lambda }_1}$, $\mathit{\alpha }$ stands as a constraint to the interval, n is the total number of observations, λ is the regularization parameter, and λ ₁ and λ ₂ are the coefficients for the L1 and L2 regularization terms, respectively (Giglio & Brown, 2018).

The objective function used in regularization includes a sum of squared errors (first term) and a second term that penalizes model complexity by decreasing the size of model coefficients (Giglio & Brown, 2018; Zou & Hastie, 2005). The first term ( L2 regularization) penalizes the size of the coefficients, while the second term ( L1 regularization) encourages sparsity (Zou & Hastie, 2003). The elastic net algorithm can adjust the weights of these terms through the constants λ, λ ₁, and λ ₂, allowing for more flexibility in the model compared to traditional L1 and L2 regularized regressions (Zou & Hastie, 2003, 2005).

Bayesian approach

Bayes' Theorem encapsulates the probability of an event occurring based on conditions related to the event (Joyce, 2003). It is defined as follows (Equation 4):

$$P\left(A|B\right)=\left(P\left(B|A\right)\times P\left(A\right)\right)/P\left(B\right)$$ (4)

where P(A|B) is the probability of A occurring given B , P(B|A) is the probability of B occurring given A , P(A) is the prior probability of A occurring, and P(B) is the prior probability of B occurring.

In this study, three Bayes' Theorem‐based algorithms, namely Bayes A, Bayes B, and Bayes C, were utilized. These algorithms are variants of Bayesian regression models commonly employed in genomic prediction and association studies. Bayes A assigns non‐zero prior probabilities to all markers (Knürr et al., 2011), Bayes B assumes a mixture of null and non‐null marker effects (Wakefield et al., 2010), and Bayes C incorporates marker effects as random variables following a distribution with shrinkage parameters (Knürr et al., 2013). Each algorithm offers distinct advantages and may be suitable for different genomic prediction scenarios.

For all the tested Bayesian algorithms, an internal number of iterations (20 000) with a burn‐in of 2000 and a thinning interval of 100 were used to obtain the highest accuracy. In addition, in order to reduce computing time, other iterations and burn‐ins were tested but found to have no impact on the prediction accuracy.

Random Forest (RF)

Random Forests is an ensemble learning technique that uses multiple decision trees to make predictions (Fawagreh et al., 2014; Yoosefzadeh‐Najafabadi et al., 2023). Each decision tree is trained on a different subset of the data, and their predictions are aggregated to produce a final estimate (Yoosefzadeh‐Najafabadi et al., 2023). The RF algorithm operates by training multiple decision trees on different randomly selected subsets of the data, thereby, reducing the risk of overfitting associated with individual decision tree. Additionally, the randomness helps improve accuracy by creating a more diverse set of decision trees. During the prediction phase, each trained decision tree contributes a prediction, which is then averaged to generate the final prediction. As such, RF harnesses the collective strength of multiple decision trees to yield a more robust and accurate model (Fawagreh et al., 2014). The general equation for a RF is expressed as follows (Equation 5):

$$Y=\frac{1}{n}\sum _{t=1}^{n}t\left(X\right)$$ (5)

where Y is the predicted value based on the input features X , N is the number of decision trees in the ensemble, t is a single decision tree in the ensemble, and t(X) is the predicted output of the decision tree t for input features X .

Support vector regression (SVR)

Support Vector Regression is a linear regression algorithm that uses support vector machine (SVM) as the predictive model (Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022). Unlike linear regression, which simply fits a straight line through the data, SVR can capture nonlinear relationships by mapping the dependent variable into a higher‐dimensional space (Yoosefzadeh‐Najafabadi, Rajcan, & Eskandari, 2022). In SVR, the goal is to find a function that best fits the given data. This function is represented as a hyperplane within a higher‐dimensional space, and the model is trained by minimizing an objective function. This function, known as the objective function, is typically a quadratic programming problem, as shown in equation (Equation 6):

$$\min f\left(w,b\right)=\frac{1}{2}\times w^2+C+\sum {\left(l_i-t_i\right)}^2$$ (6)

where w is a vector of parameters, b is the bias term, C is a regularization parameter, l _(i) is the predicted output (denoted as y(x)), and t _(i) is the target output. The objective function is minimized by adjusting the parameters w and b to their optimal values, which are found using gradient descent.

To determine the optimal values, the parameters must satisfy certain constraints. As an example, parameter vectors are typically constrained to reside within a certain margin from the data points, thereby defining a tolerance margin. Once the parameters are determined, the resulting hyperplane is used to predict data points. As such, the model is trained by minimizing the objective function, where the output of the model's output is a function of both the input data points and the parameters w and b . The goal is to find the parameters that yield the lowest error when predicting future data points.

Quantification of model performance and error estimations

In order to thoroughly evaluate each tested GS method, the results of error estimation metrics were computed using a fivefold cross‐validation (CV) technique (Schaffer, 1993) with 10 repetitions. The root mean squared error (RMSE) was calculated from the mean and standard deviation values using Equation (7).

$$\text{RMSE}=\sqrt{\frac{\sum {\left({\mathrm{Y}}^{\prime }-Y\right)}^2}{n}}$$ (7)

where Y represents the observed value, Y′ stands for the predicted value, and n is the number of observations.

Furthermore, the coefficient of determination (R ²) value of each trait was averaged over the number of repetitions to obtain an overall R ² value. R ² values range between 0 and 1, with values approaching 1 indicating a more accurate model fit, considered a perfect fit (Equation 8).

$$R^2=\frac{\mathrm{SST}-\mathrm{SSE}}{\mathrm{SST}}$$ (8)

where SSE and SST represents the sum of squares for error and total, respectively.

Reduce dimensionality using Monte Carlo Feature Selection and Interdependency Discovery (MCFS‐ID)

Monte Carlo Feature Selection and Interdependency Discovery (MCFS‐ID) was used to reduce dimensionality in genomic data. It utilizes Monte Carlo simulations and statistical testing to identify important features and interdependencies among all SNP variables, facilitating targeted and efficient dimensionality reduction (Dramiński et al., 2011). The first step involves inputting the genomic data into the algorithm. MCFS‐ID then estimates a relative importance of each SNP marker by constructing a different set of trees from randomly selecting a subset of input variables (Dramiński et al., 2010). These trees undergo training and evaluation in an inner loop using different training and testing datasets created based on a selected subset of input variables (Figure 5). This process is repeated multiple times to create a distribution of mutual information scores, enabling the determination of the statistical significance of each feature (Dramiński et al., 2010). After selecting the relevant features, MCFS‐ID then proceeds to identify interdependencies among them. This is achieved through a series of statistical tests, including Pearson correlation and mutual information analysis (Dramiński et al., 2010, 2011). The results of these tests are used to construct a dependency network, offering a visual representation of the relationships between the selected features. Features that are highly interconnected in the network are considered to have strong interdependencies, indicating their importance in understanding the underlying structure of the data.

Figure 5.

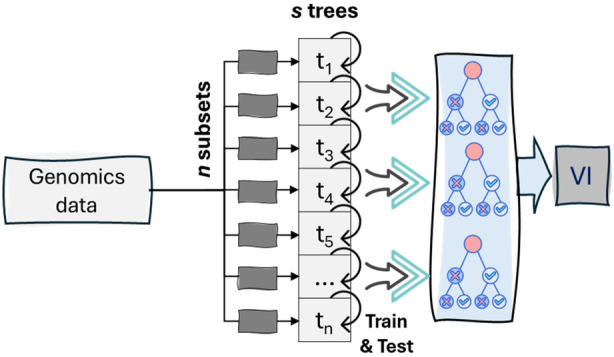
Visual representation of the key steps in the MCFS algorithm. Trees are trained and tested using different datasets (subsets), creating mutual information scores to determine the statistical significance of each feature. Relevant features are selected, and interdependencies are identified, resulting in a dependency network that shows the relationships between features. Highly interconnected features are considered important in understanding the data.

Multi‐trait genome prediction

To enhance the predictive accuracy and efficacy of our genomic selection strategies, a multi‐trait GS approach was implemented following the identification of the most effective ML algorithm from our single‐trait GS analyses. This multi‐trait approach focused on four key cannabinoids (CBD, CBG, CBC, and D9THC) which are all biosynthetically derived from the precursor CBGA. Each of these cannabinoids, along with their respective precursors, was included in the analysis to harness synergistic effects that could potentially enhance the predictive modeling. The genotypic data for these traits were integrated using the MCFS‐ID approach to refine our dataset, effectively reducing noise and focusing on genotypic information most relevant to cannabinoid biosynthesis.

Extracting putative candidate genes underlying detected SNPs

The genes that may have the potential to be candidate genes were extracted from the reference genome of C. sativa (cs10; https://www.ncbi.nlm.nih.gov/assembly/GCA_900626175.2, accessed on 28 March 2024). The flanking regions, 20 kb [based on decay distance of linkage disequilibrium (LD) to its half (Figure S1)], of peak SNPs linked with the trait of interest were used to extract genes residing within those regions (de Ronne et al., 2024). Additionally, in order to identify and understand the biological mechanisms of the genes associated with the desired trait, biomart from Ensembl Plants (Bolser et al., 2016) and Uniprot (UniProt Consortium, 2014) were used accordingly.

Visualizing and statistical analysis

The results were visualized using ggplot2 (Wickham, 2011), and ggvis packages (Dennis, 2016) in the R software version 4.3.1. All pre‐processing steps and all description statistical procedures were conducted using AllInOne preprocessing R shiny package version 1.0.5 (Najafabadi et al., 2023). Also, all ML algorithms were implemented using BWGS R package version 0.2.1 (Charmet et al., 2020) and tidymodels R package version 1.2.0 (Kuhn et al., 2020).

AUTHOR CONTRIBUTIONS

DT conceptualized, designed, and directed the experiments, and wrote the manuscript; MYN conceptualized the scheme of the analyses, developed algorithms, performed analyses, summarized results, and wrote the manuscript; MYN and DT revised the manuscript and validated the results. All authors have read and approved the final manuscript.

CONFLICT OF INTEREST STATEMENT

The authors have not declared a conflict of interest.

Supporting information

Figure S1. Linkage Disequilibrium (LD) Decay plot of the tested Cannabis panel.

Table S1. The list of detected genes for the measured cannabinoids in the tested cannabis panel.

DATA AVAILABILITY STATEMENT

The raw data supporting the conclusions of this article will be available without undue reservation.