Abstract
Determining phylogenetic relationships between species is a difficult problem, and many phylogenetic relationships remain unresolved, even among eutherian mammals. Repetitive elements provide excellent markers for phylogenetic analysis, because their mode of evolution is predominantly homoplasy-free and unidirectional. Historically, phylogenetic studies using repetitive elements have relied on biological methods such as PCR analysis, and computational inference is limited to a few isolated repeats. Here, we present a novel computational method for inferring phylogenetic relationships from partial sequence data using orthologous repeats. We apply our method to reconstructing the phylogeny of 28 mammals, using more than 1000 orthologous repeats obtained from sequence data available from the NISC Comparative Sequencing Program. The resulting phylogeny has robust bootstrap numbers, and broadly matches results from previous studies which were obtained using entirely different data and methods. In addition, we shed light on some of the debatable aspects of the phylogeny. With rapid expansion of available partial sequence data, computational analysis of repetitive elements holds great promise for the future of phylogenetic inference.
Repetitive elements, particularly SINEs (short interspersed elements) and LINEs (long interspersed elements), provide excellent markers for phylogenetic analysis: their mode of evolution is predominantly homoplasy-free, since they do not typically insert in the same locus of two unrelated lineages, and unidirectional, since they are not precisely excised from a locus with the flanking sequences preserved (Shedlock and Okada 2000). Indeed, the use of SINEs and LINEs to elucidate phylogeny has a rich history. SINEs and LINEs have been used to show that hippopotamuses are the closest living relative of whales (Shimamura et al. 1997; Nikaido et al. 1999), to determine phylogenetic relationships among cichlid fish (Takahashi et al. 2001a,b; Terai et al. 2003), and to elucidate the phylogeny of eight Primate species, providing the strongest evidence yet that chimps are the closest living relative of humans (Salem et al. 2003). In each one of these studies, the presence or absence of a repetitive element at a specific locus in a given species was determined experimentally by PCR analysis, using flanking sequences as primers. It has been suggested that such experimental studies would not make a widespread contribution to phylogenetic inference in the short term, because the time, money, and effort needed to collect data on relatively few characters would be prohibitive (Hillis 1999). We agree that the biological methods described above are highly resource-intensive. However, the set of species with partial sequence data available is rapidly expanding. Therefore, we propose instead to determine the presence or absence of a repetitive element at specific loci in each given species, and infer the resulting phylogeny, purely by computational means. Previous work has already hinted at the potential of this approach: for example, Thomas et al. (2003) identified four repetitive elements that support a Primate-Rodent clade, and Schwartz et al. (2003a) identified a repetitive element that supports a horse-Carnivore clade. Our work extends the computational analysis of repetitive elements to elucidate phylogeny to a much larger scale.
We apply our method to obtain results on the phylogeny of 28 (mostly eutherian) mammals, using sequence data from the NISC Comparative Sequencing Program (Thomas et al. 2003). We note that the phylogeny of eutherian mammals has been subject to considerable debate, as there are many instances in which previous studies reach conflicting conclusions (Amrine-Madsen et al. 2003). More recent studies (Kitazoe et al. 2004; Reyes et al. 2004) have resolved many of the differences between mitochondrial and nuclear data. However, some open questions remain. Our results shed light on these questions, and are otherwise consistent with previous results. Given the predominantly homoplasy-free, unidirectional nature of SINE/LINE insertions, and the robustness of results obtained with limited sequence, we are optimistic that, with an increased amount of sequence data available in the future, our method will be a valuable alternative to traditional phylogenetic approaches (see also Delsuc et al. 2005).
Approach
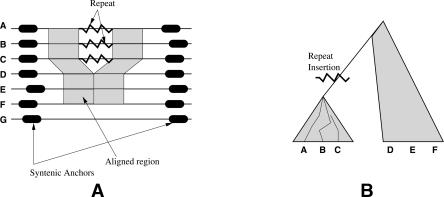
Consider a syntenic genomic region in a set of n species. Figure 1A describes this schematically for n = 7 species. The synteny is determined by flanking orthologous regions such as single-copy genes in all seven species. Further, let n1 (n1 = 3 in Fig. 1) of these n genes contain a repeat element R such that removing this repeat element results in a largely gap-free local multiple alignment of six of the seven species. The multiply aligned region is depicted by the lightly shaded areas in Figure 1A. The most parsimonious phylogeny explaining this scenario will have the three species in a clade with R inserted in a common ancestor (Fig. 1B). Any other scenario would imply either that R was inserted at exactly the same location multiple times in different species, or that the insertion of R in a species was followed by a deletion event that removed only the region containing R, and nothing else. Both of these are rare events, and therefore less plausible. The absence of a strong alignment (perhaps because of a deletion event) in G implies that neither presence, nor absence, of R can be verified. Thus, repeat R does not impose any phylogenetic constraint on G.
Figure 1.
(A) A schematic diagram of syntenic regions in three species, with a repeat insertion in A, B, and C. The lightly shaded areas correspond to regions that align well, indicating that the repeat is present in A, B, C and absent in D, E, F. Neither presence nor absence can be verified for G. (B) A likely phylogeny consistent with a parsimonious explanation of the data. Species A, B, and C belong in a clade that can be separated from D, E, and F, and the repeat was inserted in a common ancestor of the three species. There is no constraint on where G might occur. Also note that there are no constraints on where D, E, and F occur, other than they do not fall in a clade defined by the earliest ancestor of A, B, C.
As transposable repeat elements are very common, particularly in mammals, a collection of phylogenetic constraints such as the one in Figure 1B could be used to automatically construct a complete phylogeny. Through a multiple alignment procedure (to be described in detail in the Methods section), we have a collection of orthologous regions containing a subset of species in which a repeat was inserted in exactly the same location, and a disjoint subset in which the repeat was not inserted. This information is computed as an orthologous-repeats table, O (an example is shown in Table 1), with rows corresponding to species, and columns to repeats. The entries are given by
 |
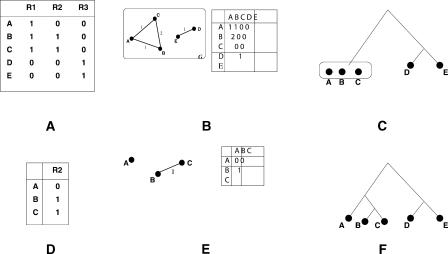
In practice, constructing accurate multiple alignments of diverged species is a challenging and highly researched problem (Bray and Pachter 2003; Brudno et al. 2003; Schwartz et al. 2003b). In order to average out possible errors in orthology computation, we use MultiPipMaker (Schwartz et al. 2003b) to compute multiple master-slave alignments, with each species in turn as the master. This leads to multiple columns for each truly orthologous Repeat, but only one column (or very few columns) for an incorrectly computed orthologous region. These columns are then filtered to retain only the ones with high sequence similarity in Repeats and flanking regions. For each column c, and triple (i, j, k), where O[i, c] = O[j, c] = 1, and O[k, c] = 0, the final phylogeny must be consistent with ((i, j), k), with the common ancestor of i and j separated from species k. Therefore, we have the following question: Given a collection of phylogenetic constraints of the form ((i, j), k), does there exist a phylogeny that is consistent with all of these constraints? This problem is well studied. Aho et al. (1981) and Pe'er et al. (2004) show that the tree, if it exists, can be constructed efficiently. M. Henzinger, V. King, and T. Warnow (unpubl.) devise a more efficient algorithm for this problem, and Kannan et al. (1998) consider many extensions. These algorithms only work if the data are error free; therefore, we cannot use them directly. Instead, we use a small modification of Aho et al.'s algorithm to handle errors. The algorithm is described below, with Figure 2 illustrating an example with n = 5 species, and three repeats.
Table 1.
An orthologous-repeats table containing a sampling of repeats
| Repeat occurrence | |||||||
|---|---|---|---|---|---|---|---|
| Human | 1 | 1 | 1 | ? | 0 | ? | ? |
| Chimp | 1 | 1 | 1 | 0 | 0 | ? | ? |
| Baboon | 1 | 1 | 0 | 0 | 0 | ? | ? |
| Mouse | 1 | 0 | 0 | 1 | 0 | ? | ? |
| Rat | ? | 0 | ? | 1 | 0 | ? | ? |
| Cat | ? | 0 | 0 | 0 | 1 | 1 | 0 |
| Dog | 0 | 0 | 0 | 0 | ? | 1 | 0 |
| Cow | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Pig | 0 | 0 | 0 | ? | 1 | ? | 1 |
Each column corresponds to a specific repeat. The symbol 1 corresponds to the presence, and 0 to the absence, of that repeat. (?) indicates missing data, when neither presence nor absence of the repeat could be confirmed.
Figure 2.
Sketch of phylogeny reconstruction from the orthologous-repeats table. (A) An orthologous-repeats table with five species and three repeats. (B) The resulting shared-repeat graph. We also illustrate the graph in matrix form. Note that the connected components of the graph correspond to clades in the final phylogeny. (C) One of the two clades has two species and is therefore resolved. The other has three species, and needs to be resolved further. (D) The orthologous-repeats subtable of species A, B, and C. Only repeat R2 contains two 1s and one 0. (E) The resulting shared-repeat subgraph resolves species A, B, and C. (F) The final phylogeny.
Construct a weighted, undirected shared-repeat graph G = (V, E, w), with each species corresponding to a vertex in G. For repeat r, let N1(r) be the subset of species that contain this repeat. For all repeats r, and all (i, j) ∈ N1(r), increment the weight w(i, j). Figure 2B illustrates the corresponding shared-repeat graph G.
Recurse to construct a subtree for each unresolved connected component of G. While recursing on a component containing the subset Nc, we only consider columns that contain at least two 1s and one 0 when restricted to rows in Nc. In the example, we only need to recurse on {A, B, C}. When restricted to those rows only R2 contains two 1s and one 0 (Fig. 2C,D,E).
Construct the tree by connecting the root to the subtrees from each connected component (Fig. 2F).
As described, the algorithm does not handle the case in which the shared-repeat graph yields a single connected component. This could happen if some repetitive elements lead to contradictory phylogenetic scenarios. Previous biological studies that used repetitive elements to elucidate phylogeny typically included a small number of contradictory loci. For example, in their analysis of Alu elements to determine Primate phylogeny, Salem et al. (2003) identified seven loci with an Alu element clearly present in human and chimp genomes and clearly absent from gorilla, and one locus with an Alu element clearly present in human and gorilla and clearly absent from chimp; they concluded that the contradictory locus was due to incomplete lineage sorting: the Alu element at that locus was polymorphic at the time of divergence of gorilla from human and chimp, remained polymorphic at the time of divergence of chimp from human, and eventually became fixed in human and gorilla lineages but not in chimp. Incomplete lineage sorting and the incompatible loci they create can complicate any phylogenetic analysis, but generally should not pose a problem in phylogenetic analyses using repetitive elements, as long as a sufficiently large number of independent loci are examined (Shedlock and Okada 2000).
In an automated analysis of thousands of repeats, rare instances of insertion homoplasy may also appear. According to Shedlock and Okada (2000), SINEs and LINEs are predominantly homoplasy-free, but hotspots of insertion may occur in exceptional cases. Indeed, Cantrell et al. (2001) have identified a locus containing two such hotspots, leading to SINE insertion homoplasy in multiple rodent species. We have found evidence of insertion homoplasy in our own data set: Figure 3 illustrates that a strong alignment appears to exist for a SINE repeat in cat and rat, while the absence of this repeat is strongly supported in baboon, cat, dog, cow, pig, and mouse, implying a phylogeny that is almost certainly incorrect. This repeat that is shared by cat and rat in an orthologous location is not an error, but accurately reflects the actual sequence data. Incomplete lineage sorting does not seem to be a plausible explanation for this example, as polymorphism of the presence or absence of the repeat would need to persist from the time of divergence of Rodents and Laurasiatheria (cat, dog, cow, pig) through the time of divergence of cat and dog, which seems unlikely. We speculate instead that this may be a rare instance of insertion homoplasy.
Figure 3.
Multiple alignment for an incompatible repeat in the orthologous-repeats table of nine species with finished sequence. Repeats annotated by RepeatMasker (A.F.A. Smit and P. Green, unpubl., RepeatMasker, http://www.repeatmasker.org/) are indicated in lowercase.
The (rare) presence of repeats that are incompatible with the correct phylogeny leads to two questions. First, how can we determine the correct phylogeny in the presence of conflicting evidence? Second, given a set of orthologous repeats that are incompatible with the correct phylogeny, how can we determine if these are instances of insertion homoplasy, incomplete lineage sorting, or erroneous alignment? In this paper, we focus primarily on the first question. Thus, we take the conservative approach of discarding repeats that are incompatible with the correct phylogeny. However, the second question is one of independent interest. For example, insertion homoplasy has important ramifications for repeat subfamily analysis, and evidence of incomplete lineage sorting may shed light on speciation hypotheses (Salem et al. 2003; Osada and Wu 2005). In the Results section, we describe putative instances of each of these causes of incompatible repeats.
We now describe our approach to discarding repeats that are incompatible with the correct phylogeny. One possibility is to look at target-site duplications, the regions on either side of a repeat element that were duplicated at the time of repeat insertion. Previous studies have used matching target-site duplications to confirm that orthologous repeats correspond to a single insertion event in a common ancestor (Thomas et al. 2003). However, target-site duplications can be difficult to identify if they are short and/or highly diverged; thus using target-site duplications to automatically discern instances of insertion homoplasy in a large-scale analysis is a considerable (and perhaps insurmountable) challenge. Therefore, we instead use the following three approaches: First, in the case of insertion homoplasy, the orthologous repeats differed at the time of insertion and hence show greater divergence. Thus, we can use the statistic
% SIMILARITY IN FLANKING REGION - % SIMILARITY IN REPEAT REGION.
Large positive values of this statistic suggest possible insertion homoplasy (see Fig. 5 below, and Results on the performance of this statistic). This statistic could also be high if the flanking regions were functionally important. However, that is a rare event, and discarding repeats with high values of the statistic is conservative. For the second approach, recall that each orthologous repeat describes a subtree that should be compatible with the overall phylogeny. Repeats that are incompatible with the true phylogeny are likely to be incompatible with subtrees from many other repeats; this incompatibility can be tested without reconstruction of the phylogeny (see Methods: Incompatibility Removal). We show in our Results that all incompatibilities in our data are explained by a small number of repeats. Finally, the presence of such repeats leads to a single connected component in the shared-repeat graph with the incompatible repeats being among the lowest weight edges. We iteratively remove minimum weight edges until the shared-repeat graph is no longer connected. In practice, we have found that the minimum weight is quite small, and the resulting phylogenies are robust (see Results). Our method includes the following steps:
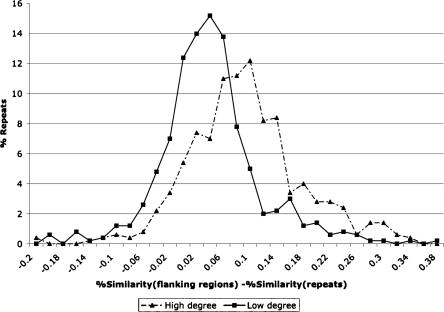
Figure 5.
Distribution of the difference statistic among columns with high and low degrees of incompatibility. The statistic measures the difference in sequence similarity between flanking and repeat regions. Repeats that show incompatibility to many other repeats may often be caused by insertion homoplasy. These repeats show larger values of the difference statistic.
Identify repeats in all of the sequences.
Use a genome multiple alignment tool to compute a multiple alignment of all sequences. The specific tool used, MultiPipMaker, builds a multiple alignment from n - 1 master-slave alignments of a single sequence against all others.
Construct an n × m orthologous-repeats table O, in which the m columns arise from orthologous repeats using each sequence in turn as a Master.
Repeat with each sequence as the Master sequence to construct a complete orthologous-repeats table.
Remove Repeats (columns in the table) that are incompatible.
Construct a complete phylogeny from the orthologous-repeats table.
Compute Bootstrap values of the phylogeny to determine robust branches.
These steps are described in detail in the Methods section.
Results
Species with finished sequence
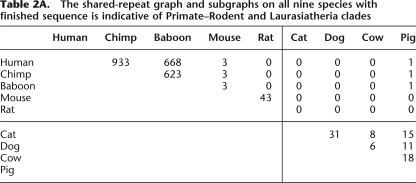
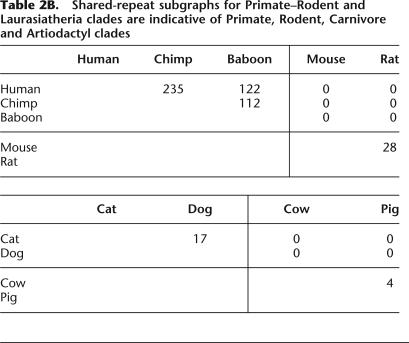
We first applied our method to nine species with finished sequence data presently available, using sequence data from the 1.5-Mb 7q31 region (see Methods). We constructed an orthologous-repeats table containing 1101 columns after removal of incompatible repeats (see Supplemental material). The resulting shared-repeat graph is displayed in Table 2A. After omitting edges of weight 1, this shared-repeat graph splits into two connected components: a Primate-Rodent clade (human, chimp, baboon, mouse, rat) and a Laurasiatheria clade (cat, dog, cow, pig). Reapplication of the method to these clades produces the shared-repeat subgraphs displayed in Table 2B. The Primate-Rodent subgraph is indicative of a Primate clade (human, chimp, baboon) and a Rodent clade (mouse, rat); the Laurasiatheria subgraph is indicative of a Carnivore clade (cat, dog) and an Artiodactyl clade (cow, pig). Finally, reapplication of the method to the Primate clade produces the shared-repeat subgraph displayed in Table 2C, which is indicative of a human-chimp clade. Combining all of these results, we obtain a phylogenetic tree of nine species (see figure in Supplemental material S1). The tree is completely consistent with a larger one of 28 mammalian species (Fig. 4).
Table 2.
Table 3.
Table 4.
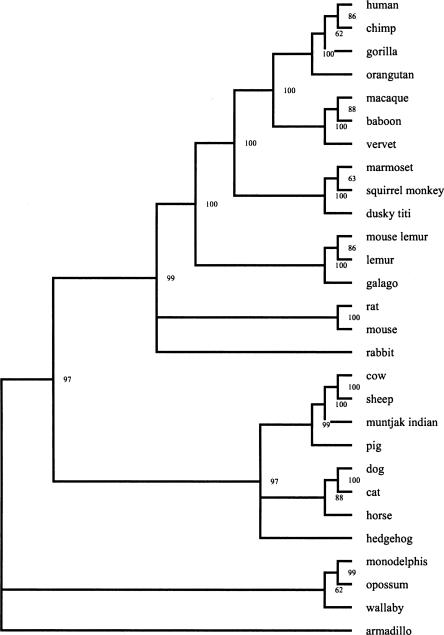
Figure 4.
Phylogenetic tree of a large set of 28 species. Bootstrap support values are based on 1000 bootstrap replicates. Tree image created using TREEVIEW (Page 1996).
A larger set of species
We subsequently applied our method to a larger set of 28 (mostly eutherian) mammals with partial sequence data available, again using sequence data from the 1.5-Mb 7q31 region (see Methods). We constructed an orthologous-repeats table containing 4775 columns after removal of incompatible repeats (see Supplemental material), and constructed a shared-repeat graph (see Supplemental material S2). The resulting phylogenetic tree is displayed in Figure 4. Each node is labeled by a bootstrap support value for that clade, obtained from an analysis of 1000 bootstrap replicates. The consensus bootstrap tree was reconstructed using Consense, part of the Phylip package (http://evolution.genetics.washington.edu/phylip.html; Felsenstein 2004). Results for parts of the tree where previous studies reached conflicting conclusions are discussed in detail below (see Discussion). Otherwise, our tree is entirely consistent with previous studies. In particular, our phylogeny of the 13 Primate species in our data set agrees exactly with the widely accepted phylogeny of Primates (Purvis 1995), and nearly all Primate phylogeny branches are supported by high bootstrap values. For example, we have identified hundreds of repeats that correctly separate (baboon, macaque, vervet, chimp, human, gorilla, orangutan) and (dusky titi, marmoset, squirrel monkey) from (galago, lemur, mouse lemur), and <10 repeats that support alternate resolutions of this trichotomy. Each one of these incompatible repeats is consistent with insertion homoplasy;4 the incompatible repeats are removed from the orthologous-repeats table during the incompatibility removal step. These numbers, and the resulting 100% bootstrap support for the correct resolution of this trichotomy, illustrate the robustness of our approach in dealing with instances of insertion homoplasy.
Assessment of incompatible repeats
As discussed earlier, a few of the repeats are instances of insertion homoplasy, which can complicate phylogenetic analyses. If there is no instance of insertion homoplasy, then each pair of columns (i.e., repeats) in the orthologous-repeats table should be “compatible” in that none of the implied phylogenies contradict each other. In the Methods section, we describe the simple three-gamete condition that can be used to check incompatibility. Such incompatibilities are common in molecular sequence data, but should be rare for repeat insertion data. We define an “incompatibility graph” on the columns of the orthologous-repeats table. Each column is a node in the graph. Two columns are connected by an edge if they are not compatible. The columns that contain an instance of insertion homoplasy lead to phylogenies that are incompatible with many others, and therefore, correspond to high-degree nodes. Note also that if the repeats were inserted independently, their divergence from the flanking regions should be higher than repeats that were inserted in a common ancestor of the sequence. For each of the columns in the table, we computed the difference in percent similarity between the flanking regions and the repeat regions. To determine if this can be used as a statistic to detect independently inserted repeats, we looked at the distribution of this number for the 500 highest and the 500 lowest degree nodes in the incompatibility graph. See Figure 5. While the true distributions overlap, they have distinct means of 8.6% for high-degree, and 3.2% for the low-degree nodes. A t-test to determine if the means were equal gave a P-value of 1.1e-32. Based on this, we remove all columns for which the difference is 7.5% or higher.
This columns removal procedure still retains some instances of insertion homoplasy, but these show up as high-degree nodes in the incompatibility graph. We constructed incompatibility graphs for the nine organism data set as well as the complete 28 organism data set. For the nine species, there were a total of 1101 columns, of which 717 nodes were connected by 821 edges. However, all edges are incident to only four nodes, and removing them would remove all incompatibilities from the graph. The 28 organism data set has similar characteristics. There were a total of 4833 columns with 28,859 edges involving 3716 columns. However, removal of 58 highest-degree columns eliminates all incompatible edges. In our method, we iteratively remove the highest degree node until no incompatible edge remains.
In order to validate our results, we manually examined each of the 58 incompatible repeats. Of these, 38 are consistent with insertion homoplasy according to the above criteria, that is, there exist two clades whose union contains all species with the repeat clearly present and no species with the repeat clearly absent. Of the 38 putative instances of insertion homoplasy, 23 correspond to Alu repeats in primates; we further analyzed the subfamily history of these repeats with respect to known Alu subfamily classification (Price et al. 2004). In nearly every case, for the two clades described above, subfamily membership was concordant within clades but discordant between clades (see Supplemental material S3), strongly supporting the insertion homoplasy hypothesis of two distinct repeat insertion events in the ancestor of each clade. For additional discussion and alignments, see Supplemental material S3.
Discussion
The phylogeny of eutherian mammals has been subject to considerable debate, as there are many instances in which previous studies reached conflicting conclusions (Amrine-Madsen et al. 2003). In particular, various placements of Rodents, horse, rabbit, and hedgehog have been reported, as we discuss below. More recent studies (Kitazoe et al. 2004; Reyes et al. 2004) have resolved many of the differences between mitochondrial and nuclear data, but leave open questions regarding the placement of armadillo and muntjak, which our results address.
We first discuss the placement of Rodents, that is, resolution of the trichotomy between Rodents, Primates, and Laurasiatheria (Carnivores, Artiodactyls, etc.). Some studies report a Primate-Rodent clade (Murphy et al. 2001; Amrine-Madsen et al. 2003), while others report the divergence of Rodent from a Primate-Laurasiatheria clade (Arnason et al. 2002; Misawa and Janke 2003). In our analysis, we identified two repeats separating Primates and Rodents from Laurasiatheria. Our results agree with Thomas et al. (2003), who identified four repetitive elements that support a Primate-Rodent clade. However, our automated approach failed to discover three of the four repeats mentioned by Thomas et al. (2003). These three repeats (all MLT10A0 repeats) failed because they (1) did not align to the flanking region on one side of the repeat, (2) showed significantly weaker alignment within the repeat region than the flanking regions, or (3) were slightly below our flanking region threshold. We note that our nine organism run was sensitive enough to select one of the aforementioned MLT10A0 repeats for support of the Primate-Rodent clade.
Another interesting example is the placement of horse in the phylogenetic tree. Early studies of horse, Carnivores, and Artiodactyls reported a horse-Artiodactyl clade (Graur et al. 1997), while more recent studies report a horse-Carnivore clade (Murphy et al. 2001; Arnason et al. 2002). In our analysis, we identified one repeat separating horse and Carnivores from Artiodactyls. It is notable that our program discovers the same L1MA9 repeat that Schwartz et al. (2003a) used to establish the horse-Carnivore clade. The alignment of this repeat (with flanking sequence) can be seen in Supplemental material S5.
The placement of rabbit in the phylogenetic tree has been the subject of considerable debate. The resolution of the trichotomy between rabbit, Primates, and Laurasiatheria has been variously reported as (Laurasiatheria, (rabbit, Primate)) (Murphy et al. 2001), (Primate, (rabbit, Laurasiatheria)) (Arnason et al. 2002), or (rabbit, (Primate, Laurasiatheria)) (Misawa and Janke 2003). We identified four repeats separating rabbit and Primates from Laurasiatheria, strongly supporting (Laurasiatheria, (rabbit, Primate)). We further note that the Murphy et al. studies confirm the Glires hypothesis of a rabbit-Rodent clade, while the Arnason et al. and Misawa and Janke studies reject the Glires hypothesis. Although we neither confirm or reject the Glires hypothesis, owing to our unresolved (rabbit, Rodent, Primate) trichotomy, our rabbit results are inconsistent with the two studies rejecting the Glires hypothesis.
Our placement of hedgehog inside the Laurasiatheria clade and armadillo outside the clade containing Primates, Rodents, and Laurasiatheria is consistent with Murphy et al. (2001), but inconsistent with Arnason et al. (2002), which places armadillo inside the Laurasiatheria clade and hedgehog outside the clade containing Primates, Rodents, and Laurasiatheria. We identified two repeats separating hedgehog and Laurasiatheria from Primates and Rodents.
Recent studies (Kitazoe et al. 2004; Reyes et al. 2004) agree with our placement of Rodents, horse, rabbit, and hedgehog, but still leave some open questions. For example, armadillo has been variously placed outside the clade containing Primates, Rodents, and Laurasiatheria (Murphy et al. 2001; Kitazoe et al. 2004); inside Laurasiatheria (Arnason et al. 2002); or inside the clade containing Primates and Rodents (Reyes et al. 2004). Our results agree with Murphy et al. and Kitazoe et al.: we identified one repeat separating Primate/Rodent and Laurasiatheria clades from armadillo. Our placement of Marsupials (wallaby, monodelphis, opossum) outside the clade containing Primates, Rodents, and Laurasiatheria is widely consistent with previous studies (Murphy et al. 2001; Arnason et al. 2002). We note that because of the inadequate representation of Marsupial repeat families in Repbase (Jurka 1998, 2000), proper placement of Marsupials in our phylogenetic tree would not have been possible without our use of the RepeatScout algorithm (Price et al. 2005) to identify additional repeat families (see Methods). Finally, we comment on the (cow, sheep, muntjak) trichotomy: Reyes et al. (2004) report a ((cow, muntjak), sheep) resolution, but we report ((cow, sheep), muntjak), supported by 23 repeats separating cow and sheep from muntjak.
Overall, we consider our generation of a phylogenetic tree of 28 mammalian species using orthologous repeats in 1.5 Mb of sequence to be an encouraging result; although other methods based on protein-coding sequence use far less data, our method can be applied to arbitrary DNA sequence, as produced by large comparative sequencing efforts. It is notable that all of our results are consistent with the Murphy et al. (2001) study, despite having been obtained via entirely different means. Our bootstrap values are slightly lower than other studies in which nearly all bootstrap support values exceed 95% (Murphy et al. 2001; Arnason et al. 2002; Misawa and Janke 2003). However, these conflicting studies, each supported by high bootstrap values, cannot all be correct. Indeed, recent articles point to exaggerated bootstrap support values for the Bayesian methods used in some of these studies (Misawa and Nei 2003). We note that our own procedure creates multiple columns for each orthologous repeat, which may lead to higher bootstrap values. Because our multiple alignment method creates multiple columns for each truly orthologous repeat but only one column (or very few columns) for an incorrectly computed orthologous repeat, we feel that this is justified.
We anticipate that with additional data and improved repeat-finding tools, we will obtain higher bootstrap values and resolve the unresolved trichotomies in our tree. In addition, we hope to further reduce the incidence of phylogenetically incompatible repeats, many of which may be due to insertion homoplasy; exploring the possible use of target-site duplications toward this goal is an important direction of our ongoing research. A caveat of our approach is that it results in a large amount of missing data; little work has been done to assess the statistical impact of missing data in phylogenetic inference, and varying opinions have been expressed in the literature on the issue of missing data in phylogenetic studies using orthologous repeats (Hillis 1999; Shedlock et al. 2000). One direction that we will consider is to adapt methods from “quartet puzzling.” The term refers to approaches for obtaining reliable ML estimates of trees by combining information from unrooted quartets (Schmidt et al. 2002). In our data set, each column corresponds to a partial tree on a subset of species, which should be amenable to quartet puzzling.
Repetitive elements provide excellent markers for phylogenetic analysis, because their mode of evolution is predominantly unidirectional and homoplasy-free. Our approach allows us to isolate and investigate the evidence from each repeat, and is robust enough to deal with thousands of repeats. We are optimistic that going forward, our method will be a valuable alternative to traditional phylogenetic approaches.
Methods
Data
Sequences were collected from the NIH Intramural Sequencing Center, NISC Comparative Sequencing Program (Thomas et al. 2003). The set of sequences used were from target reference 7q31, Encode Name Enm001, a region ∼1.5 Mb in size. The sequences themselves ranged from 1.2 Mb (pig) to 2.3 Mb (marmoset). To obtain preliminary data for organisms with unpublished 7q31 sequence, the entire 7q31 data set was scanned. GenBank files, for accession numbers from that data set, were retrieved; from these files the corresponding sequences were extracted. Contigs were joined to one another via overlap information embedded within each GenBank file. Note that the concatenated sequences are not complete, and the alignment introduces gaps.
Repeat identification
For the nine organism data set, repeat-annotated sequences were obtained from supplemental data of Thomas et al. (2003). For the 28 organism data set, repeat elements were identified by running RepeatMasker (A.F.A. Smit and P. Green, unpubl., RepeatMasker, http://www.repeatmasker.org/) using a repeat library derived from the set of mammalian repeat families in Repbase (Jurka 1998, 2000) plus additional repeat families identified by RepeatScout (Price et al. 2005). RepeatMasker was run at the default setting for speed/sensitivity.
Multiple alignments
Multiple alignments were generated via MultiPipMaker (Schwartz et al. 2003a). MultiPipMaker is a tool for aligning multiple, long (megabase size) genomic DNA sequences quickly and with good sensitivity. The program takes as input a single reference sequence and multiple secondary sequences; additionally, one of the following options must be selected: show all matches, chaining, or single coverage. Alignments are first computed by pairwise BLASTZ alignments, and subsequent refinements, between the reference organism and each secondary sequence. MultiPipMaker then looks at subalignments within the global multiple alignment to see if modifications can be made to improve the overall score of the alignment. Since our sequences were variable in length and since the alignments generated by MultiPipMaker are most relevant as alignments to the reference sequence, it was necessary to rerun MultiPipMaker with each organism as reference sequence. This generates multiple columns for a single orthologous repeat, but has the advantage of averaging over data. Repeats erroneously marked as orthologous with a single master sequence are unlikely to show up with other master sequences, and will have a low weight in the shared-repeat graph. Thus, for our n organisms we generated n multiple alignments (the ordering of the secondary sequences was irrelevant). Moreover, the chaining option was selected to avoid duplicate matches caused by the “show all matches” option, that is, a single region in the reference sequence aligning to two regions in a secondary sequence. This option was selected over single coverage because (1) the secondary sequences were assumed to be contiguous, (2) the comparisons were made with a single strand of the secondary sequence, and (3) the order of conserved regions was assumed identical in the two sequences (Schwartz et al. 2003b).
Identifying orthologous insertions
For each MultiPip alignment, our algorithm iterated through the reference organism's RepeatMasker generated repetitive element list, ignoring all nontransposable element-based repeats (such as LTRs and simple repetitive repeats). For each repeat considered, the corresponding orthologous region in each secondary organism as well as a 50-nt upstream and downstream flanking region were retrieved. For a repeat to be considered present in a secondary organism's sequence, it must strongly align in the repeat region and within both flanking regions. See Supplemental material S4 for assessment of flanking region alignments. For a repeat to be considered absent from a secondary organism's sequence, it must strongly align within both flanking regions, while gapping out the repeat region. Such an alignment may not always be possible. A deletion in the region, for example, might make it impossible to determine if the repeat was deleted after insertion, or if it was never inserted. If neither set of requirements is satisfactorily met, the presence of the repeat is considered uncertain for that secondary organism's sequence. In the case of a partial repeat, if the base organism repeat is a full-length repeat and it aligns to a partial repeat in a secondary organism (or vice versa), the repeat is considered uncertain for the secondary organism. However, if the base organism has a partial repeat and the same partial repeat region is seen within a secondary organism, it is considered to be present in the secondary organism. Using this methodology, an orthologous-repeats table is generated. Each row of the repeat represents an organism, and each column represents a given repeat. The presence of a repeat is indicated with a 1, the absence with a 0, and uncertainty with a?.
Incompatibility removal
Two repeats (columns in the orthologous-repeats table) are incompatible if they lead to conflicting phylogenies. Such incompatibility can be tested directly by using the rule of three-gamete violation. An incompatibility occurs for two columns (i, j) in the orthologous-repeats table if and only if there exist three species A, B, and C that contain 0,1, (1,0), and (1,1) in the columns i and j, as shown in Table 3A (e.g., see Gusfield 1997).
Table 3A.
Incompatible columns in the orthologous-repeats table; columns i and j are incompatible because they violate the three-gamete condition
| i | j | |
|---|---|---|
| A | 0 | 1 |
| B | 1 | 0 |
| C | 1 | 1 |
Construct an incompatibility graph. Each column is a node in the graph, and a pair of columns (i, j) forms an edge if (i, j) are incompatible. We must compute a “minimum vertex cover” of this graph (Garey and Johnnson 1979), that is, we must remove a minimum number of columns such that no incompatibilities remain. The problem is computationally hard in general, but our results show that a greedy heuristic works fine. Also, the graphs we obtain are almost bipartite (contain no cycles of odd length), for which the problem is tractable.
We iteratively remove the column with the highest degree (number of incompatible edges), and recompute the degree of each column, and repeat until no incompatibility remains. This revised orthologous-repeats table is then fed into our tree-building algorithm. We note that there are rare cases in which there is no explicitly incompatible pair but the ambiguities “?” still lead to incompatibilities, as illustrated in Table 3B. In this example, resolving the ambiguity of C at repeat i as a 0 leads to an incompatibility between i and j. On the other hand, resolving it as a 1 leads to an incompatibility between i and k. Such rare cases of indirect incompatibility lead to the shared-repeat graph having a single connected component. We deal with these cases in phylogeny reconstruction (see below).
Table 3B.
Incompatible columns in the orthologous-repeats table; columns i, j, k are incompatible together as any resolution of the ambiguity for species C in column i leads to an incompatibility
| h | i | j | k | l | |
|---|---|---|---|---|---|
| A | 1 | 1 | 1 | 0 | 0 |
| B | 1 | 1 | 0 | 0 | 0 |
| C | ? | ? | 1 | 1 | 1 |
| D | 0 | 0 | ? | 1 | 1 |
As columns i and k are supported by h and l, respectively, column j corresponds to a weak edge and is removed during phylogeny reconstruction, resolving the incompatibility.
Shared-repeat graph generation and phylogeny reconstruction
The following procedure is an implementation of the algorithm presented by Aho et al. (1981) with modifications for dealing with incompatibilities.
A subset of the orthologous-repeats table is created, in which only “relevant” rows (organisms) are considered (initially all rows, since all organisms are being considered). Within this subset of rows, only those columns in which at least two rows have a 1 and one row has a 0 are considered.
Using this subset of the original repeat occurrence table, a graph is created by iterating through the columns. If two rows both have a 1 in a given column, an edge of weight 1 is created between the two corresponding organisms. If an edge already exists between those two organisms, its weight is incremented by 1.
Multiple connected components are sought within the graph. If the graph contains a single connected component, weak edges must be eliminated. This is accomplished by removing edges, beginning with those of weight 1 and incrementally removing edges of greater weight, until multiple connected components arise.
Steps 1-3 are recursively applied to each connected component containing more than two organisms. The “relevant” rows in each run are the organisms within the connected component.
Consider the above example illustrated in Table 3B. The phylogenetic inference of column i is supported by column h, and column k is supported by column l. Thus, in the shared-repeat graph, edges (A, B) and (C, D) have weight 2, while the edge (A, C) has weight 1. Removing the minimum weight edge is akin to removing column j, which has the least support.
Finally, we perform a nonparametric bootstrapping of our data. A 1000 pseudoreplicates were generated by randomly sampling the orthologous repeats table (generated after removal of incompatible repeats) to create new orthologous repeat tables of the same size as the original. From this set of 1000 trees, we were able to obtain a consensus tree with bootstrap values using the Consense program (Felsenstein 2004).
Acknowledgments
The utilized sequence data were generated by the NIH Intramural Sequencing Center (www.nisc.nih.gov).
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.3493405.
Footnotes
[Supplemental material is available online at www.genome.org.]
In each case, there exist two clades whose union contains all species with the repeat clearly present and no species with the repeat clearly absent, supporting the hypothesis of two distinct repeat insertion events in the ancestor of each clade.
References
- Aho, A.V., Sagiv, S.Y., Szymanski, T.G., and Ullman, J.D. 1981. Inferring a tree from lowest common ancestors with an application to the optimization of relational expressions. Siam J. Comput. 10: 405-421. [Google Scholar]
- Amrine-Madsen, H., Koepfli, K., Wayne, R.K., and Springer, M.S. 2003. A new phylogenetic marker, apolipoprotein B, provides compelling evidence for eutherian relationships. Mol. Phylogenet. Evol. 28: 225-240. [DOI] [PubMed] [Google Scholar]
- Arnason, U., Adegoke, J.A., Bodin, K., Born, E.W., Esa, Y.B., Gullberg, A., Nilsson, M., Short, R.V., Xu, X., and Janke, A. 2002. Mammalian mitogenomic relationships and the root of the eutherian tree. Proc. Natl. Acad. Sci. 99: 8151-8156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray, N. and Pachter, L. 2003. MAVID multiple alignment server. Nucleic Acids Res. 31: 3525-3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno, M., Do, C.B., Cooper, G.M., Kim, M.F., Davydov, E., Green, E.D., Sidow, A., and Batzoglou, S. 2003. LAGAN and Multi-LAGAN: Efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 13: 721-731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantrell, M.A., Filanoski, B.J., Ingermann, A.R., Olsson, K., DiLuglio, N., Lister, Z., and Wichman, H.A. 2001. An ancient retrovirus-like element contains hot spots for SINE insertion. Genetics 158: 769-777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delsuc, H., Brinkmann, H., and Philippe, H. 2005. Phylogenomics and the reconstruction of the tree of life. Nat. Rev. Genet. 6: 361-375. [DOI] [PubMed] [Google Scholar]
- Felsenstein, J. 2004. PHYLIP Phylogeny Inference Package version 3.61. Distributed by the author. Department of Genome Sciences, University of Washington, Seattle. http://evolution.genetics.washington.edu/phylip.html.
- Garey, M.R. and Johnson, D.S. 1979. Computers and intractability: A guide to the theory of NP-completeness. W.H. Freeman, New York.
- Graur, D., Gouy, M., and Duret, L. 1997. Evolutionary affinities of the order Perissodactyla and the phylogenetic status of the superordinal taxa Ungulata and Altungulata. Mol. Phylogenet. Evol. 7: 195-200. [DOI] [PubMed] [Google Scholar]
- Gusfield, D. 1997. Algorithms on strings, trees and sequences: Computer science and computational biology. Cambridge University Press, Cambridge, UK.
- Hillis, D.M. 1999. SINEs of the perfect character. Proc. Natl. Acad. Sci. 96: 9979-9981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurka, J. 1998. Repeats in genomic DNA: Mining and meaning. Curr. Opin. Struct. Biol. 8: 333-337. [DOI] [PubMed] [Google Scholar]
- ———. 2000. Repbase Update: A database and an electronic journal of repetitive elements. Trends Genet. 9: 418-420. [DOI] [PubMed] [Google Scholar]
- Kannan, S., Warnow, T., and Yooseph, S. 1998. Computing the local consensus of trees. SIAM J. Comput. 27: 1695-1724. [Google Scholar]
- Kitazoe, Y., Kishino, H., Okabayashi, T., Watabe, T., Nakajima, N., Okuhara, Y., and Kurihara, Y. 2004. Multidimensional Vector space representation for convergent evolution and molecular phylogeny. Mol. Biol. Evol. 22: 704-715. [DOI] [PubMed] [Google Scholar]
- Misawa, K. and Janke, A. 2003. Revisiting the Glires concept-phylogenetic analysis of nuclear sequences. Mol. Phylogenet. Evol. 28: 320-327. [DOI] [PubMed] [Google Scholar]
- Misawa, K. and Nei, M. 2003. Reanalysis of Murphy et al.'s data gives various mammalian phylogenies and suggests overcredibility of Bayesian trees. J. Mol. Evol. 57 Suppl 1: S290-S296. [DOI] [PubMed] [Google Scholar]
- Murphy, W.J., Eizirisk, E., O'Brien, S.J., Madsen, O., Scally, M., Douady, C.J., Teeling, E., Ryder, O.A., Stanhope, M.J., de Jong, W.W., et al. 2001. Resolution of the early placental mammal radiation using Bayesian phylogenetics. Science 294: 2348-2351. [DOI] [PubMed] [Google Scholar]
- Nikaido, M., Rooney, A., and Okada, N. 1999. Phylogenetic relationships among cetartiodactyls based on insertions of short and long interspersed elements: Hippopotamuses are the closest extant relatives of whales. Proc. Natl. Acad. Sci. 96: 10261-10266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osada, N. and Wu, C.I. 2005. Inferring the mode of speciation from genomic data: A study of the Great Apes. Genetics 259-264. [DOI] [PMC free article] [PubMed]
- Page, R.D.M. 1996. TREEVIEW: An application to display phylogenetic trees on personal computers. Comput. Appl. Biosci. 12: 357-358. [DOI] [PubMed] [Google Scholar]
- Pe'er, I., Pupko, T., Shamir, R., and Sharan, R. 2004. Incomplete directed perfect phylogeny. SIAM J. Comput. 33: 590-607. [Google Scholar]
- Price, A.L., Eskin, E., and Pevzner, P.A. 2004. Whole genome analysis of Alu repeat elements reveals complex evolutionary history. Genome Res. 2245-2252. [DOI] [PMC free article] [PubMed]
- Price, A.L., Jones, N.C., and Pevzner, P.A. 2005. De novo identification of repeat families via extension of consensus seeds. ISMB (in press). [DOI] [PubMed]
- Purvis, A. 1995. A composite estimate of primate phylogeny. Phil. Trans. Roy. Soc. Lond. B 348: 405-421. [DOI] [PubMed] [Google Scholar]
- Reyes, A., Gissi, C., Catzeflis, F., Nevo, E., Pesole, G., and Saccone, C. 2004. Congruent mammalian trees from mitochondrial and nuclear genes using Bayesian methods. Mol. Biol. Evol. 21: 397-403. [DOI] [PubMed] [Google Scholar]
- Salem, A.H., Ray, D.A., Xing, J., Callinan, P.A., Myers, J.S., Hedges, D.J., Garber, R.K., Witherspoon, D.J., Jorde, L.B., and Batzer, M.A. 2003. Alu elements and hominid phylogenetics. Proc. Natl. Acad. Sci. 100: 12787-12791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt, H.A., Strimmer, K., Vingron, M., and von Haeseler, A. 2002. TREE-PUZZLE: Maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics 18: 502-504. [DOI] [PubMed] [Google Scholar]
- Schwartz, S., Elnitski, L., Li, M., Weirauch, M., Riemer, C., Smit, A., NISC Comparative Sequencing Program, Green, E.D., Hardison, R.C., and Miller, W. 2003a. MultiPipMaker and supporting tools: Alignments and analysis of multiple genomic DNA sequences. Nucleic Acids Res. 31: 3518-3524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, S., Zhang, Z., Frazer, K.A., Smit, A., Riemer, C., Bouck, J., Gibbs, R., Hardison, R., and Miller, W. 2003b. PipMaker—A Web server for aligning two genomic DNA sequences. Genome Res. 10: 577-586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shedlock, A.M. and Okada, N. 2000. SINE insertions: Powerful tools for molecular systematics. BioEssays 22: 148-160. [DOI] [PubMed] [Google Scholar]
- Shedlock, A.M., Milinkovitch, M.C., and Okada, N. 2000. SINE evolution, missing data, and the origin of whales. System. Biol. 49: 808-817. [DOI] [PubMed] [Google Scholar]
- Shimamura, M., Yasue, H., Ohshima, K., Abe, H., Kato, H., Kishiro, T., Goto, M., Munechika, I., and Okada, N. 1997. Molecular evidence from retroposons that whales form a clade within even-toed ungulates. Nature 388: 666-670. [DOI] [PubMed] [Google Scholar]
- Takahashi, K., Nishida, M., Yuma, M., and Okada, N. 2001a. Retroposition of the AFC family of SINEs before and during the adaptive radiation of cichlid fishes in Lake Malawi and related inferences about phylogeny. J. Mol. Evol. 53: 496-507. [DOI] [PubMed] [Google Scholar]
- Takahashi, K., Terai, Y., Nishida, M., and Okada, N. 2001b. Phylogenetic relationships and ancient incomplete lineage sorting among cichlid fishes in Lake Tanganyika as revealed by analysis of the insertion of retroposons. Mol. Biol. Evol. 18: 2057-2066. [DOI] [PubMed] [Google Scholar]
- Terai, Y., Takahashi, K., Nishida, M., Sato, T., and Okada, N. 2003. Using SINEs to probe ancient explosive speciation: “Hidden” radiation of African cichlids? Mol. Biol. Evol. 20: 924-930. [DOI] [PubMed] [Google Scholar]
- Thomas, J.W., Touchman, J.W., Blakesley, R.W., Bouffard, G.G., Beckstrom-Sternberg, S.M., Margulies, E.H., Blanchette, M., Siepel, A.C., Thomas, P.J., McDowell, J.C., et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424: 788-793. [DOI] [PubMed] [Google Scholar]
Web site references
- http://evolution.genetics.washington.edu/phylip.html; PHYLIP.
- http://www.nisc.nih.gov/; NIH Intramural Sequencing Center.
- http://www.repeatmasker.org/; RepeatMasker.