Abstract
Magnonics, which harnesses the unique properties of spin waves, offers promising advancements in data processing due to its broad frequency range, nonlinear dynamics, and scalability for on-chip integration. Effective information encoding in magnonic systems requires precise spatial and temporal control of spin waves. Here, we demonstrate the rapid optical control of spin-wave transport in hybrid magnonic-plasmonic structures. By using thermoplasmonic heating in yttrium iron garnet films integrated with gold nanodisk arrays, we achieve a suppression of spin-wave signals by 20 dB using single laser pulses lasting just a few hundred nanoseconds. Our results reveal a strong correlation between plasmonic light absorption and spin-wave manipulation, as supported by micromagnetic simulations that emphasize the crucial role of magnonic refraction. This study establishes thermoplasmonics as a powerful tool for controlling spin-wave propagation, bridging the fields of magnonics and plasmonics, and paving the way for the development of multifunctional hybrid magnonic devices.
Thermoplasmonic heating enables efficient and rapid optical control of spin-wave transport in a low-loss magnonic medium.
INTRODUCTION
Magnonics exploits the fundamental properties of spin waves to enable innovative data processing solutions (1–3). This emerging technology offers several compelling advantages, such as low-power operation over a broad frequency range from gigahertz to terahertz (4), nonlinear (5–7) and nonreciprocal (8–13) spin-wave dynamics, and on-chip scalability (13, 14). These characteristics position magnonics as a promising candidate for next-generation information processing systems. A critical requirement for effective information encoding in magnonic systems is the ability to actively control spin waves with high spatial and temporal resolution. Information can be encoded in the amplitude or phase of spin waves (15, 16), necessitating precise manipulation techniques. Furthermore, active control of spin-wave transport is essential for the development of other magnonic devices, such as magnonic neuromorphic systems (17–20), which could use these mechanisms to achieve task-adaptive reconfigurability (21). Spin-wave propagation can be manipulated by coupling their dynamics to other physical domains, such as electric currents (22–24), voltages (25–27), or light (28–31). Extending all-optical control of magnetism (32) to spin-wave transport holds the potential of being fast, but the diffraction of light limits its spatial resolution.
Plasmonics, a subfield of nanophotonics, explores the interaction between electromagnetic waves and free electrons in metallic nanostructures, enabling light manipulation beyond the diffraction limit (33). By confining optical fields into tiny volumes, plasmonics facilitates the design of compact optical devices, including advanced imaging and sensing technologies (34, 35). Thermoplasmonics, a subdiscipline of plasmonics, investigates the heat dynamics resulting from localized optical fields (36). When plasmonic nanostructures absorb light, they efficiently convert it into heat, creating localized temperature rises that can be precisely controlled. Heat generation in these structures occurs on ultrafast timescales—femtoseconds to picoseconds—as light energy is quickly converted into electronic excitations and subsequently phonons. This rapid initial heating is followed by a slower diffusion process, typically on the order of nanoseconds, during which heat spreads into the surrounding medium.
The convergence of magnetism and plasmonics has spurred the emergence of magneto-plasmonics (37–39), a multidisciplinary field where magnetic fields are used to influence plasmonic properties, such as the wavelength of surface plasmon polaritons (SPPs) (40) and plasmonic lasing (41). At the same time, plasmon modes are leveraged to manipulate magneto-optical and magnetic effects. For instance, magneto-plasmonics has been used to enhance magneto-optical effects (42, 43), achieve energy-efficient all-optical magnetic switching (44, 45), and generate optical gyromagnetic properties (46). Although research into magnon-plasmon interactions is still in its infancy, it is gaining momentum. Experiments have demonstrated the generation of spin currents through surface plasmon resonances in ferrimagnetic insulators (47), attributed to nonequilibrium magnon excitation. Theoretical studies have also predicted magnon-plasmon hybridization in graphene-magnetic heterostructures and two-dimensional (2D) antiferromagnets (48–50), as well as the excitation of surface plasmon-phonon-magnon polaritons in topological insulator-antiferromagnetic bilayer structures (51). Despite these promising advances, the full potential of integrating magnonics and plasmonics remains largely untapped, particularly with respect to interactions between coherent spin waves and plasmon modes on short timescales.
Here, we demonstrate of rapid optical control of propagating spin waves in hybrid magnonic-plasmonic structures. Our results show that moderate thermoplasmonic heating of an yttrium iron garnet (YIG) film by a gold (Au) nanodisk array, induced by single laser pulses lasting approximately 500 ns, results in a 20-dB suppression of spin-wave transmission between two microwave antennas. This plasmonic switching mechanism enables precise manipulation of spin-wave signals with high spatial and temporal resolution, offering substantial potential for applications in wave-based information processing.
RESULTS
Optical control of spin-wave transmission by plasmon mode excitation
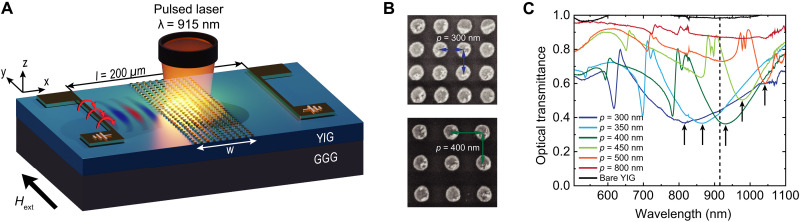
Figure 1A depicts the hybrid magnonic-plasmonic structure and measurement geometry. Two parallel microwave antennas, separated by 200 μm, are used to measure the spin-wave transmission in a 250-nm–thick YIG film integrated with an array of Au nanodisks. Plasmon resonances are excited using a pulsed laser at 915 nm wavelength. To study the effect of plasmon mode excitation on spin-wave transport in the YIG film, we vary the array period (p) from 300 to 800 nm (Fig. 1B), while keeping the Au disk diameter (d) fixed at 180 nm. Adjusting the array period shifts the wavelength of the collective surface lattice resonance (SLR), a hybrid mode resulting from the coupling of localized surface plasmon resonances (LSPRs) on the Au nanodisks to the diffracted light wave in the plane of the array (52, 53). The SLR mode for different p values is indicated by arrows in the optical transmittance spectra shown in Fig. 1C. The SLR, which red shifts with increasing array period, considerably enhances the absorption of light in the hybrid magnonic-plasmonic structure compared to the bare YIG film. At the laser wavelength (915 nm) used to manipulate spin waves in the YIG film, the plasmonic array with p = 400 nm absorbs most of the incident light. More information on SLR-mode excitation is provided in the Supplementary Text.
Fig. 1. Hybrid magnonic-plasmonic structure, measurement geometry, and optical properties.
(A) Schematic of the experimental configuration. Spin-wave transmission in a 250-nm–thick YIG film is measured between two parallel microwave antennas using a VNA. The antennas with a 3-nm Ti/120-nm Au structure are 6 μm wide and 50 μm long. The distance between the antennas is 200 μm. Plasmonic nanodisk arrays with a rectangular shape are patterned between the antennas on the YIG film. The nanodisks, consisting of 3-nm Ti and 50-nm Au, have a diameter of 180 nm. Within the array, the nanodisks are arranged on a square lattice (px = py) whose period is varied from 300 to 800 nm. The width of the arrays (w), in the direction of spin-wave propagation, is either 50 or 120 μm. Laser pulses with a wavelength of 915 nm illuminate the plasmonic array. The laser spot on the YIG film is 70 μm in diameter. The laser power and pulse length are varied in the experiments, with the maximum power reaching 16.6 W and the pulse length ranging from 100 to 600 ns. A magnetic bias field saturates the YIG film’s magnetization parallel to the antennas and perpendicular to the direction of spin-wave propagation direction, consistent with the Damon-Eshbach geometry. (B) Scanning electron microscopy images of selected Au nanodisk arrays on the YIG film. (C) Optical transmittance spectra of Au plasmonic nanodisk arrays with varying periods on the YIG film. The vertical dashed line indicates the 915-nm wavelength used in the spin-wave experiments, while the arrows mark the SLR wavelengths for the different plasmonic nanodisk arrays.
Spin waves propagating between the two microwave antennas are optically controlled by focusing the 915-nm laser onto the plasmonic array (Fig. 1A). The laser spot diameter is 70 μm. Broadband spin-wave transmission spectra, recorded by a vector network analyzer (VNA) during 150-kHz laser pulsing with 500-ns pulses at 16.6-W laser power (Fig. 2A), reveal that spin waves in the YIG film are minimally affected by laser irradiation in the absence of the plasmonic array. This is consistent with the negligible light absorption by the bare YIG film (Fig. 1C). However, when the laser illuminates a plasmonic array on top of the YIG film, the spin-wave transmission signal is substantially diminished. Notably, the nanodisk arrays do not affect the measurement when the laser is OFF (see fig. S1). The suppression of the spin-wave signal by the laser depends on the array period (Fig. 2B), with the strongest attenuation of 20 dB [corresponding to an amplitude ratio S12(ON)/S12(OFF) = 0.1] observed for p = 400 nm. Comparing the optical transmittance data (Fig. 1C) and the spin-wave transmission results (Fig. 2, A and B) reveals a clear correlation between the extent of light absorption by the plasmonic array and the degree of spin-wave suppression in the YIG film. An exception is seen for p = 450 nm, likely due to the excitation of an optical waveguide mode in the YIG film at 915 nm for this array period (see fig. S3).
Fig. 2. Optical control of broadband spin-wave transmission.
(A) Spin-wave transmission spectra recorded for a bare YIG film and the same film with different plasmonic arrays. Measurements are taken during continuous laser pulsing (150 kHz pulse frequency, 500 ns pulse length, and 16.6 W laser power). A reference spectrum, recorded with the laser OFF, is also shown. The strong signal attenuation near 2.0 GHz, present in all spectra, is attributed to hybridization between the first two branches of the dipolar spin-wave modes in the 250-nm–thick YIG film (see fig. S2). (B) Variation of the spin-wave transmission signal at 1.84 and 2.14 GHz extracted from (A), alongside the optical transmittance at 915 nm (from Fig. 1C), as a function of the plasmonic array period. (C) Spin-wave transmission spectra recorded at various laser powers (150 kHz pulse frequency, 500 ns pulse length, and 400 nm array period). (D) Spin-wave transmission signal at 1.84 GHz as a function of laser power and pulse length [from (C) and fig. S4]. (E) The same data as in (D), plotted against laser fluence. The data in (A) to (E) are recorded with a magnetic bias field of 14 mT. (F) Variation of the spin-wave transmission signal, averaged over the entire excitation spectrum, as a function of the magnetic bias field (150 kHz pulse frequency, 500 ns pulse length, 16.6 W laser power, and 400 nm array period). The plasmonic array has a width of 50 μm in all measurements.
Next, we examine the effect of laser power on the optical control of spin waves for the plasmonic array with p = 400 nm. As shown in Fig. 2C, increasing the laser power during 150-kHz laser pulsing with 500-ns pulses progressively suppresses the spin-wave signal across the excitation spectrum. Figure 2D plots the spin-wave signal at 1.84 GHz as a function of laser power for different pulse lengths (tp), with full spectra provided in fig. S4. The results demonstrate that spin-wave transmission decreases approximately linearly with increasing laser power for all pulse lengths. To evaluate whether temporal dynamics influences the results, Fig. 2E plots the same data against laser fluence. Because all the data points fall on a single curve, this indicates that the total energy absorbed by the system, rather than pulse length, governs the spin-wave suppression. A similar dataset for spin waves at 2.14 GHz is shown in fig. S5.
We also examined the effect of the magnetic bias field on optical spin-wave control. Data presented so far were recorded at a 14-mT bias field. Spin-wave transmission spectra measured at different bias fields, ranging from 5 to 30 mT, are shown in fig. S6. As the bias field increases, the spin-wave excitation spectrum shifts to higher frequencies. To quantify laser-induced spin-wave suppression at various magnetic fields, we averaged the transmission data collected with the laser OFF and during 150-kHz laser pulsing (500-ns pulses at 16.6 W) over the full spin-wave spectrum for each bias field. The results, summarized in Fig. 2F, show that the broadband suppression of the spin-wave transmission increases gradually as the magnetic bias field increases.
To monitor the magnonic response to single laser pulses, we synchronized the VNA and the pulsed laser using an external wave generator. Time-resolved data in Fig. 3A, recorded by sweeping the measurement-point delay of the VNA with respect to the trigger signal in a pump-probe manner at a constant spin-wave excitation frequency of 1.84 GHz (see Materials and Methods), demonstrate the suppression of spin-wave transmission by single laser pulses for the plasmonic array with a 400-nm period. The magnonic response to the laser turning ON is limited by heat diffusion in the YIG film (discussed in the next section) and the time required for spin waves to propagate from beneath the plasmonic array to the detecting microwave antenna. Given a spin-wave group velocity of 9 km/s (fig. S7) and an average array-antenna separation of 100 μm, we estimate the latter delay to be approximately 10 ns. While a single 100-ns pulse causes only a small reduction in the spin-wave signal, a 600-ns pulse suppresses the signal by 20 dB by the pulse’s end. After the laser is turned OFF, spin-wave transport between the two antennas recovers, with signal recovery following an exponential function. The recovery time constant ranges from 255 ns for the 100-ns pulse to 917 ns for the 600-ns pulse (see fig. S8). The duration of the optically induced magnonic response exceeds what would be expected from purely magneto-optical effects, such as magnetization dynamics driven by the inverse Faraday effect (54). Combined with the correlation between spin-wave suppression and light absorption (Fig. 1C), this suggests that thermoplasmonic heating via the SLR mode (55) is the dominant control mechanism.
Fig. 3. Time-resolved measurements of optical spin-wave control.
(A) Response of the spin-wave transmission signal to single laser pulses of varying length (16.6 W laser power). (B) Dependence of the spin-wave signal on laser power for single laser pulses (500 ns pulse length). (C) Maximum suppression of the spin-wave signal during irradiation by single laser pulses as a function of laser power and pulse length. (D) The same data as in (C), plotted against laser fluence. (E) Dependence of the spin-wave transmission signal on laser-pulse frequency (500 ns pulse length and 16.6 W laser power). (F) Variation of the spin-wave transmission signal as a function of laser power (150 kHz pulse frequency and 500 ns pulse length). In all measurements, the spin-wave excitation frequency is 1.84 GHz, the magnetic bias field is 14 mT, the period of the plasmonic arrays is 400 nm, and its width is 120 μm.
The dependence of spin-wave manipulation on laser power for single laser pulses is shown in Fig. 3B for a 500-ns pulse (complete data mapping the effects of pulse length and power are available in fig. S9). The suppression of the spin-wave signal as a function of laser power and fluence for different pulse lengths is depicted in Fig. 3 (C and D). These results confirm that the total energy absorbed by the system during single-shot laser irradiation determines the extent of spin-wave suppression. The influence of pulse length and laser power on the recovery time constant after laser pulsing is summarized in figs. S10 and S11.
Last, we investigate the effect of laser-pulse frequency. If the time between laser pulses is shorter than the cooling time required for the system to return to room temperature, a persistent temperature rise occurs. Although most cooling happens within 1 μs after the laser is turned OFF, full cooling to room temperature takes about 20 μs. Consequently, continuous laser pulsing at frequencies of 50 kHz or higher leads to a gradual temperature increase until a balance between heating during laser pulses and cooling between them is achieved. This effect is confirmed by time-resolved spin-wave measurements (Fig. 3E) for 500-ns pulses at 16.6 W (data for other pulse lengths are shown in fig. S12). The persistent temperature rise, which also depends on laser power (Fig. 3F), results in sustained spin-wave transmission suppression, with stronger effects at higher pulse frequencies.
Thermoplasmonic heating of the YIG film
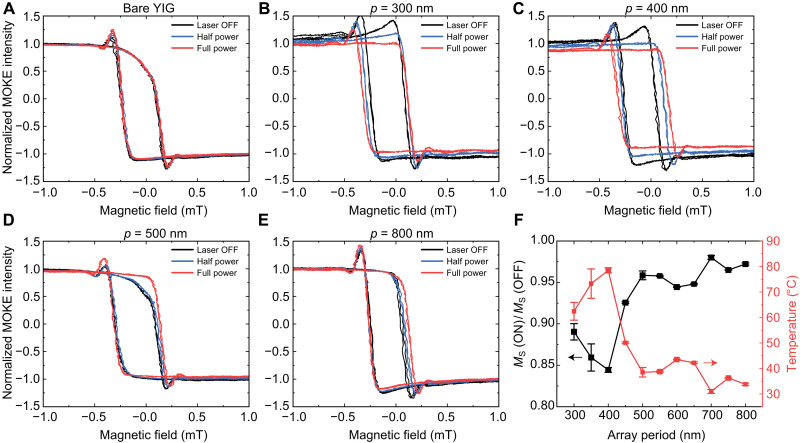
In YIG, the temperature dependence of various magnetic parameters can affect spin-wave transport during laser irradiation. For dipolar Damon-Eshbach spin waves, i.e., spin waves with a wave vector oriented perpendicular to the direction of in-plane magnetization, critical parameters include saturation magnetization, magnetic anisotropy, and magnetic damping. Our measurements do not reveal any dependence of the YIG ferromagnetic resonance (FMR) frequency on the angle of the in-plane magnetic field (fig. S13). Therefore, magnetic anisotropy can be excluded as an important parameter in our experiments. The temperature dependence of the magnetic damping parameter is measured by placing the sample on a ceramic heater and recording the FMR linewidth of the YIG film as a function of frequency (fig. S7). We find a weak non-monotonic variation of the damping parameter with temperature up to 120°C, insufficient to explain the strong suppression of spin-wave transmission during thermoplasmonic heating. Therefore, we conclude that a temporary reduction of the saturation magnetization during laser pulsing is the main reason for the optical control of spin waves in our hybrid magnonic-plasmonic structures. This is confirmed by measuring local magnetic hysteresis curves on the YIG film underneath the plasmonic array using a magneto-optical Kerr effect setup (see Materials and Methods). The hysteresis curves, recorded during continuous pulsing by the same 915-nm laser under identical conditions as in the spin-wave measurements (Fig. 2), show a clear correlation between the reduction of the YIG film magnetization and the period of the plasmonic array (Fig. 4), with p = 400 nm producing the strongest effect, consistent with the optical transmittance data (Fig. 1C).
Fig. 4. Reduction of the YIG saturation magnetization induced by thermoplasmonic heating.
(A to E) Local MOKE hysteresis curves of the YIG film, recorded beneath the plasmonic arrays during continuous laser pulsing (150 kHz pulse frequency, 500 ns pulse duration, and 16.6 W laser power). The bumps observed in the hysteresis curves near the switching field are attributed to contributions from the transverse Kerr effect. However, this effect does not influence the laser-induced reduction in saturation magnetization, which is determined from the MOKE hysteresis curves at higher magnetic fields. (F) Reduction of the saturation magnetization for different array periods, derived from the MOKE hysteresis curves. The YIG film temperature during thermoplasmonic heating is estimated from the reduction in Ms and its temperature dependence from control experiments (fig. S14).
We use the change in saturation magnetization during laser pulsing to estimate the average temperature of the YIG film underneath the plasmonic array. The variation of saturation magnetization with temperature is calibrated by placing the sample on a ceramic heater. The saturation magnetization is extracted by measuring the FMR frequency as a function of the magnetic field and fitting the data with the Kittel formula (56) (fig. S14). We find Ms(T) ≈ Ms,RT − η(T − TRT) with η = 562 AK−1 m−1 for our YIG film. Using this result and the measured reduction of Ms during laser pulsing (Fig. 4F), we estimate that the temperature of the YIG film increases to about 78°C when the 915-nm laser pulses excite an SLR mode in the plasmonic array with p = 400 nm. For the other plasmonic structures, the SLR mode is detuned from 915 nm, lowering the amount of heating through light absorption (Fig. 4F). At elevated temperatures, the reduction of Ms decreases the spin-wave group velocity, confirmed independently by temperature-dependent measurements of the spin-wave group velocity in broadband spectroscopy experiments (fig. S7).
We further analyze thermoplasmonic heating in the hybrid magnonic-plasmonic structure by conducting finite-difference time-domain (FDTD) simulations of the optical field distribution during laser pulsing (see Materials and Methods). The electric field intensity of the SLR mode excited by a normal-incident 915-nm plane wave in the plasmonic array with p = 400 nm is particularly high at the edges of the Au nanodisks and underneath the disk array in the YIG film (Fig. 5A). The effect of thermoplasmonic heating is calculated by importing the simulated optical power distribution to a HEAT solver. The temperature distribution after illuminating the plasmonic array with p = 400 nm by a 500-ns laser pulse with a power of 16.6 W is shown in Fig. 5B. The temperature increase is highest in the YIG film directly under the Au nanodisks and decreases gradually away from the Au/YIG interface. The time evolution of the temperature increase at three locations within the 250-nm–thick YIG film is depicted in Fig. 5C. When the laser pulse turns ON, the temperature at the interface between the Au nanodisks and the YIG film rises. After 500 ns of irradiation, the temperature at this interface increases to 110°C, while the temperature at the YIG/GGG interface reaches almost 80°C. Because YIG is an insulator, heat transport in the YIG film is dominated by phonons.
Fig. 5. Thermoplasmonic simulations.
(A) Electric field distribution in the hybrid magnonic-plasmonic structure with p = 400 nm simulated for a normal-incident 915-nm plane wave. Electric field distributions for the other plasmonic arrays are shown in fig. S3. (B) Temperature distribution in the same structure at the end of a 500-ns laser pulse. (C) Temperature increase during thermoplasmonic heating by a 500-nm laser pulse.
Comparing the simulated temperature during a single laser pulse (Fig. 5, B and C) and the experimental estimation of the YIG film temperature during continuous laser pulsing (Fig. 4F), it is instructive to examine the suppression of the spin-wave signal under these two conditions. The average spin-wave transmission signal at 1.84 GHz during continuous laser pulsing with f = 150 kHz, tp = 500 ns, and P = 16.6 W (Fig. 2A) is very similar to the lowest transmission signal during a single laser pulse with tp = 500 ns and P = 16.6 W (Fig. 3A). For the first condition, the YIG film temperature is estimated to be about 78°C (Fig. 4F), while FDTD simulations for single laser pulses indicate a YIG temperature of 78° to 110°C after 500 ns (Fig. 5C). The two temperature estimations and the corresponding spin-wave suppressions are in reasonable agreement, confirming thermoplasmonic heating of the YIG film as the main control mechanism of spin-wave transport.
Spin-wave suppression and redirection
To further understand the influence of thermoplasmonic heating on spin-wave propagation, we perform micromagnetic simulations using MuMax3 software (57) (see Materials and Methods). These simulations are designed to replicate the experimental configuration depicted in Fig. 1A, specifically focusing on the impact of local reductions in saturation magnetization (Ms) on spin-wave transport. For simplicity, we model two configurations: one where the reduction of Ms matches the plasmonic array’s shape and another where it corresponds to the laser spot size. In Fig. 6 (A to E), we compare the spin-wave profiles for these configurations against the profile of a bare YIG film. The reduction of Ms within the heated region is set to 85% of its room temperature value in Fig. 6 (B and D), consistent with experimental data for the plasmonic array with p = 400 nm (Fig. 4F), and it is fixed at 70% in Fig. 6 (C and E). When the shape of the heated area corresponds to that of the plasmonic array (Fig. 6, B and C), the spin-wave signal is only reduced slightly at the location of the detecting microwave antenna (x = 200 μm). This reduction, caused by a decrease of spin-wave group velocity in the heated area (fig. S7), does not fully explain the strong optical control of spin waves observed in the measurements (Figs. 2 and 3). However, when the heated area matches the laser spot size (Fig. 6, D and E), the simulated suppression of the spin-wave signal at the detecting antenna becomes more pronounced. This is due to an optically induced magnonic refraction effect (29, 30), analogous to optical refraction, where spin waves are redirected as a result of variations in the refractive index. In magnetic systems, changes in the refractive index can occur through alterations in parameters such as saturation magnetization, magnetic anisotropy, film thickness, or external magnetic field. These changes may be gradual, as in graded refractive index materials (58–60), or abrupt, occurring at magnetic interfaces (61, 62). In cases of abrupt changes, the redirection of spin waves adheres to a modified version of Snell’s law, which governs refraction at non-normal angles between the wave vector and the magnetic interface. In our hybrid magnonic-plasmonic system, the local reduction in Ms caused by laser-induced heating leads to spin-wave redirection when the heating area matches the circular laser spot size (Fig. 6, D and E). The relationship between the spin-wave signal at the detecting antenna and the reduction in Ms is summarized in Fig. 6F, with additional supporting data provided in figs. S15 and S16. The micromagnetic simulations assume a uniformly heated area in the YIG film, an assumption justified by the minimal temperature variations observed in the thermoplasmonic simulations (Fig. 5B). Moreover, Bragg scattering from the Au nanodisk array heating pattern does not occur, as the spin-wave wavelength is one to two orders of magnitude larger than the array period. This is further corroborated by the absence of bandgaps in the spin-wave transmission spectra.
Fig. 6. Micromagnetic simulations.
(A to E) Simulated spin-wave maps and line profiles at 1.84 GHz for (A) the bare YIG film, [(B) and (C)] the YIG film with a uniformly heated area matching the shape of the rectangular plasmonic array, and [(D) and (E)] the YIG film with a uniformly heated circular area matching the laser spot size. In (B) and (D), Ms is reduced to 85% of its room temperature value in the heated areas, whereas in (C) and (E), it is reduced to 70%. The shorter spin-wave wavelength in the area with reduced Ms is due to a downward shift of the dispersion curve (fig. S17). A 14-mT magnetic field is applied along the y axis in all simulations. (F) Suppression of the spin-wave signal at the detecting antenna (x = 200 μm) for the rectangular and circular heating patterns as a function of reduced Ms.
DISCUSSION
Heating as a tool of controlling spin-wave transport has been implemented through various techniques. For instance, nanoscale magnonic structures have been fabricated using thermally assisted magnetic scanning probe lithography (63, 64), which induces permanent magnetic changes. In addition, optically induced heating of thick YIG films on the millimeter scale has been explored for spin-wave redirection (29, 30) and attenuation (28, 31). In these experiments, the heating patterns were produced by continuous light illumination or by laser pulsing on a timescale of milliseconds.
Hybrid magnonic-plasmonic structures enable high-resolution, time-sensitive optical control of spin-wave transport. A collective plasmon mode dominates light absorption in our devices, decoupling it from the YIG medium, which absorbs minimally for wavelengths above 550 nm (65). This decoupling extends the operational spectral range into the infrared, facilitating thermoplasmonic manipulation of spin waves in an optically transparent YIG film. The structural parameters of the plasmonic metamaterial, such as nanodisk shape, size, and the array period, can be easily tuned to maximize light absorption at the laser wavelength.
While we focused on collective SLRs, other plasmon modes like LSPRs or SPPs could also be used in hybrid magnonic devices. On ultrashort timescales, the spatial resolution of thermoplasmonic heating is limited by plasmon mode localization. LSPRs in metal nanostructures offer excellent near-field confinement and are widely used in high-resolution biosensing (66). In magnonics, LSPRs in variously shaped nanostructures could induce high-resolution heating profiles, enabling the creation of optically controlled magnonic elements such as lenses and waveguides.
In our proof-of-principle experiments, we used laser fluences ranging from about 10 to 260 mJ/cm2 and laser powers between 3.5 and 16.6 W to manipulate spin-wave transport. These fluence values are one to two orders of magnitude higher than those typically required for all-optical switching in thin magnetic films using femtosecond laser pulses (on the order of a few mJ/cm2) (32). Similarly, the power used is one to two orders of magnitude higher than the ~100-mW laser power used in heat-assisted magnetic recording (HAMR) (67), a commercial technology that increases the storage density of hard disk drives by temporarily heating the disk material during writing. Further reductions in energy consumption can be achieved in magnonic-plasmonic hybrids through device downscaling, which brings several benefits. First, downscaling would enable laser focusing to a smaller spot, maintaining similar fluence levels while drastically reducing the laser power. Second, because the timescale of thermoplasmonic heating scales with the square of the heat source size (36), focusing the laser on a single or a few plasmonic nanostructures would not only expedite spin-wave control but also lower the necessary fluence. Third, further improvements could be made by decreasing the thickness of the YIG film and patterning it into 1D waveguides, commonly used in magnonic devices (13, 14). This would reduce the heating volume and limit lateral heat diffusion. Collectively, these optimizations could bring the required laser fluence and power well below those of other optically controlled magnetic switching technologies.
In summary, we have demonstrated the optical control of spin-wave transport in hybrid magnonic-plasmonic structures, consisting of a YIG film and a Au nanodisk array, using laser pulses with lengths of a few hundred nanoseconds. The primary mechanism behind these effects is the reduction in the YIG film’s magnetization through thermoplasmonic heating. Looking ahead, we anticipate that thermoplasmonics can be leveraged to actively manipulate the amplitude, phase, or direction of spin waves in functional devices. Plasmonics offers a versatile toolkit for designing time-dependent heating patterns in magnonics at specific wavelengths. By combining this with shorter and more intense laser pulses, it will be possible to further minimize the spatial and temporal scales of optical control, opening previously unexplored avenues for magnonic device applications.
MATERIALS AND METHODS
Sample fabrication
We grew YIG films with a thickness of 250 nm on double-sided polished GGG(111) substrates using PLD. The GGG substrates were ultrasonically cleaned in acetone and isopropanol, then degassed at 550°C for 10 min inside the deposition chamber. Following this, oxygen was introduced into the chamber, and the temperature was raised to 850°C at a rate of 5°C/min. YIG films were deposited from a stoichiometric target in an oxygen partial pressure of 0.13 mbar at this temperature. An excimer laser with a pulse repetition rate of 2 Hz and a fluence of 1.8 J/cm2 was used. After film growth, we annealed the YIG films at 750°C for 10 min in an oxygen environment of 13 mbar, then cooled them down to room temperature at a rate of −3°C/min. The deposition process resulted in single-crystal YIG films, as confirmed by x-ray diffraction and transmission electron microscopy measurements.
Plasmonic nanodisk arrays were patterned using electron beam lithography. Following the development of the polymethyl methacrylate resist, 3 nm Ti/50 nm Au was deposited using electron-beam evaporation. The plasmonic nanodisk arrays underwent liftoff in hot acetone. The geometry of the fabricated arrays and the quality of the liftoff process were inspected by scanning electron microscopy. The diameter of the plasmonic nanodisks was fixed at 180 nm and the array period was varied from 300 to 800 nm. Parallel microwave antennas with a separation of 200 μm were fabricated by maskless photolithography and liftoff. The antennas, consisting of 3-nm Ti and 120-nm Au, were 6 μm wide and 50 μm long.
Broadband spin-wave spectroscopy
We performed spin-wave transmission measurements using a two-port VNA (Agilent N5222A) and a home-built probe station equipped with a quadrupole electromagnet. Spin-wave transmission spectra were obtained by recording the S12 scattering parameter. The excitation power of the microwave signal was set at −10 dBm to avoid nonlinear spin-wave excitation. All experiments were conducted in the Damon–Eshbach configuration with a magnetic bias field applied parallel to the microwave antennas. For the optical control of propagating spin waves, we integrated a pulsed near-infrared laser diode (AeroDiode 915LD-4-2) into the setup. The laser had a wavelength of 915 nm and a maximum power of 16.6 W. In the experiments, the pulse frequency, pulse length, and laser power were varied. The laser power was experimentally calibrated using a Thorlabs S405C power sensor. The laser illuminated the plasmonic nanodisk arrays at normal incidence with a spot size of approximately 70 μm.
Time-resolved spin-wave transmission measurements
We used the internal delay-after-trigger function of the VNA (Agilent N5222A) to conduct time-resolved measurements of the S12 scattering parameter at fixed frequencies. To synchronize the VNA and the pulsed laser (AeroDiode 915LD-4-2), both devices were connected to a common trigger source, a Keysight 33220A arbitrary waveform generator. The laser diode’s synchronization module provided precise control over the delay between the laser pulse and the trigger signal. In the experiments, the trigger signal defined time zero, and the laser was set to a fixed delay of 1.3 μs from the leading edge of the trigger. The onset of the VNA’s S12 parameter measurement was also referenced to this external trigger. Time-resolved spin-wave signals were acquired by sweeping the VNA’s internal trigger-measurement delay in a pump-probe manner. To reduce noise, each delay step was averaged 5 or 10 times, with the VNA’s intermediate frequency bandwidth set to 1.5 MHz.
Magneto-optical Kerr effect measurements
We used a home-built longitudinal magneto-optical Kerr effect (MOKE) setup to estimate the reduction in saturation magnetization during laser irradiation. Local MOKE hysteresis loops of the YIG film were recorded by focusing a 405-nm p-polarized laser onto the plasmonic nanodisk array. The probe laser, incident at 45°, had a spot size of 50 μm. The measurements were conducted with nearly crossed polarizers (analyzer opening angle of approximately 7°), and the reflected light was detected using a photodiode. In this configuration, the detected light intensity reflects the longitudinal Kerr effect, which is proportional to the magnetization component parallel to the applied magnetic field. However, there is also a contribution from the transverse Kerr effect, proportional to the magnetization component perpendicular to the applied field. The transverse Kerr effect is only relevant near the magnetic switching field and does not influence the reduction in saturation magnetization derived from the MOKE hysteresis loops at higher magnetic fields. We used the same near-infrared laser diode (AeroDiode 915LD-4-2) as in the spin-wave spectroscopy measurements to excite the plasmonic arrays at 915 nm under identical conditions. The excitation laser (spot size, 70 μm) and MOKE probing laser (spot size, 50 μm) were carefully overlapped to characterize the effect of thermoplasmonic heating on the saturation magnetization of the YIG film. To reduce noise, the MOKE hysteresis loops were averaged over 20 field sweeps.
Optical transmittance measurements
We used an optical spectrometer with a supercontinuum laser (NKT Super EXW 12) and a tunable filter (SuperK SELECT) to characterize the optical transmittance of the YIG film with plasmonic nanodisk arrays for wavelengths ranging from 500 to 1100 nm. The laser beam was first polarized and then focused onto the sample at normal incidence. The transmitted intensity was detected by a broadband photodetector, and the transmittance spectrum was normalized by data obtained for the same YIG film in an area without the plasmonic nanodisk array.
Modeling of the optical field and thermoplasmonic heating
The optical and thermal properties of the hybrid magnonic-plasmonic structures were simulated using Ansys Lumerical FDTD and HEAT solvers. An area of 400 × 400 nm2 with periodic boundary conditions along the x and y axes was simulated to evaluate the properties of an infinite array of 3-nm Ti/50-nm Au nanodisks on top of a 250-nm–thick YIG film and a thick GGG substrate. The nanodisks were surrounded by air. Perfectly matched layer absorbing boundaries were applied along the z direction to absorb light at the edges of the simulation area and prevent back reflection. The structure was illuminated at normal incidence by a 915-nm linearly polarized plane wave. The input optical power was set to 0.7 mW for the unit cell, corresponding to 4.3 mW/μm2 used in the experiments. We used an internal library to extract the power absorbed by a single unit cell. These data were imported into the HEAT solver. Thermal modeling was performed with insulating boundary conditions between unit cells. Heat losses from the nanodisks and GGG substrate to air were accounted for by defining convective boundary conditions at the corresponding interfaces. The ambient temperature was set to 293 K. The thermal properties of the materials used in the simulations were taken from (68,69). To assess thermoplasmonic heating induced by a single laser pulse, the incident plane wave was activated for 500 ns. The distribution of electric field and temperature in the xy and xz planes was captured by relevant monitors.
Micromagnetic simulations
Micromagnetic simulations of spin-wave transport in the YIG film were performed using the open-source GPU-accelerated MuMax3 software (57). The effect of thermoplasmonic heating on spin-wave transmission was approximated by reducing the saturation magnetization of the YIG film in an area that either matched the shape of the plasmonic array or the laser spot. We used a simulation area of 700 × 1 × 0.25 μm3 with 1D periodic boundary conditions applied along the y axis to investigate spin-wave transport in the bare YIG film and the YIG film with reduced Ms in a 70-μm–wide, infinitely long rectangular area. For the 70-μm-diameter circular area with reduced Ms, the simulation area was set to 700 × 700 × 0.25 μm3. In both cases, the simulations were discretized into 100 × 100 × 250 nm3 cells, which suffices for long-wavelength dipolar spin waves, and the center of the area with reduced Ms was positioned at x = 100 μm. The input parameters included a saturation magnetization Ms = 197 kA/m, an exchange constant Aex = 3.1 pJ/m, and a magnetic damping parameter α = 6 × 10−4 (fig. S18). Propagating spin waves were excited by applying a sinusoidal magnetic field of 1 mT across a 6-μm–wide area at x = 0 μm. A magnetic bias field of 14 mT was applied along the y axis. Reflections from the edges of the simulation area were suppressed by high-damping boundaries. To avoid reflections from the area with reduced saturation magnetization, the value of Ms in the YIG film was changed exponentially. During continuous excitation, the time evolution of the z component of magnetization (mz) was recorded for 60 ns. Spatially resolved spin-wave intensity maps were obtained by Fourier transforming the evolution of mz on a cell-by-cell basis. We analyzed the amplitude of the transmitted spin waves at x = 200 μm, corresponding to the location of the detection antenna in the experiments.
Acknowledgments
Funding: This work was supported by the Jane and Aatos Erkko Foundation and the Technology Industries of Finland Centennial Foundation as part of the Future Makers funding program as well as the Academy of Finland under project no. 338748. N.K. acknowledges financial support by the Magnus Ehrnrooth Foundation. H.Q. acknowledges financial support by the National Key Research and Development Program of China (no. 2023YFA1406600 and no. 2022YFA1402400) and the National Natural Science Foundation of China (grant no. 12374119).
Author contributions: Conceptualization: H.Q., L.F., and S.v.D. Investigation: N.K., H.Q., L.F., and S.v.D. Methodology: N.K., H.Q., and L.F. Validation: N.K. and H.Q. Formal analysis: N.K. Software: N.K. Formal analysis: N.K. Visualization: N.K. Resources: L.F. Supervision: H.Q. and S.v.D. Project administration: H.Q and S.v.D. Writing—original draft: N.K. and S.v.D. Writing—review and editing: N.K., H.Q., L.F., and S.v.D. Funding acquisition: N.K., H.Q., L.F., and S.v.D.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S18
References
REFERENCES AND NOTES
- 1.Chumak A. V., Vasyuchka V. I., Serga A. A., Hillebrands B., Magnon spintronics. Nat. Phys. 11, 453–461 (2015). [Google Scholar]
- 2.Barman A., Gubbiotti G., Ladak S., Adeyeye A. O., Krawczyk M., Gräfe J., Adelmann C., Cotofana S., Naeemi A., Vasyuchka V. I., Hillebrands B., Nikitov S. A., Yu H., Grundler D., Sadovnikov A. V., Grachev A. A., Sheshukova S. E., Duquesne J.-Y., Marangolo M., Csaba G., Porod W., Demidov V. E., Urazhdin S., Demokritov S. O., Albisetti E., Petti D., Bertacco R., Schultheiss H., Kruglyak V. V., Poimanov V. D., Sahoo S., Sinha J., Yang H., Münzenberg M., Moriyama T., Mizukami S., Landeros P., Gallardo R. A., Carlotti G., Kim J.-V., Stamps R. L., Camley R. E., Rana B., Otani Y., Yu W., Yu T., Bauer G. E. W., Back C., Uhrig G. S., Dobrovolskiy O. V., Budinska B., Qin H., van Dijken S., Chumak A. V., Khitun A., Nikonov D. E., Young I. A., Zingsem B. W., Winklhofer M., The 2021 magnonics roadmap. J. Phys. Condens. Matter 33, 413001 (2021). [DOI] [PubMed] [Google Scholar]
- 3.Chumak A. V., Kabos P., Wu M., Abert C., Adelmann C., Adeyeye A. O., Åkerman J., Aliev F. G., Anane A., Awad A., Back C. H., Barman A., Bauer G. E. W., Becherer M., Beginin E. N., Bittencourt V. A. S. V., Blanter Y. M., Bortolotti P., Boventer I., Bozhko D. A., Bunyaev S. A., Carmiggelt J. J., Cheenikundil R. R., Ciubotaru F., Cotofana S., Csaba G., Dobrovolskiy O. V., Dubs C., Elyasi M., Fripp K. G., Fulara H., Golovchanskiy I. A., Gonzalez-Ballestero C., Graczyk P., Grundler D., Gruszecki P., Gubbiotti G., Guslienko K., Haldar A., Hamdioui S., Hertel R., Hillebrands B., Hioki T., Houshang A., Hu C.-M., Huebl H., Huth M., Iacocca E., Jungfleisch M. B., Kakazei G. N., Khitun A., Khymyn R., Kikkawa T., Kläui M., Klein O., Kłos J. W., Knauer S., Koraltan S., Kostylev M., Krawczyk M., Krivorotov I. N., Kruglyak V. V., Lachance-Quirion D., Ladak S., Lebrun R., Li Y., Lindner M., Macêdo R., Mayr S., Melkov G. A., Mieszczak S., Nakamura Y., Nembach H. T., Nikitin A. A., Nikitov S. A., Novosad V., Otálora J. A., Otani Y., Papp A., Pigeau B., Pirro P., Porod W., Porrati F., Qin H., Rana B., Reimann T., Riente F., Romero-Isart O., Ross A., Sadovnikov A. V., Safin A. R., Saitoh E., Schmidt G., Schultheiss H., Schultheiss K., Serga A. A., Sharma S., Shaw J. M., Suess D., Surzhenko O., Szulc K., Taniguchi T., Urbánek M., Usami K., Ustinov A. B., van der Sar T., van Dijken S., Vasyuchka V. I., Verba R., Kusminskiy S. V., Wang Q., Weides M., Weiler M., Wintz S., Wolski S. P., Zhang X., Advances in magnetics roadmap on spin-wave computing. IEEE Trans. Magn. 58, 3149664 (2022). [Google Scholar]
- 4.Kampfrath T., Sell A., Klatt G., Pashkin A., Mährlein S., Dekorsy T., Wolf M., Fiebig M., Leitenstorfer A., Huber R., Coherent terahertz control of antiferromagnetic spin waves. Nat. Photonics 5, 31–34 (2011). [Google Scholar]
- 5.Wang Q., Verba R., Heinz B., Schneider M., Wojewoda O., Davídková K., Levchenko K., Dubs C., Mauser N. J., Urbánek M., Pirro P., Chumak A. V., Deeply nonlinear excitation of self-normalized short spin waves. Sci. Adv. 9, eadg4609 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zheng S., Wang Z., Wang Y., Sun F., He Q., Yan P., Yuan H. Y., Tutorial: Nonlinear magnonics. J. Appl. Phys. 134, 151101 (2023). [Google Scholar]
- 7.An K., Xu M., Mucchietto A., Kim C., Moon K.-W., Hwang C., Grundler D., Emergent coherent modes in nonlinear magnonic waveguides detected at ultrahigh frequency resolution. Nat. Commun. 15, 7302 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Grassi M., Geilen M., Louis D., Mohseni M., Brächer T., Hehn M., Stoeffler D., Bailleul M., Pirro P., Henry Y., Slow-wave-based nanomagnonic diode. Phys Rev. Appl. 14, 024047 (2020). [Google Scholar]
- 9.Kruglyak V. V., Chiral magnonic resonators: Rediscovering the basic magnetic chirality in magnonics. Appl. Phys. Lett. 119, 200502 (2021). [Google Scholar]
- 10.Wang Q., Chumak A. V., Pirro P., Inverse-design magnonic devices. Nat. Commun. 12, 2636 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yu T., Luo Z., Bauer G. E. W., Chirality as generalized spin–orbit interaction in spintronics. Phys. Rep. 1009, 1–115 (2023). [Google Scholar]
- 12.Zou J., Bosco S., Thingstad E., Klinovaja J., Loss D., Reconfigurable spin-wave nonreciprocity induced by dipolar interaction in a coupled ferromagnetic bilayer. Phys. Rev. Lett. 132, 036701 (2024). [DOI] [PubMed] [Google Scholar]
- 13.Talmelli G., Devolder T., Träger N., Förster J., Wintz S., Weigand M., Stoll H., Heyns M., Schütz G., Radu I. P., Gräfe J., Ciubotaru F., Adelmann C., Reconfigurable submicrometer spin-wave majority gate with electrical transducers. Sci. Adv. 6, eabb4042 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang Q., Csaba G., Verba R., Chumak A. V., Pirro P., Nanoscale magnonic networks. Phys. Rev. Appl. 21, 040503 (2024). [Google Scholar]
- 15.Csaba G., Papp Á., Porod W., Perspectives of using spin waves for computing and signal processing. Phys. Lett. A 381, 1471–1476 (2017). [Google Scholar]
- 16.Mahmoud A., Ciubotaru F., Vanderveken F., Chumak A. V., Hamdioui S., Adelmann C., Cotofana S., Introduction to spin wave computing. J. Appl. Phys. 128, 161101 (2020). [Google Scholar]
- 17.Papp Á., Porod W., Csaba G., Nanoscale neural network using non-linear spin-wave interference. Nat. Commun. 12, 6422 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gartside J. C., Stenning K. D., Vanstone A., Holder H. H., Arroo D. M., Dion T., Caravelli F., Kurebayashi H., Branford W. R., Reconfigurable training and reservoir computing in an artificial spin-vortex ice via spin-wave fingerprinting. Nat. Nanotechnol. 17, 460–469 (2022). [DOI] [PubMed] [Google Scholar]
- 19.Körber L., Heins C., Hula T., Kim J.-V., Thlang S., Schultheiss H., Fassbender J., Schultheiss K., Pattern recognition in reciprocal space with a magnon-scattering reservoir. Nat. Commun. 14, 3954 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fripp K. G., Au Y., Shytov A. V., Kruglyak V. V., Nonlinear chiral magnonic resonators: Toward magnonic neurons. Appl. Phys. Lett. 122, 172403 (2023). [Google Scholar]
- 21.Lee O., Wei T., Stenning K. D., Gartside J. C., Prestwood D., Seki S., Aqeel A., Karube K., Kanazawa N., Taguchi Y., Back C., Tokura Y., Branford W. R., Kurebayashi H., Task-adaptive physical reservoir computing. Nat. Mater. 23, 79–87 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Demidov V. E., Urazhdin S., Demokritov S. O., Control of spin-wave phase and wavelength by electric current on the microscopic scale. Appl. Phys. Lett. 95, 262509 (2009). [Google Scholar]
- 23.Vogt K., Fradin F. Y., Pearson J. E., Sebastian T., Bader S. D., Hillebrands B., Hoffmann A., Schultheiss H., Realization of a spin-wave multiplexer. Nat. Commun. 5, 3727 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Liu C., Wu S., Zhang J., Chen J., Ding J., Ma J., Zhang Y., Sun Y., Tu S., Wang H., Liu P., Li C., Jiang Y., Gao P., Yu D., Xiao J., Duine R., Wu M., Nan C.-W., Zhang J., Yu H., Current-controlled propagation of spin waves in antiparallel, coupled domains. Nat. Nanotechnol. 14, 691–697 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Rovillain P., de Sousa R., Gallais Y., Sacuto A., Méasson M. A., Colson D., Forget A., Bibes M., Barthélémy A., Cazayous M., Electric-field control of spin waves at room temperature in multiferroic BiFeO3. Nat. Mater. 9, 975–979 (2010). [DOI] [PubMed] [Google Scholar]
- 26.Sadovnikov A. V., Grachev A. A., Sheshukova S. E., Sharaevskii Y. P., Serdobintsev A. A., Mitin D. M., Nikitov S. A., Magnon straintronics: Reconfigurable spin-wave routing in strain-controlled bilateral magnetic stripes. Phys. Rev. Lett. 120, 257203 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Qin H., Dreyer R., Woltersdorf G., Taniyama T., van Dijken S., Electric-field control of propagating spin waves by ferroelectric domain-wall motion in a multiferroic heterostructure. Adv. Mater. 33, e2100646 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vogel M., Chumak A. V., Waller E. H., Langner T., Vasyuchka V. I., Hillebrands B., von Freymann G., Optically reconfigurable magnetic materials. Nat. Phys. 11, 487–491 (2015). [Google Scholar]
- 29.Dzyapko O., Borisenko I. V., Demidov V. E., Pernice W., Demokritov S. O., Reconfigurable heat-induced spin wave lenses. Appl. Phys. Lett. 109, 232407 (2016). [Google Scholar]
- 30.Vogel M., Aßmann R., Pirro P., Chumak A. V., Hillebrands B., von Freymann G., Control of spin-wave propagation using magnetisation gradients. Sci. Rep. 8, 11099 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gubanov V. A., Kruglyak V. V., Sheshukova S. E., Bessonov V. D., Nikitov S. A., Sadovnikov A. V., Frequency-selective spin-wave propagation in magnonic waveguide with a local laser-heated region. Phys. Rev. B 107, 024427 (2023). [Google Scholar]
- 32.Kirilyuk A., Kimel A. V., Rasing T., Laser-induced magnetization dynamics and reversal in ferrimagnetic alloys. Rep. Prog. Phys. 76, 026501 (2013). [DOI] [PubMed] [Google Scholar]
- 33.Gramotnev D. K., Bozhevolnyi S. I., Plasmonics beyond the diffraction limit. Nat. Photonics 4, 83–91 (2010). [Google Scholar]
- 34.Li M., Cushing S. K., Wu N., Plasmon-enhanced optical sensors: A review. Analyst 140, 386–406 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mejía-Salazar J. R., Oliveira O. N. J., Plasmonic biosensing. Chem. Rev. 118, 10617–10625 (2018). [DOI] [PubMed] [Google Scholar]
- 36.Baffou G., Cichos F., Quidant R., Applications and challenges of thermoplasmonics. Nat. Mater. 19, 946–958 (2020). [DOI] [PubMed] [Google Scholar]
- 37.Armelles G., Cebollada A., García-Martín A., González M. U., Magnetoplasmonics: Combining magnetic and plasmonic functionalities. Adv. Opt. Mater. 1, 10–35 (2013). [Google Scholar]
- 38.Maksymov I. S., Magneto-plasmonic nanoantennas: Basics and applications. Rev. Phys. 1, 36–51 (2016). [Google Scholar]
- 39.Floess D., Giessen H., Nonreciprocal hybrid magnetoplasmonics. Rep. Prog. Phys. 81, 116401 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Temnov V. V., Armelles G., Woggon U., Guzatov D., Cebollada A., García-Martín A., Garcia-Martin J.-M., Thomay T., Leitenstorfer A., Bratschitsch R., Active magneto-plasmonics in hybrid metal–ferromagnet structures. Nat. Photonics 4, 107–111 (2010). [Google Scholar]
- 41.Freire-Fernández F., Cuerda J., Daskalakis K. S., Perumbilavil S., Martikainen J.-P., Arjas K., Törmä P., van Dijken S., Magnetic on–off switching of a plasmonic laser. Nat. Photonics 16, 27–32 (2022). [Google Scholar]
- 42.Maccaferri N., Berger A., Bonetti S., Bonanni V., Kataja M., Qin Q. H., van Dijken S., Pirzadeh Z., Dmitriev A., Nogués J., Åkerman J., Vavassori P., Tuning the magneto-optical response of nanosize ferromagnetic Ni disks using the phase of localized plasmons. Phys. Rev. Lett. 111, 167401 (2013). [DOI] [PubMed] [Google Scholar]
- 43.Kataja M., Hakala T. K., Julku A., Huttunen M. J., van Dijken S., Törma P., Surface lattice resonances and magneto-optical response in magnetic nanoparticle arrays. Nat. Commun. 6, 7072 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vergès M., Perumbilavil S., Hohlfeld J., Freire-Fernández F., Le Guen Y., Kuznetsov N., Montaigne F., Malinowski G., Lacour D., Hehn M., van Dijken S., Mangin S., Energy efficient single pulse switching of [Co/Gd/Pt]N nanodisks using surface lattice resonances. Adv. Sci. 10, 2204683 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stenning K. D., Xiao X., Holder H. H., Gartside J. C., Vanstone A., Kennedy O. W., Oulton R. F., Branford W. R., Low-power continuous-wave all-optical magnetic switching in ferromagnetic nanoarrays. Cell Rep. Phys. Sci. 4, 101291 (2023). [Google Scholar]
- 46.Yang W., Liu Q., Wang H., Chen Y., Yang R., Xia S., Luo Y., Deng L., Qin J., Duan H., Bi L., Observation of optical gyromagnetic properties in a magneto-plasmonic metamaterial. Nat. Commun. 13, 1719 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Uchida K., Adachi H., Kikuchi D., Ito S., Qiu Z., Maekawa S., Saitoh E., Generation of spin currents by surface plasmon resonance. Nat. Commun. 6, 5910 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bludov Y. V., Gomes J. N., Farias G. A., Fernández-Rossier J., Vasilevskiy M. I., Peres N. M. R., Hybrid plasmon-magnon polaritons in graphene-antiferromagnet heterostructures. 2D Mater. 6, 045003 (2019). [Google Scholar]
- 49.Dyrdał A., Qaiumzadeh A., Brataas A., Barnaś J., Magnon-plasmon hybridization mediated by spin-orbit interaction in magnetic materials. Phys. Rev. B 108, 045414 (2023). [Google Scholar]
- 50.Costa A. T., Vasilevskiy M. I., Fernández-Rossier J., Peres N. M. R., Strongly coupled magnon-plasmon polaritons in graphene-two-dimensional ferromagnet heterostructures. Nano Lett. 23, 4510–4515 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.To D. Q., Wang Z., Liu Y., Wu W., Jungfleisch M. B., Xiao J. Q., Zide J. M. O., Law S., Doty M. F., Surface plasmon-phonon-magnon polariton in a topological insulator-antiferromagnetic bilayer structure. Phys. Rev. Mater. 6, 085201 (2022). [Google Scholar]
- 52.Kravets V. G., Kabashin A. V., Barnes W. L., Grigorenko A. N., Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 118, 5912–5951 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang W., Ramezani M., Väkeväinen A. I., Törmä P., Gómez Rivas J., Odom T., The rich photonic world of plasmonic nanoparticle arrays. Mater. Today 21, 303–314 (2018). [Google Scholar]
- 54.Kimel A. V., Kirilyuk A., Usachev P. A., Pisarev R. V., Balbashov A. M., Rasing T., Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 435, 655–657 (2005). [DOI] [PubMed] [Google Scholar]
- 55.Zundel L., Malone K., Cerdán L., Martínez-Herrero R., Manjavacas A., Lattice resonances for thermoplasmonics. ACS Photonics 10, 274–282 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kittel C., On the theory of ferromagnetic resonance absorption. Phys. Rev. 73, 155–161 (1948). [Google Scholar]
- 57.Vansteenkiste A., Leliaert J., Dvornik M., Helsen M., Garcia-Sanchez F., Van Waeyenberge B., The design and verification of MuMax3. AIP Adv. 4, 107133 (2014). [Google Scholar]
- 58.Davies C. S., Francis A., Sadovnikov A. V., Chertopalov S. V., Bryan M. T., Grishin S. V., Allwood D. A., Sharaevskii Y. P., Nikitov S. A., Kruglyak V. V., Towards graded-index magnonics: Steering spin waves in magnonic networks. Phys. Rev. B 92, 020408(R) (2015). [Google Scholar]
- 59.Davies C. S., Kruglyak V. V., Graded-index magnonics. Low Temp. Phys. 41, 760–766 (2015). [Google Scholar]
- 60.Gruszecki P., Krawczyk M., Spin-wave beam propagation in ferromagnetic thin films with graded refractive index: Mirage effect and prospective applications. Phys. Rev. B 97, 094424 (2018). [Google Scholar]
- 61.Stigloher J., Decker M., Körner H. S., Tanabe K., Moriyama T., Taniguchi T., Hata H., Madami M., Gubbiotti G., Kobayashi K., Ono T., Back C. H., Snell’s law for spin waves. Phys. Rev. Lett. 117, 037204 (2016). [DOI] [PubMed] [Google Scholar]
- 62.Yu W., Lan J., Wu R., Xiao J., Magnetic Snell’s law and spin-wave fiber with Dzyaloshinskii-Moriya interaction. Phys. Rev. B 94, 140410 (2016). [Google Scholar]
- 63.Albisetti E., Petti D., Pancaldi M., Madami M., Tacchi S., Curtis J., King W. P., Papp Á., Csaba G., Porod W., Vavassori P., Riedo E., Bertacco R., Nanopatterning reconfigurable magnetic landscapes via thermally assisted scanning probe lithography. Nat. Nanotechnol. 11, 545–551 (2016). [DOI] [PubMed] [Google Scholar]
- 64.Albisetti E., Petti D., Sala G., Silvani R., Tacchi S., Finizio S., Wintz S., Calò A., Zheng X., Raabe J., Riedo E., Bertacco R., Nanoscale spin-wave circuits based on engineered reconfigurable spintextures. Commun. Phys. 1, 56 (2018). [Google Scholar]
- 65.Wemple S. H., Blank S. L., Seman J. A., Biolsi W. A., Optical properties of epitaxial iron garnet thin films. Phys. Rev. B 9, 2134–2144 (1974). [Google Scholar]
- 66.Petryayeva E., Krull U. J., Localized surface plasmon resonance: Nanostructures, bioassays and biosensing—A review. Anal. Chim. Acta 706, 8–24 (2011). [DOI] [PubMed] [Google Scholar]
- 67.Trinh T. D., Rajauria S., Smith R., Schreck E., Dai Q., Talke F. E., Dependence of optical laser power on disk radius, head-disk spacing and media properties in heat-assisted magnetic recording. Microsyst. Technol. 26, 3371–3376 (2020). [Google Scholar]
- 68.Schreier M., Kamra A., Weiler M., Xiao J., Bauer G. E. W., Gross R., Goennenwein S. T. B., Magnon, phonon, and electron temperature profiles and the spin Seebeck effect in magnetic insulator/normal metal hybrid structures. Phys. Rev. B 88, 094410 (2013). [Google Scholar]
- 69.E. Palik, Handbook of Optical Constants of Solids Academic Press Handbook Series (Elsevier Science, 1998).
- 70.Auguié B., Barnes W. L., Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 101, 143902 (2008). [DOI] [PubMed] [Google Scholar]
- 71.L. Körber, G. Quasebarth, A. Hempel, F. Zahn, A. Otto, E. Westphal, R. Hertel, A. Kákay. TetraX: Finite-element micromagnetic-modeling package. Rodare 10.14278/rodare.1418 (2022).
- 72.Körber L., Quasebarth G., Otto A., Kákay A., Finite-element dynamic-matrix approach for spin-wave dispersions in magnonic waveguides with arbitrary cross section. AIP Adv. 11, 095006 (2021). [Google Scholar]
- 73.Kalinikos B. A., Slavin A. N., Theory of dipole-exchange spin wave spectrum for ferromagnetic films with mixed exchange boundary conditions. J. Phys. C Solid State Phys. 19, 7013–7033 (1986). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S18
References