Foundation model of ECG diagnosis: Diagnostics and explanations of any form and rhythm on ECG

Summary

We propose a knowledge-enhanced electrocardiogram (ECG) diagnosis foundation model (KED) that utilizes large language models to incorporate domain-specific knowledge of ECG signals. This model is trained on 800,000 ECGs from nearly 160,000 unique patients. Despite being trained on single-center data, KED demonstrates exceptional zero-shot diagnosis performance across various regions, including different locales in China, the United States, and other regions. This performance spans across all age groups for various conditions such as morphological abnormalities, rhythm abnormalities, conduction blocks, hypertrophy, myocardial ischemia, and infarction. Moreover, KED exhibits robust performance on diseases it has not encountered during its training. When compared to three experienced cardiologists on real clinical datasets, the model achieves comparable performance in zero-shot diagnosis of seven common clinical ECG types. We concentrate on the zero-shot diagnostic capability and the generalization performance of the proposed ECG foundation model, particularly in the context of external multi-center data and previously unseen disease.

Graphical abstract

Highlights

• •A signal-language architecture-based ECG foundation model is proposed
• •Propose a signal-text-label augmented contrastive loss for multi-label learning
• •Enhance model’s zero-shot diagnostic capabilities through knowledge enhancement
• •Exhibit excellent zero-shot diagnostic abilities in diverse external environments

Tian et al. develop a foundation model for ECG diagnosis, demonstrating excellent zero-shot diagnostic performance for morphological abnormalities, rhythm abnormalities, hypertrophy, myocardial ischemia, and infarction across populations of all ages in China, the United States, and other areas. The model also diagnoses diseases not encountered during training.

Introduction

Cardiovascular disease (CVD) is the leading cause of death worldwide, and early identification of high-risk populations is crucial.¹ The electrocardiogram (ECG), recorded over 300 million times annually, serves as a primary tool for early diagnosis of CVD across a variety of clinical settings, from health screenings to intensive care.² Its convenience, cost-effectiveness, non-invasiveness, and capability for diagnosing and assessing various CVDs lend it significant clinical value. A typical cardiologist usually requires more than 12 years of training.³ However, even for experienced cardiologists, interpreting complex ECGs remains a time-consuming and error-prone task.⁴ In remote and underserved regions, providing accurate diagnoses is especially challenging due to the scarcity of cardiologists and limited resources.²

The application of artificial intelligence (AI) in ECG interpretation has shown tremendous potential. Studies indicate that AI-based ECG diagnostics have already surpassed general cardiologists in diagnosing certain specific diseases.^2,3,5,6 Furthermore, using AI to assist in diagnosis can significantly enhance cardiologists’ interpretation efficiency, reducing the time to one-third of the original and increasing accuracy by 13.5%.⁷ However, the existing mainstream automatic ECG diagnosis systems typically train on closed datasets for a few specific diseases. The differences in data distribution and the wide range of diseases from multi-center make it difficult to directly apply these existing models to the datasets of other centers. Recent studies have investigated the advancement of ECG zero-shot diagnosis.^8,9,10 Zero-shot diagnosis refers to the ability to diagnose data samples without additional training data to fine-tune a model, even when the output classes are unknown.¹¹ However, these studies have not yet conducted direct evaluation of data from other centers or examined diagnostic performance across unknown classes. This gap presents significant challenges for the application of these systems in practical multi-center scenarios. Therefore, for automatic diagnostic systems to be practically significant in large-scale multi-center clinical environments, particularly in remote and underserved regions, it is crucial to develop an ECG diagnostic system that can operate effectively without relying on annotated data after initial training.

The emergence of foundation model^12,13,14 demonstrates impressive generalization abilities in various tasks by establishing connections between text and vision and utilizing text to enhance the performance of visual tasks. Recently, several studies have explored the application of foundation models in the medical field, including cheXzero,¹⁵ MedSAM,¹⁶ PLIP,¹⁷ RETFound,¹⁸ and Med-PaLM.¹⁹ However, in the field of ECG, ECG reports are concise and highly abstract, unlike radiology reports, which provide detailed explanations describing and summarizing the patient’s condition. This conciseness in ECG reports limits contextual information for the models, posing challenges to previous methods in integrating domain knowledge with ECG signals. Therefore, it is critical to align professional medical knowledge with fine-grained features of modalities such as signals to enhance generalization ability and build ECG diagnostic foundation models that do not rely on annotated datasets.

To this end, we have developed a knowledge-enhanced automated ECG diagnosis system (KED), the foundation model in the field of ECG diagnosis. As illustrated in Figure 1, the KED is capable of querying the presence of diseases, form, and rhythm abnormalities in an ECG through natural language, subsequently offering conclusions and explanations for the queries posed. This architecture differs from previous approaches that could diagnose only specific diseases learned during the training phase. In contrast, KED supports inquiries into any potential diseases, enhancing the model’s applicability across a broad range of unknown environments. We trained the KED on 800,000 ECG records from close to 160,000 unique patients at a single center. Subsequently, we evaluated the KED’s diagnostic performance on five diverse ECG datasets, which were collected from various regions, ethnic populations, and ECG acquisition devices, without additional fine-tuning. Unlike previous studies that assessed model performance based on data from specific regions, populations, and a limited range of diseases, our approach maximizes the assessment of the model’s applicability across diverse and unknown environments. This offers a promising method for constructing an AI-ECG model capable of direct deployment in complex multi-center clinical settings involving unknown regions, diverse ethnic populations, different ECG collection devices, and previously unencountered diseases during training. This capability is particularly crucial for remote and underserved areas that require a model capable of accurately diagnosing and screening as many diseases as possible.

Figure 1.

Overview of the KED workflow

(A) The training process of KED.

(B) The deployment and testing process of KED.

See also Figure S4.

Results

Dataset and metrics

We pre-trained our model using the MIMIC-IV-ECG²⁰ clinical database, which comprises approximately 800,000 ECGs from nearly 160,000 patients. This dataset includes ECGs from the emergency department, inpatient (including ICU), and outpatient care centers of Beth Israel Deaconess Medical Center, collected using Philips equipment. Five external datasets were utilized to comprehensively evaluate the model’s diagnostic performance across various regions, ethnicities, and ECG collection devices (Figure 2A illustrates the label-matching relationships among these datasets and MIMIC-IV-ECG). These datasets are the CPSC2018,²¹ representing the Chinese population and collected from 11 hospitals in China; Chapman,²² collected from 10,646 patients at Shaoxing People’s Hospital in China using the GE MUSE ECG system; Georgia,²³ representing the southeastern United States and differing geographically from the MIMIC-IV-ECG dataset; PTB-XL,^24,25 representing other regions, constructed by Physikalisch-Technische Bundesanstalt, including 21,837 ECGs from 18,885 patients collected using Schiller AG devices, with ECG reports in German (70.89%), English (27.9%), and Swedish (1.21%), all double-checked by human doctors for test evaluations; and the Clinical Data (as shown in Figure 2B), re-annotated from Shanghai First People’s Hospital in China, collected using MedEx devices. Detailed descriptions of each dataset are available in STAR Methods. The CPSC2018, Chapman, Georgia, and PTB-XL datasets were used to assess the model’s zero-shot diagnosis (including categories not seen during training) and few-shot fine-tuning performance for rhythm, morphology, and diagnostic categories, such as conduction block, myocardial ischemia, myocardial injury, myocardial infarction, and hypertrophy, across different populations in China, the southeastern United States, and other regions. The Clinical Data was utilized to evaluate the zero-shot diagnostic performance of the model; this performance was then compared to the diagnostic capabilities of cardiologists in top-tier hospitals in well-developed regions of China. For definitions of zero-shot diagnosis and few-shot fine-tuning (as illustrated in Figure 2C), refer to the STAR Methods section.

Figure 2.

Analysis of datasets and tasks in the experiment

(A) Label distribution analysis between pre-training and downstream evaluation datasets. Definitions for the abbreviations can be found in Table S7 and Table S8.

(B) Illustration of the real clinical evaluation dataset.

(C) Description of evaluated tasks in the experiment.

To evaluate the model’s overall performance and its value in clinical decision-making, we employed comprehensive evaluation metrics to assess the model’s performance, including area under the receiver operating characteristic curve (AUROC), area under the precision-recall curve (AUPRC), accuracy (ACC), F1-score, Matthews correlation coefficient (MCC), sensitivity, specificity, positive likelihood ratio (LR+), and negative likelihood ratio (LR−). AUROC evaluates the model’s ability to correctly predict samples, AUPRC combines precision and recall for positive samples, and ACC represents the proportion of correctly classified samples. The F1-score represents the harmonic mean of recall and precision. MCC considers true positives, true negatives, false positives, and false negatives, making it suitable for imbalanced datasets. Sensitivity, also known as recall, is the ratio of detected positive samples to all positive samples, inversely related to the patient’s missed diagnosis rate. Specificity is the ratio of detected negative samples to all negative samples, inversely related to the patient’s misdiagnosis rate. LR+ quantifies the extent to which the probability of having the disease increases following a positive test result, while LR− quantifies the extent to which the probability of not having the disease increases following a negative test result. LR+ greater than 1, the larger the value, the higher the diagnostic value of the positive result; LR− less than 1, the smaller the value, the higher the exclusion value of the negative result. For the remaining metrics, higher values indicate better performance. We primarily report AUROC, sensitivity, specificity, LR+, and LR− in the main text, with the remaining metrics available in the supplementary table. In this study, unless otherwise specified, area under the curve (AUC) denotes AUROC. Detailed descriptions and formula definitions of all evaluation metrics can be found in the STAR Methods. Following the setup in other studies,²⁶ we determined the threshold for multi-label classification by maximizing the MCC on the dataset. To evaluate the calibration of the model in diagnosing different diseases in an unknown population, we introduced calibration plots. The calibration plots show the consistency between the predicted probabilities and the actual diagnostic results.²⁷ Additionally, for the clinical dataset, we utilized kappa coefficients²⁸ to evaluate the scoring consistency between cardiologists and between cardiologists and the model.

Overview of the KED framework

Our KED framework consists of two main stages: training and testing. As shown in Figure 1A, the KED utilizes ECG data and paired original ECG reports. Initially, we extract structured text labels from these reports, such as left anterior fascicular block, left ventricular hypertrophy, and premature ventricular contraction. Next, we use large language models (LLMs) to enhance the ECG reports by adding explanations of medical terminology and background knowledge on disease diagnosis. Detailed descriptions of report augmentation can be found in the STAR Methods. Therefore, each training dataset includes raw ECG signals, augmented ECG reports, and structured text labels. The KED framework comprises four modules: an ECG signal encoder, which encodes raw signals into specific dimensional representation vectors; a knowledge encoder, which encodes report or label text into corresponding dimensional representation vectors; a label query network (LQN), which, upon receiving label and ECG encodings, outputs the encoding of the label query results; and a classification head, which takes the encoding of the label query results and outputs the probability of the label’s presence in the ECG. During the training phase, we propose a novel contrastive learning strategy, augmented signal-text-label contrastive learning (AugCL), to integrate medical text knowledge into ECG signal learning and mitigate the problem of noisy labels. AugCL, optimized based on CLIP²⁹ and UniCL,³⁰ addresses the multi-label nature of ECG diagnosis by constructing independent contrastive spaces for each label through the addition of a label dimension. Initially, the ECG encoder and knowledge encoder process the ECG data and augmented reports and calculate the signal-text-label contrastive loss. Concurrently, the knowledge encoder encodes the text labels, and these encoded results serve as queries for the LQN. The ECG or report encodings function as keys and values, and we compute the binary cross-entropy loss for each label. By employing two parallel loss optimization processes, we developed a signal-language pre-training model augmented with medical knowledge. During the testing and deployment phase after model training, shown in Figure 1B, patients and doctors can query potential diseases using a 12-lead ECG or predefine a range of disease queries. The KED encodes the ECG and structured text labels separately, and the encoded results are fed into the LQN to automatically output the probability of each disease. To obtain further information on the diagnostic basis, the KED utilizes Grad-CAM³¹ and GPT³² to offer detailed diagnostic insights for specific diseases and highlights areas on the ECG that require attention. Detailed descriptions of KED can be found in the STAR Methods.

KED has achieved excellent zero-shot diagnostic performance on the Chinese population

CPSC2018 and Chapman are two ECG datasets from the Chinese population. The diagnostic performance of KED on the CPSC2018 and Chapman datasets is shown in Table 1. CPSC2018 (see Table 1 upper) includes three categories of abnormalities: rhythm abnormalities, conduction blocks, and morphological abnormalities. Among them, ST segment depression (STD) is an abnormality that the model did not encounter during training. Excluding STD, the model’s zero-shot diagnosis metrics are as follows: average AUC of 0.900, average sensitivity of 0.695, average specificity of 0.949, average LR+ of 44.788, and average LR− of 0.322. For the previously unseen STD, the metrics are as follows: AUC of 0.731, sensitivity of 0.562, specificity of 0.753, LR+ of 3.944, and LR− of 0.539, indicating that the model has developed diagnostic capabilities for STD. When we fine-tuned KED using a small portion of CPSC2018 samples (82 ECG records without overlap with the test set, with at least two samples for each abnormality), the average AUC, average sensitivity, average specificity, average LR+, and average LR− were 0.930, 0.736, 0.983, 45.697, and 0.274, respectively. For STD after fine-tuning with small samples, the AUC, sensitivity, specificity, LR+, and LR− were 0.772, 0.762, 0.691, 2.547, and 0.338, respectively. These results demonstrate that KED achieved excellent performance in the direct diagnosis of atrial fibrillation, premature beats, conduction blocks, ST segment elevation, and other abnormalities on ECG data from 11 hospitals in China. Moreover, it also developed diagnostic capabilities for previously unseen conditions. Additional evaluation metrics are provided in Table S1.

Table 1.

Diagnostic performance of KED on ECG in the Chinese population

Type	AUC	Sensitivity	Specificity	LR+	LR−
AFIB
ZS	0.978 (0.968–0.986)	0.885 (0.841–0.939)	0.980 (0.973–0.985)	45.549 (32.270–61.087)	0.117 (0.078–0.164)
FT	0.982 (0.975–0.990)	0.871 (0.817–0.939)	0.981 (0.976–0.990)	49.476 (35.239–79.826)	0.132 (0.078–0.192)
IAVB
ZS	0.779 (0.744–0.811)	0.480 (0.237–0.667)	0.892 (0.800–0.981)	6.033 (3.246–12.573)	0.575 (0.418–0.778)
FT	0.902 (0.868–0.925)	0.685 (0.580–0.804)	0.965 (0.941–0.982)	21.626 (13.068–36.315)	0.326 (0.208–0.471)
LBBB
ZS	0.972 (0.947–0.996)	0.904 (0.829–0.973)	0.994 (0.990–0.998)	175.582 (90.567–420.424)	0.097 (0.029–0.178)
FT	0.981 (0.965–0.995)	0.880 (0.765–0.970)	0.994 (0.991–0.997)	157.255 (97.059–295.699)	0.121 (0.031–0.252)
RBBB
ZS	0.908 (0.880–0.925)	0.722 (0.663–0.790)	0.960 (0.928–0.980)	20.303 (10.931–33.915)	0.289 (0.223–0.378)
FT	0.928 (0.905–0.942)	0.807 (0.672–0.870)	0.941 (0.916–0.970)	15.582 (9.874–26.217)	0.204 (0.140–0.339)
APC
ZS	0.916 (0.887–0.944)	0.740 (0.636–0.831)	0.955 (0.930–0.977)	17.991 (10.757–27.834)	0.272 (0.184–0.378)
FT	0.909 (0.880–0.936)	0.625 (0.489–0.728)	0.974 (0.954–0.986)	26.739 (14.429–36.589)	0.384 (0.289–0.518)
VPC
ZS	0.871 (0.848–0.900)	0.627 (0.218–0.918)	0.898 (0.791–0.999)	23.964 (4.204–201.050)	0.399 (0.109–0.783)
FT	0.887 (0.848–0.921)	0.720 (0.581–0.816)	0.918 (0.870–0.965)	9.572 (6.016–16.764)	0.304 (0.212–0.443)
STD∗
ZS∗	0.731 (0.688–0.765)∗	0.562 (0.177–0.932)∗	0.753 (0.431–0.996)∗	3.944 (1.603–22.155)∗	0.539 (0.179–0.905)∗
FT∗	0.772 (0.733–0.795)∗	0.762 (0.651–0.908)∗	0.691 (0.510–0.800)∗	2.547 (1.888–3.323)∗	0.338 (0.180–0.478)∗
STE
ZS	0.879 (0.817–0.940)	0.511 (0.276–0.750)	0.965 (0.926–0.997)	24.097 (9.111–91.494)	0.504 (0.269–0.726)
FT	0.921 (0.887–0.960)	0.561 (0.414–0.731)	0.984 (0.970–0.993)	39.628 (20.667–77.314)	0.446 (0.292–0.593)
Avg.Seen
ZS	0.900	0.695	0.949	44.788	0.322
FT	0.930	0.736	0.983	45.697	0.274
Avg.Total
ZS	0.879	0.679	0.925	39.683	0.349
FT	0.910	0.739	0.931	40.303	0.282
AFL
ZS	0.926 (0.911–0.938)	0.582 (0.378–0.923)	0.940 (0.839–0.988)	15.977 (5.537–31.35)	0.434 (0.094–0.699)
FT	0.930 (0.916–0.943)	0.537 (0.296–0.846)	0.956 (0.873–0.993)	25.474 (6.625–56.136)	0.477 (0.172–0.709)
AFIB
ZS	0.994 (0.992–0.996)	0.949 (0.903–0.976)	0.975 (0.963–0.987)	41.788 (26.596–67.717)	0.052 (0.024–0.102)
FT	0.993 (0.991–0.996)	0.948 (0.912–0.977)	0.975 (0.964–0.984)	39.944 (26.923–58.933)	0.053 (0.024–0.104)
AT∗
ZS∗	0.811 (0.716–0.877)∗	0.237 (0.071–0.818)∗	0.965 (0.704–1.000)∗	3.093 (0.000–28.354)∗	0.771 (0.261–0.929)∗
FT∗	0.839 (0.758–0.900)∗	0.319 (0.071–0.789)∗	0.959 (0.864–1.000)∗	65.040 (0.000–224.286)∗	0.696 (0.242–0.930)∗
SA
ZS	0.926 (0.879–0.959)	0.506 (0.354–0.679)	0.983 (0.960–0.997)	44.371 (15.999–108.800)	0.501 (0.334–0.648)
FT	0.927 (0.903–0.946)	0.554 (0.436–0.686)	0.975 (0.965–0.988)	26.501 (17.921–39.385)	0.456 (0.325–0.618)
SB
ZS	0.998 (0.995–0.999)	0.993 (0.982–1.000)	0.992 (0.988–0.996)	143.348 (79.881–251.231)	0.008 (0.000–0.018)
FT	0.998 (0.997–0.999)	0.992 (0.985–0.998)	0.991 (0.986–0.997)	146.050 (69.556–321.786)	0.008 (0.002–0.018)
ST
ZS	0.981 (0.973–0.990)	0.932 (0.896–0.966)	0.979 (0.970–0.988)	47.319 (31.154–73.534)	0.070 (0.036–0.106)
FT	0.986 (0.982–0.992)	0.941 (0.893–0.977)	0.974 (0.965–0.987)	38.151 (27.725–69.475)	0.061 (0.024–0.110)
SR
ZS	0.993 (0.989–0.997)	0.944 (0.915–0.967)	0.990 (0.984–0.995)	102.637 (58.966–181.136)	0.057 (0.033–0.086)
FT	0.992 (0.987–0.996)	0.945 (0.914–0.975)	0.992 (0.985–0.997)	147.406 (64.688–301.602)	0.056 (0.025–0.087)
SVT∗
ZS∗	0.928 (0.900–0.941)∗	0.726 (0.519–0.924)∗	0.911 (0.833–0.971)∗	12.269 (5.035–20.139)∗	0.293 (0.091–0.557)∗
FT∗	0.944 (0.926–0.954)∗	0.765 (0.512–0.926)∗	0.932 (0.889–0.980)∗	13.684 (7.850–27.870)∗	0.248 (0.083–0.499)∗
Avg.
ZS	0.945	0.733	0.967	51.350	0.273
FT	0.951	0.750	0.969	62.781	0.257

The upper section is the CPSC2018 dataset, and the lower section is the Chapman dataset. “ZS” denotes zero-shot, “FT” represents few-shot fine-tune, and the bootstrapped 95% confidence intervals (CIs) are provided in parentheses. Definitions for the remaining abbreviations can be found in Table S8. Asterisks indicate the unseen and super-sub classes. See also Table S1.

The Chapman dataset (see Table 1 lower), a single-center collection annotated by experienced cardiologists through multiple rounds, includes eight types of arrhythmias. Notably, atrial tachycardia (AT) and supraventricular tachycardia (SVT) were not encountered during the training phase. Overall, zero-shot diagnosis using the KED achieved an average AUC of 0.945, sensitivity of 0.733, specificity of 0.967, LR+ of 51.350, and LR− of 0.273 across all categories. For AT, which was not encountered during training, the model produced an AUC of 0.811, sensitivity of 0.237, specificity of 0.965, LR+ of 3.093, and LR− of 0.771. For SVT, the respective metrics were an AUC of 0.928, sensitivity of 0.726, specificity of 0.911, LR+ of 12.269, and LR− of 0.293. When fine-tuning the KED model on a small subset of the Chapman samples (126 ECG records that do not overlap with the test set and contain at least two samples of each arrhythmia), the average AUC improved to 0.951, sensitivity to 0.750, specificity to 0.969, LR+ to 62.781, and LR− to 0.257. Additional evaluation metrics are provided in Table S1.

The calibration plot for disease diagnosis using KED among the Chinese population is depicted in Figure S1. The Chapman dataset demonstrates good calibration in diagnoses of atrial fibrillation (Brier score: 0.0256) and sinus tachycardia (Brier score: 0.014). Similarly, the CPSC2018 dataset indicates good calibration for models diagnosing atrial fibrillation (Brier score: 0.042), left bundle branch block (Brier score: 0.009), and premature atrial contraction (Brier score: 0.049). However, the model tends to underestimate the risk for unseen anomalies, such as SVT (Brier score: 0.052) and STD (Brier score: 0.114).

The results indicate that despite the CPSC2018, Chapman, and the training dataset MIMIC-IV-ECG being from distinct regions, ethnicities, and ECG acquisition equipment, KED consistently demonstrates high diagnostic performance for various rhythm abnormalities, conduction blocks, and morphological abnormalities in the Chinese population. When dealing with previously unseen classes such as STD, AT, and SVT, the model still exhibited high AUC and acceptable specificity and sensitivity, suggesting robust generalization capability. Notably, following fine-tuning with a small sample (feasible through minor-scale sample collection), performance markedly improved, underscoring the model’s adaptability to new data.

KED has achieved robust zero-shot diagnostic performance among the southeastern population of the United States

Unlike MIMIC-IV-ECG, which represents ECG data from the northeastern United States population, the Georgia dataset represents a large population from the southeastern United States. As shown in Table 2, this dataset includes 20 types of ECG descriptions, such as rhythm abnormalities, morphological abnormalities, and conduction blocks, among which Q wave abnormalities (QAb) and T wave inversions (TInv) were classes not seen during training. Zero-shot diagnosis using the KED achieved an average AUC of 0.900, sensitivity of 0.696, specificity of 0.925, LR+ of 39.601, and LR− of 0.329 across all categories. For various rhythm abnormalities and conduction blocks, the AUC exceeded 0.9. For QAb, which was not encountered during training, the model achieved an AUC of 0.774, sensitivity of 0.583, specificity of 0.799, LR+ of 10.728, and LR− of 0.491. For TInv, the respective metrics were an AUC of 0.700, sensitivity of 0.494, specificity of 0.812, LR+ of 2.877, and LR− of 0.615. When a small subset of Georgia samples (98 ECG records with no overlap with the test set, with at least two samples of each class) was used to fine-tune KED, the model’s performance metrics improved across all categories. For QAb, fine-tuning with small samples enhanced AUC, sensitivity, specificity, and LR−. The calibration plot for disease diagnosis using KED in the southeastern United States population is presented in Figure S2A. The diagnostic probabilities for left anterior fascicular block (Brier score: 0.020), left bundle branch block (Brier score: 0.011), right bundle branch block (Brier score: 0.022), sinus tachycardia (Brier score: 0.025), premature atrial contraction (Brier score: 0.037), and premature ventricular contraction (Brier score: 0.036) all demonstrate good calibration. The findings suggest that models trained on northeastern US population data can achieve excellent diagnostic performance for rhythm abnormalities, conduction blocks, and morphological abnormalities when applied to the southeastern US population. Even for morphological abnormalities not encountered during training, such as QAb and TInv, the model demonstrated competent diagnostic ability. Additional evaluation metrics are provided in Table S2.

Table 2.

Diagnostic performance of KED on ECG among the southeastern population of the United States

Type	AUC	Sensitivity	Specificity	LR+	LR−
AFIB
ZS	0.933 (0.889–0.960)	0.696 (0.588–0.821)	0.991 (0.978–0.997)	112.304 (33.75–222.573)	0.307 (0.183–0.427)
FT	0.932 (0.888–0.964)	0.655 (0.530–0.810)	0.988 (0.970–0.998)	95.024 (26.103–315.549)	0.348 (0.211–0.494)
AFL
ZS	0.965 (0.951–0.979)	0.556 (0.261–0.839)	0.982 (0.956–1.000)	71.341 (0.0–265.54)	0.449 (0.178–0.75)
FT	0.958 (0.941–0.975)	0.560 (0.250–0.960)	0.980 (0.932–1.000)	50.370 (0.000–139.154)	0.445 (0.054–0.759)
IAVB
ZS	0.930 (0.909–0.950)	0.632 (0.516–0.828)	0.963 (0.920–0.984)	20.809 (9.677–35.007)	0.381 (0.187–0.498)
FT	0.969 (0.961–0.978)	0.743 (0.551–0.953)	0.962 (0.922–0.991)	27.693 (11.101–62.236)	0.264 (0.061–0.457)
IRBBB
ZS	0.943 (0.920–0.965)	0.666 (0.375–0.833)	0.964 (0.932–0.997)	31.436 (11.442–113.462)	0.344 (0.179–0.639)
FT	0.954 (0.936–0.972)	0.786 (0.643–0.923)	0.961 (0.947–0.983)	21.756 (15.625–37.800)	0.222 (0.086–0.367)
LAD
ZS	0.931 (0.917–0.946)	0.796 (0.704–0.879)	0.909 (0.878–0.947)	9.136 (6.684–13.029)	0.224 (0.147–0.332)
FT	0.932 (0.917–0.946)	0.744 (0.595–0.872)	0.921 (0.864–0.961)	10.532 (6.343–16.677)	0.276 (0.146–0.432)
LAFB
ZS	0.949 (0.932–0.962)	0.867 (0.731–1.000)	0.934 (0.907–0.953)	13.758 (9.536–18.105)	0.142 (0.033–0.324)
FT	0.963 (0.951–0.975)	0.771 (0.435–0.970)	0.954 (0.912–0.993)	23.629 (10.969–67.444)	0.237 (0.035–0.602)
LBBB
ZS	0.990 (0.983–0.996)	0.730 (0.536–0.933)	0.992 (0.979–0.999)	189.601 (41.25–692.0)	0.271 (0.07–0.477)
FT	0.992 (0.985–0.996)	0.793 (0.577–0.964)	0.992 (0.982–0.999)	166.579 (45.600–695.769)	0.208 (0.041–0.429)
LQRSV
ZS	0.849 (0.813–0.885)	0.661 (0.365–0.898)	0.863 (0.774–0.960)	6.036 (3.631–11.041)	0.379 (0.13–0.669)
FT	0.903 (0.881–0.929)	0.527 (0.327–0.804)	0.952 (0.866–0.989)	15.748 (5.943–34.460)	0.492 (0.248–0.692)
LQT
ZS	0.817 (0.788–0.850)	0.578 (0.259–0.852)	0.848 (0.655–0.979)	5.157 (2.501–12.522)	0.481 (0.215–0.757)
FT	0.855 (0.824–0.885)	0.621 (0.432–0.812)	0.891 (0.764–0.957)	6.418 (3.659–10.592)	0.421 (0.256–0.606)
NSIVCB
ZS	0.880 (0.837–0.928)	0.711 (0.474–0.900)	0.906 (0.877–0.951)	8.471 (5.683–14.168)	0.314 (0.124–0.575)
FT	0.847 (0.780–0.912)	0.587 (0.333–0.850)	0.939 (0.921–0.984)	12.606 (6.652–25.292)	0.434 (0.165–0.695)
SR
ZS	0.860 (0.839–0.880)	0.769 (0.667–0.905)	0.800 (0.699–0.868)	4.105 (2.88–5.405)	0.281 (0.142–0.396)
FT	0.895 (0.880–0.915)	0.743 (0.606–0.881)	0.861 (0.774–0.937)	6.497 (3.749–9.814)	0.292 (0.165–0.439)
PAC
ZS	0.920 (0.892–0.951)	0.686 (0.585–0.79)	0.982 (0.967–0.992)	45.365 (23.143–82.333)	0.319 (0.221–0.425)
FT	0.919 (0.889–0.949)	0.678 (0.578–0.802)	0.971 (0.944–0.986)	27.734 (13.635–44.170)	0.331 (0.214–0.431)
QAb∗
ZS∗	0.774 (0.737–0.821)∗	0.583 (0.094–0.89)∗	0.799 (0.580–0.999)∗	10.728 (2.081–61.833)∗	0.491 (0.192–0.912)∗
FT∗	0.820 (0.791–0.860)∗	0.592 (0.176–0.862)∗	0.846 (0.687–0.993)∗	7.031 (2.609–23.609)∗	0.463 (0.208–0.834)∗
RBBB
ZS	0.980 (0.961–0.993)	0.916 (0.857–0.963)	0.984 (0.978–0.991)	62.112 (40.452–98.171)	0.086 (0.038–0.148)
FT	0.985 (0.973–0.994)	0.887 (0.810–0.946)	0.987 (0.980–0.994)	78.236 (45.340–129.782)	0.114 (0.057–0.207)
SA
ZS	0.929 (0.903–0.955)	0.495 (0.373–0.68)	0.988 (0.956–0.996)	61.062 (15.427–124.1)	0.51 (0.351–0.647)
FT	0.953 (0.929–0.972)	0.710 (0.549–0.833)	0.986 (0.973–0.996)	63.331 (27.534–139.167)	0.294 (0.176–0.457)
SB
ZS	0.991 (0.986–0.995)	0.965 (0.916–0.991)	0.98 (0.97–0.993)	56.019 (32.454–131.215)	0.036 (0.009–0.086)
FT	0.992 (0.988–0.996)	0.956 (0.926–0.981)	0.983 (0.974–0.990)	61.403 (36.966–96.426)	0.045 (0.020–0.076)
ST
ZS	0.990 (0.985–0.994)	0.933 (0.894–0.965)	0.982 (0.974–0.991)	57.667 (36.661–101.333)	0.068 (0.036–0.116)
FT	0.992 (0.988–0.995)	0.917 (0.879–0.946)	0.990 (0.984–0.995)	105.344 (58.762–196.589)	0.084 (0.055–0.125)
TAb
ZS	0.866 (0.846–0.886)	0.747 (0.667–0.83)	0.848 (0.803–0.905)	5.059 (4.122–6.888)	0.297 (0.212–0.385)
FT	0.878 (0.861–0.894)	0.728 (0.633–0.837)	0.874 (0.811–0.930)	6.285 (4.305–8.950)	0.308 (0.200–0.397)
TInv∗
ZS∗	0.700 (0.659–0.743)∗	0.494 (0.356–0.685)∗	0.812 (0.723–0.895)∗	2.877 (2.092–4.326)∗	0.615 (0.438–0.744)∗
FT∗	0.707 (0.664–0.745)∗	0.637 (0.545–0.735)∗	0.731 (0.667–0.776)∗	2.426 (1.990–2.893)∗	0.494 (0.374–0.612)∗
VPC
ZS	0.809 (0.758–0.865)	0.436 (0.262–0.583)	0.971 (0.958–0.995)	18.987 (10.516–42.583)	0.58 (0.44–0.775)
FT	0.843 (0.791–0.899)	0.455 (0.356–0.587)	0.983 (0.974–0.994)	33.819 (15.576–67.234)	0.554 (0.431–0.658)
Avg.
ZS	0.900	0.696	0.925	39.601	0.329
FT	0.914	0.705	0.938	41.123	0.316

“ZS” denotes zero-shot, “FT” represents few-shot fine-tune, and the bootstrapped 95% confidence intervals (CIs) are provided in parentheses. Definitions for the remaining abbreviations can be found in Table S8. Asterisks indicate the unseen and super-sub classes. See also Table S2.

KED has achieved significant zero-shot diagnostics and few-shot fine-tuning performance on population data from other regions

The original ECG reports in PTB-XL include German, English, and Swedish, representing ECG data from populations in other regions. This dataset formats the original reports into three main categories of ECG statements: rhythm, form, and diagnosis. From these, we selected 46 statements with more than 100 samples to evaluate diagnostic performance. Table 3 illustrates 21 representative diagnostic performance examples, with the remaining results provided in Table S3. Among these 46 ECG statements, zero-shot diagnosis using the KED achieved an average AUC of 0.744, sensitivity of 0.623, specificity of 0.768, LR+ of 18.911, and LR− of 0.453. In the rhythm category, KED maintains high performance for zero-shot diagnosis (average AUC for atrial fibrillation [AFIB], sinus arrhythmia [SA], SB, SR, and ST is 0.918, average sensitivity is 0.706, average specificity is 0.921, LR+ is 43.646, and LR− is 0.314), except for the unseen SVARR, which did not perform well. However, when fine-tuned with a small subset of PTB-XL samples (218 ECG recordings, with at least two samples of each class and no overlap with the test set), the model showed significant improvement in SVARR (AUC 0.849, sensitivity 0.348, specificity 0.997, LR+ 128.918, and LR− 0.654). Additional evaluation metrics are provided in Table S4.

Table 3.

Diagnostic performance of KED on ECG in the population data from other regions

Type	AUC	Sensitivity	Specificity	LR+	LR−
AFIB
ZS	0.965 (0.952–0.973)	0.765 (0.708–0.839)	0.973 (0.964–0.982)	29.547 (22.211–42.111)	0.241 (0.176–0.311)
FT	0.983 (0.973–0.993)	0.897 (0.852–0.942)	0.995 (0.993–0.998)	211.51 (118.49–443.34)	0.104 (0.059–0.148)
STACH
ZS	0.987 (0.983–0.992)	0.769 (0.581–0.909)	0.992 (0.983–0.998)	151.936 (53.409–385.944)	0.233 (0.102–0.424)
FT	0.994 (0.991–0.996)	0.902 (0.821–0.956)	0.993 (0.989–0.996)	140.014 (84.671–217.432)	0.099 (0.049–0.180)
SVARR∗
ZS∗	0.590 (0.461–0.694)∗	0.736 (0.231–1.000)∗	0.570 (0.413–0.934)∗	1.923 (1.296–3.492)∗	0.388 (0.000–0.826)∗
FT∗	0.849 (0.802–0.915)∗	0.348 (0.154–0.600)∗	0.997 (0.995–0.999)∗	128.918 (47.890–251.423)∗	0.654 (0.463–0.877)∗
CLBBB∗
ZS∗	0.991 (0.987–0.996)∗	0.880 (0.750–0.966)∗	0.985 (0.978–0.996)∗	68.527 (41.897–157.426)∗	0.122 (0.035–0.289)∗
FT∗	0.997 (0.996–0.999)∗	0.943 (0.877–1.000)∗	0.994 (0.991–0.999)∗	194.69 (105.973–622.029)∗	0.057 (0.014–0.131)∗
LAFB
ZS	0.937 (0.928–0.946)	0.808 (0.728–0.907)	0.911 (0.884–0.935)	9.284 (7.504–12.048)	0.210 (0.114–0.294)
FT	0.964 (0.957–0.970)	0.847 (0.758–0.902)	0.940(0.926–0.966)	14.477 (11.697–20.518)	0.163 (0.104–0.312)
1AVB
ZS	0.724 (0.679–0.774)	0.429 (0.059–0.786)	0.842(0.596–1.000)	16.823 (1.924–106.987)	0.638 (0.296–0.943)
FT	0.942 (0.925–0.957)	0.621 (0.452–0.773)	0.969 (0.946–0.988)	22.263 (14.051–40.853)	0.390 (0.244–0.555)
LVH
ZS	0.700 (0.676–0.740)	0.466 (0.155–0.838)	0.802 (0.719–0.971)	2.820 (1.982–5.216)	0.650 (0.469–0.862)
FT	0.921 (0.906–0.934)	0.649 (0.537–0.744)	0.963 (0.943–0.982)	19.082 (12.110–29.002)	0.364 (0.293–0.499)
LPFB∗
ZS∗	0.748 (0.667–0.827)∗	0.289 (0.048–0.714)∗	0.931 (0.790–1.000)∗	47.402 (0.000–272.000)∗	0.733 (0.358–0.953)∗
FT∗	0.754 (0.668–0.832)∗	0.313 (0.059–0.632)∗	0.953 (0.913–1.000)∗	56.963 (0.000–362.333)∗	0.704 (0.395–0.942)∗
ASMI
ZS	0.927 (0.913–0.940)	0.740 (0.613–0.876)	0.914 (0.863–0.955)	9.302 (6.279–13.784)	0.282 (0.143–0.405)
FT	0.969 (0.961–0.977)	0.846 (0.765–0.924)	0.950 (0.920–0.972)	18.160 (11.525–28.978)	0.162 (0.087–0.247)
ILMI∗
ZS∗	0.693 (0.616–0.764)∗	0.416 (0.234–0.744)∗	0.892 (0.783–0.962)∗	5.372 (2.685–8.533)∗	0.645 (0.365–0.803)∗
FT∗	0.833 (0.798–0.881)∗	0.466 (0.132–0.774)∗	0.914 (0.729–0.998)∗	11.450 (3.083–47.711)∗	0.572 (0.295–0.870)∗
ISC_
ZS	0.888 (0.873–0.902)	0.708 (0.543–0.869)	0.873 (0.788–0.939)	6.215 (4.091–9.061)	0.329 (0.170–0.491)
FT	0.944 (0.927–0.964)	0.648 (0.515–0.764)	0.966 (0.939–0.985)	20.827 (12.428–34.622)	0.364 (0.248–0.496)
ISCAL∗
ZS∗	0.764 (0.737–0.804)∗	0.496 (0.063–0.800)∗	0.841 (0.687–0.999)∗	11.753 (2.504–57.214)∗	0.573 (0.288–0.938)∗
FT∗	0.886 (0.861–0.913)∗	0.520 (0.347–0.863)∗	0.928 (0.807–0.973)∗	10.086 (4.353–14.457)∗	0.507 (0.175–0.715)∗
INJAL∗
ZS∗	0.720 (0.612–0.814)∗	0.800 (0.579–1.000)∗	0.670 (0.350–0.836)∗	2.850 (1.538–4.913)∗	0.265 (0.000–0.573)∗
FT∗	0.823 (0.758–0.888)∗	0.788 (0.421–1.000)∗	0.805 (0.672–0.950)∗	5.242 (2.899–12.409)∗	0.243 (0.000–0.611)∗
PVC
ZS	0.968 (0.958–0.976)	0.666 (0.545–0.802)	0.980 (0.966–0.993)	39.759 (22.818–79.180)	0.340 (0.205–0.461)
FT	0.991 (0.988–0.994)	0.945 (0.885–0.983)	0.981 (0.977–0.989)	52.710 (41.792–87.222)	0.056 (0.017–0.117)
LNGQT∗
ZS∗	0.848 (0.753–0.950)∗	0.211 (0.077–0.875)∗	0.991 (0.974–1.000)∗	102.312 (0.000–624.286)∗	0.791 (0.571–0.938)∗
FT∗	0.860 (0.745–0.960)∗	0.547 (0.182–0.875)∗	0.964 (0.934–0.998)∗	38.895 (8.831–121.278)∗	0.466 (0.133–0.819)∗
DIG∗
ZS∗	0.740 (0.616–0.836)∗	0.289 (0.050–0.588)∗	0.951 (0.842–1.000)∗	53.062 (0.000–290.267)∗	0.738 (0.442–0.952)∗
FT∗	0.897 (0.867–0.943)∗	0.693 (0.231–1.000)∗	0.890 (0.737–0.991)∗	12.023 (3.807–38.375)∗	0.325 (0.000–0.799)∗
LPR
ZS	0.555 (0.480–0.644)	0.671 (0.188–1.000)	0.502 (0.150–0.935)	1.529 (1.145–2.856)	0.548 (0.000–0.920)
FT	0.961 (0.951–0.974)	0.805(0.676–0.900)	0.950 (0.928–0.971)	17.115 (12.051–26.563)	0.204 (0.106–0.362)
NST_∗
ZS∗	0.638 (0.553–0.689)∗	0.462 (0.097–0.737)∗	0.773 (0.616–0.988)∗	3.377 (1.653–9.815)∗	0.658 (0.449–0.918)∗
FT∗	0.793 (0.750–0.819)∗	0.743 (0.649–0.841)∗	0.758 (0.686–0.836)∗	3.133 (2.484–3.870)∗	0.337 (0.234–0.513)∗
STD_∗
ZS∗	0.599 (0.555–0.650)∗	0.387 (0.170–0.944)∗	0.771 (0.225–0.993)∗	2.440 (1.218–8.641)∗	0.752 (0.249–0.944)∗
FT∗	0.808 (0.780–0.828)∗	0.640 (0.347–0.831)∗	0.819 (0.692–0.952)∗	4.039 (2.721–7.551)∗	0.429 (0.262–0.689)∗
Avg.Total
ZS	0.744	0.623	0.768	18.911	0.453
FT	0.858	0.633	0.893	36.232	0.396

“ZS” denotes zero-shot, “FT” represents few-shot fine-tune, and the bootstrapped 95% confidence intervals (CIs) are provided in parentheses. Definitions for the remaining abbreviations can be found in Table S8. Asterisks indicate the unseen and super-sub classes. See also Tables S3 and S4.

Diagnostic statements mainly include conduction blocks, atrioventricular hypertrophy, and ischemic heart disease. Zero-shot diagnosis of complete left bundle branch block (CLBBB), complete right bundle branch block, incomplete right bundle branch block (IRBBB), left anterior fascicle block (LAFB), and right ventricular hypertrophy achieved excellent performance (average AUC 0.921, average specificity 0.957, average sensitivity 0.622, average LR+ 46.223, and average LR− 0.39). Ischemic heart disease primarily includes myocardial ischemia, injury, and infarction involving different areas, such as anterior, anterior septal, anterior lateral, inferior, inferior lateral, lateral, etc. KED achieved outstanding zero-shot diagnostic performance for certain ischemic heart diseases, such as anterior septal myocardial infarction (ASMI; AUC 0.927, sensitivity 0.740, specificity 0.914, LR+ 9.302, and LR− 0.282) and non-specific myocardial ischemia (ISC_; AUC 0.888, sensitivity 0.708, specificity 0.873, LR+ 6.215, and LR− 0.329). KED also demonstrated diagnostic capabilities for some unseen ischemic heart diseases, such as anterolateral myocardial ischemia (ISCAL; AUC 0.764, sensitivity 0.496, specificity 0.841, LR+ 11.753, and LR− 0.573) and subendocardial injury in anterolateral leads (INJAL; AUC 0.720, sensitivity 0.800, specificity 0.670, LR+ 2.850, and LR− 0.265). After fine-tuning with few-shot, significant improvements were observed, such as AUC for anterolateral myocardial ischemic reaching 0.886, sensitivity 0.520, specificity 0.928, LR+ 10.086, and LR− 0.507, and AUC for subendocardial injury in anterolateral leads reaching 0.823, sensitivity 0.788, specificity 0.805, LR+ 5.242, and LR− 0.243.

Following PTB-XL’s classification method, form statements mainly include abnormalities such as premature contractions, PR interval, Q wave, QRS complex, ST segment, T wave, and QT interval. For (atrial and ventricular) premature contractions, KED achieved excellent zero-shot diagnostic performance (average AUC 0.944, average specificity 0.718, average sensitivity 0.95, average LR+ 24.885, and average LR− 0.295). The model also demonstrated diagnostic capability for unseen long QT (LNGQT) interval and digitalis effect (DIG), such as zero-shot diagnosis of long QT interval (AUC 0.848, sensitivity 0.211, specificity 0.991, LR+ 102.312, and LR− 0.791) and digitalis-effect (AUC 0.740, sensitivity 0.289, specificity 0.951, LR+ 53.062, and LR− 0.738). When using few-shot fine-tuning on the target dataset, significant improvements can be achieved in the form classes where zero-shot diagnosis performs poorly. For instance, the fine-tuned KED’s prolonged PR interval (LPR) AUC increased from 0.555 to 0.961, sensitivity from 0.671 to 0.805, specificity from 0.502 to 0.950, LR+ from 1.82 to 17.115, and LR− from 0.548 to 0.204. The unseen STD AUC increased from 0.599 to 0.808, sensitivity from 0.387 to 0.640, specificity from 0.771 to 0.819, LR+ from 2.440 to 4.039, and LR− from 0.752 to 0.429. The calibration plot for disease diagnosis using KED in other populations is presented in Figure S2B. The diagnostic probabilities for complete right bundle branch block (Brier score: 0.021), myocardial ischemia (Brier score: 0.047), and inferior wall myocardial infarction (Brier score: 0.022) all demonstrate good calibration.

These results indicate that KED can achieve excellent zero-shot diagnostic performance for most rhythm disorders, conduction blocks, some ischemic heart diseases, and premature contractions in ECG from populations in other regions. KED also showcases diagnostic capability for unseen ischemic heart diseases and forms abnormalities. For classes with low zero-shot diagnosis performance, significant improvements in diagnostic capability can be achieved by fine-tuning the model with small subset of data.

The zero-shot diagnostic performance of KED is comparable to that of cardiologists in top-tier hospitals in well-developed regions of China

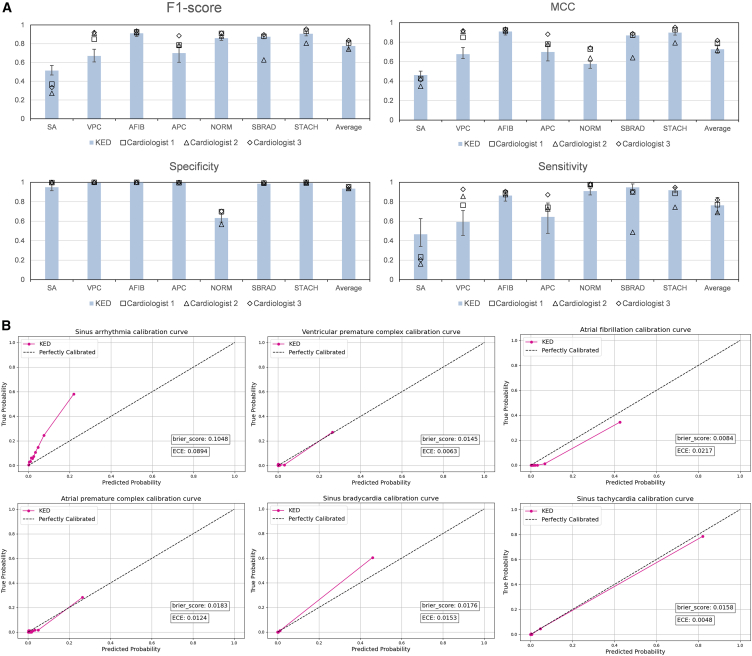
The Clinical Data is a clinical evaluation dataset we constructed, re-annotated independently by three cardiologists from top-tier hospital in well-developed region of China. The ground truth for the dataset was ultimately determined by a senior cardiologist. After maximizing the MCC to determine the classification threshold for each category, we evaluated the diagnostic performance of KED against the three cardiologists across seven ECG categories (as illustrated in the Figure 3A, with the remaining results provided in Table S5). The F1-score, MCC, specificity, and sensitivity indicate that the overall diagnostic performance of KED is comparable to that of the three cardiologists. KED achieved an F1-score of 0.776 (0.731–0.820), an MCC of 0.727 (0.629–0.740), a specificity of 0.935 (0.920–0.948), and a sensitivity of 0.763 (0.679–0.843). Notably, KED outperformed the three experts in F1-score, MCC, and sensitivity for the diagnoses of sinus arrhythmia (SA), sinus bradycardia, and sinus tachycardia (STACH), with similar specificity. For AFIB, KED demonstrated diagnostic capabilities comparable to the experts. However, KED was slightly inferior to the experts in diagnosing ventricular premature complex (VPC), atrial premature complex (APC), and normal ECG. Importantly, these results were achieved without KED having any prior information regarding the population characteristics, ECG collection equipment, or disease incidence rates from this center, whereas the dataset and the three cardiologists were all from the same hospital. The calibration plot for disease diagnosis using KED in clinical dataset is shown in Figure 3B. The diagnostic probabilities for VPC (Brier score: 0.015), AFIB (Brier score: 0.008), APC (Brier score: 0.018), sinus bradycardia (Brier score: 0.018), and STACH (Brier score: 0.016) all exhibit good calibration. Additionally, in Figure S3, we compared the inter-rater reliability between KED and three cardiologists who annotated the clinical data.

Figure 3.

Diagnostic performance of KED on clinical data

(A) Comparison of zero-shot diagnostic performance between three cardiologists and KED on the clinical dataset. Data are presented with 95% confidence intervals. Definitions for the abbreviations can be found in Table S8.

(B) Calibration plots of KED on Clinical Data.

See also Table S5.

Discussion

Previous research has primarily focused on specific tasks such as diagnosing particular rhythm abnormalities and conduction blocks,^2,5 or specific populations.^3,33 For example, although the recent HeartBEiT⁶ was pre-trained on 8.5 million ECGs, its diagnostic evaluation was limited to three tasks: hypertrophic cardiomyopathy, low left ventricular ejection fraction, and ST-segment elevation myocardial infarction. Similarly, although Lai et al.³³ recently proposed an algorithm capable of identifying 60 ECG diagnostic terms, their study was only applicable to the Chinese population and required special ECG collection equipment. Furthermore, they did not assess the diagnostic ability for previously unseen samples during training. Our research focuses on the generalization and zero-shot diagnostic capabilities of ECG diagnostic models. Specifically, it aims to learn diagnostic-relevant medical knowledge that can generalize from training on single-center data. This would enable the model to perform well on data from different regions, populations, and ECG collection devices, and even possess diagnostic capabilities for diseases not encountered during training. Our experimental results demonstrate the excellent generalization and robustness of the KED for various types of ECG diagnoses. Evaluation results from CPSC2018, Chapman, Georgia, and PTB-XL (four datasets with uniform gender distribution and comprehensive age distribution) show that our model maintains excellent diagnostic ability in ECG diagnoses across diverse populations in various regions of China, the southeastern United States, and other areas, without the need for target center data fine-tuning. This finding demonstrates that our model is not constrained by geographic, ethnic, age, gender, or ECG acquisition equipment variations. Furthermore, the results suggest that our model performs robustly and excellently in zero-shot diagnosis of diseases such as rhythm abnormalities, conduction blocks, premature contractions, hypertrophic cardiomyopathy (e.g., right ventricular hypertrophy, left ventricular hypertrophy), and some ischemic heart diseases (e.g., non-specific myocardial ischemia, ASMI). It also shows good diagnostic ability for diseases not seen during training (e.g., SVT, AT, QAb, anterolateral myocardial ischemia). The ability to diagnose various types of diseases in unknown environments has significant application value in deploying models to assist in diagnosis and early rapid screening in areas with a lack of and underdeveloped medical resources.

However, real-world environments are often more complex due to variations in ECG morphology, differences in disease incidence among diverse regions and ethnicities, and the occurrence of rare diseases. These factors may hinder the universality of KED’s zero-shot diagnosis. Therefore, we also investigated KED’s few-shot fine-tuning performance. Unlike the conventional approach of fine-tuning pre-trained models using large-scale target center data (thousands to tens of thousands of data), this method utilizes only several dozen to a few hundred ECG recordings from the target center, which is easier to collect and implement in real-world environments. Our experimental results demonstrated that KED exhibits remarkable adaptability, achieving significant performance improvements on four external evaluation datasets using merely 1% of their data. For example, fine-tuning the model with 218 ECG records in PTB-XL that did not overlap with the test set population improved the AUC for prolonged PR interval from 0.555 to 0.961, sensitivity from 0.671 to 0.805, and specificity from 0.502 to 0.950. The ability to fine-tune models with easily collectible, small-sample data to quickly adapt to the ECG pattern variability and specificity of the target population holds significant practical implications.

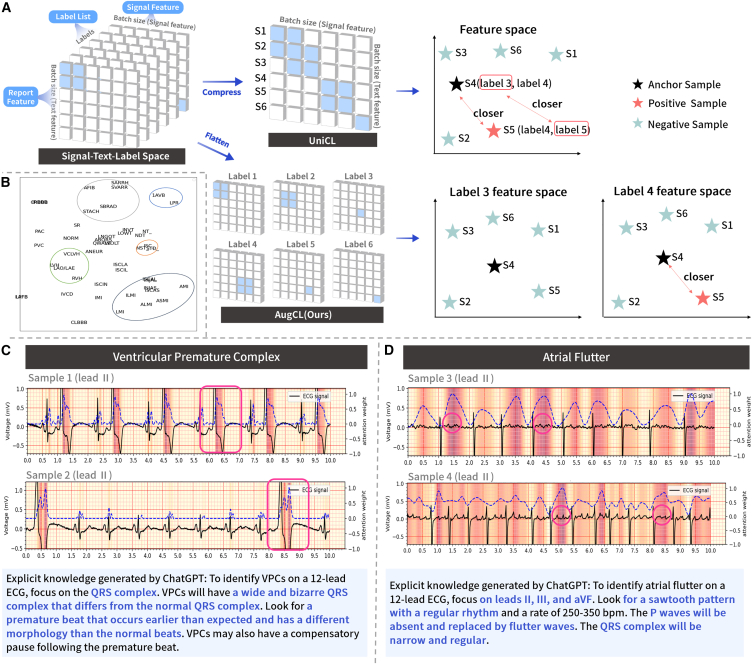
The robust performance of KED across diverse regions, ethnicities, and various equipment types from multiple manufacturers is primarily attributed to our signal-language architecture, knowledge enhancement methods, and signal-text-label contrastive representation learning. Traditional image or signal supervision model architectures are trained to predict a fixed set of predefined object categories and require additional labeled data to specify any other visual or signal concepts.^29,34 This limited form of supervision constrains their generality and usability. In contrast, our signal-language architecture employs text as the supervisory signal. Text inherently contains rich semantics, especially given that contemporary large language models typically encompass extensive knowledge with already established semantic relationships. Figure 4B depicts our query generation process, indicating the semantic space similarity of the representations encoded by different text labels (the closer the distance, the more similar the semantic relationship). For example, first-degree atrioventricular block and prolonged PR interval are completely different textual symbols, yet they exhibit similar semantic relationships within the KED representation space. Descriptions of hypertrophic cardiomyopathy also demonstrate similar semantic relationships. Prolonged QT interval, which was never encountered during training, shows similar semantic relationships with abnormalities such as QRS complex, ST segment, and T wave after KED encoding. This indicates that our model can effectively leverage the extensive knowledge and rich semantics in large language models to enhance zero-shot transfer.

Figure 4.

Module validity and interpretability analysis of KED

(A) Comparison of learning paradigms between AugCL and UniCL.

(B) A t-SNE diagram illustrating the query generation process for text labeling.

(C and D) Grad-CAM analysis of abnormal ECGs encoded by KED: highlighting model focus regions.

Secondly, to improve the generalization ability of the model, some studies incorporate open-domain medical knowledge into the model, utilizing resources such as Wikipedia, expert systems, and knowledge graphs. However, this approach demands significant effort to construct and align the knowledge base, making the process arduous and time-consuming, with uncertain results. The advent of LLMs offers an alternative solution, providing not only a rich repository of knowledge but also facilitating the integration of closed-domain models with LLMs through straightforward text prompts. Our strategy to enhance the knowledge of closed-domain training models via LLMs includes two key aspects: first, incorporating external medical knowledge during the training phase to guide the model’s representation learning, and second, using external knowledge to better guide the model in zero-shot diagnosis of previously unseen categories. This strategy’s efficacy is reflected in our ablation study results (as shown in Table S6), which indicate an improvement in diagnostic performance across five datasets when external medical knowledge is incorporated, compared to relying solely on text labels.

Lastly, UniCL enhances image-text contrastive learning with positive examples by incorporating label information, making it optimal for single-label classification tasks. Nonetheless, it tends to introduce noisy positive examples in multi-label classification settings. For instance, as shown in Figure 4A, in a task involving multi-label classification with label 3, label 4, and label 5, if there are two samples labeled (label 3, label 4) and (label 4, label 5), respectively, UniCL would consider the first sample as a positive example for the second (due to the shared label 4), thereby introducing noise in the representation learning of label 3 and label 5. Conversely, our proposed AugCL integrates a label dimension, allowing positive examples only between samples with the same label in each label’s dimension. This approach decouples multi-labels, and then reduces the influence of noise-positive examples based on a set of learnable parameters in the label dimension.

Interpretability plays a crucial role in AI-assisted applications.³⁵ It enables clinical physicians to uncover and comprehend the evidential basis upon which AI algorithms generate predictions, thereby ensuring a transparent level of AI diagnostics.³⁶ In this paper, we achieve user-oriented diagnostic result interpretability through two perspectives: the focus area of the model on the ECG and the domain knowledge of diagnosing specific diseases. Regarding interpretability, we conduct a case study; as shown in Figures 4C and 4D, it is evident that the generated knowledge and the model’s focus regions strongly align with the medically defined areas. For instance, KED diagnoses an ECG as VPC, and through Grad-CAM, we observe that KED focuses on the broad and abnormal QRS wave (the red box area) and makes the diagnosis of VPC based upon this. Concurrently, the generated diagnostic knowledge also describes, “focus on the QRS complex, VPCs will have a wide and bizarre QRS complex … ”, which is consistent with the basis for cardiologists diagnosing VPC. In addition, KED diagnoses the ECG as atrial flutter, observing that KED concentrates in the areas where the flutter waves appeared (the red circle area), and makes the diagnosis of atrial flutter based on this observation. At the same time, the generated diagnostic knowledge described “ … The P waves will be absent and replaced by flutter waves. The QRS complex will be narrow and regular.” This “image-text” format benefits beginners or cardiologists in underdeveloped areas. In the lack of sufficient educational resources or experienced doctors for guidance, it helps them in their diagnoses or self-study, thereby improving their diagnostic abilities.

Limitations of the study

Although KED has good zero-shot inference capabilities and superior downstream task adaptability, it still has certain limitations. First, despite employing various machine learning methods to mitigate erroneous labels in training datasets and conducting thorough external evaluations, it remains impossible to completely eliminate incorrect labels in large-scale datasets.^37,38 In the future, we will enhance our efforts by collecting and organizing more manually annotated or reviewed labels and utilizing advanced technologies to address label scarcity in large-scale datasets. Second, during development, KED integrates medical knowledge generated by large language models like GPT-4. However, these models inherently possess hallucination issues,³⁹ which introduce unavoidable risks in KED. To effectively mitigate these risks, it may be beneficial to first construct a validation set to evaluate the model’s overall performance in an external unknown environment before deploying it. Third, although the model can diagnose various diseases, it has not explored and evaluated conditions not explicitly mentioned in ECG reports, such as left ventricular dysfunction⁴⁰ and electrolyte imbalances.⁴¹ Our future work will focus on developing techniques for more precise alignment between ECG and medical text knowledge by integrating various data types, including tabular data, to further expand our downstream task research. Additionally, we utilize a large-scale single-center dataset to train our model. Although we strive to enable the model to learn generalizable diagnostic knowledge, our approach cannot completely eliminate biases related to demographic and clinical characteristics specific to this population. To address the limitations of single-center dataset, we plan to collect and organize large-scale datasets in future researches, perform model training based on multi-center data, and conduct extensive evaluations.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Yuanyuan Tian (tian102@sjtu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •All data presented within this study are available (see key resources table).
• •All original code has been deposited at Zenodo and is publicly available as of the date of publication. Accession links are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.

Acknowledgments

This paper is partly supported by National Postdoctoral Program for Innovative Talents (no. BX20230215), National Natural Science Foundation of China (no. 62406190), and Shanghai Municipal Science and Technology Major Project (no. 2021SHZDZX0102). This work also was partly supported by SJTU Kunpeng&Ascend Center of Excellence.

Author contributions

Y.T., Z.L., and Y.J. conceived the idea and designed the experiments. Y.T. and Z.L. wrote the code, performed the experiments, and plotted the figures. Y.T., M.W., and X.W. analyzed the results and drafted the manuscript. Y.T. and Y.J. carried out critical revisions of the manuscript and the results and discussion. L.Z. organized the re-annotation of the clinical data. Y.T., J.L., and Y.L. re-conducted the experiments and revised the manuscript format. C.L. and L.Z. supervised the projects, approved the submission, and accepted responsibility for the overall integrity of the paper.

Declaration of interests

The authors declare no competing interests.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work, the authors used Grammarly’s AI service in order to improve language and readability. After using this service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
CPSC2018	The China Physiological Signal Challenge 201821	http://2018.icbeb.org/Challenge.html
CHAPMAN	Shaoxing Hospital Zhejiang University School of Medicine22	PhysioNet: https://physionet.org/content/ecg-arrhythmia/1.0.0/
Georgia	the PhysioNet/Computing in Cardiology Challenge 202023	PhysioNet: https://moody-challenge.physionet.org/2020/
PTB-XL	Physikalisch-Technische Bundesanstalt24	PhysioNet: https://physionet.org/content/ptb-xl/1.0.2/
MIMIC-IV-ECG	Beth Israel Deaconess Medical Center20	PhysioNet: https://physionet.org/content/mimic-iv-ecg/1.0/
Clinical dataset	This paper	Zenodo: https://doi.org/10.5281/zenodo.14180221
Software and algorithms
KED	This paper	Zenodo: https://doi.org/10.5281/zenodo.14180221
xResnet1d_101	Strodthoff et al.25	Github: https://github.com/helme/ecg_ptbxl_benchmarking
BioClinicalBERT	Alsentzer et al.42	Github: https://github.com/EmilyAlsentzer/clinicalBERT
Transformer	N/A	Github: https://github.com/xiaomanzhang/KAD
Pytorch	N/A	https://pytorch.org/

Experimental model and subject details

The study protocol received approval from the medical ethics committees of the participating institutions. As this study is retrospective, patient consent was not required. A total of six datasets were used in this study, among which MIMIC-IV-ECG, CPSC2018, Chapman, Georgia, and PTB-XL are all open-source datasets. The Clinical Data has been approved by the review boards of Shanghai Jiao Tong University School of Medicine and Shanghai First People’s Hospital. MIMIC-IV-ECG represents ECG data from the northeastern U.S. population, used for model training. CPSC2018 and Chapman represent clinical ECG data from various regions in China; Georgia represents ECG data from the southeastern U.S. population; PTB-XL represents clinical ECG data from other regions (70.89% German, 27.9% English, and 1.21% Swedish). CPSC2018, Chapman, Georgia, and PTB-XL were used to evaluate zero-shot diagnostic performance across different regions, ethnicities, and ECG acquisition devices. The Clinical Data was used to compare model performance with that of cardiologists. All ECG reports in different languages (German, English, Chinese, Swedish, etc.) were standardized to English. The datasets encompass all age groups and a balanced gender ratio. More detailed demographic and clinically relevant characteristics can be found in the Method Details or the cited references. To evaluate the model’s performance in ECG diagnostics across different regions, ethnicities, ages, genders, and ECG acquisition devices, no specific screening and processing were conducted on the geographical, ethnic, age, gender, or ECG signals. Instead, screening was based on the sample size within each label to ensure sufficient evaluation samples for each disease.

Method details

Pre-training and evaluation dataset preparation

In this study, the MIMIC-IV-ECG clinical database was used to pre-train the model. This database contains about 800,000 diagnostic ECGs collected from nearly 160,000 patients (both inpatient and outpatient) during 2008–2019 for MIMIC-IV. These included ECGs from the Beth Israel Deaconess Medical Center emergency department, hospital (including ICU), and outpatient care centers. These diagnostic ECGs use 12 leads and are 10 s in length. For each ECG, the database provides a machine measurement. As the cardiologist reports are not yet published, we opted to use the text-based cardiological reports generated by the ECG machines to train the model. Under the guidance of a chief physician, we organized and standardized the 105 most frequent labels (the sample size was not less than 2000) from these unstructured cardiological reports for training, the labels are shown in Figure 2A and Table S7.

We selected four publicly available datasets and one clinical dataset to evaluate the model performance. The relationships between the ECG labels of these 5 external datasets and the labels we organized in MIMIC-IV-ECG are shown in Figure 2A and Table S8. Among the five datasets, there are 29 unique labels (50.0%) that directly appear in MIMIC-IV-ECG; 16 unique labels (27.6%) not seen, such as Atrial tachycardia and ST-segment depression, which do not appear among the MIMIC-IV-ECG; there are 13 unique labels (22.4%) that have a superclass-subclass relationship with labels in MIMIC-IV-ECG, such as complete left bundle branch block and left bundle branch block. This can be fully utilized to assess the model’s transfer learning ability and generalizability.

The PTB-XL database^24,25 comprises 21,837 clinical 12-lead ECG records, each with a duration of 10 s. These records were obtained from 18,885 patients, with 52% male and 48% female, and an age range of 0–95 years (mean: 62, interquartile range: 22). The ECG reports are available in German (70.89%), English (27.9%), and Swedish (1.21%). The annotations for the ECGs adhere to the SCP-ECG standards.²⁴ These annotations are classified into three non-exclusive categories. To ensure data reliability, we excluded categories with fewer than 100 samples, resulting in 29 diagnostic statements, 15 form statements, and 6 rhythm statements, totaling 46 statements.

The CPSC2018²¹ dataset originates from the 1st China Physiological Signal Challenge held in 2018, a central event of the 7th International Conference on Biomedical Engineering and Biotechnology (ICBEB 2018). It consists of 9,831 12-lead ECG records from 9,458 patients across 11 Chinese hospitals, with durations ranging from 6 to 60 s and a total of nine labels. The subset we utilized includes 6,877 ECGs (the rest were not released), comprising 3,178 females and 3,699 males. The ages of the patients range from 1 to 92 years (mean: 60, standard deviation: 19).

The Georgia dataset²³ represents the unique demographic characteristics of the southeastern region of the United States. This dataset includes 20,678 12-lead ECG records from 15,742 patients. Based on the PhysioNet/Computing in Cardiology Challenge 2020,²³ which released 10,344 records, we filtered out categories with fewer than 100 samples to ensure the reliability of the evaluation results, ultimately retaining 8,999 ECG records and 20 categories. Among these 8,999 ECGs, 53% are from males, with an age range of 14–89 years (mean age: 60, standard deviation: 15).

The Chapman dataset²² is a 12-lead ECG dataset developed through a collaboration between Chapman University and Shaoxing People’s Hospital. This dataset comprises 10,646 10-s 12-lead ECG records collected from 10,646 patients at Shaoxing People’s Hospital in China. The patient demographic includes 56% male, with ages ranging from 4 to 98 years (mean age of 51 years, standard deviation of 18 years). We filtered out rhythm types with fewer than 100 samples, ultimately retaining eight different rhythms.

To evaluate our model’s effectiveness in clinical screening and compare its diagnostic performance with clinical cardiologists, we collaborated with Shanghai First People’s Hospital to develop a representative dataset of 1760 ECG records from 1753 patients. Figure 2B illustrates the distribution of labels, ages, and genders in the dataset. Notably, 48% of the data is from male patients, with an age range of 1–96 years (mean of 53, standard deviation of 19). We invited three experienced cardiologists and a senior cardiologist to form a labeling committee to re-annotate the Clinical dataset. The re-annotation process was conducted in two stages. In the first stage, the three experienced cardiologists individually utilized the same labeling interface to annotate all ECG data, which only provided age, gender, and the original ECG. No discussion or communication was permitted during this process. The consistency (kappa coefficient) among the three cardiologists is shown in Figure S3. In the second stage, the senior cardiologist reviewed all ECGs and adjudicated any inconsistencies found in the first stage. The results of the first stage were used to assess the accuracy of the cardiologists, while the results of the second stage served as the final ground-truth labels for the dataset.

Report augmentation of KED

Cardiologists rely heavily on medical knowledge when analysing ECGs and making diagnostic conclusions. Specific medical knowledge is needed to diagnose a condition like Incomplete Right Bundle Branch Block (IRBBB). For example, "Look for QRS duration greater than 120 ms, fuzzy S wave in the lead I, wide R waves in leads V1 and V2. Additionally, there may be notches or fuzzy R waves in lead V1 … ". Integrating such medical knowledge into ECG representation learning is significant, as it incorporates valuable knowledge that may produce superior results compared to solely relying on diagnostic conclusions. Recently, advancements in LLMs such as GPT4,^32,43 Gemini,⁴⁴ and GLM4⁴⁵ have significantly accelerated. In this study, we utilize LLMs to integrate medical knowledge to enhance ECG reports and better guide ECG signal representation learning. Specifically, each ECG has one or multiple structured labels extracted from the report. Then, we ask GPT4 how to identify these labels from a 12-lead ECG. For reports with multiple labels, we combine multiple pieces of medical knowledge to create the background info section appended to the original ECG report. This enhanced report is used to guide ECG representation learning. Moreover, in the zero-shot diagnosis phase, when the model encounters categories it has not seen before, LLMs provide enhanced textual descriptions for these novel categories, improving the model’s comprehension. The prompt utilized in this study is:

I want you to play the role of a professional Electrocardiologist, and I need you to teach me how to diagnose {disease name} from 12-lead ECG. such as which leads or what features to focus on, etc. Your answer must be less than 50 words.

Since the quality of medical knowledge generated by different LLMs varies, we explore the impact of different LLMs on the model in the Results section.

The modules in KED

The KED framework includes four key modules: an ECG signal encoder that transforms raw signals into vector representations of specific dimensions; a knowledge encoder that converts reports or label texts into their corresponding vector dimensions; a Label Query Network, based on the Transformer architecture,⁴⁶ processes label and ECG encodings to generate the vector representations of the query results; and a classification head, specifically a Multilayer Perceptron (MLP), that interprets these query result encodings to predict the likelihood of each label’s presence in the ECG data. The ECG encoder, knowledge encoder and Label Query Network are introduced in the following.

ECG encoder. Given a 12-leads ECG $x_i\in R^{12\times W}$, we compute the features with a signal encoder:

$$x_i={\Phi }_{signal}\left(x_i\right)\in {\mathbb{R}}^{c\times d}$$ Equation (1)

where $c$ refers to the number of channels, and $d$ refers to the feature dimension, the ECG encoder architecture is shown in Figure S4A.

Knowledge encoder. Given an augmented report $t_i$ in text form, we compute its features with a pre-trained knowledge encoder:

$$t_i={\Phi }_{knowledge}\left(t_i\right)\in {\mathbb{R}}^{t\times d}$$ Equation (2)

where $t$ refers to the token number, and $d$ refers to the feature dimension. In our case, we adopt BioClinicalBERT⁴² as the knowledge encoder (see Figure S4B).

Label query network. The process of LQN, denoted as ${\Phi }_{LQN}$, is summarized in Algorithm 1, and its architecture is depicted in Figure S4C. Given a label list $L$, we generate a set of query vectors $L=\left\{l_1,l_2,...,l_L\right\}$ by the knowledge encoder, where $l_i={\Phi }_{knowledge}\left(l_i\right)$. The inputs of ${\Phi }_{LQN}$ includes $x_i$, $t_i$ and $L$; the output is the vector representations of the query results. During training, we randomly select either the encoded signal features $x_i$ or report features $t_i$ as the key and value of the LQN, this allows us to use the signal and textual embedding spaces interchangeably. During inference, the input LQN consists solely of signal features. The resulting outputs are then passed through an MLP to infer the presence of the queried label.

Algorithm 1: The process of ΦLQN.

#L: a set of text labels encoded by knowledge encoder;

#x: a batch of 12-leads ECG signal; t: a batch of augmented report.

# Transformer_decoder: a decoder model of Transformer.

For x, t in loader:

x = Φ_signal(x)

t = Φ_knowledge(t)

if mode = = training:

key = x if random.random() < 0.5 else t

value = x if random.random() < 0.5 else t

else:

key = x

value = x

query = L

s = Transformer_decoder(query, key, value)

End.

Augmented Signal-Text-Label Contrast Learning and training process of KED

Inspired by the UniCL, which combines the image-label and image-text spaces to create a novel image-text-label space, the unified space allows for more effective guidance in visual representation learning. As shown in Figure 4A (left), the constructed Signal-Text-Label space comprises three dimensions: signal, text, and label. For each batch of data during training, $z^S\in R^{b\times d}$ represents the result calculated on a batch of ECGs using Equation 1 and pooled across the channel dimension; $z^T\in R^{b\times d}$ represents the result calculated on a batch of reports using Equation 2 and pooled across the token dimension; $\overline{l}\in R^{b\times L}$ represents the one-hot encoding of the sample labels in the batch, where $b$ denotes the batch size and $L$ denotes the number of queried labels. We use $z^S$, $z^T$ and $\overline{l}$ to construct the Signal-Text-Label space for each batch, forming a three-dimensional vector of size $L\times b\times b$. This semantic space integrates the signal, report, and multi-label characteristics of each sample, constructing the semantic information of each sample. The semantic information in this space is used for subsequent comparisons of similarities and differences between different samples, referred to as contrastive learning.

As shown in the middle of Figure 4A, UniCL is designed for single-label data, which essentially further compresses the label dimension based on the three-dimensional vector of $L\times b\times b$ that we constructed. However, this compression method may result in a loss of information. This section introduces the Augmented Signal-Text-Label Contrast Learning (AugCL). This is further computed within the Signal-Text-Label space constructed by $z^S$, $z^T$ and $\overline{l}$, AugCL loss preserves the label dimension and constructs a separate space for each label. (We further discuss the difference between UniCL loss and AugCL loss in section Discussion.) It then aligns the signal-text pairs within their corresponding label space:

$$L_{S\to T}^{STL}=-\sum _{l\in L}{\omega }_l\cdot \sum _{m\in Q_{\left(l\right)}}\frac{1}{P_{\left(l\right)}}\cdot \sum _{k\in P_{\left(l\right)}}\log \left(\frac{\mathit{exp}\left(z_m^S\cdot z_k^T/\tau \right)}{\sum _{j=1}^B\mathit{exp}\left(z_m^S\cdot z_j^T/\tau \right)}\right)$$ Equation (3)

$$L_{T\to S}^{STL}=-\sum _{l\in L}{\omega }_l\cdot \sum _{m\in Q_{\left(l\right)}}\frac{1}{P_{\left(l\right)}}\cdot \sum _{k\in P_{\left(l\right)}}\log \left(\frac{\mathit{exp}\left(z_m^T\cdot z_k^S/\tau \right)}{{\sum }_{j=1}^B\mathit{exp}\left(z_m^T\cdot z_j^S/\tau \right)}\right)$$ Equation (4)

where $L$ is the label list, $w_l$ is the learnable parameters, $k\in P_{\left(l\right)}=\left\{k\mid k\in B,y_k=l\right\}$, $m\in Q_{\left(l\right)}=\left\{m\mid m\in B,y_m=l\right\}$, $y$ is the category of $\left(z^S,z^T\right)$, and $B$ is the batch size. $L_{S\to T}^{STL}$, $L_{T\to S}^{STL}$ are the signal-to-text and text-to-signal contrastive loss, respectively. The definition of augmented signal-text-label contrast loss (AugCL loss) is: $L^{STL}=L_{S\to T}^{STL}+L_{T\to S}^{STL}$.

To train our KED, we randomly select a small batch of $N$ input pairs from the training dataset and optimise the signal, text, and label contrast loss $L^{STL}$. Next, utilizing the labels as queries, we employ binary cross-entropy to predict the existence of each respective label, denoted as $L^{LQN}$. Finally, for each small batch, we aggregate $L^{STL}$ and $L^{LQN}$ as the overall loss:

$$L=L^{STL}+L^{LQN}\text{.}$$ Equation (5)

Interpretability of the KED

Deep learning models, often referred to as "black boxes," possess internal decision-making mechanisms that are not well understood.⁴⁷ As such, the interpretation and understanding of these models are crucial for elucidating their behavior, limitations, and social impact, especially in the medical field.^48,49 This study examines the interpretability of such models from two perspectives. Grad-CAM,³¹ a visualization technique employing gradients, can generate heatmaps from input signals. This technique reveals network sections that significantly impact the decision-making process, allowing us to identify the image features the model primarily focuses on, thus enhancing interpretability. We initially assess the model’s interpretability using Grad-CAM to identify the key regions on ECG signals that are essential for diagnosis. Simultaneously, we use the multi-label diagnostic results of the KED model to generate explicit text knowledge on how to diagnose specific diseases with GPT4, and apply this interpretative knowledge to assist users in learning and medical diagnosis. As shown in Figures 4C and 4D, the diagnostic interpretability for users consists of background knowledge of disease diagnosis and the area that the model focuses on specific samples.

Implementation and deployment details

Data preprocessing. In the signal-language pre-training stage, we organize each 12-lead ECG signal into 10-s segment with a sampling frequency of 100 Hz. We directly use the raw signal as the input for the model without any signal preprocessing. For the ECG report, we combine the standardized labels extracted from it with the customized prompt and interact with OpenAI’s GPT-4 model⁵⁰ in the form of interface access to obtain the model’s returned results. We then combine the returned results with the original ECG report to create the enhanced report. During the fine-tuning stage, we utilize the same strategy to preprocess the four datasets.

Model pre-training. The pre-training process is illustrated in Figure 1A. For the signal-language pre-training stage, the signal encoder is a XResNet1D_101^25,51 without fully connected layers. The knowledge encoder is initialized from BioClinicalBERT⁴² and fine-tuned during the pre-training process by adjusting the last layer of BioClinicalBERT (The parameters of the remaining layers are frozen). The LQN consists of seven layers of standard Transformer decoder.⁴⁶ The dimensionality of ECG signal and text features, $d$, is 768. The classification head contains a two-layer MLP structure. The first layer has 2048 neurons, while the second layer is the output layer and contains 2 neurons. We use AdamW⁵² optimiser with $lr=5\times 10^{-5}$ and $l{r}_{warm}=1\times 10^{-5}$. We train on a GeForce RTX A6000 with a batch size of 80 for 4 epochs. In our model, the total number of parameters amounts to 163,656,580, with 85,689,988 being trainable and 77,966,592 remaining frozen.

Model deployment. The testing and deployment phase is shown in Figure 1B. Leveraging advancements in Internet and cloud computing technologies, our team has developed a cloud-based solution wherein the trained model is deployed to cloud servers. Remote and underserved areas can upload ECG data and query potential diseases (or predefine a range of disease queries), and the cloud servers process the data and return diagnostic results. This cloud deployment distributes the computational workload, allowing resource-limited regions to require only basic internet access, which is feasible in most parts of China. Regarding privacy and data security, our cloud model necessitates only ECG data for diagnosis and does not require any additional personal information from patients.

Evaluation details

We evaluate the model performance from two perspectives: zero-shot diagnosis and few-shot fine-tuning. The definition of generalized zero-shot diagnosis is to recognize samples from both seen and unseen classes in new, unknown data that differ in distribution from the training data.¹¹ As shown in Figure 2C, where zero-shot diagnosis in this paper refers to directly diagnosing the five downstream datasets without using any additional samples after pre-training on MIMIC-IV-ECG. To evaluate the zero-shot performance of the model in multi-label classification tasks, LQN employs a query input consisting of a series of label names, and the original signal features serve as keys and values. This approach allows LQN to determine the likelihood of the presence of a particular label in the considered ECG signals. Divide the four downstream datasets into training, validation and test sets with a ratio of 7:1.5:1.5. Zero-shot diagnosis is applied directly to the test set. In addition, after being annotated by cardiologists, the clinical dataset is directly used for zero-shot inference. Few-shot fine-tuning refers to fine-tuning the pre-trained model using a small number of samples in the downstream dataset before diagnosing the downstream dataset. In the few-shot fine-tuning stage, we use the AdamW optimiser to fine-tune the model on the four datasets. The model is trained using the same learning rate and decay strategy as the pre-training phase with the batch size of 16 and epoch of 10. Similarly, divide the dataset into training, validation, and test sets. The model is fine-tuned by randomly selecting samples on the 1% training set and then evaluated on the test set.

We utilize metrics such as AUROC, AUPRC, Accuracy (ACC), Matthews Correlation Coefficient (MCC), F1-score, Sensitivity, Specificity, Positive Likelihood Ratio (LR+), and Negative Likelihood Ratio (LR-) to comprehensively evaluate the performance of the model. Among these, ACC represents the proportion of correctly classified samples, which is defined as:

$$ACC=\frac{TP+TN}{TP+TN+FP+FN}\text{,}$$ Equation (6)

where $TP$ represents the number of true positives, $TN$ represents the number of true negatives, $FP$ represents the number of false positives, and $FN$ represents the number of false negatives.

MCC takes into account true positives, true negatives, false positives, and false negatives, and its formula is defined as:

$$MCC=\frac{TP\cdot TN-FP\cdot FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}\text{.}$$ Equation (7)

Sensitivity (Sen), also known as recall, is the ratio of correctly identified positive samples to the total number of positive samples. It is negatively correlated with the rate of missed diagnoses in patients. It is defined as:

$$Sen=\frac{TP}{\left(TP+FN\right)}\text{.}$$ Equation (8)

Specificity (Spe) is the ratio of correctly identified negative samples to the total number of negative samples. It is negatively correlated with the rate of misdiagnoses in patients. It is defined as:

$$Spe=\frac{TN}{\left(FP+TN\right)}\text{.}$$ Equation (9)

F1-score represents the harmonic mean of recall and precision. It is defined as:

$$F1=\frac{2\cdot Precision\cdot Recall}{Precision+Recall}\text{.}$$ Equation (10)

where $Recall$ is equivalent to $Sen$, $Precision=\frac{TP}{TP+FP}\text{.}$

LR + indicates how much the likelihood of having the disease increases after a positive test result. When LR+ > 1, the larger the value, the higher the diagnostic value of the positive result. It is defined as:

$$LR+=\frac{Sen}{1-Spe}\text{.}$$ Equation (11)

LR-indicates how much the likelihood of not having the disease increases after a negative test result. When LR-is less than 1, the smaller the value, the higher the exclusion value of the negative result. It is defined as:

$$LR-=\frac{1-Sen}{Spe}\text{.}$$ Equation (12)

We also conduct a calibration assessment of the model, plot calibration plots, and calculate the Brier score. The definition of the Brier score is:

$$Brier\_score=\frac{1}{N}\sum _{t=1}^N{\left({\hat{y}}_t-y_t\right)}^2\text{,}$$ Equation (13)

where $\hat{y}$ is the predicted probability; $y$ is the ground truth, $N$ is the total number of samples.

Ablation study

We conduct an ablation study on the proposed knowledge enhancement method and contrastive learning method. Table S6 presents the quantitative results. Overall, the implementation of the knowledge enhancement method and the contrastive learning method significantly improves performance across five datasets. In the knowledge enhancement method, GPT-4 outperforms Gemini and GLM4 on the CHAPMAN, Georgia, and PTB-XL datasets. For example, in the Georgia dataset, when neither knowledge enhancement nor AugCL is utilized, the model’s average AUC is 0.859, with Sensitivity at 0.670, Specificity at 0.884, LR + at 30.550, and LR-at 0.358. However, with the application of knowledge enhancement (GPT-4) and AugCL, the AUC increases to 0.900, Sensitivity to 0.696, Specificity to 0.925, LR + to 39.601, and LR-decreases to 0.329.

In comparison to the model without knowledge enhancement, using GPT-4 knowledge enhancement improves the AUC by 1.1%, 0.6%, 3.8%, 2.8%, and 1.9% on the CPSC2018, Chapman, Georgia, PTB-XL, and clinical datasets, respectively. Employing AugCL as the contrastive learning objective, as opposed to UniCL, enhances the AUC by 3%, 1.1%, 1.6%, 1.4%, and 0.3% on the CPSC2018, Chapman, Georgia, PTB-XL, and clinical datasets, respectively. When combining knowledge enhancement (GPT-4) and AugCL, zero-shot diagnostic performance improves by 3.7%, 0.6%, 4.1%, 0.4%, and 1.5% AUC on the CPSC2018, Chapman, Georgia, PTB-XL, and clinical datasets, respectively.

Additionally, we qualitatively analyze the effectiveness of different language models for knowledge enhancement. Table S9 lists several diseases related to the location of myocardial infarction: anterolateral myocardial infarction (ALMI), anterior myocardial infarction (AMI), anterior septal myocardial infarction (ASMI), and inferior myocardial infarction (IMI), comparing knowledge generated by three large language models with medical definitions.⁵³ Table S10 shows the zero-shot diagnostic AUC for these diseases on the PTB-XL dataset. The results indicate that although all three models provide medical knowledge, the knowledge provided by GPT-4 is more effective in improving the zero-shot diagnostic performance of ECGs.

Quantification and statistical analysis

We perform statistical analysis using the sklearn package and report various metrics, including AUROC, AUPRC, Accuracy, F1-score, Matthews Correlation Coefficient, Sensitivity, Specificity, Positive Likelihood Ratio, and Negative Likelihood Ratio. We also report the calibration plots of KED for diagnosing various diseases in an unknown population. To calculate the 95% confidence intervals for all these metrics, we utilize a non-parametric bootstrap method to generate confidence intervals: random samples of size n (equal to the size of the original dataset) are repeatedly sampled with replacement from the original dataset 100 times.

Published: December 17, 2024