Mechanics of receptor-mediated endocytosis

Abstract

Most viruses and bioparticles endocytosed by cells have characteristic sizes in the range of tens to hundreds of nanometers. The process of viruses entering and leaving animal cells is mediated by the binding interaction between ligand molecules on the viral capid and their receptor molecules on the cell membrane. How does the size of a bioparticle affect receptor-mediated endocytosis? Here, we study how a cell membrane containing diffusive mobile receptors wraps around a ligand-coated cylindrical or spherical particle. It is shown that particles in the size range of tens to hundreds of nanometers can enter or exit cells via wrapping even in the absence of clathrin or caveolin coats, and an optimal particles size exists for the smallest wrapping time. This model can also be extended to include the effect of clathrin coat. The results seem to show broad agreement with experimental observations.

Receptor-mediated endocytosis is one of the most important processes with which viruses and bioparticles can enter or leave an animal cell. Viruses have thousands of different shapes and sizes. Most viruses show a characteristic size in the range of tens to hundreds of nanometers (1, 2). Equipped with a limited amount of nucleic acid, viruses propagate by parasitizing host cells and multiplying their viral nucleic acid and protein capsid via the biochemical machinery of the host. The life cycle of a virus follows a sequential route through various compartments of the host as illustrated in Fig. 1 (3). It takes only 20–40 min for many bacterial phages to finish one life cycle from infection to lysis. For most animal viruses, entering and leaving a host cell are mediated by specific binding of outer coat proteins (such as hemagglutinin in the case of influenza viruses) to specific mobile receptors on the host cell surface.

Fig. 1.

The life cycle of an animal virus. (a) Adsorption or docking with the host receptor protein. (b) Entry into the host cytoplasm. (c) Biosynthesis of viral components. (d) Assembly of viral components into complete viral units. (e) Budding from the host cell.

It has been generally assumed that the endocytosis of viruses is associated with the formation of a clathrin coat at the inner membrane leaflet (4). Typically, clathrin coats can generate a membrane radius of curvature as small as ≈50 nm. The formation of such small buds has been explained in terms of the bending elasticity concept by considering topological defects of the clathrin network (5). More recently, however, it has been shown that influenza viruses can enter cells even if the formation of clathrin coats are inhibited (6, 7). Here, we develop a model to explain the mechanism of clathrin-free entry of viruses into cells. This model can easily be extended to account for the effect of a clathrin coat.

The endocytic pathway is also of interest for understanding possible mechanisms by which nanomaterials might enter into human or animal cells, a significant issue for the development of gene and drug delivery tools (8, 9), as well as for assessing the potential hazard of nanotechnology on ecology and human health (10–14).

Experimental studies on targeted drug delivery into cells have identified particle size as an important factor in cellular uptake of nanomaterials. It has been shown that particles with radii <50 nm exhibit significantly greater uptake compared with particles >50 nm (15, 16). Aoyama and coworkers (17–19) made a specific investigation of the size effects and receptor contributions in glycoviral gene delivery by excluding potential complications arising from the charge effects. They concluded that receptor-mediated endocytosis is strongly size-dependent and that there is an optimal size, ≈25 nm.

Various models have been established to elucidate the mechanism of virus budding on a host membrane. Simons and Garoff (20, 21) suggested that the viral capsid may wrap itself in the host membrane via thermal fluctuations of the membrane. Lerner et al. (22) proposed several possible rate-limiting processes to explain virus budding and found that a nonzero spontaneous membrane curvature may be necessary to ensure a wrapping time in accordance with the experimentally observed upper limit of ≈20 min. Recently, van Effenterre and Roux (23) and Tzlil et al. (24) developed statistical thermodynamics models of virus budding. van Effenterre and Roux (23) derived a relationship between the volume concentration of viruses and the budding time, and they identified an optimal volume concentration of internalized particles for budding. All of these models are based on the assumption of a specific particle size. The questions of whether and how particle size affects the dynamics of entry (endocytosis) or exit (budding) remains largely unresolved.

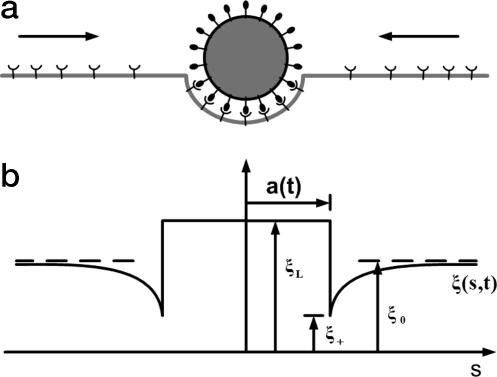
In this article, we consider how a cell membrane containing diffusive mobile receptors wraps around a cylindrical or spherical particle coated with compatible ligands. The ligands are assumed to be immobile and uniformly distributed on the particle surface, whereas the receptors are mobile and undergo rapid diffusive motion in the plane of the cell membrane. The receptors on the cell membrane diffuse to the wrapping site and bind with the ligands on the particle surface to lower the free energy of interaction. Because cells are generally much larger than viruses, we consider a particle interacting with an initially flat membrane. The receptor-ligand binding causes the membrane to locally wrap around the viral particle at the cost of elevated elastic energy associated with increased local curvature of the membrane and reduced configurational entropy associated with receptor immobilization, as shown in Fig. 2a. For such adhesive contact between cell membrane and particle, we adopt the mathematical framework developed in recent studies of curved biological membranes spreading on a flat substrate (25, 26), where results were found in good comparison with experimental observations (27, 28) on spreading of giant vesicles on integrin-coated substrates. The distribution of receptors in the membrane is determined by solving the problem of diffusion in a plane, as shown in Fig. 2b.

Fig. 2.

Schematic illustration of the problem. (a) An initially flat membrane containing diffusive receptor molecules wraps around a ligand-coated particle. (b) The receptor density distribution in the membrane becomes nonuniform upon ligand-receptor binding; the receptor density is depleted in the near vicinity of the binding area and induces diffusion of receptors toward the binding site.

Before contact with the particle, the receptors are assumed to be distributed uniformly on the cell membrane with density ξ₀, consistent with the state of maximum entropy. Once the contact starts, the receptor density within the contact area is raised to the level of ligand density ξ_L on the particle surface. Driven by a local reduction in free energy caused by ligand–receptor binding, the receptors in the immediate neighborhood of the adhesion region are drawn to the edge of the contact zone by diffusion, leading to a local depletion of receptors in the vicinity. The resulting gradient in concentration induces global diffusive motion of receptors toward the binding site. The diffusive process can be characterized by a nonuniform receptor distribution function ξ(s, t) (Fig. 2b). The size of the contact area 2a(t) increases with time t as more and more receptors are captured within it. The wrapping process begins at s = 0, t = 0 and ends when the total area of contact reaches that of the particle.

Uptake of Cylindrical Particles into Cell

We first consider the 2D configuration of an infinite flat membrane wrapping around an infinitely long cylindrical particle. We adopt the mathematical framework developed in a recent study of an initially curved membrane spreading on a flat substrate (25). The analysis has been adapted to the problem of a flat membrane wrapping around a cylindrical (this section) or spherical (next section) particle.

Assuming that the total number of receptors in the membrane remains constant during the wrapping process, we can write a global conservation condition for the receptor density ξ(s, t) as

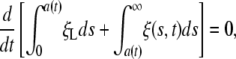[1]

where a(t) is the half-width of the contact region. The diffusive flux of receptors is assumed to be prescribed by the kinetic relation

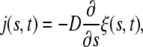where D is the diffusivity. Substituting the continuity equation

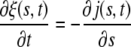[2]

into Eq. 1 while noting that ξ(s, t) → ξ₀, j(s, t) → 0 as s → ∞, and ξ(s, t) = ξ_L, j(s, t) = 0 for s < a(t) yields

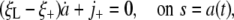[3]

where ξ₊ ≡ ξ(a⁺, t), j₊ ≡ j(a⁺, t) denote values directly in front of the contact edge.

The receptor density ξ(s, t) is determined from the diffusion equation

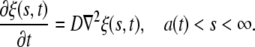[4]

This problem corresponds to the so-called Stefan problem (29). The appropriate solution has the form

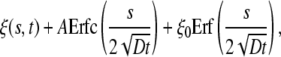[5]

where Erf(z) and Erfc(z) are the error and complementary error functions, respectively, and A is a constant of integration. One may immediately check that Eq. 5 satisfies the initial condition ξ(s, 0) = ξ₀ and correct asymptotic behavior ξ(s, t) → ξ₀, j(s, t) → 0 as s → ∞. Substituting the solution in Eq. 5 into the conservation condition in Eq. 3 gives the following equation

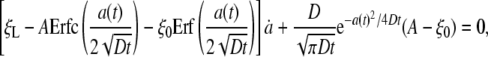[6]

which can be satisfied only if

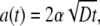[7]

where α is a constant that will be called the “speed factor.” The value of α will be determined shortly by power balance. Inserting Eq. 7 into Eq. 6 gives the constant A

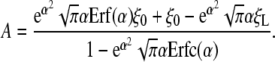[8]

The process of viruses entering and leaving a host cell may involve thermal fluctuations of the plasma membrane and hydrodynamic interactions. In this study, we consider a simplified free energy function (25) for a curved cell membrane in adhesive contact with a substrate

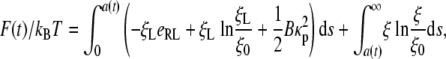[9]

where k_B is the Boltzmann constant, T is the absolute temperature, k_BTe_RL is the energy of a single receptor–ligand bond, k_BT lnξ_L/ξ₀ and k_BT lnξ/ξ₀ are the free energy per receptor associated with the loss of configurational entropy of the bound receptors and free receptors (treated as an idea gas in the membrane plane), respectively (30), and Bk_BTκ²_p/2 is the elastic bending energy of the membrane wrapping around a cylinder with radius of curvature κ_p =1/R (31), Bk_BT being the bending modulus. The free energy function in Eq. 9 thus consists of the energy of receptor–ligand binding, the configurational entropy of receptors, and the elastic energy of the cell membrane. A slightly different expression has been adopted for the entropic part of the free energy in ref. 26.

Differentiating Eq. 9 with respect to time leads to

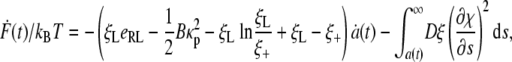[10]

where

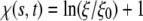[11]

is the local chemical potential of a receptor. The integral term in Eq. 10 is identified as the rate of energy dissipation associated with receptor transport along the cell membrane (25). If we require that the rate of free energy reduction gained from the wrapping process exactly balances the rate of energy dissipation consumed during receptor transport, the first term in Eq. 10 must vanish so that

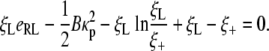[12]

Substituting Eqs. 5, 7, and 8 into the power balance relation of Eq. 12 yields an equation to determine the speed factor α,

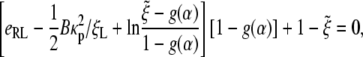[13]

where

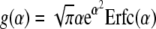[14]

and .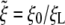

Once α is known, the particle wrapping time is obtained as

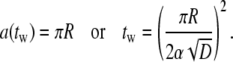[15]

Uptake of Spherical Particles into Cell

The previous 2D analysis for wrapping of a cylindrical particle by a flat cell membrane can be extended to the axisymmetric 3D problem of wrapping of a spherical particle. To retain the simplicity of an analytical treatment of the problem, we model the process of membrane wrapping around a spherical particle as an expansion of an effective contact area of receptor–ligand adhesion on a flat membrane. The exact geometry of membrane wrapping around a spherical particle is only taken into account in the free energy function.

In the axisymmetric 3D case, most of the equations are similar to 2D. For example, the continuity condition in Eq. 2 is modified as

whereas the receptor conservation condition is identical to Eq. 3. The axisymmetric solution to receptor density function has the form

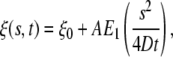[16]

where

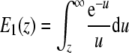is the exponent integral function and A is a constant of integration. This solution satisfies the axisymmetric diffusion equation and the correct boundary conditions ξ(s, 0) = ξ₀ and ξ(s, t) → ξ₀, j(s, t) → 0 as s → ∞. Substitution of Eq. 16 into the conservation condition Eq. 3 yields

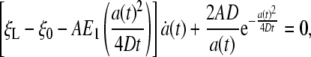[17]

which again suggests that

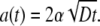[18]

Inserting Eq. 18 into Eq. 17 gives

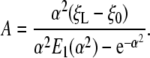[19]

Similar consideration of power balance during particle wrapping leads to an equation to determine the 3D speed factor α,

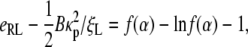[20]

where κ_p = 1/R₁ + 1/R₂ = 2/R is the effective curvature of a spherical particle (1/R₁, 1/R₂ are the Gaussian principal curvatures) and

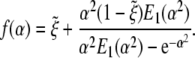[21]

Once α is known, the wrapping time is obtained as

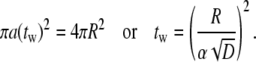[22]

Numerical Solution of a Finite Membrane Wrapping Around Particles

The previous semianalytical treatment of particle wrapping by an infinite flat membrane has the implicit assumption of an unlimited number of receptors to bind with ligands. This assumption leads to an unrealistic prediction that the membrane can take up an infinitely large particle. In practice, both the size of a cell membrane and the number of receptors available to binding are limited.

A closed-form analytical solution to diffusion equation is unavailable for the case of a finite-sized membrane wrapping around a particle. We have obtained numerical solutions with a front-tracking approach similar to that described in ref. 25. The main steps are briefly summarized below. We consider a membrane with linear extent 2L wrapping around a cylindrical particle and one with an effective area πL² wrapping around a spherical particle. We want to determine the wrapping front a(t) at each incremental time step. The conservation condition Eq. 3 and the power balance Eq. 12 are still valid for a finite membrane. The wrapping front speed ȧ(t), determined at a given time t from ξ(s, t), is used to update the wrapping front at the next time step as a(t + Δt) = a(t) + ȧ(t)Δt. At the first time step, Δt, we assume a(Δt) ≪ L and use the analytical solutions in Eq. 5 for a cylindrical particle and Eq. 16 for a spherical particle as the initial condition for the receptor density distribution ξ(s, Δt). The relevant diffusion equation subject to the boundary conditions

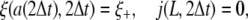[23]

can then be solved numerically in the interval a(2Δt) < s < L. The numerical solution for ξ(s, 2Δt) provides the basis for finding ξ(s, 3Δt), and these steps are repeated iteratively until the wrapping area reaches that of the particle.

Results and Discussion

For biological membranes, the bending modulus B is commonly believed to have a value on the order of 20 k_BT (31). The receptor-ligand adhesion energy e_RL is unknown (24). However, in comparison with antibody–antigen interaction, e_RL has been estimated to be on the order of 15 k_BT at the temperature of 300 K (32). The diffusion constant of membrane receptors is expected to be on the order of 10⁴ nm²/s (23, 32). Typical size of a cell membrane is assumed to be L = 10 μm. For the extensively studied model system of Semliki Forest virus, the ligand density of a viral particle can be calculated through the number of spike glycoproteins of the virus, or ≈5 × 10³ ligands per square μm (24). Based on partial experimental information, ξ₀ should be in the range of 50 to 500 receptors per square μm (24, 33, 34), so that the ratio 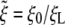should be in the range of 0.01 to 0.1. These parameters are summarized in Table 1. Some of our calculations are carried out for the receptor density ratio 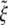varying within the entire range [0, 1].

Table 1. Physical constants in the model.

B	D, nm2/s	eRL	ξL, 1/μm2	ξ̃ = ξ0/ξL
20	104	15	5 × 103	0.01–0.1

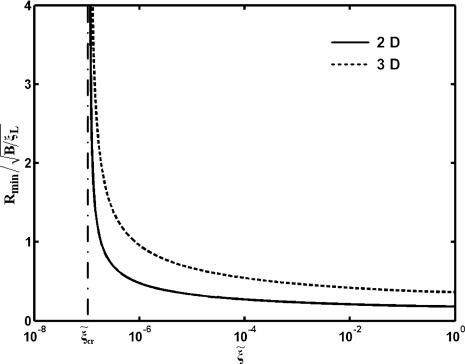
Considering that the particle can be wrapped only if the speed factor α is larger than zero, we immediately see that there exists a minimum radius of the particle and a minimum receptor density ratio for wrapping. For a cylindrical particle, letting α → 0 in the power balance Eq. 13 gives the minimum wrapping radius as

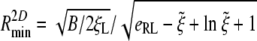[24]

and the minimum receptor density ratio as

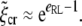[25]

For a spherical particle, the minimum receptor density ratio is identical to Eq. 25 and the minimum wrapping radius is .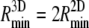

Below these critical values, there is no driving force for the advance of the wrapping front and wrapping cannot take place. As shown in Fig. 3 for e_RL = 15, a decrease in the receptor density ratio 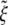leads to an increase in the normalized critical radius 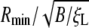. The critical radius for either 2D or 3D corresponds to the receptor density at the wrapping front approaching the remote density, i.e. ξ₊ → ξ₀.

Fig. 3.

The normalized minimum wrapping radius versus the receptor density ratio 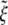for uptake of a cylindrical particle (solid curve) and a spherical particle (dashed curve) into a membranes of infinite size.

For a finite membrane, the smallest and the largest particles that can be successfully wrapped into the cell can be estimated from the conservation of receptors. A critical condition for successful wrapping of a cylindrical particle by a membrane of linear extent 2L is

[26]

and that for successful wrapping of a spherical particle by a membrane of effective area πL² is

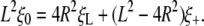[27]

Inserting the above equations into Eq. 12 leads to the following equations

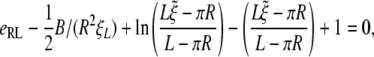[28]

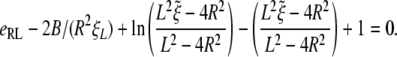[29]

If the receptor density ratio is larger than a critical value, Eqs. 28 and 29 each have two real roots, corresponding to the minimum and maximum particle radius for wrapping, respectively. The minimum value of the receptor density ratio for the existence of real roots of the above equations corresponds to the critical receptor density required for wrapping. Below the critical receptor density, Eqs. 28 and 29 have no real roots, indicating no particle can be wrapped under this situation.

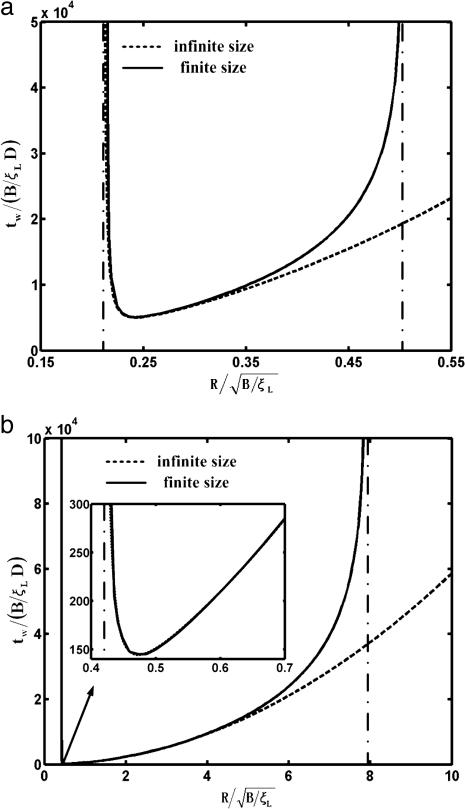
The normalized wrapping time t_w/(B/ξ_LD) is determined numerically and plotted in Fig. 4 as a function of the normalized particle radius 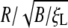for parameter values e_RL = 15 and 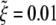. For comparison, the solutions for both infinite and finite membranes are shown in Fig. 4. For the finite membrane, we take L = 10 μm, B = 20, and ξ_L = 5 × 10³/μm². It is interesting to note that there is an optimal particle size R^* for the smallest wrapping time t^*. The optimal particle radius is a result of competition between thermodynamic driving force and receptor diffusion kinetics. For particles smaller than the optimal size, the increased elastic energy associated with bending of the membrane results in decreased driving force for wrapping and increased wrapping time. When the particle size falls below the minimum radius R_min, the wrapping causes an increase in free energy and cannot proceed at all. For particles larger than the optimal size, diffusion of receptors over a longer distance, hence a longer wrapping time, is required. For a finite membrane, if the size of the particle exceeds the maximum radius R_max, the wrapping process cannot be completed because of the limited number of receptors available to binding. Table 2 lists the estimated range of the optimal particle radius and other parameters.

Fig. 4.

The normalized wrapping time t_w/(B/ξ_LD) versus the normalized particles radius 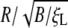with 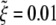and e_RL = 15 for uptake of a particle into an infinite membrane (dashed curve) and a finite membrane (solid curve). In the case of a finite membrane, B = 20, ξ_L = 5 × 10³/μm², and L = 10 μm. (a) Cylindrical particle with normalized minimum and maximum wrapping radii of 0.21 and 0.5. (b) Spherical particle with normalized minimum and maximum wrapping radii of 0.42 and 7.9.

Table 2. Estimated range of the characteristic particle radius and wrapping time.

Dimensions	R*, nm	t*, s	Rmin, nm	Rmax, nm
2D	13.7–15.3	14–2,020	12	320
3D	27–30	2–58	24	1,600

The size dependence of wrapping time shown in Fig. 4 is based on the assumed physical process of a receptor-mediated endocytosis. Particles smaller than R_min may enter cells through other mechanisms such as clathrin or caveolin coats, or transmembrane diffusion directly through membrane or protein channels. On the other hand, particles can also be ingested by phagocytosis, a process driven by the actin myosin cortex in phagocytosis competent cells such as macrophages or amoeba. Only particles near the optimal size would be most efficiently taken up by receptor-mediated endocytosis.

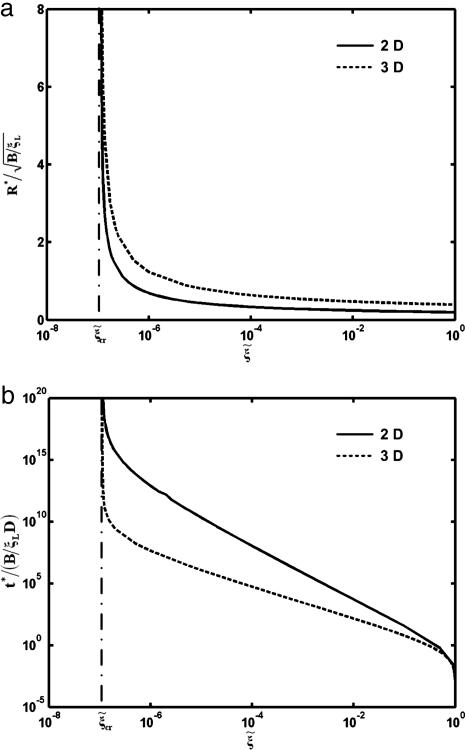
The normalized optimal particle radius 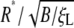and optimal wrapping time t^*/(B/ξ_LD) are numerically determined and plotted in Fig. 5 as a function of the receptor density ratio 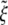for an infinite membrane with e_RL = 15. As the receptor density ratio increases, both the optimal wrapping radius and optimal wrapping time decrease. For small receptor density ratios, the optimal radius must increase to compensate the increase in entropic free energy by decreasing the bending energy. The optimal wrapping radius and time increase sharply as the receptor density ratio approach the critical density ratio. This finding confirms that wrapping cannot take place unless the receptor density ratio is larger than the critical density ratio.

Fig. 5.

The normalized optimal radius 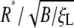and the normalized optimal wrapping time t^*/(B/ξ_LD) versus the receptor density ratio 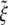for uptake of a cylindrical particle (solid curve) and a spherical particle (dashed curve) into a membrane of infinite size. Here, we have taken e_RL = 15 with the critical receptor density ratio 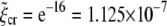. (a) Optimal radius. (b) Optimal wrapping time.

Various studies on targeted drug delivery into cells have shown that the size of the particle is indeed an important factor in cellular uptake of nanomaterials. It is generally observed that particles <50 nm in radius are preferable for drug delivery (9, 15, 16). However, in most of the existing studies, it is difficult to assess the charge effects in cellular uptake. Particles with positive surface charges could interact strongly with a negatively charged cell membrane. Such charge interactions would push the optimal wrapping size to larger particles. Recently, Aoyama and colleagues (17–19) made a careful investigation of the size effects and receptor contributions in glycoviral gene delivery by excluding potential complications arising from the charge effects. They concluded that receptor-mediated endocytosis is strongly size-dependent with an optimal radius ≈25 nm. This conclusion is in good agreement with our theoretical model that gives an optimal radius ≈27–30 nm for spherical particles. For particles smaller than the critical radius, a cluster of particles may be packaged in one endosome to reach the optimal size.

Carbon nanotubes (CNTs) have recently been explored as molecular transporters (10–12). Experiments have shown that CNTs can enter animal cells without apparent toxicity (10–12). The uptake mechanism, however, is still unclear. Kam et al. (12) reported that single-walled nanotubes (SWNTs) may enter the cells via the endocytosis pathway. They used SWNTs and small bundles of SWNTs with length in the range of 100 nm to 1 μm and radius in the range of 0.5 to 2.5 nm. From our model, uptake of an isolated SWNT via endocytic pathway seems impossible because the radius of a SWNT is much smaller than the critical radius. However, it is possible that some of the SWNTs form larger bundles via hydrophobic and van der Waals forces, and the overall radius of a bundle may reach a size comparable or larger than the critical radius. Also, the perfect and dense atomic structure of CNTs may interact strongly with cell membrane. If the adhesion energy between SWNTs and cell membrane becomes larger than that of typical receptor–ligand binding, the critical size for wrapping may decrease. Pantarotto et al. (11) observed that multiwalled CNTs (MWNTs) with apparent length of ≈200 nm and radius ≈10 nm can also enter into the cell. This radius is already on the order of the critical wrapping radius in our model for cylindrical particles. However, Pantarotto et al. found that their observed uptake of MWNTs was apparently not caused by endocytosis and suggested a possible mechanism via spontaneous flipping of lipid molecules (35). The apparent contradiction between different experiments may be caused by different functionalization of nanotube surfaces, which could give rise to different binding energy levels with a cell membrane. Another possibility of CNT uptake is phagocytosis driven by the action myosin cortex, as the HeLa cells used by Pantarotto et al. (11) as well as the HL60 and human T cells used by Kam et al. (12) all are phagocytosis-competent. Further study is obviously needed to resolve the exact mechanism(s) for uptake of CNTs into animal cells.

The main objective of the present study is to provide a theoretical basis for understanding the size effect of receptor-mediated endocytosis. The optimal size for endocytosis may provide some guidelines for designing efficient drug delivery systems. The size and surface of the particle are crucial factors in targeting and attachment of cell-specific ligands for increased efficiency and selectivity. The budding time is greatly affected by the particle or vesicle size, and this understanding may be used to optimize drug delivery and targeting systems.

While suggesting a mechanism for the clathrin-independent entry of viruses into cells, our model can also be extended to cases where clathrin (or other) coating play an important role. In these cases, the energy function should include an excess binding energy e_c and an elastic bending energy

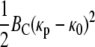caused by the presence of the coat, where B_ck_BT and κ₀ denote the bending modulus and spontaneous curvature of the coat (5). Similar calculations would lead to an equation

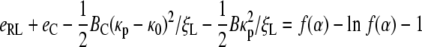[30]

for the speed factor α.

As a final note, we point out some limitations of our analysis as presented in this article. First of all, receptor molecules on a cell membrane may induce a spontaneous membrane curvature that may affect the wrapping process (22). We have also neglected deformation outside of the receptor–ligand binding zone (36). Thermal fluctuation of the cell membrane may play some significant role. As the membrane wraps around a particle, water must be squeezed out from between the membrane and the capsid. All of these factors may affect the wrapping process in some way. Although the simple model adopted here makes the central idea readily apparent, more sophisticated models can be developed to clarify these issues.