Abstract
Here, direct noninvasive neutron reflectivity measurements reveal the presence of a reduced (deuterated) water density region, with a sigmoidal density profile at the hydrophobic silane–water interface that depends on the type and concentration of dissolved gases in the water. Removal of dissolved gases decreases the width of the reduced water density region, and their reintroduction leads to its increase. When compared with recent computer simulations, a locally fluctuating density profile is proposed, whereas preexisting nanobubbles are excluded. The presence of a fluctuating reduced water density region between two hydrophobic surfaces and the attractive “depletion force” to which it leads may help explain the hydrophobic force and its reported diminution in deaerated water. Our results are also quantitatively consistent with recent dynamic surface force apparatus results that drastically revise previous estimates of the slip length of water flowing past hydrophobic surfaces from microns to ≈20 nm. Our observations, therefore, go a long way toward reconciling three quite different types of experiments and phenomena: water depletion at hydrophobic surfaces, water slip at hydrophobic surfaces, and the hydrophobic interaction.
Keywords: interfacial water, neutron reflectivity, slip conditions
Unraveling the interfacial structure of water at hydrophobic surfaces embodies potential answers to the experimentally observed finite-ranged attractive forces between hydrophobic surfaces in water (1–3) and the reduced drag on water flowing in hydrophobic channels (4–7). “Hydrophobic interactions” are involved in diverse phenomena including protein folding, amphiphile self-assembly, membrane fusion, and “superhydrophobicity” (8). The range and origin of this interaction has remained unresolved for 20 years (3, 9, 10). Suggested mechanisms for the long-range hydrophobic attraction include two mainly theoretical and two more experimental models as follows: (i) water structure (2, 3, 11), (ii) electrostatic models based on fluctuating dipoles (3, 10, 12, 13), (iii) preexisting submicroscopic bubbles that bridge the surfaces (10, 14–17), and (iv) the spontaneous nucleation of bridging cavities as two hydrophobic surfaces approach each other. In both the latter cases, the surfaces will be pulled together through capillary (Laplace pressure) forces (18). There is evidence of preexisting bubbles 50–500 nm in diameter and 5–50 nm in height on some hydrophobic surfaces (mechanism iii), but these bubbles have only been detected by invasive techniques such as atomic force microscopy (AFM) imaging (10, 14–17). Other AFM and surface forces apparatus studies have not reported seeing nanobubbles (19, 20).
Analytical theoretical studies (21) have concluded that the density of water is lower near a hydrophobic surface, with a sigmoidal density profile centered at 10–15 Å from the hydrophobic surface (where the water density is half the bulk density). In contrast, molecular dynamics computer simulations (22–24) indicate a depletion region extending at most 2.5 Å from the hydrophobic surface, whereas recent Monte Carlo simulations show that dissolved gases such as N2 adsorb as a monolayer at the hydrophobic–water interface with a density that is ≈30 times higher than in the bulk solution (25). However, no stable bubbles are predicted by these simulations, and they are not expected thermodynamically.
Neutrons are particularly useful in studies of buried solid–liquid interfaces because of their large penetration depth, angstrom resolution, and the remarkable contrast between hydrogenated and deuterated species. Previous neutron (16, 26) and x-ray (23) reflectivity measurements of water at hydrophobic interfaces have suggested a 1- to 4-nm “depleted,” “dewetting,” or “precursor gas” layer or region where the mean water density is 85–90% of the bulk value. However, the samples used in the neutron experiments had thick or multicomponent layers (16, 26), leading to uncertainty in the layer thickness and composition. In the case of the x-ray study (23), the width of the depletion region could not be quantitatively established because of the low contrast between the hydrocarbon and water phases, coupled to the presence of capillary waves. These concerns, and other issues outlined by Ball (9), have precluded accurate measurement of the extent of the depletion zone. Most importantly, these studies did not explore the effects of dissolved air or other gases, which have been heavily implicated in the hydrophobic interaction (20, 27–30).
Here, we have conducted systematic neutron reflectivity (NR) measurements on an 18-carbon chain octadecyl-tricholorosilane (OTS) monolayer chemically attached to a highly polished quartz substrate in contact with deuterated water (D2O) to enhance the scattering contrast.
Materials and Methods
D2O Treatments. Different D2O subphases were prepared as follows: (i) directly from the D2O bottle after equilibration with air at atmospheric pressure in Los Alamos, altitude of 7,500 feet (untreated D2O, Table 1); (ii) D2O bubbled with ultra-high purity Ar gas for >12 h (Ar D2O, Table 1); (iii) D2O bubbled with compressed CO2 overnight in an ice bath followed by room temperature bubbling for 2 h (CO2 D2O, Table 1); and (iv) D2O from a different bottle (Table 1, Untreated D2O subphase c) after equilibration with atmospheric air, and the same D2O was used for vacuum degassing (degassed D2O, Table 1). Vacuum was applied to a D2O-filled flask with Teflon chips and a Teflon stirrer. Continuous stirring was used to shake off the bubbles nucleated on the Teflon chips. The system was under vacuum for ≈1 h until no bubble formation was seen on the Teflon chips (20). Before each NR measurement, the OTS surfaces were cleaned with deionized water, chloroform, and ethanol, followed by drying in ultra-high-purity Ar.
Table 1. Fit results for neutron reflectivity performed on OTS against different water subphases.
| Subphase | Combined average thickness, 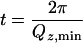 , Å , Å |
Reduced water density region offset, δ ± 0.5, Å | Width of the error-function profile, σ, Å |
|---|---|---|---|
| Untreated (naturally aerated) D2O | |||
| (a) | 34.8 | 11.3 | 3.6 ± 0.3 |
| (b) | 33.7 | 10.3 | 3.2 ± 0.5 |
| (c) | 31.0 | 7.6 | 3.4 ± 0.2 |
| Ar D2O | 26.5 | 2.0 | 4.2 ± 0.3 |
| CO2 D2O | 28.8 | 5.8 | 3.7 ± 0.8 |
| Before degassing | 31.0 | 7.6 | 3.4 ± 0.2 |
| Vacuum degassed D2O | |||
| T = 0 hr | 28.6 | 5.2 | 2.1 ± 0.2 |
| T = 5 hr | 29.1 | 5.7 | 2.9 ± 0.6 |
| T = 18 hr | 30.3 | 6.2 | 4.2 ± 0.1 |
δ and σ were obtained from Parratt fitting algorithm (see text for details). The errors on these parameters are based on a single parameter error analysis (χ2 → χ2 + 1); all δ have a maximum error of 0.5 Å.
OTS Sample Preparation. OTS monolayers were deposited according to the procedure described in refs. 31 and 32. The resulting advancing and receding water contact angles were 113.4° and 100.7°, respectively. Such a robust monolayer system has many advantages over the more diffuse interfaces previously studied (16, 26). Initial x-ray reflectivity measurements in air indicate an OTS hydrocarbon tail thickness of thc = 22.8 ± 0.5 Å, which is very close to the theoretical length for fully stretched (all-trans) octadecyl chains, tmax = 1.5 + 1.265(n - 1) = 23.0 Å for n = 18. In comparison, NR measurements in deuterated cyclohexane (C6D12) yielded thc = 25.5 ± 0.5 Å, the increased thickness being attributed to the stretching of the hydrocarbon chains due to solvent penetration.
NR. The NR experiments were performed on the SPEAR beamline at the Manuel Lujan Neutron Scattering Center (Los Alamos National Laboratory). A specular reflectivity curve measured as a function of momentum transfer vector Qz provides information on the in-plane average coherent scattering length density (SLD) profile, β(z), normal to the quartz surface (i.e., in the z-direction; Fig. 1), which is directly proportional to the mass density of the medium, ρ(z). The samples consisted of D2O sandwiched between the quartz–OTS surface and an unpolished silicon block (Fig. 1). This sandwich was enclosed in an aluminum chamber with a D2O reservoir to minimize evaporation, and NR measurements were performed with different D2O solutions using standard procedures (see above).
Fig. 1.
Schematic of the experimental set-up used for the NR measurements. kin is the neutron incident wave vector, kout is the specularly reflected wave vector, and Qz = kout - kin is the vertical momentum transfer wave vector, Qz = 4π*sinθ/λ, where θ is the angle of incidence and λ is the neutron wavelength. Because the same OTS monolayer was used against different water samples, the SLD of quartz and the roughness of the OTS–quartz interface were fixed at 4.18 × 10-6 Å-2 and 3 Å, respectively. The neutron SLD and thickness of the OTS hydrocarbon layer obtained from the fitting algorithm was SLDhc = -0.4 × 10-6 Å-2 (corresponding to a mass density of 0.9 g/cc) and thc = 22.8 Å, consistent with densely packed chains each occupying an area of 19.5 Å2. The OTS headgroup thickness thg was fixed at 3.5 Å (calculated from the sum of the Si–C bond length of 1.86 Å and the Si–O bond length of 1.65 Å) with a SLDhg of 2.06 × 10-6 Å-2. These values are consistent with those reported in the literature (43). The water density profile was fitted by a sigmoidal error function of the form erf(z/σ), which is the integral of the Gaussian that describes the interfacial profile, where 2σ is the full width, as shown [a hyperbolic tan or exponential function with offsets that are also commonly used to profile liquid–vapor interfaces (44, 45) fitted the data just as well, with exponential decay lengths of order 2.0–3.5 Å]. The midpoint of the sigmoidal curve was offset by δ from the hydrocarbon–water interface. The different results obtained for t, σ, and δ are listed in Table 1. The profiles actually shown here are for untreated (naturally aerated) D2O, for which δ = 11.3 ± 0.5 Å and σ = 3.6 ± 0.3 Å (see Fig. 2 and Table 1), which compares reasonably well with two separate measurements performed on different quartz–OTS samples (Table 1). We note that this figure shows an averaged D2O occupancy profile; because the NR measurement provides only the out-of-plane density profile and averages the in-plane density, this profile can be treated as the normalized mass density profile ρ(z)/ρbulk (see Fig. 3).
Results and Discussion
Given the extreme simplicity of the system, trends in the NR data could be analyzed by direct visualization. The presence of a low SLD D2O region adjacent to the (also) low SLD OTS monolayer, when both are sandwiched between two high-density materials (quartz and D2O), was detected as an apparent increase of the average hydrocarbon layer thickness. The combined average thickness, t, was approximated from the Qz positions of the intensity minima (33) in the NR curves by t = 2π/Qz,min (see Fig. 2). Because of the loss of phase information in the NR data, a numerical fitting procedure was used to extract the SLD profiles. We used both the model-independent B-spline approach (34, 35) and the model-dependent optical matrix method using the Parratt fitting algorithm, which describes the profile in terms of slabs (36). To describe the SLD profiles, two slabs of constant thickness, thg and thc, and SLDs were used to model the OTS headgroups and hydrocarbon tails, respectively (Fig. 1). The reduced water density region was modeled by sigmoidal error-functions, erf(z/σ) of width σ, where their midpoints (where the water density is half the bulk value) were offset by δ from the hydrocarbon–water interface. The results from fitting the data using the above model for OTS in contact with D2O subjected to different treatments are shown in Figs. 2 and 3 and are summarized in Table 1.
Fig. 2.
Fresnel divided NR data, R/RF vs. Qz, and slab-model fits (solid lines) for OTS monolayer in contact with three different aqueous media. Plotting R/RF vs. Qz compensates for the sharp decrease in the reflectivity as described by Fresnel's law, R α Qz-4. Representative error bars are shown and are based on the error propagation of the Poisson statistics.
Fig. 3.
SLD profiles corresponding to the NR fits of Fig. 2 for an OTS monolayer in different environments, as indicated. The lines at z = 0 and 26.3 Å represent the average positions of the OTS monolayer. For example, the line at 37.6 Å represents the 50% water density (midpoint of the sigmoidal profile) for untreated (naturally aerated) D2O. The in-plane average coherent SLD profile, β(z), normal to the quartz surface is directly proportional to the mass density of the medium, ρ(z). Inset shows a snapshot of a different molecular distribution (in comparison with one shown in Fig. 1) that is also consistent with the data for naturally aerated water, where local random diffuse density fluctuations (with a maximum possible lateral spacing, Y, of 10 μm with no minimum limit) are shown based on expectations from computer simulations (25, 39, 40). Other molecular models also can fit the data, such as small fluctuating cavities of about the same size as those shown here but with sharper liquid–vapor interfaces.
The smallest reduced water density region, defined by δ, was observed for a D2O subphase bubbled with Ar (Table 1); the largest was for naturally aerated D2O, i.e., with mainly N2 and O2 (Table 1), whereas CO2 fell in between (Table 1). Previous experiments (37) have suggested, and simulations (25) have shown, that dissolved gases adsorb at the hydrophobic–water interface, but it is not obvious why different gases with comparable water solubilities exhibit different adsorptions; perhaps both their size and hydrophobicities play a role. However, we note that the volume of dissolved gas present in the system alone cannot account for the reduced density, and any monolayer-like adsorption would in fact result in a higher SLD. Table 1 shows that both σ and δ fall as the D2O is vacuum degassed but slowly increase again on allowing the deaerated solution to reequilibrate with air.
Fig. 3 shows the SLD plots obtained from fitting the NR data of the three systems studied in Fig. 2. The SLD profiles indicate that there is a finite probability of finding D2O molecules at the hydrocarbon surface at z = 26.3 Å because the SLD value at this surface is greater than the hydrocarbon SLD of SLDhc = -0.4 × 10-6 Å-2.
In addition to the different profiles, which are time averages of the fluctuating water distributions shown in Fig. 1 and Fig. 3 Inset, one also might attribute the reduced water density to the presence of nanobubbles (10, 14–17). However, our NR measurements are not consistent with some AFM studies of preexisting bubbles that are tens of nanometers in size (10, 14–17). To fit our data, the surface coverage of the nanobubbles would have to be >90% and their average height would have to be <11 Å, making them thermodynamically unstable under static conditions, providing another reason for considering them as fluctuating entities (38). In addition, the amplitude and frequency of the fluctuations at one hydrophobic surface would be expected to be enhanced by the close proximity of a second hydrophobic surface, allowing for vapor bridges to form [depending on the surface separation, area, and time (25, 39, 40)] that would pull the surfaces together with a strong capillary force acting over a range significantly greater than twice the original reduced water density length, 2δ.
To test for reversibility, we vacuum degassed one D2O sample for 1 h, then allowed air to diffuse back in. Fig. 4 and Table 1 show the results and fitted parameters from this study. The shift of the position of Qz,min in the normalized reflectivity back toward the original position (before degassing) 18 h after reexposing the sample to air clearly demonstrates the reversibility (and slowness) of the effects of changing the dissolved gas concentration. Our results are consistent with the observations of Pashley and coworkers (41), who found that oil droplets can freely disperse in degassed water and that the electrostatic repulsions from the slightly charged oil droplets thus formed prevented their coalescence when gas was reintroduced. Here, the use of a single hydrophobic surface, where long-range electrostatic interactions with another surface are absent, allows us to observe the reversibility of this process.
Fig. 4.
Fresnel divided NR curves for naturally aerated and vacuum-degassed D2O, and the same sample measured 18 h after allowing air to diffuse back into the D2O (see Table 1 for details including the values after 5 h).
These measurements elucidate the experimental observations of a reduced hydrophobic attraction in deaerated water (20, 27–30) if this interaction is due to the nucleation of vapor bridges forming between two hydrophobic surfaces once they are sufficiently close to each other. The statistical nature of the nucleation process (25, 39, 40), depending as it would on the time the surfaces remain at a given separation, could make it difficult to express this interaction in terms of an equilibrium potential function, which could be the reason why experiments such as surface forces apparatus, AFM, and colloidal stability studies, which involve very different length and time scales, have often produced very different results. Nucleation of nanobubbles by another surfaces, such as an AFM tip, could conceivably explain the reported observation of such bubbles during imaging (10, 14–17).
A reduced water density region at a surface also should reduce its viscosity and boundary conditions for flow (4–7), from no-slip to partial or full-slip, which will have a significant impact on transport properties in small channels and on drag reduction in general. We find good quantitative agreement between our work and recent experimental results of Cottin-Bizonne et al. (7) that drastically revised previous estimates of the slip length of water flowing past hydrophobic surfaces from microns to ≈20 nm. Thus, the simplest model used by theoreticians assumes the existence of a homogeneous vapor film of thickness d between the bulk liquid water phase and the hydrophobic surface, for which the slip length b is given by (42)
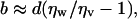 |
[1] |
where ηw and ηv are the viscosities of bulk liquid water and water vapor, respectively. Eq. 1 assumes a sharp interface between bulk vapor and bulk liquid. In contrast, in our experiments the contact density at the OTS surface is commensurate with a vapor-like density, and a sigmoidal density profile is used to describe the reduced water density region into the bulk. Because our experimental δ values correspond to ≈50% water mass density, we can assume d ≈ δ in Eq. 1. By putting d = δ and by using our typical measured value for δ (≈0.5 nm) and the known ratio ηw/ηv = 50, we obtain b ≈ 25 nm, which quantitatively reconciles theory and two quite different types of experiments and phenomena. The presence of a reduced water density at polymer and protein surfaces also may impact the hydrophobic interactions of biological surfaces and macromolecules, affecting both the hydrophobic interaction energies and, more likely, the kinetics (e.g., association rates) of macromolecular assemblies.
Notes
Because the SLD of OTS and reduced water density D2O layer are very close, NR cannot distinguish the case where the depleted layer is on top of the OTS or whether the OTS has detached from the surface and raised itself with an intervening low density layer while maintaining a few contacts with the substrate. To resolve this problem, we performed a measurement on a different sample with deuterated-OTS/D2O and confirmed that the depleted layer was indeed at the OTS–water interface.
Nucleated gas/vapor bubbles with a finite surface coverage, if present, can be viewed as a separate layer with an average SLD less than that of D2O. If they are <1,500 Å in size, oscillations corresponding to their thickness should be observed in the NR curves, and if they are >1,500 Å perturbation of the critical Qz would be observed.
Acknowledgments
We thank Prof. T. Kuhl (University of California, Davis, CA), Chad Miller (University of California, Davis, CA), and Dr. A. M. Dattelbaum (Los Alamos National Laboratory) for the OTS samples; Dr. W. Hamilton (Oak Ridge National Laboratory) for use of the mirror reflectivity fitting program; and Dr. C. Braun (Hahn–Meitner Institute, Berlin) for the parratt32 reflectivity program. This work was supported by the Los Alamos National Laboratory Laboratory Directed Research and Development program, Department of Energy Office of Science (Basic Energy Sciences), the Los Alamos National Laboratory under Department of Energy Contract W7405-ENG-36, and the Department of Energy Office of Basic Energy Sciences. D.A.D. was supported by the Los Alamos National Laboratory Director's Postdoctoral Fellowship. J.N.I. was partially supported by National Science Foundation Materials Research Laboratories Program Award DMR00-80034.
Author contributions: D.A.D., E.B.W., J.N.I., and J.M. designed research; D.A.D., E.B.W., and J.M. performed research; D.A.D. and E.B.W. contributed new reagents/analytic tools; D.A.D. and E.B.W. analyzed data; and D.A.D., E.B.W., J.N.I., and J.M. wrote the paper.
Abbreviations: AFM, atomic force microscopy; D2O, deuterated water; NR, neutron reflectivity; OTS, octadecyl-tricholorosilane; SLD, scattering length density.
References
- 1.Israelachvili, J. N. & Pashley, R. (1982) Nature 300, 341-342. [DOI] [PubMed] [Google Scholar]
- 2.Israelachvili, J. N. & Pashley, R. M. (1984) J. Colloid Interface Sci. 98, 500-514. [Google Scholar]
- 3.Christenson, H. K. & Claesson, P. M. (2001) Adv. Colloid Interface Sci. 91, 391-436. [Google Scholar]
- 4.Vinogradova, O. I. (1999) Int. J. Miner. Processing 56, 31-60. [Google Scholar]
- 5.Ruckenstein, E. & Rajora, P. (1983) J. Colloid Interface Sci. 96, 488-491. [Google Scholar]
- 6.Granick, S., Zhu, Y. X. & Lee, H. (2003) Nat. Mater. 2, 221-227. [DOI] [PubMed] [Google Scholar]
- 7.Cottin-Bizonne, C., Cross, B., Steinberger, A. & Charlaix, E. (2005) Phys. Rev. Lett. 94, 056102-056104. [DOI] [PubMed] [Google Scholar]
- 8.Israelachvili, J. (1991) Intermolecular and Surface Forces (Academic, San Diego).
- 9.Ball, P. (2003) Nature 423, 25-26. [DOI] [PubMed] [Google Scholar]
- 10.Attard, P. (2003) Adv. Colloid Interface Sci. 104, 75-91. [DOI] [PubMed] [Google Scholar]
- 11.Pratt, L. R. & Chandler, D. (1977) J. Chem. Phys. 67, 3683-3704. [Google Scholar]
- 12.Yoon, R. H. & Ravishankar, S. A. (1996) J. Colloid Interface Sci. 179, 391-402. [Google Scholar]
- 13.Rabinovich, Y. I., Guzonas, D. A. & Yoon, R. H. (1993) Langmuir 9, 1168-1170. [Google Scholar]
- 14.Tyrrell, J. W. G. & Attard, P. (2001) Phys. Rev. Lett. 87, 1761041-1761044. [DOI] [PubMed] [Google Scholar]
- 15.Ishida, N., Inoue, T., Miyahara, N. & Higashitani, K. (2000) Langmuir 16, 6377-6380. [Google Scholar]
- 16.Steitz, R., Gutberlet, T., Hauss, T., Klosgen, B., Krastev, R., Schemmel, S., Simonsen, A. C. & Findenegg, G. H. (2003) Langmuir 19, 2409-2418. [Google Scholar]
- 17.Simonsen, A. C., Hansen, P. L. & Klosgen, B. (2004) J. Colloid Interface Sci. 273, 291-299. [DOI] [PubMed] [Google Scholar]
- 18.Christenson, H. K. & Claesson, P. M. (1988) Science 239, 390-392. [DOI] [PubMed] [Google Scholar]
- 19.Tsao, Y. H., Yang, S. X., Evans, D. F. & Wennerstrom, H. (1991) Langmuir 7, 3154-3159. [Google Scholar]
- 20.Meyer, E. E., Lin, Q. & Israelachvili, J. N. (2005) Langmuir 21, 256-259. [DOI] [PubMed] [Google Scholar]
- 21.Lum, K., Chandler, D. & Weeks, J. D. (1999) J. Phys. Chem. B 103, 4570-4577. [Google Scholar]
- 22.Mamatkulov, S. I., Khabibullaev, P. K. & Netz, R. R. (2004) Langmuir 20, 4756-4763. [DOI] [PubMed] [Google Scholar]
- 23.Jensen, T. R., Jensen, M. O., Reitzel, N., Balashev, K., Peters, G. H., Kjaer, K. & Bjornholm, T. (2003) Phys. Rev. Lett. 90, 0861011-0861014. [DOI] [PubMed] [Google Scholar]
- 24.Grigera, J. R., Kalko, S. G. & Fischbarg, J. (1996) Langmuir 12, 154-158. [Google Scholar]
- 25.Leung, K., Luzar, A. & Bratko, D. (2003) Phys. Rev. Lett. 90, 0655021-0655024. [DOI] [PubMed] [Google Scholar]
- 26.Schwendel, D., Hayashi, T., Dahint, R., Pertsin, A., Grunze, M., Steitz, R. & Schreiber, F. (2003) Langmuir 19, 2284-2293. [Google Scholar]
- 27.Wennerstrom, H. (2003) J. Phys. Chem. B 107, 13772-13773. [Google Scholar]
- 28.Mahnke, J., Stearnes, J., Hayes, R. A., Fornasiero, D. & Ralston, J. (1999) Phys. Chem. Chem. Phys. 1, 2793-2798. [Google Scholar]
- 29.Ishida, N., Sakamoto, M., Miyahara, M. & Higashitani, K. (2000) Langmuir 16, 5681-5687. [Google Scholar]
- 30.Craig, V. S. J., Ninham, B. W. & Pashley, R. M. (1999) Langmuir 15, 1562-1569. [Google Scholar]
- 31.Maoz, R. & Sagiv, J. (1984) J. Colloid Interface Sci. 100, 465-496. [Google Scholar]
- 32.Kuhl, T. L., Majewski, J., Wong, J. Y., Steinberg, S., Leckband, D. E., Israelachvili, J. N. & Smith, G. S. (1998) Biophys. J. 75, 2352-2362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kjaer, K. (1994) Physica B 198, 100-109. [Google Scholar]
- 34.Pedersen, J. S. & Hamley, I. W. (1994) J. Appl. Crystallogr. 27, 36-49. [Google Scholar]
- 35.Berk, N. & Majkrzak, C. (1995) Phys. Rev. B Condens. Matter 51, 11296-11309. [DOI] [PubMed] [Google Scholar]
- 36.Parratt, L. (1954) Phys. Rev. 95, 359-369. [Google Scholar]
- 37.Beaglehole, D. (1987) J. Phys. Chem. 91, 5091-5092. [Google Scholar]
- 38.Zhang, X. Y., Zhu, Y. X. & Granick, S. (2002) Science 295, 663-666. [DOI] [PubMed] [Google Scholar]
- 39.Pertsin, A. & Grunze, M. (2004) J. Phys. Chem. B 108, 16533-16539. [Google Scholar]
- 40.McCormick, T. A. (2003) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 68, 0616011-0616015. [Google Scholar]
- 41.Maeda, N., Rosenberg, K. J., Israelachvili, J. N. & Pashley, R. M. (2004) Langmuir 20, 3129-3137. [DOI] [PubMed] [Google Scholar]
- 42.Lauga, E., Brenner, M. P. & Stone, H. A. (2005) in Handbook of Experimental Fluid Mechanics, eds. Tropea, C., Foss, J. & Yarin, A. (Springer, New York), Chap. 15, in press.
- 43.Baptiste, A., Gibaud, A., Bardeau, J. F., Wen, K., Maoz, R., Sagiv, J. & Ocko, B. M. (2002) Langmuir 18, 3916-3922. [Google Scholar]
- 44.Moseley, L. L. (1997) Int. J. Mod. Phys. C 8, 583-588. [Google Scholar]
- 45.Sides, S. W., Grest, G. S. & Lacasse, M. D. (1999) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 60, 6708-6713. [DOI] [PubMed] [Google Scholar]






