Coevolutionary arms races between bacteria and bacteriophage

Abstract

We propose a computational and theoretical framework for analyzing rapid coevolutionary dynamics of bacteriophage and bacteria in their ecological context. Bacteriophage enter host cells via membrane-bound surface receptors often responsible for nutrient uptake. As such, a selective pressure will exist for the bacteria to modify its receptor configuration and, in turn, for the phage to modify its tail fiber. A mathematical model of these trait adaptations is developed by using the framework of adaptive dynamics. Host strains differ in their efficiency of resource uptake and resistance to phage, whereas phage strains differ in their host preference for adsorption. We solve the evolutionary ecology model and find the conditions for coevolutionary branching and relevant dimensionless parameters leading to distinct quasispecies. We confirm these calculations using stochastic Monte Carlo simulations of populations evolving in a chemostat with fixed washout rate and inflow resource density. We find that multiple quasispecies of bacteria and phage can coexist in a homogeneous medium with a single resource. When diversification occurs, quasispecies of phage adsorb effectively to only a limited subset of the total number of quasispecies of bacteria, i.e., functional differences between quasispecies arise endogenously within the evolutionary ecology framework. Finally, we discuss means to relate predictions of this model to experimental studies in the chemostat, using the model organisms Escherichia coli and the virulent strain of λ phage.

Over 40 years ago the influential ecologist G. E. Hutchinson proposed “the paradox of the plankton” (1). Many phytoplankton species are functionally equivalent and live in well mixed pelagic environments, or so the paradox contends. As such, their diversity should be limited by the inevitable competitive advantage possessed by a small number of types. However, phytoplankton diversity is observed to be many orders of magnitude greater in natural samples (2) than predicted by the theory of competitive exclusion (3). This gap between theory and empirical data has been debated widely in the literature, and Hutchinson himself offered a number of ecological scenarios that purport to resolve the paradox (1). These scenarios include spatial heterogeneity in the environment, symbiotic interactions and predation, temporal switching in competitive strategies, as well as the catalytic effect of predation. These scenarios constitute a suite of possible approaches for resolving the paradox of the plankton as well as the fundamental question: why are there so many species (4, 5)? The accelerating scientific interest in studies of biodiversity in the intervening decades reflects the importance of this (increasingly practical) problem in evolutionary ecology.

In this paper, we develop a quantitative framework to address aspects of the generation and maintenance of diversity in microbial systems. Typical aquatic samples contain bacterial densities on the order of 10⁷ ml^-1 (6) and there is evidence that viral density is at least that high (2). These densities support a diversity of strains whose estimation poses a difficult experimental as well as theoretical problem (7). Nonetheless, there is an emerging consensus that there are many, perhaps millions, of uncultured and as yet unidentified strains of bacteria and phage (8). The presence of this diversity reflects the mutation–selection balance of neutral or near-neutral changes in the individual genomes as well as functional differences in the response of bacteria and phage to their environments (9, 10). The environments bacteria and phage respond to include each other; thus, a theory of the generation and maintenance of diversity should account for the evolutionary and possibly coevolutionary changes among bacteria and bacteriophage.

Previous theoretical models of coevolutionary dynamics (11, 12) of host–parasite interactions have not yet been applied to systems with fluctuating resources such as aquatic environments and the many experimental studies of coevolution of bacteria and bacteriophage in the chemostat (13–18). Coevolutionar y models designed for analysis of bacteria–bacteriophage communities have consisted of verbal mathematical constructs (2, 19, 20) or explicit calculations of the pairwise fitness of an invading mutant with respect to a single resident wild type (21). In many of these models, an assumption is made that the interaction of bacteria and bacteriophage rely on exclusive lock–key mechanisms. The biological basis for such an assumption is that bacteriophage insert their DNA into a host cell via membrane-bound surface receptors often responsible for nutrient uptake. Distinct tail fibers of bacteriophage (the key) are then presumed to adsorb exclusively to distinct conformations of a surface receptor (the lock). Changes in the conformation of the surface receptor, among other possible phenotypic changes, drive concomitant changes in the conformation of tail fibers. A possible outcome of such pairwise changes is the generation of a completely resistant bacterial host for which no host-range phage mutant exists (22, 23). However, the collapse of the host-parasitoid interaction web is by no means inevitable. Recent studies suggest the sustainability of complex host–parasitoid webs (17). An alternative view of bacteria and bacteriophage interactions is that of an imperfect lock–key mechanism, for which every tail fiber may adsorb to multiple receptor configurations, though not with equal efficiency. Likewise, a single receptor may be sensitive to adsorption by multiple tail fibers. Such a mechanism is likely to occur whenever there are severely deleterious consequences for the fitness of a bacterium mutant whose surface receptor is severely altered or eliminated altogether. Strong empirical support for such a view is found in the case of the interaction between Escherichia coli and λ phage (24–26). The theoretical model presented in this manuscript addresses the case of imperfect lock–key mechanisms.

We begin our analysis by proposing a conceptual framework that involves an ecological model, an evolutionary model, and a means to couple this pair of processes. The ecological model describes the population dynamics of bacteria and virulent phage in continuous culture. The evolutionary model describes the changes in phenotypic trait space that control host resource consumption and phage adsorption. A coupled evolutionary ecology model with a specified set of testable assumptions is then solved by the techniques of adaptive dynamics (27, 28), leading to the conditions for coevolutionary diversification. The major assumption of the conceptual model is that bacteria cannot completely block the infection of phage without also losing their ability to uptake resources. Assuming small, but finite, rates of mutagenesis, we also use stochastic simulations to assess the dynamics of coevolution and diversification in multistrain communities of bacteria and bacteriophage. Finally, we discuss the implications, for future coevolutionary studies, of prior work on the specific genetic loci affecting adsorption and uptake in the model organisms E. coli and the virulent strain of λ phage.

Coevolution Model of Bacteria–Bacteriophage Interactions

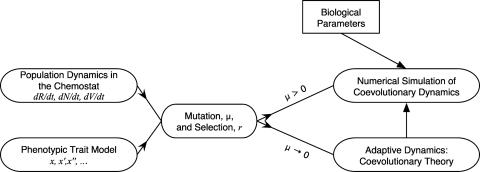
Recent advances in studies of coevolution suggest means to integrate ecological interactions into a coevolutionary framework (29–32). The system we present describes coevolutionary changes in phenotypic traits; it consists of an explicit trait-driven ecological model and a phenotypic model of trait changes in a continuous trait space. A schematic of the linkages between the analytical techniques and the stochastic simulations is contained in Fig. 1.

Fig. 1.

A schematic of the linkages between the ecological model of population dynamics, the trait model describing resource uptake and adsorption of phage, and the theoretical and numerical approaches for analyzing the evolutionary ecology. Note that adaptive dynamics is the limit of the evolutionary ecology in the small-mutation limit, results from which are combined with biological parameters to guide stochastic simulations of coevolutionary dynamics of bacteriophage and bacteria in the chemostat.

The ecological model we consider here is similar to mean field theories of predator–prey dynamics (33–35) and is a standard variant of the population dynamics of lytic phage and bacteria (36–38) in a chemostat (39); more details may be found in Appendix 1 of Supporting Text, which is published as supporting information on the PNAS web site. The change in densities of resource (R), bacteria (N), and bacteriophage (V), depend on phenotypic traits that determine uptake of nutrients and adsorption of phage. We denote the trait of the bacteria by x and the trait of the phage by y. These phenotypic traits, x and y, are one-dimensional approximations to the state space of the underlying coevolutionary dynamics occurring on what is presumably a large, but finite, number of possible types of bacteria and phage strains, respectively. The population dynamics can be written as

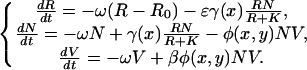[1]

This system, given a reasonable choice of parameters, possesses a nonfluctuating steady state with coexisting bacteria and phage; the derivation of the equilibrium state and its stability may be found in Appendix 1 of Supporting Text. The relevant point for the evolutionary model is that the maximal growth rate γ(x) depends on the phenotypic trait of the bacteria, whereas the adsorption rate ϕ(x, y) depends on the phenotypic traits of both the bacteria and the bacteriophage. Note that K and β are also potentially evolvable phenotypic traits of the bacteria and phage, respectively; however, they will be held constant for the sake of mathematical tractability.

We posit the following functional forms for the dependence of the maximal growth rate, γ(x), and the adsorption rate, ϕ(x, y), on the phenotypic traits

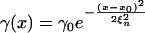[2]

and

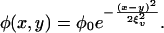[3]

Biologically, the form of γ(x) implies that there is an optimal configuration for maximal resource uptake, x = x₀, and hence an opportunity for a tradeoff between resource uptake and phage avoidance; without loss of generality, we will assume x₀ = 0. The form of ϕ(x, y) implies that, for every bacterial strain x, there is a phage strain y that maximizes the strain-specific adsorption rate. The parameter ξ_n is the stable uptake range of hosts; in the model, it is defined as the range of possible host phenotypes whose maximal growth rate is within e^-1/2 of the maximum for all phenotypes. The parameter ξ_v is the host range of phage; in the model, it is defined as the range of possible host phenotypes for which any given phage has an adsorption rate within e^-1/2 of its maximal adsorption rate.

In this model, new strains continually die or out-compete wild types, possibly drive entire classes of strains to extinction, and give rise to coexistence of multiple types. The mechanism for the introduction of mutant strains is straightforward. For example, a mutant bacteria with trait x′ appears in the system at a rate μ_nB_n(x, y), where μ_n is the mutation probability and B_n(x, y) is the birth rate of the resident bacteria. The mutant can invade only when its fitness when rare is positive, r′_n(x′; x, y) > 0, for which it has a probability p = 1 - m/b of avoiding the stochastic loss of beneficial mutations, where m is the per capita death rate and b is the per capita birth rate. When a mutant invades, the ecological model in Eq. 1 is expanded by an additional equation, corresponding to the dynamics of the mutant host population, N′. The introduction of mutants on evolutionary time scales with different trait values, x′ and y′, in turn modifies the ecological model in Eq. 1. An analogous process holds for the invasion by mutant phage.

Analytical Results on Diversification and Coexistence

It has been shown elsewhere (27) that, under the assumptions of rare and small mutations for an ecological model with a fixed-point equilibrium, the evolution of traits obeys the following dynamics

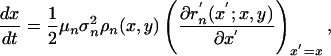[4]

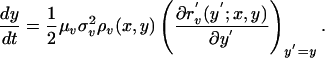[5]

In these equations, μ is the mutation probability, σ² is the variance of the mutation kernel in trait space, ρ is the equilibrium population size, and r′ is the fitness of a mutant when rare; in all cases, the subscripts n and v denote parameters associated with the bacteria and phage, respectively. In the chemostat model under consideration, the dynamics of a mutant bacteria population N′ that invades when rare is

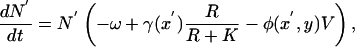[6]

and an analogous equation holds for a mutant phage population. The fitness of the mutant, r′_n, is equal to the term in large parentheses in Eq. 6, where the values of R and V are replaced by steady-state values for a given x and y. The fitness of bacteria and phage mutants can be written as

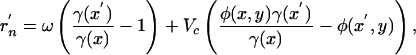[7]

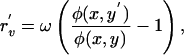[8]

respectively, where V_c is the steady-state phage density derived in Appendix 1 of Supporting Text. Eqs. 4 and 5 constitute a two-dimensional coevolutionary flow in trait space. Given 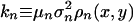, , 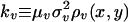two cases are relevant: (i) Limit of fast viral mutagenesis, k_v >> k_n > 0; and (ii) general case, k_n, k_v > 0. A summary of results for these two cases are included below; more details may be found in Appendix 2 of Supporting Text.

When k_v >> k_n, the sequence of evolutionary adaptations consists of viral adaptations toward an evolutionary fixed point followed by bacterial adaptations, etc. This fixed point occurs unsurprisingly at x = 0, i.e., at the optimal state for resource uptake. The evolutionary branching criterion at the fixed point (x = 0, y = 0),

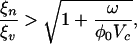[9]

requires that the stable uptake range of hosts exceed the host range of phage, where the second term under the square root of Eq. 9 expresses the degree to which ecological conditions modify the physiological control of diversification. Thus, we find two important dimensionless ratios controlling the dynamics: (i) the ratio of stable uptake range to host range; and (ii) the ratio of washout rate to maximal adsorption rate per unit host. This system of coevolutionary dynamics may also be shown to be convergence stable. Whenever the evolutionary fixed point is not an Evolutionarily Stable Strategy (ESS), the system should undergo evolutionary branching.

The general case of arbitrarily scaled trait evolution rates, k_n and k_v, is not always considered in the adaptive dynamics literature; however, see refs. 40–43. In higher dimensions (such as in coevolutionary dynamics) the asymptotic stability of an evolutionary fixed point (x_c, y_c) is determined by the Jacobian of the dynamics in trait space (34) (see Appendix 2 of Supporting Text for more details). Evaluation of the Jacobian leads to an algebraic condition for a co-ESS, 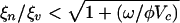, the same as the ESS condition in the case of fast viral mutagenesis. However, when this condition is not satisfied, the criterion for branching becomes

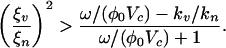[10]

Hence, the relative trait evolution rate, k_n/k_v, acts, in concert with the previously identified dimensionless ratios, ω/(ϕ₀V_c) and ξ_n/ξ_v, as a switch between coevolutionary branching and no coevolutionary branching.

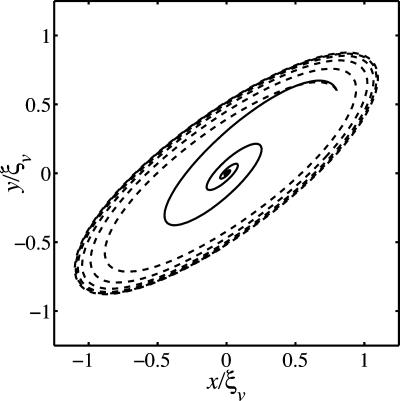
In summary, when the rate of trait evolution is unknown, the conditions for distinguishing between co-ESS and coevolutionary branching regimes are more complex than in the case of fast viral mutagenesis. For the chemostat model presented here, the condition for the co-ESS is independent of the ratio of trait evolution rates. When the evolutionary fixed point is not a co-ESS then, in general, it may exhibit evolutionary diversification or evolutionary cycles (“Red Queen” dynamics, ref. 44) depending on the relative rates k_n/k_v. There will be a critical value for large enough ratios, k_n/k_v, where the system no longer undergoes coevolutionary branching as part of the coevolutionary dynamics. We show in Fig. 2 a typical pair of trajectories for the numerical solutions of the coupled ordinary differential equations in Eqs. 4 and 5. The convergence to the evolutionary fixed point implies the potential for diversification.

Fig. 2.

An evolutionary-rate controlled switch between cyclical trait changes and convergence to the fixed point (0, 0) in a dimensionless x - y trait-space domain (40). The coupled ordinary differential equations of Eqs. 4 and 5 were numerically integrated with ξ_n/ξ_v = 4, ϕ₀V_c/ω = 0.25, along with k_n/k_v = 6.25 (dashed) and k_n/k_v = 4.56 (solid).

Numerical Simulations of Coevolution in a Chemostat

Stochastic simulations of coevolution in the chemostat are conducted for biologically meaningful parameters. Simulations are conducted by integrating in time a multistrain variant of the population dynamics described in Eq. 1

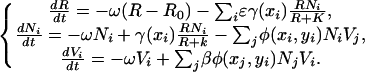[11]

Every bacteria population has a trait value x_i and density N_i; likewise, every phage population has a trait value y_i and density V_i. These traits are coupled to uptake, γ(x), and adsorption, ϕ(x, y) via the trait model defined in Eqs. 2 and 3.

Event-driven simulations of population dynamics stop under two conditions: the extinction of a strain or a mutation event. An extinction of a strain occurs when the population passes below some critical threshold. The strain is then removed from the coupled system of ordinary differential equations in Eq. 11 and the integration is allowed to proceed. A mutation event occurs at a rate that scales with the birth rate. Every mutant possesses a trait value equal to its mother strain plus a normal deviate. The probability of success of a mutant, p, depends on its fitness according to the standard formula for the survival of a branching process with death rate m and birth rate b, p = 1 - m/b (45). For the bacterial strains, m_i = ω + ∑_j ϕ(x_i, y_j)V_j and b_i = γ(x_i)R/(R + K), while for the phage strains, m_i = ω and b_i = ∑_j βϕ(x_j, y_i)N_j. Successful mutants remain in the population and so the number of strains is a dynamic variable responding to the evolution of traits and the population densities. Numerical simulations are conducted for small mutation probabilities 10^-6 < μ_n, μ_v < 10^-4 and normally distributed trait changes, 0.001 < σ_n, σ_v < 0.1. Biological parameter values are derived from the literature (36, 38) and included in Table 1. These parameter values permit the presence of bacteria–phage coexistence at the evolutionary fixed point, as derived in Appendix 2 of Supporting Text.

Table 1.

A list of parameters and values for stochastic simulation of Eq. 11

Parameter	Definition	Value
ω	Washout rate	0.2 h-1
R0	Resource density	2.2 μg/ml
ε	Resource conversion rate	2.6 × 10-6 μg/cell
γ0	Maximal growth rate	0.738 h-1
ϕ0	Maximal adsorption rate	6.24 × 10-8 ml/(hr·cell)
K	Half-saturation constant	4 μg/ml
β	Burst size	71

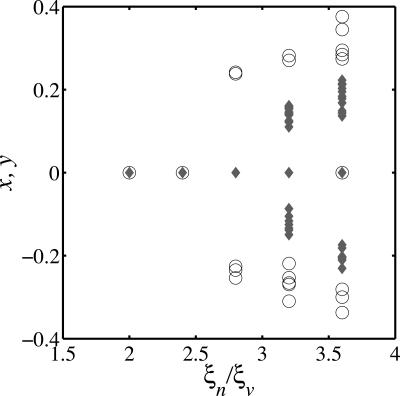
The principal result of numerical simulation is that multistrain coexistence is possible when the stable uptake range of hosts exceeds the host range of phage, 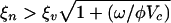. We examine the relationship between quasispecies number and the ratio ξ_n/ξ_v for a given set of biological parameters. Using the considered parameters and steady-state population densities at the evolutionary fixed point (x = 0, y = 0), the diversification condition for the adaptive dynamics model is ξ_n > 2.2ξ_v. In Fig. 3 a sequence of bifurcations is clearly visible, as ξ_n exceeds ξ_v near the value predicted by the theory of adaptive dynamics. The sequence of bifurcations occurs as a single phage and bacterium quasispecies are replaced by two bacteria and one phage quasispecies and then, as the ratio is increased, multiple numbers of each. Thus, the presence of phage acts as a catalyst that drives hosts to diversify in an effort to escape infection, which in turn provides an incentive for phage to diversify to track the hosts. However, when ξ_n < ξ_v, a host is unable to diversify beyond the reach of the host range of phage and the coevolution is limited to trait changes along an evolutionary trajectory with a single bacterial quasispecies and a single viral quasispecies. It is important to note that multistrain coexistence is not possible in this model without the phage because there is a single optimum for resource uptake.

Fig. 3.

Results from stochastic simulations of an evolutionary chemostat model with parameters as described in Table 1. In this case, the ratio of the stable uptake range of hosts to the host-range of phage, ξ_n/ξ_v, varies from 2 to 3.6. The dimensionless ratios are ϕ₀V_c/ω = 0.25 and k_n/k_v = 0.056. The y axis depicts the steady-state trait values for bacteria (circles) and phage (diamonds). The depicted strains are those with at least 1% of the total bacteria or phage population, respectively. A succession of bifurcations leading to multistrain coexistence is shown. The strains group naturally into distinct clusters of quasispecies.

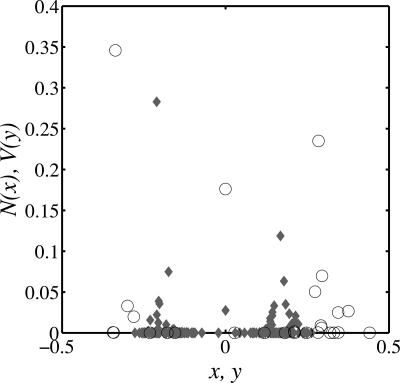
The significance of this result is that more than one sequence of coevolutionary branching occurs. Because of the complexity of the analytical derivations for the multi-strain case, we are only able to demonstrate this phenomena via numerical simulation. Although the total number of distinct strains is in the hundreds, as in Fig. 4 they are easily clustered into phenotypically distinct quasispecies which persist stably through time. The continual generation of strains does not preclude the maintenance of structured quasispecies which function in distinct ways. For example, in Fig. 4, the three quasispecies of phage adsorb preferentially to a respective quasispecies of bacteria. Interestingly, those bacteria strains which are the least efficient at the uptake of resources are the most abundant as a consequence of experiencing lower levels of phage-induced mortality.

Fig. 4.

Results from stochastic simulations of an evolutionary chemostat model with parameters as described in Fig. 3 using ξ_n/ξ_v = 3.6. Relative population density of bacteria N (circles) and phage V (diamonds) are plotted as a function of their trait values, x and y respectively. There are three quasispecies of bacteria and three of phage, despite the presence of 27 bacteria strains and 185 phage strains.

Discussion

The diversification of forms and types in the natural world are a result of evolutionary forces acting upon and within ecological communities. Theoretical analyses of diverse communities should therefore take the perspective of evolutionary ecology. In the present study of coevolutionary arms races, bacteria and bacteriophage are distinguished by state variables that determine their interactions with the environment and with each other. The particular choice of functional forms describing the interactions implies that not every phage can infect every host equally well. In addition, avoiding infection of viruses by bacteria comes with a tradeoff in terms of the host bacteria's uptake of resources (46). Given these core assumptions, the coevolutionary dynamics may lead to stable fixed points, Red Queen cycling, as well as diversification leading to multistrain coexistence. Diversification occurs despite the fact that the evolutionary ecology model of the bacteria–resource system can sustain, at most, a single bacterial strain. The presence of phage allows the system to diversify, and hence escape the limit on total strain number otherwise set by the theory of competitive exclusion, a result found in other host–parasite systems such as ref. 47.

The analytical conditions presented in Eqs. 9 and 10 demonstrate the importance of three dimensionless ratios in determining the likelihood of coevolutionary diversification: (i) ratio of stable uptake range of hosts to host range of phage, ξ_n/ξ_v; (ii) relative mutation rate, k_n/k_v; and (iii) ratio of phage-independent to phage-dependent mortality rate, ω/(ϕ₀V_c). As simple rules of thumb, diversification is promoted when ratio i is high and ratios ii and iii are low. We have demonstrated the plausibility of detecting a coevolutionary arms race leading to diversification by analytical calculations as well as by explicit numerical simulations of coevolution in a chemostat. Presumably, mortality rates and mutation rates may be manipulated by changing experimental conditions. However, testable quantitative predictions require estimates of ξ_n and ξ_v, respectively. The former may be estimated by an assay of mutant strains with altered surface receptors, the latter by standard techniques. Also of interest for comparison with theory is the determination of the structure of the resource uptake–phage evasion tradeoff.

The question of experiments is relevant to a broader aim of this paper. The coevolution of bacteria and bacteriophage in chemostat environments have been studied in a number of systems; a representative sample of work may be found in refs. 13–18. Typically, mutant bacteria arise that are partially or completely resistant to the phage. Phage may then mutate concurrently to track the mutant host strains, or decrease dramatically in population density if no host-range phage mutants arise (23). Bacteria whose membrane receptor for uptake of an available carbon source is distinct from the receptor utilized by phage are able to develop complete resistance in chemostat studies and hence stop the coevolutionary arms race altogether.

In contrast, the association between E. coli and the virulent strain of λ phage forms an ideal model system for the study of coevolutionary dynamics. λ phage infects E. coli through the LamB receptor (48, 49). If E. coli is cultured continuously in a chemostat with minimal media whose carbon source is maltose, then in principle there will be the opportunity to observe coevolutionary changes in both bacteria and phage. In fact, one experiment has already observed evidence of such changes (14), though only two concurrent strains were observed at any single observation. Bacteria strains should evolve different receptor moieties to avoid infection by phage while still accepting maltose. Likewise, phage should evolve different tail fiber conformations to adsorb, presumably nonexclusively, to alternative receptor types. Previous cross-adsorption studies of mutants of λ phage with lamB mutants show a consistently nonexclusive lock–key pattern (25). In addition to traditional uptake and strain-specific adsorptivity studies (50, 51), genetic analysis may aid in determining the degree to which the lamB gene in E. coli and the small number of tail fiber genes in λ phage undergo coevolution-induced selection.

Experiments that take place in the chemostat may be conducted under varying inflow rates, resource density, and system size. A major theoretical challenge left unresolved by the present work is a systematic study of the evolutionary stable number of coexisting strains for any given set of parameters. Is there a regime where the number of types increases in an unbounded fashion, limited only by system size? How do the present results generalize to systems where the stable uptake range of hosts, ξ_n, or the host-range of phage, ξ_v, are evolvable characters subject to selective pressure (52, 53)? Results such as these would be invaluable in directing experimental work toward distinct coevolutionary regimes. It is quite possible that unobserved diversity in chemostat coevolution experiments is waiting to be uncovered by modern genetic techniques (8, 9, 54–56). We hope that this work proves useful in providing a framework for understanding and testing how host–parasitoid interactions lead, in part, to the generation and maintenance of diversity in experimental habitats and natural environments.