Hydrophobic hydration from small to large lengthscales: Understanding and manipulating the crossover

Abstract

Small and large hydrophobic solutes exhibit remarkably different hydration thermodynamics. Small solutes are accommodated in water with minor perturbations to water structure, and their hydration is captured accurately by theories that describe density fluctuations in pure water. In contrast, hydration of large solutes is accompanied by dewetting of their surfaces and requires a macroscopic thermodynamic description. A unified theoretical description of these lengthscale dependencies was presented by Lum, Chandler, and Weeks [(1999) J. Phys. Chem. B 103, 4570–4577]. Here, we use molecular simulations to study lengthscale-dependent hydrophobic hydration under various thermodynamic conditions. We show that the hydration of small and large solutes displays disparate dependencies on thermodynamic variables, including pressure, temperature, and additive concentration. Understanding these dependencies allows manipulation of the small-to-large crossover lengthscale, which is nanoscopic under ambient conditions. Specifically, applying hydrostatic tension or adding ethanol decreases the crossover length to molecular sizes, making it accessible to atomistic simulations. With detailed temperature-dependent studies, we further demonstrate that hydration thermodynamics changes gradually from entropic to enthalpic near the crossover. The nanoscopic lengthscale of the crossover and its sensitivity to thermodynamic variables imply that quantitative modeling of biomolecular self-assembly in aqueous solutions requires elements of both molecular and macroscopic hydration physics. We also show that the small-to-large crossover is directly related to the Egelstaff-Widom lengthscale, the product of surface tension and isothermal compressibility, which is another fundamental lengthscale in liquids.

Biological self-assembly processes in aqueous solutions are driven by water-mediated interactions between constituents taking part in the assembly. Of these, hydrophobic interactions have received particular attention because of their relevance to protein folding and interactions, micelle and membrane formation, and molecular recognition (1–5). Theoretical work in this direction has been focused on the modeling of primitive hydrophobic phenomena, such as hydration and association of small hydrophobic particles in water (6–13). However, biological assembly occurs over a spectrum of lengthscales from that of an amino acid to proteins and larger. Naturally, fundamental understanding of the lengthscale dependence of hydration and association of hydrophobic solutes in water will be relevant to the quantitative modeling of realistic macromolecular processes (14, 15).

Small hydrophobic solutes can be accommodated into the open hydrogen-bonded network of liquid water without significant perturbations. Indeed, theories that model density fluctuations over small lengthscales in pure water provide a quantitative description of the hydration thermodynamics of small hard-sphere solutes in water (11, 12, 16–18). As the solute size is increased, water dewets the solute surface. Near a sufficiently large solute, the solute-water interface resembles that between vapor and liquid water, and therefore, requires interfacial thermodynamics for its description (15, 19, 20). Correspondingly, the thermodynamics of hydration changes gradually from entropic for small solutes to enthalpic for large solutes (1, 15). The theoretical approach by Lum, Chandler, and Weeks (LCW) (14) provided a quantitative description of structural and thermodynamic aspects of hydrophobic hydration over the entire small-to-large lengthscale region.

Applications of LCW theory have highlighted the importance of including lengthscales larger than molecular in the description of hydration thermodynamics. For example, the blurring of the entropy convergence in thermal unfolding of proteins (21), the drying-induced collapse of hydrophobic polymers (22), or the strong association of nanoscopic solutes in water cannot be explained based on the physics of small-solute hydration alone. Independent molecular simulation studies of various model nanoscopic solutes in water have also reported dewetting of solute surfaces and the resultant strong water-mediated interactions between those solutes (20, 23–27).

LCW theory predicts that the free energy of hydration of hard-sphere solutes increases approximately linearly with solute volume for small solutes, and with solute surface area for large solutes, and the small-to-large crossover occurs over nanoscopic lengthscales (28). The small-solute hydration is governed by microscopic density fluctuations (11, 12, 16–18), whereas large-solute hydration is described by the thermodynamics of interface formation (1, 15, 19). These two fundamentally different mechanisms will display different dependencies on thermodynamic conditions, thereby providing a mechanism for manipulation of the crossover lengthscale and the associated driving forces.

Motivated by the LCW work (14), here we use molecular dynamics (MD) simulations to probe the lengthscale-dependent hydrophobic hydration as a function of different thermodynamic conditions. Specifically, we focus on hydrophobic hydration in water under tension and in aqueous salt and ethanol solutions. Collectively, our simulation studies confirm the physical picture of lengthscale-dependent hydrophobic hydration presented by the LCW theory and extend that picture in the space of thermodynamic conditions. Specifically, we show that application of tension to water or addition of ethanol brings the small-to-large crossover down to molecular lengthscales, where it can be studied in detail by molecular simulations. By performing temperature-dependent studies under these conditions, we track the gradual transition with solute size from entropy-dominated to enthalpy-dominated hydration thermodynamics. Our simulation studies of alcohol and salt solutions provide quantitative clues to how additives can be expected to impact the small-to-large crossover lengthscale in hydrophobic hydration and the driving forces for hydrophobic aggregation. Finally, we relate the small-to-large crossover to the Egelstaff-Widom lengthscale (29), which is another fundamental lengthscale in liquids.

Methods

MD simulations were performed to calculate the free energy of hydration of hard-sphere solutes with water exclusion radius, R, in the range of 0 to 0.73 nm. Simulations were carried out in the isothermal-isobaric ensemble by using gromacs (30, 31). Berendsen's barostat and thermostat were used to maintain constant temperature and pressure (32) with coupling time constants of 0.1 ps. The extended simple point charge model (33) was used to represent water molecules explicitly. Periodic boundary conditions were applied, and the particle mesh Ewald method was used to calculate the electrostatic interactions with a grid spacing of 0.12 nm and a cutoff distance of 1 nm. A time step of 2 fs was used in all simulations.

Hydration free energy of small hard-sphere solutes (R ≤ 0.4 nm) was calculated by using Widom's test particle insertion method from pure water simulations (34, 35). To calculate the hydration free energy of larger hard-sphere solutes, we included a soft-sphere repulsive solute (acting as a biasing potential) interacting with water molecules with energy, 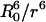, in the MD simulations. A range of R₀ values from 0.05 to 0.80 nm (in increments of 0.05 nm) was used in a set of simulations that included between 500 and 2,174 extended simple point charge water molecules. Each simulation was equilibrated for 1 ns followed by 4 ns of production run. Configurations (saved every 0.5 ps) obtained from the MD simulations containing the biasing potential were used to evaluate the hydration free energy as a function of the hard-sphere solute radius over small (≈1 Å) windows by using perturbation theory (36). These data were combined by minimizing the least-square difference in free energies in the overlapping regions to construct the ΔG(R) curve.

To obtain the dependence of ΔG(R) on thermodynamic conditions, we performed free energy calculations in systems under hydrostatic tension. Independent simulations of pure water were performed for three different system sizes to obtain an estimate of the spinodal pressure and density as described in Results and Discussion. Calculation of ΔG(R) at negative pressure requires simulation of metastable systems containing biasing solutes. The presence of such a void in the system can help nucleate phase separation over short time scales used in the simulation. This phenomenon restricts the size of the largest solute that can be simulated as well as the lowest pressure that can be applied. We performed calculations of ΔG(R) down to pressure as low as -1,000 atm (1 atm = 101.3 kPa) for R as large as 0.7 nm.

We also performed calculations of ΔG(R) at 300 K and 1 atm in ethanol–water mixtures and in sodium chloride solutions at two different concentrations each. Sodium and chloride ions were represented as spherical Lennard–Jones solutes with a unit electronic charge placed at their centers (37). The united-atom representation (38) was used to model ethanol molecules.

Entropic and enthalpic contributions to the free energy were calculated by taking temperature derivatives of the free energy values (39). To that end, we performed calculations of ΔG(R) at four different temperatures (280, 300, 310, and 320 K) at pressures of 1 atm and -1,000 atm (under tension) and in 40 mol% ethanol solution.

Results and Discussion

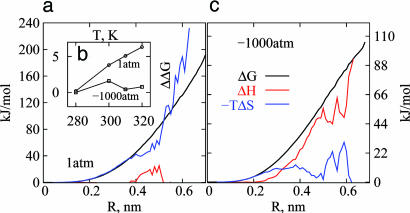
Fig. 1a shows the hydration free energy of hard-sphere solutes, ΔG(R), calculated from MD simulations. The hydration free energy is related to the probability of spontaneous formation of a solute-sized cavity in water, p₀, by ΔG = -kTlnp₀ (40). If particle number density fluctuations in a solute-sized observation volume, V, in pure water are approximately Gaussian (17), then

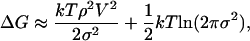[1]

where k is the Boltzmann constant, T the temperature, ρ the water number density, and σ² the variance of water number in V. Fig. 1a compares ΔG(R) predicted by Gaussian theory (16) with that obtained from MD simulations under ambient conditions. For small solutes with water exclusion radius R < 4 Å, the Gaussian theory predictions are in excellent agreement with the simulation data. Correspondingly, the probability distribution, p_n, of observing exactly n water molecules within a solute-sized observation volume in water is nearly Gaussian (11, 16) for R < 4 Å. With increasing solute size, the Gaussian predictions diverge from the measured ΔG values. Indeed, for solutes with R = 6.0 Å, Gaussian theory overestimates ΔG by as much as 30 kT. The onset of discrepancy between Gaussian predictions and MD measurements characterizes the beginning of the small-to-large lengthscale crossover in hydrophobic hydration. The origin of this discrepancy lies in the fundamentally disparate character of large-solute hydration, with

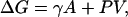[2]

where γ is the solute-water surface tension, A the solute surface area, and P the pressure. Huang and Chandler (41) have shown that the above discrepancy is reflected microscopically in the non-Gaussian nature of density fluctuations in the tails of p_n for large V (Fig. 1b), leading to a higher probability of cavity formation that is accompanied by dewetting or drying of the solute surface (14, 19, 20). The different physical mechanisms underlying small- and large-solute hydration are expected to display different sensitivities to changes in thermodynamic conditions. For example, the entropy of hydration, which characterizes the temperature dependence of free energy, is negative for small solutes and positive for sufficiently large solutes. Similarly, other thermodynamic perturbations can change the hydration free energies of small and large solutes to different extents such that the small-to-large lengthscale crossover can be manipulated in a predictable way, from molecular to nanoscopic lengthscales. In the case of the former, as we demonstrate below, the thermodynamic character of the crossover can be studied through atomistic simulations.

Fig. 1.

Density fluctuations and hydration free energy. (a and c) The free energy of formation of a cavity of radius R in water at 1 atm (a) and -1,000 atm (c) at 300 K, obtained from MD simulations (triangles) and predicted by using Gaussian theory (lines). (b) A schematic illustration of the Gaussian and non-Gaussian character of density fluctuations. (d) Shown is the ratio, p_n/Gauss(n), of probabilities measured in MD simulations of pure water and its Gaussian prediction for R = 4.0 Å as a function of the applied tension at 300 K. (e) The P_-ρ phase diagram of extended simple point charge water at 300 K in the negative pressure region for three different system sizes containing 128, 300, and 500 water molecules.

We begin by exploring hydrophobic hydration in the metastable (P < 0) region of water's phase diagram (42), which presents unique advantages. The strongly associating nature of water allows the liquid phase to withstand large tensions. Experimental studies on water inclusions in quartz crystals (43, 44), computer simulations (45), and model equations of state (46, 47) predict the spinodal pressure at 300 K to be in the range of -1,500 to -2,000 atm. By performing simulations of pure extended simple point charge water systems at 300 K in the stretched water region and fitting a polynomial to the P(ρ) curve, we estimate the spinodal pressure to be approximately -1,780 atm (Fig. 1e). As expected (48), with increasing tension, cavity formation becomes easier and ΔG values are lowered. Interestingly, Fig. 1c shows that compared with 1 atm at -1,000 atm Gaussian theory predicts ΔG accurately over a smaller range of solute sizes (R < 3.0 Å). Correspondingly, the density fluctuations become significantly non-Gaussian over molecular lengthscales. Indeed, the actual probability of formation of a 4-Å cavity at -1,000 atm is ≈80 times larger than its Gaussian prediction, leading to a 10 kJ/mol overestimate of ΔG by the Gaussian theory (Fig. 1d).

The small-to-large lengthscale transition in hydrophobic hydration is better illustrated by plotting the hydration free energy per unit solute surface area, ΔG/A, as a function of solute size (Fig. 2a). In the small-solute region, ΔG/A increases approximately linearly with the solute size, indicating that the free energy scales approximately linearly with the solute volume in this region. With increasing solute size, the ΔG/A profile becomes sublinear and is in quantitative agreement with previous calculations (28). These data can be extrapolated by using ΔG/A = γ(R) + PR/3, consistent with a gradual transition to interfacial thermodynamics with increasing solute size (Fig. 2c). The curvature dependence of γ is captured approximately by γ(R) = γ_∞(1 - 2δ/R), where δ is the Tolman length, and γ_∞ = lim_R→∞ γ(R). We use γ_∞ = 73.6 dynes/cm and δ = 0.76 Å as in ref. 28.

Fig. 2.

Crossover lengthscale in hydrophobic hydration. (a) The free energy of hydration of a hard-sphere solute per unit surface area, ΔG/4πR², as a function of the exclusion radius, R, at 300 K was obtained from MD simulations at different tensions. Independent results from Huang et al. (28) at 1 atm are also shown (•). (b) The contact density of water relative to its bulk density as a function of R at five different tensions is shown. The curves are Padé fits to g(R) data calculated from ΔG values (49). (c and d) Shown are ΔG/A curves at 1 atm (c) and -1,000 atm (d) along with linear fits to Gaussian theory prediction in the small-solute region (red) and the γ_∞(1 - 2δ/R) + PR/3 curve in the large-solute limit (blue). We calculated the dependence of γ_∞ on tension by using a molecular thermodynamic theory for water (50): γ_∞ equals 73.6 dynes/cm at 1 atm and reduces to 68 dynes/cm at -1,000 atm, shown by horizontal dashed lines. δ = 0.76 Å (28) is assumed to be a constant. Arrows indicate the crossover length as the point of intersection of small- and large-solute hydration behavior.

The asymptotic approach to the macroscopic thermodynamic description with increasing solute size is consistent with the contact density profiles (19, 24) (Fig. 2b). For small solutes, the density of water in contact with the solute, g(R), increases with R and reaches a maximum for solutes with 2 < R < 2.5 Å (49). Increasing the solute size further leads to growth of the void volume and a corresponding loss of favorable enthalpic interactions by vicinal water molecules characterized by Hummer and Garde (20) in terms of the “cavity expulsion” potential. That loss results in a gradual dewetting of hydrophobic solutes with increasing solute size. For sufficiently large solutes, g(R) varies inversely with R and its numerical value drops well below the bulk density of water (19). In this limit, the solute–water interface resembles the interface between vapor and liquid water, and therefore, surface tension dominated hydration behavior is expected (1, 15, 19).

The small-to-large crossover lengthscale characterizes the size at which macroscopic hydration thermodynamics also becomes relevant. The point of intersection of the Gaussian theory line (ΔG/A from Eq. 1) and the γ_∞(1 - 2δ/R) + PR/3 curve provides an approximate measure of that lengthscale. The crossover length calculated by using this definition is rather small (subnanoscopic) under ambient conditions, equal to ≈5 Å, which is followed by a broad transition region in the ΔG/A profile. With increasing tension, although the ΔG/A profile remains qualitatively similar, the crossover region shifts to even smaller lengthscales (≈3 Å). Why does the crossover length decrease with increasing tension? The answer lies in the characteristically different dependence of ΔG on pressure (tension) for small and large solutes, implied by Eqs. 1 and 2, respectively. With increasing tension, at 300 K, ρ decreases (Fig. 1e) and σ² increases slightly, leading to the lowering of ΔG/A values for small solutes. For large solutes, the decrease in ΔG/A with increasing tension arises directly from the PV term, and indirectly through the γA term. To our knowledge, no direct measurements of γ have been reported in metastable water. However, an approximately linear dependence of γ on ρ is expected (50). At -1,000 atm, the PV term for intermediate-sized solutes becomes comparable to the γA term, leading to the negative slope of ΔG/A line for larger solutes (Fig. 2d).

A simple thermodynamic argument provides a basis for the disparate pressure dependencies discussed above. The pressure derivative of ΔG/A is proportional to the solute size:

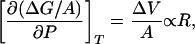where ΔV is the excess volume of hydration of the solute (51). Thus, the decrease in ΔG/A is smaller for molecular solutes compared with that for larger solutes, effectively reducing the crossover length with increasing tension.

The crossover lengthscale characterizes the region where small and large lengthscale hydration descriptions overlap. Indeed, equating Eqs. 1 and 2 [i.e., kTρ²V²/2σ² + 1/2kTln(2πσ²) = γA + PV] and neglecting the logarithmic term on the left side of the equation, we get the crossover length scale

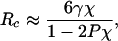[3]

where χ = σ²/kTρ²V is the microscopic compressibility. Both the surface tension and the microscopic compressibility depend on R, and therefore, values of γ and χ at R = R_c need to be used in Eq. 3. The curvature dependence of γ is given approximately by the Tolman equation (see Fig. 2c). Fig. 3a shows the R dependence of the microscopic compressibility obtained from computer simulations. For molecular volumes, χ is ≈5–10 times larger than the bulk water compressibility, χ_b, and decreases monotonically to χ_b in the thermodynamic limit. Egelstaff and Widom (29) found that, although individual values of γ_∞ and χ_b for a range of liquids vary by a factor of 150, the product γ_∞χ_b remains almost constant equal to a few tenths of an angstrom (γ_∞χ_b ≈ 0.34 Å for water). Thus, Eq. 3 suggests a remarkable relationship between the crossover lengthscale and the Egelstaff-Widom lengthscale, γ_∞χ_b, a fundamental length characteristic of liquids.

Fig. 3.

Prediction of the crossover lengthscale and its connection to the Egelstaff–Widom lengthscale. (a) The microscopic compressibility, χ = σ²/kTρ²V, as a function of the radius of spherical observation volumes calculated from MD simulations at 300 K and 1 atm is shown. The dashed line denotes the bulk water isothermal compressibility, χ_b = 4.5 × 10^-5 atm^-1. (b) A graphical solution of Eq. 3, obtained as a point of intersection of the curve y = 6γχ/(1 - 2Pχ) (solid line) and y = R (dashed line). We used χ(R) from a and γ(R) = γ_∞(1 - 2δ/R). (c) The values of R_c predicted by solving Eq. 3 as a function of the applied tension are shown.

A graphical solution of Eq. 3 provides the value of the crossover length, R_c, which is subnanoscopic (Fig. 3b). In addition, the pressure dependence of R_c predicted by Eq. 3 is consistent with our earlier observations. Specifically, application of tension reduces the crossover length to molecular sizes (Fig. 3c). The fact that the crossover length is related to the Egelstaff-Widom lengthscale is physically intuitive, because the latter quantity contains information about both molecular (χ) and macroscopic (γ) solvation physics.

Does the reduction in crossover length imply a similar transition in the thermodynamic nature of hydrophobic hydration with increasing tension? The entropic (-TΔS) and enthalpic (ΔH) contributions to ΔG calculated by taking temperature derivatives of ΔG are shown in Fig. 4. Although the calculated entropy and enthalpy values contain significant statistical uncertainties, at 1 atm, entropy makes the major contribution to the free energy over the entire solute size range considered here. In contrast, at -1,000 atm, entropy dominates over a significantly smaller range of solute sizes (R < 3 Å), with the hydration of larger solutes being predominantly enthalpic in nature. Because surface tension decreases monotonically with temperature, the entropy of hydration of sufficiently large solutes is expected to be positive (favorable). However, at -1,000 atm, the entropy of hydration of larger solutes remains small but negative (unfavorable), suggesting that crossover to large-solute hydration is not complete over the range of solute sizes studied here. That is, the region of crossover from small-to-large-solute hydration is broad, and the crossover size simply characterizes a lengthscale at which elements of large-solute hydration physics also become important.

Fig. 4.

Thermodynamics of small and large solute hydration. (a and c) The hydration free energy of a hard-sphere solute, ΔG, as a function of solute size R, at 1 atm (a) and -1,000 atm (c) at 300 K. (b) The temperature dependence of ΔG is shown with reference to its value at 280 K [ΔΔG = ΔG(T) - ΔG(T = 280K)] for a hard-sphere solute of radius 4.5 Å. (c) The enthalpic (ΔH, red) and entropic (-TΔS, blue) contributions to ΔG obtained from temperature derivatives of the free energy are shown at 300 K. Thermodynamic crossover from entropic to enthalpic hydration is clear at -1,000 atm.

The sign of the hydration enthalpy determines the temperature dependence of the solubility as well. Nonpolar gases display a minimum in their aqueous solubility with increasing temperature. The hydration enthalpy becomes positive above the solubility minimum temperature (52, 53). For small hard-sphere solutes, Gaussian theory (54) as well as the exact point-particle limit of the scaled particle theory (55) indicate that the sign of the hydration enthalpy is positive above the temperature of maximum density (TMD) of liquid water. Thus, small hard-sphere solutes will display a solubility minimum near the TMD (equal to 277 K at 1 atm). For larger hard-sphere solutes, temperature-dependent surface tension data indicate that the solubility minimum, if present at all, would be observed at temperatures <277 K (56). Thus, at 300 K, for both small and large hard-sphere solutes, solubility increases with temperature, except that the rate of that increase will be higher for larger solutes, because their solvation is enthalpy dominated.

The relatively small magnitude of the crossover lengthscale implies that, in general, thermodynamic and structural aspects of large-solute hydration are relevant even for subnanoscopic lengthscales. We note, however, that inclusion of solute–water attractive interactions reduces the hydration free energy of small solutes (54) and the extent of dewetting of solute surface (1, 24) and the corresponding surface tension of the large solute-water interface (20, 50). The relatively higher decrease in the small-solute hydration free energy caused by solute–water attractive interactions will increase the crossover lengthscale correspondingly.

In general, a thermodynamic perturbation affects small- and large-solute hydration differently, leading to a change in crossover length and associated thermodynamics. Fig. 5a shows that the addition of NaCl increases ΔG/A values for both small and large solutes, albeit numerically differently. Addition of ethanol has similar effects, but in the opposite direction. In both cases, changes in the asymptotic values (≈5 dynes/cm for 2 M NaCl and ≈30 dynes/cm for 40 mol% ethanol solution) are consistent with experimental data on vapor–liquid surface tensions of their aqueous solutions (57, 58). Further, we find that the Egelstaff-Widom lengthscale, γ_∞χ_b, increases somewhat with salt addition and decreases with ethanol addition, consistent with our calculations. The observed reduction in the crossover length in 40 mol% ethanol solution is also independently confirmed by the enthalpy dominated nature of hydrophobic hydration as shown in Fig. 5b.

Fig. 5.

Effects of salt and additives on hydrophobic hydration. (a) The free energy of hydration of a hard-sphere solute per unit surface area, ΔG/A, as a function of R at 1 atm and 300 K, in pure water, sodium chloride solutions, and ethanol-water mixtures is shown. (b) The enthalpic (red) and entropic (blue) contributions to ΔG in an aqueous solution with 40 mol% ethanol at 300 K are shown.

The lengthscale dependence of the hydration free energy of a single solute and its sensitivity to thermodynamic conditions are also relevant to the thermodynamics of aggregation processes (1, 5). Consider n small solutes each with volume v forming a globular aggregate of volume nv. ΔG_nv - nΔG_v can then be taken as a qualitative measure of the driving force for the aggregation process (1). For small solutes, ΔG_v ≈ αv, where α is a constant. For sufficiently large n, the radius of the aggregate will be larger than the crossover lengthscale, and therefore, its free energy will vary with aggregate area [ΔG_nv ≈ 4πγ(3nv/4π)^2/3]. The two terms, nΔG_v and ΔG_nv, display quantitatively disparate dependencies on thermodynamic perturbations, leading to increased or decreased driving force for aggregation. For example, the addition of salt increases both α and γ. For sufficiently large n, however, n¹ dependence dominates, leading to a higher driving force, nαv - 4πγ(3nv/4π)^2/3, for aggregation. In the case of ethanol addition, both α and γ decrease, leading to a reduced driving force for hydrophobic aggregation. This general picture is consistent with experimental data on additive effects on protein stability (58–60).

Conclusions

We have presented calculations of hydration free energies of hard-sphere solutes in water by using MD simulations of systems under various thermodynamic conditions, which include application of hydrostatic tension, or addition of ethanol and salt molecules to water. These calculations highlight characteristic lengthscale dependencies of hydration of these model hydrophobic solutes in the context of the broader picture presented by the LCW theory (14). Physical mechanisms underlying the formation of small and large cavities are different; the former is described by the approximately Gaussian nature of density fluctuations in bulk water, whereas the latter requires an interfacial thermodynamics framework for its description. Likewise, the sensitivity of small- and large-solute hydration to thermodynamic perturbations is different, which allows the manipulation of the crossover lengthscale at which the two descriptions overlap. Specifically, our calculations show that the application of tension or the addition of ethanol to water, reduces the small-to-large crossover lengthscale to subnanometer sizes, making the crossover region accessible to detailed molecular investigations. Temperature-dependent calculations further verify that hydration thermodynamics is entropic for lengthscales below the crossover but gradually becomes enthalpic for larger lengthscales. The nanoscopic lengthscale of the crossover indicates that small-solute hydration thermodynamics alone is not sufficient for modeling solution thermodynamics of biomolecular processes, such as hydration, self-assembly, and interactions.

By equating expressions for free energies for small- and large-solute hydration, we show that the crossover length is directly related to the Egelstaff-Widom lengthscale, γ_∞χ_b. The dependence of that lengthscale on thermodynamic conditions [e.g., temperature (61), pressure, and the addition of salt or ethanol] is consistent with the corresponding dependence of the crossover length observed in our simulations. Our analysis is not restricted to water and should be applicable to other condensed fluids as well. In light of this remarkable connection, it will be instructive to perform a quantitative analysis of the dependence of γ_∞χ_b on an extensive set of thermodynamic conditions for water and other liquids. Together, these results have implications for a fundamental understanding of solvation in condensed matter and applications, including extensions of protein pressure-temperature phase diagrams to metastable regions, phase behavior, and self-assembly in confined environments of interest to disparate fields of geochemistry, environmental sciences, and biotechnology (62–64).