Abstract
Feature engineering is of critical importance in the field of Data Science. While any data scientist knows the importance of rigorously preparing data to obtain good performing models, only scarce literature formalizes its benefits. In this work, we present the method of Statistically Enhanced Learning (SEL), a formalization framework of existing feature engineering and extraction tasks in Machine Learning (ML). Contrary to existing approaches, predictors are not directly observed but obtained as statistical estimators. Our goal is to study SEL, aiming to establish a formalized framework and illustrate its improved performance by means of simulations as well as applications on practical use cases.
Keywords: Feature extraction, Machine learning, Statistics
Subject terms: Applied mathematics, Computer science, Statistics
Introduction
In the field of Machine Learning (ML), the preparation and pre-processing of the data is often considered equally or even more important than the model itself. Students in data science are usually taught that 80% of the workload on an ML project is about preparing the data, while the remaining 20% are concerned with the actual choice of ML model1. This is in sharp contrast to the focus put on the modeling part in comparison to the data preparation and its benefit to models. As an illustration, the top 15 questions on Stack Overflow for the keywords “Machine learning” count 140 times more views than the top questions for “Data preparation” or “Data engineering”.
When searching for the keywords “Machine learning” (link), results count 2,279,504 views covering 109 answers, while “Data preparation” (link) counts 16,320 views and 16 answers (accessed on December 4th, 2024). Similarly, the most relevant research articles retrieved on Google Scholar with the keywords “Machine learning” accumulate 16 times more citations than articles with keywords “data preparation” or “feature engineering”. Papers for “Machine learning” (link) have a total of 62,723 citations, while “data preparation” papers (link) count 3975 citations (accessed on December 4th, 2024).
In this work, we therefore introduce Statistically Enhanced Learning, abbreviated SEL, which is a statistical feature engineering framework that allows building new features (which we will also call “covariates” in this paper) which cannot be directly observed. The idea is to enhance the performance of existing learning algorithms by extracting specifically targeted information that is not directly given by the data (we will often refer to this as “missing signal”). This allows adding the information of an unobserved or mismeasured signal under the form of a statistical covariate with a clear meaning. As we will demonstrate, SEL works for any type of data (tabular, computer vision, text) and is a general approach to improve any learning algorithm. We refer to learning as the general term since it considers the large spectrum of data-driven learning techniques (from classical statistical to advanced deep learning models). As we will see, contributions from different domains (statistics, machine learning, econometrics, computer science, ...) have already unknowingly used SEL as feature engineering technique. By our formalizing framework we will thus reunite and structure seemingly distinct approaches, which will shed new light on feature engineering.
Formalizing feature extraction
We distinguish three levels of SEL features with increasing technical complexity:
SEL 1 - Proxies: addition of one or several features to represent another variable we cannot observe or do not have available. In statistics and econometrics, a proxy is a variable which is correlated with and used in place of an omitted variable2. It can be a weak representation of the original signal, but still carries enough information from the unmeasured variable3. An illustrative example from econometrics would be the proxy feature household consumption for the abstract and not-measurable concept of standards of living.
SEL 2 - Descriptive statistics: transformation of some existing features with classical statistical tools (e.g., count, moments, quantiles, etc.) to summarize information in a meaningful way. Such summaries are particularly relevant with a large amount of predictors which would be meaningless to add on their own. For example, in the prediction of sports matches between two teams of 30 players each, the average age is a useful predictor contrary to individual ages of players.
SEL 3 - Advanced modeling features: higher level of abstraction to extract information from available variables (that cannot be used as predictors themselves) via more advanced statistical tools (e.g., maximum likelihood estimators, causal estimands, moving averages, etc.). It is important for the resulting covariates to bear a statistical nature, meaning that their uncertainty should be quantifiable and they should have a concrete meaning to users. These variables should also add new information to the model to enhance its learning. Hence, this excludes dimensionality reduction techniques such as principal component analysis. As an illustrative example, the forecasting of wind energy production can be improved by adding exponentially weighted moving averages (EWMA)4 of wind speed measurements over the past 7, 14, 21 and 28 days.
To illustrate the above concepts on a concrete example, we now analyze the study of Felice et al.5 on the prediction of handball games by means of machine learning models under the light of SEL. In their analysis, they consider around 5000 matches of female handball teams from European clubs between September 2019 and April 2023 as training set and 250 games from April to June 2023 as test set. They consider the following features for their prediction: game information (day of the week the game takes place, hour of the game, importance of the game, days left until the end of the competition), factors describing a team’s structure (average and variance of height, weight and age of players per position on the field, travel distance to the place of the game, nationalities of the players, and percentage of international players) and factors describing the team’s strength (attack strength, defense strength). Among these features
The “travel distance” is a proxy for the fatigue of the away team and hence SEL1;
Averages and variances of heights, weights and ages per position on the field are SEL2;
The attack and defense strengths are quantities taken from Felice6 and defined as combinations of the estimated parameters from a Conway-Maxwell-Poisson distribution fitted (estimated by means of maximum likelihood, a statistical technique that chooses the parameter values in such a way that the likelihood of all match outcomes is maximized) to the results of several handballs games, therefore they correspond to SEL3.
Interestingly, the age features are also SEL1 as they are proxies for a player’s experience. This illustrates the fact that the boundaries between the different levels of SEL features are quite porous. Since proxy variables might sometimes not be available, one would have to estimate them with descriptive statistics or advanced modeling. In these situations, a feature would fall into two distinct levels. In the case of the age features, they are of type SEL1 and SEL2 as they represent a proxy for experience and are descriptive statistics of the individual player’s age. The attack and defense strength parameters drastically enhance the prediction accuracy of each machine learning model considered in Felice et al.5. For instance, the best-performing model, a random forest, went from 60.11% to 81.32% accuracy in game outcome prediction by adding these SEL3 features. Moreover, these features were found to be the most influential in the predictions when looking at variable importance measures.
This concrete example underlines the power of statistically enhancing existing (machine) learning models. This enhancement is obviously not only due to the addition of new features, as meaningless features would not improve the models and would certainly not be selected as most influential. SEL, rather, is a means to recover information from signals that cannot be detected. The strength of SEL can best be perceived by adopting the perspective of Granger causality: Granger7 defines a causal relation when a predictor of a phenomenon contains information that cannot be retrieved from another predictor. In other words, if all possible predictors of a certain phenomenon 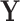 are contained in our set of predictors
are contained in our set of predictors 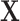 , then we can consider the relation to be causal.
, then we can consider the relation to be causal.
Putting this statement in the context of SEL, we can summarize the workflow with the diagram from Fig. 1.
Fig. 1.
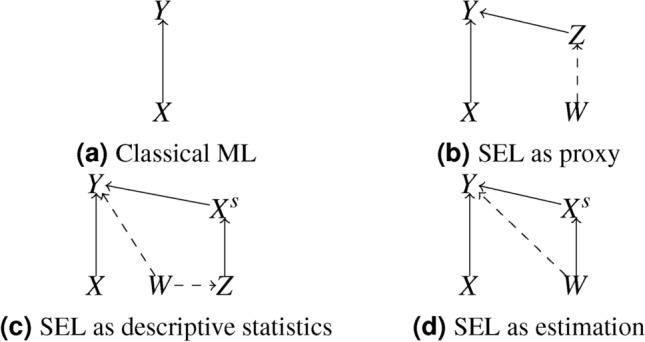
Representation of SEL variables in a Granger causality view. The classical (modeling and) learning approaches under setting (a) consider an input 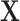 that influences the target variable
that influences the target variable 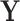 . The modeler then tries to estimate the relation
. The modeler then tries to estimate the relation 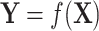 , with f being any (potentially nonlinear) transformation of the input. With Granger’s logic7, if
, with f being any (potentially nonlinear) transformation of the input. With Granger’s logic7, if 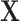 contains all variables influencing
contains all variables influencing 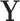 and we know that
and we know that 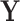 does not cause
does not cause 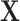 , then the relation between
, then the relation between 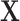 and
and 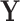 can even be considered as causal. SEL comes at play in the different situation when
can even be considered as causal. SEL comes at play in the different situation when 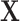 does not contain all the signals influencing the target
does not contain all the signals influencing the target 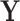 (see settings (b–d)). Instead, we know that other factors
(see settings (b–d)). Instead, we know that other factors 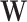 have a direct influence on
have a direct influence on 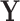 but they cannot be observed. The modeler then uses new substitute variables, denoted
but they cannot be observed. The modeler then uses new substitute variables, denoted 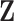 or
or 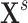 in the diagram, to represent the missing signal. In other words, since the relation
in the diagram, to represent the missing signal. In other words, since the relation 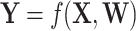 cannot be explicitly written because
cannot be explicitly written because 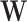 is not observed, the modeler substitutes
is not observed, the modeler substitutes 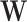 by
by 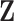 or
or 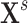 and focuses on estimating the relation
and focuses on estimating the relation 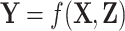 or
or 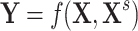 .
.
The three levels of SEL correspond to the following representations.
The dashed link in Fig. 1b exists but cannot be observed so the scientist has to use
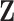 as an alternative source of information to model the phenomenon Y. In our handball example,
as an alternative source of information to model the phenomenon Y. In our handball example,  corresponds to the not measurable fatigue of players due to their journey (typically by bus) to the game. Therefore the travel distance is used as proxy
corresponds to the not measurable fatigue of players due to their journey (typically by bus) to the game. Therefore the travel distance is used as proxy 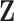 .
.The link between the variable of interest
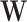 and the target
and the target 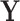 as illustrated in Fig. 1c is indirect. In situations like the handball predictions, we know that the information contained in
as illustrated in Fig. 1c is indirect. In situations like the handball predictions, we know that the information contained in 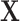 is not sufficient to model
is not sufficient to model 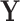 accurately. The maturity of players as the true missing signal
accurately. The maturity of players as the true missing signal 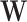 is too important to be ignored as a predictor. The players’ ages (variable
is too important to be ignored as a predictor. The players’ ages (variable 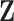 ) are a good indicator (proxy) for their maturity. However, the ages of individual players cannot be used alone as predictors and would be meaningless to the model. Hence, instead the players’ average age per position (
) are a good indicator (proxy) for their maturity. However, the ages of individual players cannot be used alone as predictors and would be meaningless to the model. Hence, instead the players’ average age per position (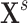 ) should be used.
) should be used.In the last situation, depicted in Fig. 1d, the signal
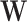 causing
causing 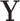 cannot be observed either but SEL is used to estimate the relation via
cannot be observed either but SEL is used to estimate the relation via 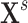 . SEL is no longer a proxy with the goal to add information but instead an actual estimation of the missing signal
. SEL is no longer a proxy with the goal to add information but instead an actual estimation of the missing signal 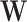 . In the handball example, the missing signal
. In the handball example, the missing signal 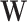 is the concept of a team’s attack and defense strength, which has been estimated, as explained above, by the quantities defined in Felice6.
is the concept of a team’s attack and defense strength, which has been estimated, as explained above, by the quantities defined in Felice6.
We now properly contextualize SEL within the domains of learning and data science. We define Statistically Enhanced Learning as inherited from three different fields:
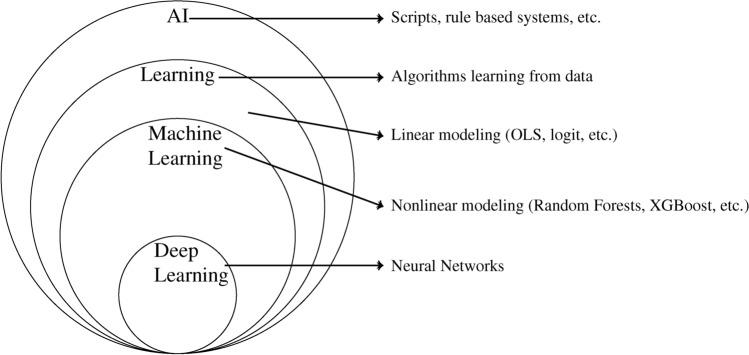
Learning: General field aiming to process some input and generate predictions. It can be as general as machine and deep learning as illustrated in Fig. 2 below, adapted from Goodfellow et al. 8. Quoting Hastie et al. 9: “Using this data we build a prediction model, or learner, which will enable us to predict the outcome for new unseen objects. A good learner is one that accurately predicts such an outcome.”
Data processing: Field that includes data preparation steps to later enhance the learning performance. It can be compared to information processing as defined by Ralston 10 and includes steps such as data cleaning and data preparation.
Statistics: In a wide sense, field that includes descriptive statistics, inference, statistical modeling and causality.
Fig. 2.
Venn diagram for Artificial Intelligence and Learning (inspired from Goodfellow et al. 8 and adapted according to the differences between Statistical (Linear) Learning and (Nonlinear) Machine Learning laid out by Ley et al. 13).
We visually represent these fields in Fig. 3. We can identify their intersections as follows:
Fig. 3.
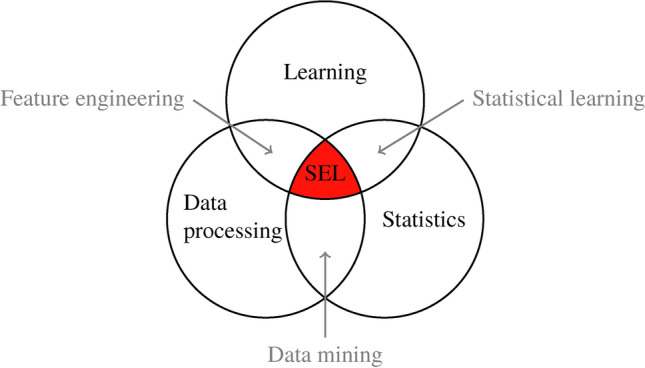
Statistically Enhanced Learning as the intersection between three fields.
Statistical learning = Learning
 Statistics: any learning algorithm that we work with (e.g., linear regression, random forests, neural networks). It is an interdisciplinary field by nature as it intersects with artificial intelligence and domains areas, such as engineering or others9.
Statistics: any learning algorithm that we work with (e.g., linear regression, random forests, neural networks). It is an interdisciplinary field by nature as it intersects with artificial intelligence and domains areas, such as engineering or others9.Feature engineering = Learning
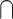 Data processing: First and crucial part before the modeling exercise in view of predictions. It consists in the preparation of the data set by processing the input data (cleaning, scaling, etc.)11
Data processing: First and crucial part before the modeling exercise in view of predictions. It consists in the preparation of the data set by processing the input data (cleaning, scaling, etc.)11Data mining = Statistics
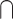 Data processing: Part of the literature which consists in extracting information/knowledge from data12. Extracted information can be used in inferential statistics, learning or generated business knowledge and metrics.
Data processing: Part of the literature which consists in extracting information/knowledge from data12. Extracted information can be used in inferential statistics, learning or generated business knowledge and metrics.
SEL is at the intersection of these fields as illustrated in Fig. 3. It consists of augmenting a data set with easy-to-understand features from one of the three SEL levels in order to improve the performance of any learning algorithm. It thus allows retrieving information about a missing signal. As they are not measured directly, SEL variables bear an extra layer of uncertainty, which one can quantify using SEL covariates of statistical nature. We also note that SEL unifies statistics and machine learning14.
We now provide examples of contributions whose methodology falls under the umbrella of SEL. We analyze these works under the formal SEL framework and, hence, shed new light on them. To show the universal applicability of SEL, we will consider a subdivision based on the type of data.
Tabular linear setting
Econometricians often face the problem of unobserved variables to model complex phenomena. Important variables to a model (such as income, willingness to pay, feelings) are either not available to the modeler or not measurable. The use of proxy variables, hence SEL 1, is a solution to compensate the lack of necessary signals. As already mentioned, Montgomery et al.3 analyze the benefit of the use of proxies such as household consumption from demographic surveys to represent standards of living and show that even weak proxy variables can still capture the desired signal from the unobserved feature. They also claim that adding proxies can help reduce the inconsistency of the estimated parameters.
The two-stage least squares approach (aka. 2SLS2) is another indirect modeling strategy which is used to incorporate a feature that cannot directly be included in the regression model when it contradicts the OLS assumptions (when the covariates X are not independent from the residuals 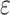 ). Therefore, including an instrumental variable (IV) as a two-stage approach is preferred by first regressing the conflicting variable Z as a function of some regressors W, thus we regress
). Therefore, including an instrumental variable (IV) as a two-stage approach is preferred by first regressing the conflicting variable Z as a function of some regressors W, thus we regress 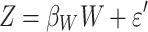 for some error term
for some error term 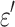 . The estimated variable Z then feeds the main regression model by
. The estimated variable Z then feeds the main regression model by 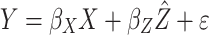 , and this is clearly an instance of SEL 3. A generalization of IV methods15 formalizes the framework which can be applied to discrete modeling or in the context of high heteroscedasticity.
, and this is clearly an instance of SEL 3. A generalization of IV methods15 formalizes the framework which can be applied to discrete modeling or in the context of high heteroscedasticity.
It also happens frequently that observed variables are noisy and therefore cannot be used as predictors. In such cases, modelers pre-process those variables via statistical methods such as kernel composition/decomposition or Fourier transforms16. Such techniques help deal with mis-measured variables (or measured with noise) and prepare a cleansed signal that will enhance the learning step. This approach falls under the umbrella of SEL 3.
Tabular nonlinear setting
17 use moments of some longitudinal features to classify abnormal bitcoin network addresses. They add the first four moments (namely mean, variance, skewness and kurtosis) from time-dependent variables to extract intrinsic information of the variable to classify bitcoin addresses. Their method outperforms existing models and shows the high importance of the moment-based variables, hence of SEL 2.
In the context of football goals prediction of national teams, Groll et al.18,19 use a so-called hybrid approach to estimate unobserved variables and augment the data set for a Random Forest model. On the one hand, they build a novel covariate as the average age of players, which is of course SEL 2. On the other hand, they add a statistical feature which aims to represent the strength of the two opponents. To this end, they consider historical games of all national teams over an 8-year-period preceding the tournament whose matches they intend to predict and model the joint distribution of goals scored by home and away teams (i and j, respectively) by the bivariate Poisson distribution. Hereby, the parameters 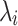 and
and 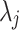 represent the mean parameters of the Poisson process and are assumed to be of the form
represent the mean parameters of the Poisson process and are assumed to be of the form 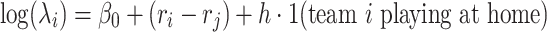 , where
, where 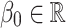 is a common intercept and
is a common intercept and 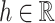 is the effect of playing at home. The real-valued parameters
is the effect of playing at home. The real-valued parameters 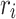 and
and 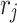 are the strength parameters of the home team i and away team j, and they are estimated by means of weighted maximum likelihood. The weights are chosen such that more importance is given to more recent matches. These estimated strength parameters are then included as a new covariate to the final model for predicting scores. As shown in Groll et al.18,19, this approach helps reduce the RMSE and allows even outperforming the bookmakers, which are a golden standard in sports prediction. This hybrid approach clearly falls in the category of SEL 3, and the authors also showed that the SEL 3 variables have the highest variable importance in their Random Forest model. Their approach has inspired the handball prediction model of Felice et al.5, which we have extensively discussed already.
are the strength parameters of the home team i and away team j, and they are estimated by means of weighted maximum likelihood. The weights are chosen such that more importance is given to more recent matches. These estimated strength parameters are then included as a new covariate to the final model for predicting scores. As shown in Groll et al.18,19, this approach helps reduce the RMSE and allows even outperforming the bookmakers, which are a golden standard in sports prediction. This hybrid approach clearly falls in the category of SEL 3, and the authors also showed that the SEL 3 variables have the highest variable importance in their Random Forest model. Their approach has inspired the handball prediction model of Felice et al.5, which we have extensively discussed already.
Computer vision
To analyze and classify images, Xuan et al.20 build a data set only composed of moment features to determine whether an image contains a hidden message in a picture or not. The moments are derived from the wavelet subbands of an image to represent the color histogram of a picture. These extracted color distributions help create features (by means of moments) that are important covariates sensitive to the change of colors and help improve the detection of hidden messages. This approach in computer vision falls under the umbrella of SEL 2. Other contributions also extract moments from images21 or temporal signals22 for classification purposes.
Natural language processing
In the field of text classification and analysis, the main challenge consists in capturing information carried by the word tokens. Some techniques consist in counting characters in a text to create new features for the data set23,24, which is part of SEL 2. A more advanced approach of counting words, which however still falls under SEL 2, is the Term Frequency-Inverse Document Frequency (TF-IDF) technique25, which weights the counts by the frequency of the words appearing in a corpus, thus representing the importance of a word. Another popular approach to deal with textual inputs is Word2Vec26. This semantic-based technique uses neural networks with embeddings to produce numeric representation of words in a high-dimensional vector space. The trained model helps compare words with the vector of semantically similar words. At first sight, Word2Vec does not appear to be part of SEL 3 as it is a complex machine learning feature extraction method, however very recently Dey et al.27 showed that, under a copula-based statistical model for text data, Word2Vec can be interpreted as a statistical estimation method for estimating the point-wise mutual information, hence qualifying it as part of SEL 3.
Lilleberg et al.28 use a combination of TF-IDF and Word2Vec to classify text into defined sentiment categories. In our framework, their approach can be perceived as a double enhancement, as an SEL 2 technique is applied on SEL 3 type features.
A unifying framework
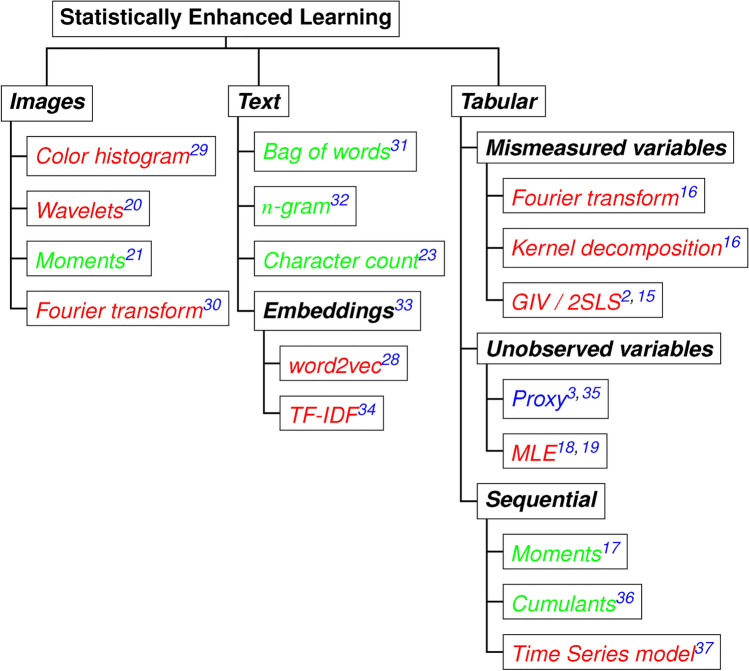
As these examples show, our proposed Statistically Enhanced Learning is a general framework that gives a structure to hitherto distinct approaches. For illustrative purpose, we summarize them in the diagram from Fig. 4.
Fig. 4.
A list of Statistically Enhanced Learning methods by type of data. Each method can be assigned one level of SEL which we represent by a color. In blue are SEL 1 - Proxies, in green we represent SEL 2 - Descriptive statistics and in red SEL 3 - Advanced modeling features.
Somewhat related to SEL is the recently proposed Probabilistic Random Forest38, which sets itself in the field of mismeasured variables. It is an adaptation of Breiman’s Random Forest14 to account for the noise of measured features. It considers quadruplets of the form 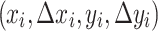 instead of the usual pair
instead of the usual pair 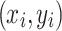 , where
, where 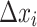 (resp.,
(resp., 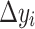 ) represents the uncertainty when measuring
) represents the uncertainty when measuring 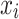 (resp.,
(resp., 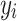 ). In particular, the authors assume that each observed value is drawn from some normal distribution where
). In particular, the authors assume that each observed value is drawn from some normal distribution where 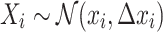 , so the additional quantity
, so the additional quantity 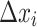 is added to the model and can be considered as a statistically estimated quantity. Indeed, in fields such as astronomy, data often come from multiple sources (e.g., satellites) where the same observation is measured by different instruments. The measure then contains uncertainty. Not only did the authors include this additional source of information, but they adapted the Random Forest logic to account for this uncertainty. The split from a node in a tree depends on this quantity
is added to the model and can be considered as a statistically estimated quantity. Indeed, in fields such as astronomy, data often come from multiple sources (e.g., satellites) where the same observation is measured by different instruments. The measure then contains uncertainty. Not only did the authors include this additional source of information, but they adapted the Random Forest logic to account for this uncertainty. The split from a node in a tree depends on this quantity 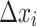 and is no longer a boolean true or false. This gives the model probabilistic considerations that improve its performance when uncertainty in measurements increases, but also allows deriving probability distributions of the target.
and is no longer a boolean true or false. This gives the model probabilistic considerations that improve its performance when uncertainty in measurements increases, but also allows deriving probability distributions of the target.
Applications
So far we have defined Statistically Enhanced Learning, presented its detailed structure, contextualized it within the realm of Data Science and Artificial Intelligence, and showed how existing approaches from the literature are embraced by SEL. Next, we will demonstrate the learning performance enhancement of SEL by means of various examples, starting with synthetic data.
Benchmarking with simulated data
By means of Monte Carlo simulations, we will compare the performance of ML models with SEL covariates versus regular ML models. For our simulations, we consider 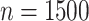 observations and p predictors, whose values are simulated from a Gaussian distribution. Before computing the response variable, we generate some underlying process
observations and p predictors, whose values are simulated from a Gaussian distribution. Before computing the response variable, we generate some underlying process 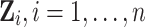 of length
of length 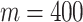 for each of the n individuals. This process follows a Cauchy distribution whose parameter
for each of the n individuals. This process follows a Cauchy distribution whose parameter 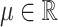 (the location parameter) will directly constitute a variable in the data set. Formally, for an individual i, the regression function writes
(the location parameter) will directly constitute a variable in the data set. Formally, for an individual i, the regression function writes
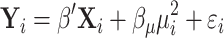 |
1 |
where 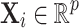 is the p-dimensional vector of observed covariates,
is the p-dimensional vector of observed covariates,  is the residual term,
is the residual term, 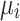 is the location parameter of the underlying Cauchy process
is the location parameter of the underlying Cauchy process 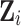 and
and 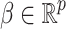 and
and 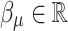 are the parameters to be learnt/estimated. We assume that we cannot observe the parameter
are the parameters to be learnt/estimated. We assume that we cannot observe the parameter 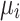 but only the underlying process
but only the underlying process 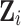 .
.
To learn the regression function (1) from data, we prepare three models using XGBoost39. A first baseline model considers that we can only observe the matrix of p covariates 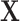 . A second model – that we denote “SEL 2” – uses the underlying process
. A second model – that we denote “SEL 2” – uses the underlying process 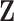 and computes the empirical mean, so that for each individual i we have
and computes the empirical mean, so that for each individual i we have 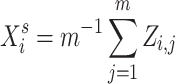 . A last model – denoted “SEL 3” – estimates the parameter of the Cauchy distribution via maximum likelihood estimation (we index the resulting estimator with MLE) from the underlying process
. A last model – denoted “SEL 3” – estimates the parameter of the Cauchy distribution via maximum likelihood estimation (we index the resulting estimator with MLE) from the underlying process 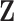 . We then have
. We then have 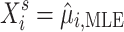 . Since we consider that we do not know the form of the actual variable in the model, we input the estimated parameter
. Since we consider that we do not know the form of the actual variable in the model, we input the estimated parameter 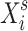 with no further transformation as an additional variable into the XGBoost algorithm.
with no further transformation as an additional variable into the XGBoost algorithm.
For replicability purposes, the full details on the simulations and data generation can be found in the repository referred in the Code availability Section.
We report in Fig. 5 the ratio of Root Mean Squared Error (RMSE) for the baseline model versus the SEL approaches as a function of the number of variables p. Simulations are run 10,000 times to derive values and credible intervals.
Fig. 5.
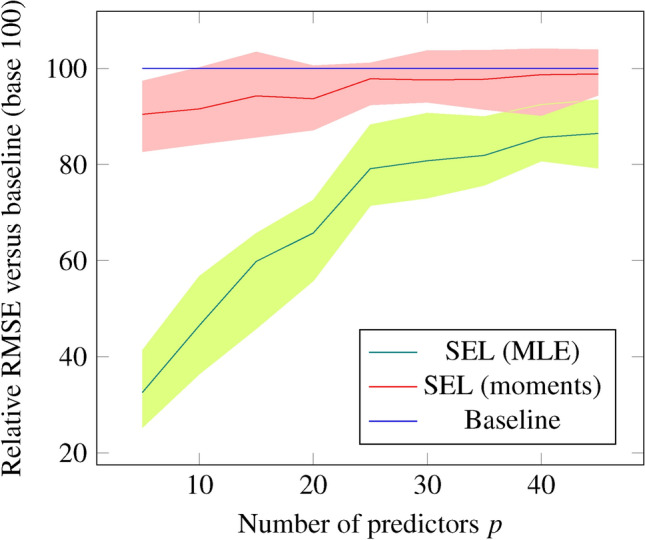
Comparison of the XGBoost model on the simulation test set with and without SEL. The baseline RMSE (set to base 100) assumes that the model does not have the variable 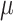 from Eq. (2), which is not observable. We use SEL to estimate the missing covariate via moments (SEL 2) and Maximum Likelihood Estimation (SEL 3). The ratio
from Eq. (2), which is not observable. We use SEL to estimate the missing covariate via moments (SEL 2) and Maximum Likelihood Estimation (SEL 3). The ratio 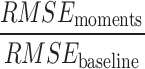 and
and 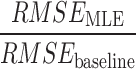 , evaluated on the simulation test set for different number of predictors p, indicates how much SEL helps improve the performance of the model (the lower the ratio of RMSE the better). SEL significantly helps reduce the RMSE when the number of total covariates p is relatively low. The RMSE of the SEL model converges towards the baseline as p increases, suggesting that the information brought by the SEL covariate gets diluted within the overall model.
, evaluated on the simulation test set for different number of predictors p, indicates how much SEL helps improve the performance of the model (the lower the ratio of RMSE the better). SEL significantly helps reduce the RMSE when the number of total covariates p is relatively low. The RMSE of the SEL model converges towards the baseline as p increases, suggesting that the information brought by the SEL covariate gets diluted within the overall model.
We can observe that the performance of the SEL models tends to be consistently better than the baseline approach, in particular when only few observable variables are present in the model. This suggests that the relative importance of the SEL features is quite high compared to the other covariates. We also analyzed the performance of the XGBoost model with the SEL 3 variable for one iteration with 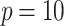 . The formula used to generate our data in this case is defined by
. The formula used to generate our data in this case is defined by
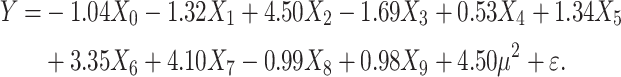 |
2 |
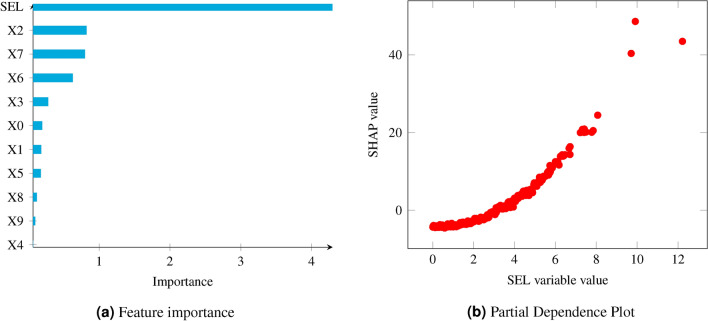
When analyzing the feature importance of the model using TreeSHAP40,41, we can observe that the estimated parameter 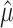 (denoted “SEL” in Fig. 6a) comes as the most important variable of the model. Other features are as important as their weight from the formula defined in Eq. (2).
(denoted “SEL” in Fig. 6a) comes as the most important variable of the model. Other features are as important as their weight from the formula defined in Eq. (2).
Fig. 6.
Analysis of the XGBoost model with TreeSHAP on the simulation test set for the SEL model with 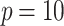 variables. (a) shows that the SEL covariate is considered, by far, to be the most important covariate in the model. The order of the other covariates remains the same when we train the model without our SEL variable (i.e. considered as not available). The Partial Dependence Plot in (b) depicts the relationship learnt by the model between the target variable Y and the SEL variable. We can see that it recovers the quadratic relationship between
variables. (a) shows that the SEL covariate is considered, by far, to be the most important covariate in the model. The order of the other covariates remains the same when we train the model without our SEL variable (i.e. considered as not available). The Partial Dependence Plot in (b) depicts the relationship learnt by the model between the target variable Y and the SEL variable. We can see that it recovers the quadratic relationship between 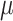 and Y as defined in Eq. (2).
and Y as defined in Eq. (2).
Furthermore, we can also see in Fig. 6b that the model is able to correctly learn the quadratic relation between the SEL variable 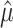 and the target
and the target 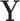 . Our nonlinear model can learn the correct relationship between the SEL variable and the target, which highlights its predominant importance in the model.
. Our nonlinear model can learn the correct relationship between the SEL variable and the target, which highlights its predominant importance in the model.
Application to image data
In order to show the benefit of the SEL methodology on a large spectrum of use cases, we apply it to computer vision data sets. We use three common data sets for model benchmarking. The first one, the MNIST data set42, is composed of 60,000 images of hand written digits from 0 to 9. The data set is widely used in machine learning and served as a set for comparing human performance versus machines in reading handwritten digits. The second one, the Fashion-MNIST43 data set, is a derivative of the original MNIST data with clothes images. It is also composed of 10 categories of images from T-Shirts, trousers to bags and boots. The third data set we use is CIFAR-1044. This database is composed of 60,000 colored images of animals and vehicles. It consists of 10 categories ranging from dog, horse to airplane or truck.
To evaluate our methodology on the aforementioned data bases, we use the same deep learning architecture on the three data sets. We use the VGG architecture45, which consists of stacking double convolutional layers (stacking two layers of 2-dimensional convolutions with max-pooling) to process the image before feeding fully connected layers before the final classification. This Convolutional Neural Network (CNN) architecture is widely used in computer vision and we will refer to it as the regular approach. For the SEL approach, we use the same architecture but add more variables on top of the convolutional layers. For each of our three data sets, we extract the distribution of colors on the images29. The MNIST and Fashion-MNIST data being in black and white, the color histogram will correspond to the gray intensity. The CIFAR-10 being in color, we will extract three histograms from the RGB (red, green and blue) representation of the images. An illustration of a color histogram for a colored image can be found in Fig. 7. From the histogram, we then compute the first four moments (mean, standard deviation, skewness and kurtosis) that will correspond to our SEL 2 features to add to the model.
Fig. 7.
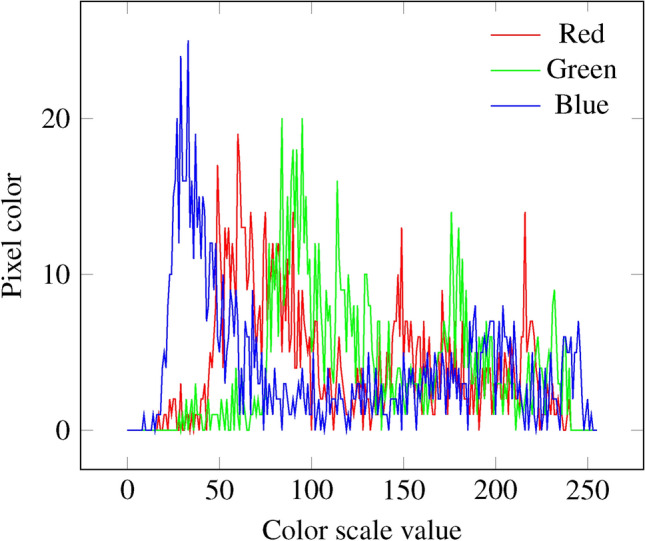
Example of the color histogram of the picture of a horse in the CIFAR-10 dataset. The curves represent the density of each color on the picture.
Our deep learning VGG architecture is only augmented with fully connected layers in parallel of the CNN to ingest the information from the SEL covariates. If we were to compare the regular and SEL models, we can consider the regular architecture as a constrained model of our SEL, where weights for the fully connected layers to learning from the moment variables are set to zero.
We report the classification performance of both methodologies on our different data sets in Table 1. We observe that the SEL features consistently help the model performance. Although the accuracy uplift can be modest, such a gain can sometimes be crucial in highly regulated sectors (such as financial institutions, security industry, etc.), where the performance of a model needs to be as high as possible and not acceptable below certain thresholds. Note that our goal in this exercise is not to reach the least error rate on these data sets (some literature already focuses on this objective by using fine-tuned state-of-the-art model architectures). Our aim is rather to illustrate that data augmentation via SEL is beneficial to any model, even for a fixed architecture.
Table 1.
Comparison of model classification accuracy for regular CNN architecture versus SEL augmented model.
| Dataset | Regular | SEL |
|---|---|---|
| MNIST | 99.01% | 99.05% |
| Fashion | 90.57% | 91.17% |
| CIFAR-10 | 69.09% | 69.49% |
We can further observe that the modest uplift of performance on the MNIST data set can be explained by an already high performance of the model (99.01% for the regular model). Although one of the goals of the convolutional layers is to recognize the color when analyzing the pixels in the image, having a higher level of information with, for example, moments from the color histogram helps the model eliminate obvious non-candidates more easily. In the case of the CIFAR-10 data set, having the overall color of the image can help understand the context. For instance, images with high representation of blue can hint to airplanes in the sky or boats on the sea. This would help remove candidates such as horses or deer, for which we would expect more green colors.
Adding information about the distribution of the gray color can impact the model performance. The variability of gray on MNIST will mostly represent the size of the digit to recognize and will help the model remove some candidates to help better classify similar digits (e.g. a “1” versus a “7”). Alternatively, high variability in the shades of gray on Fashion-MNIST can highlight numerous colors on the original image. This will hint to either shirt, dress or shoes and remove candidates such as trousers or bag, for instance. Later, the shape will further help the model decide on the final attribute. This high-level summary of the image can then help the model better navigate over the image with some context in memory.
Discussion
Statistically Enhanced Learning (SEL) brings a fresh perspective to the forefront of Machine Learning, emphasizing the often underestimated significance of data preparation. The paper’s exploration of SEL’s three levels, ranging from simple proxies to advanced modeling features, provides a comprehensive framework for extracting meaningful information from data. We have illustrated how SEL works through the concrete example of the handball prediction study of Felice et al.5, which we have revisited here under the light of the SEL framework. This example also sheds light on the huge potential of SEL by showing the very strong increase of performance of machine learning models thanks to the SEL3 feature engineering that led to attack and defense strengths. The increase in power has further been shown on simulated data and, though to a lesser extend, on image data. Through these examples, we could also illustrate that SEL contributes to the interpretability of a model, as the resulting features are easy to interpret (especially when obtained in collaboration with human domain experts, see for instance the attack and defense strengths in handball which thus summarize the information from a large list of past matches played not only by the teams for which we predict a match, but also other teams involved in the competition) or the moments of the color distribution in the image data analysis.
From a practical perspective, Statistically Enhanced Learning is not a new algorithm that can be presented under the form of a generally applicable code. Instead, it indicates how users can improve their models by a novel smart feature engineering, creating new impactful features for unobservable yet important information. This creation of new features from otherwise hard-to-use informtion differentiates SEL from dimensionality reduction techniques such as principal component analysis or autoencoders. Proxies (SEL1) and descriptive statistics (SEL2) are accessible to novices in data analysis; the definition of advanced modeling features (SEL3) is more challenging and requires a thorough thought process, yet they bear the highest promises in terms of improving prediction accuracy. In order to apply SEL to their own work, we recommend the interested reader to start by thinking what information, that is currently not present in their features (e.g., a team’s strength or fatigue) or too big to be directly usable (e.g., the individual ages of players), he/she judges useful, and then reflect whether it can be integrated as proxy, by simple statistical summaries, or by advanced modelling. All examples we encountered so far have strongly benefited from this additional effort. The versatility of SEL may also be perceived as a limitation, as it is not a general code that one can directly apply to a given problem. SEL requires a deep enough understanding of the data and needs to be done on a case-by-case basis. Depending on the chosen SEL level, this statistical feature engineering might also come with a certain computational cost.
Furthermore, the formalization of SEL establishes a bridge between different disciplines like statistics, machine learning, and econometrics. This cross-disciplinary approach sheds light on the diverse applications of SEL, unifying seemingly distinct feature engineering techniques. The paper’s significance lies in providing a formal definition of SEL, offering researchers and practitioners a systematic approach to improving learning performance. By identifying the intersections between Statistics, Enhanced (data processing), and Learning, the paper lays the groundwork for a more nuanced and informed application of SEL across a wide array of learning problems.
Our paper, by the establishment of the new discipline “Statistically Enhanced Learning”, not only contributes to the theoretical understanding of feature engineering but also offers practical insights for improving the performance of learning algorithms. The framework’s versatility and applicability make it a valuable addition to the field, opening avenues for further exploration and application in diverse domains.
Author contributions
F.F. and C.L. wrote the main manuscript text, F.F. and C.L. conceived the experiments, F.F. conducted the experiments, F.F. and C.L. analysed the results. All authors reviewed the manuscript.
Data availibility
The code and software materials have been deposited to the GitHub page at https://github.com/florianfelice/StatisticallyEnhancedLearning.
Declarations
Competing interests
The authors declare no competing interests. This work is not related to Amazon.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Florian Felice and Christophe Ley contributed equally to this work.
References
- 1.Press, G. Cleaning big data: Most time-consuming, least enjoyable data science task, survey says. Forbes15 (2016). Section: Tech.
- 2.Wooldridge, J. M. Introductory Econometrics: A Modern Approach (Cengage Learning, 2015).
- 3.Montgomery, M. R., Gragnolati, M., Burke, K. A. & Paredes, E. Measuring living standards with proxy variables. Demography37, 155–174. 10.2307/2648118 (2000). [PubMed] [Google Scholar]
- 4.Holt, C. C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast.20, 5–10. 10.1016/j.ijforecast.2003.09.015 (2004). [Google Scholar]
- 5.Felice, F. & Ley, C. Predicting handball matches with machine learning and statistically estimated team strengths. J. Sports Anal. (2024).
- 6.Felice, F. Ranking handball teams from statistical strength estimation. Comput. Stat.10.1007/s00180-024-01522-0 (2024). [Google Scholar]
- 7.Granger, C. W. J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica37, 424. 10.2307/1912791 (1969). [Google Scholar]
- 8.Goodfellow, I., Bengio, Y. & Courville, A. Deep learning (MIT Press, 2016). [Google Scholar]
- 9.Hastie, T., Tibshirani, R. & Friedman, J. H. The elements of statistical learning: Data mining, inference, and prediction. Springer Series in Statistics (Springer, 2017), second edn, corrected at 12th printing 2017 edn.
- 10.Ralston, A. Data processing. in Encyclopedia of computer science, 502–504 (John Wiley and Sons Ltd., GBR, 2003).
- 11.Zheng, A. & Casari, A. Feature engineering for machine learning: Principles and techniques for data scientists (“O’Reilly Media, Inc.”, 2018).
- 12.Chakrabarti, S. et al. Data mining curriculum: A proposal (Version 1.0). Intensive working group of ACM SIGKDD curriculum committee 140, 1–10 (2006).
- 13.Ley, C. et al. Machine learning and conventional statistics: Making sense of the differences. Knee Surg. Sports Traumatol. Arthrosc.30, 753–757. 10.1007/s00167-022-06896-6 (2022). [DOI] [PubMed] [Google Scholar]
- 14.Breiman, L. Random forests. Mach. Learn.45, 5–32. 10.1023/A:1010933404324 (2001). [Google Scholar]
- 15.Chesher, A. & Rosen, A. M. Generalized instrumental variable models, methods, and applications. in Handbook of Econometrics7, 1–110. 10.1016/bs.hoe.2019.11.001 (Elsevier, 2020).
- 16.Schennach, S. M. Mismeasured and unobserved variables. in Handbook of Econometrics7, 487–565. 10.1016/bs.hoe.2020.07.001 (Elsevier, 2020).
- 17.Lin, Y. -J., Wu, P. -W., Hsu, C. -H., Tu, I. -P. & Liao, S. -W. An evaluation of bitcoin address classification based on transaction history summarization. Tech. Rep. arXiv:1903.07994. 10.48550/arXiv.1903.07994 (2019).
- 18.Groll, A., Ley, C., Schauberger, G. & Van Eetvelde, H. A hybrid random forest to predict soccer matches in international tournaments. J. Quant. Anal. Sports15, 271–287. 10.1515/jqas-2018-0060 (2019). [Google Scholar]
- 19.Groll, A. et al. Hybrid machine learning forecasts for the UEFA EURO 2020, 10.48550/arXiv.2106.05799 (2021). ArXiv:2106.05799 [cs, stat].
- 20.Xuan, G. et al. Steganalysis based on multiple features formed by statistical moments of wavelet characteristic functions. in Barni, M., Herrera-Joancomartí, J., Katzenbeisser, S. & Pérez-González, F. (eds) Information Hiding, 262–277, 10.1007/1155885920 (Springer, 2005).
- 21.Soranamageswari, M. & Meena, C. Statistical feature extraction for classification of image spam using artificial neural networks. in 2010 Second International Conference on Machine Learning and Computing, 101–105, 10.1109/ICMLC.2010.72 (2010).
- 22.Borith, T., Bakhit, S., Nasridinov, A. & Yoo, K.-H. Prediction of machine inactivation status using statistical feature extraction and machine learning. Appl. Sci.10, 7413. 10.3390/app10217413 (2020). [Google Scholar]
- 23.Senthil Murugan, N. & Usha Devi, G. Detecting streaming of twitter spam using hybrid method. Wireless Pers. Commun.103, 1353–1374. 10.1007/s11277-018-5513-z (2018). [Google Scholar]
- 24.Søgaard, A. et al. Inverted indexing for cross-lingual NLP. in Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers) 1713–1722 (2015).
- 25.Ramos, J. Using TF-IDF to determine word relevance in document queries. in Proceedings of the First Instructional Conference on Machine Learning242, 29–48 (2003).
- 26.Mikolov, T., Chen, K., Corrado, G. & Dean, J. Efficient estimation of word representations in vector space. ArXiv:1301.3781 [cs] (2013).
- 27.Dey, N., Singer, M., Williams, J. P. & Sengupta, S. Word embeddings as statistical estimators. ArXiv:2301.06710 [stat] (2023).
- 28.Lilleberg, J., Zhu, Y. & Zhang, Y. Support vector machines and Word2vec for text classification with semantic features. in 2015 IEEE 14th International Conference on Cognitive Informatics & Cognitive Computing (ICCI*CC), 136–140, 10.1109/ICCI-CC.2015.7259377 (2015).
- 29.Novak, C. & Shafer, S. Anatomy of a color histogram. in Proceedings 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 599–605, 10.1109/CVPR.1992.223129 (IEEE Comput. Soc. Press, Champaign, IL, USA, 1992).
- 30.Li, W., Zhang, D. & Xu, Z. Palmprint identification by Fourier transform. Int. J. Pattern Recognit Artif Intell.16, 417–432. 10.1142/S0218001402001757 (2002). [Google Scholar]
- 31.Tsai, C.-F. Bag-of-words representation in image annotation: A review. ISRN Artif. Intell.1–19, 2012. 10.5402/2012/376804 (2012). [Google Scholar]
- 32.Ahuja, R., Chug, A., Kohli, S., Gupta, S. & Ahuja, P. The impact of features extraction on the sentiment analysis. Proc. Comput. Sci.152, 341–348. 10.1016/j.procs.2019.05.008 (2019). [Google Scholar]
- 33.Selva Birunda, S. & Kanniga Devi, R. A review on word embedding techniques for text classification. in Raj, J. S., Iliyasu, A. M., Bestak, R. & Baig, Z. A. (eds.) Innovative data communication technologies and application, vol. 59, 267–281, 10.1007/978-981-15-9651-323 (Springer, 2021). Series Title: Lecture Notes on Data Engineering and Communications Technologies.
- 34.Aizawa, A. An information-theoretic perspective of TF–IDF measures. Inf. Proc. Manag.39, 45–65. 10.1016/S0306-4573(02)00021-3 (2003). [Google Scholar]
- 35.Wooldridge, J. M. On estimating firm-level production functions using proxy variables to control for unobservables. Econ. Lett.104, 112–114. 10.1016/j.econlet.2009.04.026 (2009). [Google Scholar]
- 36.Abu-Romoh, M., Aboutaleb, A. & Rezki, Z. Automatic modulation classification using moments and likelihood maximization. IEEE Commun. Lett.22, 938–941. 10.1109/LCOMM.2018.2806489 (2018). [Google Scholar]
- 37.Briand, J., Deguire, S., Gaudet, S. & Bieuzen, F. Monitoring variables influence on random forest models to forecast injuries in short-track speed skating. Front. Sports Active Living4, 896828. 10.3389/fspor.2022.896828 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Reis, I., Baron, D. & Shahaf, S. Probabilistic random forest: A machine learning algorithm for noisy data sets. Astron. J.157, 16. 10.3847/1538-3881/aaf101 (2018). [Google Scholar]
- 39.Chen, T. & Guestrin, C. XGBoost: A scalable tree boosting system. in 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, 785–794, 10.1145/2939672.2939785 (Association for Computing Machinery, 2016).
- 40.Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. in Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, 4768–4777 (Curran Associates Inc., Red Hook, 2017).
- 41.Lundberg, S. M. et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell.2, 56–67. 10.1038/s42256-019-0138-9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.LeCun, Y., Cortes, C. & Burges, C. The MNIST database of handwritten digits. (1998).
- 43.Xiao, H., Rasul, K. & Vollgraf, R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. ArXiv:1708.07747 [cs, stat] (2017).
- 44.Krizhevsky, A. & Hinton, G. Learning multiple layers of features from tiny images (2009).
- 45.Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. ArXiv:1409.1556 [cs] (2015).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The code and software materials have been deposited to the GitHub page at https://github.com/florianfelice/StatisticallyEnhancedLearning.