Advances in modeling cellular state dynamics: integrating omics data and predictive techniques

ABSTRACT

Dynamic modeling of cellular states has emerged as a pivotal approach for understanding complex biological processes such as cell differentiation, disease progression, and tissue development. This review provides a comprehensive overview of current approaches for modeling cellular state dynamics, focusing on techniques ranging from dynamic or static biomolecular network models to deep learning models. We highlight how these approaches integrated with various omics data such as transcriptomics, and single-cell RNA sequencing could be used to capture and predict cellular behavior and transitions. We also discuss applications of these modeling approaches in predicting gene knockout effects, designing targeted interventions, and simulating organ development. This review emphasizes the importance of selecting appropriate modeling strategies based on scalability and resolution requirements, which vary according to the complexity and size of biological systems under study. By evaluating strengths, limitations, and recent advancements of these methodologies, we aim to guide future research in developing more robust and interpretable models for understanding and manipulating cellular state dynamics in various biological contexts, ultimately advancing therapeutic strategies and precision medicine.

Introduction

Manipulation and intervening cell phenotypes have long been a central objective in the field of biology primarily due to their potential in advancing therapeutic strategies and understanding disease mechanisms. Phenotypic changes in cells, such as alterations in morphology, proliferation rates, and gene expression profiles, are often driven by external stimuli or genetic modifications, providing crucial insights into cellular function and dysfunction. The capability to engineer and control cell phenotypes has led to significant advancements in areas such as regenerative medicine, cancer treatment, and immune therapies (Kim et al. 2024a). For instance, reprogramming of somatic cells to induced pluripotent stem cells (Takahashi and Yamanaka 2006) has demonstrated a profound impact of modulating cellular states for therapeutic purposes. More recently, advancements in CRISPR-Cas9 gene-editing technology have further facilitated precise interventions at the molecular level, allowing for targeted changes of cell phenotypes and paving the way for personalized medicine approaches (Doudna and Charpentier 2014). These breakthroughs underscore the pivotal role of phenotype manipulation in both fundamental biology and translational medicine.

Strategies for researching the intervention of cell phenotypes have evolved significantly, transitioning from traditional experimental trial-and-error approaches that rely on isolated findings to more sophisticated methods grounded in a comprehensive understanding of biomolecular mechanisms. Initially, much of cellular biology research has focused on altering phenotypes based on single-gene experiments or individual pathway perturbations, often resulting in limited predictability and inconsistent outcomes. However, with the advent of high-throughput technologies and omics-based data such as genomics, transcriptomics, proteomics, and metabolomics, researchers can now map complex cellular networks and identify key regulatory components at the systems biology level. This shift enables a more holistic approach to phenotype modulation, where interventions are designed based on the integration of large-scale data to pinpoint molecular drivers of cellular behavior (Barabasi et al. 2011; Aebersold and Mann 2016). As a result, researchers can now alter components within these identified mechanisms with a higher accuracy, transforming the field from empirical experimentation to predictive and mechanism-based interventions that are key to advancing personalized medicine and regenerative therapies.

Recent studies have increasingly focused on intervening cell phenotypes through systematic modeling of cellular state dynamics, leveraging omics data to capture the complex and dynamic nature of cellular processes. These models utilize large-scale datasets of various omics profiles, allowing researchers to construct computational frameworks that can simulate cellular responses to various stimuli or perturbations. By analyzing these models, it becomes possible to predict phenotypic outcomes based on molecular alterations and to identify key regulatory genes for targeted interventions (Trapnell et al. 2014). Such approaches have opened new avenues for precision medicine, tissue engineering, and drug discovery, offering the potential to manipulate cell states with unprecedented specificity. However, it is crucial for the scientific community to assess these emerging methodologies critically and evaluate their advantages – such as the ability to capture dynamic interactions and predict long-term phenotypic changes – against their limitations such as the complexity of model validation and the potential for overfitting due to noisy or incomplete data. Comprehensive review of these recent approaches will help us refine their applications and ensure that models are robust and generalizable, ultimately advancing the field of cellular phenotypic control. To assist readers in navigating the key technical terms and concepts used throughout this review, a glossary of definitions has been included as Table 1.

Table 1.

Glossary of key concepts.

Attractors in network models	Stable states of a system in dynamic models, representing phenotypes or biological processes like differentiation or apoptosis.
Boolean networks (BN)	A mathematical model where biological systems are represented as networks of genes or proteins, each with binary states (active or inactive), used to study state transitions.
Cell reprogramming	The process of converting one cell type into another, such as somatic cells into induced pluripotent stem cells, often for therapeutic applications.
Cellular state dynamics	The study of changes in cellular states (phenotypes) over time, often in response to internal genetic regulation or external stimuli. Used to understand processes such as cell differentiation, disease progression, and cellular reprogramming.
Critical state transitions	Key points where cellular states shift dramatically, often associated with the onset of diseases or major phenotypic changes.
Deep learning in biology	Machine learning methods using neural networks to analyze large-scale biological data, predict cellular behavior, and simulate responses to perturbations.
Dynamic vs. Statis models Dynamic models Static models	Represent temporal changes in cellular states, capturing transitions and interactions over time. Represent regulatory interactions as fixed snapshots, useful for identifying critical genes or pathways
Gene regulatory networks (GRNs)	Networks depicting regulatory interactions among genes, essential for understanding the control of cellular functions and responses.
Genome-scale models	Computational models that incorporate data from entire genomes to simulate cellular metabolism, gene regulation, or interaction networks.
Omics data	Comprehensive datasets that include information about various molecular layers of cells, such as genomics (DNA sequences), transcriptomics (gene expression), proteomics (protein expression), and metabolomics (metabolite profiles).
Pathway activity inference	Predicting the activity of biological pathways based on gene or protein expression data to understand cellular responses or identify intervention points.
Perturbation	Any alteration or intervention in a biological system, such as gene knockouts, drug treatments, or environmental changes, used to study system responses and predict outcomes.
Petri-net	A graphical and mathematical modeling tool used to represent concurrent processes in biological systems, incorporating both qualitative and quantitative data to simulate interactions and dynamics of complex networks.
Probabilistic Boolean networks (PBN)	An extension of Boolean networks incorporating probabilistic rules to account for biological variability and uncertainty in regulatory mechanisms.
Single-cell RNA sequencing (scRNA-seq)	A technique for analyzing gene expression at the single-cell level, offering insights into cellular heterogeneity and dynamic state transitions.
State space	A conceptual representation of all possible cellular states and the transitions between them, often visualized as a landscape where valleys represent stable states (attractors).
Time-series omics data	Sequentially collected data that captures temporal changes in omics profiles, allowing for the modeling of dynamic biological processes.

Models of cellular state dynamics

Concept of cellular states and cellular state dynamics

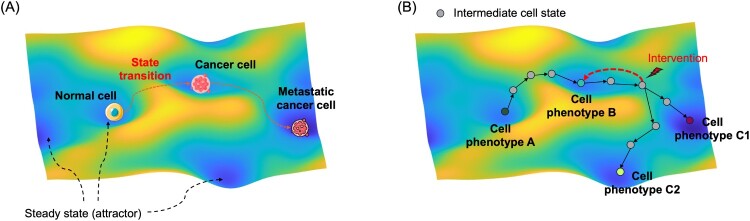
The concept of representing cell phenotypes as discrete states within a dynamic landscape of cellular state transitions offers a powerful framework for understanding cellular behavior and its regulation. In this concept, each cell phenotype characterized by a unique combination of gene expression, protein activity, and metabolic functions can be considered a steady state within a cellular state space (Figure 1(A)). Transitions between phenotypes such as those observed during differentiation, reprogramming, and disease progression are viewed as shifts in cellular state dynamics governed by both intrinsic molecular regulatory networks and extrinsic environmental cues (Moris et al. 2016; Jeong et al. 2023). These transitions often occur along defined paths within the cellular state space, where cells traverse through intermediate or unsteady states before reaching a new phenotype. By modeling cell phenotypes as cellular states and their transitions as dynamic processes, it becomes possible to predict cellular responses to perturbations, identify critical regulatory factors, and even manipulate cell fate (Figure 1(B)). This framework has been particularly useful for understanding complex biological processes such as cancer metastasis and stem cell differentiation, where multiple phenotypic states and transitions are involved (Gupta et al. 2011). As such, modeling the dynamics of cellular states provides a unifying approach to studying phenotypic changes of cells and mechanisms underlying them. Many different modeling approaches have been used. Representative strategies of modeling cellular state dynamics will be covered in the following subsections.

Figure 1.

Cellular state space and state dynamics. (A) An example of representing different cell phenotypes as steady states within the landscape of cellular state. Bright-colored space represents the area of unstable states, and the dark colored space represents the area of stable steady states. (B) Concept of cellular state transitions between steady states of cell phenotypes through unstable intermediate states. Gray-colored states are intermediate states that will converge to nearby steady states, where several steady states of different phenotypes can be present. The approach of controlling cell state dynamics is applying intervention on the cell state space and altering the trajectory of cell state changes.

Modeling dynamics of cellular states using boolean and probabilistic boolean networks

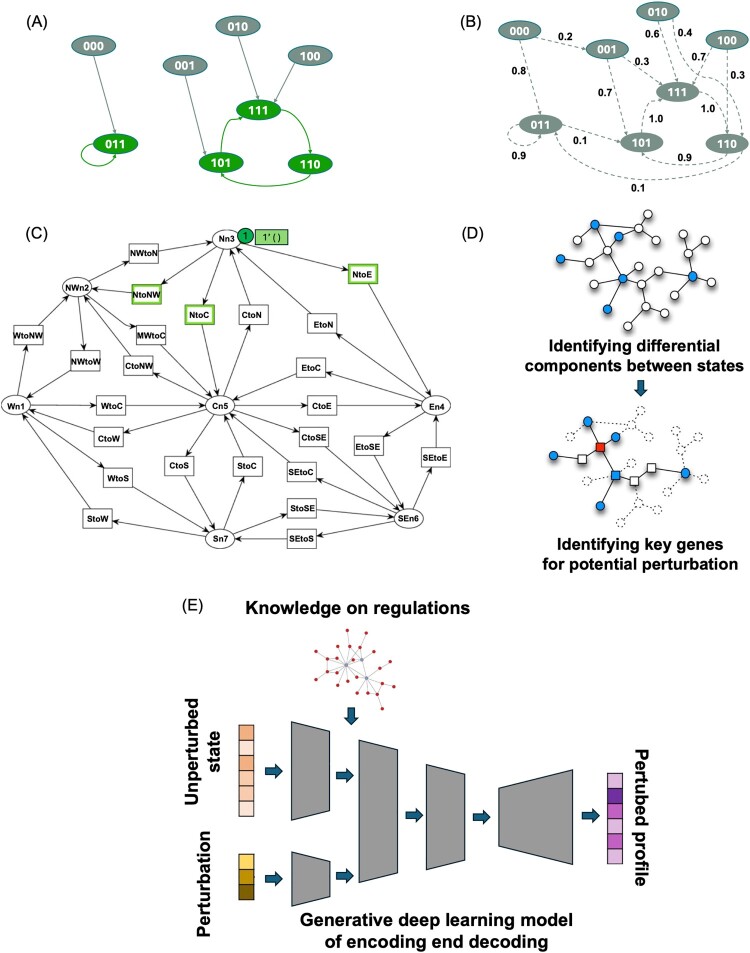
A Boolean network (BN) is a discrete mathematical model used to represent regulatory interactions between components of biological systems, such as genes or proteins, where each component is assigned a binary state (0 or 1, representing inactive or active, respectively) (Figure 2(A)). The state of each component at any time is determined by a Boolean function of the states of its regulators at the previous time point. These Boolean functions define logical rules governing the system's behavior. Over time, the model transitions through different cellular states and forms a trajectory in a cellular state space. The state dynamics of a BN describes how the model evolves from an initial cellular state, following its update rules at each discrete time step. These dynamics eventually reach a steady state or an attractor, which can be a fixed point where the cell settles into a single state or a cyclic attractor where the cell oscillates between a set of states. Attractors correspond to the long-term behavior of a biological system and often represent stable cellular phenotypes or biological processes such as cell differentiation and apoptosis. Many studies (Barman and Kwon 2017; Munoz et al. 2018; Liu et al. 2021; Trinh and Kwon 2021; Choi et al. 2022; Liu et al. 2022; Argyris et al. 2023; Benes et al. 2023; Kim et al. 2023; Singh et al. 2023; Kim et al. 2024b) have utilized BN to model the dynamics of cellular states. For instance, BN has been used to study gene regulatory networks (GRNs), focusing on steady-state gene expression data (Trinh and Kwon 2021). Similarly, fibroblast-like synoviocytes in rheumatoid arthritis have been simulated (Singh et al. 2023), predicting drug responses based on steady state of cell dynamics. BN has many applications for modeling cellular state dynamics, demonstrating the utility of BN in capturing the complex regulatory behavior of biological systems through dynamic and steady-state properties of cells.

Figure 2.

Popular models for studying dynamics of cellular states. (A) An example of Boolean network of three genes. Each state is represented as a node with three 0 (inactive) or 1 (active) as values. Each state will go to another state in the next time step in a deterministic way. Green states are attractor (steady) states and gray states are unstable intermediate states. (B) An example of Probabilistic Boolean network of three genes. State transition occurs probabilistically based on the specified probability. (C) An example of a Petri-net model. Circles represent places and rectangles represent transitions. (D) Estimating key intervention points from static regulatory models. Static regulatory model is built from data of multiple cellular states. Regulatory components that are different between states are identified (blue-colored nodes). Based on identified regulatory components of difference, key biological components or genes (red-colored nodes) of high impact on the difference are identified as potential interventions that can drive differences between states. (E) Deep learning approach of estimating changed cellular state (omics profile) based on a current state and perturbation information. Prior knowledge on genetic regulations is often integrated in the process of learning and data embedding. Generative models can be used to construct a new profile of cellular state after perturbation.

A Probabilistic Boolean network (PBN) is a mathematical model used to represent the dynamics by extending the traditional BN framework to incorporate stochastic elements (Figure 2(B)). In a PBN, the state of each gene is represented as a binary variable (0 or 1), like the representation in BN. However, the state of a gene evolves over time based on a set of probabilistically selected Boolean functions instead of a single Boolean function. This probabilistic selection accounts for inherent biological uncertainty and noise in gene expression. The state of the cell evolves according to the probabilistically chosen Boolean functions, generating a stochastic dynamic system of cellular state transitions. Over time, the cell may reach a steady state, where distribution of cellular states becomes stationary. Several studies (Tercan et al. 2022; Šliogeris et al. 2023) have applied PBNs to model cellular dynamics in cancer and transdifferentiation, respectively, emphasizing the importance of identifying key attractors in predicting cellular outcomes. Additionally, methods have been proposed for designing PBNs that can achieve desired cellular steady-state distributions (Kobayashi and Hiraishi 2017), offering insights into how interventions in gene networks can control cell states. These works demonstrate the utility of PBNs in modeling the probabilistic and dynamic nature of cellular state regulation.

These BN and PBN modeling are widely used approaches to studying dynamics of cellular states by representing mechanisms of dynamics as discrete systems. One of the key advantages of both BN and PBN modeling is their ability to simulate cell state transitions over time, enabling the discovery of steady states, some of which may represent unknown or unobserved cell phenotypes. This is particularly important for identifying hidden cellular behaviors or potential disease states. Additionally, they allow for the simulation of dynamic responses to interventions, such as activating or inhibiting specific genes and altering regulatory interactions, providing a powerful framework to explore therapeutic strategies in silico. Despite these advantages, both BN and PBN approaches face limitations in scalability because the size of the cellular state space grows exponentially with the number of genes, making it computationally challenging to model large biological mechanisms. This restricts their applicability to small – or medium-scale networks, particularly when high-resolution cellular state transition dynamics are required. Furthermore, although simplification of gene expression into binary states is practical, it might overlook finer gradations of gene activity that play critical roles in complex cellular processes.

While BNs and PBNs provide discrete frameworks for modeling cellular dynamics, ordinary differential equations (ODEs) are widely used to model the continuous evolution of molecular states. For example, ODE-based models have been used to capture dynamic interactions in signaling pathways, such as the MAPK signaling cascade, where time-resolved molecular concentrations are predicted under different perturbations (Kholodenko 2000). Another study applied ODEs to model the Wnt signaling pathway, providing insights into the regulatory mechanisms of stem cell differentiation (Giuraniuc et al. 2022). These approaches highlight the ability of ODEs to offer a detailed, time-dependent understanding of cellular processes, complementing the discrete perspectives of Boolean models.

Modeling cellular state dynamics using petri-net

Petri-net is a mathematical modeling tool widely used for representing and analyzing networks, particularly those involving concurrent processes and complex biochemical interactions (Murata 1989). It consists of places, transitions, and tokens, which represent biological entities (e.g. metabolites or states), reactions, and their current states, respectively (Figure 2(C)). Petri-net’s ability to incorporate both qualitative and quantitative aspects of biological systems make it particularly suited for modeling metabolic pathways, gene regulatory networks, and signaling cascades.

For example, a Petri-net can be used to simulate metabolic flux in systems biology by capturing the dynamic behavior of metabolites and enzymatic reaction over time (Baldan et al. 2010). This approach has been employed in studies of systems-level phenomena such as cellular metabolism under stress conditions and drug interaction effects on signaling pathways. Additionally, the extension of Petri-net to stochastic Petri-nets allows for modeling the inherent randomness in gene expression and molecular interactions, offering insights into noise-driven phenomena in cellular systems (Peter and Peccoud 1998).

One of the strengths of Petri-net is its graphical representation, which provides an intuitive way to visualize complex interactions. Furthermore, Petri-nets can integrate multi-omics data, enabling researchers to model system-wide interactions with high precision. However, challenges such as scalability and the need for accurate parameterization remain key limitations, particularly for large-scale networks.

Predicting cellular states using deep learning

Deep learning, a subset of machine learning, involves using neural networks with multiple layers to learn hierarchical representations of data, enabling models to capture complex patterns and interactions. In biological contexts, deep learning can be enhanced by integrating prior biological knowledge such as genetic interactions and GRNs to inform the learning process. By embedding this knowledge into a deep learning model (Roohani et al. 2024), prediction of multigene perturbation outcomes improves in accuracy, even for gene combinations not previously observed experimentally (Figure 2(E)). Similarly, a deep generative model ca be leveraged to infer effects of gene knockouts on cellular states without the need for physical knockout data (Yang et al. 2023) using variational graph autoencoders to simulate GRNs. These approaches illustrate how deep learning models, when coupled with prior biological knowledge, can predict novel cellular states, enable exploration of unseen genetic perturbations and simulation of complex cellular responses, and advance the field of modeling cellular state dynamics and genetic perturbation prediction.

Predicting cellular state dynamics by analyzing static biomolecular networks

Analyzing static biomolecular network structures has been also a popular approach for predicting effective intervention points that can guide cellular states toward desirable phenotypes (Gao et al. 2014; Sun et al. 2015; Alvarez et al. 2016; Hu et al. 2019; Zhong et al. 2023). This approach involves comparing biomolecular network structures between different cellular states, such as healthy and diseased conditions, to identify critical genes or interactions that might play a pivotal role in driving cell state transitions (Figure 2(D)). By leveraging network-based metrics and control theory, researchers can suggest specific genes or proteins that, when targeted, may modulate the network's behavior and potentially reverse or halt disease progression. For example, an approach has been introduced to detect tipping points in cellular systems by analyzing network entropy changes at a single-sample level (Zhong et al. 2023), revealing early warning signals of critical state transitions in complex diseases. Similarly, a method has been developed for applying network controllability theory to estimate optimal control genes in disease-perturbed networks (Hu et al. 2019), suggesting them as potential targets for combination therapies. These studies exemplify how comparative network analysis can uncover key regulators and synergistic intervention points, offering insights into effective strategies for therapeutic interventions.

Scalability of modeling the dynamics of cellular states

Modeling of cellular state dynamics can be approached through various methodologies, each offering distinct levels of scalability and resolution. State-space models such as BN (discrete state) and ordinary differential equations (continuous state) generally do not have high scalability due to exponential increase of cellular states with a large number of genes, making them suitable for capturing cellular states of small biomolecular mechanisms. Machine learning-based models, particularly deep learning approaches, exhibit flexibility in capturing complex dynamics with varying scalability and resolution. However, they often require large datasets for training. Thus, the choice of modeling approach depends on trade-offs between scalability and resolution, which are determined by specific characteristics and goals of the study.

Modeling the dynamics of cellular states in small scale with high-resolution state information

Traditionally, BN modeling has been widely used to study the dynamics of cellular states at the scale of tens of genes, allowing researchers to capture key regulatory interactions governing cellular processes in a simplified and qualitative manner. This approach is exemplified by many studies (Munoz et al. 2018; Choi et al. 2022; Kim et al. 2023), where BNs have been applied to infer or simulate cellular behavior with manageable computational complexity, focusing on relatively small networks. However, as the complexity of biological systems requires more comprehensive representations, recent advancements have developed strategies to increase the scalability of BN-based modeling to encompass hundreds of genes. These strategies often involve integrating machine learning techniques, optimization algorithms, and more sophisticated data integration methods. For instance, a strategy has been introduced to combine machine learning with BN (Kim et al. 2024b), while a constrained genetic algorithm-based inference method has been developed to handle larger models (Trinh and Kwon 2021). A novel encoding scheme has been proposed for efficient Boolean function representation (Liu et al. 2021), and mutual information-based feature selection has been utilized to scale up the modeling (Barman and Kwon 2017). Additionally, large-scale Boolean models have been constructed by integrating extensive signaling pathways to simulate disease-specific cellular behaviors (Singh et al. 2023). These advancements demonstrate that it is now feasible to model dynamics of cellular states at a larger-scale, enabling more comprehensive simulations of complex cellular systems.

PBNs have been also used to model the dynamics of cellular states due to their ability to incorporate stochasticity and uncertainty inherent in biological systems. However, the scalability of PBNs is often further limited, typically up to tens of genes, because the stochastic nature of the model can lead to a rapid increase in computational complexity with the number of genes. For instance, a PBN inference method has been demonstrated directly from steady-state gene expression data (Šliogeris et al. 2023). However, it could only feasibly model up to a few dozen genes due to exponential growth of cellular state space. To address such limitation, a sampled network approach has been recently introduced (Tercan et al. 2022), which can significantly reduce computational demands, thereby enabling the modeling of cellular state dynamics involving hundreds of genes. This approach marks a promising advancement in applying PBNs to more complex and larger-scale models of cellular state dynamics, expanding the potential of PBNs for capturing intricate biological processes at a broader scale.

Modeling the dynamics of cellular states in large scale

Deep learning-based approaches have demonstrated significant scalability in modeling the dynamics of cellular states particularly due to their ability to handle high-dimensional data and learn complex, non-linear relationships among thousands of genes. These methods leverage advanced deep learning architectures that can integrate large-scale data with gene regulatory networks to model intricate gene interactions. For instance, a graph-based deep learning model has been utilized to infer gene knockout effects using wild-type scRNA-seq data (Yang et al. 2023), effectively capturing regulatory changes across thousands of cells and gene interactions. Similarly, the scalability of deep learning models has been demonstrated (Roohani et al. 2024), which integrate a knowledge graph of gene–gene relationships to predict transcriptional outcomes of both single and multigene perturbations at a scale involving over 1,500 perturbations and 170,000 cells. The scalability of these approaches is rooted in their ability to efficiently encode complex gene relationships and perturbational effects into the model, allowing for simultaneous analysis of thousands of genes and prediction of novel genetic interactions. This scalability is crucial for advancing our understanding of cellular processes and for developing precise genetic interventions.

Static network-based analysis of cellular state changes also offers a scalable approach that can efficiently handle thousands of genes, making it suitable for analyzing large biological systems. This scalability arises from the fact that static networks represent interactions between genes as fixed connections, allowing for the use of well-established algorithms to identify critical genes or pathways without considering the concept of state dynamics. This makes the construction and analysis of static models computationally simpler and more feasible compared to those of dynamic models, which require extensive data to accurately capture temporal changes in cellular states. The Sample-Perturbed Network Entropy (SPNE) method has been introduced for identifying critical transitions in biological systems (Zhong et al. 2023), while a method has been developed to identify optimal control genes in disease-perturbed networks for combination therapy (Hu et al. 2019). Both methods leveraged static network representations to identify critical genes and pathways effectively. However, this approach has limitations compared to dynamic network-based modeling, as it cannot capture temporal or causal relationships inherent in cellular processes, potentially missing transient interactions or regulatory events that occur during cellular state transitions. Thus, while static network analysis is more scalable and easier to implement than dynamic network analysis, it provides a less detailed view of the dynamic changes in cellular states.

Necessary data for modeling cellular state dynamics

Gene expression data of one or more steady states

To model cellular state dynamics, many methods have been tried to capture the dynamics model that can represent one or more observed steady states. Each steady state represents a distinct cellular phenotype. These methods allow for the analysis of cellular state transitions, including shifts between different phenotypes. Such models can help identify critical regulatory pathways and predict cellular responses to perturbations. For instance, several studies (Trinh and Kwon 2021; Šliogeris et al. 2023) have focused on inferring cellular dynamics using data from a single steady state, enabling the reconstruction of PBNs and BNs, respectively, from such limited data. This approach provides insights into underlying regulatory mechanisms of a particular cellular phenotype without requiring data of various cellular states. In contrast, some studies (Tercan et al. 2022; Zhong et al. 2023) have used data from multiple steady states to construct models that can capture the dynamics between different cellular phenotypes. These models provide a more comprehensive understanding of transitions between phenotypes, such as during transdifferentiation and disease progression, by identifying critical states and molecular mechanisms driving these changes.

Single-cell RNA-Seq and multi-omics data

Single-cell RNA-seq (scRNA-seq) provides a high-resolution snapshot of the transcriptomic landscape at the individual cell level, allowing researchers to capture the heterogeneity and dynamic transitions of cellular states. By collecting scRNA-seq data from cells of various types or states, it is possible to construct models that can map the trajectories of cellular differentiation, activation, or reprogramming processes, thereby elucidating dynamic pathways and transitions between distinct cellular states (Huynh-Thu et al. 2010; Lim et al. 2016; Matsumoto and Kiryu 2016; Aibar et al. 2017; Chan et al. 2017; Matsumoto et al. 2017; Specht and Li 2017; Papili Gao et al. 2018; Woodhouse et al. 2018; Moerman et al. 2019; Kartha et al. 2022; Osorio et al. 2022; Fleck et al. 2023; González-Blas C et al. 2023; Kamimoto et al. 2023; Shin and Cho 2023; Wang et al. 2023; Zhang et al. 2023; Lee et al. 2024a). Additionally, scRNA-seq data from perturbed cells, such as those exposed to drugs, genetic modifications, or environmental stressors, can be used to directly model the impact of these perturbations on cellular profiles (Lotfollahi et al. 2019; Osorio et al. 2022; Yang et al. 2023; Roohani et al. 2024). This approach enables the identification of GRNs, pathway alterations, and specific molecular mechanisms that drive cellular responses to perturbations, thus providing insights into how cells adapt or transition under various conditions. By integrating temporal or pseudotime analysis with scRNA-seq data, researchers can further infer the progression and lineage relationships of cellular states, making it a powerful tool for understanding cellular dynamics in development, disease, and response to treatment.

Single-cell multi-omics data, which simultaneously captures transcriptomic, epigenomic, and proteomic layers, also offers unparalleled resolution in understanding cellular state dynamics (Lee et al. 2024b). The inclusion of epigenetic data, such as DNA methylation and histone modifications, provides critical insights into the regulatory mechanisms that govern cellular transitions and fate decisions. For instance, single-cell ATAC-seq combined with RNA-seq has been used to map the chromatin accessibility landscape alongside gene expression profiles, enabling a more comprehensive modeling of stem cell differentiation processes (Buenrostro et al. 2015). Incorporating epigenetic status into multi-omics data for cellular state modeling allows for a deeper understanding of how chromatin structure and regulatory elements influence dynamic cellular behaviors.

Time-series omics data

The modeling of cellular state dynamics using time-series omics data provides an opportunity to capture temporal changes in biological systems, enabling the construction of models that can more accurately reflect the dynamic nature of cellular states over time, rather than relying on static or steady-state profiles. This approach is particularly useful for understanding complex biological processes as it allows for the identification of regulatory relationships and interactions that change in response to different conditions or stimuli. For instance, the effectiveness of using time-series gene expression data has been demonstrated to infer BNs with high accuracy (Liu et al. 2021), thereby reconstructing temporal dynamics of GRNs. Similarly, a method has been employed to infer BNs from time-series data (Barman and Kwon 2017), improving the ability to predict both the structure and dynamics of cellular states. More recently, time-series data has been used to build large-scale dynamic models (Borzou et al. 2023), integrating protein–protein interactions and biochemical reactions to capture genome-wide changes in cellular states over time. A limitation in using time-series data is the difficulty of obtaining time-series profiles over short time periods to accurately capture the changing status of cellular dynamics. Nevertheless, these studies exemplify the utility of time-series data in developing models that represent the evolving nature of cellular states, providing deeper insights into underlying mechanisms of complex biological systems.

Useful omics atlas databases

In addition to individually available omics data, omics atlas databases provide valuable resources for modeling cellular states by integrating multi-layered data. For instance, the Human Cell Atlas (Regev et al. 2017) offers high-resolution transcriptomic data, which are critical for understanding cellular heterogeneity and dynamic state transitions. The Mouse Organogenesis Cell Atlas (Cao et al. 2019) provides high-resolution single-cell RNA-sequencing data across various stages of mouse development, offering a valuable resource for modeling cellular states during organogenesis. Furthermore, resources like scMoresDB (Chen et al. 2024) and SMARTdb (Liu et al. 2024) include integrated multi-omics data, enabling more comprehensive modeling of regulatory mechanisms underlying cellular state changes.

Applications of modeling cellular state dynamics

Modeling organ development process

Modeling the dynamics of cellular states is a powerful approach to understanding intricate processes that govern organ development. By capturing interactions and regulatory mechanisms between genes, proteins, and other molecular components, researchers can construct models to predict how cellular behavior evolves over time, ultimately leading to the formation and differentiation of tissues and organs. For example, regulatory dynamics has been modeled for Arabidopsis thaliana's flower and root development (Munoz et al. 2018). This demonstrates the potential of modeling the dynamic behavior of cellular states, thereby offering valuable insights into fundamental processes that drive organ development.

Predicting result of gene knockout or target intervention

Modeling the dynamics of cellular states can be also used to predict effects of perturbations, such as gene knockouts and targeted interventions. This process typically involves three main steps: (1) constructing a dynamic model that captures the behavior of cellular states, (2) introducing perturbations to the model to simulate gene knockouts or drug treatments, and (3) simulating the model to identify new steady states and understand cellular dynamics after perturbation. For instance, this approach has been applied to predict gene functions under virtual knockout conditions using scRNA-seq data (Yang et al. 2023). Similarly, steady-state gene expression dynamics has been modeled (Trinh and Kwon 2021), revealing regulatory structures that could be influenced by gene knockouts. Drug synergies have been predicted in rheumatoid arthritis (Singh et al. 2023), demonstrating how dynamic modeling can guide therapeutic interventions. Cellular responses to perturbations have been also simulated (Kim et al. 2024b), highlighting its use in predicting anti-cancer drug responses. Transcriptional outcomes have been predicted in response to multigene perturbations (Roohani et al. 2024). Additionally, a method has been presented to identify optimal control genes in disease-perturbed networks (Hu et al. 2019), serving as targets for combination therapy. Cellular responses to treatments have been also simulated in diseases such as colorectal cancer (Borzou et al. 2023). These studies collectively demonstrate the potential of dynamic modeling in predicting the impact of genetic or pharmacological interventions on cellular states, providing valuable insights for systems biology and precision medicine.

Modifying cellular states to desired phenotypes

Another promising application of modeling cellular state dynamics is identifying optimal interventions that can modify cells from initial to desired states, providing insights into how cellular behaviors can be controlled for therapeutic applications. This process typically involves collecting data from multiple cellular states, constructing a model that captures dynamic interactions within the cellular system, and then simulating the model to identify interventions capable of driving the transition from an initial state to a desired state. For instance, transcription factors have been identified that could induce transdifferentiation between immune cell types (Tercan et al. 2022). Key interventions have been predicted to trigger cellular state changes in tumor progression and cell differentiation (Zhong et al. 2023). In another study (Kim et al. 2023), a cellular state dynamics model was constructed based on epithelial-to-mesenchymal transition (EMT) data, allowing the identification of interventions that could reverse EMT in lung cancer cells while avoiding intermediate hybrid states. Similarly, transcriptomic data has been used to construct a cellular state dynamics model of basal-like breast cancer cells and identified the inhibition of BCL11A and HDAC1/2 as optimal interventions for reprogramming these cells into a less aggressive luminal A phenotype (Choi et al. 2022). These studies exemplify how dynamic cellular state modeling, informed by experimental data, can be leveraged to discover targeted interventions that could guide cellular transitions toward desired outcomes in various biological contexts.

Discussion

This review provides a comprehensive overview of current studies used to model the dynamics of cellular states, a crucial aspect in understanding complex biological processes such as cell differentiation, disease progression, and tissue development. We examined a broad spectrum of modeling approaches, ranging from BN and PBN that offer insights into the regulatory logic of gene interactions to deep learning methods that leverage large-scale data to predict cellular behavior with high accuracy. We also highlighted the increasingly important role of scRNA-seq data in unraveling the heterogeneity and transitions of cellular states, thus offering high-resolution insights into cellular processes. Metrics such as predictive accuracy, robustness to noise, and computational efficiency are also essential for evaluating these modeling approaches, ensuring their generalizability and utility across diverse biological contexts (Perumal and Gunawan 2011; Lotfollahi et al. 2019; Kamimoto et al. 2023).

The versatility of these modeling approaches enables researchers to understand cellular state transitions in different contexts, such as predicting outcomes of gene knockouts, designing therapeutic interventions, and simulating organ development. While BNs excel in capturing discrete state transitions of small-to-medium-scale networks, deep learning and static network analysis have demonstrated superior scalability, enabling modeling of more complex, large-scale biological systems. A summary of representative studies from these perspectives is listed in Table 2, and a comparative summary of the methodologies mentioned in this review is provided in Table 3. Our review emphasized the necessity of integrating multiple data types, including steady-state gene expression, time-series omics, and scRNA-seq, to construct accurate and generalizable models of cellular state dynamics.

Table 2.

Representative studies of modeling cellular state dynamics.

Study	Used model	Application	Input data	Size of model
Roohani et al. (2024)	Deep learning	Predicting multigene perturbation effect	scRNA-seq	5,000 genes
Borzou et al. (2023)	Static network + ODE	Drug treatment effect prediction	Time-series proteomics	3,347 biomolecules
Kim et al. (2023)	BN	Modifying cell phenotype	Manual model construction	31 genes
Yang et al. (2023)	Deep learning	Predicting gene knock-out effect	scRNA-seq	3,000 genes
Zhong et al. (2023)	Static network	Key gene identification	Bulk or scRNA-seq	Scale of whole genome
Choi et al. (2022)	BN	Cancer subtype alteration	Manual model construction	28 genes
Tercan et al. (2022)	PBN	B cell transdifferentiation	scRNA-seq	30 transcription factors
Hu et al. (2019)	Static network	Drug treatment prediction	RNA-seq	5,959 genes

Table 3.

Comparative summary of the methodologies, highlighting their features and limitations.

Methodology	Key features	Advantages	Limitations
BN	Discrete states; deterministic transitions	Simulates state transitions; identifies attractors	Limited scalability due to exponential state space growth; oversimplifies continuous data
PBN	Incorporates stochasticity in state transitions	Models uncertainty and noise in gene expression	High computational complexity; typically limited to small networks
ODEs	Continuous, time-resolved state modeling	Captures detailed molecular interactions over time	Parameter estimation is challenging; limited scalability for genome-wide networks
Petri-nets	Graphical representation of concurrent processes	Combines qualitative and quantitative data; intuitive visualization	Parameterization challenges; scalability issues with complex networks
Deep learning	Learns complex, non-linear patterns from data; scalable to high-dimensional data	Handles large-scale data; integrates prior biological knowledge; predicts unseen scenarios	Requires large datasets; interpretability and robustness concerns
Static biomolecular networks	Analyzes fixed network structures between states	Computationally efficient; scalable to whole-genome data	Does not capture temporal or causal relationships in cellular processes

Contributions of this review to the scientific research community are multifold. Firstly, it serves as a valuable reference for researchers seeking to understand or apply various modeling techniques to study cellular state dynamics. Secondly, this review underscores the importance of combining data-driven approaches with systems biology frameworks, promoting a more holistic understanding of cellular behavior. Lastly, by highlighting strengths and limitations of current methodologies, this review offers guidance for future research directions, encouraging the development of more scalable, accurate, and interpretable models that can advance our understanding of cell biology.

In conclusion, modeling of cellular state dynamics is a rapidly evolving field that holds great promise for unlocking complexities of cellular function and disease mechanisms. As high-throughput technologies and computational methods continue to advance, we anticipate that integrating multi-omics data with sophisticated modeling techniques will lead to even more refined and predictive models, ultimately enhancing our ability to manipulate cellular states for therapeutic purposes and furthering our understanding of fundamental biological processes.

Funding Statement

This work was supported by a National Research Foundation of Korea (NRF) grant number [2022R1A2C1007345] funded by the Ministry of Science and ICT (MSIT), Republic of Korea.

Disclosure statement

No potential conflict of interest was reported by the author(s).