Synchronizing genetic relaxation oscillators by intercell signaling

Abstract

The ability to design and construct synthetic gene regulatory networks offers the prospect of studying issues related to cellular function in a simplified context; such networks also have many potential applications in biotechnology. A synthetic network exhibiting oscillatory behavior has recently been constructed [Elowitz, M. B. & Leibler, S. (2000) Nature (London) 403, 335–338]. It has also been shown that a natural bacterial quorum-sensing mechanism can be used in a synthetic system to communicate a signal between two populations of cells, such that receipt of the signal causes expression of a target gene [Weiss, R. & Knight, T. F. (2000) in DNA6: Sixth International Meeting on DNA-Based Computers, June 13–17, 2000, Leiden, The Netherlands]. We propose a synthetic gene network in Escherichia coli which combines these two features: the system acts as a relaxation oscillator and uses an intercell signaling mechanism to couple the oscillators and induce synchronous oscillations. We model the system and show that the proposed coupling scheme does lead to synchronous behavior across a population of cells. We provide an analytical treatment of the synchronization process, the dominant mechanism of which is “fast threshold modulation.”

Cellular protein levels are determined by the interplay between the rates of gene expression and protein degradation. Because the regulation of expression occurs mainly at the level of DNA transcription (1, 2), cells often manipulate their protein levels through the modification of relevant transcription rates. Such regulation is accomplished by specific regulatory proteins called transcription factors and can occur in a positive or negative sense. Positive regulation refers to an increase in transcription rate, usually accomplished by enhancing RNA polymerase binding at a promoter site. Negative regulation, in turn, usually refers to the inhibition of polymerase binding at a promoter site. In both cases, expressed proteins act to regulate their own production and/or that of other proteins. Such regulatory feedback can lead to complex network dynamics, and an important theme in “postgenomic” research will be to understand these dynamics and how they affect cellular behavior.

The design and construction of de novo synthetic gene networks (3–6) provides a natural framework for reducing the complexity of gene regulation. This approach combines tools from nonlinear dynamics and statistical physics with the extensive array of techniques in traditional molecular biology (7, 8). Mathematical models are utilized in the design and analysis of the various features of the network, and, to date, the qualitative agreement between model and experiment has supported the notion of such an engineering-based approach (3–6). The power of this methodology is that it can be used to study simplified systems to gain insight into the general “themes” of gene regulation. These themes include subnetworks that act as switches (5, 9–13) or oscillators (3, 14–21), as well as networks that utilize feedback to dampen the effects of internal noise (6, 22). In addition to the insights gleaned from the construction of small networks, such genetic modules may have important biotechnological applications in their own right. In this context, synthetic gene circuits may provide a means for controlling complex biochemical systems in much the same way that digital and analog circuits provide a means for controlling electronic and mechanical systems.

Recently, a synthetic network capable of producing sustained oscillations in protein concentration was presented (3). The “repressilator” consisted of three genes (for simplicity, call them a, b, and c), expressing three proteins (respectively, A, B, and C). The network formed a ring: protein A repressed transcription of gene b; B repressed c; and C repressed a. For certain biochemical parameters, this cyclic repression produced self-sustained roughly sinusoidal oscillations over the entire growth phase of the host Escherichia coli cells. One intriguing aspect of this study was its relationship to naturally occurring oscillatory networks, such as circadian clocks. A random phase drift was observed in each cellular oscillator, and because there was no inherent means for the cells to synchronize, this caused the phases of the oscillators to drift apart over time. These variations suggest that, to circumvent the effects of noise, naturally occurring oscillators might need some additional form of control (18).

In this work, we present a model for controlling a synthetic gene network of coupled oscillators. Unlike the repressilator, our proposed oscillator (23) consists of only two genes (x and y) and is of the relaxation type. In our oscillatory gene network, both proteins are under the control of a promoter that is activated by the protein X, and protein Y is a protease for X. Oscillations arise because Y degrades X and thus reduces its own expression level (because X activates transcription of y). Our proposed control consists of cell to cell coupling, which acts to maintain synchrony across the population. We utilize the quorum-sensing apparatus of the bacterium Vibrio fischeri (24, 25). (Quorum-sensing refers to the ability of bacteria to detect and respond to their population density.) This cell to cell communication system operates by diffusing a small molecule [called autoinducer (AI)] into the environment. When this molecule binds to a regulatory protein (LuxR), it activates transcription from the lux operator region (see Fig. 1). Recent experiments (4) have shown that such a mechanism can be used by a synthetic gene network. In that work, two populations of cells were engineered: “sender” cells containing the autoinducer synthase (LuxI) under the control of a chemically inducible promoter, and “receiver” cells containing a reporter protein [green fluorescent protein (GFP)] controlled by the lux operator region. The experiments demonstrated that a complete cell–cell signaling pathway was active in the synthetic system. When the sender cells were induced to express LuxI, AI was produced and diffused into the extracellular environment. The AI then entered the receiver cells and stimulated production of GFP by activating the lux region.

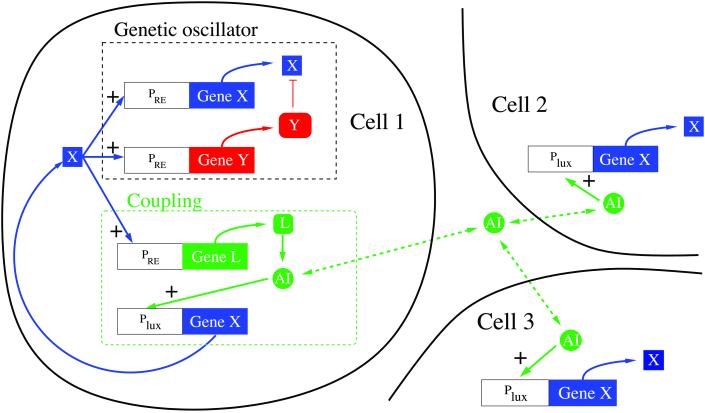
Figure 1.

Schematic of the proposed gene network. Proteins X (CII) and Y (FtsH) constitute the relaxation oscillator; protein L (LuxI) synthesizes the diffusible signal molecule called the AI, which passes through the cellular membrane in both directions. AI binds to the lux operator region (mediated by protein LuxR, not shown) and stimulates production of X.

We begin by describing the proposed synthetic network and proceed to formulate a model of the cellular and population-level behavior. We then consider the effect of the coupling on synchronization. For the near-synchrony case, we provide analytical results. For initial conditions far from synchrony, we show by simulation that the system is rapidly brought into synchrony by the coupling.

Model

The synthetic network is shown in Fig. 1. We use a variant of the genetic relaxation oscillator proposed in ref. 23 based on proteins CII and FtsH, both under the control of the P_RE promoter from the λ phage virus. Protein CII is the autocatalytic portion of the oscillator, whereas FtsH is a protease that degrades CII. Transmission of the coupling signal between oscillators is effected by placing the protein LuxI, which acts to synthesize the autoinducer signal molecule, under the control of the P_RE promoter. The signal is received when the autoinducer binds to the regulatory protein LuxR and activates transcription of CII from the lux operon. Thus, when an oscillator is in its high-CII state, it expresses LuxI and produces autoinducer, generating a signal that “encourages” other oscillators to jump to the high-CII state.

We define the following chemical species: X, protein CII; Y, protein FtsH; L, protein LuxI; A, the AI (diffusible signal); R, protein LuxR; C, the LuxR–AI complex; D, the DNA protein-binding site in promoter P_RE; D^L, the DNA protein-binding site in the lux operator region; and P, RNA polymerase.

The fast reactions involve the binding of proteins to one another (multimerization), to the DNA (regulatory binding), and to the autoinducer (LuxR–AI complex formation):

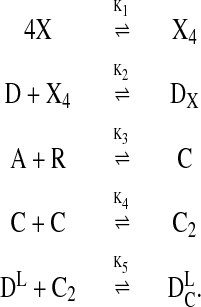[1]

The slow reactions involve transcription of mRNA and translation of proteins (here treated as a single combined process), autoinducer synthesis (by protein LuxI, acting on substrates native to the E. coli cell), and degradation of proteins and autoinducer:

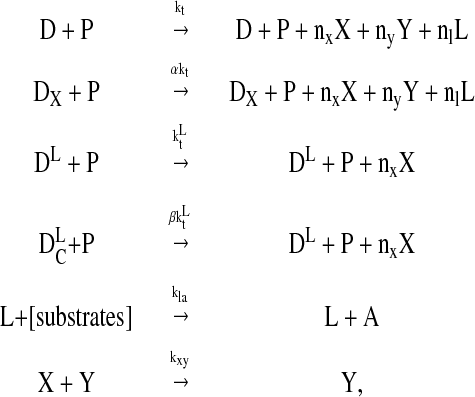[2]

where n_i is the number of proteins molecules per transcript of gene i. Species X, Y, L, and A degrade, respectively, at rates k_x, k_y, k_l, and k_a.

We formulate the model by using a rate equation approach (26, 27), neglecting fluctuations and using concentrations as our dynamical variables. Taking the fast reactions to be in equilibrium, we eliminate variables as follows: [X₄] = K₁[X]⁴; [D_X] = K₁K₂[X]⁴[D]; [C] = K₃[A][R]; [C₂] = K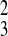K₄([A][R])²; and [D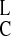] = KK₄K₅([A][R])²[D^L].

The rate equation for the concentration of protein CII is given by

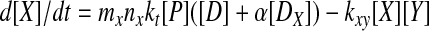3

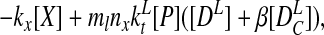where m_x and m_l are plasmid copy numbers. We eliminate the fast variables, note that the total number of DNA-binding sites is conserved in each of the P_RE and lux regions (D_T = [D] + [D_X] and D = [D^L] + [D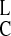]), and nondimensionalize by setting τ = t(n_xk_t[P]d_T(K₁K₂)^1/4) ≡ t/t*, x = [X](K₁K₂)^1/4 ≡ [X]/X*, y = [Y]/X*, l = [L]/X*, and a = [A][R]_oK₃(K₄K₅)^1/2 ≡ [A]/A*, where [R] = constant = [R]_o. The dimensionless equation is then

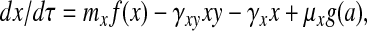4

where f(x) = (1 + αx⁴)/(1 + x⁴), γ_xy = k_xyt*X*, γ_x = k_xt*, μ_x = m_l(k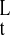/k_t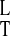)(D/D_T), and

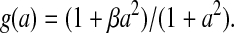The equations for y and l are derived similarly:

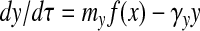5

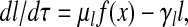6

where γ_y = k_yt*, γ_l = k_lt*, and μ_l = m_l(n_l/n_x). The appearance of the same production term f(x) in Eqs. 4–6 reflects the fact that all three proteins are under the control of the same promoter.

As a first approximation, we ignore spatial effects except to partition the volume of interest into the fraction inside the bacterial cells (volume fraction ρ) and the fraction in the extracellular space (1 − ρ) (28). Autoinducer is synthesized by LuxI (we assume that the underlying substrates are not depleted), diffuses through the cell walls at a rate η, and undergoes degradation, leading to the equation

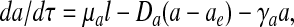7

where μ_a = k_lat*X*/A*, D_a = ηt*/ρ, a_ext = [A_e]/A*, and γ_a = k_at*. The extracellular autoinducer concentration, [A_e], is governed by

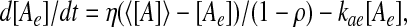8

where k_ae gives the rate of decay of the autoinducer in the extracellular space and 〈[A]〉 represents the average autoinducer concentration inside the cells. As in ref. 28, we make the simplifying assumption that [A_e] is in a quasisteady state, so that [A_e] = Q 〈[A]〉, with Q = η/[η + (1 − ρ)k_ae]. In terms of dimensionless quantities, a_e = Q 〈a〉.

Parameter values are as follows: α ∼ 600 (29); K₁ ∼ 1.8 × 10¹⁸ M⁻³ (30); K₂ ∼ 5 × 10⁶ M⁻¹ (31); from earlier estimates (n_xk_t[P]d_T) ∼ 88 nM min⁻¹ (23); k_al ∼ 1.1 min⁻¹ (32, 33); η ∼ 9 min⁻¹ (34). The degradation rates of the various molecules are not known. We use the nondimensionalized values γ_a = 0.2 (corresponding to the rate arising from dilution by cell growth), and γ_x = γ_y = 0.5 (a rate slightly above dilution). We use a high degradation rate for l (γ_l = 25), which avoids lingering production of AI after the oscillator is no longer in the high state; protein degradation rates may be artificially increased by using SsrA tags (peptide sequences appended to the protein to make it a target for proteases in the cell) (3, 35). In wild-type E. coli, CII has a half-life on the order of 2 min (36, 37), with the degradation thought to be caused largely by the influence of FtsH. The lack of a figure for the concentration of FtsH in the cell makes the value of k_xy uncertain; we use k_xy ∼ 2 × 10⁴ nM⁻¹ min⁻¹ (whence γ_xy ≃ 5). The dimensionless parameter Q varies fairly weakly with the extracellular AI degradation rate, k_ae, over a wide range of half-lives; we choose k_ae to make Q = 0.6. For the volume fraction found inside bacterial cells we use ρ = 0.5; this is the fraction occupied by loosely packed spheres, but of course E. coli are not spherical, and their density will vary depending on experimental conditions. Plasmid copy number choices give m_x = 10, m_y = 1, and μ_l = μ_x = 50. The degree to which bound LuxR–AI complexes stimulate transcription, β, is not available, but ref. 38 suggests that it is significantly greater than 4; we use β = 10 (note that our analysis indicates that β does not critically affect the synchronization behavior). The binding strengths that make up the factor K₃(K₄K₅)^1/2 ≡ K_AR are also not known; we use the reasonable but somewhat arbitrary value K_AR ∼ 10⁻⁶ nM⁻². Inaccuracy in this value should not be fatal to the design effort. We can compensate for the influence of K_AR by adjusting [R]_o with a tunable promoter; here, we take [R]_o = 100 nM. The dimensional scaling constants are t* ∼ 6.7 min, X* ∼ 580 nM, and A* ∼ 10 μM. The remaining dimensionless constants are μ_a ∼ 0.4 and D_a ∼ 120.

To summarize the system, each cell is governed by Eqs. 4–7; x and y constitute the oscillator, whereas l and a implement the coupling, operating through the quantity a_e.

Results

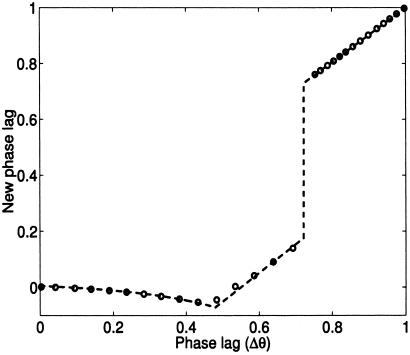
To analyze the synchronization, we address the near-synchrony case where the bulk of the population is synchronous, whereas a single outlier cell (or a small fraction of the population) is out of phase. This situation could be arranged experimentally by augmenting the design with a chemically inducible promoter expressing, say, protein X (CII). By flooding the system with the appropriate inducer, we could force all cells to a nonoscillatory fixed point, then remove the inducer to obtain a population that would start to oscillate at least approximately in synchrony. In this case, it is possible to derive analytical expressions for the effect of the coupling; the analysis is somewhat technical, and we defer the details to the Appendix. Briefly, when the outlier cell lags the population, its level of a is increased by the ambient a_e diffused by the population. This shifts the oscillator's transition threshold (see Fig. 4) and causes the cells to jump quickly from the low-x to the high-x state; this transition reduces the phase difference between the outlier cell and the population. A slower synchronization mechanism prevails when the outlier cell leads the population. As Fig. 2 shows, the closed-form solution matches well with the results of numerically integrating Eqs. 4–7 for a population of 1,000 cells, with a single outlier cell initialized with various phase lags.

Figure 2.

Effect of coupling on cycle to cycle phase differences for the near-synchrony case. Dashed line: analytical result. Circles: results from numerical integration of Eqs. 4–7 for 1,000 cells with one outlier cell. Varying the coupling strength (β) does not affect the quality of the match between numerics and theory (simulations not shown). Rapid phase compression via fast threshold modulation occurs for the range 0 ≤ Δθ ≤ θ_j (where θ_j = 0.72); see the Appendix for definitions of these terms. Outside this range we have slower synchronization via the mechanism discussed in the Appendix.

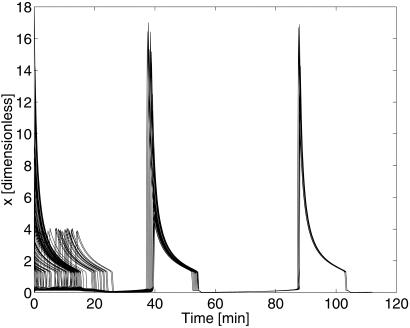
Fig. 3 illustrates that even cells initially at randomly scattered phases are quickly brought into synchrony by the coupling. Heuristically, the effect is caused by the cells initially in the high-x state producing enough AI to saturate the levels of a in the cells initially in the low-x state, causing rapid transitions and quickly condensing the range of phases in the population. On subsequent cycles, the cells are close enough to synchrony that the near-synchrony mechanism discussed in the Appendix is approximately applicable, and the population exhibits the rapid synchronization seen in Fig. 2.

Figure 3.

Synchrony achieved from random initial phases. The plot overlays the time courses of 100 cells, chosen at random from a population of 1,000 coupled cells; the initial phase for each cell was chosen with a uniform distribution in [0, 1]. Synchrony is essentially complete within two periods of the oscillation.

Discussion

In this article, we have proposed a design for a synthetic network implementing coupling between genetic oscillators and we have shown through modeling that the proposed design is capable of producing synchronous behavior across a population of such oscillators. Our analytical results enable us to predict, for a given set of parameter values, whether or not the intercell coupling will act to synchronize the cells. This will assist in producing a working experimental implementation of the design, enabling us to assess, at least approximately, the expected effect of varying parameters.

Our proposed oscillator is of the relaxation type, whereas the previously implemented “repressilator” (3) is a phase oscillator: it has a sinusoidal waveform and does not exhibit multiple time scales. This distinction is key, because it has been shown (39–42) that the mechanism underlying the approach to synchrony is very different in the two cases. Relaxation oscillators generally synchronize more rapidly than their phase-oscillator counterparts and approach synchrony at a rate relatively independent of the coupling strength. It would be of interest to investigate these differences directly, carrying out both modeling and experimental work on a system in which the repressilator phase oscillator was coupled across a population by using the same type of signaling mechanism outlined here.

The model presented here simplifies a number of aspects of the system. The effects of noise and heterogeneity are of particular interest. Gene expression levels in cells exhibit fluctuations, often attributed to the relatively small particle numbers involved (13, 44–46). It is possible to augment the rate equations with stochastic terms capturing these fluctuations (13, 46); in the case of the relaxation oscillators, the effect would presumably be most critical near the transition points, where small fluctuations could cause early entry into the fast phases of the oscillation. Although we have treated the plasmid copy numbers as constants, they may in fact vary across a population, causing a corresponding variation in the internal dynamics of the cells. Further modeling and analysis may be able to elucidate how such a variation will affect the synchronization behavior. Interestingly, previous theoretical work (40) indicates that arrays of coupled relaxation oscillators are able to compensate for heterogeneity in their internal dynamics, altering their waveforms while retaining synchrony in the timing of the fast jumps.

There are a number of potential applications for a synthetic network of the type described here. Existing gene therapy approaches typically deal with transfected genes that are fixed in either an “on” or “off” state. As our ability to implement cellular control improves, more sophisticated medical interventions may require particular proteins to be expressed on a periodic schedule, and in such cases we would want all cells in a given tissue to oscillate synchronously. Further, there has been considerable recent interest in genetic “reverse engineering”; that is, in probing complex natural gene networks to deduce their network connectivity. Inserting an artificial oscillator into the natural system of interest would provide an input whose induced response could provide valuable information about the system's internal dynamics; keeping oscillations synchronous across a population would prevent the introduction of drift in the input signal from cell to cell.

Abbreviation

AI

autoinducer

Analysis

In Eqs. 4–7, the variables l and a act to shift the nullclines of the x–y dynamics. We may thus consider motion only in the x–y plane, provided that we properly account for the motion of the nullclines under the influence of the other two variables. For our parameter values, l and a rapidly approach steady-state values (with time scales on the same order as the fast dynamics of the oscillator); we will thus take l ≃ l̄ = μ_lf(x)/γ_l and a ≃ ā = (μ_al̄ + D_aa_e)/(D_a + γ_a). The ẏ = 0 nullcline is given by y = m_yf(x)/γ_y, whereas the cubic-shaped ẋ = 0 nullcline is given by

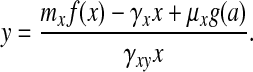9

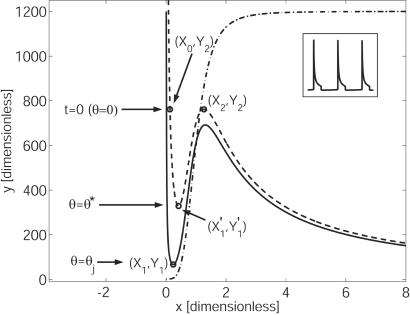
The ẋ = 0 nullcline is in fact a family of curves parametrized by a, where increasing the level of autoinducer shifts the nullcline upwards. For low levels of a, g(a) = 1; substituting g(a) = 1 into Eq. 9 gives us what we will call the a⁻ nullcline. At high levels of a, g(a) = β; substituting g(a) = β into Eq. 9 gives us the a⁺ nullcline. Both of these curves are shown in Fig. 4. The transition points [(X₁, Y₁) and so on] have been found explicitly as functions of the parameters, by solving for the extrema of Eq. 9.

Figure 4.

Nullclines for Eqs. 4 and 5. Dash-dotted line: ẏ = 0 nullcline. Solid line: ẋ = 0 nullcline, no coupling (g(a) = 1); the a⁻ nullcline. Dashed line: ẋ = 0 nullcline, maximum coupling (g(a) = β); the a⁺ nullcline. θ* = 0.24 and θ_j = 0.72.

We begin by examining the dynamics of a single isolated cell with no coupling influence; that is, we take a_e = 0. Consider such a cell starting on the left branch of the a⁻ nullcline (see Fig. 4). On this branch, f(x) ≃ 1 and g(ā) ≃ 1; the cell proceeds down the left branch to the “knee” at (X₁, Y₁), at which point it makes a rapid transition to the right branch. For large x we have f(x) ≃ α, g(ā) ≃ β [for our parameters, simulations show g(ā) = 0.95β], and the cell moves upwards along the right-hand branch of the a⁺ nullcline to (X₂, Y₂), where it rapidly jumps back down to the left branch. After this transition, g(ā) quickly drops back to 1, the cell moves down the a⁻ nullcline, and the cycle repeats. Note that the cell's own local production of a is sufficient to shift the ẋ = 0 nullcline from the a⁻ to (nearly) the a⁺ state.

A population of synchronously oscillating cells behaves essentially identically to a single cell; the presence of higher levels of a_e has little effect on the x–y dynamics because g(ā) is bounded by β. To estimate the period of the oscillations, we use the saturating form of f(x) to solve Eq. 5 on the left branch (f(x) ≃ 1) and on the right branch (f(x) ≃ α). We may then write expressions for the time taken to move from a point y₁ to a point y₂:

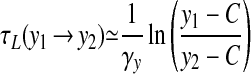10

on the left branch, and

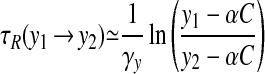11

on the right branch, where C ≡ m_y/γ_y. Taking the fast jumps to be instantaneous, we may write the period as

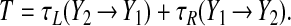12

For our parameters this predicts T ≃ 46 min, compared with T ≃ 48 min obtained by numerical integration of Eqs. 4–7. We define the phase as θ = t/T, taking t = 0 at the point marked in Fig. 4.

To analyze the approach to synchrony, we address the near-synchrony case mentioned in Results: the bulk of the population is synchronous, while a single outlier cell is out of phase. Throughout this analysis, we apply ideas from the work on “fast threshold modulation” (FTM) presented in refs. 39, 40, and 43.

The synchronous portion of the population may be lumped together into a single oscillator, so that we are effectively considering two coupled oscillators: O_p, the population (with associated phase θ_p), and O_c, the outlier cell (phase θ_c). O_p affects both its own value of ā and that of O_c; O_c, on the other hand, has no influence on O_p but affects its own level of ā. We are interested in the effect of the leftward and rightward transitions on the separation in time of the two oscillators; that is, how long it would take for one oscillator, moving along the cycle, to reach the current position of the other oscillator. Phase compression is said to have taken place if, after a transition, the time separation is reduced. Successive compressions yield an approach to synchrony at a geometric rate (39).

Consider first the situation where O_c lags O_p, with both starting on the left branch of the a⁻ nullcline; we define the phase lag as Δθ = θ_p − θ_c. When the population reaches (X₁, Y₁) and jumps to the right branch, a_e rises rapidly and the cell's value of ā is increased to the point where g(ā) → β; the cell thus finds itself governed by the a⁺ nullcline. For sufficiently short lags (0 ≤ Δθ ≤ θ_j − θ*), the cell is now past the “knee” of its new nullcline, and jumps instantly to the right. Phase compression occurs if

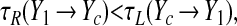13

where Y_c is the cell's y position when the population jumps. Substituting our parameters into Eqs. 10 and 11 shows that we do in fact have τ_R ≪ τ_L for all points in this range of phases.

For longer lags (θ_j − θ* < Δθ ≤ θ_j), the cell jumps first to the left branch of the a⁺ nullcline then makes its rightward transition when it reaches (X′₁, Y′₁) (marked in Fig. 4). During the delay before the cell jumps, the population moves upward along the right branch of the a⁺ nullcline, reaching a point Y_p (explicitly calculable in terms of the parameters). Phase compression occurs in this case if

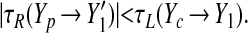14

The absolute value sign on τ_R reflects the fact that Y_p may fall above or below Y′₁, leading to negative or positive values of τ_R, respectively; in either case, the phase separation between the two oscillators is reduced if the new absolute time difference is smaller than the original difference. Once again, evaluation of the inequality for our parameter values shows rapid phase compression for all points in the range.

When O_c lags O_p at the leftward transition at (X₂, Y₂), there is no effect on the phase separation of the two oscillators: the cell's local production of a keeps it on the a⁺ nullcline, so there is no difference in the trajectories and thus no phase compression.

We now move to the case where O_c leads O_p; that is, the outlier cell is ahead of the population in the cycle. Here, the rightward transition at (X₁, Y₁) has no effect on the phase separation, once again because of the cell's local production of a. The leftward transition at (X₂, Y₂) now leads to relatively slow synchronization, as follows. The cell makes its leftward transition, but travels down the left branch of the a⁺ nullcline rather than that of the a⁻ nullcline, reaching some point Y_c; the time separation between points on this branch may be written as

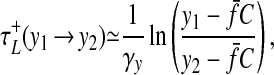15

where

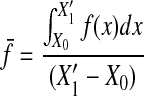16

is an approximation used to obtain a closed-form solution. When the population makes its leftward transition, the cell returns to the a⁻ nullcline, and we have a synchronizing effect if

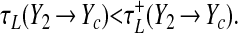17

This inequality is always satisfied, as may be seen by examining Eq. 5: because the function f(x) is monotonically increasing, motion down the a⁺ nullcline is slower everywhere than motion down the a⁻ nullcline, and thus τ_L(Y₂ → Y) < τ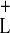(Y₂ → Y) for all Y. However, the synchronization is not rapid in this case, because f̄ is only slightly greater than f(x) ≃ 1.

Combining the effects at the leftward and rightward transitions, and explicitly calculating the values of τ_L, τ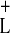, and τ_R for various initial phase lags, we produce an analytical prediction of the map from the phase lag (Δθ = θ_p − θ_c) on one cycle to the new phase lag on the next cycle (see Fig. 2). For phase lags in the range 0 ≤ Δθ ≤ θ_j − θ*, the lagging outlier cell undergoes a rightward transition nearly instantly when the population jumps, whereas for θ_j − θ* < Δθ ≤ θ_j the cell makes its rightward transition after spending some time on the left branch of the a⁺ nullcline, as discussed above. The entire range 0 ≤ Δθ ≤ θ_j exhibits rapid synchronization via the fast threshold modulation mechanism: all phase lags in this range are mapped, on the next cycle, to values near zero. For Δθ > θ_j, the curve is close to the identity map; in this region, the synchronization is governed by the slower mechanism discussed above.