Protein folding mediated by solvation: Water expulsion and formation of the hydrophobic core occur after the structural collapse

Abstract

The interplay between structure-search of the native structure and desolvation in protein folding has been explored using a minimalist model. These results support a folding mechanism where most of the structural formation of the protein is achieved before water is expelled from the hydrophobic core. This view integrates water expulsion effects into the funnel energy landscape theory of protein folding. Comparisons to experimental results are shown for the SH3 protein. After the folding transition, a near-native intermediate with partially solvated hydrophobic core is found. This transition is followed by a final step that cooperatively squeezes out water molecules from the partially hydrated protein core.

The energy landscape theory and the funnel concept combined with a new generation of experiments provide a new framework for understanding the protein folding problem. According to this “new view,” the folding landscape for proteins (at least for small fast folding proteins) resembles a partially rough funnel riddled with traps where the protein can transiently reside (1–8). Recent theoretical and experimental evidence fully support this picture and suggests that, because the energetic roughness of the landscape is sufficiently small (low level of energetic frustration), the global characteristics of the structural heterogeneity observed in the transition state ensemble for two-state fast folding proteins are most strongly determined by the native state topology. For this reason, theoretical energetically unfrustrated models have been shown to reproduce nearly all experimental results for the global geometrical features of the transition state ensemble of a large number of real proteins, which are two-state or three-state folders, on whose native structures they are based (9–24).

Some concerns have been raised, however, about the applicability of these models. For example, solvent effects are incorporated implicitly into the energetic interactions between residues. Such implicit equilibrium models for solvation are unable to capture effects such as desolvation of the hydrophobic core; therefore, understanding the potential of mean force for the interaction between solutes in an aqueous solvent attracts the attention of many research groups (25–30). The potential of mean force (PMF) between two methane-like particles exhibit two minima—a contact minimum at the van der Waals distance between the particles and a solvent-separated minimum. The two minima are separated by a desolvation barrier with a width of approximately one water molecule diameter. Recently, Hillson et al. (31, 32) advertised the importance of the desolvation effect by taking into account the process of expelling a water molecule in a pairwise interaction between hydrophobic particles. Assuming that the time scale for water penetration and escape are faster than the contact formation in proteins (33), the shape of this potential energy function implies that there are free-energy costs for protein (de)solvation (27). The time scale separation assumption may not be always valid and its limitations are discussed at the following section. The results obtained in these preliminary studies (31, 32) have been obtained by Monte Carlo sampling, and therefore they only provide kinetic information indirectly.

In this article, we generalize these minimalist models to include the interplay between structure-search in a funnel landscape and water desolvation in determining the protein folding mechanism. Practically, we provide a phenomenological model where the parameters are adapted from previous studies by Hummer et al. (27). This model features a barrier that plays a dominant role in determining the desolvation and solvation dynamics during the protein folding event. Its details are described in the Appendix A. Applications are shown for the SH3 protein model, which has a hydrophobic core buried within beta sheets in the native structure (36). Our results show an initial structural collapse to an overall native shape that is followed by water expulsion from the hydrophobic core region of SH3 during the final step before the native state is reached. This folding mechanism is in total agreement with earlier results using energy landscape theory of folding [e.g., similar ensemble of structures at the transitions state (22)], with the additional feature that residue–residue interactions are now generalized to include the possibility of water solvation/desolvation.

A Minimalist Model for Water-Mediated Interaction

The interaction potential used is an extension of the energetically unfrustrated models described above to include the possibility of protein (de)solvation. This idea is implemented by generalizing Gō (37) type interactions; that is, only attractive interactions are assigned to the native contacts and repulsive interactions are assigned to the nonnative ones. The nonnative interactions, U_rep(r), are given by hard-core repulsions that follow C × r⁻¹², where the constant C is optimized to guarantee a minimally frustrated energy landscape. Again, although no nonnative attractive interactions are included in these unfrustrated models, what appears to be unrealistic, recent theoretical and experimental results support their applicability. In addition to the experimental citations earlier in the introduction, several recent theoretical/simulational approaches have shown the geometrical features of the folding mechanism are robust to energetic frustration as long as it is small relative to the bias toward the native configuration (34, 35).

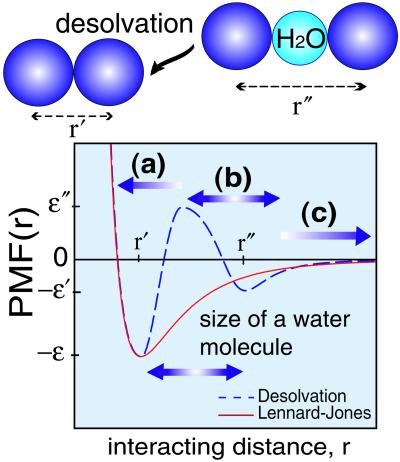
Therefore, even when neglecting the effects of energetic frustration, these Gō models have been shown to reproduce nearly all-global geometrical features of the transition state ensemble and intermediates of the real, fast folding proteins (16, 20, 22). The new interactions, however, include not only the standard minimum for the direct contacts between residues, but also a barrier separating this minimum from a weak secondary one for the water-separated contacts. As demonstrated in this paper, this barrier plays a major role in the water solvation/desolvation mechanism during the kinetic events in the funnel landscape. This potential is described in details in Fig. 1 and Appendix A. Three different regions characterize the nature of contact formation: (i) when residues (modeled by atoms at the C_α positions) are separated by a distance shorter than the position of the desolvation barrier, then a native contact is formed; (ii) when this separation is around the second minimum (i.e., a single water molecule exists between the residues), defined as a “pseudo contact” (i.e., the first hydration shell); (iii) for larger separations, which are associated to larger amounts of water between residues, neither sort of contact is formed.

Figure 1.

A schematic representation of a phenomenological potential for tertiary contact formation which includes the possibility of desolvation. r′ and r" label the residue–residue contact minimum and the single water molecule-separated contact minimum, respectively. The parameters for energies are adapted from the refs. 27 and 31, where ɛ" − ɛ′/ɛ′ − ɛ = 1.33, ɛ′/ɛ = 1/3. The desolvation barrier allows for a clear determination of whether a native contact is formed. Three regions are defined: (i) when the separation distance between residues r is shorter than the range of the desolvation barrier, then a native contact is formed; (ii) when the residues are separated from the desolvation barrier by a single water molecule (3 Å) distance, then a “pseudo contact” (i.e., the first hydration shell) is formed; (iii) when the residues are separated by multiple hydration shells, no contact is formed. By using this simple rule, the degree of nativeness of any configuration is easily determined. The normalized density of the native contacts (Q) and the native “pseudo contacts” (pseudo Q) are appropriate parameters to characterize the degree of nativeness and of desolvation. For comparison, a Lennard–Jones type potential (in red) is presented in the figure.

The two-dimensional free-energy profiles plotted as a function of the two folding parameters Q and pseudo Q, at the folding temperature (T_f, k_BT_f/ɛ = 1.28), is shown in Fig. 2A and at 0.88T_f in Fig. 2B. Q measures the normalized density of formed native contacts (varying between 0 and 1). Pseudo Q is the equivalent parameter for the single water separated contacts. Because the desolvation barrier for the interaction potential is relatively high (about 1.22k_BT_f), it causes some difficulties for canonical sampling schemes. This problem can be overcome by incorporating multicanonical sampling methods into molecular dynamics simulations.§ The algorithm for multicanonical sampling (38–41) is briefly described in Appendix B. Fig. 2 A and B shows that the folding mechanism for SH3 is governed by two distinct events, although the energy landscape is slightly different for the two temperatures. First, a folding transition occurs between regions around Q ∼ 0.3 and Q ∼ 0.8. This step involves overcoming a transition state ensemble (TSE) barrier (Q between 0.4 and 0.6). At Q ≈ 0.8, an ensemble of structures with an overall shape similar to the folded motif but with substantial internal solvation is reached. This is followed by a second transition that is associated to expelling water from the hydrophobic core. These hydrated hydrophobic cores, of conformations near the native state, have also been observed in free-energy profiles obtained from all-atom simulations (43), where the authors propose that these waters provide a lubrication mechanism during folding. This agreement with all-atom simulations provides additional support for our simplified water representation. These solvated cores are also consistent with experimental evidence discussed later.

Figure 2.

A and B show the free-energy diagrams plotted as the function of folding parameters Q and pseudo Q at the folding temperature (T_f, where k_BT_f/ɛ = 1.28) and 0.88T_f, respectively. Q and pseudo Q are the normalized density of native contacts and pseudo native contacts (see Fig. 1). Free energies are measured in units of k_BT (T = T_f in A or 0.88T_f in B) where blue (red) stands for low (high) value of these. Pseudo Q ranges are approximately between 0 and 0.3. Pseudo Q appears to decline sharply at Q ≥ 0.8, indicating the system expels water at this stage. A typical folding trajectory is superimposed on the free-energy landscape at T = 0.88T_f (D). In addition, Q, pseudo Q (C) and contact energy (E) are plotted as a function of integration time step. Using the same desolvation potential presented in Fig. 1, this trajectory is simulated by Langevin dynamics. The folding run was recorded for another 10⁶ steps after Q reaches 1. According to the distinct transitions indicated by the contact energy in (E), the folding mechanism is characterized by two stages: a structural collapse toward a nearly native ensemble at a time τ₁, which is followed by water expulsion from the hydrophobic core at a time τ₂. To have a better understanding of the kinetics, several snapshots of the chain are shown in which a blue sphere is used to identify pseudo contacts (i.e., single water molecule-separated residues). In addition, we color the residues with formed native contacts in red to specify the folded portion of the protein and the unfolded portion in gray. In this trajectory, (a) shows an unfolded configuration where only the short-range native contacts are formed. This early step is followed by a transition indicating the structural collapse to the nearly native ensemble (b → c) in which Q increases and pseudo Q decreases. The configuration shown in (b) has 31 pseudo contacts formed. After excluding the possibility that some of these pseudo contacts use the same water molecules, 23 “water” molecules are expelled cooperatively during this transition (the principle of excluded volume is used to determine whether pseudo contacts possibly use the same water molecule). Notably, the native contact formation between the diverging turn (Dv) and the distal loop (Dt) (indicated by a broken green circle) is crucial for this structural collapse. This region overlaps with the experimentally determined high φ-value regions (46, 47). The final transition involves the mechanism of water expulsion from the partially hydrated hydrophobic core (d → e). This transition involves the formation of long-range tertiary contacts across the two sandwiched β-sheets. Configuration (d) has 20 pseudo contacts in the hydrophobic core and the terminal regions. After excluding the possibility that some of these pseudo contacts use the same water molecules, 17 “water” molecules are expelled cooperatively during this final transition. Configuration (e) has only a few residual “water” molecules in the terminal regions. To emphasize this collective behavior of water expulsion during the interval of the final transition, an Inset in C shows that the number of native pseudo contacts decreases abruptly (N is the number of total native contacts).

Kinetic and Thermodynamic Views of Folding Mechanism

In addition to computing the free-energy profile, several folding (unfolding) simulations were performed using Langevin dynamics simulations.§ One of the main advantages of these minimalist representations for proteins is that not only thermodynamic studies but also a fully kinetic analysis is computationally feasible. These kinetic runs allow us to fully confirm that the transition regions identified in the free-energy profile correspond to the kinetic steps observed during the folding event. Therefore, the kinetic desolvation events observed during these kinetic events are exactly the same as those shown in Fig. 2B. To facilitate visualization of the folding mechanism, a comparison is shown for a typical folding run at 0.88T_f in Fig. 2 B–E. The two transitions described above can be clearly identified in the kinetic run: the folding transition in this trajectory occurs after a time τ₁ and the water expulsion from the hydrophobic core occurs a time τ₂ later. The relative duration of these times may change for different proteins because both topology and energetics play a major role in determining the transition barriers. Also, the ratio of τ₁ and τ₂ depends on the parameterization of the potential of mean force, which may vary with the experimental conditions, such as pressure (27). In this paper, however, we only consider systems under near-native conditions.

To better illustrate these two transitions, several snapshots along the trajectory are shown in Fig. 2E. Unfolded parts of the chain are colored in gray, whereas folded regions of the chain are shown in red. Pseudo contacts (single water separated contact pairs) are represented by blue spheres between the corresponding residues. Unfolded regions with no blue sphere in between have a larger solvation. The first transition involves a structural collapse, where the contact formation between the diverging turn (Dv) and distal loop (Dt) is crucial for assuring the proper alignment of the tertiary contacts needed to later pack the hydrophobic core. These regions overlap with the experimentally determined high φ-value regions (9, 45, 46), where contacts are basically formed in the transition states. The next transition is mainly responsible for the water expulsion out of hydrophobic core region. Interestingly, there are 20 pairs of solvated pseudo contacts distributed about the hydrophobic core and termini regions. For visualization purposes, water molecules are presented as spheres, and the principle of excluded volume is used to determine whether different pseudo contacts could possibly use the same water molecule. However, we emphasize that no explicit water molecules are used in the simulation. After excluding the possibility that some of these pseudo contacts use the same water molecule, we determined that ≈17 “water” molecules are expelled cooperatively during this transition. To emphasize this collective behavior of water expulsion during the interval of the final transition, an inset in Fig. 2C shows that the number of native pseudo contacts decreases abruptly, and this decrease matches the number of contacts being formed. Most trajectories share similar characteristics during the folding collapse, which is controlled by topological constraints (the need for the early formation of the region between Dt and Dv, otherwise folding is not possible), as well as during the water expulsion mechanism from the hydrophobic core. This final kinetic feature was absent in the previous minimalist models using implicit-solvent. More specifically, quantitative aspects of this feature are very sensitive on the profile of desolvation barrier (data not shown). These results allow us now to appreciate the relative roles of structure-search toward the native structure and water desolvation in determining the protein folding mechanism.

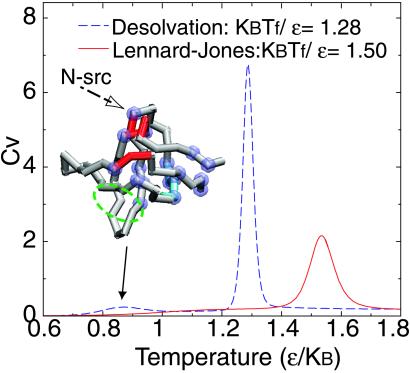
The validity of using the sum of two-body contributions to represent the many-body nature of hydrophobic effect is often questioned. Czaplewski et al. (47) found that three-body cooperative term accounts for 10% of the total hydrophobic association free energy; it is not too small to be negligible. Shimizu et al. (48) claimed that, in addition to the radial dependence of the potential of mean force, the angular dependence of the potential of mean force can modulate the sign of the cooperativity. These results are consistent with earlier observations by Takada et al. (49). Despite that we cannot quantitatively address these questions using simplified models, we observe a stronger cooperativity in the folding transition using our desolvation potential when compared with results using Lennard–Jones interactions. This is clear from thermodynamics properties such as the specific heat (Fig. 3). Because the enthalpy change for both models at individual folding temperatures is basically the same, the sharper profile of the specific heat in the desolvation model indicates a much stronger cooperativity of folding. Although an increase in the cooperativity of folding is obtained by using a two-body interaction featuring desolvation, such an enhancement is still too weak to account for the entire cooperativity observed experimentally.

Figure 3.

The cooperativity of folding of models using the desolvation and Lennard–Jones potentials are compared by plotting specific heat as a function of temperature. The enthalpy change for both models at individual folding temperatures is the same. The sharper profile of the specific heat implies stronger cooperativity of folding in the desolvation model than that for the Lennard–Jones model. Noticeably, at low temperature, there is a broad but small peak in the desolvation model. This low temperature feature corresponds to minute fluctuations of the native structure (where Q ≤ 0.93, pseudo Q ≤ 0.07). The origin of the fluctuation at low temperature is attributed to very few sporadically formed pseudo contacts found at the termini regions, hydrophobic core, several intrahairpins, or loops that are in the proximity of the termini. In the Inset with an SH3 structure, the top 30% residues that possibly form pseudo contacts at low temperatures are highlighted with purple balls. In comparison, the regions colored in red are the binding site of the protein to the proline-rich peptide. The green broken circles label the experimentally determined high φ-value regions (45, 46). The β-sheet colored in cyan is the region, in addition to termini and loops regions, suggested by the NMR experiments (50, 51) to account for the conformational changes under near-native conditions as temperature mildly increases.

In addition to a sharper peak at the folding temperature in the specific heat curve obtained for the desolvation model, there is another distinct thermodynamic signature found at lower temperatures where a small peak is observed (Fig. 3). This low temperature feature corresponds to minute fluctuations of the native structure (where Q ≤ 0.93, pseudo Q ≤ 0.07). The origin of these fluctuations is attributed to few sporadically formed pseudo contacts found at the termini regions, hydrophobic core, several intrahairpins, or loops that are in the proximity of the termini.

Conclusions

In this study, we have found a near-native intermediate with a partially solvated hydrophobic core. This intermediate corresponds to a loosely compact and structured, partially denatured ensemble recently identified in experiments for N-terminal SH3 domain of Drosophila adapter protein drk, using a N-15/H-2-labeled samples to observe long range amide nuclear Overhauser effects (NOE) (50, 51). The residues observed experimentally to be partially hydrated in the vicinity of the core are in good agreement with our theoretical predictions (50). Experimentally, this “structured” ensemble was found to have a near-native “collapsed” structure that is strongly confined in the conformational space and close to the native structure; after this state is achieved, folding required only a simple step to match the well aligned contact pairs. In this article we have identified this additional step as a desolvation process that squeezes out water molecules in the vicinity of partially hydrated core. More precisely, we have determined that the folding process of SH3 can be characterized as a “structure-search collapse” that is followed by a separate “desolvation” step of this nearly native ensemble.

Is there a biological advantage of having this nearly native ensemble? It has been found that this ensemble exists under physiological conditions and is equally populated compared with native state (51). Also, experimental evidence suggests that conformational changes in the core region take place during ligand binding (52). We would like to point out that the desolvation effect might provide a more “efficient” (kinetically) and “inexpensive” (thermodynamically) way to conduct conformational changes (i.e., without significant structural rearrangement) and switch the protein between functional (liganded) and nonfunctional states. Interestingly, the ligand-binding site of SH3 is far from its high φ-value regions (such as RT-loop and Dv-turn); thus, the functional dynamics of SH3 cannot be simply addressed by φ-value analysis.

In summary, by introducing the feature of desolvation in the tertiary contacts pair potential, we have been able to capture functional aspects of SH3 dynamics and folding by using a minimalist model. In particular, we have identified the nearly native ensemble that might have profound biological significance under physiological conditions. Such a state contributes to the ensemble of conformations existent in the bottom of the folding funnel. Although local conformational changes [specifically (de)solvation] of the hydrophobic core are not the only mechanism for SH3 liganding and functioning, the combination of theoretical and experimental evidence strongly suggests its importance during folding and function of this protein. Despite the fact that our theoretical studies have been limited to only one protein, this interplay between structure-search and desolvation mechanisms is probably general during the folding of different proteins. The detailed effect on the overall folding mechanism should vary for different systems, because it will depend on their topological and/or energetic features.

Design of the Desolvation Model

The desolvation potential, U(r), is designed as a function of the interacting distance, r, between residues involved in Gō contacts (37), where r′ is the minimum of the first potential well, r^† is the maximum of the desolvation barrier, and r" is the minimum of the second potential well. The separation between r′ and r" is the size of a single water and set to be 3.0 Å (ref. 31; see Fig. 1). We set r^† = (r′ + r")/2.

We required this function to be dependent on several known parameters, such as the depth of the first well (ɛ), the height of the desolvation barrier (ɛ"), the depth of the second well (ɛ′), and the location of two minima and desolvation barrier. Moreover, we demand adjustable exponents to control the short- and long-range behaviors. The function is therefore segmented into three parts for better controlling these parameters.

In the equation below, for r < r′, we demanded a Lennard–Jones type of interaction, where k controlled the width of the first potential well. For r > r^†, we set one boundary to be r^† such that U(r^†) has a positive value. Once r increases, U(r) decreases toward the most negative value at r = r". Finally, the long tail behavior is controlled by the power of r²/r^2m. Therefore, U(r) converges to zero when r is large and m > 2. As to r′ < r < r^†, we demanded that at the junctions both force and potential have to be continuous. The function is therefore segmented into three sections separated by r′ and r^†.

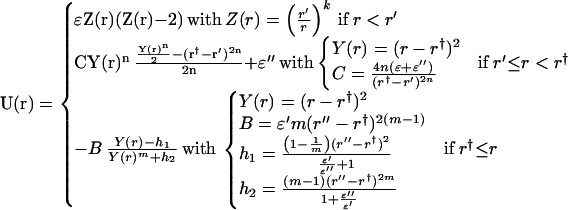Multicanonical Sampling Method

In the canonical ensemble at a temperature T, the probability distribution, P_c, of the potential energy E is given by P_c(E; T) = (1/Z_c)n(E)e^−E/k_BT , with n(E) as the spectral density and Z_c = ∑_En(E)e^−E/k_BT.

In our study, the roughness of the energy landscape increases because of the presence of the desolvation barrier. Consequently, trapping in local minima of the energy landscape is easily encountered. Once sampling difficulty emerges, we overcome it by a multicanonical ensemble sampling techniques. This ensemble is defined by a flat energy distribution function, P_mc: P_mc(E) = (1/Z_mc)n(E)e^−W(E) = constant, where W(E), the weight function, is a function of E, and Z_mc = ∑_En(E)e^−W(E).

After the simulations, the reweighting formula converts P_mc back into the canonical distribution, P_c, at a temperature T (42): P_c(E; T) = (Z_mc/Z_c)P_mc(E)e^{W(E)−E/k_BT}. W(E) is not known a priori, and needs to be refined through iterated multicanonical simulations at a high temperature T_o until it covers sufficient wide range of E.