Abstract
Giemsa staining has been used for identifying individual human chromosomes. Giemsa-dark and -light bands generally are thought to correspond to GC-poor and GC-rich regions; however, several experiments showed that the correspondence is quite poor. To elucidate the precise relationship between GC content and Giemsa banding patterns, we developed an “in silico chromosome staining” method for reconstructing Giemsa bands computationally from the whole human genome sequence. Here we show that 850-level Giemsa bands are best correlated with the difference in GC content between a local window of 2.5 megabases and a regional window of 9.3 megabases along a chromosome. The correlations are of strong statistical significance for almost all 43 chromosomal arms. Our results clearly show that Giemsa-dark bands are locally GC-poor regions compared with the flanking regions. These findings are consistent with the model that matrix-associated regions, which are known to be AT-rich, are present more densely in Giemsa-dark bands than in -light bands.
Distinct patterns of Giemsa-dark (G) and -light (R) bands observed on mitotic chromosomes reflect regional differences in chromatin higher-order structures and functions at various levels. Giemsa bands are related to functional nuclear processes such as replication or transcription in the following points. First, DNA replication timing during the cell cycle differs; R bands are early-replicating, whereas G bands are late-replicating (1, 2). Second, R bands are gene-rich and contain most housekeeping genes as well as a large number of CpG islands, whereas G bands are gene-poor and preferentially contain tissue-specific genes (3, 4). Giemsa bands are related also to chromatin structures; the chromatins in G bands are more condensed than those in R bands during both metaphase and interphase (5, 6). Recently, G- and R-band DNAs were demonstrated to form discrete domains in the interphase cell nucleus, and they are differently located in the nucleus; G-band DNA is localized at the nuclear periphery, whereas R-band DNA is in the interior of the nucleus (7).
Bernardi et al. (8, 9) proposed that the human genome is composed of isochores, long DNA segments (≫300 kb) that are homogeneous in GC content. G and R bands generally were thought to correspond to GC-poor and -rich isochores, respectively. Recently, 338 clones were mapped to 850-level bands of varying staining intensity, and the sequence analysis of the regions surrounding these clones confirmed that G bands are more AT-rich than R bands with statistical significance (10). However, the general correspondence between isochores and cytogenetic bands is only an approximation. Compositional maps of human chromosomes revealed that (i) G bands are homogeneous in GC content and essentially consist of GC-poor isochores, and in contrast, (ii) R bands are heterogeneous and contain both GC-rich and -poor isochores (11, 12). These results indicate that Giemsa banding patterns cannot be explained only by the difference in base composition. Thus, the relationship between the nucleotide sequence and cytogenetic bands still has remained elusive. The purpose of this study is to elucidate the precise relationship between Giemsa bands and genome sequences by using the draft sequence of the whole human genome (13). In this article, we show that G bands are the regions in which the GC content is relatively lower than that of the surrounding regions.
Materials and Methods
Data.
DNA sequences of the draft human genome (the version of October 7, 2000) were downloaded from the web site genome.ucsc.edu/(13). The relative position of each boundary between neighboring Giemsa bands in relation to the total euchromatic portion of each chromosomal arm was obtained from Francke (14).
Calculation of the Similarity Score.
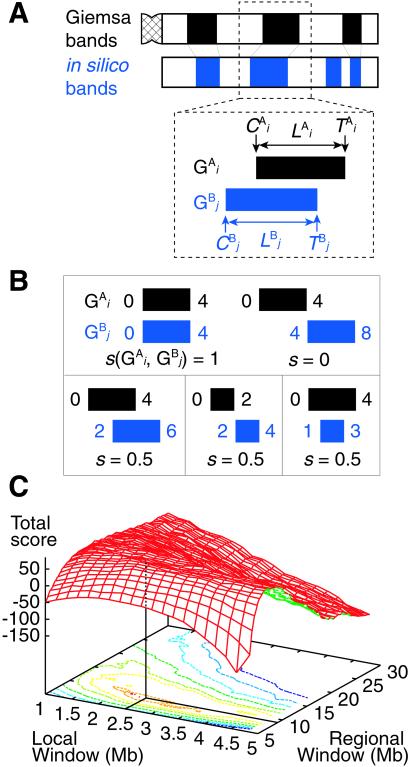
The basic idea to calculate the similarity score S between Giemsa bands and in silico bands is to determine the optimal “alignment” of G bands by using dynamic programming (15). Let the i-th G band in a Giemsa banding pattern (pattern A) and the j-th G band in an in silico banding pattern (pattern B) be G and G
and G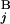 , respectively (Fig. 2A). The local score s(G
, respectively (Fig. 2A). The local score s(G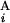 , G
, G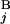 ) between G
) between G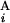 and G
and G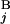 is calculated by the expression s(G
is calculated by the expression s(G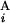 , G
, G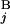 ) = 1 − (|C
) = 1 − (|C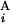 − C
− C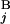 | + |T
| + |T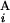 − T
− T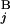 | + |L
| + |L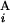 − L
− L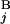 |)/2L, where C
|)/2L, where C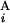 (C
(C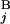 ), T
), T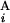 (T
(T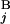 ) and L
) and L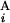 (L
(L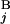 ) stand for the position of the centromeric end of G
) stand for the position of the centromeric end of G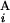 (G
(G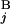 ), the position of the telomeric end of G
), the position of the telomeric end of G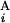 (G
(G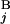 ), and the length of G
), and the length of G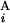 (G
(G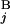 ), respectively. L stands for the average length of G bands at an 850-band level among all chromosomes. Based on the experimental data of relative band sizes (14) and the DNA length of each chromosomal arm, L is calculated as ≈4.0 megabases (Mb). We calculate the local score s(G
), respectively. L stands for the average length of G bands at an 850-band level among all chromosomes. Based on the experimental data of relative band sizes (14) and the DNA length of each chromosomal arm, L is calculated as ≈4.0 megabases (Mb). We calculate the local score s(G , G
, G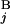 ) for all the combinations of G
) for all the combinations of G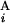 and G
and G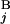 . The optimal alignment of two banding patterns is found by dynamic programming (15). Gap penalties g(G
. The optimal alignment of two banding patterns is found by dynamic programming (15). Gap penalties g(G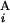 ) and g(G
) and g(G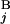 ) are defined as L
) are defined as L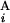 /L and L
/L and L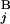 /L, respectively. We constructed a matrix F by the following recurrence equation: Fi,j = max[Fi−1,j−1 + s(G
/L, respectively. We constructed a matrix F by the following recurrence equation: Fi,j = max[Fi−1,j−1 + s(G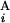 , G
, G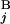 ), Fi−1,j − g(G
), Fi−1,j − g(G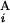 ), Fi,j−1 − g(G
), Fi,j−1 − g(G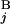 )]. The initial conditions were as follows: F0,0 = 0, Fi,0 = −Σ
)]. The initial conditions were as follows: F0,0 = 0, Fi,0 = −Σ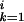 g(G
g(G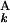 ), F0,j = −Σ
), F0,j = −Σ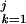 g(G
g(G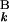 ). Fm,n gives the score of the optimal alignment, where m and n are the numbers of G bands in the patterns A and B. Fm,n is defined as the similarity score S between banding patterns A and B.
). Fm,n gives the score of the optimal alignment, where m and n are the numbers of G bands in the patterns A and B. Fm,n is defined as the similarity score S between banding patterns A and B.
Figure 2.
(A) Calculation of the similarity score S between Giemsa and in silico bands (see Materials and Methods). (B) Examples of the calculation of s(G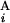 , G
, G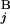 ). The coordinates of the centromeric and the telomeric ends of G
). The coordinates of the centromeric and the telomeric ends of G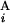 (G
(G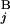 ) are shown in Mb at the ends of G
) are shown in Mb at the ends of G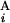 (G
(G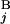 ). In the case of a perfect match, the expression of s(G
). In the case of a perfect match, the expression of s(G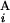 , G
, G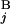 ) gives one (Upper Left). When the positions of G
) gives one (Upper Left). When the positions of G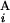 and G
and G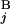 are different by L = 4 Mb, s(G
are different by L = 4 Mb, s(G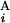 , G
, G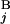 ) is equal to zero (Upper Right). Depicted are three examples of “half matches,” i.e., s(G
) is equal to zero (Upper Right). Depicted are three examples of “half matches,” i.e., s(G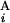 , G
, G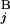 ) = 0.5 (Lower). (C) The sum of the similarity scores for all 43 chromosomal arms. The total scores were calculated for all the combinations of local and regional window sizes. These window sizes were changed independently by 0.1-Mb steps from 1 to 5 Mb for a local window and 5 to 30 Mb for a regional window. The local and regional window sizes that maximize the total score are 2.5 and 9.3 Mb, respectively. Contours are plotted at −50, −25, 0, 25, 50, 62.5, 75, and 80 (from blue to red).
) = 0.5 (Lower). (C) The sum of the similarity scores for all 43 chromosomal arms. The total scores were calculated for all the combinations of local and regional window sizes. These window sizes were changed independently by 0.1-Mb steps from 1 to 5 Mb for a local window and 5 to 30 Mb for a regional window. The local and regional window sizes that maximize the total score are 2.5 and 9.3 Mb, respectively. Contours are plotted at −50, −25, 0, 25, 50, 62.5, 75, and 80 (from blue to red).
Statistical Test.
The sequence of each chromosomal arm was split into 10-kb fragments, and these fragments were shuffled randomly, yielding a shuffled sequence with the same length and average GC content as the whole sequence of the chromosome. For each shuffled sequence, in silico staining was conducted by using a local window of 2.5 Mb and a regional window of 9.3 Mb. The similarity score Sexp between Giemsa bands and the banding pattern constructed from the shuffled sequence was calculated. The simulation scheme was iterated 10,000 times. By using a normal distribution, the probability P for the observed similarity score Sobs was calculated for each chromosomal arm.
Results
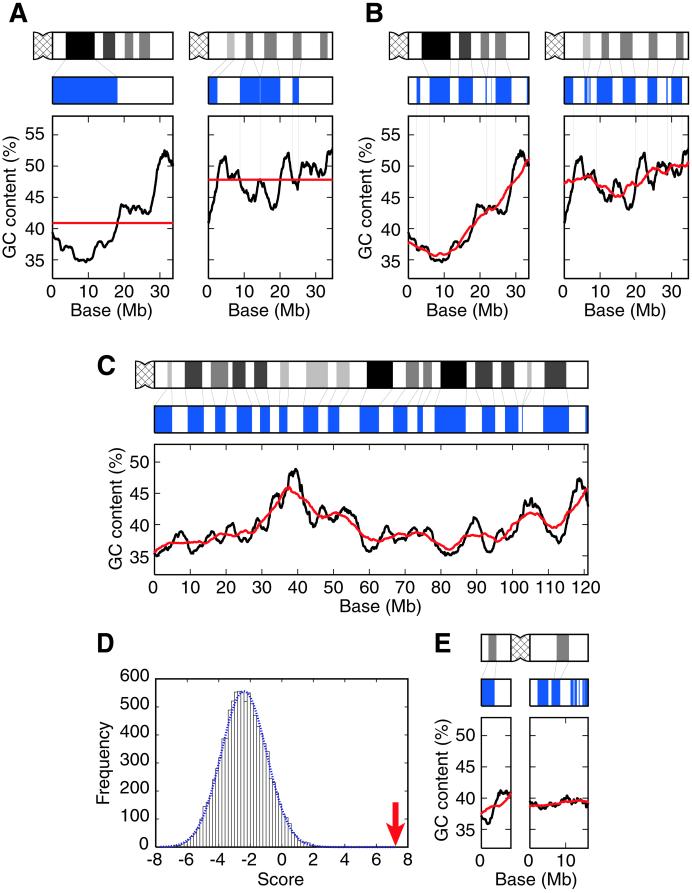
Fig. 1A shows the variation in GC content for human chromosomes 21 and 22, the complete DNA sequences of which are known (16, 17). We computationally stained the genomic regions in which the GC content in a window is lower than the average GC content over the chromosome, obtaining completely different patterns from the Giemsa bands experimentally observed. Therefore, the simple correspondence between GC-poor regions and G bands or that between GC-rich regions and R bands is not precise. Fig. 1A rather implies a possible correspondence between G bands and locally GC-poor regions compared with the flanking regions. Therefore, we invented a “two-window analysis” in which two windows with different sizes are used for detecting the regions in which the GC content is lower than that of the flanking regions (Fig. 1B). The diagrams in blue were obtained by computationally staining the regions in which the GC content for a local window (2.5-Mb) is lower than that for a regional window (9.3-Mb). The sizes of the two windows were chosen to optimize the correspondence between in silico bands and Giemsa bands (see below). We refer to the method of two windows for computationally producing such patterns as “in silico staining,” and the patterns obtained by in silico staining as “in silico bands.” In silico bands are very similar to Giemsa bands in both chromosomes with the exception of the centromeric or telomeric regions (Fig. 1B).
Figure 1.
Reconstruction of Giemsa bands in silico. (A) No correspondence between G bands and GC-poor regions or R bands and GC-rich regions in chromosomes 21 (Left) and 22 (Right). The Giemsa banding pattern shown in black (Top) was obtained from Francke (14). The diagram in blue (Middle) was obtained by computationally staining the regions in which the GC content for a 2.5-Mb window is lower than the average GC content over the chromosome. The graph at Bottom shows the variation in GC content for a 2.5-Mb window sliding in 10-kb steps across the chromosome (black line) and the average GC content (red line)—40.9% (Left) and 47.8% (Right). The number of nucleotides used for the calculation of the GC content becomes smaller than 2.5 Mb when the window contains chromosomal ends or strings of Ns (ambiguous nucleotides or sequence gaps). (B) Correlation between Giemsa bands and in silico bands in chromosomes 21 (Left) and 22 (Right). Giemsa bands are shown in black (Top). The diagram in blue (Middle) shows in silico bands obtained by computationally staining the regions in which the GC content for a 2.5-Mb window is lower than that for a 9.3-Mb window. The graph at Bottom shows the variation in GC content for a 2.5-Mb local window (black line) and a 9.3-Mb regional window (red line) sliding in 10-kb steps across the chromosome. The thin lines between Giemsa and in silico bands denote aligned G bands. (C) The best correlation between Giemsa bands and in silico bands observed for chromosome 3q. Giemsa bands are shown in black (Top) and in silico bands are shown in blue (Middle). The black and red lines in the graph at Bottom show the variation in GC content for 2.5- and 9.3-Mb windows, respectively. The thin lines between Giemsa and in silico bands denote aligned G bands. (D) Distribution of the similarity scores in a simulation for chromosome 3q. The dotted blue line represents a normal distribution having the values of the mean and the standard deviation calculated from 10,000 random samples. The arrow shows the observed similarity score between in silico and Giemsa bands (P = 9 × 10−12). (E) A poor correspondence between Giemsa and in silico bands for chromosome Y. The representation is the same as that described for C.
We quantified the similarity between Giemsa bands and in silico bands by defining a similarity score S. The basic idea to calculate S is to find out the best alignment of G bands by using dynamic programming (15). The aligned G bands of a perfect match contribute by one to the score S (Fig. 2B, Upper Left). Therefore, the score S has a meaning of the total number of aligned G bands. More similarity gives a higher score. For example, the similarity scores between Giemsa and in silico bands are 1.93 and 2.63 for chromosomes 21 and 22, respectively (see Fig. 1B); in contrast, the similarity scores between Giemsa bands and the blue diagrams shown in Fig. 1A are −3.70 and 0.59 for chromosomes 21 and 22, respectively. Therefore, the score S is an informative measure for detecting the similarity between two banding patterns. To optimize the sizes of local and regional windows, we calculated the sum of the scores for all 43 chromosomal arms by using all the combinations of local and regional window sizes. These window sizes were changed independently by 0.1-Mb steps. We then found that the total score reaches the maximum when the local and regional window sizes are 2.5 and 9.3 Mb, respectively (Fig. 2C). Fig. 3 shows the comparisons between Giemsa and in silico bands obtained by using windows of 2.5 and 9.3 Mb for all chromosomes.
Figure 3.
Giemsa and in silico bands for all chromosomes. Short (p) and long (q) arms are positioned left and right, respectively. Giemsa bands obtained from Francke (14) are shown in black ideograms. The bands depicted in black, gray, and white represent euchromatins, and the darkness of each band reflects the shading. Pericentromeric heterochromatin and heteromorphic regions of chromosomes 1, 3, 9, 16, 19, and Y are depicted by crosshatched and horizontal lines, respectively. In silico bands constructed by using windows of 2.5 and 9.3 Mb are shown in blue. The thin lines between Giemsa and in silico bands denote aligned G bands. The coordinates of in silico bands for each chromosomal arm are available at the web site www.cib.nig.ac.jp/dda/home.html.
To evaluate the statistical significance of the similarities between Giemsa and in silico bands, we performed computer simulations for each of 43 chromosomal arms. Table 1 shows the result of the statistical test. Of 43 chromosomal arms, 33 are significant at a 5% level, and 30 are significant at a 1% level. The best correspondence between Giemsa and in silico bands is observed for chromosome 3q (P ≈ 10−11; Fig. 1 C and D). We can see almost perfect one-to-one correspondence of G bands throughout the chromosomal arm, although it is more than 120 Mb long. Of 10 chromosomal arms that do not show significant correlation, three arms are very short (<20 Mb). Note that our method does not work well for regions so close to the chromosomal end that a regional window cannot be taken. Thus, it is reasonable that a very short chromosomal arm such as chromosomes Yp or Yq shows a poor correlation (Fig. 1E). It also explains the observation that the correlation is relatively weak in the regions close to the chromosomal ends. Therefore, we conclude that Giemsa banding patterns are reconstructed successfully by in silico staining for almost all the chromosomal arms.
Table 1.
Statistics of in silico staining
| Chromosome | Sobs | Sexp | P | Length, Mb |
|---|---|---|---|---|
| 1p | 2.50 | −3.49 ± 1.48 | 3 × 10−5* | 133 |
| 1q | −0.23 | −3.85 ± 1.42 | 5 × 10−3* | 118 |
| 2p | −0.18 | −3.07 ± 1.21 | 9 × 10−3* | 94 |
| 2q | 3.84 | −5.25 ± 1.61 | 7 × 10−9* | 155 |
| 3p | 1.10 | −1.68 ± 1.36 | 2 × 10−2† | 103 |
| 3q | 7.22 | −2.40 ± 1.43 | 9 × 10−12* | 121 |
| 4p | 0.51 | −3.08 ± 0.96 | 9 × 10−5* | 52 |
| 4q | 2.69 | −6.39 ± 1.63 | 1 × 10−8* | 147 |
| 5p | 1.47 | −1.70 ± 0.97 | 5 × 10−4* | 50 |
| 5q | −1.02 | −8.31 ± 1.54 | 1 × 10−6* | 149 |
| 6p | 4.00 | −0.68 ± 1.02 | 2 × 10−6* | 64 |
| 6q | 2.50 | −4.45 ± 1.46 | 1 × 10−6* | 115 |
| 7p | 2.86 | −0.01 ± 0.99 | 2 × 10−3* | 58 |
| 7q | 2.51 | −2.95 ± 1.32 | 2 × 10−5* | 105 |
| 8p | 2.40 | −2.11 ± 0.93 | 7 × 10−7* | 48 |
| 8q | 6.35 | −1.36 ± 1.36 | 6 × 10−9* | 101 |
| 9p | 1.16 | 0.95 ± 0.87 | 4 × 10−1 | 45 |
| 9q | 4.68 | 2.37 ± 1.05 | 1 × 10−2† | 74 |
| 10p | 0.63 | 0.19 ± 0.84 | 3 × 10−1 | 41 |
| 10q | 1.08 | −2.25 ± 1.34 | 7 × 10−3* | 100 |
| 11p | 3.60 | −1.53 ± 1.00 | 1 × 10−7* | 53 |
| 11q | 2.24 | −2.09 ± 1.28 | 4 × 10−4* | 94 |
| 12p | 0.80 | −0.06 ± 0.77 | 1 × 10−1 | 35 |
| 12q | 2.23 | −1.40 ± 1.36 | 4 × 10−3* | 105 |
| 13q | 4.73 | −0.25 ± 1.40 | 2 × 10−4* | 103 |
| 14q | 4.78 | 0.26 ± 1.20 | 8 × 10−5* | 90 |
| 15q | 3.89 | 1.63 ± 1.14 | 2 × 10−2† | 84 |
| 16p | 1.58 | −1.54 ± 0.79 | 4 × 10−5* | 40 |
| 16q | 2.65 | −0.92 ± 0.85 | 1 × 10−5* | 48 |
| 17p | −0.53 | −1.07 ± 0.51 | 1 × 10−1 | 24 |
| 17q | 0.94 | −0.05 ± 0.96 | 2 × 10−1 | 61 |
| 18p | −0.47 | −0.51 ± 0.54 | 5 × 10−1 | 18 |
| 18q | 1.12 | −4.79 ± 1.01 | 2 × 10−9* | 65 |
| 19p | −1.62 | −1.97 ± 0.59 | 3 × 10−1 | 28 |
| 19q | 1.59 | −1.10 ± 0.89 | 1 × 10−3* | 43 |
| 20p | 1.99 | −0.86 ± 0.67 | 1 × 10−5* | 27 |
| 20q | 2.98 | 0.21 ± 0.78 | 2 × 10−4* | 35 |
| 21q | 1.93 | −1.10 ± 0.70 | 7 × 10−6* | 33 |
| 22q | 2.63 | 0.81 ± 0.70 | 4 × 10−3* | 34 |
| Xp | 0.21 | −0.05 ± 0.95 | 4 × 10−1 | 53 |
| Xq | 1.60 | −5.57 ± 1.33 | 3 × 10−8* | 106 |
| Yp | 0.47 | 0.02 ± 0.34 | 9 × 10−2 | 8 |
| Yq | −1.31 | −1.04 ± 0.42 | 7 × 10−1 | 16 |
The observed similarity score, Sobs, is calculated using Giemsa and in silico bands. The expected similarity score, Sexp, is calculated using Giemsa bands and a pattern generated from a random sequence. Sexp is given as mean ± s.d.
, P < 0.01. †, P < 0.05.
It is known that the staining intensity is not uniform among G bands. G bands in Fig. 3 are depicted by four different degrees of darkness: solid black, light black, dark gray, and light gray. To understand the relationship between the degree of darkness and the GC content, we calculated the average GC content over all the in silico G bands that correspond to a particular degree of darkness of G bands. The GC contents for the four different degrees of darkness are calculated as 36.5, 38.0, 40.3, and 41.8% for solid black, light black, dark gray, and light gray, respectively. Thus, we support the idea that the difference in the staining intensity of G bands is related to the difference in the GC content (18).
Discussion
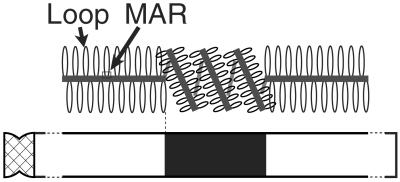
The successful reconstruction of Giemsa bands by in silico staining could be explained from the viewpoint of chromatin structures. Chromatin DNA is composed of loops and matrix-associated regions (MARs), the regions of DNA attaching to nuclear scaffolds. Saitoh and Laemmli (5) experimentally detected a lineup of MARs named AT-queue using specific dye. They proposed a model of a metaphase chromatin structure in which G bands are the regions where AT-queue is tightly folded, whereas R bands are the regions where AT-queue is unfolded and located along a longitudinal axis of a chromatin (Fig. 4). According to Saitoh and Laemmli's model, MARs are present densely in G bands and sparsely in R bands. MARs are known to be AT-rich (≈70%) but lack any clear consensus motifs (19), although some patterns common to MARs have been reported (20). Our finding of the correlation between G bands and the regions in which the GC content is lower than that of the flanking regions would be explained in the following way. Suppose that a genomic region is under a functional constraint to have a compact chromatin structure. A decrease in GC content would be selectively advantageous in the region or an increase in GC content would be disadvantageous in the region, because many different sites can function as MARs in an AT-rich region. Note that MARs are AT-rich but do not have any clear consensus motifs. Therefore, the regions under the constraint of compact chromatin structures would be subject to a selective pressure for reducing the GC content or against increasing the GC content. That is, structural constraint would keep the region in a G band more AT-rich than the flanking R-band regions.
Figure 4.
Model of a metaphase chromatin structure adapted from Saitoh and Laemmli (5).
The optimal sizes of local and regional windows, 2.5 and 9.3 Mb, respectively, are reasonable because of the following reasons. The average length of Giemsa bands among all chromosomes is ≈4 Mb (see Materials and Methods). Because a 9.3-Mb regional window generally contains both a G band and its flanking R band, this size of a regional window can reflect properly the GC content of the surrounding region of a local window. On the other hand, the entire region of a 2.5-Mb local window generally can be contained in either a G or an R band, because almost all bands are larger than 2.5 Mb. Because a local window with a size smaller than 2.5 Mb tends to yield larger degrees of statistical fluctuation, 2.5 Mb is considered to be an appropriate size for a local window to detect sensitively the difference in GC content between a G band and the flanking R band. It implies that the performance of our method may not be good for fine bands that are smaller than the local window size. For example, the correspondences of in silico bands to two G bands at the positions of ≈4 and 105 Mb in chromosome 3q (Fig. 1C) are relatively poor, because those bands are experimentally shown very small, approximately only 1.2-Mb long for both.
The correlation between Giemsa and in silico bands is expected to improve further by using the data of genome-wide fluorescence in situ hybridization mapping (10). This expectation is made because, first, we assume that the terminus of a DNA sequence of each chromosomal arm exactly corresponds to a boundary between a C band (constitutive heterochromatin) and the first euchromatic band. However, the DNA sequences used for the analyses would contain constitutive heterochromatin regions as well as euchromatin regions. For chromosome 22q, for example, the in silico G band at the centromeric end does not correspond to any G bands experimentally observed (Fig. 1B). This observation is explained well by the idea that the available DNA sequence of chromosome 22q contains the pericentromeric heterochromatin region, because constitutive heterochromatins are highly AT-rich. Such extra in silico G bands at the centromeric ends are observed also in chromosomes 1q, 5q, 7q, 10q, 12p, 14q, 16q, and 19q (Fig. 3). Second, in silico bands predicted from a DNA sequence is aligned to cytogenetic bands without considering the difference of DNA density. In other words, a compaction ratio between G and R bands is assumed to be one, although it is known that G bands are more condensed than R bands (5, 6). Therefore, the performance would improve by taking into account the difference of a compaction ratio. The improvement of the performance may not be expected much, because the ratio of the G-band length to the length of an R band containing the same amount of DNA would be on the order of only the cube root of the compaction ratio. Although these assumptions may cause a limited number of poorly corresponding in silico bands, the correspondence would improve by incorporating the fluorescence in situ hybridization mapping data into our analysis.
The origin of isochores is in a longstanding controversy. Bernardi et al. (8, 9) proposed that isochores arose from adaptive evolution. They argue that an increase in GC content is advantageous in warm-blooded organisms, because G–C bonds contribute to greater thermodynamic stability of RNA, DNA, and proteins. The opposing view is that isochores arose from mutational biases (21–23). Our results imply the relationship between isochores and chromatin structures, inferring a different mechanism of isochore formation. We propose that the functional constraint for retaining compact chromatin would be one contributor to forming isochores. Note that our method of two-window analysis for identifying Giemsa bands implies the presence of another factor that determines the regional trend in GC content. The mechanism of determining the regional trend in GC content, however, remains an open question.
Acknowledgments
We thank H. Akashi, T. D. Andrews, W. M. Fitch, T. Imanishi, H. Iwama, N. Sueoka, A. Wyndham, and all the members of the DNA Data Analysis Laboratory for valuable comments and discussion. Y.N. is supported financially by the Japan Society for the Promotion of Science. T.G. is supported by a grant from the Ministry of Education, Science, Sports, and Culture.
Abbreviations
- G
Giemsa-dark
- R
Giemsa-light
- Mb
megabase(s)
- MAR
matrix-associated region
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Drouin R, Holmquist G P, Richer C-L. Adv Hum Genet. 1994;22:47–115. doi: 10.1007/978-1-4757-9062-7_2. [DOI] [PubMed] [Google Scholar]
- 2.Tenzen T, Yamagata T, Fukagawa T, Sugaya K, Ando A, Inoko H, Gojobori T, Fujiyama A, Okumura K, Ikemura T. Mol Cell Biol. 1997;17:4043–4050. doi: 10.1128/mcb.17.7.4043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Craig J M, Bickmore W A. BioEssays. 1993;15:349–354. doi: 10.1002/bies.950150510. [DOI] [PubMed] [Google Scholar]
- 4.Cross S H, Bird A P. Curr Opin Genet Dev. 1995;5:309–314. doi: 10.1016/0959-437x(95)80044-1. [DOI] [PubMed] [Google Scholar]
- 5.Saitoh Y, Laemmli U K. Cell. 1994;76:609–622. doi: 10.1016/0092-8674(94)90502-9. [DOI] [PubMed] [Google Scholar]
- 6.Yokota H, Singer M J, van den Engh G J, Trask B J. Chromosome Res. 1997;5:157–166. doi: 10.1023/a:1018438729203. [DOI] [PubMed] [Google Scholar]
- 7.Cremer T, Cremer C. Nat Rev Genet. 2001;2:292–301. doi: 10.1038/35066075. [DOI] [PubMed] [Google Scholar]
- 8.Bernardi G, Olofsson B, Filipski J, Zerial M, Salinas J, Cuny G, Meunier-Rotival M, Rodier F. Science. 1985;228:953–958. doi: 10.1126/science.4001930. [DOI] [PubMed] [Google Scholar]
- 9.Bernardi G. Gene. 2000;241:3–17. doi: 10.1016/s0378-1119(99)00485-0. [DOI] [PubMed] [Google Scholar]
- 10.The BAC Resource Consortium. Nature (London) 2001;409:953–958. [Google Scholar]
- 11.Gardiner K, Aissani B, Bernardi G. EMBO J. 1990;9:1853–1858. doi: 10.1002/j.1460-2075.1990.tb08310.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Saccone S, De Sario A, Wiegant J, Raap A K, Della Valle G, Bernardi G. Proc Natl Acad Sci USA. 1933;90:11929–11933. doi: 10.1073/pnas.90.24.11929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.International Human Genome Sequencing Consortium. Nature (London) 2001;409:860–921. [Google Scholar]
- 14.Francke U. Cytogenet Cell Genet. 1994;65:206–219. doi: 10.1159/000133633. [DOI] [PubMed] [Google Scholar]
- 15.Needleman S B, Wunsch C D. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 16.Hattori M, Fujiyama A, Taylor T D, Watanabe H, Yada T, Park H-S, Toyoda A, Ishii K, Totoki Y, Choi D-K, et al. Nature (London) 2000;405:311–319. doi: 10.1038/35012518. [DOI] [PubMed] [Google Scholar]
- 17.Dunham I, Hunt A R, Collins J E, Bruskiewich R, Beare D M, Clamp M, Smink L J, Alinscough R, Almeida J P, Babbage A, et al. Nature (London) 1999;402:489–495. doi: 10.1038/990031. [DOI] [PubMed] [Google Scholar]
- 18.Federico C, Andreozzi L, Saccone S, Bernardi G. Chromosome Res. 2000;8:737–746. doi: 10.1023/a:1026797522102. [DOI] [PubMed] [Google Scholar]
- 19.Boulikas T. Int Rev Cytol. 1995;162:279–388. doi: 10.1016/s0074-7696(08)61234-6. [DOI] [PubMed] [Google Scholar]
- 20.Singh G B, Kramer J A, Krawets S A. Nucleic Acids Res. 1997;25:1419–1425. doi: 10.1093/nar/25.7.1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sueoka N. Proc Natl Acad Sci USA. 1988;85:2653–2657. doi: 10.1073/pnas.85.8.2653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wolfe K H, Sharp P M, Li W-H. Nature (London) 1989;337:283–285. doi: 10.1038/337283a0. [DOI] [PubMed] [Google Scholar]
- 23.Francino M P, Ochman H. Nature (London) 1999;400:30–31. doi: 10.1038/21804. [DOI] [PubMed] [Google Scholar]