Abstract

Metal injection molding (MIM) is an advanced manufacturing technology for producing complex metal parts with precise dimensions. Multiattribute decision making (MADM) can convert multiple quality attributes into a single overall quality score (OQS). To improve multiple quality attributes of the MIM compacts, a reasonable multiobjective optimization method should be applied. This paper proposes a Taguchi-MADM-based hybrid optimization method of the MIM process. It consists of the following main steps: (1) designing the experiment using a Taguchi orthogonal array, (2) conducting the experiment and measuring multiple quality attributes at each experimental trial, (3) calculating the OQS values at every experimental trial using some popular MADM methods, (4) selecting the best suitable MADM method from among some MADMs, and (5) determining optimal MIM process parameters to maximize the OQS obtained from the selected MADM using the Taguchi method. By using this method, this work determines the optimal MIM process parameters (injection pressure, injection temperature, powder loading, mold temperature, holding pressure, and injection speed) for improving multiple quality attributes (flexural strength, density, and surface appearance) of the MIM compacts with 3l6L stainless steel powder. The proposed method could be actively applied to many practical multiple quality attribute optimization problems in the manufacturing industry.
1. Introduction
Metal injection molding (MIM)/powder injection molding (PIM) is an advanced manufacturing technology that fabricates complex metal parts with precise dimensions, and it is similar to traditional plastic injection molding.1 The MIM is a combination of powder metallurgy and injection molding technology, and it requires low production cost to manufacture complex parts with small size in mass production.2,3 It involves the injection molding of feedstock blended metal powder and binders, debinding, and sintering. The MIM provides a rapid and convenient technique for mass manufacture of components with complex shape, small size, and superior surface finish.4 The MIM technology consists of four major steps: mixing, injection, debinding, and sintering.5
To improve the quality of the MIM spectra, it is necessary to introduce optimization techniques. The optimization of the MIM process is one of the major issues in MIM practice, and it is vital to satisfy the increasing quality demands of the MIM compacts.
The common optimization method is a trial and error method, and it is very time-consuming and costly because it requires massive experiments.5 Many works have applied various experimental design methods and optimization methods to analyze the effects of the MIM process parameters and determine the optimal process parameters. Tatt et al.5 applied the Taguchi method to determine the optimal molding process parameters for green defects and green density of MIM feedstock. Chen et al.6 used the Taguchi method to determine the optimal process parameters for improving the products’ quality and decreasing the costs. Amin et al.7 analyzed the effects of PIM process parameters on the density of the green body of cemented carbide (WC-Co)-based PIM feedstock and optimized the process parameters using the Taguchi Method with L18 orthogonal array (OA). Mustafa et al.8 optimized the green strength of the parts manufactured by MIM using the Taguchi method. Xie et al.9 investigated the effects of the process parameters on flexural strength and density of ultrafine WC/12Co powder injection molding (PIM) compacts and optimized the process parameters using the Taguchi method with L16(45) OA and analysis of variance (ANOVA). They determined the optimal process parameters on the flexural strength and density of molded compacts, respectively. Zhao et al.10 reviewed some experimental design methods such as Taguchi orthogonal design, central composite design (CCD), Box-Behnken design (BBD), and sampling methods, mathematical modeling methods that considered nonlinear relationship between control factors, and optimization goals using multiple regression analysis, artificial neural networks, and optimization methods of PIM process parameters. Jannah et al.11 analyzed the effects of three process parameters (temperature, holding time, and addition of Sn) on density in the MIM sintering process and determined the optimal values of the process parameters using the Taguchi method.
The Taguchi method is commonly used to optimize a single quality attribute. In the MIM process practice, it is desirable to determine reasonable process parameters to improve multiple quality attributes, simultaneously. Huang et al.3 analyzed the effects of the injection molding and sintering process parameters on dimensions and mechanical properties of stainless steel MIM compact and determined three sintering process parameters to optimize simultaneously dimensional shrinkage rate, density, and hardness of the compacts using the Taguchi method and principal component analysis (PCA). They calculated the composite quality indicator as the sum of the first and second principal components obtained from the PCA and then determined the optimal process parameters to optimize the sum. However, there was significant information loss because the method used only two principal components. Askari and Momeni12 optimized the injection parameters such as injection speed, injection temperature, mold temperature, holding pressure for Fe–2Ni–2Cu feedstock in the MIM process, and influence of the process parameters on the density and flexural strength using the Taguchi method. Rezaei and Askari13 studied the MIM of the thin surgical component using the palm-stearin-based SS316L feedstock. They determined the optimal solids loading of the feedstock, developed the moldability index, and established the process window based on the experiments to present appropriate injection parameters. They evaluated the significance and mutual coupling of each MIM process parameter using an analysis of variance. They optimized the process parameters, including injection temperature, injection speed, holding pressure, holding time, and injection pressure to maximize the green density.
Many practical MIM process optimization problems have multiple quality attributes to be optimized, not only one attribute. Therefore, it needs to optimize multiple quality attributes, simultaneously. It becomes a multiobjective optimization (MOO) problem. The MOO problem could be solved by converting it to a single objective optimization (SOO) problem. To convert the multiple quality attributes into a single overall quality attribute, some popular multiattribute decision making (MADM) methods such as simple additive weighting (SAW) method, weighted product method (WPM), technique for order preference by similarity to ideal solution (TOPSIS), gray relational analysis (GRA), and rank sum ratio (RSR) method are applicable.
Some works converted the multiple quality attributes into a single overall quality attribute using MADMs, and then, the optimal process parameters were determined to improve the overall quality attribute. Lin et al.4 determined the optimal MIM processing parameters that maximize powder concentration uniformity and minimize volume shrinkage simultaneously using a hybrid approach based on the Taguchi method and GRA. Nor et al.14 determined the optimal injection molding parameters to improve three quality attributes (defects, strength, and density) for titanium alloy powder mixed with palm stearin and polyethylene using the Taguchi method and GRA. Moayyedian and Mamedov15 proposed a multiobjective optimization for minimizing shrinkage, warpage, and short shot based on the feasible moldability index using finite element analysis, Taguchi method, fuzzy analytic hierarchy process (AHP), and TOPSIS.
As mentioned above, different MADMs have been applied to convert multiple quality attributes into a single overall quality attribute. However, it is unknown which is the best MADM, and how to select the best suitable MADM for the given problem. The previous works did not consider why the specific MADMs were applied in their works and lacked full consideration to address this issue.
In this paper, we proposed the Taguchi-MADM-based hybrid optimization method of the MIM process and applied it to multiple quality optimizations of the MIM compacts with 3l6L stainless steel powder.
2. Methods
2.1. Experiment Procedure
The metal powder used in this study was gas-atomized 316L stainless steel powder with a density of 7.93 g/cm3 mixed with a binder consisting of poly(ethylene glycol), methyl polymethacrylate, and stearic acid. The binder composition was 73 wt % polyethylene glycol, 25 wt % polymethacrylate, and 2 wt % stearic acid. The size distributions of powder metal particles are in a bimodal distribution consisting of 70 wt % of coarse powder. The powder mixing equipment (SK-160 Two Roll Plastics Mixing Mill) was used to prepare the feedstock by mixing them for 2 h at the temperature of 150 °C. The injection molding was performed in a CJ80TB injection molding machine to produce the samples with 13 mm in diameter and 13 mm in height at injection temperatures of 130, 140, and 150 °C, injection pressures of 350, 450, and 550 bar, injection rates of 10, 15, and 20 ccm/s, holding pressure of 700, 900, and 1100 bar, and 45, 48, and 51 °C of mold temperature.
The density (D) of the compact was measured by the Archimedes method and by using the following equation:
| 1 |
where ρ is the density of the specimen, ρL is the density of the liquid, Wa is the weight in air, and WL is the weight in the liquid.
The flexural strength (FS) was measured using a 3-point bending flexural strength test in accordance with ISO20795-1. The specimens of 64 mm (length) × 10 mm (width) × 3.3 mm (thickness) were prepared. The specimens were investigated using a universal testing machine with two supports 20 mm apart and a crosshead speed of 5 mm/min. The FS was calculated in MPa as follows:
| 2 |
where L is the maximum load at fracture, d is the distance between the supports (=20 mm), w is the specimen thickness, and h is the height.
2.2. Taguchi-MADM-Based Hybrid Optimization Method of the MIM Process
This subsection proposed the Taguchi-MADM-based hybrid optimization method of the MIM process.
Let L quality attributes of the MIM compacts be y1, y2,···, and yL, and p controllable MIM process parameters be x1, x2,···, and xp. (L ≥ 2, p ≥ 2)
The main steps are as follows:
Step 1: Set the levels of the MIM process parameters and select a suitable Taguchi OA according to the numbers of the process parameters and their levels.
Step 2: Conduct the experiment according to the OA and measure the multiple quality attributes at every experimental trials.
Let xij be the value
of jth MIM process parameter, and yik be the measurement value of kth quality attribute at ith experimental
trial ( ), where n is the number
of experimental trials. The MIM process parameter values of every
experimental trial construct a process parameter matrix X= (xij)n×p, and the quality attribute
values of every experimental trial construct a decision matrix Y= (yik)n×L.
), where n is the number
of experimental trials. The MIM process parameter values of every
experimental trial construct a process parameter matrix X= (xij)n×p, and the quality attribute
values of every experimental trial construct a decision matrix Y= (yik)n×L.
Step 3: Calculate the overall quality score (OQS) values from L quality attributes at all the experimental trials using some popular MADMs such as SAW, WPM, TOPSIS, GRA and RSR.
For each MADM, the OQS at each experimental trial is as follows:
simple weighted sum in SAW,
weighted product in WPM,
relative closeness value in TOPSIS,
gray relational degree in GRA, and
rank sum ratio in RSR.
Step 4: Select the best suitable MADM method from among some available MADMs.
Step 4-1: Calculate the mean rank correlation coefficients (MRCs) and mean rank deviations (MRDs) between the OQS values from each MADM and those from other MADMs.
The MRC and MRD between the OQS
values from each MADM and other
MADMs are as follows: ( )
)
| 3 |
| 4 |
where Rmk is the rank correlation coefficient between the OQS values Sm1,···, Smi,···, Smn from mth MADM and the OQS values Sk1,···, Ski,···, Skn from kth MADM, and
| 5 |
is the mean deviation between the OQS ranks Srm1,···, Srmi,···, and Srmn from mth MADM and the OQS ranks Srk1,···, Srki,···, and Srkn obtained from kth MADM.
The higher the value of MRC is (the lower the value of MRD is), the better the OQS ranks from the MADM coincide with the OQS ranks from the other MADMs, and it is a more suitable MADM for the given problem. Namely, the MRC and MRD become the evaluating measures of the MADM.
Step 4-2: Ranks the MRCs and MRDs and selects the MADM with maximum MRC and minimum MRD as the best suitable MADM.
Step 5: Analyze the influences of the MIM process parameters using range percentages of the process parameters.
Step 5-1: Calculate the mean OQS values according to each level and their ranges for every process parameters as follows:
| 6 |
where Slk is the mean OQS value obtained from the selected MADM according to lth level for kth process parameter.
Step 5-2: Calculate the range percentages (RPs) of the process parameters as follows:
| 7 |
The higher the RP value, the larger the influence of the MIM process parameter is.
Step 6: Determine the optimal process parameters using the Taguchi optimization method.
The optimal condition consists of the levels with maximum mean OQS values at every MIM process parameters.
The main steps of SAW method are as follows:16
Step 1: Construct the normalized decision-matrix Z = (zik)n×L from Y = (yik)n×L using the following linear min–max normalization formula:
| 8 |
where K+ and K– are the index sets for the benefit and cost attributes, and ykmax and ykmin are the maximum and minimum values of the kth quality attribute, respectively.
Step 2: Calculate the simple weighted sums at every experimental trials using the following formula:
| 9 |
where wk denotes the weight of kth quality attribute ( ).
).
The calculated S1, ···, Si, ···, and Sn are the overall quality score values at every experimental trials. The higher the value is, the better the overall quality is.
The formula to calculate the
quality attribute weights using the
entropy weighting method is as follows (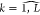 ):17
):17
| 10 |
where
| 11 |
The flowchart of the proposed multiple quality optimization method is shown in Figure 1.
Figure 1.
Flowchart of the proposed multiple quality optimization method.
There are many optimization techniques such as genetic algorithm (GA), simulated annealing (SA) algorithm, particle swarm optimization (PSO) algorithm, Taguchi method, etc. The Taguchi method is a pretty simple, clear, and practical optimization method because it requires small experimental trials and requires no additional operation parameters, while the intelligent optimization techniques such as GA, SA, and PSO require additional operation parameters and it is difficult to determine the reasonable values of the operation parameters. Because of its simplicity, feasibility, and practicability, this work selected the Taguchi method as an optimization technique for the MIM process.
2.3. Design of Experiment
The MIM process consists of mixing, injection, debinding, and sintering. This work selects six injection process parameters such as injection pressure (IP), injection temperature (IT), powder loading (PL), mold temperature (MT), holding pressure (HP), and injection speed (IS) as the main controllable MIM process parameters and keeps the other parameters to constants. This work also considers three quality attributes such as flexural strength (FS), density (D), and surface appearance (SA) of the injection-molded green compacts. The FS and D are the benefit attributes (higher-the-better), and SA is the cost attribute (lower-the-better). In this work, the MIM process parameters and their levels were determined on the basis of previous works and experiments.
Table 1 shows the MIM process parameters and their levels.
Table 1. MIM Process Parameters and Their Levels.
| levels | process parameters | |||||
|---|---|---|---|---|---|---|
| IP (bar) | IT (°C) | PL (% vol) | MT (°C) | HP (bar) | IS (ccm/s) | |
| level 1 | 350 | 130 | 64 | 45 | 700 | 10 |
| level 2 | 450 | 140 | 64.5 | 48 | 900 | 15 |
| level 3 | 550 | 150 | 65 | 51 | 1100 | 20 |
The ranges (lower and upper limits) and levels of the MIM process parameters were selected based on the related previous studies and the preliminary experiment. Namely, the ranges and levels of the IP and IT were limited by the rheological result of the feedstock from the previous study (refs (18) and (19)), and the range and levels of the PL were selected based on the critical powder loading from the previous study (ref (20)). The ranges of the other MIM process parameters were selected based on the preliminary experiment done prior to the optimization using the design of the experiment (DOE).
As the number of process parameters is 6 and the number of levels is 3, Taguchi OA L27(313) is selected for the design of experiment. The six process parameters are assigned to 1st, 2nd, 5th, 9th, 12th, and 13th columns in the OA (Table 2).
Table 2. Taguchi OA L27(313) with Six Process Parameters.
| trial no. | MIM process parameters | |||||
|---|---|---|---|---|---|---|
| IP | IT | PL | MT | HP | IS | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 |
| 4 | 1 | 2 | 1 | 2 | 3 | 3 |
| 5 | 1 | 2 | 2 | 3 | 1 | 1 |
| 6 | 1 | 2 | 3 | 1 | 2 | 2 |
| 7 | 1 | 3 | 1 | 3 | 2 | 2 |
| 8 | 1 | 3 | 2 | 1 | 3 | 3 |
| 9 | 1 | 3 | 3 | 2 | 1 | 1 |
| 10 | 2 | 1 | 1 | 2 | 2 | 3 |
| 11 | 2 | 1 | 2 | 3 | 3 | 1 |
| 12 | 2 | 1 | 3 | 1 | 1 | 2 |
| 13 | 2 | 2 | 1 | 3 | 1 | 2 |
| 14 | 2 | 2 | 2 | 1 | 2 | 3 |
| 15 | 2 | 2 | 3 | 2 | 3 | 1 |
| 16 | 2 | 3 | 1 | 1 | 3 | 1 |
| 17 | 2 | 3 | 2 | 2 | 1 | 2 |
| 18 | 2 | 3 | 3 | 3 | 2 | 3 |
| 19 | 3 | 1 | 1 | 3 | 3 | 2 |
| 20 | 3 | 1 | 2 | 1 | 1 | 3 |
| 21 | 3 | 1 | 3 | 2 | 2 | 1 |
| 22 | 3 | 2 | 1 | 1 | 2 | 1 |
| 23 | 3 | 2 | 2 | 2 | 3 | 2 |
| 24 | 3 | 2 | 3 | 3 | 1 | 3 |
| 25 | 3 | 3 | 1 | 2 | 1 | 3 |
| 26 | 3 | 3 | 2 | 3 | 2 | 1 |
| 27 | 3 | 3 | 3 | 1 | 3 | 2 |
3. Results and Discussion
This section conducts multiple quality optimizations of the MIM compacts with 3l6L stainless steel powder using the proposed method.
We developed the MATLAB program for the proposed method in MATLAB R2012a environment and applied it to the given optimization problem.
Table 3 shows the experimental results according to OA L27(313). At each experimental trial according to OA L27(313), three specimens were prepared and the average values of FS, D, and SA of the specimens were taken.
Table 3. Experimental Results According to OA L27(313).
| trial no. | MIM process parameters | quality attributes | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IP | IT | PL | MT | HP | IS | FS (MPa) | D (kg/m3) | SA | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10.59 | 5299 | 4.3 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 9.88 | 5286 | 4.2 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 | 8.00 | 5336 | 3.7 |
| 4 | 1 | 2 | 1 | 2 | 3 | 3 | 10.72 | 5355 | 2.7 |
| 5 | 1 | 2 | 2 | 3 | 1 | 1 | 9.7 | 5321 | 3.1 |
| 6 | 1 | 2 | 3 | 1 | 2 | 2 | 11.03 | 5506 | 3.7 |
| 7 | 1 | 3 | 1 | 3 | 2 | 2 | 9.32 | 5255 | 1.3 |
| 8 | 1 | 3 | 2 | 1 | 3 | 3 | 0.84 | 5368 | 3.7 |
| 9 | 1 | 3 | 3 | 2 | 1 | 1 | 8.92 | 5299 | 5.0 |
| 10 | 2 | 1 | 1 | 2 | 2 | 3 | 9.37 | 5158 | 5.3 |
| 11 | 2 | 1 | 2 | 3 | 3 | 1 | 10.24 | 5308 | 5.5 |
| 12 | 2 | 1 | 3 | 1 | 1 | 2 | 10.76 | 5521 | 2.9 |
| 13 | 2 | 2 | 1 | 3 | 1 | 2 | 9.84 | 5246 | 2.1 |
| 14 | 2 | 2 | 2 | 1 | 2 | 3 | 10.94 | 5358 | 4.1 |
| 15 | 2 | 2 | 3 | 2 | 3 | 1 | 9.87 | 5290 | 3.7 |
| 16 | 2 | 3 | 1 | 1 | 3 | 1 | 11.07 | 5358 | 3.5 |
| 17 | 2 | 3 | 2 | 2 | 1 | 2 | 10.13 | 5335 | 4.3 |
| 18 | 2 | 3 | 3 | 3 | 2 | 3 | 7.32 | 5246 | 3.9 |
| 19 | 3 | 1 | 1 | 3 | 3 | 2 | 9.06 | 5125 | 2.6 |
| 20 | 3 | 1 | 2 | 1 | 1 | 3 | 11.45 | 5424 | 2.2 |
| 21 | 3 | 1 | 3 | 2 | 2 | 1 | 8.41 | 5103 | 4.1 |
| 22 | 3 | 2 | 1 | 1 | 2 | 1 | 10.31 | 5320 | 5.3 |
| 23 | 3 | 2 | 2 | 2 | 3 | 2 | 10.31 | 5325 | 3.4 |
| 24 | 3 | 2 | 3 | 3 | 1 | 3 | 7.51 | 5131 | 6.1 |
| 25 | 3 | 3 | 1 | 2 | 1 | 3 | 9.53 | 5252 | 4.1 |
| 26 | 3 | 3 | 2 | 3 | 2 | 1 | 8.08 | 5189 | 4.3 |
| 27 | 3 | 3 | 3 | 1 | 3 | 2 | 11.15 | 5421 | 5.9 |
The weights of quality attributes FS, D, and SA were calcuated using the entropy weighting method, and they are, respectively, 0.126, 0.438, and 0.436.
To convert three quality attributes FS, D, and SA into a single OQS, we selected five MADMs such as SAW, WPM, TOPSIS, GRA, and RSR methods in consideration of the clarity of principle, excellent feasibility, computational simplicity, and descriptive frequency ranking of the methods.21,22
Table 4 shows the normalized decision matrix. Table 5 shows the OQS values and ranks obtained from 5 MADM methods.
Table 4. Normalized Decision Matrix.
| trial no. | FS | D | SA |
|---|---|---|---|
| 1 | 0.919 | 0.469 | 0.375 |
| 2 | 0.852 | 0.438 | 0.396 |
| 3 | 0.675 | 0.557 | 0.500 |
| 4 | 0.931 | 0.603 | 0.708 |
| 5 | 0.835 | 0.522 | 0.625 |
| 6 | 0.960 | 0.964 | 0.500 |
| 7 | 0.799 | 0.364 | 1.000 |
| 8 | 0.000 | 0.634 | 0.500 |
| 9 | 0.762 | 0.469 | 0.229 |
| 10 | 0.804 | 0.132 | 0.167 |
| 11 | 0.886 | 0.490 | 0.125 |
| 12 | 0.935 | 1.000 | 0.667 |
| 13 | 0.848 | 0.342 | 0.833 |
| 14 | 0.952 | 0.610 | 0.417 |
| 15 | 0.851 | 0.447 | 0.500 |
| 16 | 0.964 | 0.610 | 0.542 |
| 17 | 0.876 | 0.555 | 0.375 |
| 18 | 0.611 | 0.342 | 0.458 |
| 19 | 0.775 | 0.053 | 0.729 |
| 20 | 1.000 | 0.768 | 0.812 |
| 21 | 0.713 | 0.000 | 0.417 |
| 22 | 0.893 | 0.519 | 0.167 |
| 23 | 0.893 | 0.531 | 0.563 |
| 24 | 0.629 | 0.067 | 0.000 |
| 25 | 0.819 | 0.356 | 0.417 |
| 26 | 0.682 | 0.206 | 0.375 |
| 27 | 0.972 | 0.761 | 0.042 |
Table 5. OQS Values and Ranks Obtained from 5 MADM Methods.
| trial no. | OQS values | OQS ranks | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SAW | WPM | TOPSIS | GRA | RSR | SAW | WPM | TOPSIS | GRA | RSR | |
| 1 | 0.485 | 0.463 | 0.445 | 0.515 | 0.425 | 15 | 14 | 16 | 16 | 17 |
| 2 | 0.472 | 0.456 | 0.436 | 0.501 | 0.394 | 17 | 15 | 17 | 18 | 19 |
| 3 | 0.547 | 0.545 | 0.534 | 0.527 | 0.593 | 11 | 11 | 11 | 12 | 11 |
| 4 | 0.690 | 0.683 | 0.662 | 0.630 | 0.794 | 5 | 4 | 4 | 5 | 4 |
| 5 | 0.606 | 0.599 | 0.582 | 0.568 | 0.655 | 8 | 7 | 7 | 8 | 7 |
| 6 | 0.761 | 0.724 | 0.692 | 0.743 | 0.800 | 3 | 3 | 3 | 2 | 3 |
| 7 | 0.696 | 0.624 | 0.629 | 0.719 | 0.624 | 4 | 5 | 5 | 4 | 10 |
| 8 | 0.496 | 0.000 | 0.542 | 0.513 | 0.644 | 14 | 26 | 10 | 17 | 9 |
| 9 | 0.401 | 0.365 | 0.377 | 0.469 | 0.332 | 22 | 18 | 22 | 23 | 23 |
| 10 | 0.232 | 0.183 | 0.207 | 0.414 | 0.184 | 26 | 24 | 26 | 26 | 26 |
| 11 | 0.381 | 0.291 | 0.359 | 0.478 | 0.355 | 23 | 21 | 23 | 21 | 21 |
| 12 | 0.846 | 0.831 | 0.787 | 0.811 | 0.896 | 1 | 1 | 2 | 1 | 2 |
| 13 | 0.620 | 0.566 | 0.578 | 0.613 | 0.586 | 7 | 9 | 8 | 6 | 12 |
| 14 | 0.569 | 0.546 | 0.529 | 0.562 | 0.650 | 10 | 10 | 12 | 11 | 8 |
| 15 | 0.521 | 0.509 | 0.489 | 0.523 | 0.510 | 12 | 12 | 13 | 14 | 14 |
| 16 | 0.625 | 0.614 | 0.589 | 0.591 | 0.772 | 6 | 6 | 6 | 7 | 5 |
| 17 | 0.517 | 0.495 | 0.483 | 0.526 | 0.496 | 13 | 13 | 14 | 13 | 15 |
| 18 | 0.427 | 0.418 | 0.410 | 0.469 | 0.341 | 20 | 17 | 19 | 22 | 22 |
| 19 | 0.439 | 0.232 | 0.435 | 0.521 | 0.457 | 19 | 22 | 18 | 15 | 16 |
| 20 | 0.817 | 0.814 | 0.795 | 0.742 | 0.935 | 2 | 2 | 1 | 3 | 1 |
| 21 | 0.272 | 0.000 | 0.285 | 0.427 | 0.238 | 25 | 26 | 25 | 25 | 24 |
| 22 | 0.413 | 0.339 | 0.386 | 0.490 | 0.402 | 21 | 19 | 21 | 19 | 18 |
| 23 | 0.590 | 0.581 | 0.559 | 0.562 | 0.685 | 9 | 8 | 9 | 10 | 6 |
| 24 | 0.109 | 0.000 | 0.124 | 0.370 | 0.079 | 27 | 26 | 27 | 27 | 27 |
| 25 | 0.441 | 0.424 | 0.407 | 0.485 | 0.375 | 18 | 16 | 20 | 20 | 20 |
| 26 | 0.340 | 0.311 | 0.317 | 0.440 | 0.234 | 24 | 20 | 24 | 24 | 25 |
| 27 | 0.474 | 0.221 | 0.452 | 0.565 | 0.543 | 16 | 23 | 15 | 9 | 13 |
Table 5 demonstrates that the OQS values and ranks from five MADMs do not coincide with one another.
To select the best suitable MADM from among 5 MADMs such as SAW, WPM, TOPSIS, GRA and RSR, we calculated the MRCs and MRDs. The MRC and MRD are introduced as the evaluating measures of the MADMs, and they were calculated using eqs 1 and 2. The values of MRCs and MRDs of 5 MADMs are listed in Table 6. From Table 6, we found that the SAW had the maximum MRC value and minimum MRD value, and the OQS ranks from the SAW best coincided with the OQS ranks from the other MADMs. Consequently, we concluded that the SAW was the most representative MADM from among five MADMs for this problem. Moreover, the SAW has better clarity, simplicity, and feasibility than the other MADMs. As a result, we selected the SAW as the most suitable MADM method for this problem.
Table 6. MRCs and MRDs of 5 MADMs.
| SAW | WPM | TOPSIS | GRA | RSR | |
|---|---|---|---|---|---|
| MRC | 0.956 | 0.866 | 0.947 | 0.932 | 0.918 |
| MRD | 1.463 | 2.500 | 1.481 | 1.796 | 2.056 |
Table 7 shows the MIM process parameters and the values of the OQS obtained from the SAW.
Table 7. MIM Process Parameters and Their OQS Values were Obtained from SAW.
| Trial no. | MIM process parameters | OQS values | |||||
|---|---|---|---|---|---|---|---|
| IP | IT | PL | MT | HP | IS | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.485 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 0.472 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 | 0.547 |
| 4 | 1 | 2 | 1 | 2 | 3 | 3 | 0.690 |
| 5 | 1 | 2 | 2 | 3 | 1 | 1 | 0.606 |
| 6 | 1 | 2 | 3 | 1 | 2 | 2 | 0.761 |
| 7 | 1 | 3 | 1 | 3 | 2 | 2 | 0.696 |
| 8 | 1 | 3 | 2 | 1 | 3 | 3 | 0.496 |
| 9 | 1 | 3 | 3 | 2 | 1 | 1 | 0.401 |
| 10 | 2 | 1 | 1 | 2 | 2 | 3 | 0.232 |
| 11 | 2 | 1 | 2 | 3 | 3 | 1 | 0.381 |
| 12 | 2 | 1 | 3 | 1 | 1 | 2 | 0.846 |
| 13 | 2 | 2 | 1 | 3 | 1 | 2 | 0.620 |
| 14 | 2 | 2 | 2 | 1 | 2 | 3 | 0.569 |
| 15 | 2 | 2 | 3 | 2 | 3 | 1 | 0.521 |
| 16 | 2 | 3 | 1 | 1 | 3 | 1 | 0.625 |
| 17 | 2 | 3 | 2 | 2 | 1 | 2 | 0.517 |
| 18 | 2 | 3 | 3 | 3 | 2 | 3 | 0.427 |
| 19 | 3 | 1 | 1 | 3 | 3 | 2 | 0.439 |
| 20 | 3 | 1 | 2 | 1 | 1 | 3 | 0.817 |
| 21 | 3 | 1 | 3 | 2 | 2 | 1 | 0.272 |
| 22 | 3 | 2 | 1 | 1 | 2 | 1 | 0.413 |
| 23 | 3 | 2 | 2 | 2 | 3 | 2 | 0.590 |
| 24 | 3 | 2 | 3 | 3 | 1 | 3 | 0.109 |
| 25 | 3 | 3 | 1 | 2 | 1 | 3 | 0.441 |
| 26 | 3 | 3 | 2 | 3 | 2 | 1 | 0.340 |
| 27 | 3 | 3 | 3 | 1 | 3 | 2 | 0.474 |
Table 8 shows the mean values of the OQS values corresponding to each level and their ranges for the MIM process parameters using the Taguchi method.
Table 8. Mean Values of the OQS Values Corresponding to Each Level and Their Ranges of MIM Process Parameters.
| MIM process parameters | IP | IT | PL | MT | HP | IS |
|---|---|---|---|---|---|---|
| level 1 | 0.573 | 0.499 | 0.516 | 0.610 | 0.538 | 0.449 |
| level 2 | 0.526 | 0.542 | 0.532 | 0.460 | 0.465 | 0.602 |
| level 3 | 0.433 | 0.491 | 0.484 | 0.463 | 0.529 | 0.481 |
| ranges | 0.140 | 0.051 | 0.048 | 0.150 | 0.073 | 0.152 |
| RPs (%) | 22.801 | 8.306 | 7.818 | 24.430 | 11.889 | 24.756 |
| ranks | 3 | 5 | 6 | 2 | 4 | 1 |
Figure 2 shows the plot of the mean OQS values of the six MIM process parameters at three levels.
Figure 2.
Plot of mean OQS values of MIM process parameters at three levels: (a) IP, (b) IT, (c) PL, (d) MT, (e) HP, and (f) IS.
From Table 8 and Figure 2, we can find that the optimal levels of the MIM process parameters are IP at the first level, IT at the second level, PL at the second level, MT at the first level, HP at the first level, and IS at the second level (IP1 IT2 PL2 MT1 HP1 IS2). As a result, the optimal values of the MIM process parameters were as follows:
IP: 350 bar, IT: 140 °C, PL: 64.5%vol, MT: 45 °C, HP: 700 bar, and IS: 15 ccm/s.
From Table 7, we can also know that the effect ranking of the MIM process parameters is as follows:
It demonstrates that IS is the most significant MIM process parameter, and the next are MT, IP, HP, TI, and PL.
The influencing analysis result was in accordance with the result obtained from the works by Askari and Momeni.12 According to the works,12 the IS played a significant role in increasing the D and FS, and there were optimum points for IT and MT, while HP did not significantly influence the D and FS. The result was also in good accord with the result obtained from the works by Rezaei and Askari.13 According to the work,13 the impact of IS was greater than other parameters, while HP showed little effect.
To justify the optimal parameters, we conducted the confirmation test according to the optimal parameters (IP: 350 bar, IT: 140 °C, PL: 64.5% vol, MT: 45 °C, HP: 700 bar, and IS: 15 ccm/s) and compared them with the experimental results according to OA L27(313) given in Table 3. Table 9 shows the confirmation test and comparison results.
Table 9. Confirmation Test and Comparison Results.
As can be seen in Table 9, the quality attributes D and SA of the MIM compact according to the optimum parameters were better than the best values of D and SA in Table 3, while the value of quality attribute FS (11.23) was slightly worse than the best value of FS (11.45) in Table 3. Since the importance weights of quality attributes FS, D, and SA are, respectively, 0.126, 0.438, and 0.436, D and SA are the major quality attributes, and FS is comparatively minor one, although the FS value of the MIM compact according to the optimal parameters is slightly worse than the best value of FS in Table 3; we can conclude that the quality performance of the MIM compact according to the optimal parameters is better than the quality performance according to best values of quality attributes given in Table 3.
4. Conclusions
In this work, we proposed the Taguchi-MADM-based hybrid optimization method of the MIM process and applied it to multiple quality optimizations of the MIM compacts with 3l6L stainless steel powder.
The conclusions were drawn as follows:
For the 3l6L stainless steel powder MIM process, the optimal values of the MIM process parameters are injection pressure of 350 bar, injection temperature of 140 °C, powder loading of 64.5% vol, mold temperature of 45 °C, holding pressure of 700 bar, and injection speed of 15 ccm/s.
The injection speed, mold temperature, and injection pressure are the major MIM process parameters that we have to pay more attention to during the MIM process, and the others are comparatively minor ones.
The significance and innovation of this work are as follows:
The selection method of a suitable MADM based on MRC and MRD enables us to select a more reasonable MADM from among some available MADMs, and the selected MADM can more reasonably and more scientifically evaluate the OQS of the fabricated MIM in full consideration of the multiple quality attributes and their importance weights.
The proposed hybrid optimization method can simultaneously and significantly improve the multiple quality attributes of the MIM compacts.
The proposed optimization method can quantitatively and exactly evaluate the influences of the process parameters using the range percentages.
The deficiencies of this work are as follows:
This work determined the importance weights of the process parameters using only the entropy weighting method, and therefore, the weights never reflect the experts’ subjective knowledge and practical experience for the importance of the process parameters.
This work did not consider the sensitivity of the importance weights of the process parameters on the OQS.
This work performed the DOE without respect to the potential interactions between the significant parameters and did not discuss the impact of the interactions on the MIM quality attributes.
In our future work, we will improve the reasonability of the importance weights of the multiple quality attributes by combining the objective weighting method such as the entropy weighting method with the subjective weighting method such as AHP. Our future work also needs to consider the sensitivity of the importance weights of the process parameters on the OQS. Our future work will investigate the potential interactions between the MIM process parameters and the impact of the interactions on the MIM quality attributes. Moreover, there are other available MADMs such as vise kriterijumska optimizacija kompromisno resenje (VIKOR), elimination and choice expressing reality (ELECTRE), and preference ranking organization method for enrichment of evaluations (PROMETHEE). When we applied the other available MADMs as well as SAW, WPM, TOPSIS, GRA, and RSR to convert the multiple quality attributes into a single overall quality score, a better reasonable MIM optimization result may be obtained.
By using the proposed Taguchi-MADM hybrid approach, we can reasonably determine the optimal MIM process parameters that simultaneously optimize the multiple quality attributes of the injection molded green compacts with comparative smaller experimental trials in consideration of the importance of the attributes, and it can effectively save time and cost for MIM optimization in the MIM practice.
The proposed method could be widely applied to not only MIM process optimization but also other advanced manufacturing process optimization problems with multiple quality attributes. To optimize the other manufacturing process, we need to select suitable process parameters and quality attributes suited to the manufacturing process, and then we can determine the optimal process parameters using the proposed method.
Acknowledgments
This work was supported by Kim Chaek University of Technology, Democratic People’s Republic of Korea. The supports are gratefully acknowledged. The authors express their gratitude to the editors and the reviewers for their helpful suggestions for improvement of this paper.
Appendix 1. Main Steps of WPM, TOPSIS, GRA, and RSR
A.1. WPM
Step 1. Construct a normalized decision matrix Z = (zik)n×L from the decision matrix Y = (yik)n×L using eq 6.
Step 2. Calculate the weighted products (OPSs) of n alternatives as follows:
| A1 |
A.2. TOPSIS
Step 1. Construct a normalized decision-matrix Z = (zik)n×L from Y = (yik)n×L using eq 6.
Step 2. Construct the weighted normalized decision matrix V= (vik)n×L as follows:
| A2 |
Step 3. Determine the positive and negative ideal solutions (PIS and NIS) V+ = (v+1, ···, v+k, ···, v+L) and V– = (v–1, ···, v–k, ···, v–L) as follows:
| A3 |
Step 4. Calculate the distances from the alternatives to the PIS and NIS as follows: (i = 1,2,···,n)
| A4 |
Step 5. Calculate the relative closeness values (OPSs) of n alternatives as follows: (i = 1,2,···,n)
| A5 |
A.3. GRA
Step 1. Construct a normalized decision matrix Z = (zik)n×L from Y = (yik)n×L using eq 6.
Step 2. Set {(zi1,···, zik,···, ziL); i = 1,2,···,n } as n comparative sequences.
Step
3. Determine the PIS Z+ = (z+1, ···, z+k, ···, z+L) and set it as a reference sequence, where  .
.
Step 4. Calculate the maximum and minimum values of the absolute deviations between the PIS (reference sequence) Z+ = (z+1, ···, z+k, ···, z+L) and n alternatives (comparative sequences) {(zi1,···, zik,···, ziL); i = 1,2,···,n} as follows:
where
| A6 |
Step 5. Calculate the gray relational coefficients between jth criteria of ith alternative and PIS as follows:
| A7 |
where ρ is the distinguishing coefficient and it is normally selected as 0.5.
Step 6. Calculate the grey relational grades (OPSs) of n alternatives as follows: (i = 1,2,···,n.)
| A8 |
A.4. RSR
Step 1. Construct a normalized decision matrix Z = (zik)n×L from the decision matrix Y = (yik)n×L using eq 6.
Step 2. Determine the ranks r1k, r2k,···, rnk of n alternatives in the descending order based on the values of the attribute values z1k, z2k,···, znk (k = 1,2,···,L), and construct a rank-matrix R = (rik)n×L.
Step 3. Calculate the rank sum ratios (OPSs) of n alternatives as follows: (i = 1,2,···,n)
| A9 |
Appendix 2. Analysis of variance (ANOVA) Results
The aim of ANOVA is to determine the statistically significant factors (MIM process parameters) influencing the quality attributes and their ranks in the designed experimental study.23Tables 10–13 shows the ANOVA results for FS, D, SA, and OQS.
Table 10. ANOVA Result for FS.
| factors | degree of freedom | sum of squares | variance | F-test | contribution (%) | rank |
|---|---|---|---|---|---|---|
| IP | 2 | 6.347 | 3.174 | 0.695 | 5.774 | 3 |
| IT | 2 | 12.164 | 6.082 | 1.332 | 11.065 | 2 |
| PL | 2 | 4.320 | 2.160 | 0.473 | 3.930 | 5 |
| MT | 2 | 5.496 | 2.748 | 0.602 | 4.999 | 4 |
| HP | 2 | 2.859 | 1.429 | 0.313 | 2.600 | 6 |
| IS | 2 | 14.834 | 7.417 | 1.625 | 13.494 | 1 |
| error | 14 | 63.913 | 4.565 | 58.138 | ||
| sum | 26 | 109.934 |
Table 13. ANOVA Result for OQS.
| factors | degree of freedom | sum of squares | variance | F-test | contribution (%) | rank |
|---|---|---|---|---|---|---|
| IP | 2 | 0.091 | 0.046 | 1.722 | 11.954 | 3 |
| IT | 2 | 0.014 | 0.007 | 0.258 | 1.789 | 5 |
| PL | 2 | 0.011 | 0.005 | 0.200 | 1.388 | 6 |
| MT | 2 | 0.132 | 0.066 | 2.488 | 17.278 | 1 |
| HP | 2 | 0.029 | 0.014 | 0.544 | 3.774 | 4 |
| IS | 2 | 0.116 | 0.058 | 2.191 | 15.213 | 2 |
| error | 14 | 0.372 | 0.027 | 48.604 | ||
| sum | 26 | 0.765 |
From Tables 10–13, we can evaluate the statistical significance of the MIM process parameters and influencing ranks.
From Table 10, the influencing ranks of the MIM process parameters on the FS is as follows:
From Table 11, the influencing ranks of the MIM process parameters on the D is as follows:
Table 11. ANOVA Result for D.
| factors | degree of freedom | sum of squares | variance | F-test | contribution (%) | rank |
|---|---|---|---|---|---|---|
| IP | 2 | 31968.519 | 15984.259 | 3.433 | 11.392 | 2 |
| IT | 2 | 4758.296 | 2379.148 | 0.511 | 1.696 | 6 |
| PL | 2 | 19891.185 | 9945.593 | 2.136 | 7.088 | 3 |
| MT | 2 | 127586.074 | 63793.037 | 13.699 | 45.466 | 1 |
| HP | 2 | 14268.074 | 7134.037 | 1.532 | 5.085 | 5 |
| IS | 2 | 16949.407 | 8474.704 | 1.820 | 6.040 | 4 |
| error | 14 | 65194.074 | 4656.720 | 23.233 | ||
| sum | 26 | 280615.630 |
From Table 12, the influencing ranks of the MIM process parameters on the FS is as follows:
Table 12. ANOVA Result for SA.
| factors | degree of freedom | sum of squares | variance | F-test | contribution (%) | rank |
|---|---|---|---|---|---|---|
| IP | 2 | 2.220 | 1.110 | 0.639 | 6.263 | 3 |
| IT | 2 | 0.187 | 0.093 | 0.054 | 0.527 | 6 |
| PL | 2 | 3.387 | 1.693 | 0.975 | 9.554 | 2 |
| MT | 2 | 1.040 | 0.520 | 0.299 | 2.934 | 4 |
| HP | 2 | 0.260 | 0.130 | 0.075 | 0.733 | 5 |
| IS | 2 | 4.027 | 2.013 | 1.159 | 11.360 | 1 |
| error | 14 | 24.327 | 1.738 | 68.629 | ||
| sum | 26 | 35.447 |
From Table 13, the influencing ranks of the MIM process parameters on the OQS is as follows:
On the other hand, from Table 8, the influencing ranks of the MIM process parameters on the OQS is as follows:
I
The above results show that the influencing ranks from the ANOVA for the OQS mostly well coincided with the influencing ranks from the RPs for the OQS. It illustrates the reasonability of the influencing ranking method of the factors based on the RPs.
As can be seen in Tables 8 and 13, the RPs of the MT and IS were 22.801 and 24.756 in Table 8, and the contributions of the MT and IS were 17.278 and 15.213 in Table 13. There was no significance in the differences. Meanwhile, the ranks of the other process parameters were the same. Consequently, we concluded that the influencing ranks of the MIM process parameters are (MT, IS) > IP > HP > IT > PL. Namely, the MT and IS have the highest influencing ranks, the next is IP, HP, and IT, and the last is PL. Also, from the viewpoint of the values of the RPs and contributions of each process parameter, we can find that IP, MT, and IS are the major process parameters that we have to pay more attention to because the values of the process parameters were pretty higher than the values of the other process parameters.
Data Availability Statement
All data that support the findings of this work are included within this article.
Accession Codes
The code for this study is available from the corresponding author according to a reasonable request.
This research did not receive the external funding.
The authors declare no competing financial interest.
References
- Czepiel M.; Ba′nkosz M.; Sobczak-Kupiec A. Advanced injection molding methods: review. Materials 2023, 16 (17), 5802. 10.3390/ma16175802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- German R. M.; Bose A.. Injection Molding of Metals and Ceramics; Metal Powder Industries Federation: Princeton, NY, 1997. [Google Scholar]
- Huang M. S.; Hsu H. C. Influence of injection moulding and sintering parameters on properties of 316L MIM compact. Powder Metallurgy 2011, 54 (3), 299–307. 10.1179/003258909X12502679013819. [DOI] [Google Scholar]
- Lin C. M.; Hung Y. T.; Tan C. M. Hybrid Taguchi–Gray Relation Analysis Method for Design of Metal Powder Injection-Molded Artificial Knee Joints with Optimal Powder Concentration and Volume Shrinkage. Polymers 2021, 13 (6), 865. 10.3390/polym13060865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatt T. K.; Muhamad N.; Haron C. H. C.; Sulong A. B. Parametric Optimization of Metal Injection Moulding Process Using Taguchi Method. Int. J. Integrated Eng. 2020, 12 (4), 210–219. 10.30880/ijie.2020.12.04.019. [DOI] [Google Scholar]
- Chen W. C.; Fu G. L.; Tai P. H.; Deng W. J. Process parameter optimization for MIMO plastic injection molding via soft computing. Expert Syst. Appl. 2009, 36, 1114–1122. 10.1016/j.eswa.2007.10.020. [DOI] [Google Scholar]
- Amin S. Y. M.; Muhamad N.; Jamaludin K. R. Optimization of Injection Molding Parameters for WC-Co Feedstocks. Jurnal Teknol. 2013, 63 (1), 51–54. 10.11113/jt.v63.1454. [DOI] [Google Scholar]
- Mustafa N.; Ibrahim M. H. I.; Asmawi R.; Aimin A. M.; Masrol S. R. Green strength optimization in Metal Injection Molding applicable with a Taguchi Method L9(3)4. Appl. Mech. Mater. 2015, 773–774, 115–117. 10.4028/www.scientific.net/AMM.773-774.115. [DOI] [Google Scholar]
- Xie X. C.; Lin C. G.; Jia C. C.; Cao R. J. Effects of process parameters on quality of ultrafine WC/12Co injection molded compacts. Int. Journal of Refractory Metals and Hard Materials 2015, 48, 305–311. 10.1016/j.ijrmhm.2014.09.022. [DOI] [Google Scholar]
- Zhao T.; Ei B. Z.; Wang X. W.; Qi G. H.; Lowe H.. Research Progress on Optimization Methods of Powder Injection Molding Process Parameters. In Proceedings of the 1st International Conference on New Materials, Machinery and Vehicle Engineering; Xu J. Y.; Cai Y. K.; Mansori M. E., Eds.; IOS Press: 2022; pp 257–262. [Google Scholar]
- Jannah W.; Yudistiro D.; Asrofi M.; Darsin M.; Maulana A. R. Effect of Temperature, Holding Time, and Addition of Sn on Density on Metal Injection Molding Sintering Process. J. Eng. Technol. Sci. 2023, 55 (2), 143–152. 10.5614/j.eng.technol.sci.2023.55.2.4. [DOI] [Google Scholar]
- Askari A.; Momeni V. Rheological investigation and injection optimization of Fe–2Ni–2Cu feedstock for metal injection molding process. Mater. Chem. Phys. 2021, 271, 124926 10.1016/j.matchemphys.2021.124926. [DOI] [Google Scholar]
- Rezaei S.; Askari A. Moulding of SS316L surgical component using palm-stearin feedstock: Rheological analysis, process window and parametric optimization. Powder Metall. 2024, 67, 246. 10.1177/00325899241273501. [DOI] [Google Scholar]
- Nor N. H. M.; Muhamad N.; Ariffin A. K.; Ruzi M.; Jamaludin K. R.; Sufizar A. Injection Molding Parameter Optimization of Titanium Alloy Powder Mix with Palm Stearin and Polyethylene for Multiple Performance Using Grey Relational Analysis. J. Appl. Sci. 2011, 11 (10), 1833–1838. 10.3923/jas.2011.1833.1838. [DOI] [Google Scholar]
- Moayyedian M.; Mamedov A. Multi-Objective Optimization of Injection Molding Process for Determination of Feasible Moldability Index. Procedia CIRP 2019, 84, 769–773. 10.1016/j.procir.2019.04.213. [DOI] [Google Scholar]
- Yang W. C.; Kang H. S.; Ri G. S.; Kim J. S. Consistency Improvement Method of Pairwise Matrix Based on Consistency Ratio Decreasing Rate and Attribute Weighting Method Considered Decision Makers’ Levels in Analytic Hierarchy Process: Application to Hip Joint Prosthesis Material Selection. Math. Probl. Eng. 2022, 2022, 1–22. 10.1155/2022/1463006. [DOI] [Google Scholar]
- Yang W. C.; Choe C. M.; Kim J. S.; Om M. S.; Kim U. H. Materials selection method using improved TOPSIS without rank reversal based on linear max-min normalization with absolute maximum and minimum values. Mater. Res. Express 2021, 9 (6), 065503 10.1088/2053-1591/ac2d6b. [DOI] [Google Scholar]
- Jamaludin K. R.; Muhamad N.; Amin S. Y. M.; Rahman M. N. A.; Murtadhahadi Rheological behavior of SS3161 gas atomized powder in bimodal particle size distribution in a composite binder system. Int. J. Mech. Mater. Eng. 2008, 3, 108–114. [Google Scholar]
- Jamaludin K. R.; Muhamad N.; Rahman M. N. A.; Murtadhahadi; Ahinad S.; Ibrahim M. H. I.; Nor N. H. M. Rheological investigation of water atomized Metal Injection Molding (MIM) feedstock for processibility prediction. Adv. Mater. Res. 2010, 83–86, 945–952. 10.4028/www.scientific.net/AMR.83-86.945. [DOI] [Google Scholar]
- Ismail M. H.; Mohamad Nor N. h.; Jai J.. Characterization of Homogenous Feedstock for Metal Injection Molding Process. In Faculty of Mechanical Engineering; University Technology: MARA, Malaysia, 2005. [Google Scholar]
- Zolfani S. H.; Hasheminasab H.; Torkayesh A. E.; Zavadskas E. K.; Derakhti A. A Literature Review of MADM Applications for Site Selection Problems-One Decade Review from 2011 to 2020. Int. J. Inf. Technol. Decis. Making 2021, 21, 7–57. 10.1142/S0219622021300019. [DOI] [Google Scholar]
- Basilio M.; Pereira V.; Costa H.; Santos M.; Ghosh A. A Systematic Review of the Applications of Multi-Criteria Decision Aid Methods (1977–2022). Electronics 2022, 11, 1720. 10.3390/electronics11111720. [DOI] [Google Scholar]
- Li K.; Yan S. L.; Zhong Y. C.; Pan W. F.; Zhao G. Multi-Objective Optimization of the Fiber-reinforced Composite Injection Molding Process using Taguchi method, RSM, and NSGA-II. Simulation Modelling Practice and Theory 2019, 91, 69. 10.1016/j.simpat.2018.09.003. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data that support the findings of this work are included within this article.




