Iron-rich silicates in the Earth's D″ layer

Abstract

High-pressure experiments and theoretical calculations demonstrate that an iron-rich ferromagnesian silicate phase can be synthesized at the pressure–temperature conditions near the core–mantle boundary. The iron-rich phase is up to 20% denser than any known silicate at the core–mantle boundary. The high mean atomic number of the silicate greatly reduces the seismic velocity and provides an explanation to the low-velocity and ultra-low-velocity zones. Formation of this previously undescribed phase from reaction between the silicate mantle and the iron core may be responsible for the unusual geophysical and geochemical signatures observed at the base of the lower mantle.

Modern deep-Earth mineralogical research began with high-pressure experiments on iron silicate, a major component in the solid Earth. The discovery of the fayalite (Fe₂SiO₄) olivine–spinel transition in 1959 (1) marked the first known transition beyond the upper mantle. The disproportionation of fayalite spinel into mixed oxides using the newly invented laser-heated and resistive-heated diamond–anvil cell in the early 1970s (2, 3) marked the first phase transition under lower mantle conditions. In the Earth's crust, upper mantle, and transition zone, iron silicates form extensive solid solutions with the magnesium endmembers in major rock-forming minerals, e.g., fayalite in α-(Fe,Mg)₂SiO₄ (olivine), ferrosilite in (Fe,Mg)SiO₃ (pyroxene), almandine in (Fe,Mg)₃Al₂Si₃O₁₂ (garnet), and fayalite spinel in γ-(Fe,Mg)₂SiO₄ (ringwoodite). No iron-rich silicate, however, was known to exist under the high pressure–temperature (P–T) conditions beyond the 670-km discontinuity that accounts for approximately three-quarters of the Earth's total silicates and oxides. Following Birch's 1952 postulation (4), iron-rich silicates break down to mixed oxides in the lower mantle.

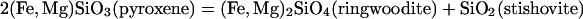[1]

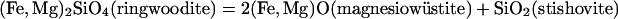[2]

In the lower-mantle silicate, (Fe_xMg_1–x)SiO₃ perovskite, iron can only participate as a minor component with x < 0.15 (5), even at the core–mantle boundary with an unlimited supply of iron from the core. Without a stable iron-rich silicate phase, previous explanations of the complex geochemical and geophysical signatures of the D″ layer have been limited to heterogeneous, solid/melt mixtures of iron-poor silicates and iron-rich metals and oxides (6, 7).

Recently, MgSiO₃ has been found to transform from perovskite to CaIrO₃ structure under the P–T conditions of the D″ layer (8–12). This postperovskite (ppv) phase also was observed to coexist with silicate perovskite and magnesiowüstite in experiments with orthopyroxene and olivine starting materials with x up to 0.4, but the iron content in this phase is undefined because of the unknown Fe/Mg distributions among multiple coexisting ferromagnesian phases (13). Here, we report experimental and theoretical investigations across the ferrosilite (FeSiO₃)–enstatite (MgSiO₃) join. We found that iron-rich (Fe_xMg_1–x)SiO₃ with x as high as 0.8 formed a single-phase ppv silicate rather than mixed oxides at the pressures of the D″ layer (≈130 GPa).

Materials and Methods

Five orthopyroxene samples with x = 0.2, 0.4, 0.6, 0.8, and 1.0 (denoted Fs20, Fs40, Fs60, Fs80, and Fs100, respectively) were synthesized in a piston-cylinder apparatus. The starting oxide mixtures were prepared by weighing MgO, Fe₂O₃, and SiO₂ in pyroxene stoichiometry with different iron contents, followed by grinding under acetone in an agate mortar. The oxide mixtures then were placed in a CO₂–CO gas-mixing furnace at a temperature of 1,473 K and oxygen fugacity (fO₂) of 10^–10.5 for 24 h to reduce all Fe³⁺ to Fe²⁺. The treated mixtures were reground and sealed in Au capsules, which then were compressed in the piston-cylinder apparatus for 48 h at 1,273 K and 1.2 GPa. The product was confirmed by x-ray diffraction as a single-phase orthopyroxene.

We compressed Fs20, Fs40, Fs60, Fs80, and Fs100 samples to 120–150 GPa in symmetrical diamond-anvil cells. Beveled diamond anvils with flat culet diameters of 90–100 μm were used to generate the pressure, and rhenium gaskets with laser-drilled-hole diameters of 35–50 μm were used to confine the samples. Multiple sample configurations (with or without Pt black as a laser absorber, with or without NaCl thermal insulation layers, and with or without additional Au and Pt as pressure markers) were used to optimize the synthesis conditions and to distinguish overlapping diffraction peaks. Rhenium at the sample–gasket interface also was used as a secondary pressure marker (14). Double-side YLF laser systems at 13ID-D and 16ID-B stations of the Advanced Photon Source were used for heating, and monochromatic x-ray beams of λ = 0.3344, 0.3888, 0.4008, and 0.4233 Å were used for x-ray diffraction. The primary x-ray beam was focused down to 5–10 μm through a diamond anvil and impinged on the samples. Diffraction rings up to 2θ = 21° exited through the second diamond anvil and cubic boron nitride seat and were recorded on a charge-coupled device detector for in situ measurements at simultaneous high P–T conditions or an image-plate detector for temperature-quenched sample at high pressures. The diffraction patterns were processed and analyzed with fit2d software (www.esrf.fr/computing/scientific/FIT2D).

Results

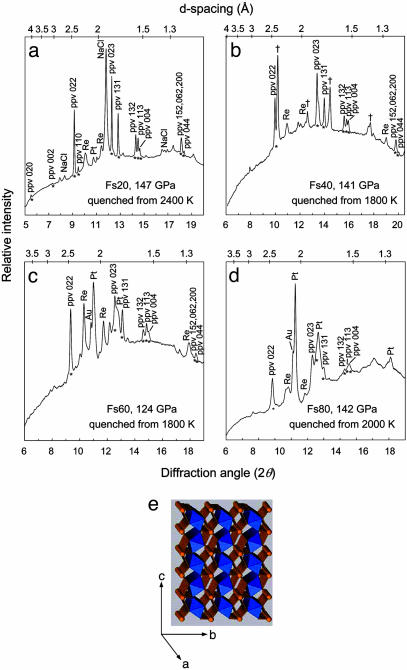
X-ray diffraction at low pressures showed well-crystallized orthopyroxene patterns. Above 20–30 GPa, sharp diffraction rings disappeared and were replaced by a broad background, indicating pressure-induced amorphization of the silicate crystals. Laser-heating of Fs40 and Fs60 at 30–100 GPa produced assemblages of silicate perovskite, magnesiowüstite, and stishovite. Heating samples compressed directly to 120–150 GPa at 2,000 K, Fs20, Fs40, Fs60, and Fs80 transformed to the ppv without a trace of silicate perovskite or mixed oxides (Fig. 1), whereas the Fs100 sample still produced mixed oxides. All characteristic lines of ppv, including the most intense 022 peak, the 023–131 doublet, and the 132–113-004 triplet, are present in the iron-bearing silicates. Indexing of the peaks and fitting to the ppv Cmcm orthorhombic unit cell are listed in Tables 1 and 2.

Fig. 1.

X-ray diffraction patterns. Patterns are shown for Fs20 at 147 GPa (λ = 0.3888 Å) (a), Fs40 at 141 GPa (λ = 0.4233 Å) (b), Fs60 at 124 GPa (λ = 0.4008 Å) (c), and Fs80 at 138 GPa (λ = 0.4057 Å) (d). ppv peaks are additionally marked with *. Re oxide peaks are marked with †. Pressures were determined from the equation of state of Pt (28). (e) The crystal structure of ppv is shown with silicon octahedrons in blue and iron and magnesium cations in orange.

Table 1. Lattice parameters for ppv phases Fs20, Fs40, Fs60, and Fs80.

ppv phase	a, Å	b, Å	c, Å	V, Å3
Fs20, 147 GPa	2.458 (2)	8.064 (5)	6.104 (2)	121.0 (1)
Fs40, 141 GPa	2.463 (3)	8.047 (8)	6.115 (3)	121.2 (2)
Fs60, 124 GPa	2.475 (3)	8.183 (7)	6.159 (3)	124.7 (2)
Fs80, 142 GPa	2.463 (2)	8.111 (9)	6.113 (2)	122.1 (2)

Values in parentheses represent the standard deviations.

Table 2. Observed and calculated d-spacings for ppv.

hkl peak	Fs20, 147 GPa d-spacing, Å		Fs40, 141 GPa d-spacing, Å		Fs60, 124 GPa d-spacing, Å		Fs80, 142 GPa d-spacing, Å
	Observed	Calculated	Observed	Calculated	Observed	Calculated	Observed	Calculated
020	4.034	4.032	—	—	—	—	—	—
022	2.443	2.444	2.437	2.434	2.460	2.460	2.444	2.441
110	2.351	2.352	—	—	—	—	—	—
023	1.815	1.817	1.816	1.818	1.834	1.835	1.820	1.821
131	1.739	1.739	1.740	1.739	1.759	1.757	1.744	1.745
132	1.560	1.559	1.561	1.560	1.576	1.575	1.565	1.564
113	1.539	1.539	1.542	1.541	1.551	1.551	1.542	1.541
004	1.525	1.526	1.528	1.529	1.539	1.540	1.528	1.528
062*	1.239	1.239	1.232	1.233	1.247	1.248	—	—
044	1.217	1.217	1.218	1.217	1.231	1.230	—	—

—, not observed.

^*The 062 peak contains contributions from the 152, 062, and 200 reflections.

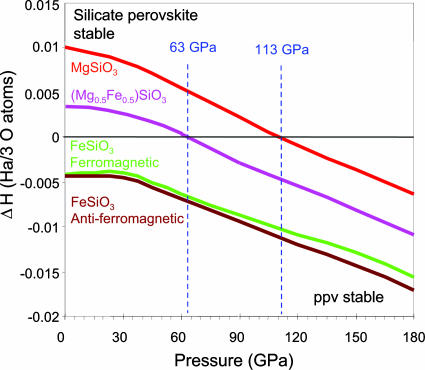
With first-principles calculations, we confirmed that indeed iron-rich (Fe,Mg)SiO₃ is stabilized in the ppv rather than silicate perovskite structure at the core–mantle boundary. Spin-polarized calculations were performed by using the generalized gradient approximation (15) of density functional theory (16, 17) as implemented in the code abinit (18). We use Troullier–Martins-type pseudopotentials, generated with the fhi98pp code (19). The core electronic configuration is [Ar], [Ne], [Ne], and [He] for Fe, Mg, Si, and O, respectively. We use a 38 Hartree (1 Hartree = 27.2116 eV) kinetic energy cut-off. The calculations are performed on 4 × 4 × 4 and 6 × 6 × 4 grids of special k points (20) for silicate perovskite and ppv phases, respectively. Convergence tests showed a precision in energy of >1 milli-Hartree per molecule and in pressure of ≈1 GPa. We computed the enthalpy of silicate ppv referencing to silicate perovskite (the zero horizontal line) for three compositions, MgSiO₃, Mg_0.5Fe_0.5SiO₃, and FeSiO₃ (Fig. 2). For ppv enthalpies of >0, silicate perovskite is stable, and at <0, ppv is stable. The silicate perovskite–ppv transition pressure occurs at ≈113 GPa for MgSiO₃ and at 63 GPa for x = 0.5, and the ppv phase is stable at all pressures with respect to silicate perovskite for the pure FeSiO₃ end-member (Fig. 2). The difference in enthalpy between the ferro- and anti-ferromagnetic configurations for ppv-FeSiO₃ is <23 meV per formula unit at pressures of <90 GPa (specific volume >34.6 ų per formula unit), which increases with pressure to ≈40 meV per formula unit at 150 GPa (specific volume ≈31.6 ų per formula unit).

Fig. 2.

Enthalpy of ppv with respect to the silicate perovskite phase of the same composition (the zero horizontal line) in the MgSiO₃–FeSiO₃ system.

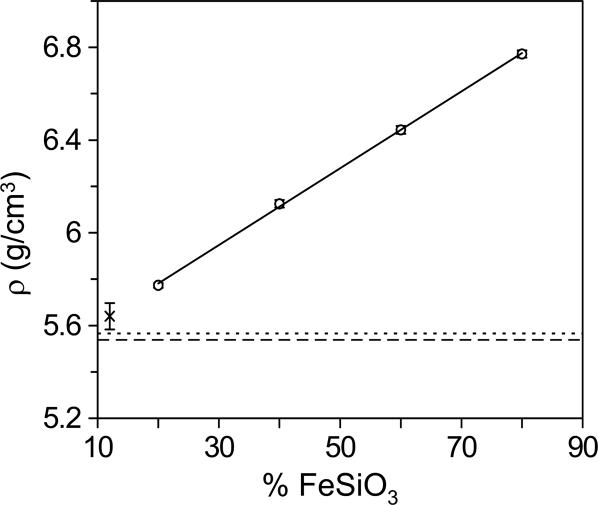
With atoms in close-packed configurations, densities of D″ minerals essentially depend on the amount of iron, which stands out as the predominant heavy element. In Fig. 3, we plot experimental results of densities of Fs20, Fs40, Fs60, and Fs80 (normalized to 130 GPa) for comparison and evaluation of the effects of iron content. The density of the ppv increases sharply with increasing iron content (∂lnρ/∂x = 0.30). Although the densities of other lower-mantle silicates, including ferromagnesian silicate perovskite and CaCl₂-type and α-PbO₂-type SiO₂ (8, 21), cluster around 5.6 gm/cm³ (±2%), the density of the iron-rich ppv silicate increases by as much as 20% depending on the iron content. Such high density in silicate would have a major impact on the seismic and geodynamic properties of the D″ layer. For a first approximation, seismic velocities are reduced inversely proportional to the square root of the increasing density due to the iron enrichment. For instance, a ppv silicate with x = 0.66 would be sufficient to lower seismic velocities by 10% as observed in ultra-low-velocity zones.

Fig. 3.

Density of the ppv phase as a function of x. For comparison, results are corrected to the same pressure at 130 GPa using the theoretical bulk modulus and elastic constants (11, 29). Density is shown with comparison to Fs12 silicate perovskite (× symbol shown with 1% error bar) (21) and the α-PbO₂-type (dotted line) and CaCl₂-type (dashed line) SiO₂ phases (30).

The vast reservoirs of iron and silicates at the core–mantle boundary provide favorable chemical–physical conditions for the formation of high-iron ppv silicate, which holds the key to understanding the geophysical and geochemical properties of the D″ layer (6, 22–24). Contrary to the previous thinking that the mantle composition was essentially unchanged by contact with the core, i.e., the composition of the mantle silicate remains within its iron-poor solubility limit of x < 0.15, this scenario calls for a reaction layer of denser silicates with much higher iron content, resulting in the observed low-velocity zones and ultra-low-velocity zones (25). Comprehensive studies of the equation of state, elastic anisotropy, diffusivity, rheology, magnetism, and reversible phase relation of ppv as a function of temperature and iron concentration are needed for developing the new paradigm for this most enigmatic layer in the solid Earth (26, 27).