Abstract
The lipids of biological membranes and intact biomembranes display chain melting transitions close to temperatures of physiological interest. During this transition the heat capacity, volume and area compressibilities, and relaxation times all reach maxima. Compressibilities are thus nonlinear functions of temperature and pressure in the vicinity of the melting transition, and we show that this feature leads to the possibility of soliton propagation in such membranes. In particular, if the membrane state is above the melting transition solitons will involve changes in lipid state. We discuss solitons in the context of several striking properties of nerve membranes under the influence of the action potential, including mechanical dislocations and temperature changes.
Keywords: sound, action potential, compressibility, Hodgkin–Huxley theory
The lipid membrane is the major building block of biological membranes, which consist mainly of large numbers of different lipids and proteins with a composition specific to the particular membrane under consideration. The isolated lipids of biomembranes display order–disorder transitions in the temperature regime of about –20°C to +60°C in which membranes absorb heat (25–40 kJ/mol), and both the lateral order and chain order of the lipid molecules are lost. This transition is accompanied by an increase in volume of ≈4% and an increase in area of ≈25%. The low and high temperature phases are called solid-ordered and liquid-disordered, respectively, indicating the simultaneous change in lateral crystalline arrangement and chain order. They are also known as gel and fluid phase, respectively. Mixed systems display a wealth of different phase diagrams. The melting profiles of lipid mixtures are therefore generally more complex than those of single lipids and cover a wider temperature range. Both peripheral and integral proteins change lipid melting caused by molecular interactions that influence the cooperative nature of the membrane fluctuations as a whole (1). Fluctuations in volume and area, and the related fluctuations in curvature, give rise to pronounced changes in elastic constants, e.g. compressibilities, bending elasticity, and relaxation times, all of which have maxima in the region of the chain melting transition. It has been suggested on theoretical and experimental grounds that these response functions are all simple functions of the heat capacity (2–4). The sound velocities of lipid dispersions obtained with ultrasonic measurements and the bending elasticities of giant vesicles are practically identical to the profiles calculated from the heat capacity (5–8). Within certain limits, it is thus possible to calculate the response functions from the heat capacity without detailed knowledge of the composition of the lipid mixture. In the transition region, membranes thus become more compressible and easier to bend. Relaxation times grow and are found to be in the range of 10–3 s–1·min (4, 9). In unilamellar vesicles of single lipids, these changes can be pronounced. In comparison to the fluid lipid phase, the bending modulus of dipalmitoyl phosphatidylcholine (DPPC) unilamellar vesicles changes by 1 order of magnitude, as does the lateral compressibility. For multilamellar vesicles that display a more cooperative transition, these effects are even more pronounced. In lipid mixtures, where heat capacity anomalies extend over a broader temperature range and the magnitude of the heat capacity is smaller, the change in elastic constants is less pronounced, but it is present whenever a heat capacity anomaly can be measured.
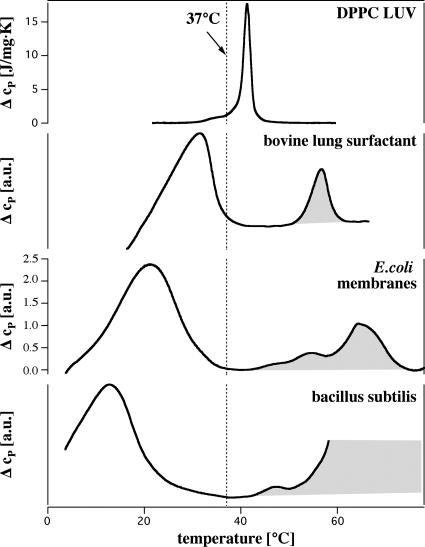
It is less known that melting transitions can also be found in biological membranes, e.g., in Escherichia coli and Bacillus subtilis membranes (this work) and lung surfactant (3), which exists on the lung surface as a monolayer–bilayer equilibrium. In these systems the intact membranes, including all proteins, display pronounced lipid melting peaks slightly below physiological temperature (see Fig. 1). In the E. coli system the lipid melting peak changes with growth temperature and pH. It would be of importance to understand how the adaptable lipid composition influences the physical features of the membranes. Unfortunately, the lipid and protein composition of biomembranes is so diverse that it is seemingly impossible to understand the corresponding phase diagrams in detail. It is clear, however, that even these complex systems are thermodynamic ensembles with fluctuations in state, volume, area, and local composition. Their response functions are related to one another because they all are second-order derivatives of the entropy, e.g., heat capacity anomalies in biological membranes are simply related to the lateral compressibility. Because sound propagation velocities are related to the compressibility, sound propagation in a membrane is also related to these changes. This relation has been shown for both single lipid membranes and mixtures for sound propagation in three dimensions (2, 5, 6).
Fig. 1.
Heat capacity profiles of artificial unilamellar DPPC vesicles, bovine lung surfactant extract, E. coli membranes, and B. subtilis membranes. Transition peaks associated with protein unfolding are shaded in gray. The dotted line indicates T = 37°C, which is the bovine body temperature and the growth temperature of E. coli and B. subtilis.
Various authors have speculated whether mechanical perturbations can travel along nerve axons (10) (note also two monographs by K. Kaufmann from 1989 available online at http://membranes.nbi.dk/Kaufmann). In fact, mechanical forces and dislocations as well as temperature responses of nerve membranes in-phase with the action potential have been found experimentally (11–16). They are accompanied by changes in the fluorescence of membrane probes and changes in turbidity and birefringence (17). None of these phenomena play a role in the Hodgkin–Huxley theory (18) that is the accepted model of nerve pulses. Most interestingly, the initial temperature increase in the nerve during the action potential is followed by a cooling, which is in-phase with voltage changes (13). This seemingly isentropic behavior of the nerve pulse is clearly not contained in the Hodgkin–Huxley theory.
This article deals with membranes close to a thermal melting transition and considers an interesting mechanical implication of these transitions: the possibility of soliton propagation in cylindrical membranes. Nonlinear and dispersive 1D systems often permit a continuum of localized density excitations, which propagate without distortion. We will loosely refer to such objects as solitons. After introducing a suitable dispersion term, we will argue that such solitons may play a role in pulse propagation in biological membranes, in particular in nerves. We will further suggest that the general features of the compression moduli for lipid mixtures (i.e., the proximity of a thermal melting transition) lead to a variety of interesting properties for such solitons.
Materials and Methods
Lipids were purchased from Avanti Polar Lipids and used without further purification. For the preparation of unilamellar vesicles, the dry lipids were hydrated in the suitable amount of buffer (2 mM Hepes/1 mM EDTA, pH 7.5) above the phase transition temperature. Unilamellar vesicles were prepared from the multilamellar lipid dispersion by ultrasonication with 50 W for several minutes by using a model W185 sonifier from Heat Systems/Ultrasonics, resulting in small unilamellar vesicles. After subsequent storage at 4°C, the small vesicles fuse to large unilamellar vesicles with a diameter of ≈120 nm. Bovine lung surfactant was a gift from Fred Possmeyer (University of Western Ontario, London, Canada). E. coli bacteria (XL1 blue with tetracycline resistance) and B. subtilis were grown in LB medium at 37°C. The bacterial membranes were then disrupted in a French press at 1,200 bar (Gaulin, APV Homogenisers, Lübeck, Germany) and centrifuged at low speed in a desk centrifuge to remove solid impurities. The remaining supernatant was centrifuged at high speed in an Beckmann ultracentrifuge (250,000 × g) in a Ti70 rotor (Beckman Coulter) to separate the membranes from soluble proteins and nucleic acids. This membrane fraction was measured in a calorimetrer. Lipid melting peaks and protein unfolding can be distinguished easily in pressure calorimetry because of their characteristic pressure dependences. [The pressure dependence of lipid transitions is much higher than that of proteins (3).] Details regarding the lung surfactant and E. coli measurements are given in ref. 19. Heat capacity profiles were obtained by using a VP-scanning calorimeter (MicroCal Software, Northampton, MA) at scan rates of 5 deg/hr (lipid vesicles) and 30 deg/hr for lung surfactant and E. coli plasma membranes.
Theory and Results
Heat Capacity and Compressibilities. Examples of heat capacity profiles in artificial and biological membranes are shown in Fig. 1. We have previously shown that these results can be used to estimate the temperature dependence of the elastic constants. The heat capacity (cP), the isothermal volume compressibility (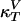 ), and the lateral compressibility (
), and the lateral compressibility (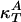 ) are related to fluctuations in enthalpy, volume, and area as
) are related to fluctuations in enthalpy, volume, and area as
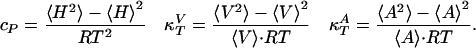 |
[1] |
It was found experimentally that the excess enthalpy, ΔH, excess volume change, ΔV, and excess area change, ΔA, of the lipid melting transitions obey the relation ΔV(T) = γVΔH(T) (2, 3) and, more indirectly, that ΔA(T) = γAΔH(T) (2, 7, 8). The constants γV = 7.8 × 10–4 cm3/J and γA = 8.9 × 103 cm2/J, which are identical within experimental error for various phosphatidylcholines, lipid mixtures, lung surfactant, and E. coli membranes (3). These relations can now be used to calculate the elastic constants from the heat capacity as
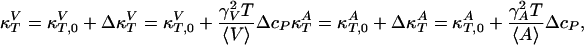 |
[2] |
where 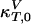 and
and 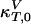 are the compressibilities outside of the transition range. Their values must be taken from the literature. These relationships show that changes in the elastic constants can be deduced from the heat capacity.
are the compressibilities outside of the transition range. Their values must be taken from the literature. These relationships show that changes in the elastic constants can be deduced from the heat capacity.
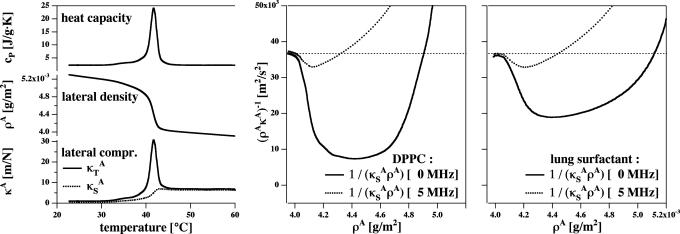
Sound Propagation. As shown in Fig. 2, elastic constants close to the chain melting vary significantly with density. The elastic modulus decreases with increasing lateral pressure for a membrane slightly above the transition, and the system resembles a spring that becomes softer when compressed. Here, we consider some of the consequences of this fact.
Fig. 2.
Thermodynamic data for DPPC vesicles and lung surfactant. (Left) Heat capacity of DPPC large unilamellar vesicle (Top), lateral area density, ρA (Middle), and the corresponding lateral compressibility (Bottom) (isothermal area compressibility, solid curve, corresponding to a low-frequency case and adiabatic area compressibility, dotted line, corresponding to a 5-MHz ultrasonic experiment), as calculated from the heat capacity. (Center) The lateral sound velocity c2 = 1/κSAρA [m2/s2] for the low-frequency and the 5-MHz case, as a function of membrane area density, ρA [g/m2]at T = 45°C. (Right) c2 profiles for lung surfactant at T = 37°C calculated from the heat capacity in Fig. 1.
Sound propagation velocities in elastic media, 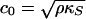 , are functions of the isentropic compressibilities,
, are functions of the isentropic compressibilities, 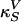 and
and 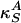 . Using Maxwell's relations (20) one can show that
. Using Maxwell's relations (20) one can show that
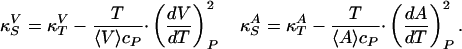 |
[3] |
These heat capacities, which describe the heat sink, depend on the time scale of the compression so that cP = cP(ω). On time scales much longer than that of relaxation processes in the membrane, the entire aqueous environment of the membrane serves as a heat reservoir. As a result, cP is large, and κS ≈ κT. For experiments faster than the dominant relaxation process, the isentropic compressibility approaches zero. If ΔA ∝ ΔH, all quantities required for the determination of the isentropic compressibility can be determined from the heat capacity at constant pressure, e.g., 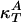 and (dA/dT)P. Ultrasonic velocity measurements at a frequency of 5 MHz show that ultrasound velocities as a function of temperature can be calculated accurately from the heat capacity if it is assumed that there is no heat transfer between the membrane and the aqueous medium. This fact means that cP(ω) = cP,lipids, excluding the aqueous environment at such frequencies. For processes slower than 2 × 10–7 s, the isentropic compressibility is larger than that found at 5 MHz but smaller than the isothermal compressibility.
and (dA/dT)P. Ultrasonic velocity measurements at a frequency of 5 MHz show that ultrasound velocities as a function of temperature can be calculated accurately from the heat capacity if it is assumed that there is no heat transfer between the membrane and the aqueous medium. This fact means that cP(ω) = cP,lipids, excluding the aqueous environment at such frequencies. For processes slower than 2 × 10–7 s, the isentropic compressibility is larger than that found at 5 MHz but smaller than the isothermal compressibility.
Although we will be concerned with lateral compressibility, we have chosen to discuss the relations for the 3D compressibility as well because they have been verified experimentally (3, 5, 6). The validity of these relations in the 2D case can only be established indirectly. The bending elasticity of membranes is related to their lateral compressibility (21). The elasticity changes predicted from heat capacity profiles are identical to those found in experiments (7, 8). The heat capacity, lateral density, and isothermal and isentropic lateral compressibilities for unilamellar DPPC vesicles and lung surfactant are given in Fig. 2 Left. Details of the determination of these quantities from the heat capacity profiles are given in refs. 2 and 6. The parameters used are given in ref. 2. It was further assumed that the total melting enthalpy and elastic parameters of the lung surfactant are comparable to those of DPPC because DPPC is the major lipid component of lung surfactant.
Solitons. We now consider 1D sound propagation along a cylindrical membrane with coordinate x. If the membrane is a long and narrow cylinder, we can reduce the problem to propagation in one direction, x. In the absence of dispersion, sound propagation is governed by the equation
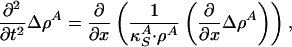 |
[4] |
where 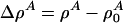 is a function of x and t. If the compressibility is approximately constant and if
is a function of x and t. If the compressibility is approximately constant and if 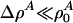 , this reduces to
, this reduces to
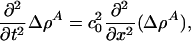 |
[5] |
where 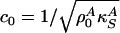 is the velocity of small amplitude sound. Recall, however, that the lateral compressibility
is the velocity of small amplitude sound. Recall, however, that the lateral compressibility 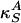 depends strongly on Δρ A if one is close to a transition in the membrane. We thus expand
depends strongly on Δρ A if one is close to a transition in the membrane. We thus expand
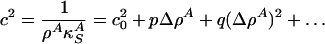 |
[6] |
where 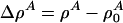 with
with 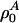 as the equilibrium lateral density. Because the compressibility at 5 MHz is always smaller than the zero frequency compressibility (approaching the isothermal compressibility), we obviously find dispersion in the system, which renders the sound velocity frequency-dependent. For the data for unilamellar DPPC vesicles shown in Fig. 2 (low-frequency case), we obtain c0 = 176.6 m/s,
as the equilibrium lateral density. Because the compressibility at 5 MHz is always smaller than the zero frequency compressibility (approaching the isothermal compressibility), we obviously find dispersion in the system, which renders the sound velocity frequency-dependent. For the data for unilamellar DPPC vesicles shown in Fig. 2 (low-frequency case), we obtain c0 = 176.6 m/s, 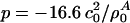 , and
, and 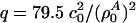 with
with 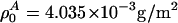 , assuming a bulk temperature of T = 45°C. For the corresponding lung surfactant data we obtain c0 = 171.4 m/s,
, assuming a bulk temperature of T = 45°C. For the corresponding lung surfactant data we obtain c0 = 171.4 m/s, 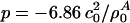 , and
, and 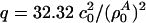 with
with 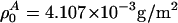 , assuming a bulk temperature of T = 37°C.
, assuming a bulk temperature of T = 37°C.
Higher frequencies result in higher propagation velocities, v, because the isentropic compressibility is a decreasing function of frequency as shown in Fig. 2. We will approximate the dispersive effects discussed above by introducing a dispersive term, –h∂4ΔρA/∂z4 with h > 0.
The equation governing sound propagation is then
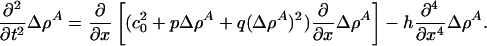 |
[7] |
This equation is closely related to the Boussinesq equation (22, 23). For periodic low-amplitude solutions with 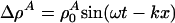 , we thus obtain the dispersion relation
, we thus obtain the dispersion relation
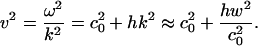 |
[8] |
The sound velocity thus increases with increasing frequency as required by the experimental observation of decreasing compressibility with increasing frequency.
We now consider the possibility of propagating solitons and seek solitonic solutions of the form Δρ A(z) with z = x – vt. Eq. 7 can be rewritten as
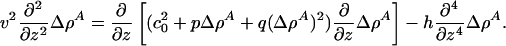 |
[9] |
Let us further assume that the solitons are localized and vanish for |z| → ∞. This allows us to perform two integrals immediately to obtain
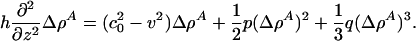 |
[10] |
Note that the desire for localized solutions requires that |v| < c0 (otherwise the density pulse does not decay to zero faraway from the pulse maximum) for which 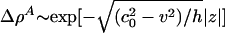 as |z| → ∞.
as |z| → ∞.
Now multiply both sides of Eq. 10 by ∂(Δρ A)/∂z and integrate once more to yield
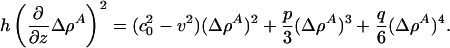 |
[11] |
The message of Eq. 11 is clear. The soliton profile must have a maximum [at which ∂(ΔρA)/∂z = 0], and it must be symmetric about this maximum. Because both 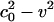 and q are positive, p must be < 0 if we are to have an exponentially localized solution. Fortunately, this is the case for the experimental examples given in Figs. 1 and 2. Moreover, Eq. 11 shows us that the maximum value of ΔρA (
and q are positive, p must be < 0 if we are to have an exponentially localized solution. Fortunately, this is the case for the experimental examples given in Figs. 1 and 2. Moreover, Eq. 11 shows us that the maximum value of ΔρA (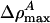 ) is independent of h. At the maximum, the left side of Eq. 11 is 0, and the right side can be solved for ΔρA. When v is very close to c0, we see that
) is independent of h. At the maximum, the left side of Eq. 11 is 0, and the right side can be solved for ΔρA. When v is very close to c0, we see that 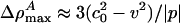 . In other words, soliton amplitudes become small as v → c0. However, if v is too small, ∂zΔρA will not vanish, ΔρA will not have a maximum, and solitons will not exist. This occurs when the right side of Eq. 11 has only one solution for ΔρA:
. In other words, soliton amplitudes become small as v → c0. However, if v is too small, ∂zΔρA will not vanish, ΔρA will not have a maximum, and solitons will not exist. This occurs when the right side of Eq. 11 has only one solution for ΔρA:
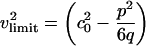 |
[12] |
with an amplitude of
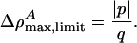 |
[13] |
In the case of unilamellar DPPC vesicles (Fig. 2), these relations imply that vlimit = 0.650 c0 ≈ 115 m/s and 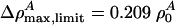 . In cas eof lung surfactant we obtain vlimit = 0.8702 c0 ≈ 149 m/s, and
. In cas eof lung surfactant we obtain vlimit = 0.8702 c0 ≈ 149 m/s, and 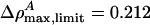 . This minimum velocity soliton has the largest maximum value of ΔρA. At maximum amplitude the membrane is forced partially through the melting transition.
. This minimum velocity soliton has the largest maximum value of ΔρA. At maximum amplitude the membrane is forced partially through the melting transition.
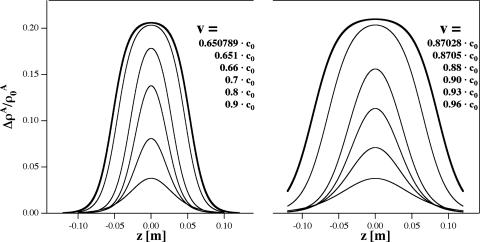
Given a value of the dispersion parameter h, soliton profiles can be calculated by solving Eq. 11 numerically. The only effect of h is to set the linear scale of the soliton, and we have set h = 2 m4/s2 to produce pulses of a few centimeters width as found in some nerves. Resulting soliton profiles are shown in Fig. 3 for several velocities. We stress that dispersion is necessary for the existence of solitons and is clearly present in the data of Fig. 2. Although the specific form of the dispersive term in Eq. 7 is ad hoc, we have confirmed that other forms yield soliton profiles strikingly similar to those of Fig. 3.
Fig. 3.
Soliton profiles. (Left) Soliton profiles for the DPPC large unilamellar vesicle membrane at T = 45°C obtained for velocities between v = 0.48 and 0.8 c0. Larger profiles correspond to smaller velocities. The largest profile is essentially the limiting soliton. (Right) Soliton profiles for lung surfactant at T = 37°C obtained for velocities between v = 0.83 and 0.95 c0. The maximum amplitude of the limiting soliton is very close to that found for the DPPC membrane.
Each of the solitons shown in Fig. 3 has an associated energy. The precise soliton shape depends on the energy of the excitation. It can be seen from Fig. 3 that the width of the soliton increases as v approaches vlimit, and the maximum amplitude approaches 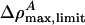 . As a result, a soliton becomes arbitrarily broad as more energy is provided without changing the shape of its tail, maximum amplitude, or velocity. For sufficiently large excitation energies, only maximum amplitude solitons will propagate. They correspond to 21% area density change at maximum for both DPPC large unilamellar vesicles and lung surfactant. The total area change in the transition of DPPC is 24.6% (2), which means that, at the peak maximum, the soliton forces the membrane ≈85% through the lipid melting transition. The energy density of a soliton has both potential and kinetic energy contributions and can be calculated by using a Lagrangian formalism (24). The energy density is given by
. As a result, a soliton becomes arbitrarily broad as more energy is provided without changing the shape of its tail, maximum amplitude, or velocity. For sufficiently large excitation energies, only maximum amplitude solitons will propagate. They correspond to 21% area density change at maximum for both DPPC large unilamellar vesicles and lung surfactant. The total area change in the transition of DPPC is 24.6% (2), which means that, at the peak maximum, the soliton forces the membrane ≈85% through the lipid melting transition. The energy density of a soliton has both potential and kinetic energy contributions and can be calculated by using a Lagrangian formalism (24). The energy density is given by
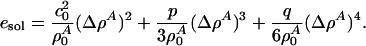 |
[14] |
The total soliton energy is the integral over dz. Given the empirical determination of the compression modulii used, this energy includes contributions from the electrostatic potential, which is a consequence of compression if the membrane is asymmetrically charged. We do not know the charge asymmetry of biological membranes. However, we can assume a maximum voltage change at the peak of the soliton, V0, which can in principle be determined experimentally. We therefore assume that the capacitive energy of a membrane is a consequence of compression and the accompanying voltage change. In the low potential limit of the Gouy–Chapman theory (relevant for medium to high ionic strength conditions and a small fraction of charged lipids), the membrane potential is proportional to the charge density and hence to the density change, ΔρA (25). We assume that the capacitive energy density is given by
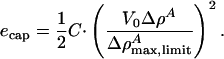 |
[15] |
Volume changes in lipid transitions are significantly smaller than area changes. Because the membrane density changes in the soliton, the membrane thickness must also change. For lipid membranes, the area change is proportional to the volume change and the thickness change. The volume change when going through the transition is 4.7% for DPPC, the corresponding area change is 24.6%, and the thickness change is –16% (corresponding to –7.4 Å). If the solitons at maximum display an area density change of 21% (corresponding to 85% of the transition), the thickness change must be of the order +6.4 Å. This distortion results in a change in the thickness of a membrane cylinder of +12.8 Å. Voltage changes and thickness changes should be proportional.
Discussion
We have discussed the influence of the melting transition on the propagation of sound and isentropic waves in the plane of the membrane. If a membrane is slightly above the melting temperature, the response to compression is an initial lowering of the elastic modulus, followed by a steep increase. Solitons exist as a consequence of a balance between nonlinear and dispersive effects. Nonlinearities are clearly present in the empirical compression modulus (Fig. 2). Dispersion effects, approximated here by –h∂4ΔρA/∂z4, are related to the experimental frequency dependence of sound velocities. Both the form and magnitude of this term can be checked experimentally by investigating the velocity of small amplitude sound. The value of h adopted here and the dispersion relation 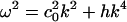 suggest an increase in the sound velocity of ≈4% at a frequency of 5 kHz. In 3D experiments (5, 6), the sound velocity is known to be approximately constant well above and below the transition. Within the transition, the compression modulus at 5 MHz is drastically reduced in comparison with the isothermal (or low frequency) case. The frequency dependence of lipid membranes close to melting transitions was investigated by Mitaku and Date (26). Although they confirmed a pronounced frequency dependence, appropriate data are unavailable in the ms regime. We emphasize that, given experimental confirmation of the dispersive term, the soliton profiles can be predicted uniquely as shown above.
suggest an increase in the sound velocity of ≈4% at a frequency of 5 kHz. In 3D experiments (5, 6), the sound velocity is known to be approximately constant well above and below the transition. Within the transition, the compression modulus at 5 MHz is drastically reduced in comparison with the isothermal (or low frequency) case. The frequency dependence of lipid membranes close to melting transitions was investigated by Mitaku and Date (26). Although they confirmed a pronounced frequency dependence, appropriate data are unavailable in the ms regime. We emphasize that, given experimental confirmation of the dispersive term, the soliton profiles can be predicted uniquely as shown above.
Our calculations have been performed for a quasi-1D cylinder slightly above the cooperative melting transition. As biological examples we chose lung surfactant (which exists as a surface film on lungs in a bilayer/monolayer equilibrium) and E. coli and B. subtilis membranes (which display similar lipid melting features slightly below body or growth temperature). Although we have no direct data on the melting of nerve axon membranes, the biological implications of such a phenomenon seem to be particularly striking regarding the propagation of the action potential.
The resting potential of nerve membranes is about –70 mV. It is the consequence of pronounced differences of ion concentrations inside and outside of the cell (Nernst potential), e.g., ≈400 mM K+ inside and only 20 mM K+ outside of the squid giant axon. The nerve pulse or action potential is associated with the propagation of a voltage pulse along a cylindrical membrane. Hodgkin and Huxley (18) considered the nerve membrane simultaneously as a capacitor and a conductor, and they related the pulse to the opening and closing of specific protein channels (sodium and potassium channels in squid axons) that alter the membrane potential in a voltage- and time-dependent manner. This theory was supported by the discovery of localized ion fluxes by Neher and Sakmann (28) by using the patch–clamp technique. Their microscopic findings seem consistent with macroscopic steady-state voltage clamp measurements. In 1998, the K+ channel was crystallized by MacKinnon and coworkers (29), and a mechanism for the selective transport of K+ versus Na+ was proposed.
Nevertheless, a number of unanswered questions regarding nerve propagation remain. Tasaki and coworkers presented data showing that nerve pulses can also be obtained in the absence of sodium or other monovalent cations in the external medium (30) and that tetrodotoxin, believed to block the sodium channel, alters the excitibility of nerves even in the absence of sodium (31). These findings speak against the sodium channel as an indispensable element responsible for nerve activity. Moreover, the Hodgkin–Huxley theory (18) is based on equivalent circuits (Kirchhoff circuits). It is not a thermodynamic theory, and its language contains neither temperature and pressure nor entropy, heat, or volume. Various authors have noted that the action potential is accompanied by reversible mechanical dislocations, changes in volume and temperature (11–16, 27, 32), and changes in fluorescence, turbidity, and birefringence (17). In particular, data indicate that heat release is exactly in phase with the action potential (12, 13), and that there is no net heat release after completion of the action potential. This finding suggests that the action potential is isentropic. A. V. Hill's early work on heat production in nerves is considered in Hodgkin's book (33), where it is noted that the heat release and absorption response during the action potential is important but is not understood (11). Given the many experimental features not explained within the Hodgkin–Huxley theory, it is surprising that it remains as unchallenged dogma. The thermodynamic data on nerves reveal many similarities to an adiabatic wave. The Hodgkin–Huxley theory is based on irreversible processes, i.e., fluxes of ions along their chemical potential gradient (across the nerve membrane or along the axon). If one assumes as here that the nerve pulse is related to the propagation of an isentropic pulse, a temporal correlation between mechanical dislocations, forces, voltage, and heat release would not be surprising but rather an intrinsic property of the pulse. Further, measured propagation velocities, which are ≈100 m/s in myelinated nerves, find a satisfying explanation. In nonmyelinated nerves, propagation velocities are usually significantly slower.
Our description of solitons is based on the assumptions (i) that membranes are at slightly higher temperatures than the melting transition of the membrane and (ii) that the system is quasi-1D.† The first of these assumptions is clearly true for lung surfactant and E. coli and B. subtilis membranes (Fig. 1), but we have not presented evidence for such a transition in nerve membranes. However, indications for such transition events accompanying the nerve pulse can be found in the literature (e.g., ref. 34 and references therein and ref. 35). Howarth et al. (12) discussed in detail the initial heat release and the subsequent reabsorption, which is in phase with the square of the voltage changes (13) as is the energy of a charging capacitor (see Fig. 4b). They found typical temperature changes on the order of 80 μK (pike olfactory nerve) and heat changes at the maximum of the action potential of 200 μcal/g of nerve (garfish olfactory nerve). They concluded that neither heats of ion dilution nor heat dissipation by charging and uncharging the capacitor can explain the magnitude of the measured heat response. In fact, they concluded that the most likely explanation for the measured heat is the reversible change of entropy (and zero net change of entropy) of the membrane itself during the pulse, a feature that is exactly shared by the present model of an adiabatically propagating density pulse.
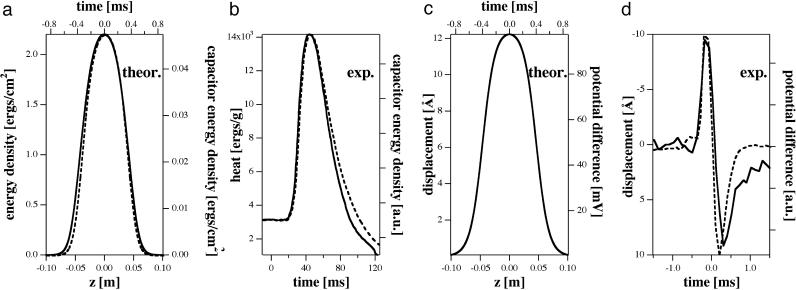
Fig. 4.
Properties of solitons and nerves. (a) Calculated total energy and capacitive energy densities stored in the soliton during the passage. Both functions display similar time dependence. (b) Experimental heat changes during the action potential of garfish olfactory nerve (solid line) and the energy of charging the membrane's capacitor. Both functions display similar time dependence (adapted from ref. 13). (c) Calculated thickness change of a membrane cylinder (displacement) and corresponding voltage changes. Both functions display identical time dependence. (d) Experimentally determined differential displacement of the squid axon and the corresponding action potential (adapted from ref. 27). Both functions display identical time dependence. The different shape of the profiles as compared with b are a consequence of the experimental setup.
It is therefore of interest to compare the energy carried by solitons with the electrostatic energy associated with the conventional description of pulse propagation in nerves. In Fig. 4a we show the energy density and capacitive energy calculated for a soliton in slightly asymmetrically charged cylindrical membranes with properties similar to those of DPPC for v = 0.651 c0 with the corresponding capacitive energy density calculated from Eqs. 11 and 14. To estimate the latter, we note that the capacitance of the membranes considered here is ≈C = 1 μF/cm2 and the maximum voltage is approximately V0 = 100 mV. Using the parameters introduced above for the isothermal compression modulus, we find an electrostatic energy density of ≈0.05 ergs/cm2. This value is >1 order of magnitude smaller than the energy of the corresponding soliton. If one assumes that the total energy density is the upper limit for the reversible heat released during the pulse, our finding is in good agreement with that of Ritchie and Keynes (13). In another study, Iwasa and Tasaki (27) found a change in nerve diameter of ≈10 Å during the pulse, in phase and with the same shape as the voltage change (Fig. 4d). This value is nearly the same as the value calculated here for the thickness change of the two opposing membranes (12.8 Å) of a cylinder. Furthermore, we also predict that voltage and thickness changes are in phase with a similar functional form. Because the calculated soliton amplitudes and the empirical shape of the solitons in DPPC membranes and those in lung surfactant are nearly the same, we expect similar energies and displacements in biological membranes as compared with the model membranes. Our description of the voltage pulse is based on simplifying assumptions regarding membrane properties. Possibly important details, including the existence of magnetic field responses (36) and the existence of free electrons in the membranes (34, 37), have not been addressed.
The above suggests that the role of solitons in pulse propagation can be confirmed or denied by experimental determinations of the total (i.e., mechanical, electrostatic, heat, etc.) energy associated with a single pulse. If the empirical pulse energy is greater than the electrostatic energy, the conventional mechanism for pulse propagation is insufficient and must be supplemented. This inequality, in fact, has been shown by Howarth et al. (12). As mentioned, it had been proposed earlier that transitions are involved in the nerve pulse. Whereas Kinnunen and Virtanen (34) favor the view that the membrane itself undergoes a transition, Tasaki (35) proposed a sol–gel transition in the cytoskeleton of the nerve axon. It should be noted that our theory can be applied to all 1D systems that undergo transitions. While a sol–gel transition would also tend to produce solitary solutions, the present contribution has focused exclusively on a lipid membrane mechanism.
Conclusions
It is clear that the Hodgkin–Huxley model fails to explain a number of features of the propagating nerve pulse, including the reversible release and reabsorption of heat and the accompanying mechanical, fluorescence, and turbidity changes. The most striking feature of the isothermal and isentropic compression modulus is its significant undershoot and striking recovery. These features lead generically to the conclusions (i) that there is a minimum velocity of a soliton and (ii) that the soliton profiles are remarkably stable as a function of the soliton velocity. There is a maximum amplitude and a minimum velocity of the solitons that is close to the propagation velocity in myelinated nerves. In addition, solitons propagate without distortion of their form. It would be surprising if nature did not exploit these features.
Acknowledgments
We thank Dr. Konrad Kaufmann for discussions and his persistence while introducing us to the interesting problem of the thermal and mechanical response during the action potential; Prof. Benny Lautrup (The Niels Bohr Institute) and Prof. Ichiji Tasaki (National Institutes of Health, Bethesda) for critical reading of our manuscript; Prof. Fred Possmeyer for a donation of bovine lung surfactant; and Denis Pollakowski from our group and Dr. Manfred Konrad (Max-Planck-Institute for Biophysical Chemistry, Göttingen, Germany) for allowing us to show the heat capacity profile of E. coli and B. subtilis membranes before detailed publication.
Author contributions: T.H. and A.D.J. designed research, performed research, analyzed data, and wrote the paper.
Abbreviation: DPPC, dipalmitoyl phosphatidylcholine.
Footnotes
The assumption of quasi one-dimensionality suggests that our model is primarily applicable to myelinated nerves, which are better able to resist curvature fluctuations.
References
- 1.Ivanova, V. P., Makarov, I. M., Schäffer, T. E. & Heimburg, T. (2003) Biophys. J. 84, 2427–2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Heimburg, T. (1998) Biochim. Biophys. Acta 1415, 147–162. [DOI] [PubMed] [Google Scholar]
- 3.Ebel, H., Grabitz, P. & Heimburg, T. (2001) J. Phys. Chem. B 105, 7353–7360. [Google Scholar]
- 4.Grabitz, P., Ivanova, V. P. & Heimburg, T. (2002) Biophys. J. 82, 299–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Halstenberg, S., Heimburg, T., Hianik, T., Kaatze, U. & Krivanek, R. (1998) Biophys. J. 75, 264–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schrader, W., Ebel, H., Grabitz, P., Hanke, E., Heimburg, T., Hoeckel, M., Kahle, M., Wente, F. & Kaatze, U. (2002) J. Phys. Chem. B 106, 6581–6586. [Google Scholar]
- 7.Dimova, R., Pouligny, B. & Dietrich, C. (2000) Biophys. J. 79, 340–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heimburg, T. (2000) Biophys. J. 78, 1154–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.van Osdol, W. W., Biltonen, R. L. & Johnson, M. L. (1989) J. Bioener. Biophys. Methods 20, 1–46. [DOI] [PubMed] [Google Scholar]
- 10.Pollack, G. H. (2001) Cells, Gels and the Engines of Life: A New, Unifying Approach to Cell Function (Ebner & Sons, Seattle).
- 11.Abbott, B. C., Hill, A. V. & Howarth, J. V. (1958) Proc. R. Soc. London Ser. B 148, 149–187. [DOI] [PubMed] [Google Scholar]
- 12.Howarth, J. V., Keynes, R.D. & Ritchie, J. M. (1968) J. Physiol. (London) 194, 745–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ritchie, J. M. & Keynes, R. D. (1985) Q. Rev. Biophys. 392, 451–476. [DOI] [PubMed] [Google Scholar]
- 14.Tasaki, I. (1988) Physiol. Chem. Phys. Med. NMR 20, 251–268. [PubMed] [Google Scholar]
- 15.Tasaki, I., Kusano, K. & Byrne, M. (1989) Biophys. J. 55, 1033–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tasaki, I. & Byrne, M. (1990) Biophys. J. 57, 633–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tasaki, I., Watanabe, A., Sandlin, R. & Carnay, L. (1968) Proc. Natl. Acad. Sci. USA 61, 883–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hodgkin, A. L. & Huxley, A. F. (1952) J. Physiol. (London) 117, 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pollakowski, D. (2004) Master's thesis (University of Göttingen, Göttingen, Germany).
- 20.Wilson, A. H. (1957) Thermodynamics and Statistical Mechanics (Cambridge Univ. Press, Cambridge).
- 21.Evans, E. A. (1974) Biophys. J. 14, 923–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Boussinesq, J. (1871) Comptes Rendus Acad. Sci. Paris 72, 755–759. [Google Scholar]
- 23.Boussinesq, J. (1872) J. Math. Pure Appl. 7, 55–108. [Google Scholar]
- 24.Manoranjan, V. S., Ortega, T. & Sanz-Serna, J. M. (1988) J. Math. Phys. 294, 1964–1968. [Google Scholar]
- 25.Träuble, H., Teubner, M. & Eibl, H. (1976) Biophys. Chem. 43, 319–342. [DOI] [PubMed] [Google Scholar]
- 26.Mitaku, S. & Date, T. (1982) Biochim. Biophys. Acta 688, 411–421. [DOI] [PubMed] [Google Scholar]
- 27.Iwasa, K. & Tasaki, I. (1980) Biochem. Biophys. Res. Commun. 95, 1328–1331. [DOI] [PubMed] [Google Scholar]
- 28.Neher, E. & Sakmann, B. (1976) Nature 260, 779–802. [DOI] [PubMed] [Google Scholar]
- 29.Doyle, D. A., Morais Cabral, J., Pfuetzner, R. A., Kuo, A., Gulbis, J. M., Cohen, S. L., Chait, B. T. & Mackinnon, R. (1998) Science 280, 69–77. [DOI] [PubMed] [Google Scholar]
- 30.Tasaki, I., Watanabe, A. & Singer, I. (1966) Proc. Natl. Acad. Sci. USA 56, 1116–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Watanabe, A., Tasaki, I., Singer, I. & Lerman, L. (1967) Science 155, 95–97. [DOI] [PubMed] [Google Scholar]
- 32.Howarth, J. (1975) Philos. Trans. R. Soc. London 270, 425–432. [DOI] [PubMed] [Google Scholar]
- 33.Hodgkin, A. L. (1964) The Conduction of the Nervous Impulse (Liverpool Univ. Press, Liverpool, U.K.).
- 34.Kinnunen, P. K. J. & Virtanen, J. A. (1986) in Modern Bioelectrochemistry, eds. Gutmann, F. & Keyzer, H. (Plenum, New York), pp. 457–479.
- 35.Tasaki, I. (1999) Ferroelectrics 220, 305–316. [Google Scholar]
- 36.Wikswo, J. P., Barach, J. P. & Freeman, J. A. (1980) Science 208, 53–55. [DOI] [PubMed] [Google Scholar]
- 37.Calvin, M., Wang, H. H., Entine, G., Gill, D., Ferruti, P., Harpold, M. A. & Klein, M. P. (1969) Proc. Natl. Acad. Sci. USA 63, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]