Tunable polarization entangled photon-pair source in rhombohedral boron nitride

Abstract

Entangled photon-pair sources are pivotal in various quantum applications. Miniaturizing the quantum devices to meet the requirement in limited space applications drives the search for ultracompact entangled photon-pair sources. The rise of two-dimensional (2D) semiconductors has been demonstrated as ultracompact entangled photon-pair sources. However, the photon-pair generation rate and purity are relatively low, and the strong photoluminescence in 2D semiconductors also makes the operational wavelength range limited. Here, we use the spontaneous parametric down conversion (SPDC) of rhombohedral boron nitride (rBN) as a polarization entangled photon-pair source. We have achieved a generation rate of more than 120 hertz (a record-high SPDC coincidence rate with 2D materials) and a high-purity photon-pair generation with a coincidence-to-accidental ratio of above 200. Tunable Bell state generation is also demonstrated by simply rotating the pump polarization, with a fidelity up to 0.93. Our results suggest rBN as an ideal candidate for on-chip integrated quantum devices.

The SPDC of rBN makes it an ideal candidate for polarization entangled photon-pair sources for on-chip integrated quantum devices.

INTRODUCTION

Entangled photon pairs are fundamental in quantum technologies such quantum communication (1), quantum sensing and imaging (2, 3), quantum computing schemes (4, 5), and quantum metrology (6–9). Spontaneous parametric down conversion (SPDC), a second-order nonlinear process, is commonly used to generate these entangled quantum light states (10–14). Conventionally, SPDC sources are bulk nonlinear crystals [such as beta barium borate (BBO) and potassium titanyl phosphate (KTP)], which have low nonlinear coefficients χ⁽²⁾, requiring larger sizes for sufficient efficiency (11–15). Normally, the creation of entangled photon pairs are based on the interference of two SPDC processes and using two crossed nonlinear crystals by combining different down conversion paths in Sagnac and linear interferometers (14, 15). These properties make these bulk SPDC sources unsuitable for compact application environments such as in a satellite or a mobile phone (16, 17).

There are demonstrations of on-chip photon pair sources with integrated nonlinear photonic platforms such as LiNbO₃, Si, and Si₃N₄ (18–21). With large scale integration of spatial and temporal multiplexing systems, near-deterministic entangled multi-photon states can be implemented. However, they are restricted with sizes for achieving phase matching. Moreover, they have difficulty to generate polarization entanglement due to the polarization preferences of the photonic structures. To search for a phase-matching free and polarization entangled quantum source, 2D van der Waals (vdW) materials with giant nonlinearities compared to conventional bulk nonlinear crystals (22, 23) have attracted broad attention due to the subwavelength thickness and relaxation of phase-matching constraints. However, because of short interaction length in monolayer materials, the absolute signal is weak. When the layer thickness increases, in normal hexagonal stacking order cases, the nonlinear response quenches with neighboring layers (24, 25), which limits the scalability for high efficiency SPDC. The highly disordered material NbOCl₂ has been demonstrated as efficient SPDC source for photon-pair generation (26). However, NbOCl₂ intrinsically lacks polarization entanglement (27), which is pivotal for practical qubit encoding. Specific device architecture can help NbOCl₂ to induce entanglement (27), while it also complicates the device design and fabrication.

Recently, rhombohedral stacked transition-metal dichalcogenides (TMDCs) are demonstrated as polarization-entangled photon pairs (28, 29). They have large second-order susceptibility for enhancing photon-pair generation and broken lattice centrosymmetry for scalable nonlinearity. Besides, they have intrinsic polarization entanglement with generated photon-pair. However, 2D TMDCs usually have strong photoluminescence (PL) signals, which add to the background noise, and increase the accidental counts, making the isolation of the entangled photon pairs difficult and reducing the purity of nonlinear excitation signals (30, 31). This can be overcome by selecting a signal wavelength out of the PL spectrum (28, 29), which also limits the operation wavelength of the quantum entangled photon pairs.

2D boron nitride is widely used in many quantum applications (32), including quantum emitters (33) and quantum sensing (34–36). Besides, it has broad spectrum transparency (37, 38), large nonlinear coefficient χ⁽²⁾ (39–41), excellent physicochemical stability (42) and high laser damage threshold (43, 44). Hence, it has been regarded as a promising candidate for nonlinear optical material (32). However, in the normal hexagonal boron nitride (hBN), similar to normal 2H-stacked TMDCs, the nonlinear response quenches with increased layers, making it unsuitable for nonlinear optical applications (39). Instead, its counterpart, rhombohedral BN (rBN) exhibits broken both out-of-plane and in-plane inversion symmetry, which increases the nonlinear signal with increasing layers, making it an ideal nonlinear optical material (45, 46).

In this work, we explore the usage of rBN as a tunable entangled photon-pair source. The unique crystal symmetry makes it possible to intrinsically emit polarization entangled photon-pairs. Unlike 2D TMDCs, rBN is wide-bandgap material, hence does not have strong PL in visible and infrared range, making the application wavelength spectrum much broader. Besides, the excellent physicochemical stability and high laser damage threshold also make it ideal for SPDC source. Our results show a highest SPDC generation rate (>120 Hz) in rBN among all the vdW materials reported so far. We also experimentally demonstrate the generation of polarization entangled photon-pairs in rBN, realizing quantum entanglement in a vdW insulator. By simply rotating the pump-field polarization, we can control the state of the generated photon-pairs and verify the quantum coherence of them. Different Bell states can be generated by aligning the pump polarization to zigzag or armchair direction of the crystal.

RESULTS AND DISCUSSION

SPDC signal from rBN

When a laser pumps on the rBN sample, entangled photon-pair will be generated and reflected by the substrate, as illustrated in Fig. 1A. The inherent physical structure of rBN can make the light and matter interaction scale up with increasing number of layers. The nonlinear optical process in rBN is similar to that observed in 3R TMDCs, which is discussed in (28, 29) in details. The optical measurement setup is shown in Fig. 1B. In this work, we use a 405-nm laser as the pump. The signal at around 810-nm wavelength is collected in the back-reflection mode. We use a Hanbury Brown-Twiss setup to characterize the generated photon pairs. Figure 1C shows a typical coincidence measurement result, which was excited by a 6.4-mW laser pump and collected without polarization selection in 2 min. A distinctive coincidence peak can be observed at a zero time difference between the two photon detectors, indicating biphoton generation. We calculate the coincidence count rate by accumulating all the coincidences within the center ±2-ns gate, subtracting the base noise counts, and dividing the collection time. As the pump laser power increases, the coincidence count rate also increases linearly, as expected, shown in Fig. 1D. Here, we can obtain a coincidence count rate over 120 Hz with a laser power of 13.11 mW. Besides, the photon count rate from the photon detector is also linearly increasing with the pump laser power as shown in fig. S1A.

Fig. 1. The schematic and experimental setup of SPDC generation in rBN.

(A) Schematic illustration of the entangled photon-pair generation from rBN. The right bottom corner shows the x (along with zigzag direction) and y (along with armchair direction) axis we used for the measurements in this work. (B) Optical setup for SPDC generation measurements with a 405-nm continuous-wave laser as the pump, including a 100× microscope lens (numerical aperture: 0.95), dichroic mirror (DM), half-wave plate (H), linear polarizer (P), 425-nm long-pass filter (LP), 810 (±5)–nm band-pass filter (BP), and a silver mirror (M). The signal is coupled into a fiber beam splitter and collected by two avalanche photon diodes (APDs). The electrical signals from APDs are then analyzed by time-correlated single-photon counting (TCSPC). (C) Coincidence histogram obtained from rBN with a pump power of 6.4 mW and integration time of 2 min. (D) Coincidence count rate measurements in rBN with different pump powers, which shows a linear relationship between the coincidence rate and the pump power. The black square dots are the experimental data, and the red line is the linear fitting plot. (E) Correlation versus pump power, which exhibits a reversal relationship.

The coincidence-to-accidental ratio (CAR) is related to normalized second-order correlation function $g^{(2)}(0)$, $\text{CAR}=g^{(2)}(0)-1$ (47). Even at the highest laser power and a coincidence rate of more than 120 Hz, we still have a CAR value of more than 13.7. At a lower laser power of 0.082 mW, we can obtain a CAR value of more than 200, and a coincidence rate of more than 1 Hz. Detailed $g^{(2)}$ results of different laser powers are shown in fig. S2. Overall, while the coincidence count rate exhibits a linear increase with the laser power, the second-order correlation function $g^{(2)}$ exhibits an inverse relationship with the laser power, as shown in Fig. 1E. This trend is because of the increase in accidental counts with higher pump laser powers. PL measurements of the sample and substrates under different laser powers are also performed and shown in fig. S1B. Under low laser pump power of 1 mW, there is negligible PL signal observed. When the laser pump power is high up to 13.11 mW, we can observe some weak PL signal at the 810-nm wavelength from both the substrate and sample. We also notice that prolonged laser irradiation can quench the PL signal from the sample and increase the CAR of SPDC. At the beginning of the measurement, we also performed a power dependence of coincidence measurements, as shown in fig. S3. The results in Fig. 1E are from the same location in the sample. However, after 2 weeks of consistent laser irradiation, while the coincidence count rate is almost the same, the CAR is significantly improved after prolonged laser irradiation on the sample. For example, with a same laser power of 6.4 mW, the CAR is increased from ~13.2 at the beginning to ~40 after 2-week laser irradiation on the sample. This should be due to photobleaching of the PL signal, which is usually observed in hBN (33, 48). This is usually an unwanted effect for quantum emitters however in this case it proves useful.

Polarization analysis of the generated photon pairs

Because of the symmetry of ${\mathrm{\chi }}_{\mathit{\text{yyy}}}^{(2)}=-{\mathrm{\chi }}_{\mathit{\text{yxx}}}^{(2)}=-{\mathrm{\chi }}_{\mathit{\text{xxy}}}^{(2)}=-{\mathrm{\chi }}_{\mathit{\text{xyx}}}^{(2)}$ in the nonlinear coefficients of rBN, there exists a special polarization relationship between the pump, signal, and idler light

$$\begin{array}{c}{\mid R⟩}_{\mathrm{p}}\stackrel{\text{SPDC}}{\to }{\mid L⟩}_{\mathrm{s}}{\mid L⟩}_{\mathrm{i}}\hfill \\ {\mid L⟩}_{\mathrm{p}}\stackrel{\text{SPDC}}{\to }{\mid R⟩}_{\mathrm{s}}{\mid R⟩}_{\mathrm{i}}\hfill \end{array}$$ (1)

$R$ and $L$ are represented by the horizontal polarization basis $H$ and the vertical polarization basis $V$ as $R=\frac{1}{\sqrt{2}}(H-\mathit{iV})$ and $L=\frac{1}{\sqrt{2}}(H+\mathit{iV})$. According to Eq. 1, the polarization evolution process of SPDC during H and V polarization pumping is as follows

$$\begin{array}{c}{\mid H⟩}_{\mathrm{p}}\stackrel{\text{SPDC}}{\to }\frac{1}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}}-{\mid V⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}})\hfill \\ {\mid V⟩}_{\mathrm{p}}\stackrel{\text{SPDC}}{\to }\frac{-1}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}}+{\mid V⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}})\hfill \end{array}$$ (2)

When the pump light is of arbitrary linear polarization, defined the angle between it and the V-polarization direction as ${\mathrm{\phi }}_{\mathrm{p}}$, the quantum state after SPDC can be written as

$$\frac{-\text{cos}{\mathrm{\phi }}_{\mathrm{p}}}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}}+{\mid V⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}})+\frac{\text{sin}{\mathrm{\phi }}_{\mathrm{p}}}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}}-{\mid V⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}})$$ (3)

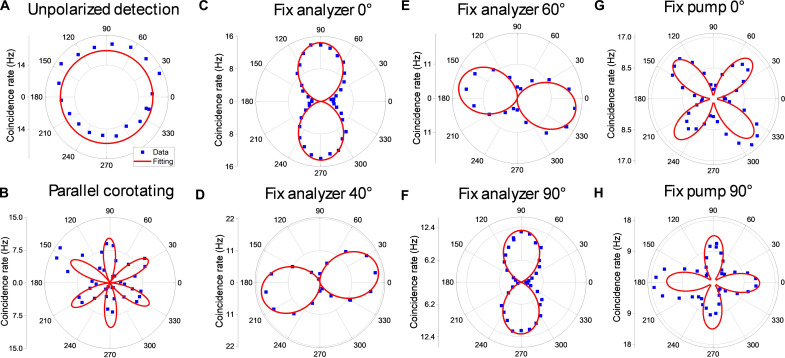
The specific form of the nonlinear tensor of rBN leads to a characteristic polarization dependence of the generated photon-pairs and the pump. Without using a polarizer on the detector, if we only rotate the polarization of the pump laser, then we observe a constant SPDC coincidence rate as expected (29, 49), shown in Fig. 2A. We firstly consider the case of using one polarizer before the SPDC photons are split into two. The angle of linear polarization selected by the polarizer is defined as ${\mathrm{\phi }}_{\text{pol}}+90°$; therefore, the quantum state selected by the polarizer can be written as $\mid {\text{pol}⟩}_{\mathrm{s}}\mid {\text{pol}⟩}_{\mathrm{i}}$, where $\mid \text{pol}⟩=\text{cos}{\mathrm{\phi }}_{\text{pol}}\mid H⟩-s\text{in}{\mathrm{\phi }}_{\text{pol}}\mid V⟩$. Performing a polarization projection measurement on the quantum state of Eq. 3, the dependence of the SPDC count rate ($R_{\text{SPDC}}$) on pump polarization angle ${\mathrm{\phi }}_{\mathrm{p}}$ and analyzer angle ${\mathrm{\phi }}_{\text{pol}}$, $R_{\text{SPDC}}\propto {\text{sin}}^2(2{\mathrm{\phi }}_{\text{pol}}+{\mathrm{\phi }}_{\mathrm{p}})$. When we keep the polarization of the analyzer and the pump in parallel ${\mathrm{\phi }}_{\text{pol}}={\mathrm{\phi }}_{\mathrm{p}}$ and rotate both of them simultaneously, we can obtain a sixfold, coaligned pattern as shown in Fig. 2B, which matches the theoretical expectation $R_{\text{SPDC}}\propto {\text{sin}}^2(3{\mathrm{\phi }}_{\mathrm{p}})$. The SPDC minimum angle corresponds to the zigzag direction of the crystal, and the SPDC maximum angle corresponds to the armchair direction. If we fix the analyzer angle in the zigzag direction (0°), then the coincidence rate corresponds to ${\text{sin}}^2{\mathrm{\phi }}_{\mathrm{p}}$, peaking when the pump polarization is in the armchair direction, as shown in Fig. 2C. By rotating the analyzer, the coincidence rate is proportional to ${\text{sin}}^2({\mathrm{\phi }}_{\mathrm{p}}+2{\mathrm{\phi }}_{\text{pol}})$. The results in Fig. 2 (C to F) agree well with the theoretically derived polarization dependence. If we fix the pump angle and rotate the analyzer polarization, then the coincidence count rate is still proportional to ${\text{sin}}^2(2{\mathrm{\phi }}_{\text{pol}}+{\mathrm{\phi }}_{\mathrm{p}})$, which is confirmed by our experimental results shown in Fig. 2 (G and H).

Fig. 2. Polarization analysis of photon-pairs generated in rBN.

(A) Coincidence rates measurements for rotating the pump polarization angle ${\mathrm{\phi }}_{\mathrm{p}}$ without using polarizer on the detector side. (B) Coincidence rate measurements for rotating the pump and detector polarization simultaneously, ${\mathrm{\phi }}_{\mathrm{p}}={\mathrm{\phi }}_{\text{pol}}$. $R_{\text{SPDC}}\propto {\text{sin}}^2(3{\mathrm{\phi }}_{\mathrm{p}})$ dependence is observed. (C to F) Coincidence rate measurements for rotating the pump polarization angle ${\mathrm{\phi }}_{\mathrm{p}}$ and keep analyzer polarizations at (C) ${\mathrm{\phi }}_{\text{pol}}=0°$, (D) $40°$, (E) 60°, and (F) 90°. $R_{\text{SPDC}}\propto {\text{sin}}^2(2{\mathrm{\phi }}_{\text{pol}}+{\mathrm{\phi }}_{\mathrm{p}})$ dependence is observed. (G and H) Coincidence rate measurements while keeping the pump at (G) 0° and (H) 90° and rotating the analyzer polarization angle ${\mathrm{\phi }}_{\text{pol}}$. $R_{\text{SPDC}}\propto {\text{sin}}^2(2{\mathrm{\phi }}_{\text{pol}}+{\mathrm{\phi }}_{\mathrm{p}})$ dependence is also observed. The blue square dots are the measured results, and the red lines are theoretical fitting curves for all.

Quantum entanglement of photon pairs in rBN

To further characterize the polarization dependence and entanglement of the quantum state, we separate the signal and idler photons with a nonpolarized beam splitter and apply polarization selection on each arm of the detector, as shown in Fig. 3A. In this situation, we can rotate the signal polarization separately while keeping the pump and idler polarization constant. For example, if we fix the pump polarization at 0°, according to Eq. 3, then the expected state should be $\mid \mathrm{\psi }⟩=\frac{-1}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}}+{\mid V⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}})$, which is equivalent to $\frac{1}{\sqrt{2}}({\mid H⟩}_{\mathrm{s}}{\mid V⟩}_{\mathrm{i}}+{\mid V⟩}_{\mathrm{s}}{\mid H⟩}_{\mathrm{i}})$. The signal and idler should emerge with a polarization perpendicular to each other. Thus, if the idler polarization is fixed at 45°[$D$, where $D=\frac{1}{\sqrt{2}}(H+V)$], then the signal should peak at a polarization angle of 135°[$A$, where $A=\frac{1}{\sqrt{2}}(H-V)$], which is confirmed by our experimental result shown in Fig. 3B. If the polarization of the pump is at 90°, then the state should be $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HH}⟩-\mid \mathit{VV}⟩)$, in which case the signal polarization should be parallel to the idler. This is also confirmed by our experimental result shown in Fig. 3D. Furthermore, in the $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HV}⟩+\mid \mathit{VH}⟩)$ state (${\mathrm{\phi }}_{\mathrm{p}}=0°$), the signal and idler photons should always be perpendicular to each other. Hence, if we keep the two with a perpendicular polarization and rotate them simultaneously, then we can always obtain a maximum coincidence rate, while keeping the two with a parallel polarization always gives a minimum coincidence rate, as shown in Fig. 3C. The opposite state $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HH}⟩-\mid \mathit{VV}⟩)$ (${\mathrm{\phi }}_{\mathrm{p}}=90°$), is also shown in Fig. 3E.

Fig. 3. Setup of quantum-state tomography measurements and polarization analysis of the setup.

(A) Optical setup for quantum polarization-state tomography measurements. Differently from the previous one shown in Fig. 1, the polarization selection is after the unpolarized beam splitter (BS), making the signal and idler separated. Additional quarter-wave plates (Q) are applied here for circular polarizations. (B and C) Coincidence rate measurements with pump at 0°, (B) rotating the signal polarization angle while keeping the idler at 45° and (C) simultaneously rotating both the signal and idler polarization while keeping them in perpendicular (blue circles) and parallel (red circles). (D and E) Coincidence rate measurements with pump at 90°, (D) rotating the signal polarization angle and (E) corotating the signal and idler. The circles and curves represent the experimental and fitting data in (B) to (E), respectively.

To characterize the polarization quantum state and show entanglement between signal and idler photon, we perform a tomographic measurement, requiring that each photon is measured in $\mid H⟩$, $\mid V⟩$, $\mid D⟩$, $\mid A⟩$, $\mid R⟩$, and $\mid L⟩)$ basis (50). When the pump polarization is set to 90°, the Bell state should be $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid HH⟩-\mid VV⟩)$. The ideal and experimental density matrices are shown in Fig. 4 (A and B). The fidelity of the measured states is 0.917 ± 0.013, confirming that the prepared quantum state is highly consistent with the ideal Bell state. The calculated purity and concurrency are 0.877 and 0.829, respectively (51). In the other Bell state $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HV}⟩+\mid \mathit{VH}⟩)$, with pump polarization at 0°, the ideal and measured density matrices are shown in Fig. 4 (C and D), exhibiting a fidelity of 0.933 ± 0.010, a purity of 0.912, and a concurrence of 0.885, indicating a high quality of Bell state. The experimental results show that high quality polarized entangled quantum states can be easily prepared using rBN. Furthermore, the $C_3$ symmetry of the crystal can support continuously tunable polarization entangled states by simply adjusting the pump polarizations, which is a notable advantage in practical quantum technologies (52).

Fig. 4. Quantum state tomography of the polarization-entangled photon-pairs generated from rBN.

The density matrix of a quantum state can be completely represented by two bar graphs representing the real $\mathrm{Re}(\widehat{\mathrm{\rho }})$ and imaginary $\mathrm{Im}(\widehat{\mathrm{\rho }})$ components. Density matrix of the ideal and experimental results of the generated quantum state (A and B) with a pump polarization at 90°, expecting a quantum state of $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HH}⟩-\mid \mathit{VV}⟩$ and (C and D) with a pump at 0°, expecting a quantum state of $\mid \mathrm{\psi }⟩=\frac{1}{\sqrt{2}}(\mid \mathit{HV}⟩+\mid \mathit{VH}⟩$.

In conclusion, we have demonstrated a high-rate polarization entangled photon pairs generated by SPDC in rBN, a vdW insulator, with which, we have obtained the highest coincidence count rate in 2D vdW materials so far, three orders of magnitude more than that in MoS₂ (29), with a high purity at the same time. Integration with resonant cavities or metasurfaces can be used to further enhance photon-pair generation efficiency in rBN (53, 54). Direct engineering on rBN to make nanophotonic devices may be applied to not only enhance the efficiency of photon-pair generation but also make operational quantum nanophotonic devices directly (55). This ultracompact, intrinsically tunable polarization-entangled photon-pair source will facilitate quantum technologies such as quantum computation and quantum sensing in compact devices and may bring new physics to quantum applications.

MATERIALS AND METHODS

Sample preparation

The rBN crystalline films were prepared by the stacking-controlled continuous precipitation strategy on the FeNi foils (42). A typical wet transfer technique was applied for transferring the rBN samples onto the target substrates. Initially, rBN/FeNi samples were suspended on the surface of an FeCl₃ solution for over 20 hours to etch away the Fe and Ni constituents. Subsequent thorough rinsing with deionized water eliminated the residual etchant, and then the films were carefully transferred onto predetermined substrates.

The transfer process was further refined through the use of a polypropylene carbonate (PPC) film, which was initially spin-coated onto a poly(dimethylsiloxane) (PDMS) stamp for the purpose of picking up the rBN flakes. The rBN/PPC film was subsequently overlaid onto a SiO₂/Si wafer substrate and was detached from the PDMS stamp through thermal release at 130°C. Upon achieving complete separation, the rBN samples underwent an annealing treatment at 400°C for 10 hours under a low-pressure condition (<200 Pa) with Ar [500 standard cubic centimeter per minute (sccm)] and H₂ (50 sccm). The annealing process was critical for the elimination of PPC residue and the removal of interlayer air bubbles, ensuring the integrity and purity of the rBN samples for subsequent analysis.

Optical measurements

First, the SPDC signal was measured without any polarization selection at the detector. The pump, a continuous wave (CW) of 405-nm laser (model: BDS-SM-405-FBC), is reflected by a dichroic mirror (Thorlabs, DMLP425R) toward the sample. The signal excited from the sample passed through a dichroic mirror. A 425-nm long-pass filter (LP, Edmund, #84-742) and an 810 (±5)–nm band-pass filter (Thorlabs, FBH810-10) was used to filter out the noise signal by emanating from wavelengths other than the SPDC signal. A half wave plate (HWP; or H in Fig. 1B, Thorlabs, AHWP10M-600) and a linear polarizer (P in Fig. 1B, Thorlabs, LPVIS050-MP2) was used to select the signal polarization. The signal was then reflected by a silver mirror and coupled into an optical fiber with a fiber beam splitter (Thorlabs, TM200R5F1B, core diameter = 200 μm) that lastly splits into two and reaches two avalanche photon diodes (PerkinElmer, SPCM-AQR-14-FC). The fibers are then connected to a TCSPC (PicoQuant, TimeHarp 260) for coincidence measurement. The polarization analysis in Fig. 2 is based on the setup shown in Fig. 1, with polarization selection before the fiber beam splitter.

For quantum tomography measurements, we applied polarization selection after the SPDC signal was split into idler and signal separately. Here, additional quarter wave plates (Thorlabs, WPQ05M-830) were used to enable polarization state selection.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S8

References