Solvent‐Controlled Separation of Integratively Self‐Sorted Pd₂L^A ₂L^B ₂ Coordination Cages

Abstract

The integrative implementation of multiple different components into metallosupramolecular self‐assemblies requires sophisticated strategies to avoid the formation of statistical mixtures. Previously, the key focus was set on thermodynamically driven reactions of simple homoleptic into complex heteroleptic structures. Using Pd₂ L^A ₂ L^B ₂‐type coordination cages, we herein show that integrative self‐sorting can be reversed by a change of solvent (from DMSO to MeCN) to favor narcissistic re‐segregation into coexisting homoleptic species Pd₂ L^A ₄ and Pd₃ L^B ₆. Full separation (“unsorting”) back to a mixture of the homoleptic precursors was finally achieved by selective precipitation of Pd₃ L^B ₆ with anionic guest G¹ from MeCN, keeping pure Pd₂ L^A ₄ in solution. When a mixture of homoleptic Pd₃ L^B ₆ and heteroleptic Pd₂ L^A ₂ L^B ₂ is exposed to a combination of two different di‐anions (G¹ and G² ) in DMSO, selective guest uptake gives rise to two defined coexisting host–guest complexes. A joint experimental and deep theoretical investigation via liquid‐state integral equation theory of the reaction thermodynamics on a molecular level accompanied by solvent distribution analysis hints at solvent expulsion from Pd₂ L^A ₄ to favor the formation of Pd₂ L^A ₂ L^B ₂ in DMSO as the key entropic factor for determining the solvent‐specific modulation of the cage conversion equilibrium.

Two shape‐complementary ligands coordinate with Pd(II) to form either heteroleptic or homoleptic cage species. The equilibrium of the products can be controlled by choosing DMSO or MeCN as a solvent. Joint experimental and theoretical analyses elucidate the driving force behind this separation.

Introduction

Metallosupramolecular self‐assembly allows to straightforwardly generate a multitude of nanoscopic objects of defined sizes and shapes. While most reported structures are based on a single ligand type per assembly, recent developments are aimed at the integrative (as opposed to narcissistic) incorporation of multiple different building blocks in a single assembly product. Therefore, a number of strategies has been developed with the common goal to avoid the formation of statistical mixtures.[ ¹ , ² ] In the field of coordination cages, we and others have used methods such as shape‐complementary assembly (SCA),[ ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ ] coordination‐sphere engineering (CSE),[ ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ ] and adjacent backbone interactions (ABI)[ ²⁰ , ²¹ ] to achieve integrative self‐sorting. The main focus was usually set on realizing some sort of thermodynamic preference for the formation of the heteroleptic self‐sorted structure as opposed to the homoleptic precursors. As key factors, the release of strain (energetic component)[ ³ , ²² ] and the reduction of assembly nuclearity (lowering the count of components per assembly concomitant with an increase in the number of independent particles in solution; entropic component)[ ³ , ²¹ , ²³ ] were identified. While often qualitatively convincing, such rather simplified explanations may recklessly neglect the strong influence of the solvent on the underlying equilibria. Indeed, a solvent dependency of the assembly and guest uptake of metallosupramolecular species is often observed.[ ²¹ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² , ³³ , ³⁴ ]

Also for homo‐ and heteroleptic Pd(II)‐based assemblies, experimental evidence for strong solvation effects was reported, e.g. concerning chiral‐self sorting, ^[35] isomer selection in cages based on unsymmetrical ligands, ^[36] the dominant ring sizes formed from bis‐monodenate ligands,[ ²⁵ , ³⁷ ] the switch between monomeric lantern‐shaped Pd₂L₄ cages and their interpenetrated dimers[ ³⁸ , ³⁹ , ⁴⁰ ] and the formation of different heteroleptic topologies from shape‐complementary ligands. ^[41] Noteworthy, the physical reasons for these solvent influences have not yet been unraveled beyond empirical attempts to find explanations based on, e.g., differences in solvent polarity, H‐bond donor/acceptor character or molecular size. While experimentally notoriously difficult to tackle, advanced theoretical methods, aimed at modeling solvation environments, have just become available to allow deeper insights into the complex solvent contributions in such systems.[ ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ ]

Here we show how the integrative self‐sorting of two homo‐ into one heteroleptic assembly, which spontaneously proceeds in one solvent (DMSO) and is reversed in another solvent (MeCN), can be reproduced and interpreted by atomistic thermodynamic calculations. We further show how the assembly segregation process can be completed by adding a dianionic guest that selectively precipitates only one of the homoleptic assemblies while keeping the other one in MeCN solution (Figure 1). Finally, we show that a mixture of a homoleptic and a heteroleptic assembly gives rise to two defined coexisting host–guest complexes when exposed to a combination of two different di‐anions in DMSO.

Figure 1.

Two shape‐complementary ligands L^A and L^B are able to separately react with Pd(II) cations to homoleptic, strained helicate Pd₂ L^A ₄ or trinuclear ring Pd₃ L^B ₆, respectively. When mixed in DMSO, they quantitatively assemble to heteroleptic cage Pd₂ L^A ₂ L^B ₂ that can be partially reconverted into narcissistically coexisting helicate and ring by changing the solvent to MeCN. Full separation can be achieved by selective precipitation of the ring with an anionic guest.

Results and Discussion

Experiments

Ligand L^A and its homoleptic helical assembly Pd₂ L^A ₄ were previously reported to react with bis‐monodentate ligands with rather divergent coordination vectors to yield dinuclear heteroleptic assemblies. ^[3] Here, we combine this with ligand L^B , ^[49] a phenanthrene derivative with para‐pyridyl donors attached via alkynyl linkers, that reacts with L^A in DMSO to quantitatively form multicomponent cage Pd₂ L^A ₂ L^B ₂, carrying both ligands in a cis‐relationship. Alternatively, both homoleptic assemblies Pd₂ L^A ₄ and Pd₃ L^B ₆, can be combined in a 3 : 2 ratio to yield Pd₂ L^A ₂ L^B ₂ via a cage‐to‐cage transformation pathway.

Clean formation of the heteroleptic cage in DMSO was shown by ¹H NMR analysis, where the integrative assembly product shows a series of signals that are shifted with respect to the signals of the free ligands and also do not stem from any of the homoleptic assemblies (Figure 2a, bottom). Most indicative is the strongly downfield shifted proton H_a of ligand L^A in Pd₂ L^A ₂ L^B ₂ (see numbering Scheme in Figure 1), appearing at 10.4 ppm in the heteroleptic assembly, while experiencing a significant upfield shift to 9.4 ppm due to the neighboring isoquinoline π‐surfaces in the highly twisted homoleptic helicate Pd₂ L^A ₄. In addition, the high‐resolution ESI mass spectrum clearly indicates the exclusive formation of the non‐statistical assembly product by showing peaks of the species [Pd₂ L^A ₂ L^B ₂+n BF₄]⁽⁴⁻ⁿ⁾⁺ (n=0–2) and a perfect match between measured and calculated isotopic patterns (Figure 2b).

Figure 2.

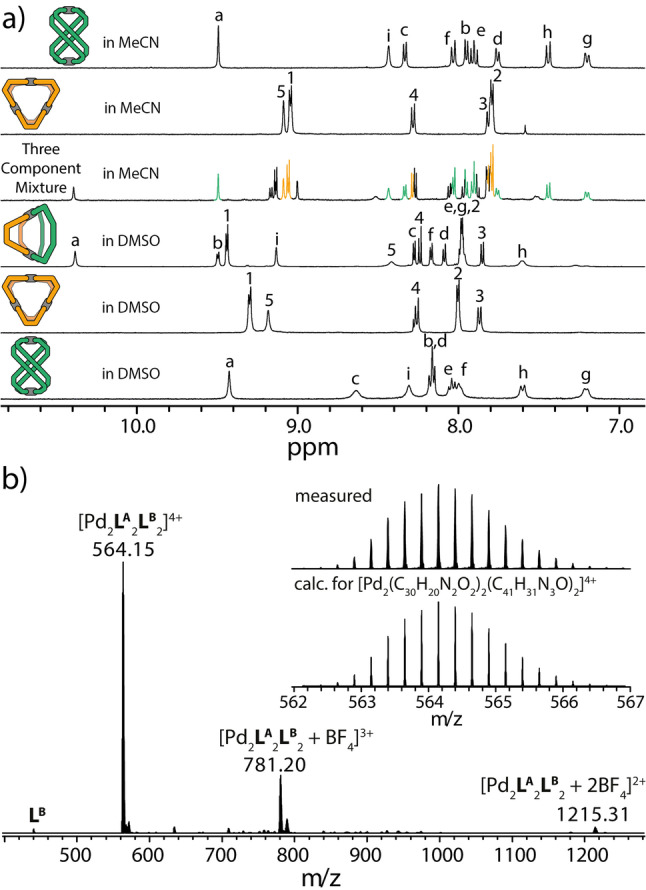
a) NMR spectra of (from bottom to top): helicate Pd₂ L^A ₄, ring Pd₃ L^B ₆ and heteroleptic cage Pd₂ L^A ₂ L^B ₂ in DMSO‐d₆ (298 K), the equilibrated mixture formed from Pd₂ L^A ₂ L^B ₂ after solvent exchange to MeCN, pure Pd₃ L^B ₆ and pure Pd₂ L^A ₄ in MeCN (298 K), b) ESI mass spectrum of Pd₂ L^A ₂ L^B ₂ (* trace of a Pd₂ L^B ₄ species).

Next, the effect of changing the solvent from DMSO (Reichardt polarity E_T (30)=45.1 ^[50] ) to the slightly more polar acetonitrile (E_T (30)=45.6) was examined by means of ¹H NMR analysis. Therefore, the system was either prepared in CD₃CN (1 : 1 stoichiometry with respect to both ligands) or the DMSO‐solution of Pd₂ L^A ₂ L^B ₂ was completely freed from DMSO by lyophilization, the solids were redissolved in acetonitrile, followed by heating at 70 °C. In both cases, ¹H NMR analysis clearly showed the formation of a three‐component mixture of assemblies, consisting of helicate Pd₂ L^A ₄, three‐membered ring Pd₃ L^B ₆ and heteroleptic cage Pd₂ L^A ₂ L^B ₂ (Figure 2a, top; Figures S7, S9). Furthermore, a single signal in the ¹⁹F{¹H} NMR spectrum appearing at a chemical shift expected for free BF₄ ⁻ indicates the absence of a strong counter anion effect (Figure S8). Based on the concentrations of homo‐ and heteroleptic assemblies after equilibration at room temperature, a Gibbs free energy change Δ_r G ⁰ of –1.31 kcal mol^‐1 was calculated for the reaction in Eq. (1). Hence, dissolution in acetonitrile leads to an equilibrium shift towards the homoleptic cages. In order to dissect the observed solvent‐induced equilibrium shift into entropic and enthalpic contributions, we determined the equilibrium constant K at temperatures ranging from 298 K to 343 K (Figures S10, S11). Van't Hoff analysis revealed that the reaction is of endothermic nature but accompanied by a gain in entropy (Table 1).

Table 1.

Contributions [kcal mol⁻¹] to the total reaction, gas phase reaction, and solvation thermodynamics for the cage separation reaction (1) from experimental analysis (for MeCN only, converting enthalpic and isobaric‐entropic contributions of 7.42±1.36 and −8.74±1.36 kcal mol^‐1, respectively, to the canonical ensemble via Eqs. (15) and (16) provided in the SI) and from the QM and the FF approaches in both solvents (see Supporting Information for raw data and Figure 4 for a graphical illustration).

	Solvent	[b,c]	${\Delta }_{\mathrm{r}}U$ [b,c]	${\left.-T{\Delta }_{\mathrm{r}}S\right|}_V$ [b,c]	${\Delta }_{\mathrm{r}}{A}_{\mathrm{gas}}$	${\Delta }_{\mathrm{r}}{U}_{\mathrm{gas}}$	${\left.-T{\Delta }_{\mathrm{r}}{S}_{\mathrm{gas}}\right|}_V$	${\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}A$ [c]	${\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}U$ [c]	${\left.-T{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}S\right|}_V$ [c]
Exp.	MeCN	−1.31±0.14	7.62±1.36	−8.93±1.36	‐	‐	‐	‐	‐	‐
	DMSO	>0	‐	‐	‐	‐	‐	‐	‐	‐
	Diff. (Δtr)[a]	>0	‐	‐	‐	‐	‐	‐	‐	‐
QM	MeCN	−3.11±0.38	−0.06±0.16	−3.05±0.23	54.31	46.62	7.69	−57.42±0.38	−46.68±0.16	−10.74±0.23
	DMSO	2.27±0.21	−3.00±1.68	5.27±1.47	54.31	46.62	7.69	−52.04±0.21	−49.62±1.68	−2.43±1.47
	Diff. (Δtr)[a]	5.38±0.44	−2.93±1.69	8.32±1.49	0.00	0.00	0.00	5.38±0.44	−2.93±1.69	8.32±1.49
FF	MeCN	−2.84±0.16	−1.93±0.11	−0.91±0.05	56.39	45.82	10.57	−59.23±0.16	−47.75±0.11	−11.48±0.05
	DMSO	2.92±0.21	2.93±2.54	−0.01±2.33	56.39	45.82	10.57	−53.47±0.21	−42.89±2.54	−10.58±2.33
	Diff. (Δtr)[a]	5.76±0.26	4.86±2.54	0.90±2.33	0.00	0.00	0.00	5.76±0.26	4.86±2.54	0.90±2.33

[a] The difference corresponds to the transfer from MeCN to DMSO (MeCN→DMSO). [b] Error margins in experimental quantities result from an estimated concentration uncertainty of 10 % propagated to , while energy/entropy errors result from the uncertainty of the van't Hoff least‐squares regression parameters. [c] Statistical uncertainties of the calculations originate from the single‐parameter least‐squares regression optimization of the solvation models that have been calibrated with respect to small molecule solvation free energy reference data (see SI).

Next, we set out to find a way to complete the segregation into the homoleptic species under consumption of the entire remnant of the heteroleptic cage. The addition of a certain guest molecule, namely 1,3‐propane disulfonate (G¹ ) in MeCN turned out to be successful as it could be shown that a precipitate forms that consists only of G¹ and three‐membered ring Pd₃ L^B ₆, while helicate Pd₂ L^A ₄ could be shown to remain exclusively in solution. Interestingly, it took three equivalents of G¹ per ring Pd₃ L^B ₆ to fully complete the precipitation process, thus balancing the net charge of +6 of each ring with 6 negative charges of guests (Figure S12). This suggests that the formation of a charge‐neutral aggregate of sum formula G¹ ₃@Pd₃ L^B ₆ is the reason for the decrease in solubility. The precipitate was removed by filtration and redissolved in DMSO for analysis. The ¹H NMR spectra of the precipitate and the filtrate showed only signals for the host–guest complex of ring Pd₃ L^B ₆ with G¹ and helicate Pd₂ L^A ₄, respectively, demonstrating that the cage‐to‐cage transformation occurred quantitatively (Figure S13).

Noteworthy, the high affinity of G¹ for ring Pd₃ L^B ₆ allowed for an exclusive binding event while the signals of helicate Pd₂ L^A ₄ and cage Pd₂ L^A ₂ L^B ₂ remained unaffected. This motivated us to test for co‐existing host–guest complexes of ring Pd₃ L^B ₆ and cage Pd₂ L^A ₂ L^B ₂ (helicate Pd₂ L^A ₄ lacks a cavity for guest binding). For this, we chose G² as second guest since we showed previously that cages with anisotropic cavity show a preference for bent‐shaped guests. ^[3] We turned back to DMSO in order to increase the solubility of the host–guest complexes (Figures S14, S15, S17, S18). Separate binding studies of G¹ and G² to cage Pd₂ L^A ₂ L^B ₂ revealed that bent‐shaped guest G² has indeed a slightly higher binding constant (K _G2=10750±535 M⁻¹) as compared to G¹ (K _G1=7995±652 M⁻¹) (Figure S20–S23). However, the difference in binding affinity was not sufficient for achieving selective encapsulation of G² in a three‐component mixture of Pd₂ L^A ₂ L^B ₂ and the two guests (Figure S24). Excitingly, addition of the two guests to a preformed mixture of ring Pd₃ L^B ₆ and cage Pd₂ L^A ₂ L^B ₂ yielded an NMR spectrum that closely resembles the NMR spectra of the individual host–guest complexes G¹ @Pd₃ L^B ₆ and G² @Pd₂ L^A ₂ L^B ₂ (Figure S25, S26). For quantifying the observed binding preferences, we turned to ESI MS. In accordance with the results obtained by ¹H NMR, host–guest complexes G¹ @Pd₃ L^B ₆ and G² @Pd₂ L^A ₂ L^B ₂ have a six‐ and nine‐times higher abundances as compared to G¹ @Pd₃ L^B ₆ and G² @Pd₂ L^A ₂ L^B ₂, respectively (Figure 3, Figure S28). Hence, judicious choice of host–guest systems that are size and/or shape complementary allowed to achieve nearly complete guest partitioning.

Figure 3.

a) Partitioning of aromatic guest G² and aliphatic guest G¹ in heteroleptic cage Pd₂ L^A ₂ L^B ₂ and in ring Pd₃ L^B ₆, respectively, from the mixture of all components, b) ESI mass spectrometric evidence for the selective formation of host–guest complexes G¹ @Pd₂ L^A ₂ L^B ₂ and G² @Pd₃ L^B ₆ (both patterns are from the same mass spectrum, see Supporting Information for further details).

Theory

To rationalize the observed solvent dependence of the assembly reaction we modeled the stoichiometric reaction equation

(1)

by thermodynamic calculations based on atomic structures in the solvents DMSO and MeCN, respectively. The key quantity to describe the solvent propensity is the standard Gibbs energy of reaction, ${\Delta }_{\mathrm{r}}{G}^0$ , which can be decomposed into energetic (U) and entropic (S) contributions according to

$${\displaystyle {\Delta }_{\mathrm{r}}{G}^0={\Delta }_{\mathrm{r}}U-{\left.T{\Delta }_{\mathrm{r}}S\right|}_V={\Delta }_{\mathrm{r}}{U}_{\mathrm{gas}}-{\left.T{\Delta }_{\mathrm{r}}{S}_{\mathrm{gas}}\right|}_V+{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}U-{\left.T{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}S\right|}_V.}$$ (2)

This way, not only the total energy/entropy contributions can be evaluated, but also the pure gas‐phase components (subscript “gas”) of the thermodynamic cycle can be distinguished from the solvent‐specific parts (subscript “solv”). For full details of the derivation and the technical implementation, including the splitting into terms formally obtained in a constant‐volume ensemble, see SI. Briefly, we described the reaction species within the rigid‐rotor harmonic oscillator (RRHO) approach[ ⁵¹ , ⁵² ] for the gas‐phase leg, while solvation contributions were determined using the three‐dimensional reference interaction site model (3D RISM) integral equation theory, for both a force field (FF) model of the molecular energetics and for a high‐level quantum‐mechanical (QM) approach including electron correlation at the MP2 level of theory. In the latter case, we refer to the embedded cluster RISM (EC‐RISM) model, which has been developed and used by us in the past for a wide range of chemical processes in solution, covering thermodynamic and spectroscopic predictions, see Refs. [53–56] and references cited therein. The 3D RISM ansatz not only allows for thermodynamic decomposition but also facilitates an illustration of the solvation patterns via 3D and (radially integrated) 1D solvent site distribution functions (g). Note that the counterion (BF₄ ⁻) does not appear in the stoichiometric Eq. (1), hence it has been neglected in the calculations. Only if it were strongly bound and therefore localized near or within the cages there would be reason to add it explicitly to the equation. Hence, counterions were here treated to merely represent a background effect, possibly detectable by non‐unity activity coefficients of the species that are, however, strongly diluted such that a non‐ideality of the solution was chosen to be ignored here.

Thermodynamic results are summarized and depicted in Table 1 and Figure 4. We first note that the Gibbs energy of reaction (${\Delta }_{\mathrm{r}}{G}^0$ ) in MeCN (favoring the homoleptic cages), for which experimental reference data is available by concentration determination from NMR, is captured well by both the FF and the QM approaches. The (simpler) FF model is closer to the reference than QM results, though the difference is not statistically significant within the error bars associated with the regression‐based solvent model optimization (see SI). Both models also agree in the qualitative experimentally observed tendency that the heteroleptic cage is favored in DMSO, computationally by more than 5 kcal mol^‐1. While the pure gas phase free energy difference (${\Delta }_{\mathrm{r}}{A}_{\mathrm{gas}}$ ) is clearly dominated by the energetic component (${\Delta }_{\mathrm{r}}{U}_{\mathrm{gas}}$ ), which strongly favors the heteroleptic cage, solvation plays a counteracting role and is actually responsible for the formation of the heteroleptic complex.

Figure 4.

Calculated contributions [kcal mol⁻¹] to the total reaction, gas phase reaction, and solvation thermodynamics (with temperature dependent PMV correction factor) for the cage separation reaction shown (1) from the QM (left) and the FF (middle) approach in both solvents using data in Table 1. The difference (right) corresponds to the transfer from MeCN to DMSO (MeCN→DMSO).

Importantly, for interpreting the relative solvent propensities only the solvation contributions are relevant as the gas phase leg cancels. Therefore, we have

$${\displaystyle \left({\Delta }_{\mathrm{r}}U{\left.-T{\Delta }_{\mathrm{r}}S\right|}_V\right)\left(\mathrm{DMSO}\right)-\left({\Delta }_{\mathrm{r}}U{\left.-T{\Delta }_{\mathrm{r}}S\right|}_V\right)\left(\mathrm{MeCN}\right)\equiv {\Delta }_{\mathrm{tr}}{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}U|{\left.-T{\Delta }_{\mathrm{tr}}{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}S\right|}_V}$$ (3)

and we can analyze the solvation components alone for rationalizing the solvent control of cage formation. Table 1 shows that the energy/entropy components deviate more strongly when QM and FF models are compared. This is not unexpected as it is well known that free energies typically are better reproduced by calculations than their components as a result of entropy‐energy (or enthalpy) compensation. ^[57] Errors in energy and entropy compensate each other to some extent and are notoriously more difficult to predict. Fortunately, temperature‐dependent NMR experiments in MeCN allowed for a van't Hoff determination of reaction enthalpy and entropy, which are transformed to the canonical (constant volume) ensemble in Table 1 in order to match the computational model setup (see Supporting Information for methodical background). Comparison of experimental with computational total reaction energy and entropy shows that the QM model, though still considerably off by ca. 7–8 and 5–6 kcal mol^‐1, respectively, appears to catch reality better, so that we focus on QM data for interpreting the thermodynamic origin of the differential solvent effect.

With all caution due to the large uncertainty with respect to experimental data, the QM results from EC‐RISM calculations show that ${\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}U$ values are strongly negative and similar in both solvents and essentially compensate for the largest fraction of the strongly positive gas‐phase part ${\Delta }_{\mathrm{r}}{U}_{\mathrm{gas}}$ . Relatively larger differences in ${\left.-T{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}S\right|}_V$ therefore translate into a stronger effect of solvation entropy on the overall ${\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}A$ , leading for the hypothetical transfer process MeCN→DMSO of the cage conversion to ${\Delta }_{\mathrm{tr}}{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}U$ = –2.9 kcal mol^‐1 and ${\left.-T{\Delta }_{\mathrm{tr}}{\Delta }_{\mathrm{r}}{\Delta }_{\mathrm{solv}}S\right|}_V$ = +8.3 kcal mol^‐1, meaning that entropy is more important than energy and that the homoleptic cages (product side of the reaction Eq. (1)) are predominantly entropically favored in MeCN and disfavored in DMSO while the solvation energies exhibit the opposite trend, yet relatively smaller in absolute terms.

The relevance of solvation entropy is directly visible by looking at individual numbers per cage form, see Table S5 in the SI. Notably, the Pd₂ L^A ₄ shows an increase of ${\left.-T{\Delta }_{\mathrm{solv}}S\right|}_V$ by ca. 12 % relative to Pd₂ L^A ₂ L^B ₂ in DMSO whereas there is no significant change in MeCN. For Pd₃ L^B ₆ relative to Pd₂ L^A ₂ L^B ₂ the solvation entropy difference is ca. 32 % in both solvents. Similar results are found for the FF model (Table S6), giving rise to some confidence in the interpretation. This trend shows that Pd₂ L^A ₄ with its special twisted geometry and narrower internal cavity is the key species for understanding solvent selection, as the stronger entropic penalization of Pd₂ L^A ₄ in DMSO is an indication for a reduction of the accessible volume of, i.e. stronger solvent expulsion from the narrower cavity for the larger solvent molecule, DMSO, whereas the smaller MeCN is not as strongly excluded from internal solvation. More evidence for this interpretation is provided by visualizing a spatially resolved entropy density, which is possible in 3D RISM theory since the free energy is given as an integral over space. Hence, the integrand represents a free energy density which can be point‐wise differentiated w.r.t. temperature to yield a corresponding solvation entropy density. Details and results are presented in the Supporting Information (Figure S31), which show that the largest part of the entropic penalization of DMSO over MeCN is localized inside the cages, compatible with the solvent expulsion view discussed above.

To corroborate this hypothesis and to illustrate the effect of solvation entropy, a look at 3D and 1D distributions of certain solvent site is instructive. as depicted in Figure 5. The solvation patterns in the 3D representation show a strong tendency of both solvents to coordinate predominantly with the Pd atoms, both from an intra‐cage and an outside perspective. A difference between the wider cages Pd₂ L^A ₂ L^B ₂ and Pd₃ L^B ₆ and the twisted Pd₂ L^A ₄ with its less voluminous cavity can be observed in that the wider ones allow for more pronounced off‐Pd intra‐cage solvent enrichment, unlike Pd₂ L^A ₄. A more quantitative corroboration can be deduced from the 1D radial distribution functions around the geometric cage centers and their integral function that yields the number of solvent molecules within a certain distance as also shown in Figure 5. Here we observe a shift of the O_DMSO peak away from the center compared to N_MeCN, which is accompanied by a larger number of intra‐cage MeCN molecules compared to DMSO for Pd₂ L^A ₄. Hence, again with all precautions due to computational uncertainty, solvent‐structural analysis is in line with the assumption of solvent expulsion of the larger DMSO molecules relative to MeCN in the narrow homoleptic Pd₂ L^A ₄ cavity as playing the role of the entropic driving force for solvent‐controlled cage conversion, which, however, needs to be further investigated.

Figure 5.

a) Perspective view of QM‐optimized cage structures, from left to right: [Pd₂ L^A ₂ L^B ₂]⁴⁺, [Pd₂ L^A ₄]⁴⁺, [Pd₃ L^B ₆]⁶⁺. Hydrogen atoms have been omitted for clarity. Carbon atoms of L^A are shown in green while L^B is shown in orange. In addition, calculated EC‐RISM solvent distributions for DMSO (upper row) and MeCN (lower row) are shown. Red and yellow surfaces represent oxygen and sulfur distributions of DMSO, while blue and gray surfaces characterize nitrogen and carbon distributions of MeCN. All isosurfaces are shown for g(r)=9.5. b) Radial solvent distribution functions g(r) for the DMSO oxygen (blue) and MeCN nitrogen (orange) sites around the individual cages obtained from EC‐RISM calculations; upper row: around the cavities in the geometric centers; lower row: around the palladium atoms of each cage, respectively. For each distribution, additionally the spherical integral of g(r) from 0 to r′ yielding the solvent particle number N is shown as a darker, dashed line.

Conclusions

We introduce an integratively self‐sorted cage Pd₂ L^A ₂ L^B ₂ which undergoes cage‐to‐cage transformation to a mixture of homo‐ and heteroleptic assemblies upon switching the solvent from DMSO to MeCN. Exploitation of the host–guest properties allowed for an entire shift of the equilibrium to the homoleptic assemblies through precipitation of the host–guest complex as well as for separation of the two homoleptic assemblies through filtration. Furthermore, introduction of two different, suitable guest molecules to a mixture of heteroleptic cage Pd₂ L^A ₂ L^B ₂ and homoleptic ring Pd₃ L^B ₆ allowed for partitioning of the guest molecules due to differentiable binding preferences of the two hosts.

Thermodynamic calculations covering the energetic, entropic, and solvation contributions to the reaction free energy were performed using cutting‐edge computational methodology, guided by an experimental van't Hoff analysis to gain insight into the driving force for the solvent‐dependent equilibrium shift. Most importantly, the consistency of experimental and theoretical free energy estimates confirmed the plausibility of the approach while the experimental van't Hoff data allowed for selecting the best model (QM/EC‐RISM). Despite absolute energetic/entropic contributions having higher uncertainty compared to the free energy (approaching the current theoretical prediction limit using our expensive high‐level calculations), a clear molecular interpretation of the phenomenon emerges: The gas phase energy clearly favors the heteroleptic cage, while solvation counteracts as the key factor for stabilizing homoleptic cages. Solvation entropy is attributed the driving force for cage conversion in the sense that the accessible volume is more reduced for DMSO compared to the smaller MeCN molecule particularly for the homoleptic Pd₂ L^A ₄ cage with its less voluminous cavity, as illustrated by quantitative density distribution analysis from calculations.

Our work combines experimental and results that advance the atomistic understanding of solvent‐dependent changes in the speciation of complex self‐assembled systems in equilibrium, often observed and phenomenologically described in the past, but poorly understood. An interesting perspective for future work would be to confirm the solvent size hypothesis by using intermediate‐sized solvent molecules such as acetone, and to explore continuous tuning of the equilibrium by solvent mixtures.

Supporting Information

The authors have cited additional references within the Supporting Information.[ ⁵⁸ , ⁵⁹ , ⁶⁰ , ⁶¹ , ⁶² , ⁶³ , ⁶⁴ , ⁶⁵ , ⁶⁶ , ⁶⁷ , ⁶⁸ , ⁶⁹ , ⁷⁰ , ⁷¹ , ⁷² , ⁷³ , ⁷⁴ , ⁷⁵ , ⁷⁶ , ⁷⁷ , ⁷⁸ , ⁷⁹ , ⁸⁰ , ⁸¹ , ⁸² , ⁸³ , ⁸⁴ , ⁸⁵ , ⁸⁶ , ⁸⁷ , ⁸⁸ , ⁸⁹ , ⁹⁰ , ⁹¹ , ⁹² , ⁹³ , ⁹⁴ , ⁹⁵ , ⁹⁶ , ⁹⁷ , ⁹⁸ , ⁹⁹ , ¹⁰⁰ , ¹⁰¹ , ¹⁰² , ¹⁰³ , ¹⁰⁴ , ¹⁰⁵ , ¹⁰⁶ , ¹⁰⁷ , ¹⁰⁸ , ¹⁰⁹ , ¹¹⁰ , ¹¹¹ , ¹¹² , ¹¹³ , ¹¹⁴ , ¹¹⁵ ] Raw data is provided in the RESOLVdata repository in machine‐readable form at https://doi.org/10.17877/RESOLV‐2024‐lyebgvd1. [Note to editor and reviewers: temporary link for reviewing: https://data.tu‐dortmund.de/privateurl.xhtml?token=10c074d6‐ad52‐4c4b‐baed‐38b9d2f9713e]

Conflict of Interests

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Ebbert K. E., Sendzik F., Neukirch L., Eberlein L., Platzek A., Kibies P., Kast S. M., Clever G. H., Angew. Chem. Int. Ed. 2025, 64, e202416076. 10.1002/anie.202416076

Data Availability Statement

The data that support the findings of this study are openly available in the RESOLVdata repository in machine‐readable form at https://doi.org/10.17877/RESOLV‐2024‐lyebgvd1.