Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2025 Jan 8;41(2):1480–1490. doi: 10.1021/acs.langmuir.4c04588

Topologies of Nanoscale Droplets upon Head-On Collision from Large Molecular Dynamics Simulations

Leonie Tugend 1, Simon Homes 1, Jadran Vrabec 1,*
PMCID: PMC11755786  PMID: 39778150

Abstract

graphic file with name la4c04588_0011.jpg

The binary collision of nanoscale droplets is studied with molecular dynamics simulation for droplets consisting of up to 2 × 107 molecules interacting via a truncated and shifted form of the Lennard-Jones potential. Considering head-on collisions of droplets with a temperature near the triple point that occur in a saturated vapor of the same fluid, this work explores a range of collision topologies. Four droplet sizes, with a radius ranging from 30 to 120 molecule diameters, are simulated with a varying initial relative collision velocity, covering 36 cases in total. Due to the relatively large size of the droplets, this study aims to resolve the differences in the collision behavior between droplets on the micro- and on the macroscale. By analyzing various metrics of the impact, four distinct collision regimes are found: coalescence, stable collision, holes and shattering. Coalescence, observed at low Weber and Reynolds numbers, is the formation of a stable droplet without significant deformations of the merging objects. Stable collisions, characterized by the formation of one stable droplet with notable deformations during collision, occur within a Weber number range between 10 and 505. The holes regime is only observed for droplet radii greater than 30 molecule diameters and a Weber number between 505 to 750, while collision cases surpassing this Weber number fall into the shattering regime, resulting in the breakup into satellite structures.

Introduction

Droplet collision processes play an important role in natural sciences1 and engineering.2−4 The collision of liquid droplets influences processes like atmospheric raindrop formation, where droplets coalesce within clouds until they are sufficiently large to form rain. Knowledge about the behavior of droplets during collision also aids in understanding the behavior of sprays in combustion engines or materials manufacturing, such as surface coating. Furthermore, technologies employed for solar collectors, in which a suspension is used to increase the absorption of solar radiation, also depend on droplet interactions. To optimize the corresponding technical processes, it is important to better understand the mechanisms governing droplet collision phenomena on a molecular level.

Droplet collisions have been investigated and characterized for different parameter variations, the most common of which being the Weber number5,6

graphic file with name la4c04588_m001.jpg 1

which relates the inertia forces, embodied by the product of droplet radius R0, liquid density ρl and squared initial relative velocity v2r, to the surface tension γ.7 Another important dimensionless property, the Reynolds number5

graphic file with name la4c04588_m002.jpg 2

relates the inertia forces to the viscous forces through the shear viscosity η.8

Laboratory experiments on droplet collisions usually consider a setup consisting of two droplet generators at a certain angle to each other, which emit droplets with a certain frequency to observe the topology of the process. Brenn et al.9−11 studied the behavior of droplets for a wide Weber number range and varying nondimensional impact parameter, categorizing the observed collisions into different regimes: permanent coalescence, separation of head-on or nearly head-on collisions and the formation of satellite droplets due to stretching separation. Ashgriz and Poo1 conducted an experimental investigation to identify two types of separation regimes for macroscale droplets, the reflexive separation regime, which occurs for head-on or near head-on collisions, and the stretching separation regime, occurring at a large nondimensional impact parameter. Qian and Law12 investigated water and hydrocarbon droplets in different ambient gases under varying pressure and found five regimes: bouncing, coalescence with and without notable deformations as well as stretching for head-on and off-center collisions. Willis and Orme13,14 conducted studies with water droplets in vacuum to eliminate the influence of the ambient gas, finding that atmospheric pressure allows for stretching of water droplets at lower Weber numbers than in a vacuum environment. Experimentally, droplet collisions have been studied extensively for a large range of the Weber number and nondimensional impact parameter.

While laboratory experiments are conducted on a macroscopic scale, collision processes occur rapidly and microscopic phenomena are excepted. Therefore, computer simulations are a powerful supplement and also offer insights into quantities which are hard to capture with experiments, e.g., highly resolved local temperature distributions. Molecular dynamics (MD) simulation is particularly suited due to its predictive power. Greenspan and Heath15 conducted such simulations to investigate the coalescence, separation and shattering regimes for nanoscale droplets. Wyatt16 used MD to study binary collisions of microscale water droplets. Ming et al.17 conducted one of the first systematic investigations of argon droplet collisions and also found the three regimes coalescence, separation and shattering. Svanberg et al.18 conducted a similar study with large water clusters. Murad and Law19 simulated head-on droplet collisions with MD and investigated the bouncing and coalescence regimes. Further investigations of argon droplets were conducted by Chun et al.20 More recent studies from Zhang et al.21 considered nanodroplets to investigate the bouncing and coalescence regimes, while Jiang et al.22 investigated the collision dynamics of nanodroplets. Moreover, Zhang and Luo6 and Zhang et al.23 studied the effects of the ambient pressure on nanodroplet collisions with MD to find the holes regime, extending the regime map of nanoscale binary droplet collisions. They found how expected regime outcomes change as the droplet size goes from the nanoscale toward the macroscale (i.e., how the probability of the holes regime decreases with rising droplet size). Further, MD was used by Liu et al.24 and Wang et al.25 to study the coalescence of nanodroplets for a wide range of Weber and Ohnesorge numbers, varying the nondimensional impact parameter, considering coalescence, stretching separation and shattering.

This work focuses on collisions of droplets which are in equilibrium with their surrounding vapor. In addition, the present systems involve a much larger number of molecules (up to 2 × 107) compared to previous studies. By simulating collisions with such a high molecular count, this study explores collision dynamics involving large droplet radii, which might help to bridge the gap between the nano- and the macroscale. Compared to other work in the literature, which usually considers only one or two radii, this work also investigates the influence of droplet size through four different radii ranging from 30 to 120 molecule diameters. By using such large droplet radii, it is possible to attempt to investigate the differences between the micro- and the macroscale behavior during collision. Also unique is the wide initial relative velocity range simulated for each radius. The droplets in the present work are assigned with their true saturated liquid density and placed in a vapor environment with the corresponding saturated vapor density to avoid superimposed evaporation processes. Moreover, it goes beyond analyzing collision topology by offering a more comprehensive analysis of collision dynamics. Based on spatially resolved density, velocity and temperature distributions throughout the collision process, deeper insights into various physical properties are gained. E.g., the spatially resolved density allows for the quantitative analysis of the collision topology that is often accompanied by the formation of a disc with a rim. Moreover, the region where the kinetic impact energy is primarily converted to thermal energy is clearly identified.

Methods

This work considers head-on26 nanoscale6 droplet collisions as outlined in Figure 1. To better categorize the 36 collision cases studied in this paper, different criteria, like Weber number and topological collision result, are summarized in Table 1, which were used for the classification of the outcomes into separate regimes.

Figure 1.

Figure 1

Open in a new tab

Schematic of the initial setup of head-on nanoscale droplet collisions (a) and the cylindrical sampling grid (b) used to sample the relevant volume. Due to rotational symmetry, the simulation data were averaged onto a plane (c).

Table 1. Classification of the Collision Regimes.

regime topology Weber number result
bouncing6,13,26 droplet sides facing each other flatten during approach; build-up of ambient gas pushes droplets away from each other very low (∼100) two separate droplets
coalescence27−29 droplets merge with little to no deformations during collision low (∼101) one stable droplet
stable collision26 formation of a disc during collision low to moderate (∼102) one stable droplet
holes6 formation of a disc with a rim during collision; formation of holes in the disc; formation of a torus-like geometry before droplet formation high (∼103) one stable droplet
shattering6 formation of a disc with a rim during collision; formation of holes in the disc; breakup of the disc and the rim very high (∼103) many satellite droplets
Open in a new tab

The Lennard-Jones (LJ) potential30,31 was employed to describe the intermolecular interactions32

graphic file with name la4c04588_m003.jpg 3

with r being the distance between the two molecules, ε the energy parameter and σ the size parameter,27 which roughly coincides with the molecule diameter. The first term ∼r–12 represents the repulsive forces due to Pauli exclusion, whereas the second term ∼r–6 considers the attractive forces due to dispersion.33

The truncated and shifted Lennard-Jones (LJTS) fluid is a form of that model in which the potential energy is truncated and shifted to zero at a certain cutoff radius rc

graphic file with name la4c04588_m004.jpg 4

meaning that for molecule pairs with a distance beyond the cutoff radius, the potential energy is set to zero.34 This work used a cutoff radius of rc = 2.5 σ. Due to the truncation, no long-range corrections need to be considered, which is particularly beneficial for inhomogeneous systems that undergo topology changes.35 The LJTS potential is nonetheless a good choice as it properly describes the thermodynamic properties of simple fluids, such as the noble gases and methane.36,37 Moreover, thermodynamic properties and equations of state are well established for this model fluid. When working with LJ fluids, all physical properties are usually reduced using a dimensional analysis based on the potential parameters, cf. Table 2. Most results are presented here in this reduced form, omitting the asterisk that is often used to indicate this reduction. Consequently, the results are valid for any combination of σ, ε and m, including the specific model parameters of argon,36 with σ = 0.33916 nm, ε/kB = 137.90 K and m = 39.948 g/mol, where kB denotes the Boltzmann constant. Note that for argon, a time interval in reduced units Δt = 1 corresponds to about 2 ps.

Table 2. Physical Properties in Reduced Units34,38,39.

property reduced SI unit
length z* = z/σ m
time Inline graphic s
velocity 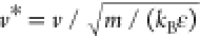Inline graphic m/s
temperature T* = TkB/ε K
density (molar) ρ* = ρσ3NA mol/m3
pressure p* = pσ3/ε N/m2
surface tension γ* = γσ2/ε N/m
shear viscosity 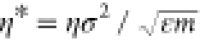Inline graphic N·s/m2
thermal conductivity Inline graphic W/(m·K)
Open in a new tab

The density of the saturated liquid ρl constituting the droplets and its coexisting vapor ρv were specified according to Vrabec et al.34 At the temperature under investigation, the density ρl of very small droplets is up to 0.6% larger than the saturated liquid density of a bulk phase ρ′ and the vapor density ρv is also by up to 12% larger than the saturated vapor density of the bulk ρ″ due to the small droplet radius R0. This is rationalized by the Laplace equation

graphic file with name la4c04588_m005.jpg 5

where Δp is the pressure difference between the coexisting phases due to the surface tension acting on a (strongly) curved interface. In this study, colliding droplets and the surrounding vapor phase were prepared such that it was accounted for the increased vapor pressure.40

The surface tension was calculated with a function that was fitted to data presented by Vrabec et al.34 Therein, it was sampled via the Irwing–Kirkwood pressure tensor for varying temperature and droplet size, as the surface tension is a function of these parameters. The fit created in this work for the surface tension on the basis of data by Vrabec et al. is given by

graphic file with name la4c04588_m006.jpg 6

Due to the fact that this work considered only droplets with an initial temperature of T = 0.7, the surface tension in eq 6 is only a function of the radius. The macroscopic limit R0 → ∞ was included in the fit, representing the surface tension of the planar interface, cf. Figure 2.

Figure 2.

Figure 2

Open in a new tab

Surface tension γ at T = 0.7 as a function of droplet radius R0 based on data from Vrabec et al.,34 considering the planar surface tension at R0 → ∞.

The shear viscosity41 and the thermal conductivity42 of the LJTS fluid were calculated according to Lautenschläger et al.43 The speed of sound and the isochoric heat capacity were determined with the perturbed truncated and shifted (PeTS) equation of state.44

The present work used the eccentricity to determine the deformation of the colliding droplets, which is given as

graphic file with name la4c04588_m007.jpg 7

where a is the length of the semimajor axis from the center and b is the length of the semiminor axis from the center. A sphere is characterized by e = 0 and a disc by 0 < e < 1. The closer e gets to unity, the flatter the disc is.45

As the droplets collide, their size in radial direction a increases, while it decreases in axial direction b. When calculating the eccentricity at the point of maximum deformation, conclusions can be drawn with respect to the topology of the colliding droplets.

For collisions in the coalescence regime, it is expected that the eccentricity remains close to zero, since the inertia forces are small compared to the surface tension, which limits their deformation due to inertia forces. The colliding droplets remain rather spherical and hence have an eccentricity close to zero. For stable collisions at a higher Weber number and in the holes regime, the droplets’ inertia increases, creating a disc-like structure. The thinner this disc becomes, the eccentricity approaches unity and the more unstable the resulting droplet becomes during collision. This is due to its increasing maximum extension in radial direction, which eventually reaches a point where the surface tension cannot balance the inertia forces. For collisions in the shattering regime, the eccentricity looses its interpretability, since the colliding droplets completely disintegrate. Therefore, it was not used for the shattering regime.

In addition to the eccentricity, a scaling law was used to quantify the maximum deformation of the colliding droplets. It is given by46

graphic file with name la4c04588_m008.jpg 8

where amax is the maximum radius of the disc.

The parallelized MD47 code ls1 mardyn(48) was used to simulate the influence of droplet radius and initial relative velocity on the droplet dynamics during collision at a constant temperature T = 0.7 and ambient pressure of p ≈ 0.005. The Prandtl number49 Pr ≈ 0.83 was almost constant for all cases. Table 3 lists all 36 droplet collision cases investigated in this work. To get an idea of the magnitude of the velocities, they can be compared to the speed of sound which is in reduced units cv ≈ 1.05 in the vapor and cl ≈ 4.9 in the liquid under the present conditions. The software MegaMol(50,51) was used to visualize and categorize the collision processes into regimes based on their topology according to the criteria in Table 1.

Table 3. Droplet Collision Cases Investigated in the Present Work.

  initial relative velocity vr
radius R0 0.25 0.5 0.75 1.0 1.25 1.5 1.75 2.0 2.5 3.0 3.5
30 x x x x x x x x x x x
60 x x x x x x x x x x  
90 x x x x x x x x x    
120   x   x x x x x      
Open in a new tab

To obtain detailed information on the process, a sampling tool was used to measure temperature, density and hydrodynamic velocity during collision by dividing the domain into cylindrical shells, cf. Figure 1. By plotting the sampled property profiles in a two-dimensional form, the collision outcomes were further analyzed. Due to rotationally symmetric decomposition and averaging, the quantities were sampled in cylindrical coordinates. Care has to be taken concerning the temperature. Since the temperature is associated exclusively with the thermal, i.e., undirected, velocity of the molecules, the local hydrodynamic velocity must be subtracted from each molecule’s individual velocity. In cylindrical coordinates, the hydrodynamic velocity components of an ensemble of N molecules are given by

graphic file with name la4c04588_m009.jpg 9
graphic file with name la4c04588_m010.jpg 10
graphic file with name la4c04588_m011.jpg 11

with the velocity vector of molecule i in Cartesian (vx,i, vy,i, vz,i) and cylindrical coordinates (vr,i, vθ,i, vz,i). The Cartesian distances xi and yi of the respective molecule i are measured from the rotation axis. Based on these velocities, the temperature can then be calculated by52

graphic file with name la4c04588_m012.jpg 12

for the present monatomic molecules.

Results and Discussion

For each of the cases simulated in this work, the collision outcome was analyzed based on the topology seen in the visualization software MegaMol. Table 4 lists the conditions under which these collisions took place.

Table 4. Parameters and Outcome of the Collision Cases Simulated in the Present Work.

R0 vr We Re regime
30 0.25 5.26 5.34 coalescence
30 0.5 21.0 10.7 stable collision
30 0.75 47.3 16.0
30 1.0 84.1 21.4
30 1.25 131.4 26.7
30 1.5 189.3 32.1
30 2.0 257.6 37.4
30 2.5 336.5 42.7
60 0.25 10.3 10.8
60 0.5 41.1 21.6
60 0.75 92.5 32.5
60 1.0 164.7 43.3
60 1.25 256.8 54.1
60 1.5 369.9 64.9
60 1.75 503.4 75.7
90 0.25 15.3 16.3
90 0.5 61.2 32.5
90 0.75 137.7 48.9
90 1.0 244.8 65.2
90 1.25 382.5 81.5
120 0.5 81.3 43.5
120 1.0 325.3 87.1
120 1.25 508.2 108.8
60 2.0 657.5 86.5 holes
90 1.5 550.8 97.8
90 1.75 749.7 114.1
120 1.5 731.9 130.6
30 3.0 757.1 64.1 shattering
30 3.5 1031 74.8
60 2.5 1027 108.2
60 3.0 1479 129.8
90 2.0 979.2 130.3
90 2.5 1530 162.9
120 2.0 1301 174.2
Open in a new tab

It has been shown in the literature that the bouncing regime occurs for nanoscale droplets at a very low Weber number if at least one additional gas species with sufficient ambient pressure is present.6,53 The bouncing regime was not encountered in this work due to the presence of a pure fluid in the entire simulation domain.54

This work observed one case in the coalescence regime, which is characterized by the merger of two droplets with low kinetic energy and is associated with weak deformations during the collision process, leading to one stable droplet. Even with the final outcome being the same as in the stable collision regime, this work still differentiates between the two due to the topology difference during collision.

Figure 3 shows snapshots of the progression in the coalescence regime. In these visualizations, all molecules that were initially part of the vapor phase as well as molecules diffusing into the vapor were graphically taken out so that the droplets can be seen more clearly. Of course, molecules constituting the vapor phase also diffuse into the droplets, but both processes are not visible in Figure 3 because the relevant molecules were graphically taken out. The defining topology of coalescence is a lack of significant deformations, as two droplets simply merge. The change of length in radial direction shows this as well. Because no disc-like structure forms during collision, no true maximum extension in radial direction is attained, which can also be seen in terms of eccentricity for this collision case.

Figure 3.

Figure 3

Open in a new tab

Topology of the four observed regimes over time: coalescence (far left), stable collision (center left), holes (center right) and shattering (far right). Note that the time origin t = 0 was set to the moment of contact and time proceeds from top to bottom. The shown cases are Coalescence R0 = 30, vr = 0.25; Stable collision R0 = 30, vr = 1.75; holes R0 = 60, vr = 2.0 and shattering R0 = 90, vr = 2.5.

Since we studied coalescence with MD in much detail in preceding work,27 accompanied by phase-field CFD modeling, the focus was laid here on the other regimes.

This work categorized events into the stable collision regime based on the formation of a disc-like structure during collision, without any holes or tears therein, and the emergence of a single, stable droplet at the end of the process. This regime has to be differentiated from the coalescence regime as it occurs at higher velocities and larger droplet radii, which are associated with larger kinetic energies and greater deformations during the collision process. Table 4 lists the 24 collisions sampled in this work that were categorized into this regime.

Figure 3 depicts the progression of an exemplary collision case in this regime to show the deformations that can occur. At the beginning, the droplets form a bridge in between them, but they do not simply glide into each other as in the coalescence regime. For the depicted case at the time instance t = 14.6 and later, it can be observed that the merging object stretches out in radial direction, creating a rim sticking out and stretching the droplet into a disc with a rim at t = 29.2, for example. Once the expansion of the disc reaches its maximum, the droplet retracts due to surface tension, eventually stabilizing into one unit, as seen at t = 291.8 and 437.7.

The holes regime was observed in this study for all droplet radii, except for the smallest R0 = 30, which may be too small to enter the holes regime. Other studies of nanoscale droplets, such as by Kalweit and Drikakis,38 have also not observed the holes regime. It is important to note that the droplets simulated in their study38 were much smaller than the ones considered in this work, but they concluded that the holes regime only appears above a certain droplet radius threshold. Table 4 lists the four cases in which the holes regime was observed here.

Figure 3 shows the topology of a typical case in the holes regime. Here, an angular view from the top was chosen to depict the holes formed in the planar structure. In this regime, the initial stage is similar to the stable collision regime, since a disc-like structure is formed. However, the spread in radial direction is greater than in the stable collision regime, leading to an even thinner disc with a rim. This very thin disc with a rim then tears, leading to the formation of holes in the disc as surface tension forces retract the droplet. As this continues, the holes grow and merge into a single hole within a torus-like structure, as seen at t = 1021.3. Surface tension forces proceed to dominate so that this torus-like structure merges into one stable droplet at t = 1458.9.

The shattering regime was observed in this work in seven cases encompassing all droplet radii, cf. Table 4. Figure 3 shows the two droplets colliding, with deformations occurring early on in the collision process. The disc-like structure that is formed disintegrates at its edges, a process supported by the high temperature in this region, with small holes forming therein, as opposed to the disc-like structure formed in the holes regime, which appears more as a disc with smooth edges. Later on, at t = 218.3, the formation of holes can be seen along the outer edges of the disc as well as in the center. The disc then ruptures and disperses into many satellite droplets.

Using the rotationally averaged cylindrical sampling data, the density profile was employed to measure the deformation of the droplets during collision by examining the variation of its axes lengths in radial and axial directions. Figure 4 depicts the progression of a density profile. Here, the outline of the droplet’s interface was detected by a threshold based on the density condition ρ ≈ ρl, identifying contours in the data, the largest of which representing the droplet interface. The area within this contour was then used to measure the change of length in radial direction and axial length from the top edge of the droplet to the center.

Figure 4.

Figure 4

Open in a new tab

Rotationally averaged density profile of the collision case R0 = 60 and vr = 1.75. The yellow curve indicates the interface, while the straight lines show the semimajor axis a (orange) and the semiminor axis b (red).

These lengths were then plotted for all collision cases for a given droplet radius so that the collisions can also be classified according to the change in axes lengths, cf. Figure 5.

Figure 5.

Figure 5

Open in a new tab

Plots depicting the change in the length of the semimajor axis (top) and the semiminor axis (bottom) for the R0 = 90 droplets with a varying initial relative velocity vr.

Figure 5 (top) shows the change in radial axis length. Since the measurements started at the moment of contact, the initial radial axis length was zero. Then the colliding droplets begin to merge, leading to an increase in radial length. In the coalescence regime observed in this work, the droplets simply merge to become one unit so that the curve monotonously increases to converge toward the maximum expansion, which can be seen for R0 = 30 in Figure A6 in the Supporting Information (SI). The curve then stagnates, showing a clear difference compared to the change in radial direction of collisions in the stable collision regime. For stable collisions, a disc with a rim is formed during collision, entailing an increase in length in radial direction that peaks and then reclines to converge against a constant. The maximum of this curve depends on the Weber and Reynolds numbers. The holes regime can be classified by a sudden drop in length in radial direction. The droplets first expand into a disc with a rim, then form holes within the disc, which leads to the torus-like structure seen in Figure 3. Once the ring retracts to form a droplet, the length in radial direction suddenly increases again. The shattering collision can be identified by the sudden stop early on in the collision process since satellite droplets break off here.

Figure 5 (bottom) depicts the change of length in axial direction. Since these plots show the progression for the R0 = 90 droplet, the lengths start at 180 (the moment when the droplets meet). As the droplets merge, becoming more and more disc-like, the axial length falls. If the droplets form a stable droplet at the end, the length in axial direction rises and converges toward a constant value. If the droplets shattered, the lengths were not recorded after disintegration.

For each droplet collision, the eccentricity was calculated by taking the maximum value of the radial length and its corresponding axial length value. This allows for the eccentricity to be measured at the maximum extension in radial direction when the disc with a rim is most pronounced. The closer the eccentricity value is to unity, the flatter the formed disc. Figure 6 depicts the Weber number over eccentricity. It shows that the closer the eccentricity is to unity (to the left in Figure 6), the more unstable the collisions become since the holes regime occurs at e → 1. For the stable collision regime, it can be seen that the higher the relative velocity, and therefore the Weber number, the wider the disc spreads, which promotes the instability of the collision. Moreover, the only collision case where e → 0 was observed is the coalescence case, which shows that even at maximum extension, the topology of coalescing droplets is still close to that of a sphere, which differentiates this collision from the stable collision cases.

Figure 6.

Figure 6

Open in a new tab

Weber number over 1 – e, where e is the eccentricity.

Figure 7 shows the square root of the Weber number over the ratio of maximum disc deformation and initial radius. For the cases in the coalescence and stable collision regimes, an almost linear proportionality can be observed, which is largely independent on the initial radius. In case of the holes regime, the measured maximum deformation is slightly too large to match this linear relation. This is directly connected to the formation of holes, which allows the disc to spread wider.

Figure 7.

Figure 7

Open in a new tab

Square root of the Weber number over the radius ratio amax/R0.

Figure 8 shows velocity profiles during an exemplary droplet collision. The vectors depict the local hydrodynamic velocity, showing that at the beginning, the liquid propagates with the initially assigned relative velocity, and then stalls in the center of the bridge formed during collision.

Figure 8.

Figure 8

Open in a new tab

Hydrodynamic velocity profiles of the collision case with R0 = 60 and vr = 2.0 over time. The arrows indicate the direction and magnitude of the local hydrodynamic velocity.

It becomes apparent that the liquid spreads out radially with the initial relative velocity, until coming close to the point of maximum expansion. At time instance t = 36.5, for example, the center of the formed droplet has a velocity close to zero, but the outskirts still have a velocity close to the initial relative velocity as the colliding droplets flow outward to form the disc.

When examining droplet collisions for a given droplet radius R0, the liquid density ρl and surface tension γ remain fairly constant, leading to the initial relative velocity vr being the only influence on the Weber number. For example, when looking at droplet collisions with R0 = 60, it can be seen that for low relative velocities, the droplets form a stable droplet and are part of the stable collision regime. As the initial relative velocity increases, and with it the Weber number, the holes regime starts to dominate, before moving on into the shattering regime. Therefore, as expected, the higher the initial relative velocity, and thus the Weber number, the more unstable a collision becomes.

The initial relative velocity has an impact not only on the topology, but also on other phenomena that occur during collision, such as the conversion of kinetic energy into thermal energy.55,56Figure 9 compares droplet collision cases with varying vr with respect to this aspect. Temperature profiles are depicted at the same length in radial direction a since this indicates a comparable instantaneous topology during the collision for different vr.

Figure 9.

Figure 9

Open in a new tab

Temperature profiles during the collision of droplets with R0 = 60 for varying initial relative velocity vr.

Figure 9 shows that the higher the initial relative velocity, the more kinetic energy is converted into thermal energy during the collision process.56,57 As the droplets collide, repulsive molecule interactions dominate in the bridge along the axial coordinate, which pushes the droplet outward in radial direction. Primarily at the radial edge, the conversion of kinetic energy into thermal energy occurs. In addition to this conversion, a part of the kinetic energy is also transformed to surface energy due to the increasing interface area during collision.

As expected, from the Weber number it can be seen that also the radius has an influence on the collision process. For example, at constant initial relative velocity vr = 2.0, the resulting collision regime varies with the radius. For a small radius R0 = 30, the stable collision regime dominates. However, with increasing R0 at a constant initial relative velocity, first the holes regime and then the shattering regime prevails.

The collision cases simulated in this work allow for conclusions on the regime ranges so that other collision scenarios can be anticipated. Figure 10 shows the collision regimes and their boundaries that were observed in this work. Note that the estimates for the collision outcome that can be made from this work are only valid within the ranges of the varied parameters, while the present initial droplet radius R0 was converted to SI units assuming potential parameters for argon.

Figure 10.

Figure 10

Open in a new tab

Weber number over Reynolds number and estimated regime boundaries based on the present work and literature data by Kalweit and Drikakis38 as well as Juang et al.58 For this comparison, the present data were converted to SI units using the potential parameters for argon.

Figure 10 shows the regime boundaries that were concluded from the present simulation results. The coalescence regime is treated as a part of the stable collision regime, occurring at very small velocities, before moving on to the stable collision regime with rising Weber and Reynolds numbers. The holes regime dominates for droplet radii of R0 = 60, 90, and 120. The regime boundary lines are assumed to bend, as this regime can only be observed for nanoscale droplets. Thus, it can be assumed that with increasing droplet radius, the possibility for this regime decreases. Furthermore, the collision case R0 = 120 and vr = 1.25 seems to be very close to this regime boundary, since when observing its topology in detail, it became evident that tiny holes did form during the collision and closed rapidly before being able to develop and spread. The shattering regime then dominates at high Weber and Reynolds numbers. Table 5 shows the ranges in which this work estimates the separate regimes to be for the LJTS fluid in the investigated parameter range.

Table 5. Comparison of Estimated Regime Ranges with the Literature.

  this work Zhang and Luo6 Zhang et al.23
droplet fluid argon water water
droplet radius [nm] 10.2, 20.3, 30.5, 40.7 10 10
ambient pressure [bar] ∼0.69 ∼2.7 0
Collision Regimes: Weber Number Ranges
coalescence ≲10    
stable collision ∼10–505 ≲ 530 277 (one case)
holes ∼505–750 ∼530–667 426 (one case)
shattering ≳750 ≳667 540 (one case)
Open in a new tab

First, it should be noted that the type of liquid, temperature and ambient pressure under which collisions occur influence the collision regime boundaries so that a direct comparison with other findings is not always straightforward. The results of this work are compared with literature data in Figure 10, where two other MD studies using argon are included. This was done by converting the reduced units used in those studies to reduced units comparable to this study. Kalweit and Drikakis38 studied droplet collisions with MD simulations using a 12–6 LJ potential by varying the initial relative velocity and impact parameter. For comparison, only their findings with an impact parameter of zero were used, since this work focuses on head-on collisions. For the radius R0 = 1.35 nm used in their work, they found that the coalescence/stable collision regime dominates until vr ≈ 5.02 and We ≈ 802.79, leaving the final collision case examined at vr ≈ 5.9 and We ≈ 1108.93 in the shattering regime. Note that no holes regime was found by them. A similar study by Juang et al.58 investigated head-on collisions of argon droplets, also using a 12–6 LJ potential. Here, a wider Weber number range was considered, with coalescence/stable collision regimes being observed up to a Weber number of 482.30, while the shattering regime was observed at We = 600.78 and 753.61. Furthermore, it should be noted that the ambient pressure under which these collisions occur affects the collision regime. With higher system pressure, the coalescence/stable collision regimes occur at higher Weber numbers, since a larger ambient pressure acts as a cushion. Therefore, only collision cases from Juang et al. under an ambient pressure of p = 0.56 bar (close to the ambient pressure of p ≈ 0.69 bar in this work) are compared.

The collisions investigated by Kalweit and Drikakis as well as Juang et al. considered a smaller initial droplet radius than this work. As discussed, it has been found that smaller droplet radii lead to a larger stable collision regime, so that the shattering regime occurs at a higher Weber number than with larger droplet radii. Since both Kalweit and Drikakis as well as Juang et al. simulated droplets with much smaller radii, this could be the factor that led to the stable collision regime occurring up to higher Weber numbers than the collision cases simulated in the present work. This, along with the consideration that different fluids or ambient pressures were used, could explain the discrepancies, with the coalescence/stable collision regime occurring at a much higher Weber number. Nonetheless, the literature studies support the assumption that the droplet radius impacts collision dynamics by decreasing the boundary of the stable collision regime with rising droplet radius. Furthermore, the general trend observed in this work with increasing initial relative velocity leading to more unstable collisions was also found by Kalweit and Drikakis as well as Juang et al.

Another fluid that has often been used to simulate droplet collisions is water, which is not as straightforwardly comparable through a conversion of reduced units. However, the findings of these works still relate to the trends found here, cf. Table 5.

Zhang and Luo6 used MD to simulate water droplets in a nitrogen gas ambient. The droplets had an initial radius of 10 nm and droplet collisions for a Weber number range were simulated at 0, 2.7, and 8 bar. Since the ambient pressure has an influence on the collision regime boundaries, with a higher pressure resulting in stable collisions for higher Weber numbers, the findings of Zhang and Luo for an ambient pressure of 2.7 bar (roughly 4 times the ambient pressure of 0.68 bar used in this work) are discussed here. Zhang and Luo found that the coalescence/stable collision regime occurs until about a Weber number of 530 for water droplets in nitrogen gas ambient and that the holes regime occurs between a Weber number of ∼530 to 667. This work found the stable collision regime to occur up to a Weber number of 505, which is somewhat below that of Zhang and Luo. This could be due to the higher ambient pressure of Zhang and Luo, which acts as a cushion to prevent early holes formation or shattering during collision. However, especially when comparing the shattering regime, which occurs at Weber numbers slightly smaller than the findings of this work, it is likely that earlier shattering is due to the difference in fluid properties.

Zhang et al.23 conducted a study simulating water droplets in vacuum, with an initial droplet radius of 10, 50, and 100 nm. Since this work simulated droplet radii of up to 40.7 nm, the findings for their 50 nm droplet radius are discussed here. Zhang et al. did not specify regime boundaries in their work, but discussed characteristic collisions for each regime. The characteristic collisions found in their study, the stable collision regime at We = 277 and the holes regime at We = 500, occur at slightly lower Weber numbers than the regime boundaries identified in this work, but remain largely within the present regime boundaries. This correlates with the assumption that the difference in ambient gas allows for the holes and shattering regime to occur at different Weber numbers and that the fluid properties of water lead to slightly different collision dynamics. Another important finding of Zhang et al. is the transition from nanoscale to macroscale droplet collisions. As discussed above, nanoscale droplet collisions present five main regimes, i.e., bouncing, coalescence, stable collision, holes and shattering. By simulating larger droplets at 50 and 100 nm, Zhang et al.23 were able to find the transition in the expected regimes for larger droplets.

A transition from the holes regime to a reflexive separation regime occurs when the droplet radius increases.23 Zhang et al. found that for a droplet radius of 50 nm, the holes regime was still observed. However, when simulating droplets with an initial radius of 100 nm, a reflexive separation regime occurred at Weber numbers where the holes regime is expected. This correlates with the estimations made in this work, that with higher droplet radius the occurrence of the holes regime decreases, as can be seen in the regime boundaries drawn in Figure 10. Therefore, it can be said that the regime ranges in this work are confirmed by other findings, considering the discrepancies of fluid properties, ambient pressure and droplet radius investigated.

Conclusions

This work employed large molecular dynamics simulations to investigate binary droplet collisions of nanoscale droplets consisting of 0.33, 2.5, 8.3, and 20 × 106 molecules interacting via the 12–6 LJTS potential. Head-on collisions were simulated with a constant nondimensional impact parameter of X = 0 at four different radii of R0 = 30, 60, 90, and 120 molecule diameters, which might help to bridge the gap to experiments due to the comparably large size of the droplets. For each droplet radius, collisions were sampled for 11 initial relative collision velocities of vr = 0.25 to 3.5, except for the R0 = 120 droplet, where seven collision cases were considered, covering a somewhat smaller initial relative velocity range.

Of the five regimes that are known for head-on nanodroplet collisions (bouncing, coalescence, stable collision, holes and shattering), this work observed the latter four. The coalescence regime was found to occur at very low Weber and Reynolds numbers (collision case R0 = 30 and vr = 0.25). The stable collision regime that results, like coalescence, in one stable droplet, but with significant deformations during the collision process, was found to occur within a Weber number range of approximately 10 to 505. Furthermore, the holes regime was observed for droplets of R0 = 60, 90, and 120 in a Weber number range of approximately 505 to 750. Collision cases with a higher Weber number were categorized into the shattering regime, where many satellite droplets form.

This work found that for the LJTS fluid at the simulated temperature conditions, the holes regime occurred for a droplet radius of R0 = 60, 90, and 120. It was also observed that the probability of the holes regime expands first with a larger radius, and then declines, since for the largest radius R0 = 120 a stable collision case was observed for an initial relative velocity that would have resulted in a holes regime at R0 = 90.

The scaling law Inline graphic was found to be confirmed by the present nanoscale droplets, which aids in bridging the gap between the micro- and the macroscale. Due to the direct accessibility of physical properties, like locally resolved temperature, the present work elucidated where and how the energy conversion takes place and gave valuable insights into the mechanisms of droplet collisions. While the validity of the scaling law on the microscale is in accordance with the macroscale, differences to the macroscopic scale were revealed since no separation but the holes regime was found for such nanoscopic droplet collisions.

Acknowledgments

The present work [project MaST: Macro/Micro-simulation of Phase Decomposition in the Transcritical Regime] is funded by dtec.bw - Digitalization and Technology Research Center of the Bundeswehr which we gratefully acknowledge. dtec.bw is funded by the European Union - NextGenerationEU. The simulations were performed on the national supercomputer HPE Apollo (Hawk) at the High-Performance Computing Center Stuttgart (HLRS) in the scope of the project MMHBF2 and on the cluster Noctua2 at the Paderborn Center for Parallel Computing (PC2).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.4c04588.

  • Detailed description of the simulation setup and the analysis; process flow chart showing the setup of the droplet collision; simulation domain during the second step to simulate the equilibrated droplet; plots depicting the change in semimajor axis (top) and semiminor axis (bottom) (PDF)

  • Video of droplet collision with R0 = 30 and vr = 1.0 (MP4)

  • Video of droplet collision with R0 = 60 and vr = 1.0 (MP4)

  • Video of droplet collision with R0 = 60 and vr = 2.0 (MP4)

  • Video of droplet collision with R0 = 60 and vr = 3.0 (MP4)

The authors declare no competing financial interest.

Supplementary Material

la4c04588_si_001.pdf (1.8MB, pdf)
la4c04588_si_002.mp4 (25.4MB, mp4)
la4c04588_si_003.mp4 (59.9MB, mp4)
la4c04588_si_004.mp4 (133.9MB, mp4)
la4c04588_si_005.mp4 (26.6MB, mp4)

References

  1. Ashgriz N.; Poo J. Y. Coalescence and separation in binary collisions of liquid drops. J. Fluid Mech. 1990, 221, 183–204. 10.1017/S0022112090003536. [DOI] [Google Scholar]
  2. Williams A.Spray Combustion in Engines. In Combustion of Liquid Fuel Sprays; Butterworth-Heinemann: Oxford, 1990, Chapter 11; pp 243–265. [Google Scholar]
  3. Fukumoto M.; Nishioka E.; Nishiyama T. New criterion for splashing in flattening of thermal sprayed particles onto flat substrate surface. Surf. Coat. Technol. 2002, 161, 103–110. 10.1016/S0257-8972(02)00471-1. [DOI] [Google Scholar]
  4. Okada M.; Suzuki T. Natural convection of water-fine particle suspension in a rectangular cell. Int. J. Heat Mass Transfer 1997, 40, 3201–3208. 10.1016/S0017-9310(96)00365-1. [DOI] [Google Scholar]
  5. Rapp B. E.Microfluidics: Modelling, Mechanics and Mathematics; Elsevier: Amsterdam, 2017; p 258. [Google Scholar]
  6. Zhang Y. R.; Luo K. H. Regimes of Head-On Collisions of Equal-Sized Binary Droplets. Langmuir 2019, 35, 8896–8902. 10.1021/acs.langmuir.8b04277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Principles and Emerging Applications in Biology and Chemistry: Integrated Analysis Systems; Day P.; Manz A.; Zhang Y., Eds.; Springer: New York, 2012; Vol. 9, p 9. [Google Scholar]
  8. Whittlesey R.Vertical Axis Wind Turbines: Farm and Turbine Design. In Wind Energy Engineering; Letcher T. M., Ed.; Academic Press: Cambridge, MA, 2017, Chapter 10; pp 185–202. [Google Scholar]
  9. Brenn G.; Valkovska D.; Danov K. The formation of satellite droplets by unstable binary drop collisions. Phys. Fluids 2001, 13, 2463–2477. 10.1063/1.1384892. [DOI] [Google Scholar]
  10. Brenn G.; Frohn A. Collision and merging of two equal droplets of propanol. Exp. Fluids 1989, 7, 441–446. 10.1007/BF00187061. [DOI] [Google Scholar]
  11. Brenn G.; Frohn A. Collision and coalescence of droplets of various liquids. J. Aerosol Sci. 1989, 20, 1027–1030. 10.1016/0021-8502(89)90753-2. [DOI] [Google Scholar]
  12. Qian J.; Law C. K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 1997, 331, 59–80. 10.1017/S0022112096003722. [DOI] [Google Scholar]
  13. Willis K. D.; Orme M. E. Experiments on the dynamics of droplet collisions in a vacuum. Exp. Fluids 2000, 29, 347–358. 10.1007/s003489900092. [DOI] [Google Scholar]
  14. Willis K.; Orme M. Binary droplet collisions in a vacuum environment: an experimental investigation of the role of viscosity. Exp. Fluids 2003, 34, 28–41. 10.1007/s00348-002-0526-4. [DOI] [Google Scholar]
  15. Greenspan D.; Heath L. F. Supercomputer simulation of colliding microdrops of water. Comput. Math. Appl. 1990, 19, 91–97. 10.1016/0898-1221(90)90197-R. [DOI] [Google Scholar]
  16. Wyatt B. Collisions of microdrops of water. Comput. Math. Appl. 1994, 28, 175–208. 10.1016/0898-1221(94)00192-8. [DOI] [Google Scholar]
  17. Ming L.; Marković N.; Svanberg M.; Pettersson J. B. C. Collision Dynamics of Large Argon Clusters. J. Phys. Chem. A 1997, 101, 4011–4018. 10.1021/jp964060w. [DOI] [Google Scholar]
  18. Svanberg M.; Ming L.; Marković N.; Pettersson J. B. C. Collision dynamics of large water clusters. J. Chem. Phys. 1998, 108, 5888–5897. 10.1063/1.475999. [DOI] [Google Scholar]
  19. Murad S.; Law C. K. Molecular simulation of droplet collision in the presence of ambient gas. Mol. Phys. 1999, 96, 81–85. 10.1080/00268979909482940. [DOI] [Google Scholar]
  20. Chun I.-B.; Ha M. Y.; Jang J.; Yoon H. S. Molecular Dynamics Study on the Binary Collision of Nanometer-Sized Droplets of Liquid Argon. Bull. Korean Chem. Soc. 2011, 32, 2027–2031. 10.5012/bkcs.2011.32.6.2027. [DOI] [Google Scholar]
  21. Zhang Y. R.; Jiang X. Z.; Luo K. H. Bounce regime of droplet collisions: A molecular dynamics study. J. Comput. Sci. 2016, 17, 457–462. 10.1016/j.jocs.2016.03.011. [DOI] [Google Scholar]
  22. Jiang X. Z.; Zhang Y. R.; Luo K. Dynamics of Nano Cluster Collisions in Carbon Nanotubes. J. Nanosci. Nanotechnol. 2016, 16, 8380–8386. 10.1166/jnn.2016.11758. [DOI] [Google Scholar]
  23. Zhang Y. R.; Zhao Z.; Luo K. H.; Shi B. Size effects on dynamics of nanodroplets in binary head-on collisions. J. Mol. Liq. 2021, 341, 117383 10.1016/j.molliq.2021.117383. [DOI] [Google Scholar]
  24. Liu W.; Li N.; Sun Z.; Wang Z.; Wang Z. Binary droplet coalescence in shear gas flow: A molecular dynamics study. J. Mol. Liq. 2022, 354, 118841 10.1016/j.molliq.2022.118841. [DOI] [Google Scholar]
  25. Wang Y. F.; Wang Y. B.; Cai Z. H.; Ma Y. R.; Yang Q.; Zheng S. F.; Lee D. J.; Wang X. D. Binary collision dynamics of equal-sized nanodroplets. J. Fluid Mech. 2024, 979, A25 10.1017/jfm.2023.1069. [DOI] [Google Scholar]
  26. Handbook of Atomization and Sprays: Theory and Applications; Ashgriz N., Ed.; Springer: New York and Heidelberg, 2011. [Google Scholar]
  27. Heinen M.; Hoffmann M.; Diewald F.; Seckler S.; Langenbach K.; Vrabec J. Droplet coalescence by molecular dynamics and phase-field modeling. Phys. Fluids 2022, 34, 042006 10.1063/5.0086131. [DOI] [Google Scholar]
  28. Jin J.; Ooi C. H.; Dao D. V.; Nguyen N. Coalescence Processes of Droplets and Liquid Marbles. Micromachines 2017, 8 (11), 336 10.3390/mi8110336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Verdier C.; Brizard M. Understanding droplet coalescence and its use to estimate interfacial tension. Rheol. Acta 2002, 41, 514–523. 10.1007/s00397-002-0249-8. [DOI] [Google Scholar]
  30. Jones J. E. On the Determination of Molecular Fields. I. From the Variation of the Viscosity of a Gas with Temperature. Proc. R. Soc. London, Ser. A 1924, 106, 441–462. [Google Scholar]
  31. Jones J. E. On the Determination of Molecular Fields. II. From the Equation of State of a Gas. Proc. R. Soc. London, Ser. A 1924, 106, 463–477. 10.1098/rspa.1924.0082. [DOI] [Google Scholar]
  32. Bardia R.; Liang Z.; Keblinski P.; Trujillo M. F. Continuum and molecular-dynamics simulation of nanodroplet collisions. Phys. Rev. E 2016, 93, 053104 10.1103/PhysRevE.93.053104. [DOI] [PubMed] [Google Scholar]
  33. Adams J. B.; Buschow K. H. J.; Cahn R. W.; Flemings M. C.; Ilschner B.; Kramer E. J.; Mahajan S.; Veyssière P.. Encyclopedia of Materials: Science and Technology; Elsevier: Oxford, 2001; pp 763–767. [Google Scholar]
  34. Vrabec J.; Kedia G. K.; Fuchs G.; Hasse H. Comprehensive study of the vapour-liquid coexistence of the truncated and shifted Lennard-Jones fluid including planar and spherical interface properties. Mol. Phys. 2006, 104, 1509–1527. 10.1080/00268970600556774. [DOI] [Google Scholar]
  35. Damasceno D.; Mesquita E.; Rajapakse N. Mechanical Behavior of Nano Structures Using Atomic-Scale Finite Element Method (AFEM). Lat. Am. J. Solids Struct. 2017, 14, 2046–2066. 10.1590/1679-78254050. [DOI] [Google Scholar]
  36. Rutkai G.; Thol M.; Span R.; Vrabec J. How well does the Lennard-Jones potential represent the thermodynamic properties of noble gases?. Mol. Phys. 2017, 115, 1104–1121. 10.1080/00268976.2016.1246760. [DOI] [Google Scholar]
  37. Stephan S.; Thol M.; Vrabec J.; Hasse H. Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment. J. Chem. Inf. Model. 2019, 59, 4248–4265. 10.1021/acs.jcim.9b00620. [DOI] [PubMed] [Google Scholar]
  38. Kalweit M.; Drikakis D. Collision dynamics of nanoscale Lennard-Jones clusters. Phys. Rev. B 2006, 74, 235415 10.1103/PhysRevB.74.235415. [DOI] [Google Scholar]
  39. Homes S.; Vrabec J. Resistivities across the vapor-liquid interface of a simple fluid: An assessment of methods. Phys. Fluids 2024, 36, 022122 10.1063/5.0193522. [DOI] [Google Scholar]
  40. Horsch M.Molecular Dynamics Simulation of Heterogeneous Systems; Ph.D. Thesis; Technische Universität Kaiserlautern, 2016. [Google Scholar]
  41. Zierep J.; Bühler K.. Grundzüge der Strömungslehre, 11th ed.; Springer Fachmedien Wiesbaden: Wiesbaden, 2018. [Google Scholar]
  42. Baehr H. D.; Kabelac S.. Thermodynamik—Grundlagen und Technische Anwendungen, 16th ed.; Springer: Berlin and Heidelberg, 2016. [Google Scholar]
  43. Lautenschlaeger M. P.; Hasse H. Transport properties of the Lennard-Jones truncated and shifted fluid from non-equilibrium molecular dynamics simulations. Fluid Phase Equilib. 2019, 482, 38–47. 10.1016/j.fluid.2018.10.019. [DOI] [Google Scholar]
  44. Heier M.; Stephan S.; Liu J.; Chapman W.; Hasse H.; Langenbach K. Equation of state for the Lennard-Jones truncated and shifted fluid with a cut-off radius of 2.5σ based on perturbation theory and its applications to interfacial thermodynamics. Mol. Phys. 2018, 116, 2083–2094. 10.1080/00268976.2018.1447153. [DOI] [Google Scholar]
  45. Bartsch H. J.Taschenbuch Mathematischer Formeln, 18th ed.; Hanser-Verlag: München, 1998. [Google Scholar]
  46. Planchette C.; Lorenceau E.; Brenn G. The onset of fragmentation in binary liquid drop collisions. J. Fluid Mech. 2012, 702, 5–25. 10.1017/jfm.2012.94. [DOI] [Google Scholar]
  47. Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: Cambridge, MA, 2001; Vol. 1. [Google Scholar]
  48. Niethammer C.; Becker S.; Bernreuther M.; Buchholz M.; Eckhardt W.; Heinecke A.; Werth S.; Bungartz H. J.; Glass C. W.; Hasse H.; Vrabec J.; Horsch M. ls1 mardyn: The massively parallel molecular dynamics code for large systems. J. Chem. Theory Comput 2014, 10, 4455–4464. 10.1021/ct500169q. [DOI] [PubMed] [Google Scholar]
  49. Wu G.; Chen S. On the collision of a moving droplet against a moving particle with heat transfer. Int. Commun. Heat Mass Transfer 2023, 144, 106752 10.1016/j.icheatmasstransfer.2023.106752. [DOI] [Google Scholar]
  50. Grottel S.; Krone M.; Müller C.; Reina G.; Ertl T. MegaMol - A prototyping framework for particle-based visualization. IEEE Trans. Visualization Comput. Graphics 2015, 21, 201–214. 10.1109/TVCG.2014.2350479. [DOI] [PubMed] [Google Scholar]
  51. Gralka P.; Becher M.; Braun M.; Frieß F.; Müller C.; Rau T.; Schatz K.; Schulz C.; Krone M.; Reina G.; Ertl T. MegaMol - A comprehensive prototyping framework for visualizations. Eur. Phys. J. Spec. Top. 2019, 227, 1817–1829. 10.1140/epjst/e2019-800167-5. [DOI] [Google Scholar]
  52. Heinen M.; Vrabec J. Evaporation sampled by stationary molecular dynamics simulation. J. Chem. Phys. 2019, 151, 044704 10.1063/1.5111759. [DOI] [PubMed] [Google Scholar]
  53. Huang K.-L.; Pan K.-L. Transitions of bouncing and coalescence in binary droplet collisions. J. Fluid Mech. 2021, 928, A7 10.1017/jfm.2021.797. [DOI] [Google Scholar]
  54. Sprittles J. E. Gas Microfilms in Droplet Dynamics: When Do Drops Bounce?. Annu. Rev. Fluid Mech. 2024, 56, 91–118. 10.1146/annurev-fluid-121021-021121. [DOI] [Google Scholar]
  55. Miljkovic N.; Enright R.; Wang E. Effect of droplet morphology on growth dynamics and heat transfer during condensation on superhydrophobic nanostructured surfaces. ACS Nano 2012, 6, 1776–1785. 10.1021/nn205052a. [DOI] [PubMed] [Google Scholar]
  56. Poulikakos D.; Arcidiacono S.; Maruyama S. Molecular dynamics simulation in nanoscale heat transfer: A review. Microscale Thermophys. Eng. 2003, 7, 181–206. [Google Scholar]
  57. Lehtinen K. E. J.; Zachariah M. R. Effect of coalescence energy release on the temporal shape evolution of nanoparticles. Phys. Rev. B 2001, 63, 205402 10.1103/PhysRevB.63.205402. [DOI] [Google Scholar]
  58. Juang R. R.; Lee Y. M.; Chiang C. H.; Wu J. S.; Hsu Y. L.; Chau S. W. Parallel molecular dynamics simulation of head-on collision of two nanoscale droplets with low relative speed. J. Comput. Theor. Nanosci. 2009, 6, 46–53. 10.1166/jctn.2009.1005. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la4c04588_si_001.pdf (1.8MB, pdf)
la4c04588_si_002.mp4 (25.4MB, mp4)
la4c04588_si_003.mp4 (59.9MB, mp4)
la4c04588_si_004.mp4 (133.9MB, mp4)
la4c04588_si_005.mp4 (26.6MB, mp4)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES