Abstract
Background
Advanced cell culture techniques such as 3D bioprinting and hydrogel-based cell embedding techniques harbor many new and exciting opportunities to study cells in environments that closely recapitulate in vivo conditions. Researchers often study these environments using fluorescence microscopy to visualize the protein association with objects such as cells within the 3D environment, yet quantification of concentration profiles in the microenvironment has remained elusive.
Objective
Demonstrate an assay that enables near real-time in situ biomarker detection and spatiotemporal quantification of biomarker concentration in 3D cell culture.
Methods
A distributed bead-based immuno-assay was used in 3D cell culture to continuously measure the time-dependent concentration gradient of various biomarkers by sequestering soluble target molecules and concentrating the fluorescence intensity of these tagged proteins. Timelapse confocal microscopy was used to measure the in situ fluorescence intensity profile and a calibration curve was separately generated. Application of a calibration transfer function to in situ data is used to quantify spatiotemporal concentration.
Results
Example assays utilize an osteosarcoma spheroid as a case study for a quantitative single-plexed gel encapsulated assay, and a qualitative multi-plexed 3D-bioprinted assay. In both cases, a time-varying cytokine concentration gradient is measured. An estimation for the production rate of the IL-8 cytokine per second per osteosarcoma cell results from fitting an analytical function for continuous point source diffusion to the measured concentration gradient and reveals that spheroid production approaches nearly 0.18 fg/s of IL-8 after 18 h in culture.
Conclusions
Theoretical and experimental demonstration of bead-based immunoassays in diffusion-limited environments such as 3D cell culture is shown, and includes example measurements of various cytokines produced by an osteosarcoma spheroid. Proper calibration and use of this assay is exhaustively explored for the case of diffusion-limited Langmuir kinetics of a spherical adsorber.
Keywords: Biomarker, Bead-based ELISA, 3D cell culture, Immunoassay, Osteosarcoma
Introduction
The tumor microenvironment creates a protective immunosuppressive barrier and represents a significant obstacle to therapies[1–4]. Local measurements of the secreted cytokines and signaling molecules involved in immunoregulation within this interphase between tumor tissue and the non-cancerous surrounding tissues are particularly challenging due to difficulties in probing this exquisitely small volume. On cellular dimensions ( O(10) µm in thickness), this total volume of the interphase region can be as small as a microliter (depending on the tumor size) [5]; in vitro interphase volumes further exacerbate the difficulty of measurement since the tumor explants and tumoroids are often much smaller than in vivo with interphase volumes of O(1–10)nL. The second major challenge with local measurements is that the in vitro tumor models are increasingly becoming three-dimensional, which introduces significant sampling and imaging challenges [6]. Accurate measurements of local concentrations over nano-liter volumes in 3D pose significant challenges in both collection and detection. To overcome these challenges, we have suspended ELISA beads within traditional matrigel-based 3D culture as well as 3D-bioprinted liquid-like solid (LLS) culture — a continuously deformable yield stress fluid medium amenable to 3D bioprinting [7]. These suspended ELISA beads are then able to participate in capture dynamics and, when imaged in a standard confocal microscope, allow for quantifiable in situ detection of cytokines in the immediate tumor vicinity. In this manuscript, we will discuss the approach of using fields of ELISA beads to measure biometric data such as spatiotemporal concentration gradients and cellular production rates.
Standard benchtop in vitro experiments enjoy a plethora of techniques to quantify biomarker concentrations [8]. Often centered around media samples captured during cell feeding, the majority of immunoassays offer robust measurement of biomarkers for time-point analysis (Fig. 1A). Although these benchtop immunoassays are the gold standard for many biomarkers, they typically do not have a sensitivity high enough for biomarkers that are scarcely produced and can only measure the average biomarker concentration in the entire assay volume. To overcome this issue, researchers have developed an in situ immunoassay called FluoroSpot which enables the simultaneous measurement of multiple biomarkers on a 2D plane located at the bottom of the culture dish [9]. In this assay, the cells act as a point source for the diffusion of biomarkers; thus, a gradient of captured biomarkers surrounds each cell; this gradient is detected through the use of a fluorophore-conjugated antibody which binds to the captured biomarkers in a fashion commonly referred to as the sandwich ELISA [10]. A fluorescence measurement device can then be used to measure the resulting intensity gradient and further analyzed to reveal the concentration gradient profile. Fluorospot is often used to quantify soluble biomarker production at the single-cell level by seeding cells on a plane containing capture antibodies. Since the biomarker gradients produced by single cells are very close to this plane, a high-quality signal develops. For 3D culture models, however, the lack of full 3D spatial measurement complicates analysis. For example, since the concentration of analyte diminishes rapidly with increasing distance from the source, the distance of the spheroid or organoid from the detection plane is inversely related to the quality of the signal generated. This limitation may be prohibitive in many advanced culture systems. Thus, a 3D analogy to the FluoroSpot assay may be an enabling technology for the development of modern in vitro models.
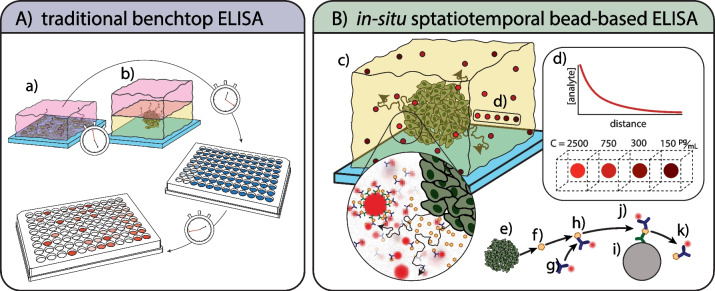
Fig. 1.
Overview of traditional ELISA methods versus our approach: (A) typical bench-top methods for measuring biomarkers with immunoassays from (a) 2D cell culture and (b) 3D cell culture rely on the diffusion of biomarkers into a bath of growth media which is collected at various timepoints. These methods dilute the biomarker concentration by the total volume of growth media in the bath. Furthermore, the sample collection and testing can often take multiple days to obtain results. (B) Our method pictured in (c) utilizes immunosorbent beads scattered throughout the volume of a 3D cell culture assay. The bead fluorescence intensity corresponds to the local concentration of biomarker within a local bead volume of approximately 20nL and these local concentrations may decrease with increasing distance from a source following a concentration gradient of a continuous point source (d). For a continuous source of biomarker from a collection of cells (e), each biomarker (f) released from a cell will bind to a detection antibody (g) to form a pair (h); this antibody biomarker pair then adsorbs to the immunosorbent bead (i) via conjugated capture antibodies (j). The antibody biomarker pair will desorb (k) from the capture antibody at some reverse reaction rate, kr. Through this process, the capture beads will produce a time-varying signal proportional to the local concentration of biomarker at any time
Recent advancements in immunoassay development have enabled the detection of multiple biomarkers from a single sample by utilizing antibody-conjugated microbeads, commonly known as bead-based multiplexed ELISA assays. These assays are becoming increasingly popular with many off-the-shelf biomarker detection kits available from numerous manufacturers. Most of these assays utilize the sandwich ELISA method to capture and detect biomarkers in a solution through the use of proprietary flow cytometers such as Magpix®, LUNARIS™, and Quanterix®[11]. Manufacturers of bead-based assays typically require the use of custom-designed flow cytometers for the detection of fluorescence intensity with their bead-based immunoassay to maximize the fluorescence intensity signal and achieve high sensitivity and linearity of the assay. Although these detection systems are custom-built, they all utilize the same basic principles outlined in Fulton et al. [12]. Briefly, microbeads with one or more unique fluorescence signatures are used to identify the biomarker specificity of each bead while other fluorescence signatures are used to detect biomarker concentration through a calibration curve transfer function [13]. Great care is taken in the design of the bead adsorption kinetics to optimize and further enhance the detectability of the biomarkers [14].
Here, we utilize these bead-based immunoassays to develop an in situ biomarker detection method for 3D cell culture. This technique uses fluorescence microscopy to detect the fluorescence intensity of immunoassay beads distributed in 3D as they sequester analyte from their local environment, as overviewed in Fig. 1B. Using this method, we are able to quantify the biomarker concentration in a singleplex assay and show that this technique is able to capture in situ spatiotemporal information of biomarker concentration in near real-time. Qualitative detection of biomarker production is also described in a multiplex assay using a much-simplified version of the quantitative method. Adaptation of the quantitative method for use in such a multiplex assay is straightforward but not presented. Furthermore, protocols for incorporating capture beads into standard 3D culture systems are developed for liquid-like solid 3D bioprinting [15] and typical gel-based 3D culture [16]. These results show the first implementation of a commercially available real-time in situ immunoassay for 3D cell culture and 3D bioprinting assays in both quantitative, and qualitative fashions.
Assay use
General assay workflow
This technique uses immunoassay beads distributed throughout a 3D culture system to detect the local concentration of analyte surrounding a cellular construct (i.e., spheroids or organoids) in a single pot sandwich-ELISA configuration. The analyte produced by the spheroid is released into the 3D environment solution containing an abundance of fluorophore-conjugated detection antibodies. The analyte is then tagged by the fluorophore-conjugated antibodies and subsequently sequestered by capture antibodies coating the surface of the distributed immunoassay beads (Fig. 1B). Tagged analytes sequestered by the capture beads can be visualized at any time via fluorescence microscopy. The use of a calibration function for the conversion of the beads’ measured fluorescence intensity to concentration can be used to produce quantitative measurements. Production rates of analyte can be measured by fitting a theoretical model of a continuous point source to the measured data. This assay provides a rapidly deployable tool to the researcher by combining in situ fluorescence microscopy and immunoassay beads to gather spatiotemporal information regarding analyte concentration profiles in 3D. Potential users of this technique are strongly encouraged to utilize the appendix for a thorough explanation of background mathematics describing assay kinetics in detail.
Qualitative biomarker detection assay
The simplest form of this assay can be implemented in a qualitative manner with relative ease resulting in spatial information of biomarker presence within detectable ranges. In practice, a combination of cytometric beads and detection antibody within a 3D assay can provide a Boolean interpretation of biomarker presence via fluorescence-enabled microscopy. In short, if a mean fluorescence intensity (MFI) exists in the proper channel after background subtraction, then the biomarker is present at detectable levels, and vice versa. However, the authors suggest careful consideration of Appendix 2 before use of a qualitative assay due to various issues related to the kinetics of singlepot-ELISA. For example, the use of custom cytometric beads or overly dense bead concentrations may lead to poor or misleading results. Nevertheless, this level of the assay can allow a user to rapidly probe an experiment to provide real-time spatial information about the state of soluble biomarkers in a 3D culture system. Best practices for detection and measurement of bead MFI can be found in Appendix 1.
Quantitative biomarker detection assay
The assay described here utilizes cytometric beads in a manner that is far from the manufacturer’s intended use. For example, measurement of the fluorescence intensity is achieved using a fluorescence microscope which has many associated issues with capturing quantitative information [17–19]. These issues ultimately lead to relatively large uncertainties of measured biomarker concentration; however, the ability to capture the spatiotemporal concentration of biomarker in real-time remains an attractive feature. The adaptation of these commercial assays to capture in situ quantitative information for 3D culture systems demands attention to three critical considerations: the conversion of MFI to biomarker concentration, determination of acceptable bead density, and the measurement method of analyte production rates.
Typically, bead-based assays assume a pure convection boundary at the bead surface coupled with an abundance of biomarker in solution much beyond the total capture capacity of the beads. These assumptions cannot be made upon adaptation to 3D culture systems which typically have minimal or no convection [20]. This leads to diffusion-limited reactions in the 3D environment and thus special considerations must be taken to ensure that measured bead MFI is calibrated correctly. For this calibration, a standard curve is generated under pure diffusion, and we introduce a dynamic measurement based on the concentration gradient of the biomarker with known boundary conditions. The dynamic measurement is based on a flat wall diffusion gradient of biomarker from a fully mixed convective chamber into a 3D culture analog. The purpose of the diffusion chamber is to ensure the density of capture beads used in the assay is appropriate to the assay kinetics.
Generation of a calibration function for MFI to concentration
To overcome these challenges, a calibration is performed that would be familiar to benchtop ELISA users but is adapted for use in fluorescence microscopy. Briefly, a custom device shown in Fig. 2 (A,B) uses multiple wells to distribute a serial dilution of analyte into a constant concentration of detection antibody. Each well also contains at least 50 immunoassay beads which are allowed to rest at the bottom of each well. The device is placed above a fluorescence microscope and the fluorescence intensities of the immunoassay beads are measured. Measured fluorescence intensities of immunoassay beads are compared to the serial analyte dilution to develop a calibration transfer function (Fig. 2C). A detailed description of calibration curve generation and error analysis can be found in Appendix 2. Importantly, the microscopy settings used in calibration (laser, gain, etc.) should be tuned to the dynamic range of the immunoassay used, then saved for use during in situ fluorescence measurement.
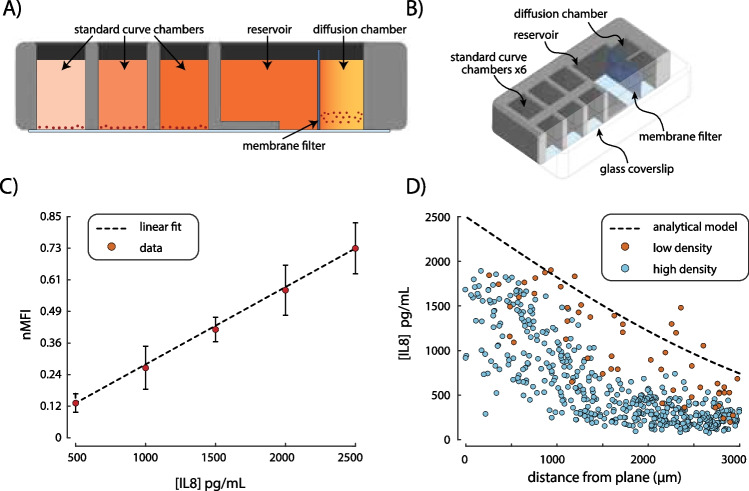
Fig. 2.
Calibration device for standard curve and dynamic diffusion curve analysis. (A) A cross-sectional view of the calibration device showing the standard curve wells, reservoir, diffusion chamber, and membrane filter. The color scale from light pink to dark orange signifies the concentration of biomarkers from low to high respectively. (B) An isometric view of the calibration device shows the overall construction. (C) The standard curve is generated using a linearly spaced concentration of biomarker from 0 to 2500 pg/mL in 500 pg/mL increments, corresponding to this assay’s linear range. The MFI of each bead is measured and then normalized (nMFI) by the top of the dynamic range. Vertical error bars represent population standard deviation of bead nMFI. A linear best fit of the nMFI data is found using an MC simulation which considers uncertainty in nMFI, and concentration of the standards used. (D) Beads in the diffusion chamber are measured after 10 h and the nMFI is transferred into cytokine concentration using the standard curve. An analytical model for flat wall diffusion (black dashed line) is compared to two bead densities Γ = 0.1 (low density, red circles) and Γ = 1 (high density, blue circles). These results show that as Γ becomes much less than one, the beads’ measurement more closely follows the expected value with R2 = -0.49 and 0.54 for Γ = 1 and Γ = 0.1 respectively
Estimation of appropriate bead density
Each capture bead sequesters some amount of biomarker from the local environment dependent upon Langmuir equilibrium kinetics resulting in the formation of a local concentration gradient. When beads are too densely packed, local concentration gradients may overlap, effectively lowering the detected local concentration. This inter-bead competition is defined by a balance of the capture-site equilibrium kinetics () and bead density () versus expected local biomarker concentration (), and can be described by the non-dimensional equation:
| 1 |
A detailed derivation of this relationship, and importantly how to derive , can be found in Appendix B.2. Appropriate prediction of capture bead density is identified by values of much below unity. Nonetheless, the effect of the capture bead concentration on the assay should be experimentally verified using the bead calibration device shown in Fig. 2A,B. Measured concentration gradients within the diffusion chamber should approximate the expected value based on a flat wall diffusion model (presented in Appendix B.1 Eq. 3) as seen in Fig. 2D. Measurement of the bead density within an assay can be quickly achieved using fluorescence microscopy by taking the ratio of the number of beads within the max intensity projection to the known imaging volume.
Estimation of biomarker production rates
For diffusion-limited systems, the concentration of products produced within a sphere is well approximated by a continuous point source after one diameter from the sphere center. An analytical solution for this continuous point source is given by Crank [21] in Eq. 2.
| 2 |
The analyte production rate is determined using a Monte Carlo (MC) simulation to find the least squares regression of Eq. 2 onto using as a free variable. A random normally distributed uncertainty is assigned to each measured concentration based on the uncertainty in the calibration transfer function. Uncertainty in bead locations (), diffusion coefficient of the conjugate detection antibody and analyte (D), and the assay time in seconds () are randomly assigned within some known uncertainty range for each simulation run. The resulting MC uncertainty analysis uses simulations for each timepoint to gather the mean and standard deviations of .
Methodology in demonstration
Culture of osteosarcoma spheroids
OS521 was cultured in a T-75 flask (Corning) using a complete culture medium with 0.3 mg/mL G418 (Mediatech) at 37 °C, 5% CO2 [22]. After reaching confluence, cells were released from the flask using a trypsin dissociation reagent (TrypLE, Gibco) and resuspended in culture media to a density of approximately cells/mL. This cell suspension was then distributed to an ultra-low attachment round-bottom 96-well plate (Corning) and incubated at 37 °C, 5% CO2 for 72 h with daily media changes until tight spheroids were formed. Immediately before use in assays, spheroids were dyed using CellTracker Green CMFDA dye using standard manufacturer-specified protocols prior to the experiment.
Preparation of gel-based distributed bead assay
A human IL-8 cytometric bead array (CBA) kit (BD biosciences) consisting of three components, IL8 capture beads, fluorophore-conjugated detection antibody, and lyophilized human IL8 standard was used in a matrigel-based culture of osteosarcoma spheroids. First, the detection antibody was diluted in a solution of culture media as well as a solution of matrigel at a ratio of 1:200. This ratio may vary between assays and manufacturers since the detection antibody concentration is not consistent. For this assay, the target detection antibody concentration allows for 10 × the number concentration of detection antibodies to the highest local number concentration of biomarkers expected. The detection antibody concentration can be determined using the protocol outlined in Appendix C.4. Next, the capture beads were added to the matrigel solution at a concentration of 50 beads/μL (the concentration of capture beads given in BD CBA kits is approximately 3000 beads/μL), gently pipette mixed, and placed on ice. An osteosarcoma spheroid, chilled on ice, was then added to the matrigel-bead solution and gently pipette mixed. The solution was then pipetted onto a glass-bottom well to form a dome, the spheroid was gently moved towards the center, and the sample was placed in an incubation chamber at 37 °C, 5% CO2 until the matrigel was set (approximately 2 min). Finally, the media + detection antibody solution was added to the culture dish ensuring the matrigel was fully submerged. The sample was then placed on a fluorescent microscope and imaged every 4 h using laser channels of the following: GFP, to capture the OS521 spheroid; cy5, to capture bead positions; and TRITC, to capture detection antibody intensity.
Preparation of 3D-printed bead assay
Four BD CBA kits of human IL-11, human IL-8, human IL-6, and human VEGF are checked for cross-reactivity by consulting the BD CBA manual. A solution of LLS is created using culture media according to the protocol outlined in Bhattacharjee et al. [7]. Detection antibodies from each kit are diluted into culture media as well as a solution of LLS at a ratio of 1:200 v/v. Capture beads from each kit are combined with the LLS solution in separate aliquots at a concentration of 50 beads/μL. In a separate aliquot, an osteosarcoma spheroid is combined with a small amount of the LLS solution and printed into a glass-bottom petri dish filled with LLS following a method outlined in Bhattacharjee et al. [7]. Each capture bead solution is then printed in a 4-arm configuration centered about the osteosarcoma spheroid as shown in Fig. 3C. Finally, the media + detection antibody solution is carefully added atop the printed structures being careful not to disturb the sample. The sample is then placed on a fluorescent microscope and imaged every 4 h using both the bead detection (cy5) channel as well as the detection antibody (TRITC) channels.
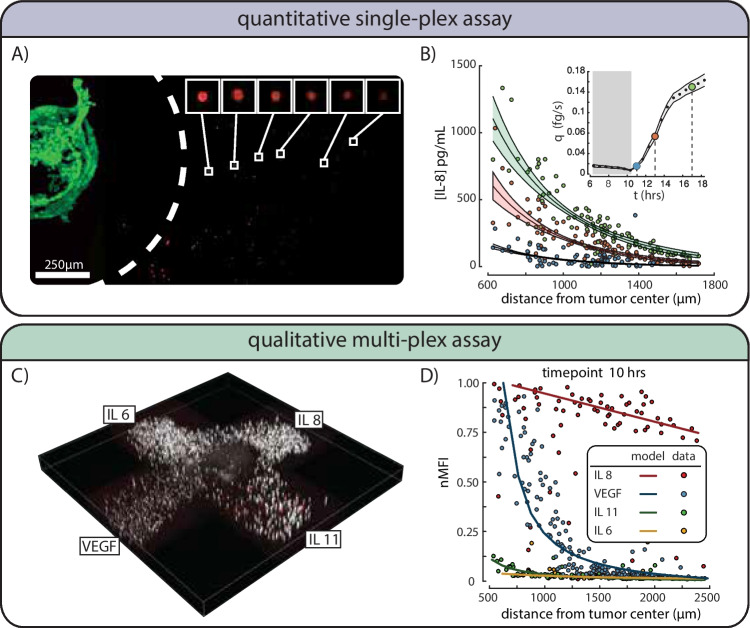
Fig. 3.
Quantitative single-plex, and qualitative multi-plexed assay results for an osteosarcoma spheroid. (A) A max intensity z-projection shows a 500-μm-diameter osteosarcoma spheroid in green on the left with a white dashed line corresponding to the area where no detection beads are found. Breakouts of six beads at various radial distances from the spheroid show a decreasing intensity with increasing radial distance. (B) Results of IL8 concentration and associated MC analysis for three timepoints are shown. Inset shows the resulting production rate across the timelapse starting at 6 h. Measured IL8 bead intensities for timepoints 11.5 h (blue), 13 h (orange), and 17 h (green) are shown with the mean best fit of the MC and shaded region showing standard deviation of best fit. The production rate q over time shown in the inset is reported as the mean (black dots) and standard deviation (shaded gray region). Select timepoint markers are color matched with the concentration profile fits and placed over corresponding black dots. IL8 production rate for the spheroid appears to climb to nearly 0.16 fg/s by the end of the timelapse; all production rate data prior to the 10-h point is not trustworthy due to insufficient quality of bead MFI data (gray region) - this timeframe however is commensurate with the expected diffusion time of biomarker from the exclusion zone. (C) A 3D-printed bead array surrounding an osteosarcoma tumoroid shows the relative position of four bead types IL6, IL8, IL11, and VEGF. (D) The detectability of each biomarker can be compared directly with IL8 and VEGF showing relatively high readings for each, and relatively low readings for IL-11 and IL-6. These readings would qualitatively indicate that IL-8 and VEGF are present while IL-11 and IL-6 are not being produced in sufficient quantities to be measured. Lines are the least square regression fit of Eq. 2 onto uncalibrated immunoassay bead nMFI data. No error bars shown as calibration was not performed
Results
Calibration
We developed a PDMS device for the calibration of MFI versus the biomarker concentration using a serial dilution of biomarker standard as well as the validation of bead kinetics; the schematic of this device can be seen in Fig. 2A,B. For this study, we first find the assay kinematic variables of the human IL-8 CBA kit using the protocols outlined in Appendix 3. The kinematic variables were found to be , = , and Using these kinematic variables with a biomarker concentration at an MFImax of 2994, the equilibrium bead coverage was found to be 0.12 using Eq. 12. Next, we produce a calibration transfer function for the bead MFI to concentration following the method outlined in Appendix B.1. A linear transfer function with a slope of 3458 pg/mL and uncertainty of 11.7% was found to fit calibration data with an of 0.94 and can be seen in Fig. 2C. We also used the calibration device to produce a concentration gradient profile for two bead concentrations 50 and 500 beads/μL with a flat wall boundary condition of constant 2500 pg/mL. The results presented in Fig. 2D) show that the bead concentration of 50 beads/μL produces a concentration profile similar to the analytical model described by Eq. 3 while the bead concentration of 500 beads/μL greatly underpredicts the analytical model. Using Eq. 1 with these bead densities and measured kinematic variables reveals the sequestration ratio for bead concentrations of 50 beads/μL and 500 beads/μL to be 0.1 and 1 respectively. This result demonstrates that Eq. 1 can accurately predict the appropriate bead density when the sequestration ratio is < < 1.
Singleplex matrigel-based assay
OS521 is known to produce the IL-8 cytokine in abundance, so we chose to focus on this cytokine for our trial study [23]. After the IL-8 capture bead density and MFI vs concentration calibration curve were found, we analyzed the resulting intensity gradient of the bead MFI surrounding the spheroid to recover the concentration gradient for three timepoints 10, 14, and 18 h as shown in Fig. 3A,B). The rate of cytokine production for the 500-μm-diameter spheroid (estimated to be ~ 10 k cells) was found for multiple timepoints by fitting Eq. 2 to the concentration gradients. Best fits of the radial concentration data were found using an MC simulation as described in Appendix B.3. The evolution of the production rate over time is plotted in Fig. 3B, inset), with the mean and uncertainty of found using the MC simulation described in Appendix B.3. These results are only valid after the 10-h timepoint since bead MFI data for all previous timepoints had very low signal to noise. After the 10-h timepoint, we measure a steady increase in the IL8 production rate for the spheroid and this rate appears to climb to nearly 0.16 fg/s by the end of the timelapse. This period of time likely corresponds to the biomarker loading period for the exclusion area surrounding the spheroid, generated during bioprinting. This region has a characteristic timescale of approximately 10 hours given the measured diffusion coefficient.
Multiplex LLS-based assay
Bead-based immunoassays are often used to measure multiple biomarkers from the same sample, and thus the detection and capture antibodies have been optimized to ensure little to no cross-reactivity. We utilize this capability in a 3D-bioprinted assay by separating the bead types by location in a 4-arm configuration centered around the spheroid as shown in Fig. 3C. The bead intensity gradient for the IL-11, IL-8, IL-6, and VEGF was measured for multiple timepoints and presented in Fig. 3D. These results show that the four cytokines measured have different concentration gradient time profiles and thus four different production rates. No calibration was completed for this multiplexed assay so results remain qualitative.
Discussion
The rise of 3D culture provides exciting opportunities to study in vitro biological systems in their closest analogous configuration to in vivo [20, 24–26]. These methods offer potentially enhanced biological complexity through mass transport modification, 3D intercellular contact, cell–matrix signaling, customizable geometric configuration of tissues, tissue shielding, and complex immune interaction. The addition of perfusion into these 3D culture systems allows for long-duration cultures providing opportunity for emergent biological complexity to flourish in vitro [27–30]. Such methods are of keen interest in the pharmaceutical industry as the development and deployment of in vivo–like high-throughput drug screening may offer better drug development outcomes [31, 32]. Unfortunately, interrogating biochemical compositions of 3D in vitro systems using standard bioassays can be extremely challenging to near impossible. Therefore, new developments in bioassay technologies are needed to provide the insights researchers have come to know as a standard for 2D in vitro systems.
In this study, we have examined the potential for the use of a commercially available bead-based immunosorbent assay as a viable method for the in situ measurement of cytokine concentration within 3D culture assays. This assay method not only represents the first of-its-kind measurement for 3D culture systems but is also easily implemented using this manuscript as a guide. Additionally, we have shown that this assay can be implemented in simple gel-based culture systems as well as more advanced 3D bioprinting systems at low cost. Typical bead-based assays supply approximately 300,000 beads, and more than enough detection antibody to coat each bead at the highest standard. The 3D assays used in this study used a bead density of 50 beads/μL with a total gel volume of approximately 100μL per sample. At this ratio, this experiment can be repeated 60 times at a total cost of a single bead-based assay kit. At the time of this writing, an IL-8 CBA kit costs approximately $278.00 making the cost of each experiment less than five dollars. If a 3D printing technique were implemented, as we have done in this manuscript, this cost can be reduced significantly.
Microfluidic platforms are often used to study the biomarker response of either individual cells [33, 34] or cellular aggregates since the volumes of nutrient media used are small with respect to traditional culture methods. One microfluidic model of note incorporates immunoassay beads into a feature containing a small amount of culture media and a single spheroid surrounded by an oil; this system then measures the biomarker production within this closed system over time [35]. The small volumes associated with microfluidic culture allow for relatively high concentrations of analyte assuming the analyte production rate is constant. Furthermore, microfluidic systems typically have low Reynolds number flows, and thus some flow geometries can result in regions with no mixing or flow velocity. Although this is often a burden in microfluidic design, the intentional implementation of these features could be used to create diffusion-limited regions. If cells of interest are located in these diffusion-limited regions, the bead-based assay described here may be useful to measure the real-time concentration profiles within advanced organ-on-a-chip models.
Bead-based immunoassays are not typically designed to be used in the manner we prescribe here. Some assays may not be viable due to incompatible assay kinetics, background saturation, cross-reactivity, etc. For example, the immunoassay must be capable of single-pot capture and detection which requires the antigen to have unique binding epitopes for the paratopes of the capture and detection antibodies. Many assays are capable of single-pot capture and detection but do not recommend this incubation method due to a reduction in assay sensitivity via the inclusion of detection antibodies within the sample which may obscure signals at the low end of the detection range. In our experience, these factors typically result in a 10% to 20% reduction of the assays reported range when used in our method. However, since our assay assumes the pure diffusion of biomarkers from one or more point sources, the local concentration of biomarkers accumulates over time and may eventually become detectable. Finally, the active implementation of this assay may limit biological interaction. The inclusion of detection antibody and subsequent conjugation of the detection antibody in solution may affect intercellular chemokine signaling and, as a result, change cellular behavior. This challenge could be circumvented by the cycling of detection antibody for periods before imaging, especially in thin sections of 3D gel-based assays or through perfusion pulsation in LLS-based experimental platforms.
Conclusions
We developed a novel method for the utilization of commercially available bead-based immunosorbent assays for use in 3D cell culture platforms. Two 3D culture systems, a simple matrigel-based assay, and an advanced 3D bioprinting assay were studied using osteosarcoma spheroids to generate and measure multiple cytokines of interest. Protocols to back out the kinematic variables from commercial cytometric assays have been developed and allow users to easily calculate the ideal beads density and the detection antibody concentration appropriate for an individualized assay. Finally, we show that this assay can be easily implemented and adapted for use in multiple 3D culture systems in both qualitative and quantitative capacities.
Appendix 1. Bead measurements
Commercial bead-based multiplex immunoassays use one or more fluorescent dyes incorporated into the bead to identify the antigen specificity within a mixture of many bead types [36, 37]. This internal fluorescence can be used to locate the bead centers within a volumetric scan of the 3D assay. Each bead in the volumetric scan should be cropped into individual max-intensity projections using the centroid of the bead as measured by the internal fluorescence channel. Once the bead has been located and cropped, each bead image should then be analyzed in the fluorescence channel of the respective detection antibody using the MFI of a circular masked region with dimensions equal to the diameter of the bead in real-world units. The uncropped inverse space of the full volume can then be used to develop a background fluorescence intensity used for background subtraction. Positive fluorescence intensity for any bead can be interpreted as detection of the respective biomarker in that location.
Appendix 2. Calibration and use of quantitative biomarker detection assay
Appendix B.1 Calibration curve generation
This assay utilizes a bead fluorescence intensity measurement using a fluorescence microscope and assumes the intensity is proportional to the local concentration of biomarkers due to one or more point sources in a 3D cell culture assay. This relationship between bead intensity and local biomarker concentration must be experimentally calibrated. To accomplish this, we have created a PDMS chip featuring six wells, and a reservoir + diffusion chamber which is a rectangular well separated by a filter membrane (as shown in Fig. 2A,B). The six wells are used to create a standard curve by creating a serial dilution of the biomarker standard. Detection antibodies and beads are added to the standards and the beads are allowed to sink to the bottom of each well. The detection antibody associates with the biomarker in solution and the beads are allowed to reach an adsorption equilibrium for their respective concentrations in a diffusion-limited reaction.
To measure the assay kinetics within a 3D culture system, the diffusion chamber is first filled with the 3D culture medium mixed with capture beads and detection antibody distributed in a manner described in “Preparation of gel-based distributed bead assay” and “Preparation of 3D-printed bead assay.” In the reservoir, a solution of the highest concentration standard mixed with detection antibodies is filled to the same level as the 3D culture medium.
The sample is placed onto a fluorescence microscope and the beads within the standard wells are used to calibrate the microscope intensity settings such that the dynamic range is maximized for the lowest and highest bead intensities used in the standards. Once a dynamic range is established, the bead MFI should be measured according to the protocol outlined above to establish the standard curve. The detection settings (laser power, gain, lens, zoom, etc.) should be recorded and kept constant for all future measurements referring to this standard calibration. The standard concentration versus measured bead MFI should be analyzed according to the manufacturer’s instructions to create a calibration curve. This calibration curve should then be used to transform the intensity measurements from the assay into biomarker concentration.
Beads within the diffusion chamber are measured every 2 h until an intensity gradient fills the view. The resulting concentration profile is then compared to the analytical function for flat wall diffusion given by Crank [21] in Eq. 3.
| 3 |
where C(x,t) is the time-varying concentration at some distance from the flat wall of constant concentration and is the diffusion coefficient for the biomarker + detection antibody. This diffusion coefficient can be measured using the protocol outlined in Appendix C.1. If the measured concentration profile does not match the analytical function, the bead density must be decreased. Refer to Appendix B.2 for more information related to bead density.
Uncertainty in calibration of the standard curve was determined using the MC method for uncertainty analysis by combining calibration solution uncertainty and bead nMFI error. Calibration solution concentration uncertainty was determined using combined standard uncertainty analysis [38] of a dilution equation with associated uncertainties in pipette volumes used. The pipette volume uncertainty was determined by repeatedly pipetting and recording deviation in pipetted volumes. Bead error was determined as the standard deviation of nMFI at each concentration condition with > 50 bead samples. Table 1 shows reported values of concentration, uncertainty in concentration, bead nMFI, and associated nMFI standard deviation. An MC simulation used a normally distributed random perturbation from the nominal concentration versus nMFI value to create 106 linear fits anchored at zero. The mean of the resulting slope was found to be 3458 pg/mL and is used as a calibration transfer function for nMFI to concentration. The standard deviation of all slopes was used to find the associated uncertainty and was found to be 11.7%.
Table 1.
List of nominal values and associated uncertainties used in an MC simulation of a linear fit of the standard curve data
| IL-8 concentration (pg/mL) | Uncertainty in concentration (pg/mL) | nMFI (> 50 bead samples) | Standard deviation of nMFI (> 50 bead samples) |
|---|---|---|---|
| 2500 | 39.05 | 0.731 | 0.098 |
| 2000 | 32.3 | 0.569 | 0.097 |
| 1500 | 25.42 | 0.417 | 0.047 |
| 1000 | 18.27 | 0.269 | 0.083 |
| 500 | 10.39 | 0.134 | 0.036 |
Appendix B.2 Determination of ideal bead density
Langmuir kinetics can be used to approximate the sequestration of biomarkers by each bead within the 3D assay with the number of sequestered biomarkers reaching an equilibrium surface concentration () for some given local concentration (C) according to Eq. 4.
| 4 |
The equilibrium constant describes the binding affinity of the capture antibody on the bead surface to the biomarker. This equilibrium constant is unique to each assay and can be determined using Eq. 9 after the kinetic variables have been found (refer to Appendix 3 for more information). To find the maximum bead density for each 3D assay, we consider the ratio of the total number of surface sites occupied at equilibrium () versus the number of biomarkers () within some local bead volume () surrounding the bead for a given local concentration (). This sequestration ratio can be found using Eq. 5.
| 5 |
where is the number of capture sites on the bead, and is the surface coverage at equilibrium. When the ratio given in Eq. 5 is much less than one, the sequestration of biomarkers from a bead does not significantly affect the local concentration of neighboring beads. In this case, the maximum bead density can be calculated using Eq. 6.
| 6 |
Appendix B.3 Monte Carlo simulation method for measuring biomarker production rates
The uncertainty in the measured analyte production rate can be determined using an MC simulation of bead concentration data. Each simulation uses a least squares regression of Eq. 2 (with as a free variable) onto the radial and time-dependent concentration data points while adding random variability to each measured concentration data point. A random normal distribution of bead locations (), diffusion coefficient (D), and assay time in seconds ( is generated for each simulation using the variables respective uncertainty as distribution standard deviation. Table 2 shows the nominal values and associated uncertainty of each variable used in the simulation. Collecting all of the simulated data allows for the determination of mean and standard deviation of the protein production rate. Additionally, accumulating the resulting best fits allows for the calculation of the mean and standard deviation of the fitted line. The result of this analysis is shown in Fig. 3B as a shaded region of uncertainty around the mean line of best fit for each timepoint.
Table 2.
List of nominal values and associated uncertainties used in an MC simulation of a fit of the radial concentration data using Eq. 2. The uncertainty in the timepoint measurement is half the scan time of the volume since data is collected using a max intensity projection. The uncertainty in the radius describes the uncertainty in the tumor margin (how spherical is the spheroid). Uncertainties for D and C are discussed in Appendix C.1 and Appendix B.1 respectively
| Variables | q | D | t | r | C |
|---|---|---|---|---|---|
| Nominal values |
Free parameter |
20 μm2/s | (Frame #)*20 min | Independent variable | Dependent variable |
| Uncertainty | Calculated as a result | 10μm2/s | 10 min | 50 μm | 11.7% |
Appendix 3. Estimation of bead assay kinetic variables
Many of the variables used in Appendix 2 are considered proprietary information by the manufacturer of the bead assay and thus are not readily available. However, these variables can be found through experimentation. The following sections outline the procedures for estimating the kinetic variables for any commercially available assay in a diffusion-limited system.
Appendix C.1 Estimation of detection antibody + biomarker diffusion coefficient
A solution of detection antibody mixed with a 1:1 ratio of biomarker is added to the gel solution used in the 3D culture platform then set within a glass-bottom culture dish. Fluorescence recovery after photobleaching (FRAPS) is then used to determine the diffusion coefficient according to the protocol outlined in Deschout et al. [39]. An MC simulation of the fits to this data allows for the calculation of uncertainty measurements given known uncertainties of each variable.
Appendix C.2 Estimation of the reaction rates
The detection antibody and biomarker both attach and detach from the capture bead at a forward reaction rate and reverse reaction rate . The forward reaction rate can be approximated using Eq. 7 adapted from the Einstein–Smoluchowski equation describing the diffusional association of two reactive species in solution [40, 41].
| 7 |
where is the radius of the capture bead, is the number of capture sites on the bead, and is the detection antibody + biomarker diffusion coefficient.
The reverse reaction rate should be determined experimentally since this rate is determined by the antibody-antigen binding affinity. Begin by transferring a bead that has reached equilibrium surface coverage of biomarker and detection antibody1 to a buffer solution with a zero concentration of biomarker and detection antibody. The fluorescence intensity of the bead should then be measured every 5 min for 20 min. The resulting MFI measured at some time can be used to find the reverse reaction rate using Eq. 8
| 8 |
where is the initial mean fluorescence intensity and is the background fluorescence intensity. This exponential decay is predicted by the Langmuir adsorption model [42].
The equilibrium constant is simply the ratio of the forward and reverse reaction rate as seen in Eq. 9..
| 9 |
Appendix C.3 Estimation of the number of capture sites and equilibrium surface coverage
Kinematic variables for the Langmuir equilibrium surface coverage versus local biomarker concentration can be found using the MFI versus data provided by the standard curve. First, the biomarker concentration versus MFI profile is cropped in the linear range. This allows for the assumption that the MFI normalized by the maximum reported MFI will be proportional to normalized by the maximum equilibrium surface coverage at the highest biomarker concentration in the linear region according to Eq. 10.
| 10 |
Substituting Eq. 9 into Eq. 4 reveals the relationship between and the assay kinematic variables for diffusion-limited reactions.
| 11 |
Finally, substituting Eq. 11 into Eq. 10 allows the reported MFI vs concentration profile within its linear range to be used to fit Eq. 12 using the number of capture sites on each bead and as free variables.
| 12 |
Appendix C.4 Estimation of detection antibody concentration
The concentration of the detection antibody should be high enough to ensure all biomarkers generated within the 3D culture assay are captured by the detection antibody before reaching the embedded capture bead. However, the background fluorescence signal increases with increasing detection antibody concentration. We, therefore, utilize the calibration device to determine the detection antibody concentration in the following manner. The diffusion chamber from the calibration device is filled with a PBS 1X buffer solution and the detection antibody solution is added to one side of the chamber separated by the membrane filter. The fluorescence intensity of the second chamber is continuously measured every 5 min until an intensity gradient fills the image of a fluorescent microscope. Assuming the MFI of each pixel is directly proportional to the antibody concentration, the flat wall diffusion equation from Eq. 3 can be used to fit the intensity versus distance profile from the filter membrane using the concentration as a free variable. The diffusion coefficient of the detection antibody can be found using the FRAP method described in Appendix C.1.
Acknowledgements
The authors would like to thank Dr. Parker Gibbs for generously donating OS521Oct4 cell lines to this work.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Use of the beads within the highest concentration standard is preferred.
The original online version of this article was revised: The reference to Figure 1A has been inserted. The reference to Figure 2D has been corrected. Figure 3 has been corrected.
Change history
2/9/2023
A Correction to this paper has been published: 10.1007/s44164-023-00042-3
References
- 1.Tabassum DP, Polyak K. Tumorigenesis: it takes a village. Nat Rev Cancer. 2015;15:473–83. 10.1038/nrc3971. [DOI] [PubMed] [Google Scholar]
- 2.Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell. 2011;144:646–74. 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 3.Discher DE, Mooney DJ, Zandstra PW. Growth factors, matrices, and forces combine and control stem cells. Sci. 2009;324:1673–7. 10.1126/science.1171643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vidi P-A, Bissell MJ, Lelièvre SA. Three-dimensional culture of human breast epithelial cells: the how and the why. In: Randell SH, Fulcher ML, editors. Epithelial cell culture protocols: second edition. Totowa, NJ: Humana Press; 2013. 193–219. 10.1007/978-1-62703-125-7_13. [DOI] [PMC free article] [PubMed]
- 5.Milo R, Phillips R. Cell Biology by the numbers. 1st Edition. Garland Sci; 2015. 10.1201/9780429258770.
- 6.Drost J, Clevers H. Organoids in cancer research. Nat Rev Cancer. 2018;18:407–18. 10.1038/s41568-018-0007-6. [DOI] [PubMed] [Google Scholar]
- 7.Bhattacharjee T, Gil CJ, Marshall SL, Urueña JM, O’Bryan CS, Carstens M, et al. Liquid-like solids support cells in 3D. ACS Biomater Sci Eng. 2016;2:1787–95. 10.1021/acsbiomaterials.6b00218. [DOI] [PubMed] [Google Scholar]
- 8.Cox KL, Devanarayan V, Kriauciunas A, Manetta J, Montrose C, Sittampalam S. Immunoassay methods. Eli Lilly & Company and the National Center for Advancing Translational Sciences; 2019. Available: https://www.ncbi.nlm.nih.gov/books/NBK92434/. Accessed 1 Jan 2022.
- 9.Janetzki S, Rueger M, Dillenbeck T. Stepping up ELISpot: multi-level analysis in FluoroSpot assays. Cells. 2014;3:1102–15. 10.3390/cells3041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aydin S. A short history, principles, and types of ELISA, and our laboratory experience with peptide/protein analyses using ELISA. Peptides. 2015;72:4–15. 10.1016/j.peptides.2015.04.012. [DOI] [PubMed] [Google Scholar]
- 11.Djoba Siawaya JF, Roberts T, Babb C, Black G, Golakai HJ, Stanley K, et al. An evaluation of commercial fluorescent bead-based luminex cytokine assays. PLoS One. 2008;3:e2535. 10.1371/journal.pone.0002535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fulton RJ, McDade RL, Smith PL, Kienker LJ, Kettman JR Jr. Advanced multiplexed analysis with the FlowMetrix system. Clin Chem. 1997;43: 1749–1756. Available: https://www.ncbi.nlm.nih.gov/pubmed/9299971. Accessed 3 Jan 2022. [PubMed]
- 13.Morgan E, Varro R, Sepulveda H, Ember JA, Apgar J, Wilson J, et al. Cytometric bead array: a multiplexed assay platform with applications in various areas of biology. Clin Immunol. 2004;110:252–66. 10.1016/j.clim.2003.11.017. [DOI] [PubMed] [Google Scholar]
- 14.Huovinen T, Lindenburg L, Minter R, Hollfelder F. Multiplexed affinity characterization of protein binders directly from a crude cell lysate by covalent capture on suspension bead arrays. Anal Chem. 2021;93:2166–73. 10.1021/acs.analchem.0c03992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bhattacharjee T, Zehnder SM, Rowe KG, Jain S, Nixon RM, Sawyer WG, et al. Writing in the granular gel medium. Sci Adv. 2015;1:e1500655. 10.1126/sciadv.1500655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ravi M, Paramesh V, Kaviya SR, Anuradha E, Solomon FDP. 3D cell culture systems: advantages and applications. J Cell Physiol. 2015;230:16–26. 10.1002/jcp.24683. [DOI] [PubMed] [Google Scholar]
- 17.Jonkman J, Brown CM, Wright GD, Anderson KI, North AJ. Tutorial: guidance for quantitative confocal microscopy. Nat Protoc. 2020;15:1585–611. 10.1038/s41596-020-0313-9. [DOI] [PubMed] [Google Scholar]
- 18.Royer CA. Characterizing proteins in their cellular environment: examples of recent advances in quantitative fluorescence microscopy. Protein Sci. 2019;28:1210–21. 10.1002/pro.3630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fricker M, Runions J, Moore I. Quantitative fluorescence microscopy: from art to science. Annu Rev Plant Biol. 2006;57:79–107. 10.1146/annurev.arplant.57.032905.105239. [DOI] [PubMed] [Google Scholar]
- 20.Nguyen DT, Famiglietti JE, Smolchek RA, Dupee Z, Diodati N, Pedro DI, et al. 3D in vitro platform for cell and explant culture in liquid-like solids. Cells. 2022;11:967. 10.3390/cells11060967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Crank J. The mathematics of diffusion. 2nd ed. London, England: Oxford University Press; 1979. [Google Scholar]
- 22.Levings PP, McGarry SV, Currie TP, Nickerson DM, McClellan S, Ghivizzani SC, et al. Expression of an exogenous human Oct-4 promoter identifies tumor-initiating cells in osteosarcoma. Cancer Res. 2009;69:5648–55. 10.1158/0008-5472.CAN-08-3580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gross AC, Cam H, Phelps DA, Saraf AJ, Bid HK, Cam M, et al. IL-6 and CXCL8 mediate osteosarcoma-lung interactions critical to metastasis. JCI Insight. 2018;3. 10.1172/jci.insight.99791. [DOI] [PMC free article] [PubMed]
- 24.Alhaque S, Themis M, Rashidi H. Three-dimensional cell culture: from evolution to revolution. Philos Trans R Soc Lond B Biol Sci. 2018;373. 10.1098/rstb.2017.0216. [DOI] [PMC free article] [PubMed]
- 25.Jacks T, Weinberg RA. Taking the study of cancer cell survival to a new dimension. Cell. 2002;111:923–5. 10.1016/s0092-8674(02)01229-1. [DOI] [PubMed] [Google Scholar]
- 26.Lv D, Hu Z, Lu L, Lu H, Xu X. Three-dimensional cell culture: a powerful tool in tumor research and drug discovery (Review). Oncol Lett. 2017;14:6999–7010. 10.3892/ol.2017.7134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Eiraku M, Takata N, Ishibashi H, Kawada M, Sakakura E, Okuda S, et al. Self-organizing optic-cup morphogenesis in three-dimensional culture. Nature. 2011;472:51–6. 10.1038/nature09941. [DOI] [PubMed] [Google Scholar]
- 28.Oshima M, Ogawa M, Tsuji T. Regeneration of complex oral organs using 3D cell organization technology. Curr Opin Cell Biol. 2017;49:84–90. 10.1016/j.ceb.2017.12.011. [DOI] [PubMed] [Google Scholar]
- 29.Jackson EL, Lu H. Three-dimensional models for studying development and disease: moving on from organisms to organs-on-a-chip and organoids. Int Bio (Cam). 2016;8:672–83. 10.1039/c6ib00039h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Balasubramanian S, Yu K, Cardenas DV, Aubin-Tam M-E, Meyer AS. Emergent biological endurance depends on extracellular matrix composition of three-dimensionally printed Escherichia coli biofilms. ACS Synth Biol. 2021;10:2997–3008. 10.1021/acssynbio.1c00290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lovitt CJ, Shelper TB, Avery VM. Advanced cell culture techniques for cancer drug discovery. Biol. 2014;3:345–67. 10.3390/biology3020345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hughes JP, Rees S, Kalindjian SB, Philpott KL. Principles of early drug discovery. Br J Pharmacol. 2011;162:1239–49. 10.1111/j.1476-5381.2010.01127.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen A, Vu T, Stybayeva G, Pan T, Revzin A. Reconfigurable microfluidics combined with antibody microarrays for enhanced detection of T-cell secreted cytokines. Biomicrofluidics. 2013;7:024105. 10.1063/1.4795423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Han Q, Bradshaw EM, Nilsson B, Hafler DA, Christopher LJ. Multidimensional analysis of the frequencies and rates of cytokine secretion from single cells by quantitative microengraving. Lab Chip. 2010;10:1391–400. 10.1039/B926849A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Saint-Sardos A, Sart S, Lippera K, Brient-Litzler E, Michelin S, Amselem G, Baroud CN. High-Throughput measurements of intra-cellular and secreted cytokine from single spheroids using anchored microfluidic droplets. John Wiley & Sons, Ltd, pp 2020;2002303. 10.1002/smll.202002303. [DOI] [PubMed]
- 36.Holmes D, She JK, Roach PL, Morgan H. Bead-based immunoassays using a micro-chip flow cytometer. Lab Chip. 2007;7:1048–56. 10.1039/b707507n. [DOI] [PubMed] [Google Scholar]
- 37.Breen EJ, Polaskova V, Khan A. Bead-based multiplex immuno-assays for cytokines, chemokines, growth factors and other analytes: median fluorescence intensities versus their derived absolute concentration values for statistical analysis. Cytokine. 2015;71:188–98. 10.1016/j.cyto.2014.10.030. [DOI] [PubMed] [Google Scholar]
- 38.Taylor BN, Kuyatt CE. Guidelines for evaluating and expressing the uncertainty of NIST measurement results. [cited 10 Oct 2022]. Available: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote1297.pdf.
- 39.Deschout H, Hagman J, Fransson S, Jonasson J, Rudemo M, Lorén N, et al. Straightforward FRAP for quantitative diffusion measurements with a laser scanning microscope. Opt Express. 2010;18:22886–905. 10.1364/OE.18.022886. [DOI] [PubMed] [Google Scholar]
- 40.Mv Smoluchowski. Grundriß der Koagulationskinetik kolloider Lösungen. Kolloid-Zeitschrift. 1917;21:98–104. 10.1007/BF01427232. [Google Scholar]
- 41.Berg OG, von Hippel PH. Diffusion-controlled macromolecular interactions. Annu Rev Biophys Biophys Chem. 1985;14:131–58. 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 42.Langmuir I. The adsorption of gases on plane surfaces of glass, mica, and platinum. J Am Chem Soc. 1918;40:1361–403. 10.1021/ja02242a004.