基于细胞生长与成骨分化的不同孔径生物支架流体力学有限元分析

Abstract

目的

应用流体力学有限元分析方法，建立相同孔隙率、不同孔径的三周期极小曲面(triply periodic minimal surfaces，TPMS)螺旋形(Gyroid)多孔支架模型，模拟体内微环境，通过比较不同孔径支架的流体流速、壁面剪切应力、渗透率等相关参数变化，分析不同孔径的多孔支架对细胞黏附、增殖和成骨分化的可能影响。

方法

利用nTopology软件建立3组孔径的Gyroid多孔支架模型，支架尺寸为10 mm×10 mm×10 mm，孔径大小分别为400、600、800 μm，内部结构为各向同性。利用ANSYS 2022R1软件划分为非结构四面体网格，网格总数300⁺万。设定边界条件，流场域入口速度分别为0.01、0.1、1 mm/s，出口压力为0 Pa。根据Navier-Stokes方程计算流体流经支架时的压力、流速、壁面剪切应力，根据达西定律(Darcy’ s law)计算渗透率，使用ANSYS 2022R1软件中的Static structural模块对上述3种孔径支架的结构模型进行抗压强度分析。

结果

当入口流速分别为0.01、0.1、1 mm/s时，壁面剪切应力与流体流速呈线性关系，流速增加会导致壁面剪切应力增大。在0.1 mm/s流速下，当流体流经孔径为400、600、800 μm的3组支架时，压力呈梯度分布并逐渐减小，入口端压力依次为0.272、0.083、0.079 Pa；平均流速依次为0.093、0.078、0.070 mm/s；平均壁面剪切应力依次为2.955、1.343、1.706 mPa；渗透率依次为0.54×10^-8、1.80×10^-8、1.89×10^-8 m²。计算3组支架内部最适合细胞黏附、增殖与成骨分化的壁面剪切应力范围所在区域占比，其中600 μm孔径支架该剪切应力范围内的内表面面积占比最大(27.65%)，其次是800 μm孔径支架(17.30%)，400 μm孔径支架占比最小(1.95%)。400、600和800 μm孔径支架的抗压强度依次为23、26、34 MPa。

结论

3组孔径的Gyroid支架在压应力作用下，应力分布均匀；600和800 μm孔径的Gyroid支架渗透率明显高于400 μm组，600 μm孔径的支架平均壁面剪切应力最小，且内部适合细胞生长与成骨分化的壁面区域占比最大，可能更适合于细胞黏附、增殖与成骨分化。

在组织工程学中，生物支架为细胞生长分化提供支持和微环境^[1]。理想的生物支架材料需具备生物相容性和生物降解性，确保在体内不会引起免疫反应，并能够在组织修复完成后自然降解。此外，材料还需提供足够的机械支持，并拥有良好的表面特性以促进细胞附着和生长。常见的支架材料包括天然材料(如胶原蛋白、纤维素)和合成材料(如聚乳酸、羟基磷灰石)等^[2-3]。除了材料本身，支架的微观结构同样影响其性能。3D打印技术为精确完成复杂的生物支架微观结构提供可行性，其中立体光刻技术打印的精度最高，平均误差为(0.132±0.018) mm^[4]。复杂的内部孔结构可以提供多方向的机械支持，有效分散应力，以增强支架的机械性能；同时，不同的孔隙几何形态，如立方形(Cubic)、六边形(Hexagon)、钻石形(Diamond)等，表现出不同的流体力学特征，进而可能影响细胞的黏附和增殖。三周期极小曲面(triply periodic minimal surfaces，TPMS)是更为复杂的一种结构形态，具有平均曲率为零的特点，这与人骨平均曲率相近，又分为多种结构形态，其中螺旋形(Gyroid)结构是一种常用的结构形态。吴其右等^[5]研究比较了4种不同结构形态的生物支架(Cubic、Hexagon、Diamond和Gyroid)，发现Gyroid结构的支架能够提供更均匀的应力分布和优化的流体力学特征，更有利于细胞在支架上附着和生长。

支架的孔隙率、孔径等特征因素也对其细胞活性及力学环境具有重要影响。Luan等^[6]通过体外细胞实验研究不同孔隙率的生物支架对成骨分化的影响，将小鼠胚胎成骨细胞(MC3T3-E1)与不同孔隙率的支架共培养，检测发现孔隙率为65%和78%支架的成骨相关蛋白及转录因子的表达量显著高于孔隙率为55%的支架，表明较大孔隙率的支架更适合成骨细胞的分化。Ma等^[7]设计了5种孔隙率为75.1%~88.8%的Gyroid支架，将人骨肉瘤细胞放入支架共培养7 d，通过扫描显微镜观察细胞数量，结果显示孔隙率为88.8%的支架上细胞数量最高；但随着孔隙率增加，支架的力学性能下降。Wu等^[8]总结以往学者的研究，建议选择60%~80%孔隙率的支架，以此平衡生物性能和机械强度之间的关系。有学者认为^[9]较大孔径(大于300 μm)可以保证支架内细胞成骨分化顺利进行。Ouyang等^[10]将MC3T3-E1与不同孔径的支架共培养后植入新西兰白兔股骨中，通过显微CT观察骨组织形成状况，孔径为650 μm时最有利于骨组织形成；当多孔支架的孔径超过850 μm时，则成骨减少。另一项研究将骨形态发生蛋白-2与不同孔径的羟基磷灰石支架共培养后放入Wistar大鼠皮下，结果显示，300~400 μm孔径支架在碱性磷酸酶活性、骨钙素含量和新骨形成方面表现最佳^[11]。总结以往关于支架内部孔径对细胞增殖和成骨分化影响的研究，结果没有统一的定论，一方面可能是由于实验对象、条件和操作的差异，另一方面是由于很多研究中存在不同孔径的支架设计，其孔隙率也不尽相同，而孔隙率恰恰同样影响多孔支架对细胞成骨分化的促进作用。目前尚缺少在控制相同孔隙率的情况下，分析不同孔径对多孔支架促进细胞成骨分化的影响。

为了更好地模拟体内环境下细胞的生长和分化，研究人员开发了3D动态灌注系统，能够模拟体内细胞生长条件及其所经历的机械力(如张力、压力和剪切应力等)。王林等^[12]研究发现，3D动态灌注系统培养下，细胞均匀增殖在整个支架中，细胞活力也明显高于静态培养。然而，3D动态灌注系统也存在一些缺点，如系统复杂和操作难度较大。有限元分析和流体力学能够计算支架环境中的应力应变分布和模拟流体在生物支架中的流动情况，模拟其对细胞行为的影响，可用于优化设计支架，减少3D动态灌注系统细胞实验的次数和材料消耗；并通过计算机调整孔径等参数，平衡多孔支架的生物性能和力学性能。本研究应用流体力学有限元分析，模拟体内微环境，建立相同孔隙率、不同孔径Gyriod支架模型，比较不同孔径支架中的流体流速、壁面剪切应力、渗透率等相关参数变化，分析支架孔径对细胞增殖和成骨分化可能的影响。

1. 材料与方法

1.1. 3D支架模型的设计与建立

通过调整隐式三角函数的参数来构建Gyriod支架，其函数表达式见公式1^[13]:

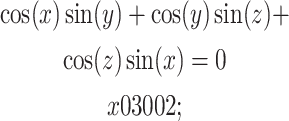1

利用nTopology软件，通过TPMS隐式法设计三组Gyriod单元结构支架，整体尺寸为10 mm×10 mm×10 mm，通过改变公式2的参数，控制支架孔隙率约70%，孔径分别为400、600、800 μm，支柱厚度分别为260、390、510 μm，分别命名为P400、P600和P800。支架内部为穿通孔，结构为各向同性。通过公式3计算支架的比表面面积：

2

式中Φ为孔隙率，孔隙率指多孔结构中孔隙空间所占百分比；V为支架总体积；V_solid为多孔结构的体积。

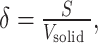3

式中δ为比表面积，比表面积指多孔结构的内表面面积与实体体积之比；S为内表面面积，指多孔结构中固体与孔隙的交界面；V_solid为多孔结构的体积。

通过上述公式得到支架主要参数(表 1)和支架结构示意图(图 1)。

表 1.

3组支架主要参数

Main parameters of three scaffold groups

Scaffold	Porosity/%	Pore size/μm	Strut size/μm	Volume of porous scaffold/mm3	Surface area/mm2	Specific surface area/(mm2/mm3)
P400	68.98	400	260	310.2	3590.94	11.58
P600	70.76	600	390	292.4	2366.90	8.09
P800	71.53	800	510	284.7	1755.36	6.17

图 1.

3组支架结构示意图

Schematic diagram of three scaffold groups

A, structural diagram of the three different pore sizes; B, blue arrows indicate the pore sizes, while the red arrows represent the struts.

1.2. 流体力学中的流场域、网格和边界条件的确定

流场域和网格：在Unigraphics NX软件中提取多孔支架外流场域，将支架结构出入口流场域增加至3倍支架长度，以保证出入口流场的稳定性。支架左侧为流场域入口，右侧为流场域出口，中间和侧面均为无滑移壁面(图 2)。网格采用ANSYS 2022R1软件划分为非结构四面体网格，多孔支架表面网格加密，网格总数300⁺万，以保证表面流动计算的准确性。设定3种流场域入口速度，分别为0.01、0.1、1 mm/s，出口采用静压边界(0 Pa)，忽略流体流动引起的支架变形，采用ANSYS 2022R1软件中的CFX模块对多孔支架结构流场域求解。流体性质：使用α-改良Eagle’ s培养基(alpha modification of Eagle’ s medium, MEM)，温度37 ℃，密度1 000 kg/m³，动力黏度1.45×10^-3 Pa·s，该流体被认定为牛顿流体，均匀且不可压缩^[10]。

图 2.

流场域和网格示意图

Schematic diagram of the flow field domain and the mesh

A, left side is the inlet of the flow field domain, and the right side is the outlet; B, surface of the porous scaffold was refined and meshed into unstructured tetrahedral elements.

1.3. 计算机流体力学模拟

将3组孔径的支架导入ANSYS软件中的CFX模块，利用Navier-Stokes方程(公式4)计算^[14]当流体经过不同孔径的多孔支架时的压力、流速、壁面剪切应力和分布，通过达西定律(Darcy’ s law)求解渗透率:

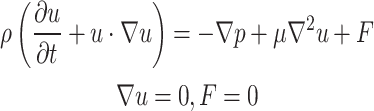4

式中ρ为流体的密度(kg/m³)；u为流体的速度矢量(m/s)；t为时间(s)；p为压力(Pa)；μ为流体的动力黏度(Pa·s)；F为外力矢量(N/m³)；▽p为压力梯度力，表示流体因压力差而受到的力；μ▽²u为黏性力项，表示由于流体内的摩擦引起的力。

1.3.1. 壁面剪切应力

壁面剪切应力是流体流过支架壁面时所施加的切向阻力(公式5)：

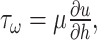5

式中τ_ω为壁面剪切应力，μ为流体的动力黏度(Pa·s)，u为流速(m/s)，h为x，y，z三个方向的高度^[15]。根据Porter等^[16]结论，壁面剪切应力在0.05~ 1 mPa范围内，适合细胞生长和分化。根据公式5计算支架中所有面的壁面剪切应力，通过ANSYS软件中CFX模块的表面分析功能，提取壁面剪切应力在0.05~1 mPa的内表面面积区域，并计算该剪切应力范围内的内表面面积占支架总内表面面积的比例。

1.3.2. 渗透率计算方法

渗透率(k)反映了流体通过多孔支架的难易程度，渗透率越高说明渗透性能越好。根据达西定律计算渗透率^[17](公式6)：

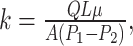6

式中Q为流过支架流体的体积流量(m³/s)，L为支架模型的长度(m)，μ为流体动力黏度(Pa·s)，A为多孔支架截面积(m²)，P₁为流体流经支架前压力(Pa)，P₂为流体流经支架后压力(Pa)。

1.4. 抗压强度分析

使用ANSYS软件中的Static structural模块对上述3组孔径支架结构模型进行抗压强度分析。支架材料主要为羟基磷灰石，是线性弹性材料，设定弹性模量为10 GPa，泊松比(Poisson’ s ratio)为0.3，密度为3 000 kg/m³。支架边界约束为多孔结构，底边固定，四周壁面为自由状态，由Static structural模块自动划分为四面体网格^[13](图 3)，逐渐增加压应力，直至支架结构发生破坏，记录此时的数值，为抗压强度。

图 3.

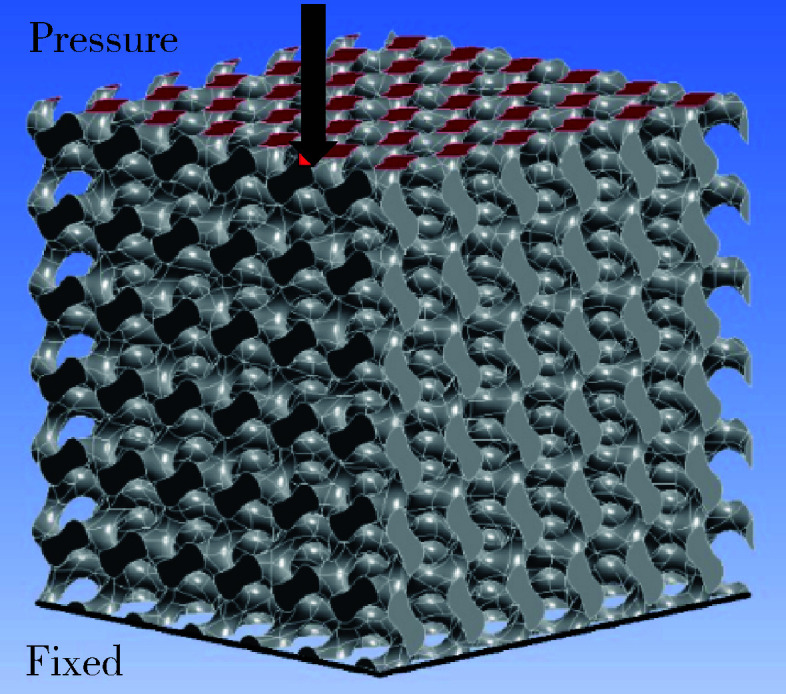
抗压强度分析时边界条件设置示意图

Schematic diagram of boundary condition settings for compressive strength analysis

2. 结果

2.1. 压力

在入口速度为0.1 mm/s的条件下，对3组孔径的支架进行压力分布分析，得到压力分布云图(图 4)，可以观察到孔径对流体流经支架表面时的压力和压力梯度变化有影响。总体趋势显示，随着孔径增大，支架内部的流体阻力逐渐减小，压力梯度变得平缓。压力在入口处最高，在出口处接近零。P400、P600、P800三组支架平均压力依次为0.134、0.041、0.039 Pa，最大压力为0.272、0.083、0.079 Pa。P400组的压力梯度变化最为明显，P600和P800组压力梯度变化小，压力分布相对均匀。在入口流速分别为0.01和1 mm/s时，压力梯度变化分别过小和过大，结果不具有参考意义。

图 4.

入口速度0.1 mm/s时3组支架的压力分布云图

Pressure distribution Cloud chart of the three scaffold groups at an inlet velocity of 0.1 mm/s

2.2. 流速

3组支架内部的流体平均流速和最大流速与流体的入口速度成相同的倍数关系。在相同的入口流速下，最大流速随孔径增大略增加，但3组支架差异不明显，而平均流速随孔径增大略减小，P400组平均流速变化最明显(表 2)。

表 2.

不同流速下流体流经3组支架时的平均流速和最大流速

Average and maximum velocities of fluid flow through three scaffold groups under different inlet velocity

Inlet velocity/(mm/s)	P400			P600			P800
	Average velocity/(mm/s)	Maximum velocity/(mm/s)		Average velocity/(mm/s)	Maximum velocity/(mm/s)		Average velocity/(mm/s)	Maximum velocity/(mm/s)
0.01	0.009	0.032		0.008	0.033		0.007	0.033
0.1	0.093	0.312		0.078	0.330		0.070	0.331
1	0.939	3.168		0.792	3.273		0.704	3.279

入口速度为0.1 mm/s时流速分布云图所示：流速分布较为均匀，没有出现流场中断，3组支架在流道中间部流速较高，而在边缘区域流速明显降低(图 5)。

图 5.

入口速度0.1 mm/s时3组支架的流速分布云图

Velocity distribution Cloud chart of three scaffold groups at an inlet velocity of 0.1 mm/s

2.3. 壁面剪切应力

通过计算得到不同流速下3组支架的壁面剪切应力和云图(表 3、图 6)，支架内部的平均壁面剪切应力和最大壁面剪切应力与流体的入口速度成正比，P600组的平均壁面剪切应力最小(表 3)。当入口速度为0.01 mm/s，3组支架的平均壁面剪切应力依次为0.295、0.134、0.170 mPa，可能有利于细胞初期黏附生长，但入口速度过低不利于营养物质的交换。当入口速度为1 mm/s时，3组支架的平均壁面剪切应力依次为29.935、13.715、17.326 mPa，过高的壁面剪切应力使得细胞难以黏附生长。在0.1 mm/s入口速度下，壁面剪切应力平均值接近Porter等^[16]发现利于细胞增殖和分化的范围，通过计算该范围内的内表面面积占支架总内表面面积的比例，结果显示P600组支架在该面积占比最大，为27.65%；其次是P800组支架，为17.30%；而P400组支架的占比最小，为1.95%。

表 3.

不同入口流速下3组支架的平均壁面剪切应力和最大壁面剪切应力

Average wall shear stress and maximum wall shear stress of three scaffold groups under different inlet velocity

Inlet velocity/(mm/s)	P400			P600			P800
	Average wall shear stress/mPa	Maximum wall shear stress/mPa		Average wall shear stress/mPa	Maximum wall shear stress/mPa		Average wall shear stress/mPa	Maximum wall shear stress/mPa
0.01	0.295	1.499		0.134	0.508		0.170	0.616
0.1	2.955	13.885		1.343	5.097		1.706	6.123
1	29.935	138.447		13.715	51.738		17.326	63.048

图 6.

3组支架的壁面剪切应力云图

Wall shear stress Cloud chart of three scaffold groups

2.4. 渗透率

3组支架渗透率计算结果显示，P800组的渗透率为1.89×10^-8 m²，P600组为1.80×10^-8 m²，两者渗透率相差不大，均明显高于P400组，P400组渗透率为0.54×10^-8 m²。

2.5. 力学性能分析

对3组支架施加压应力，结果显示P400、P600和P800 3组支架的抗压强度分别为23、26、34 MPa，抗压强度差距较小，应力分布较均匀(图 7)。

图 7.

3组支架的应力分布云图

Stress distribution Cloud chart of three scaffold groups

3. 讨论

在组织工程学中，生物支架对于细胞黏附、增殖和分化具有重要作用。孔径、孔隙率、支架内部支柱厚度是支架设计中的关键参数，不仅决定了支架的机械强度和渗透率，还直接影响流体在支架内部的流速和壁面剪切应力。王真^[18]对不同孔隙率的圆孔支架进行力学性能研究，结果显示55%、70%孔隙率的支架抗压强度分别为31、27 MPa，而85%孔隙率的支架抗压强度为15 MPa，仅为70%孔隙率支架抗压强度的一半。有研究表明人体松质骨孔隙率为50%~95%^[19]，抗压强度约1.5~45 MPa。本研究选用的支架模拟人体骨结构的孔隙率，设计不同孔径的支架孔隙率约为70%。当孔径变大时，支柱厚度相应增加，从而提高了大孔径支架的抗压强度，减少因孔径增大带来的力学性能减弱^[20]。本研究结果显示3组孔径的支架抗压强度差别不大，满足颅骨、颌骨等承载部位的要求。

生物支架的渗透率是影响细胞生长和组织再生的重要因素之一。渗透率影响营养物质和氧气扩散，以及代谢废物排出。低渗透率会限制这些物质的输送，导致细胞活力下降和组织再生能力减弱；反之，过高的渗透率则可能导致流体流动过快，增加剪切应力，不利于细胞的黏附和增殖^[21]。有研究表明, 人松质骨渗透率约为2.5×10^-11~7.43×10^-8 m²，样本取自跟骨、股骨和脊柱等^[22]。Chan等^[21]研究表明人体骨骼渗透率为0.5×10^-8~5×10^-8 m²，本研究结果显示孔径400 μm支架的渗透率是0.542× 10^-8 m²，而孔径为600 μm和800 μm的支架渗透率结果近似，分别为1.80×10^-8 m²和1.89×10^-8 m²，约是孔径400 μm支架的3倍，支架的渗透率随着孔径增大而升高，当孔径从400 μm增加到600 μm时，渗透率显著上升；而600 μm到800 μm时，渗透率的增长趋于缓和。Chan等^[21]通过对不同孔径和不同结构的生物支架进行流体力学模拟分析，认为无论是圆形还是六边形结构，当孔径从250 μm增至650 μm时，支架的渗透率均呈线性增长，这一研究虽然和本研究的结果近似，但本研究中渗透率为非线性变化，这种非线性变化可能与支架内部几何结构的复杂程度密切相关，不同形态的结构可能会对流体流动路径产生影响，从而导致与线性趋势的偏离。本研究制备支架的渗透率均在骨小梁渗透率范围内，其中孔径600 μm和800 μm的支架渗透率更高，更利于营养物质、废物的交换。

细胞的生长和增殖需要稳定的力学环境。剧烈波动的力学环境可能导致细胞内应力过度反应、细胞膜通透性频繁变化，干扰细胞的正常代谢和功能，从而影响其生长和分化。相反，稳定的力学环境有助于细胞的适应和正常生理状态的维持，促进生长。有研究表明，成骨类细胞的增殖和分化与压力大小密切相关，适度且均匀分布的压力有助于细胞的增殖和分化，而过高或过低的压力可能抑制这些过程^[23-24]。Chen等^[25]通过设置不同压力条件分析其对成骨细胞的影响，发现压力可以通过激活Wnt/β-catenin信号通路来促进成骨分化，在适度的压力下，成骨分化相关基因的表达最高；而在较高的压力变化下，这些基因的表达水平明显降低。

Porter等^[16]通过建立3D动态灌注系统对MC3T3-E1进行研究，采用晶格玻尔兹曼法(Boltzmann’ s method)分析细胞在生物支架中受到的壁面剪切应力，结果显示, 当壁面剪切应力为0.05 mPa时，细胞存活率和增殖率最高；随着壁面剪切应力增大至1 mPa时，Runt相关转录因子2、骨钙素和碱性磷酸酶等成骨标志基因表达上调。Yu等^[26]也证实了低壁面剪切应力(1.5~52.6 mPa)刺激人成骨细胞碱性磷酸酶基因表达；当超过412 mPa时，则抑制成骨细胞增殖和分化。过高的流速导致细胞所受的壁面剪切应力超过其黏附力，导致细胞从支架表面脱落或受到机械损伤^[27]，而过低的流速产生的壁面剪切应力无法提供足够的机械刺激，进而影响细胞增殖和分化。本研究对3种入口流速进行筛选，发现0.1 mm/s流速下产生的壁面剪切应力有利于细胞增殖和分化，且与骨髓组织液的流速大致相当，能够更真实地模拟体内微环境，表明在此流速下，孔径600 μm的支架内部平均壁面剪切应力最小，支架内适合细胞增殖和分化的壁面面积占比最大，推论这一孔径结构在促成骨细胞增殖和分化方面可能具有优势。

流体力学有限元分析可用于优化生物支架的形态结构设计，通过调整支架孔径、孔隙率、内部支柱厚度等参数，平衡生物性能和力学性能，为骨组织工程中生物支架的设计提供了新的思路。未来可以应用3D动态灌注系统实验技术，结合流体力学有限元分析的结果进行细胞实验以及进一步的动物实验，以验证其有效性，通过在不同流速、灌注模式、压力、pH值和温度等条件下进行测试，更真实地模拟细胞在体内不同部位的生理环境，为骨组织再生支架的设计提供理论基础。

Funding Statement

国家自然科学基金(52111530189)

Supported by the National Natural Science Foundation of China(52111530189)