Critical mobility in policy making for epidemic containment

Abstract

When considering airborne epidemic spreading in social systems, a natural connection arises between mobility and epidemic contacts. As individuals travel, possibilities to encounter new people either at the final destination or during the transportation process appear. Such contacts can lead to new contagion events. In fact, mobility has been a crucial target for early non-pharmaceutical containment measures against the recent COVID-19 pandemic, with a degree of intensity ranging from public transportation line closures to regional, city or even home confinements. Nonetheless, quantitative knowledge on the relationship between mobility-contagions and, consequently, on the efficiency of containment measures remains elusive. Here we introduce an agent-based model with a simple interaction between mobility and contacts. Despite its simplicity, our model shows the emergence of a critical mobility level, inducing major outbreaks when surpassed. We explore the interplay between mobility restrictions and the infection in recent intervention policies seen across many countries, and how interventions in the form of closures triggered by incidence rates can guide the epidemic into an oscillatory regime with recurrent waves. We consider how the different interventions impact societal well-being, the economy and the population. Finally, we propose a mitigation framework based on the critical nature of mobility in an epidemic, able to suppress incidence and oscillations at will, preventing extreme incidence peaks with potential to saturate health care resources.

Introduction

The importance of human mobility in shaping the spreading of infectious diseases is one of the pillars of Computational Epidemiology^1–5. Along the years, hundreds of works confirmed the paramount role of mobility^6–12—at all scales: from urban commuting^13–18 to intercontinental air travel^9,19,20— in driving disease diffusion. For this reason, containment policies based on non-pharmaceutical interventions often involve a strong reduction in human mobility and different levels of confinements with the aim of reducing contacts within and between populations^21–24.

A paradigmatic example of the application of these strategies has been the measures to fight against the COVID-19 pandemic. Forced by the lack of pharmaceutical solutions and the availability of vaccines, most countries around the world had to rely on social-distancing measures and mobility restrictions to slow-down community transmission of SARS-CoV-2 and limit the collapse of healthcare systems²⁵. Although countries adopted different types of interventions²⁶, they all aimed at reducing social mixing by limiting mobility, creating social clusters where cases can be detected and isolated. For almost all the strategies, policy-makers linked the strength and duration of interventions to the epidemiological situation^26,27—i.e. imposing thresholds on different parameters such as the effective reproduction number , the disease incidence per 100,000 individuals or the number of ICU patients. Those policies that, in most cases, implied home confinement^28,29, curfews³⁰ and mobility reductions of more than ^31–33 with respect to normal periods, eventually led to a consistent reduction of COVID-19 incidence and transmission rates^34–37, with data directly linking mobility reductions and decreased community transmission^38–41. However, lifting limitations led to a rapid resurgence of incidence cases and transmission^42–44 with many countries having experienced a or even a wave of the epidemic⁴⁵.

This oscillatory behavior, as we will demonstrate, can be attributed to delays and inaccuracies intrinsic to epidemiological measures. The effective reproduction number , for example, estimates the average number of secondary cases generated by an infected individual. However, its measurement is affected by biological, social and technological lags—e.g. the disease incubation period or delays in testing and processing. Thus, measured today accounts for infections occurred in the previous 2 or 3 weeks. Similar delays are inherent to other parameters as well. E.g. the number of ICU patients or deaths suffer from even larger delays since several weeks can pass from infection to hospitalization or death. Combined together these delays create a shift between the time of infection and the evaluation of the epidemiological situation, that is, measurements represent an epidemiological scenario up to 3 or 4 weeks in the past, making hard a real-time control of the transmission.

In a recent work, Nouvellet et al.⁴⁶ proposed a statistical framework to directly link human mobility in one area at time t with the effective reproduction number in that area. Their results, relative to COVID-19 infections in 52 countries, demonstrate an excellent agreement between the two measures, especially for the first wave of the epidemic, when individual immunity was extremely low and other preventive measures like face-masks and closure of indoor spaces were absent. These results, along with providing a methodology for estimating from mobility data, also have a more subtle implication: the existence of a critical mobility threshold below which allowing for a direct control of community transmission.

Here we develop a simple, yet meaningful, modeling framework able to grasp the connection between local mobility and individual contacts. In this way we are able, not only to confirm the existence of the critical mobility range needed to contain community-level spreading hypothesised empirically, but also to estimate its value for different immunity levels. Moreover, building on the link between mobility range and the effective reproduction number, we revisit intervention principles employed in the recent pandemic and propose an epidemic containment strategy where mobility range is used to assess the epidemiological situation and guide interventions, reducing the delay between epidemiological measurements and interventions. Although in practice an accurate estimation of the critical mobility level may not be available, we develop an heuristic procedure based on the knowledge gained from this model to approximate this range and gain its benefits with minimal information. Finally, reviewing the different strategies improves our understanding of the consequences of each intervention and can help make informed decisions to minimise healthcare system’s overload while controlling stress in both the economy and the population.

Methods

Minimal data layer

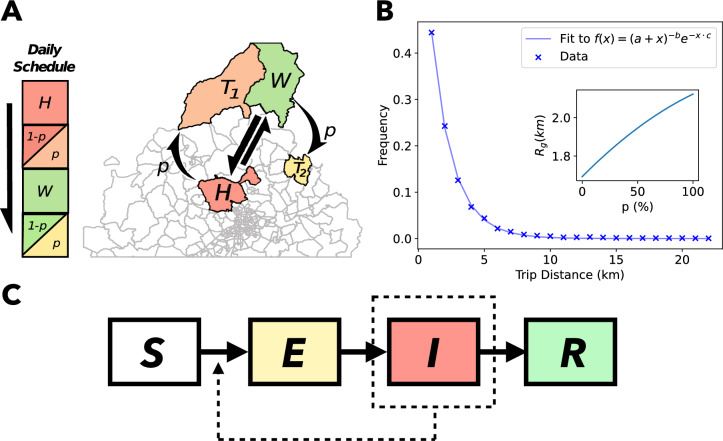
We use a substrate of data to make the model minimally realistic, but without losing generality. Any population and mobility data can be used or even a brand new set can be generated. In this work, we have employed the population distribution of the city of Madrid together with cell phone data provided by Kido Dynamics, dividing the province around the city in 1398 polygons. Mobility is measured through Call Detail Records from a major telecom operator in Spain, covering 13 million users over 42 weeks (January 10, 2020, to October 18, 2024). The dataset captures an average of approximately 100 data points per day, with a user’s residence defined as the most frequently visited census section from 10 PM to 6 AM each month. The sample is scaled to statistically represent the total Spanish population as reported by INE. These polygons correspond to the smallest possible tesselation of space that can guarantee the preservation of privacy when collecting data so at least 25 users where registered in each polygon. The data is comprised of scaled-to-census trips in the form R-O-D, i.e., origin O-destination D fluxes separated by residence place R of the individuals. The trip distance distribution obtained from the data (Fig. 1B), which will determine the behaviour of the main mobility metrics, is consistent with the literature^47–49.

Fig. 1.

Summary of our model. (A) Sketch of zones where agents can be seen during the day. H and W represent house and workplace respectively, with fixed mobility between them represented in straight arrows. and represent extra trips that may occur with a probability p, represented with curved arrows. (B) Trip distance statistics from the data used with the relationship between the mobility metric and the trip probability p as an inset. A fit to the trip distance data is shown with parameters , and , consistent with the power law behaviour in known literature⁴⁷. (C) Compartmental model. Transition rates and other parameters are listed in Table 1. The compartments consist of the following states: susceptible S, exposed E, infected I and recovered R.

Model

We developed a metapopulation agent based model which has agents moving and producing social contacts via visiting subdivisions of the Madrid region in Spain. Due to the parameter choice, every timestep corresponds to a day. Agents daily commute between a home (H) and workplace (W) sampled from the distributions obtained from the data. Moreover, along with the home-work commute, they can also perform an additional trip from both home and workplace independently with a probability p, as shown in Fig. 1A.

Implementation of mobility

We assume that the base level mobility, home-work (H-W), is always present (straight arrows in Fig. 1A). An agent’s home area H is sampled from the distribution P(H) given by census data, with the agent’s workplace W sampled once at the start of each simulation from the distributions of trips leaving area H by residents of H , obtained from the data. Additional contacts and mobility, called “Trips” (T), can be included from any of the two locations H and W with a trip probability p by sampling the trip distributions obtained from the data, and respectively, every time extra mobility is required. By tuning the parameter p, we can thus pass from a situation with a basal mobility to other situations with a maximum of 4 social trips per agent and day. For convenience, we can refer to these 2 periods of the day related to Home+Trip 1 and Workplace+Trip 2 as “morning” and “afternoon”. So a standard day is formed at least by a trip from home to work in the morning plus the return in the afternoon, with one potential extra trip in each time period.

Epidemic spreading

Spreading of the disease is simulated via a mass-action principle applied to the occupants of each subdivision of the region at different times of day. Figure 1C shows the compartmental model used to represent the different stages of infection, with rates and generation times listed in Table 1 similar to the recent COVID-19 pandemic, although any infectious process with non-zero incubation period will qualitatively display the same phenomenology. The compartments are comprised of an infectious state I and non-infectious state S for susceptible, E for exposed and R for recovered. Exposed individuals are developing the disease but are not yet contagious. The compartments correspond to an SEIR model, the simplest compartmental model to display a non-zero mode in the generation time distribution⁵⁰, relevant for the interplay between generation times, detection and mobility, plus being pertinent to most epidemic-prone diseases. The transition rates between compartments are inspired by the recent COVID-19 pandemic (see the parameter sources listed in Table 1), with no intention to replicate this disease with major accuracy, desiring only to obtain realistic timescales for the different infection stages.

Table 1.

Transition rates of the epidemic compartmental model. Values have been selected to be compatible with the timescales of COVID-19 infections⁵¹. t.s.=timesteps.

Transition	Rate

All simulations start with the introduction of a seed of 100 infected, i.e., an incidence at of 10 cases per 100,000 individuals. To make our simulations robust against stochastic fluctuations that may extinguish the epidemic in near-critical scenarios, we introduce 1 case per 100,000 individuals as a Poisson point process with rate , i.e., on average once every 100 timesteps. Simulations are prevented from being extinguished due to stochastic noise via the seeding introduced. In order to deem that an outbreak has naturally concluded and is not in fact being sustained by seeding, simulations are deemed to be finished when we do not observe at least the same amount of cases as seeds introduced in 1000 timesteps, i.e., the effective reproductive number .

We assume that individuals have an average of k contacts per location. If we call the infectiousness of the disease per contact c and the probability of infection upon visiting a location P, for every susceptible in a population of N individuals with I infected follows a mass action principle in the form:

1

where the infectivity is . As this is true per location, a higher mobility implies more locations per agent, thus an augmented number of contacts between individuals in our population. The baseline contact level, always present, is given by interactions in the Home and Workplace areas. The visit to other places, or , amplify the number and variety of potential contacts. To ensure no contacts are repeated when there is no extra social mobility associated to it, a pair of agents with no extra-trips will not interact twice at home or the workplace.

Characterizing population mobility levels

The agent-based nature of our simulations allows us to directly explore and employ methodology tried and tested for recent data driven studies of human mobility. To have a quantitative metric on the level of mobility within the population, we use the so-called radius of gyration ^47,52. For an individual i, we can define a radius of gyration, based on movements from the residence location as

2

where is the vector marking the centroid of an area j visited by agent i, is the vector pointing to the centroid of the area of residence (H) of the agent and the index j runs over the trips of the agent. Increasing p will increase the number of trips performed by an agent, thus inducing a larger radius of gyration. To characterise the whole mobility level in the population, which we will name , we calculate the mean of the distribution of all of all the agents so

3

The mean of the distribution, , provides a completely smooth, monotonous and unambiguous relationship with p as can be seen in the inset in Fig. 1B. It is important to stress that is an observable that can be measured both in the model and in the empirical data -e.g. out of mobile phone records-, while the control parameter p is an abstraction that refers only to our model. Thus, to measure results, we use to quantify mobility from now onward.

Results

Epidemic threshold connection to mobility

As a direct consequence of the relation introduced between contacts and mobility, our model shows an epidemic threshold that depends on both the immunisation and the population mobility level via its descriptive metric . Note that this has been a feature hypothesised out of empirical data in the literature^46,52. Figure 2 shows how much mobility is necessary to spark an epidemic with a seed of infected under different initial proportions of immune population. The dependent variable displayed in the figure is the final size, understood as the fraction of population infected at the end of our simulations. A mobility boundary depending on the immunity level in the population is observed, inducing 2 phases; one with exponentially growing outbreaks and one without significant epidemic activity (exponential decay of outbreaks). The critical mobility boundary between both phases can be estimated via the contour lines of Fig. 2. We have chosen the contour line corresponding to a 5% outbreak scenario as a proxy for the critical mobility boundary separating the stale phase from the outbreak phase.

Fig. 2.

Epidemic size, i.e., the fraction of individuals who suffered infection during simulation time, as a function of the population mobility and the initial immunity levels for infectivity . We include the critical mobility level and the 10% outbreak contour line.

Our model with other implementations of mobility (see Figs. S1–5 in Supplementary Material, SM) or a more realistic epidemic model for COVID-19 as the one of Ref.²⁹ (see Fig. S6D in SM) also produce two phases with a similar critical curve for the relation between mobility and affected population for an intermediate range of infectivity values, especially for those in which the final fraction of infected lays between , as in this range containment interventions on mobility can have an effect. On the extremes, if is very large, the critical boundary will shift upwards in Fig. 2, making nearly all infections happen at the minimum mobility, thus leaving a minimal chance for improvement with interventions (see SM, in Fig. S7). Conversely, with a very small infectivity, the critical boundary will shift downwards and thus herd immunity will be located at a very small fraction of immune, limiting the length and epidemic size of our simulations and leaving us, yet again, a small margin to evaluate the effectiveness of measures (see SM, in Fig. S7).

Interventions

Two possible types of non-pharmaceutical interventions are implemented in our model. All of them aim to control spiking incidences via a reduction of p and, consequently, of the contacts between the individuals. Simulations start at and try to drive the system to with the least epidemiological impact possible. In the first intervention procedure, inspired by the COVID traffic light system introduced in many European countries, the mobility reductions are triggered by exceeding the established incidence thresholds²⁶. The second type of intervention takes as the main reference variable, trying to keep mobility under control and follow the curve of in Fig. 2. This can be achieved by either estimating the value of via data and epidemiological forecasting or via tentative approximation of the curve due to its monotonously increasing nature with immunity. Various epidemiological and mobility indicators help us compare each of the interventions.

Besides non-pharmaceutical interventions, we can also consider two scenarios regarding population immunisation: i) a baseline scenario without vaccination in which only infected individuals can enter the R compartment, and ii) mimicking a vaccination campaign where susceptible individuals S pass directly to the removed compartment R at a constant rate each time-step. We show results for the no vaccination scenario as a progressive vaccination campaign yields no qualitative difference in the interplay between mobility and the epidemic and constitutes only a narrowing of the simulation window before herd immunity at is attained (Fig. S8 in SM).

Incidence threshold-based interventions

In this type of interventions, the main variable to monitor is the accumulated incidence per 100, 000 inhabitants during the last 14 days, . The ideal objective is to have the epidemic under control whilst driving the mobility as swiftly as possible towards , mimicking the lifting of control measures by the authorities. The value of p allowed is revised every timesteps and adjusted following table 2 in correspondence to the cumulative incidence. The selected values are arbitrary and another set can be selected to work with (Fig. S9). In an effort to make the simplest assumptions about this procedure, we choose equally-spaced intervals for the mobility parameter p and incidence intervals similar to those seen in the recent COVID-19 pandemic^53,54. Due to the segmented, start-stop, nature of the intervention, we will interchangeably refer to this intervention as “traffic lights”. We define a “strict traffic light” intervention as an incidence threshold-based intervention where mobility values are adjusted immediately whenever a revision is held.

Table 2.

Mobility states, i.e., values for the trip probability p, utilised to control mobility for each 14 day accumulated incidence rate in our incidence threshold-based interventions.

	p
[0,50)	1
[50,100)	0.6
[100,150)	0.3
[150,)	0

In a real case scenario, enforcing drastic and strict restrictions may be unfeasible in a practical sense and might very well also entail enormous impacts to societal well-being and economic stability. Thus exploring an inaccurate adoption of measures is relevant. In consequence, we introduce a less stringent intervention, characterised by higher revision times and by limiting the magnitude of closures and re-openings, even if it means reaching the intended mobility state late. In this intervention, the maximum allowed adjustment in the parameter p is described by . The aforementioned procedure defines a “lenient traffic light” intervention.

Figure 3 exemplifies how incidence based interventions induce oscillations in both the epidemic and mobility. More so, drifting away from a strict approach to this system not only significantly increases the period of oscillations but also their amplitude. This can be attributed to extended times of both above and below the critical mobility level , causing higher peaks and deeper valleys as shown in Fig. 3B,D. The strict approach, even when the traffic light values may be distant to the critical mobility curve, approximates the optimum value via fast-oscillations in mobility (Fig. 3E). We can thus measure this behaviour via an “effective mobility” defined as the moving average of the curve in a sufficiently large window; which in Fig. 3E stays close to the critical value. In contrast, Fig. 3G shows an effective mobility with a higher deviation from , remaining frequently above the 10% outbreak mobility limit (yellow curve Fig. 2). This implies that in a sufficiently small window as to not build epidemiological inertia, strict traffic light interventions manage to approximate the critical mobility level at the cost of frequent closures and re-openings, with the inherent social and economic stress induced. Metrics to better understand and quantify the results of these interventions are introduced and commented in subsection Performance differences below.

Fig. 3.

Examples of incidence threshold-based interventions for infectivity . (Left column) Incidence per 100,000 inhabitants and mobility curves throughout a realisation of strict traffic light interventions without vaccination. Mobility is adjusted every timesteps and adopts the values stated in Table 2 immediately. (Right column) Epidemic and mobility curves throughout a realisation of lenient traffic light interventions without vaccination. Mobility aims to adopt the values stated in Table 2 progressively, in changes of revised every timesteps. The grey dashed line in (A) and (B) represents an incidence rate of 10 daily cases per 100,000 individuals. (E) and (G) show the effective mobility level, calculated as an average of the mobility from the 180 timesteps prior to each date. (F) and (H) System trajectories in the immunity-mobility space of Fig. 2 for each intervention. All mobility curves are accompanied by the critical mobility levels at different contours shown in Fig. 2.

-based interventions

Imagining that it was possible to accurately estimate the mobility threshold for any state of our population, the way to control the epidemic with a minimal intervention would be to conduct the mobility to . Note that as the population gets immunised, either by infection or vaccination, can only grow, and, therefore, mobility policies would comprise of a gradual, smooth and strictly increasing change of over time, in contrast to the on-and-off dynamics of the traffic light interventions. This is, from the epidemiological impact perspective, an optimal type of intervention that we are going to illustrate with our model. Later, we will discuss alternatives for situations in which the curve of displayed in Fig. 2 is not available. We start the simulation by estimating given the initial immunisation conditions using the contours extracted from Fig. 2. After this, due to having a bijection between p and , a value of can be translated into a critical value of p, , in our model. As in the threshold-based case, we need to establish an intervention revision interval . After each , the mobility parameter p is increased to match the new estimation of .

Unfortunately, calculating out of empirical data is not a trivial task. An approximated estimation is suggested in recent works^46,52. For simplicity and to illustrate the power of the critical insight gained thus far, we will later show a heuristic method to remain close to without delicate modelling and information required. For now, we will use the contour lines of Fig. 2 to obtain an approximation of (and ) for our model given the epidemic parameters and a certain initial immunity level in the population. We chose the 5% contour line in order to lead the epidemic to herd immunity with the minimum incidence possible as vaccination isn’t included in this model. Thus, every timesteps, if the 14-day cumulative incidence is below 50 points, the mobility parameter p is updated to following:

4

An example of this procedure is shown in the left column of Fig. 4. The intervention manages to maintain a minimal incidence rate whilst monotonically increasing mobility, thus no stress of sudden behavioural changes or difficulties in applying strict changes in short periods apply. The only relevant incidence spikes are found at the start of the simulations where, due to outbreak contour lines being closer together at lower immunity levels in Fig. 2, any stochastic overshoot in mobility can lead to a higher incidence outcome.

Fig. 4.

Examples of -based interventions for infectivity . (Left column) Incidence per 100,000 inhabitants and mobility curves throughout a realisation of an -based intervention with theoretically estimated (outbreak contour 5%) without vaccination. Mobility is adjusted every timesteps following 4. (Right column) Epidemic and mobility curves throughout a realisation of staircase interventions without vaccination. The mobility parameter p is forced to be monotonically increasing through time in gradual steps of every timesteps. The grey dashed line in (A) and (B) represents an incidence rate of 10 daily cases per 100,000 individuals. (E) and (G) show the effective mobility level, calculated as an average of the mobility from the 180 timesteps prior to each date. (F) and (H) System trajectories in the immunity-mobility space of Fig. 2 for each intervention. All mobility curves are accompanied by the critical mobility levels at different contours shown in Fig. 2.

Due to the delayed relationship between epidemiological evolution and mobility/social contacts, the previously mentioned methods for estimating the critical mobility level can only produce results retroactively. This means that the critical mobility level estimated for the time period can only be determined via correlating the corresponding epidemic curves at a posterior time period with and . To estimate the current critical mobility level at any given time with these techniques, a precise epidemiological, demographic and mobility model most be developed to predict the epidemiological outcome of mobility levels at the moment and then use the aforementioned procedures. The complexity and precision these models entail, plus the vast amount of detailed data required to make these predictions accurate, can make this enterprise prohibitive for many governments and institutions. This challenge becomes particularly difficult when it comes to collecting precise and relevant data on social contacts and patterns.

Staircase approach to

Fortunately, the knowledge gained from analysing the existence and evolution of the critical mobility level can help us design a heuristic to approximate this threshold without needing prior modeling and field knowledge. As we saw in Fig. 3, epidemic thresholds with a sufficiently quick update speed can stabilize the system in a low incidence regime but a great back on forth in mobility is needed to approximate the critical level. To avoid this social stress due to fast oscillations in mobility policies and restrictions, we can attempt to move with the critical mobility level. As stated, the monotonous increase of the critical level allows us to correct any overshoot in mobility by maintaining the mobility level until immunity makes the critical level catch up to the mobility. This allows us to design an intervention based on a progressive, yet always increasing re-opening, yielding very small incidence rates with no modeling necessary. This is done by only observing the incidence curves and staying on the safe side of the critical mobility level, only releasing mobility by a small increase if incidence is decreasing and the epidemic is deemed controlled. Thus, for every revision of measures at timesteps:

The right column of Fig. 4 shows the epidemiological outcome and the behaviour of mobility resulting from the aforementioned procedure. Incidence shows only minimal peaks, predominantly below an incidence rate of 10 points, caused by any small overshoot of mobility above the critical mobility level, which we see is easily stabilised by holding mobility in place.

Performance differences

We are going to calculate the following epidemic and mobility metrics to each simulation in order quantify the performance of the different intervention protocols:

• The proportion of cases happening above 10 incidence points per 100,000 expressed as a percentage of the total population, designated as “surplus incidence”, to focus on possible health care system saturation and also omit large periods of lockdown where the epidemic is not active.

• Peak incidence, as another indicator of possible healthcare saturation²⁹.

• Standard deviation of the relative mobility, , as a measure of mobility fluctuations relative to the critical level.

• An accumulated measure of the effective mobility above the 10% outbreak mobility limit as a measure of when, even when oscillating, the intervention is staying a significant time in the outbreak phase of the immunity-mobility diagram.

The distribution of these metrics over 100 realisations of all previously described interventions are summarised in Fig. 5. With no vaccination, all simulations arrive stably at a epidemic size, as expected from Fig. 2, independently of the intervention typology. The first column of Fig. 5 shows different parameter combinations for traffic light interventions. As expected, higher revision intervals and less reactive mobility adjustments produce higher peaks and surplus incidence (Fig. 5A,B). Many reactive and frequent revisions () manage to achieve a less than a 5% surplus incidence rate. In contrast, the lenient example shown in the right column of Fig. 3 can produce surplus incidence rates of up to 30%. This is also manifested in the peak incidence metrics, where a strict approach causes peaks of up to 50 incidence points whilst the lenient approach can produce peaks of over 300 incidence points. Regarding metrics related to mobility, traffic light systems produce the largest standard deviation around the critical mobility level from all interventions tested (Fig. 5C,H,M), as their efficacy is inherently tied to fast oscillations that can approximate the effective mobility to the critical mobility level as seen in Fig. 3. This is supported by Fig. 5D where we can observe slower traffic light applications leading to more effective time above the 10% outbreak level. Due to having the worst epidemic performance, outbreak duration times (Fig. 5E,J,O) are lower than the rest of the interventions as more individuals get infected per timestep, leading to a faster arrival to herd immunity in the absence of vaccination.

Fig. 5.

Histograms and gaussian kernel density estimation (KDE) of the different metrics and interventions tested. Legends on the first row show the parameter combinations plotted. The number of simulations for each intervention is 100. First row: Surplus incidence as a percentage of the total population. Second row: Peak incidence as incidence per 100,000. Third row: Standard deviation of . Fourth row: Accumulated effective mobility (180 t.s. window) above the 10% outbreak level. Fifth row: Duration of the simulations. The center column of the figure shows modelled as different contours of Fig. 2.

Concerning focused interventions, both interventions show extremely low epidemic metrics (Fig. 5F,K,G,L) with all of the cases tested. Surplus incidence rates and peak incidences manage to stay comparable to the best performing case of traffic light interventions, even with approximate methods such as the staircase approach. Of course, by design, they show much better performing mobility metrics, with standard deviations and effective mobilities over the 10% outbreak level staying lower than their traffic light counterparts. Naturally, due to having extremely low incidence rates, epidemic duration times are almost guaranteed to be larger than for traffic light interventions, which is not an issue having in mind that in a real case scenario, vaccination is set to arrive at some moment, by which we expect to have caused the minimum amount of epidemic impact if possible.

Discussion

The increasing precision and availability of mobility data calls to try new ways in which to monitor and contain epidemics. From individual-based approaches such as app-based digital contact tracing to wider, policy-based approaches such as monitoring commuting flows and general mobility levels, recent studies have been proposing a possible critical mobility level due to the coupling between epidemic outbursts and mobility observed through various sources of data and their derived metrics. In this work, we have introduced a very simple connection between mobility and epidemic contacts, together with a compartmental model with timescales similar to the recent COVID-19 pandemic, and have observed this to be sufficient to not only witness the appearance of a critical mobility level, but also to capture the evolution and behaviour of this critical level throughout an epidemic. This model has allowed us to comprehend, evaluate, and compare different interventions based on their approach towards mobility and the epidemic information available, and has allowed us to verify the various effects on the oscillatory behaviour of an epidemic produced by the proposed couplings between mobility and the incidence.

Our agent based model with mobility reduced to a single parameter, the trip probability p, allows us perfectly relate epidemic contacts to the empirically measurable observable . The proposed model also incorporates mobility data from Call Detail Records, reproducing known social behaviours such as a distribution of trip distances that decays with an exponent close to the inverse square of the distance. With these simple assumptions and minimal data, our model is capable of reproducing a phase diagram with a critical mobility level, separating an outbreak phase from a stale phase. Together with epidemic observables such as the incidence per 100,000 inhabitants, we are able to monitor the state of the system and define interventions to safely conduct the population to herd immunity, aiming to minimise the oscillation of the system into the outbreak phase.

Having mainly separated interventions in 2 categories: threshold-based interventions and mobility-based interventions, we have been able to understand the principles and consequences behind the use of both kinds of interventions, plus how to better use these interventions to avoid harmful side effects such as saturation of healthcare resources and economic-social stress due to an unstable climate of restrictions and re-openings.

Traffic light interventions are inherently short-sighted and work by applying restrictions and re-openings just by observing the current epidemic state of the system. The fact that the system is forced into a handful of states, in our case 4 (see Table 2), depending on the epidemiological state means this system is blind to the key factor in this mobility-driven system; the value of the current critical mobility threshold. Restricting the states of the system means the system requires rapid oscillations between states so that the effective mobility, a key observable to understand the observed phenomena, is close to the critical threshold in a sufficiently small window of time. Additionally, looking only at the incidence to correct the status of your system is inherently a sub-optimal approach to interventions as the information provided inevitably carries a delay of weeks; the incidence observed at any time is a direct consequence of the events and contacts of a few weeks prior. These interventions become less accurate with worst case detection, a higher incubation period and a high infectivity of a possible asymptomatic case. Combining an overlooking of the critical mobility level of the system, the inherent delay and a possible lenient application of the measures will probably drive the system into a highly oscillatory regime of overshooting and undershooting, as seen in Fig. 3. Quickness and decisiveness when applying changes in mobility, plus the social stress they inevitably entail, are paramount if one desires to keep both the average incidence and peaks to a minimum when using a traffic light system, as shown via comparison in Fig. 5.

On the other hand, the proposed interventions based on mobility are fundamentally about utilising the knowledge and insight gained from observing and understanding the system in terms of its critical mobility level and outbreak phases. In the both examples mentioned, interventions with a modelled and the staircase heuristic, we either directly set the mobility level to as close to the critical value as possible (assuming it is known) as in the former intervention (left column of Fig. 4) or we try to approximate it by tentatively increasing and sustaining mobility in reaction to outbreaks in order to follow its ascent as we did for the latter approach (right column of Fig. 4). These methods seem extremely well behaved, displaying minimal oscillations and very low peak incidences (Figs. 4A and B). In essence, the staircase approach to would also be looking at the threshold, and thus could be subject to the same problems as the traffic light counterparts presented earlier. The real difference between the staircase approach and the traffic light system, even though they both look at the epidemic state to decide the next mobility level, is in incorporating the knowledge gained from observing , and most importantly, on the increasing nature of , plus allowing a relaxation of the spectrum of states the mobility can be in. By doing this tentative increase and sustaining of the mobility, the staircase manages to approximate the critical level well enough to not produce large overshoots and undershoots when changing state. This would allow administrations that do not count with precise data and modelling to benefit from the knowledge of the critical mobility threshold. Whichever the case, utilising the notion of a critical mobility level and an outbreak phase is of the utmost importance in order to minimise epidemic impact.

Other very important benefits of -based interventions are related to the effects interventions and restrictions have on economy and social tissue. Although these interventions do not maximise mobility above (Fig. 5I,N), they provide less unnecessary closures (mobility below ) and less stress from oscillations (Fig. 5H,M). The progressive and monotonous increase in mobility allows for a better adaptation and planning for businesses and individuals, plus it can eliminate the stress and uncertainty sudden and drastic closures may produce on the public. The most notorious downside of these interventions is their extremely slow rate of achieving herd immunity, achieving simulation times of double or even triple length compared to traffic light measures. If vaccination is not an option, societies are not able to withstand their economy with closures happening along a very prolonged amount of time. As we have seen with some countries in the recent COVID-19 pandemic, governments had to choose a trade-off between economic collapse and public health. This downside can be solved with other complementary interventions, as -based measures can buy time and keep the population safe whilst other developments such as vaccines can be developed and put into use, accelerating the journey towards herd immunity.

In practice, a sufficiently accurate model of would provide better results than the one presented in this work. This is due to our choice in modelling as, for simplicity purposes, we keep mobility always a fix amount above by using the 5% contour line. As we have seen, the 10% outbreak mobility level is closer to at the start of the epidemic and then leaves more room for error. Most negative effects of this intervention shown in this work are due to not correcting the distance between and as the epidemic evolves, leaving less distance at the start and increasing mobility respect to as times advances. In any real scenario, if an outbreak is detected by using this approach, mobility can be held or even lowered if necessary, options not included in our model for simplicity’s sake.

The limitations of our setting and model are evident. Our model assumes mobility as being the only factor in disease spreading and incorporates no information on variable transmissibility, variable behaviour on each stage of the compartmental model, seasonal mobility and changes in social contacts, demography, precise social contact modelling, realistic vaccination campaigns, improved detection and tracking of the incidence, and the problem of how to precisely estimate immunity in the population. Another crucial limitation for a real case application would be that, apart from absolute lockdown, any given mobility policy may have an undetermined reaction by the population. A population may ignore or overreact to a policy depending on their knowledge of the disease, opinion, beliefs and even the amount of time they have been under stress due to containment policies. The recent pandemic has seen some incidence spikes due to pandemic paranoia and lockdown/restriction-induced psychological ill-being in the population, where epidemic risk warnings were relatively or completely ignored due to burnout with the hopes of returning as soon as possible to a normal life regime. Thus a natural progression of this work would be to not only focus on mobility as the single factor to produce this critical phenomena, but also how to incorporate changes in disease transmissibility, include other strains and variants of the disease and changes in average number of contacts, as this would change the parameter without necessarily increasing the mobility level . In policy making practice, it is in fact very complicated to know exactly how policies impact mobility with precision. If jobs and activities can be ordered or classified depending on how essential they are to society or how many contacts they can potentially generate, this could be a way to decide which shops and services are allowed to re-open and allow the citizens to attend those places. Anyhow, any proposed policy can be monitored via the radius of gyration. A precise modelling of human behaviour related to complying with policy making and how that affects the observed mobility level and contact patterns would also be necessary to improve results. Note that, although the infectivity depends on other factors, these would only alter the critical boundary in the vs immunity diagram, but not the validity of our analysis and control framework. More so, even with our assumptions, mobility and immunity are not the only factors that can cause outbreaks as the current prevalence of the disease in the population plays a great role. Further works must add this third axis to the phase diagram as outbreaks stemming from a given mobility and immunity level will surely be affected by the disease prevalence in the population. Possible future works include incorporating better data on contacts and transmission, mobility, incidence and demography in an attempt to produce estimations for the critical mobility level and check via the known methods if a more refined model can accurately predict these critical thresholds. Precise information and observation of the critical mobility threshold would take us a step closer to shifting epidemiological interventions primarily into prevention territory and not mainly into mitigation efforts, as we have seen in the recent COVID-19 pandemic.

Thanks to the knowledge gained from studying the criticality associated to mobility in epidemics and the increasing amount of data available for administrations and research bodies, we hope our study can help to retroactively clarify the role of mobility in the observed phenomena during the recent COVID-19 pandemic together with designing better strategies for policy making in the case of future epidemic events; minimising the impact of the disease on the population whilst allowing for a better, smoother transition to normality for both the economy and society alike.

Author contributions

J.A.M.L., A.H., S.M. and J.J.R. designed research; J.A.M.L., S.M. and J.J.R. performed research; J.A.M.L., D.M. and A.H. analyzed data; J.A.M.L., S.M. and J.J.R. wrote the paper; All the authors revised and approved the manuscript.

Data Availability

The code and data used to perform simulations is available at https://gitlab.ifisc.uib-csic.es/jeslop/critical-interventions-open

Declarations

Competing interests

The authors declare no competing interests

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-86759-5.