Skip to main content
NCBI home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2002 Jun;13(6):2157–2169. doi: 10.1091/mbc.02-01-0608

A Polymer Model for Large-scale Chromatin Organization in Lower Eukaryotes

Joseph Ostashevsky 1,†
Editor: Hugh R B Pelham1
PMCID: PMC117632  PMID: 12058077

Abstract

A quantitative model of large-scale chromatin organization was applied to nuclei of fission yeast Schizosaccharomyces pombe (meiotic prophase and G2 phase), budding yeast Saccharomyces cerevisiae (young and senescent cells), Drosophila (embryonic cycles 10 and 14, and polytene tissues) and Caenorhabditis elegans (G1 phase). The model is based on the coil-like behavior of chromosomal fibers and the tight packing of discrete chromatin domains in a nucleus. Intrachromosomal domains are formed by chromatin anchoring to nuclear structures (e.g., the nuclear envelope). The observed sizes for confinement of chromatin diffusional motion are similar to the estimated sizes of corresponding domains. The model correctly predicts chromosome configurations (linear, Rabl, loop) and chromosome associations (homologous pairing, centromere and telomere clusters) on the basis of the geometrical constraints imposed by nuclear size and shape. Agreement between the model predictions and literature observations supports the notion that the average linear density of the 30-nm chromatin fiber is ∼4 nucleosomes per 10 nm contour length.

INTRODUCTION

Chromosome structure plays an essential role in regulating many biological processes, such as gene activity, DNA replication, and DNA damage repair. The rules that determine the interphase chromosome structure and the nuclear architecture are not well understood. Chromosome structure has several levels of organization: DNA; nucleosome; the 30-nm chromatin fiber; the chromatin fiber folding or a so-called higher-order chromatin structure above the 30-nm fiber; and at the scale of the whole chromosome: configurations (e.g., linear vs. loop) and interchromosome associations (e.g., homologous chromosome pairing; van Holde, 1989; Manueldis, 1990; Marshall et al., 1997a; Wolffe, 1998; Belmont et al., 1999; Marshall and Sedat, 1999; Cremer et al., 2000; Mahy et al., 2000; Cremer and Cremer, 2001; Hayes and Hansen, 2001; Wolffe and Hansen, 2001; Woodcock and Dimitrov, 2001). Nucleosomes and the chromatin fiber represent the universal units of chromosome structure in eukaryotes, whereas structural levels above the 30-nm fiber are present in many, but not in all, eukaryotic species. Homologous chromosome pairing occurs in meiosis in all eukaryotic species, while only a few species (e.g., Drosophila) show such pairing in interphase.

Some chromosome configurations are accompanied by anchoring of centromeres and/or telomeres to the nuclear structures (e.g., the nuclear envelope [NE], the nuclear lamina, nucleolus). These attachments are a focus of intensive research in recent years by biochemical, cytological, and genetic approaches, particularly because gene silencing is related to the location of such genes in proximity of telomeres or centromeres, which are often located near the nuclear periphery (Cockell and Gasser, 1999; Gasser, 2001). In the folded (so-called “Rabl”) chromosome configuration the centromere and telomeres serve as anchors, with the centromeres often forming a cluster at one side of the NE, while the telomeres are located at another side (see, e.g., Marshall et al., 1997a). The loop chromosome configuration is formed by telomeres clustering at the NE, as in the “bouquet” stage of meiosis (see, e.g., Yamamoto and Hiraoka, 2001).

The random-walk behavior of chromatin fibers, on the scale up to ∼1 Mb in euchromatin regions, was demonstrated in many studies (van den Engh et al., 1992; Sachs et al., 1995; Yokota et al., 1995, 1997). This is consistent with the diffusional, albeit confined, nature of chromatin motion in the interphase nucleus (Abney et al., 1997; Marshall et al., 1997b). In its turn, confinement of chromatin motion is consistent with a discreteness of chromatin domains ranging from whole chromosomes, to chromosome arms, to different chromosomal replication regions (reviewed in Cremer and Cremer, 2001).

Chromatin domains may fill all available nuclear space, as supported by the fluorescence microscopy in situ observations showing that neighboring domains are in contact, with negligible space between them (Visser and Aten, 1999; Cremer et al., 2000). On the other hand, large interchromatin voids were seen under electron microscopy (Cremer et al., 1993; Visser et al., 2000). The apparent contradiction can be reconciled by the fact that electron microscopy images reflect the static volume of the chromosomes (i.e., of the fibers themselves), whereas the fluorescence imaging reflects the dynamic volumes formed by the fluctuating fibers.

The aim of this work was to develop a quantitative biophysical model describing the rules for large-scale chromatin organization and its relationship to nuclear size and shape. The model is based on the random-walk behavior of the chromosomal fiber and the tight packing of chromatin domains in a nucleus. An important aspect of the model, which differentiates it from other polymer models of the chromosomal fiber (Sachs et al., 1995; Munkel and Langowski, 1998; Ostashevsky, 1998), is the treatment of chromatin anchoring as a means to organize chromosomes geometrically and to confine chromatin diffusional motion. The model is limited to cases of flexible chromosomal fibers, which do not have a higher-order structure and consist of either a single or multiple-parallel 30-nm chromatin fiber(s). Several constraints imposed by nuclear dimensions on chromatin organization are considered in the model. Because no adjustable parameters are used in the calculations, the results can be directly compared with the observed data. We applied the model to the nuclei of budding yeast Saccharomyces cerevisiae, fission yeast Schizosaccharomyces pombe, fruit fly Drosophila (embryonic and polytene cells), and the nematode Caenorhabditis elegans. For these species, the model correctly predicts chromosome configurations (linear, Rabl, loop) and chromosome associations (pairing, centromere and telomere clusters) from nuclear size and shape data.

THE MODEL'S BASIS

Chromatin Fiber Properties

As was mentioned in the Introduction, the model is limited to flexible chromosomal fibers. In this case, the mean square distance (h2, μm2) between two markers located on a single fiber is proportional to the DNA mass (M, Mb) between them. This dependence,

graphic file with name M1.gif 1a

with B (μm2/Mb) as the coefficient, which relates mass to squared-distance, has been observed for euchromatic regions of mammalian G1 chromosomes on the scale up to ∼1 Mb (van den Engh et al., 1992; Sachs et al., 1995; Yokota et al., 1995, 1997). In the experiments with human fibroblasts under conditions maintaining the physiological nuclear volume, B was found to be ∼0.5 μm2/Mb for gene-poor AT-rich Giemsa-dark minibands and ∼1.3 μm2/Mb for gene-rich CG-rich Giemsa-light minibands (Yokota et al., 1997).

Another equivalent expression for h2 is

graphic file with name M2.gif 1b

where L is the fiber contour length and a is the persistence length, a measure of the fiber's resistance to bending (see, e.g., Grosberg and Khokhlov, 1994). Equations 1a and 1b apply only to long fibers, i.e., those with a contour length, L ≫ a, their persistence length.

Chromatin fiber compactness can be characterized by n, the linear density of nucleosomes, the number of nucleosomes per 10 nm contour length. The contour length, L = 10 M/(ni), with i as the nucleosomal DNA mass. Substituting this expression into Eq. 1b and equating Eqs. 1a and 1b, one obtains a relationship between the parameters, B and n:

graphic file with name M3.gif 2

where i ranges between 160 and 240 base pairs (bp), depending on species (van Holde, 1989).

Measurements on single G1 chromatin fibers showed that a = 30 nm and n = 4 nucleosomes per 10 nm (Cui and Bustamante, 2000; Katritch et al., 2000). For a = 30 nm, n = 4, and i = 190 bp (as for human cells; van Holde, 1989), Eq. 2 yields B = 0.8 μm2/Mb, which is similar to the average of the Giemsa-dark and Giemsa-light values observed for B (see above). The persistence length corresponds to ∼12 nucleosomes (= 4 × 30/10) containing ∼2–3 kb DNA (=12i).

G2 chromosomal fibers consist of two side-by-side parallel cohesive sister chromatids. It is assumed that Eq. 1a is applicable to a G2 chromosomal fiber, with M representing the DNA mass (Mb) for one chromatid only. To the best of our knowledge, there are no direct measurements of the coefficient B and the persistence length (a) for G2 chromosomes in the literature. One estimate of the persistence length for G2 chromosomal fibers comes from consideration of two elastic isotropic cylindrical rods (approximation of sister chromatids) with either very low or very high degrees of side-by-side cohesion (see the Appendix). This consideration yields a between one and six times the value for a single chromatid.

Chromosome associations in paired homologous interphase chromosomes as, e.g., in Drosophila embryonic cycles, are likely to be loose because adjacent contacts between the associated chromosomes are relatively distant (Fung et al., 1998). In the model, the persistence length of the chromosomal fibers is assumed to not be affected by chromosome association per se.

A polytene chromosome, the thickness of which is a few μm, consists of up to a few thousand sister chromatids neatly aligned in parallel arrays (Urata et al., 1995). These chromosomal fibers appear to behave as flexible coils without a higher-order structure, as follows from their appearance in Drosophila nuclei (see, e.g., Figure 3 in Hochstrasser and Sedat, 1987a). We assume, as for G2 chromosomes, that Eq. 1a is applicable to a polytene chromosome, with M representing the DNA mass (Mb) for one chromatid only.

Mitotic and meiotic chromosomes become condensed and rigid and therefore do not obey Eq. 1a. An exception is the S. pombe meiotic chromosomes, which remain flexible in prophase (Bahler et al., 1993).

Chromosome Configurations

We consider several chromosome configurations (see Figure 1), differing in their pattern of chromatin attachments to the nuclear structures, which can include, for example, the nuclear envelope (NE), the nuclear lamina, and nucleolus. In the model, it does not matter to what the fiber is attached but only that it is attached to something. The following configurations are considered: (I) linear, unattached chromosomes; (II) linear, anchored by both telomeres; (III) the Rabl orientation: folded, anchored by the centromere and both telomeres; and (IV) loop formed by an adjacent anchoring of both telomeres. Additional attachments (other than by telomeres and centromeres) along the chromosomal fiber are possible in configurations II–IV.

Figure 1.

Figure 1

Open in a new tab

Schematic drawing of chromosome configurations in a nucleus. The configurations differ in their pattern of chromatin attachments to the nuclear structures: the nuclear envelope, nucleolus (crossed-hatched areas), etc. The chromosomal fiber can be anchored by telomeres (filled circles), centromeres (squares), and other sites (empty circles). The dashed lines represent discrete chromatin domains with length Hd and width Qd. The chromosome length and width are H and Q, respectively. (A) Configuration I: linear, unattached chromosomes; (B) configuration II: linear, anchored by both telomeres; (C) configuration III: the Rabl orientation: folded, anchored by the centromere and both telomeres; (D) configuration IV: loop formed by an adjacent anchoring of both telomeres. The nuclei are ellipsoid (A–C) and pear-shaped (D).

Domains are defined as discrete units of chromatin, nonoverlapping with other domains. For simplicity, we consider equal-size domains. Suppose, C (Mb) is the total euchromatin mass in a nucleus and N is the number of chromosomes in the case of configurations I and II, or the number of chromosome arms in the case of configurations III and IV (The loop in configuration IV can be represented as two equal paired branches). Thus, M (Mb) = C/N is the chromosome mass in the case of configurations I and II or the arm mass in the case of configurations III and IV. In the presence of additional attachments, chromatin domains are seen as arcs between two adjacent anchors. Suppose, k is the number of such domains per chromosome in the case of configurations I and II or per arm in the case of configurations III and IV. Thus, the domain mass, Md (Mb) = M/k, and the total number of domains per nucleus is kN.

Domain Dimensions and Nuclear Parameters

Because the chromosomal fiber behaves as a random coil, the domain squared length Hd2 and squared width Qd 2 can be expressed in terms of Md using expressions obtained for random coils in polymer theory:

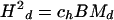graphic file with name M4.gif 3a
graphic file with name M5.gif 3b

where (see, e.g., Volkenstein, 1963) the coefficients ch = 2, cq = 1/2, and ch/cq = 4 for configuration I, which has both ends unattached; ch = 1, cq = 1/3, and ch/cq = 3 for configurations II and III, where both ends are anchored; for configuration IV, which has one end unattached, the values of the coefficients are between those for configuration I and II and III, i.e., 1 ≤ ch ≤ 2, 1/3 ≤ cq ≤ 1/2, and 3 ≤ ch/cq ≤ 4.

The domain shape can be approximated as that of an ellipsoid of rotation. Taking π/6 as the packing factor (as for cubed solid spheres), the volume of the space assigned for a domain in a nucleus, Vd = Hd Qd 2. Substituting Eqs. 3a and 3b in this expression, one obtains:

graphic file with name M6.gif 4

where α = √2 for configuration I, α = 3 for configurations II and III, and √2 ≤ α ≤ 3 for configuration IV.

A chromatin domain formed by a flexible fiber is more or less empty because the volume of the fiber it contains is much smaller than Vd, the domain volume. Looseness of random coils makes it possible for two or more chromosomes to share the same nuclear space, as occurs, for instance, with homologous chromosome pairing. Taking chromosome associations into account, the total space occupied by domains in the nucleus can be expressed as kNVd/p, where p is the association index (e.g., p = 1 for unassociated chromosomes; p = 2 for paired chromosomes).

The volume available for euchromatin in the nucleus is γVn, where Vn (μm3) is the nuclear volume, and the coefficient γ (γ ≤ 1) corrects for space occupied by heterochromatin and nonchromatin objects in the nucleus (e.g., nucleolus). To analyze the effects of the nuclear shape and size separately, Vn can be expressed through the nuclear shape coefficient, β, as follows: Vn = βD3, where D is the nuclear length. For spherical or ellipsoidal nuclei, β = (π/6)ε2, where ɛ is the nuclear width/length ratio. For cylinders, β = (π/4)ε2. For cones with a cone angle = 2ϕ, the coefficient β = (π/3) tan2ϕ. For pear-shaped nuclei, which can be represented as a cone with a hemi-spherical cap, β = (π/3) (1 + 2 tanϕ) tan2ϕ/(1+tanϕ)3.

The Volume Constraint

The model assumes that the chromatin domains occupy all available nuclear space:

graphic file with name M7.gif 5

Substituting Eq. 4 into Eq. 5 and making transformations, one obtains

graphic file with name M8.gif 6

where the symbols are as defined previously.

Equation 6 yields the average (over the nucleus) value of B. In the case of multiple-parallel-chromatid chromosomes, the values of the parameters C, N, and p are each proportional to the number of chromatids per chromosome. In Eq. 6, however, these values can be taken as those for a G1 nucleus because their interrelationship cancels this chromatid number dependence.

For the cases where the persistence length (a) of the chromosomal fiber is known, as in the case of G1 chromosomes, one can obtain n, the average (over the nucleus) number of nucleosomes per 10 nm contour length per fiber by combining Eqs. 6 and 2:

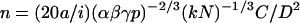graphic file with name M9.gif 7

For G1 chromatin fibers, a = 30 nm and n = 4 nucleosomes per 10 nm (Cui and Bustamante, 2000; Katritch et al., 2000).

Equations 6 and 7 enable one to calculate B and n from the nuclear size D and the nuclear shape coefficient β, assuming various chromosomal configurations (different α) and degrees of association (different p). Comparison of the values B and n measured with those calculated from Eqs. 6 and 7 provides a constraint on the possible chromosomal configurations and degrees of association. This can be called the volume constraint since it was derived from consideration of the nuclear volume.

The Linear Constraint

The linear constraint states that the chromosome length (H) should not exceed the nuclear length: H ≤ D. If the value of the coefficient B is known as, for example, in the case of G1 chromosomes, H can be estimated directly from Eq. 3a using the chromosome mass, M. However, Hmax, the length of the largest chromosome (configurations I and II) or of the largest arm (configurations III and IV) provides a greater constraint than does the average chromosome length:

graphic file with name M10.gif 8

where Mmax is the mass (Mb) of the largest chromosome or of the largest arm.

For the cases where the value of B is unknown, a relative approach can be used. Substituting B from Eq. 6 into Eq. 3a, one obtains Hd/D, the relative domain length:

graphic file with name M11.gif 9

The relative length of the largest chromosome, Hmax/D = (Hd/D) k1/2 (Mmax/M)1/2. Thus, the relative linear constraint is

graphic file with name M12.gif 10

It follows from Eqs. 9 and 10 that the relative dimensions depend only on nuclear shape (β) but are independent of nuclear size, and therefore, can be calculated without measurement of D.

The constraint imposed by Eqs. 8 and 10 provides a necessary but not sufficient condition because there could be cases where the limit for the chromosome length is smaller than the nuclear length. The chromosome linear limitation in such cases depends on nuclear geometry and hence should be considered separately for each case. The same is true for the cases where the nucleolus and/or heterochromatin occupy a significant fraction of the nucleus.

The Cross-section Constraint

The cross-section constraint requires that the sum of the chromatin domain cross-section areas should not exceed the corresponding nuclear cross-section area. An important application of this constraint is the limitation on the number of centromeres or telomeres, which can be clustered at a certain point in the nucleus. For example, chromosomes in the Rabl configuration may form a single centromere cluster in the nucleus only if m, the maximum possible number of branches is greater than Na/p, the number of discrete arm domains in the nucleus: m ≥ Na/p.

The maximum possible number of branches per cluster, m can be approximately estimated as follows:

graphic file with name M13.gif 11

where An is the nuclear cross-section area at the middomain level; Ad is the domain cross-section area: Ad = (π/4)Qd2= (π/4)(cq/ch)Hd2, where Qd2, Hd2, and cq/ch are, respectively, the domain squared width, squared length, and their ratio (see Eqs. 3a and 3b); δ is the two-dimensional packing factor (δ = π/4 for m ≥ 2, and δ = 1 for m = 1). The nuclear cross-section (An) strongly depends on the nuclear shape; this defines a dependence of m on the nuclear shape.

Let us consider several examples of telomere or centromere clusters, which include different nuclear shapes and chromosomal configurations II–IV. By definition, unattached chromosomes (configuration I) do not form telomere or centromere clusters.

1. A nucleus is spherical, and the telomere or centromere cluster is attached to the NE. For a spherical nucleus, the cross-section at the middomain level, An = (π/4)Hd2 [2(Hd/D)−1 − 1], where Hd/D is the domain relative length (see Eq. 9). Substituting this expression into Eq. 11, one obtains

graphic file with name M14.gif 12a

2. The cluster is located at the major axis apex of an ellipsoid of rotation with minor/major axis ratio, ɛ (see Figure 1c). For such a prolate ellipsoid, An = (π/4)ɛ2Hd2 [2(Hd/D)−1 − 1], and as follows from Eq. 11:

graphic file with name M15.gif 12b

3. The cluster is located at the minor axis apex of a flat (oblate) ellipsoid of rotation. In this case, An = (π/4) Hd2 [2(Hd/D)−1 − ɛ−1]. Thus, for an oblate ellipsoid,

graphic file with name M16.gif 12c

In Eqs. 12a–12c, m is independent of nuclear size (D), because the ratio Hd/D is independent of D (see Eq. 9).

4. The cluster is located at the nuclear apex of a pear-shaped nucleus with cone angle = 2ϕ. The corresponding nuclear cross-section is An = (π/4)(H tanϕ)2. Substituting this expression into Eq. 11, one obtains for a pear-shaped nucleus:

graphic file with name M17.gif 13a

5. The same as in case 4, but with rigid “linear elements” in chromosomes such as those observed in loop chromosomes of S. pombe in late meiotic prophase (Bahler et al., 1993; Kohli, 1994). In this case, the loop width decreases by a factor k1/2 (k is the number of arcs per half-loop), and therefore:

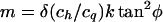graphic file with name M18.gif 13b

RESULTS AND DISCUSSIONS

In this section, we apply the model's equations to the nuclear data for yeast (budding S. cerevisiae and fission S. pombe), Drosophila (embryonic cycles 10 and 14, and polytene nuclei), and worm C. elegans. A given chromosome configuration should meet all three constraints in order to be feasible. The volume constraint calculated from Eq. 7 checks if a given configuration provides the linear density of nucleosomes, n = 4 per 10 nm (Cui and Bustamante, 2000; Katritch et al., 2000). The linear constraint states that the largest chromosome maximal dimension (length) calculated from Eqs. 8 and 10 cannot exceed the nuclear length. The cross-section constraint calculated from Eqs. 12–13 limits the number of branches per cluster. The three constraints (volume, relative linear, and cross-section) are independent of each other because the volume constraint condition (n = 4) was not used to derive Eqs. 10 and 12–13.

Fission Yeast S. pombe

Haploid genome: the DNA content, C = 13.8 Mb; the number of chromosomes, Nc = 3; the average chromosome = 4.6 Mb; the largest chromosome = 5.7 Mb; the largest chromosome arm = 3.8 Mb. The nucleosomal DNA mass, i = 165 bp (van Holde, 1989).

A. Karyogamy, Haploid, G1 Chromosomes.

Observations: Nuclear shape is approximated as pear-like (a cone with hemi-sphere at the top); the cone-angle, 2ϕ = 55o and the nuclear length, D = 2.3 μm (both taken from Figure 4 in Chikashige et al., 1994). Thus, the nuclear shape coefficient β = 0.17 (since for pear-shaped nucleus, β = (π/3)(1 + 2 tanϕ) tan2ϕ/(1+ tanϕ)3, see above). The chromosomes have been observed associated in one domain with their telomeres clustered and attached to the nuclear apex (loop configuration; Yamamoto et al., 1999; see Table 1).

Table 1.

S. pombe; karyogamy, haploid; G1 chromosomes

Nuclear data m, domains/cluster n, nucleosomes/10 nm Hmax (μm), loop length Chromosome I (Mmax = 2.9 Mb)
C = 13.8 Mb; Nc = 3 0.8–1.1 2.5–4.1 1.6–2.3
D = 2.3 μm
Cone-angle = 55°
Open in a new tab

The cross-section constraint for a telomere cluster: Let us estimate m, the maximal number of discrete loop domains. It follows from Eq. 13a that m = 0.8–1.1 for a cone with the angle 2ϕ = 55o. This means that only loops associated in a single domain (m = 1) can be accommodated in this cone-angle.

The volume constraint: Let us estimate n, the linear density of nucleosomes. Substituting β = 0.17 into Eq. 7 yields n = 2.5–4.1 for a single loop domain (the association index, p = 6), which meets the volume constraint (consistent with n = 4).

The linear constraint for the largest chromosome: Let us estimate the maximal dimension of the largest chromosome (Hmax) in the loop configuration. The coefficient B = 0.9 μm2/Mb for G1 yeast chromosomes (see Eq. 2 for i = 165 bp). It follows from Eq. 8 that Hmax = 1.6–2.3 μm for Mmax = 2.9 Mb (= 5.7 Mb/2). This estimate of Hmax ≤ D and therefore satisfies the linear constraint.

B. Meiotic Prophase, Wild-type, Early and Late Prophase.

Observations: The S. pombe chromosomes do not form the typical synaptonemal complex structure in meiotic prophase, but rather remain flexible with internal rigid “linear elements” (Bahler et al., 1993; Kohli, 1994; see Table 2). The flexibility of these meiotic chromosomes makes them suitable for consideration in the model's framework.

Table 2.

S. pombe; meiotic prophase; wild type (wt) versus dynein (dhc-1) mutant

Nuclear data: C = 27.6 Mb; Nc = 6 wt, early prophase pear-shaped nucleus Cone-angle 55°; k = 1 wt, late prophase “horse-tail” nucleus Cone-angle 30°; k = 3–4 dhc-1, early prophase Flat ellipsoid nucleus, ɛ = 0.5; k = 1
m, domains/cluster 0.8–1.1 0.8–1.1 7–8
Hmax/D, relative length 0.9–1.0 0.8–0.9 0.4–0.5
Open in a new tab

At the beginning of meiotic prophase, the nucleus is pear-shaped with a cone-angle = 55o (taken from Figure 4 in Chikashige et al., 1994), the same as in karyogamy. Later, the nucleus takes on a “horse-tail” shape with a cone-angle = 30o (taken from Figure 4 in Chikashige et al., 1994). This is accompanied by the appearance of 24 rigid “linear elements” (Bahler et al., 1993; Kohli, 1994) and the formation of a centromere cluster (Chikashige et al., 1994). Thus, a half-loop consists of k = 3–4 small arcs, where k = 4 (=24/12 + 1 + 1) for half-loops containing a centromere, and k = 3 (=24/12 + 1) for half-loops not containing a centromere.

For the cone angles = 55o and 30o, the nuclear shape coefficient β = 0.17 and 0.06, respectively (see above the expression for β).

The cross-section constraint for a telomere cluster: At the beginning of prophase, a pear-shaped nucleus with cone angle = 55o can accommodate all six loops only if they are associated into a single domain: m = 0.8–1.1 (see above). When the cone-angle decreases to 30o, no full-length flexible loop can be accommodated into such a nucleus in the absence of small arcs (k = 1): the corresponding m = 0.2–0.3 < 1 for 2ϕ = 30o (see Eq. 13a). However, the associated loops can be accommodated (m = 1) if there are small arcs: Eq. 13b yields m = 0.8–1.1 for 2ϕ = 30o and k = 3–4.

The relative linear constraint for the largest chromosome: Absolute linear constraint cannot be calculated for meiotic chromosomes because their coefficient B is unknown (has not been determined). However, the relative linear constraint can be calculated because it is independent of B. For the shape coefficient β = 0.17 (for 2ϕ = 55o), Eq. 10 yields the relative length of the largest loop chromosome, Hmax/D = 0.9–1.0 (≤1, meets the constraint). For β = 0.06 (for 2ϕ = 30o), the relative Hmax/D = 0.8–0.9 (<1).

C. The Dynein Heavy-Chain (dhc-1) Mutant, Diploid, Meiotic Prophase.

Observations (Yamamoto et al., 1999): The nucleus is an oblate-ellipsoid with a minor/major axis ratio, ɛ = 0.5, and the loop chromosomes are clustered at the minor axis apex (see Table 2). The homologous chromosomes of the mutant fail to associate properly.

The relative linear constraint for the largest chromosome: For unassociated loops (Na/p = 6), Eq. 10 yields the relative length of the largest loop, Hmax/D = 0.45–0.5. This is compatible with the loop cluster being located at the minor axis apex of the nucleus: Hmax/D ≤ ɛ.

The cross-section constraint for a telomere cluster: For Na/p = 6, Eq. 9 yields the relative length of average loop, Hd/D = 0.40–0.44. Substituting these values of Hd/D into Eq. 13c, one obtains the maximal possible number of domains per cluster, m = 7–8 > 6. Thus, an oblate-ellipsoid nucleus with ɛ = ∼0.5 provides enough space for six unassociated loop chromosomes. This is consistent with the mutant's homologous chromosomes failing to pair (Yamamoto et al., 1999; Yamamoto and Hiraoka, 2001).

D. Diploid, G2 Chromosomes.

Observations (Funabiki et al., 1993; Chikashige et al., 1997): The nucleus is a sphere with diameter ∼ 4.5 μm and the nucleolus occupying the other hemi-sphere: γ = 0.5 (see Table 3). The six chromosomes are in Rabl configuration with one cluster of centromeres on one side of the NE and 3–4 clusters of telomeres. Hence, the number of discrete chromosome arm domains per nucleus, Na/p = 3–4.

Table 3.

S. pombe, diploid, G2 cells

Nuclear data: Hmax/D, relative the largest arm m domains/cluster B (μm2/Mb) a (nm), the persistence length
Na/p = 3–4; 0.7–0.8 5–6 3.0–3.5 100–115
D = 4.5 μm
ɛ = 1; γ = 0.5
Open in a new tab

The relative linear constraint for the largest chromosome arm: Because the coefficient B has not been determined for G2 chromosomes, only the relative linear constraint can be calculated. It follows from Eq. 10 that the relative length of the largest chromosome arm, Hmax/D = 0.8 < 1 (meets the constraint).

The cross-section constraint for a centromere cluster: It follows from Eq. 12a that the maximal possible number of nonoverlapping arm domains per centromere cluster, m = 5–6 > Na/p = 3–4. This means that one centromere cluster per nucleus is possible, which is consistent with the observations (see above).

Estimates of the coefficient B and the persistence length a: Substituting D = 4.5 μm into Eq. 6, one obtains the coefficient B = 3.0–3.5 μm2/Mb, which corresponds to a = 100–115 nm (as follows from Eq. 2 for n = 4), i.e., 3–4 times that for a single fiber. It is shown in the Appendix that the maximal increase in a for two tightly cohesive flexible rods is sixfold.

Budding Yeast S. cerevisiae

The haploid nucleus has 16 chromosomes with a total chromatin/DNA content, C = 12.1 Mb; the average chromosome = 0.75 Mb (see Table 4). The largest chromosome (4) contains 1.5 Mb; the largest chromosome arm = 1.1 Mb. The nucleosomal DNA mass, i = 165 bp (van Holde, 1989).

Table 4.

S. cerevisiae; haploid and diploid (young and aged); G1 cells

Chromosomal configurations I (unattached) II (telomere-attached) III (centromere- and telomere-attached) IV (loop)
n nucleosomes/ 10nm
 Haploid young
  D ∼ 1.9 μm; γ ∼ 0.8 6.9a 4.2 3.3 2.1–3.4
  C = 12.1 Mb; Nc = 16
 Diploid young
  D = 2.3 μm; γ ∼ 0.8 7.4a 4.5 3.6 2.2–3.7
  C = 24.1 Mb; Nc = 32
 Old mother
  D ∼ 4.5 μm, γ ∼ 1/4; 4.2 2.5* 2.0* 1.3–2.1*
  C = 24.1 Mb; Nc = 32
Hmax (μm), length 1.7 1.2 1.0 0.8–1.2
Chromosome IV (Mc = 1.5 Mb; Ma = 1.1 Mb)
Open in a new tab
a

Inconsistent with n ∼ 4. 

A. Young, Haploid and Diploid Cells, G1 Phase.

Observations: The diameter of spherical nuclei, D is ∼1.9 μm in haploid (Heun et al., 2001b), and D is ∼2.3 μm in diploid (Laroche et al., 1998) cells. The nucleolus has a crescent shape, γ = 0.8 (Garcia and Pillus, 1999). Chromosome 3 has been shown to have the loop configuration (Dekker et al., 2002). Telomeres are attached to the NE (Gotta et al., 1996; Laroche et al., 1998; Tham et al., 2001), and there are 3–8 and 6–10 perinuclear telomere clusters in haploid and diploid nuclei, respectively (Gotta et al., 1996; Laroche et al., 1998; Heun et al., 2001c). The centromeres form a rosette-like cluster at the interior of the nucleus (Jin et al., 2000; Heun et al., 2001a). Homologous chromosomes are either unassociated or loosely associated, mainly in the centromere region (Marshall et al., 1997b; Burgess et al., 1999; Aragon-Alcaide and Strunnikov, 2000).

The volume constraint: For unassociated chromosomes (p = 1) in haploid cells, Eq. 7 yields the linear density of nucleosomes, n = 6.9 for configuration I, n = 4.2 for configuration II, n = 3.3 for configuration III, and n = 2.1–3.4 for configuration IV (for latter, p = 2). For diploid cells, Eq. 7 yields n = 7.4, 4.5, 3.6, and 2.2–3.7 for configurations I, II, III, and IV, respectively. Thus, according to the volume constraint (n = 4), configuration I is not feasible in these nuclei, but configurations II–V are equally probable. This agrees with attachment of telomeres to the NE (see above).

The linear constraint for the largest chromosome: Substituting B = 0.9 μm2/Mb (as follows from Eq. 2 for i = 165 bp) in Eq. 9, one obtains the length of the largest chromosome in G1 phase, Hmax = 1.7, 1.2, 1.0, and 0.8–1.2 μm in configurations I, II, III, and IV, respectively. These estimates of Hmax are consistent (≤) with the nuclear diameter of haploid (D = 1.9 μm) and diploid (D = 2.3 μm) cells.

The cross-section constraint for telomere clusters: Let us estimate m, the maximal number of telomeres in a peripheral cluster. For haploid cells, Eq. 9 yields the relative length of an average domain, Hd/D = 0.43, 0.34, and 0.43–0.47 for configurations II, III, and IV, respectively. Substituting these values of Hd/D into Eq. 12a, one obtains m = 9, 12, and 8–9 for configurations II, III, and IV, respectively. These values of m correspond to the minimal number ∼3–4 (=32/8–12) telomere clusters per haploid nucleus, which is consistent (≤) with the observed number (3–8) of telomere clusters in haploid cells. Agreement between the estimated and observed numbers of telomere clusters is also obtained for diploid cells: Eq. 12a yields m = 11, 16, and 10–12 for configurations II, III, and IV, respectively. These numbers correspond to the minimal number ∼4–6 (=64/10–16) telomere clusters per nucleus, comparable to 6–10 observed.

The cross-section constraint for a centromere cluster: Eq. 12a (which is applicable to clusters located near the NE, see above) yields m = 12 and 16 for configuration III for haploid and diploid nuclei, respectively (see above). This means that a single centromere cluster located at the NE is not feasible in these nuclei: m ≤ Na/p, the number of nonassociated chromosome arms, = 32 (haploid) and 64 (diploid). The conclusion about the lack of a peripheral centromere cluster in G1 cells is consistent with the observations of a rosette-like centromere cluster at the interior of the nucleus (Jin et al., 2000; Heun et al., 2001a).

B. Old Mother, Senescent Diploid Cells.

Observations: The nuclear diameter of old mother cells is approximately twice that for young cells: D = 4.5 μm and an enlarged and fragmented nucleolus covers the nuclear periphery: γ = 1/4 (Sinclair et al., 1998).

The volume constraint: Eq. 7 yields n = 4.2, 2.5, 2.0, and 1.3–2.1 for configurations I, II, III, and IV, respectively. Thus, only configuration I meets the volume constraint (n = 4) in senescent cells. That chromosomes become detached from the NE in senescent cells is consistent with the observation that the SIR complexes, which participate in tethering of telomeres to the NE in young cells, relocate from the nuclear periphery to the nucleolus in aged cells (Sinclair et al., 1998).

C. Comparison with Chromatin Motion Data.

Observations: In a diploid nucleus, the diffusion motion of a probe located near the centromere of chromosome 3 (Mc = 0.32 Mb; Ma = 0.2 Mb) was confined within a sphere of diameter 0.6 μm (Marshall et al., 1997b). In a G1 haploid nucleus, the amplitude of the diffusion of the probes located at chromosome 4 (Mc = 1.5 Mb; Ma = 1.1 Mb) and chromosome 14 (Mc = 0.8 Mb; Ma = 0.6 Mb) was ∼0.8–1.0 and 0.7 μm, respectively (estimated from data on Figures 1 and 2 of Heun et al., 2001b).

Calculations: By definition of a domain, the diffusion distance of a bound probe inside the domain should be similar to the domain dimensions. It follows from Eq. 3a for B = 0.9 μm2/Mb that the maximal domain dimensions in configurations II–IV, Hd = 0.4–0.5, 1–1.2, and 0.7–0.8 μm, respectively, for chromosomes 3, 4, and 14. These estimates are similar to the observed boundaries of diffusional motion for corresponding chromatin probes (see above). This supports the notion of discrete chromatin domains (See also the calculations for the chromatin motion in Drosophila embryonic nuclei below).

Fruit Fly Drosophila

A. Embryo, Cycles 10 and 14, G1 and G2 Chromosomes.

Observations: Total diploid DNA content = 330 Mb in 10 approximately equal chromosome arms; euchromatic regions contain 240 Mb (see Table 5). Compact heterochromatin does not seem to form in the rapidly dividing nuclei of cycle 10 (Hiraoka et al., 1993) but is present in cycle 14. Thus, C = 330 Mb, Mmax = 40 Mb, and γ = 1 for cycle 10; and C = 240 Mb, Mmax = 28 Mb, γ = 0.8 for cycle 14. The nucleosomal DNA mass, i = 200 bp (van Holde, 1989).

Table 5.

Drosophila embryo; diploid; cycles 10 and 14

Cycle
10 14
C = 330 Mb; Mmax = 40 Mb; γ = 1.0
C = 240 Mb; Mmax = 28 Mb; γ ∼ 0.8
G1 chromosomes G2 chromosomes D = 5.5 μm, ɛ = 1 D = 10.5 μm; ɛ = 1 D = 4.1–5.1 μm; ɛ ∼ 0.9 D = 12.5 μm; ɛ ∼ 0.5
p, the association index 1 2 1 2
G1 chromosomes
 n, nucleosomes/10 nm 4.5 2.9a 5.0–7.8a 3.2–4.9
 m, domains/cluster 20 15 17 13
 Hmax/D, relative length 0.9 1.2b 0.8 1.0
 Hmax (μm), length
  Chromosome X or 3R 5.5 4.6
G2 chromosomes
 Hmax/D, relative length 0.9 1.2b 0.5 0.7
 m, domains/cluster 20 15 8c 6
 B, μm2/Mb 2.5 3.9 1.6 2.6
Open in a new tab
a

Inconsistent with n ∼ 4; 

b

Hmax/D > 1; 

c

m < Na/p = 10 for unpaired chromosomes. 

The nuclei are spherical in cycle 10 with diameter increasing from 5.5 μm at the beginning to 10.5 μm at the interphase end (Foe and Alberts,1985). In the beginning of cycle 14, the nuclei are slightly ellipsoid with the ratio of minor/major axis, ɛ = 0.9 and the major axis, D = 4.1–5.1 μm (the range represents two independent measurements; Foe and Alberts, 1985; Fung et al., 1998). In the end of the cycle 14 interphase, the nuclei becomes highly ellipsoid with ɛ = 0.5 and D = 12.5 μm (Foe and Alberts, 1985; Fung et al., 1998; Wilkie et al., 1999).

In both cycles, chromosome arms have been observed in the Rabl configuration with the centromere cluster located at the major axis apex (Foe and Alberts, 1985; Dernburg et al., 1996; Marshall et al., 1996). Chromosomes have ∼15 attachments to the NE per arm (Marshall et al., 1996). Thus, the small chromatin domains in the nucleus are the arcs with Md = 1.5–2 Mb formed by the adjacent NE anchors. Homologous chromosomes are unpaired in cycle 10, but pairing is almost complete in cycle 14 (Foe and Alberts, 1985; Fung et al., 1998).

The volume constraint for G1 chromosomes: Substituting the number of small arcs per arm, k = 16, into Eq. 7, one obtains n = 4.5 for unpaired and n = 2.9 for paired chromosomes for the beginning of cycle 10. For the beginning of cycle 14, n = 5.0–7.8 for unpaired and n = 3.2–4.9 for paired, chromosomes. Thus, according to the volume constraint (n = 4), homologous chromosomes are paired in cycle 14, but not in cycle 10; this is consistent with what has been observed (see above).

The linear constraint for G1 chromosomes: For G1 chromosomes, the coefficient B = 0.75 μm2/Mb (see Eq. 2 for n = 4 and i = 200 bp). As follows from Eq. 8, the largest arm length, Hmax = 5.5 μm for cycle 10 (Mmax = 40 Mb), which is consistent with the observed D = 5.5 μm (Foe and Alberts, 1985). For the beginning of cycle 14 (Mmax = 28 Mb), Eq. 8 yields Hmax = 4.6 μm, which is consistent with D = 5.1 μm (Foe and Alberts, 1985) but not with D = 4.1 μm (Fung et al., 1998).

The relative linear constraint for the largest chromosome arm: The relative linear constraint depends on the shape of the nucleus and can be applied for both G1 and G2 chromosomes. For the spherical nuclei of cycle 10, the relative arm length, Hmax/D = 0.94 (<1) and 1.2 (>1) for unpaired and paired homologous chromosomes, respectively, as follows from Eq. 10. Thus, the paired chromosomes are unfavorable in cycle 10, in agreement with the observations (see above). For paired G1 and G2 chromosomes in ellipsoidal nuclei of cycle 14, the values of Hmax/D = 1.0 and 0.67, respectively, were obtained from Eq. 10 (ɛ = 0.9 and 0.5 for G1 and G2 nuclei, respectively).

The cross-section constraint for a centromere cluster: Substituting the relative domain length Hd/D obtained from Eq. 9 into Eq. 12b, one obtains the maximal possible number of nonoverlapping arms per cluster, m = 20 > Na/p = 10 for unpaired chromosomes in cycle 10, and m = 6–13 > Na/p = 5 for paired chromosomes in cycle 14. In contrast, m = 8 < Na/p = 10 for unpaired chromosomes in cycle 14. Thus, the centromeres can be clustered in a single center in cycle 14, as observed, only if homologous chromosomes are paired there.

Estimates of the coefficient B and the persistence length a for G2 chromosomes: Substituting the corresponding nuclear data into Eq. 6 yields B = 2.5 μm2/Mb for unpaired G2 chromosomes of cycle 10, and B = 2.6 μm2/Mb for paired G2 chromosomes of cycle 14. The values of B = 2.5–2.6 μm2/Mb correspond to a = 100–105 nm (as follows from Eq. 2). This estimate is close to a = 100–115 nm obtained above for the S. pombe G2 chromosomes.

B. Comparison with Chromatin Motion Data.

Observations: During embryonic cycle 13, the diffusion motion of a site on the X chromosome is confined within a sphere of diameter 1.8 μm (Marshall et al., 1997b).

Calculations: Let us estimate the maximal dimension of a chromatin domain with Md = 1.5–2 Mb (see above). The values of B = 0.75 μm2/Mb for G1 chromosomes and B = 2.5–2.6 μm2/Mb for G2 chromosomes (see above). It follows from Eq. 3a that Hd changes from 1.1–1.2 μm at the beginning of interphase, to Hd = 1.9–2.3 μm at the interphase end. These estimates bracket, and their average is similar to, the observed diameter of the diffusion confinement sphere = 1.8 μm.

As was discussed above for budding yeast, the similarity between the estimated maximal dimension of chromatin domains and the observed diameters of confinement spheres of chromatin motion supports the notion of discrete chromatin domains in the model. Moreover, differences in the diffusion amplitude observed for different chromosomes of yeast and Drosophila can be explained by size differences between corresponding domains.

C. Polytene Nuclei of Different Tissues.

Observations: Polytene chromosomes have sister chromatids neatly aligned in parallel arrays (see Urata et al., 1995). The DNA content = 120 Mb per haploid (five arms) set (see Table 6).

Table 6.

Drosophila polytene nuclei

Tissue Nuclear data Hmax/D, m B a (μm)
C = 120 Mb; Na/p = 5; Mmax = 28 Mb relative length domains per chromocenter μm2/Mb the persistence length
Salivary gland (SG) D = 35 μm; ɛ = 1; γ = 1 0.93 8 37 1.5
 k = 4.0; d = 3.2 μm
Prothorasic gland (PG) D = 23.5 μm; ɛ = 1; γ = 0.95 0.96 10 19 0.8
 k = 5.6; d = 1.8 μm
Midgut cells (MG) D = 44 μm; ɛ =0.5; γ = 1 0.57 3.5a 22 0.9
 k = 3.4; d = 2.0 μm
Open in a new tab
a

m < Na/p = 5. 

Chromosomes are in the Rabl configuration having one chromocenter in the salivary gland (SG) nucleus and the prothorasic gland (PG) nucleus and two chromocenters in the midgut (MG) nucleus (Hochstrasser and Sedat, 1987a, 1987b). In SG, chromosomes have a total of 15 attachments to the NE, which corresponds to the number of the small arc domains per arm, k = 4.0 (=15/5 + 1). There are 23 attachments (k = 5.6) in the PG nucleus, and 12 attachments (k = 3.4) in the MG nucleus (Hochstrasser and Sedat, 1987a, 1987b).

The number of chromatids per chromosomal fiber is different in these tissues providing a difference in chromosomal fiber thickness, d = 3.2, 1.8, and 2.0 μm for SG, PG, and MG chromosomes, respectively (Hochstrasser and Sedat, 1987a, 1987b).

The cross-section constraint for a centromere cluster: Eq. 12b yields that the maximal possible number of arms per chromocenter, m = 8–10 (≥5) for spherical SG and PG nuclei but m = 3.5 (<5) for ellipsoid MG nuclei with ɛ = 0.5. An ellipsoidal nucleus has a smaller cross-section area and therefore can accommodate a smaller number of the clustered chromosome arms than can a spherical nucleus. Embryonic nuclei in the end of cycle 14 have the same shape as do MG nuclei but their chromosomes form a single chromocenter (m = 6 > 5; see Table 5). This is because the arc domains in embryonic nuclei are smaller (relative to the nuclear size) than those in MG nuclei: there are 15 attachments per arm in the former (Marshall et al., 1996) versus 2.4 in the latter (Hochstrasser and Sedat, 1987a, 1987b).

Thus, the model predicts that SG and PG but not a MG nucleus can accommodate all five arms in a single centromere cluster. This agrees with the observations (see above).

The relative linear constraint for the largest chromosome arm: Eq. 10 yields the relative length of maximal chromosome arm, Hmax/D = 0.9, 1.0, and 0.6, respectively, for SG, PG, and MG, all ≤1. The values of Hmax/D for spherical nuclei of SG and PG are smaller than those obtained for paired homologous chromosomes in embryonic spherical nuclei (=1.2 > 1; see Table 5) because of a lower number of domains per arm for polytene chromosomes: k = 4.0–5.6 in SG and PG nuclei versus k = 16 in embryo nuclei (see above).

Estimates of the coefficient B and the persistence length a: Substituting the nuclear parameters into Eq. 6, one obtains values of B = 37, 19, and 22 μm2/Mb, respectively, for SG, PG, and MG chromosomes. Assuming that polytene chromosomes have the same linear density per chromatid as interphase chromosomes, i.e., n = 4, Eq. 2 yields the values of a = 1.5, 0.8, and 0.9 μm, for SG, PG, and MG, respectively. These values are close to the corresponding chromosomal fiber radii: 1.6, 0.9, and 1.0 μm for SG, PG, and MG chromosomes, respectively (see above). The estimated values of B and a for polytene chromosomes could be tested by direct measurements.

Nematode Worm C. elegans, G1 Cells

Observations: Diploid G1 DNA mass, C = 195 Mb; the largest chromosome, Mmax = 21 Mb; Nc = 12, chromosomes are holocentric; the average chromosome size = 16 Mb (see Table 7). Premeiotic G1 cells have spherical nuclei with diameter, D = 4.0 μm (taken from Figure 5 of MacQueen and Villeneuve, 2001). A large nucleolus (∼0.5D) occupies the nuclear interior; γ = 0.85.

Table 7.

C. elegans, diploid, G1 cells

Chromosome configurations I
II
C = 195 Mb; Nc = 12; D ≈4 μm; ɛ = 1; γ ≈0.85
Hmax (μm), length, 5.6b
4.0
Chromosome V (Mmax = 21 Mb)
p, the association index 1 2 1 2
                               
n, nucleosome/10 nm 22a 14a 13a 8.3a
 if k = 1
k, attachments per chromosome to provide n =4 nucl/10 nm N/A N/A 36 9
m, domains/cluster N/A N/A 30 14
Open in a new tab
a

Inconsistent with n ∼ 4; 

b

Hmax > D ∼ 4 μm. 

The linear constraint for the largest chromosome: For B = 0.75 μm2/Mb (as follows from Eq. 2 for n = 4 and i = 200 bp), Eq. 8 yields a length of the largest chromosome, Hmax = 5.6 μm (>D) for configuration I (unattached chromosomes), and Hmax = 4.0 μm (≤ D) for configuration II (telomere-attached chromosomes). (The centromere-attached Rabl configuration (III) is impossible for holocentric chromosomes.) Thus, configuration II, but not I, meets the linear constraint.

The volume constraint: Configuration I cannot meet the volume constraint, as follows from n = 14 and n = 22, calculated from Eq. 7 for paired and unpaired chromosomes, respectively. In contrast, configuration II can provide n = 4 if each chromosome has, on average, ∼35 attachments to the NE (k = 36, Md = 0.5 Mb) per unpaired chromosome, or ∼8 attachments (k = 9, Md = 1.8 Mb) per paired chromosome. These estimates of k and Md can be tested by measurement of chromatin contacts to the NE and nucleolus.

The cross-section constraint for a telomere cluster: Let us test whether all 12 chromosomes in configuration II can form a single telomere cluster. For the above values of k, Eq. 12a yields the maximal possible number of domains per cluster, m = 30 > Nc/p = 12 for unpaired, and m = 14 > Nc/p = 6 for paired, chromosomes. Thus, the telomere cluster is possible in these nuclei. This prediction can be tested directly.

CONCLUSION

A simple polymer model presented here deals quantitatively with large-scale chromosome organization for budding and fission yeast, Drosophila and C. elegans. Agreement between the results of the model calculations and the observations supports the notion that for these species, the chromosome-nucleus relationship can be understood in terms of different patterns of chromatin anchoring and chromosome associations. It also follows from this agreement that the average linear density of the 30-nm chromatin fiber is ∼4 nucleosomes per 10-nm contour length.

Chromatin attachments to nuclear structures (e.g., the nuclear envelope, nucleolus) play an important role in the geometric organization of chromosomes by changing the chromosome volume. That changes in chromosome configuration affect the chromosome volume follows from the coil-like behavior of chromosomal fibers, because only for coils do the fiber attachments to nuclear structures decrease the chromosome volume. If chromatin fibers were rigid rods (as opposed to coils), fiber anchoring would not affect the chromosome volume because the latter would have been equal to the volume of the fiber itself.

The observed sizes of confinement spheres for chromatin diffusional motion are similar to the model-based estimates of maximal dimensions of the corresponding domains. Size differences in the diffusion confinement spheres observed for different chromosomes are explained in the model by differences in size of corresponding domains.

The model shows how information about nuclear size and shape can be used to predict chromosome configurations and associations. The following examples are interesting.

1. For S. pombe chromosomes in meiosis, the model shows that only loops associated in a single domain can fit into the observed cone-angle of the pear-shaped nucleus at the beginning of prophase. No full-length flexible loops can be accommodated in the even more narrow ‘horse-tail’ nuclei at late prophase. However, as the model shows, it is possible to fit the flexible loops into the ‘horse-tail’ nucleus in the presence of rigid “linear elements.”

2. The model shows that the ellipsoidal nucleus of the S. pombe dynein heavy chain (dhc-1) mutant can accommodate all six loops as separate domains clustering at the minor axis apex. This is consistent with the mutant's failure to pair homologous chromosomes.

3. The calculations for S. cerevisiae show that chromosomes in telomere-attached, Rabl, and loop configurations are equally feasible in G1 nuclei. The estimated minimal number of telomere clusters attached to the NE is consistent with those observed. Chromosomes seem to become unattached in old mother cells. This prediction is consistent with the observation that the SIR complexes tethering telomeres to the NE in young cells, relocate from the nuclear periphery to the nucleolus in senescent cells.

4. For the Drosophila polytene midgut nucleus, the calculations show that due to the combination of ellipsoid-shaped nucleus and a lower number of chromatin attachments to the NE, not more than three (of five) chromosomal arms can cluster at the nuclear apex. In contrast, the salivary gland and prothorasic gland spherical nuclei can accommodate all five arms in one cluster. This is consistent with the latter two having a single chromocenter, whereas the former has two chromocenters.

It is beyond the scope of the model to consider whether a nucleus determines the chromosome size or chromosomes determine the nuclear size. The assembly of the nuclear lamina and nuclear envelope occurs on the chromosome surfaces in late mitosis (reviewed in Wolffe and Hansen, 2001); this agrees with the latter case.

The model can be tested in several ways. First, more accurate measurements of the nuclear parameters would permit one to test the results of the calculations more rigorously. Second, the model can be applied to many other eukaryotes with relatively low chromatin content. Third, the model's estimates of the coefficient B and the persistence length a made for multichromatid chromosomal fibers can be tested in experiments. Because polytene chromosomes are visible under the microscope, the persistence length can be measured from the chromosome bending in the same way as was done for mitotic chromosomes (Marshall et al., 2001). Cohesion between sister chromatids seems to result in a three- to fourfold increase in the persistence length for the G2 chromosomal fiber versus that for a single chromatid, as estimated for fission yeast and Drosophila.

ACKNOWLEDGMENTS

The author thanks C.S. Lange for helpful discussions and careful reading of the manuscript and A. Berens for drawing Figure 1.

Appendix

The persistence length for an isotropic elastic rod, a = E I/kBT, where E is Young's modulus (a measure of the rod's resistance to stretching), I is the moment of inertia of the rod's cross-section, kB is the Boltzman constant, and T is the absolute temperature (Landau and Lifschitz, 1970). For a cylindrical rod, the moment of inertia, I = πR4/4, where R is the cross-section radius.

Let us consider two isotropic flexible rods bound side by side, either continuously along their line of contact or only at rare sites. In the latter limiting case, the value of a of the system is the same as that of a single rod. In the former limiting case, the principal moment of inertia about the axis connecting the rod's centers in their cross-section, I1 = 2 (π/4) R4, whereas the principal moment about the perpendicular axis, I2 = 2(5π/4)R4. Because I = ½(I1 + I2), half of the sum of the principal moments, I = (6π/4)R4, i.e., six times the single fiber value.

Thus, because the persistence length a is proportional to I, the estimate of a for two cohesive rods has a range one- to sixfold that for a single rod.

Footnotes

Article published online ahead of print. Mol. Biol. Cell 10.1091/mbc.02–01–0608. Article and publication date are at www.molbiolcell.org/cgi/doi/10.1091/mbc.02–01–0608.

REFERENCES

  1. Abney JR, Cutler B, Fillbach ML, Axelrod D, Scalettar BA. Chromatin dynamics in interphase nuclei and its implications for nuclear structure. J Cell Biol. 1997;137:1459–1468. doi: 10.1083/jcb.137.7.1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aragon-Alcaide L, Strunnikov AV. Functional dissection of in vivo interchromosome associations in Saccharomyces cerevisiae. Nat Cell Biol. 2000;2:812–818. doi: 10.1038/35041055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Belmont AS, Dietzel S, Nye AC, Strukov YG, Tumbar T. Large-scale chromatin structure and function. Curr Opin Cell Biol. 1999;11:307–311. doi: 10.1016/S0955-0674(99)80041-6. [DOI] [PubMed] [Google Scholar]
  4. Burgess SM, Kleckner N, Weiner BM. Somatic pairing of homologs in budding yeast: existence and modulation. Genes Dev. 1999;13:1627–1641. doi: 10.1101/gad.13.12.1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chikashige Y, Ding D-Q, Funabiki H, et al. Telomere-led premeiotic chromosome movement in fission yeast. Science. 1994;364:270–273. doi: 10.1126/science.8146661. [DOI] [PubMed] [Google Scholar]
  6. Chikashige Y, Ding D-Q, Imai Y, Yamamoto M, Haraguchi T, Hiraoka Y. Meiotic nuclear reorganization: switching the position of centromeres and telomeres in fission yeast Schizosaccharomyces pombe. EMBO J. 1997;16:193–202. doi: 10.1093/emboj/16.1.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cockell M, Gasser SM. Nuclear compartments and gene regulation. Cur Opin Genet Dev. 1999;9:199–205. doi: 10.1016/S0959-437X(99)80030-6. [DOI] [PubMed] [Google Scholar]
  8. Cremer T, Cremer C. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet. 2001;2:292–301. doi: 10.1038/35066075. [DOI] [PubMed] [Google Scholar]
  9. Cremer T, Kreth G, Koester H, et al. Chromosome territories, interchromatin domain compartment and nuclear matrix: an integrated view of the functional nuclear architecture. Crit Rev Eukar Gene Expres. 2000;12:179–212. [PubMed] [Google Scholar]
  10. Cremer T, Kurz A, Zirbel R, et al. Role of chromosome territories in the functional compartmentalization of the cell nucleus. Cold Spring Harbor Symp Quant Biol. 1993;58:777–792. doi: 10.1101/sqb.1993.058.01.085. [DOI] [PubMed] [Google Scholar]
  11. Cui Y, Bustamante C. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc Natl Acad Sci USA. 2000;97:127–132. doi: 10.1073/pnas.97.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
  13. Dernburg AF, Broman KW, Fung JC, Marshall WF, Philips J, Agard DA, Sedat JW. Perturbation of nuclear architecture by long-distance chromosome interactions. Cell. 1996;85:749–759. doi: 10.1016/s0092-8674(00)81240-4. [DOI] [PubMed] [Google Scholar]
  14. Foe VE, Alberts BM. Reversible chromosome condensation induced in Drosophila embryos by anoxia: visualization of interphase nuclear organization. J Cell Biol. 1985;100:1623–1636. doi: 10.1083/jcb.100.5.1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Funabiki H, Hagan I, Uzawa S, Yanagida M. Cell cycle-dependent specific positioning and clustering of centromeres and telomeres in fission yeast. J Cell Biol. 1993;121:961–976. doi: 10.1083/jcb.121.5.961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fung JC, Marshall WF, Dernberg A, Agard DA, Sedat JW. Homologous chromosome pairing in Drosophila melanogaster proceeds through multiple independent initiations. J Cell Biol. 1998;141:5–20. doi: 10.1083/jcb.141.1.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Garcia SN, Pillus L. Net results of nucleolar dynamics. Cell. 1999;97:825–828. doi: 10.1016/s0092-8674(00)80794-1. [DOI] [PubMed] [Google Scholar]
  18. Gasser S. Positions of potential: nuclear organization and gene expression. Cell. 2001;104:639–642. doi: 10.1016/s0092-8674(01)00259-8. [DOI] [PubMed] [Google Scholar]
  19. Gotta M, Laroche T, Formenton A, Maillet L, Scherthan H, Gasser SM. The clustering of telomeres and colocalization with Rap1, Sir3, and Sir4 proteins in wild-type Saccharomyces cerevisiae. J Cell Biol. 1996;134:1349–1363. doi: 10.1083/jcb.134.6.1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Grosberg AY, Khokhlov AR. Statistical Physics of Macromolecules. AIP Series in Polymers and Complex Materials. New York: American Institute of Physics Press, Chapter; 1994. 1. [Google Scholar]
  21. Hayes JJ, Hansen JC. Nucleosomes and the chromatin fiber. Curr Opin Genet Dev. 2001;11:24–129. doi: 10.1016/s0959-437x(00)00168-4. [DOI] [PubMed] [Google Scholar]
  22. Heun P, Laroche T, Raghuraman MK, Gasser S. The positioning and dynamics of origin of replication in the budding yeast nucleus. J Cell Biol. 2001a;152:385–400. doi: 10.1083/jcb.152.2.385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Heun P, Laroche T, Shimada K, Furrer P, Gasser S. Chromosome dynamics in the yeast interphase nucleus. Science. 2001b;294:2181–2186. doi: 10.1126/science.1065366. [DOI] [PubMed] [Google Scholar]
  24. Heun P, Taddei A, Gasser S. From snapshots to moving pictures: new perspectives on nuclear organization. Trends Cell Biol. 2001c;11:519–525. doi: 10.1016/s0962-8924(01)02174-2. [DOI] [PubMed] [Google Scholar]
  25. Hiraoka Y, Dernburg AF, Parmelee SJ, Rykowski MC, Agard DA, Sedat JW. The onset of homologous chromosomal pairing during Drosophila melanogaster embryogenesis. J Cell Biol. 1993;120:591–600. doi: 10.1083/jcb.120.3.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hochstrasser M, Sedat JW. Three-dimensional organization of Drosophila melanogaster interphase nuclei. I. Tissue-specific aspects of polytene nuclear architecture. J Cell Biol. 1987a;104:1455–1470. doi: 10.1083/jcb.104.6.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hochstrasser M, Sedat JW. Three-dimensional organization of Drosophila melanogaster interphase nuclei. II. Chromosome spatial organization and gene regulation. J Cell Biol. 1987b;104:1471–1483. doi: 10.1083/jcb.104.6.1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Jin Q, Fuchs J, Loidl J. Centromere clustering is a major determinant of yeast interphase nuclear organization. J Cell Sci. 2000;113:1903–1912. doi: 10.1242/jcs.113.11.1903. [DOI] [PubMed] [Google Scholar]
  29. Katritch V, Bustamante C, Olson WK. Pulling chromatin fibers: computer simulations of direct physical micromanipulations. J Mol Biol, 2000;295:29–40. doi: 10.1006/jmbi.1999.3021. [DOI] [PubMed] [Google Scholar]
  30. Landau LD, Lifschitz EM. Theory of Elasticity. Oxford: Pergamon Press, Chapter; 1970. 2. [Google Scholar]
  31. MacQueen AJ, Villeneuve AM. Nuclear reorganization and homologous chromosome pairing during meiotic prophase require C. elegans chk-2. Genes Dev. 2001;15:1674–1687. doi: 10.1101/gad.902601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mahy NL, Bickmore WA, Tumbar T, Belmont AS. Linking large-scale chromatin structure with the nuclear structure. In: Elgin SCR, Workman JL, editors. Chromatin Structure and Gene Expression. New York: Oxford University Press; 2000. [Google Scholar]
  33. Manuelidis L. A view of interphase chromosomes. Science. 1990;250:1533–1540. doi: 10.1126/science.2274784. [DOI] [PubMed] [Google Scholar]
  34. Marshall WF, Dernburg AF, Harmon B, Agard DA, Sedat JW. Specific interactions of chromatin with the nuclear envelope: positional determination within the nucleus in Drosophila melanogaster. Mol Biol Cell. 1996;7:825–842. doi: 10.1091/mbc.7.5.825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Marshall WF, Fung JC, Sedat JW. Deconstructing the nucleus: global architecture from local interactions. Curr Opin Genet Dev. 1997a;7:259–263. doi: 10.1016/s0959-437x(97)80136-0. [DOI] [PubMed] [Google Scholar]
  36. Marshall WF, Straight A, Marko JF, Swerdlow J, Dernburg A, Belmont A, Murray AW, Agard DA, Sedat JW. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol. 1997b;7:930–939. doi: 10.1016/s0960-9822(06)00412-x. [DOI] [PubMed] [Google Scholar]
  37. Marshall WF, Sedat JW. Nuclear architecture. In: Ohlsson R, editor. Genomic Imprinting. Berlin: Springer; 1999. pp. 283–301. [DOI] [PubMed] [Google Scholar]
  38. Marshall WF, Marko JF, Agard DA, Sedat JW. Chromosome elasticity and mitotic polar ejection force measured in living Drosophila embryos by four-dimensional microscopy-based analysis. Curr Biol. 2001;11:569–578. doi: 10.1016/s0960-9822(01)00180-4. [DOI] [PubMed] [Google Scholar]
  39. Munkel C, Langowski J. Chromosome structure predicted by a polymer model. Phys Rev E. 1998;57:5888–5896. [Google Scholar]
  40. Ostashevsky JY. A polymer model for the structural organization of chromatin loops and minibands in interphase chromosomes. Mol Biol Cell. 1998;9:3031–3040. doi: 10.1091/mbc.9.11.3031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sachs RK, van den Engh G, Trask BJ, Yokota H, Hearst J. A random-walk/giant-loop model for interphase chromosomes. Proc Natl Acad Sci USA. 1995;92:2710–2714. doi: 10.1073/pnas.92.7.2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Sinclair DA, Mills K, Guarente L. Molecular mechanisms of yeast aging. Trends Biol Sci. 1998;23:131–134. doi: 10.1016/s0968-0004(98)01188-8. [DOI] [PubMed] [Google Scholar]
  43. Tham W-H, Wyithe JSB, Ferrigno PK, Silver PA, Zakian VA. Localization of yeast telomeres to the nuclear periphery is separable from transcriptional repression and telomere stability functions. Mol Cell. 2001;8:189–199. doi: 10.1016/s1097-2765(01)00287-8. [DOI] [PubMed] [Google Scholar]
  44. Urata Y, Parmelee SJ, Agard DA, Sedat JM. A three-dimensional structural dissection of Drosophila polytene chromosomes. J Cell Biol. 1995;131:270–295. doi: 10.1083/jcb.131.2.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. van den Engh G, Sachs R, Trask BJ. Estimating genomic distance from DNA sequence location in cell nuclei by a random walk model. Science. 1992;257:1410–1412. doi: 10.1126/science.1388286. [DOI] [PubMed] [Google Scholar]
  46. van Holde KE. Chromatin. New York: Springer-Verlag, Chapter; 1989. 7. [Google Scholar]
  47. Visser AE, Aten JA. Chromosomes as well as chromosomal subdomains constitute distinct units in interphase nuclei. J Cell Sci. 1999;112:3353–3360. doi: 10.1242/jcs.112.19.3353. [DOI] [PubMed] [Google Scholar]
  48. Visser AE, Jaunin F, Fakan S, Aten JA. High resolution analysis of interphase chromosome domains. J Cell Sci. 2000;113:2585–2593. doi: 10.1242/jcs.113.14.2585. [DOI] [PubMed] [Google Scholar]
  49. Volkenstein MV. Configurational Statistics of Polymeric Chains. New York: Interscience Publishers, Chapter; 1963. 4. [Google Scholar]
  50. Wilke GS, Shermoen AW, O'Farrell PH, Davis I. Transcribed genes are localized according to chromosomal position within polarized Drosophila embryonic nuclei. Curr Biol. 1999;9:1263–1266. doi: 10.1016/s0960-9822(99)80509-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wolffe AP. Chromatin: Structure and Function, 3d edition. London: Academic Press; 1998. [Google Scholar]
  52. Wolffe AP, Hansen JC. Nuclear visions: functional flexibility from structural instability. Cell. 2001;104:631–634. doi: 10.1016/s0092-8674(02)01453-8. [DOI] [PubMed] [Google Scholar]
  53. Woodcock CL, Dimitrov S. Higher-order structure of chromatin and chromosomes. Curr Opin Genet Dev. 2001;11:130–135. doi: 10.1016/s0959-437x(00)00169-6. [DOI] [PubMed] [Google Scholar]
  54. Yamamoto A, West RR, McIntosh JR, Hiraoka Y. A cytoplasmic dynein heavy chain is required for oscillatory nuclear movement of meiotic prophase and efficient meiotic recombination in fission yeast. J Cell Biol. 1999;145:1233–1249. doi: 10.1083/jcb.145.6.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Yamamoto A, Hiraoka Y. How do meiotic chromosomes meet their homologous partners?: lessons from fission yeast. BioEssays. 2001;23:526–533. doi: 10.1002/bies.1072. [DOI] [PubMed] [Google Scholar]
  56. Yokota H, van den Engh G, Hearst JE, Sachs RK, Trask BJ. Evidence for the organization of chromatin in megabase pair-size loops arranged along a random-walk path in the human G0/G1 interphase nucleus. J Cell Biol. 1995;130:1239–1249. doi: 10.1083/jcb.130.6.1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Yokota H, Singer MJ, van den Engh, Trask BJ. Regional differences in the compactness of chromatin in human G0/G1 interphase nuclei. Chromosome Res. 1997;5:157–166. doi: 10.1023/a:1018438729203. [DOI] [PubMed] [Google Scholar]

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES