Abstract
The bending rigidities of mitotic chromosomes isolated from cultured N. viridescens (newt) and Xenopus epithelial cells were measured by observing their spontaneous thermal bending fluctuations. When combined with simultaneous measurement of stretching elasticity, these measurements constrain models for higher order mitotic chromosome structure. We measured bending rigidities of B ∼10−22 N · m2 for newt and ∼10−23 N · m2 for Xenopus chromosomes extracted from cells. A similar bending rigidity was measured for newt chromosomes in vivo by observing bending fluctuations in metaphase-arrested cells. Following each bending rigidity measurement, a stretching (Young's) modulus of the same chromosome was measured in the range of 102 to 103 Pa for newt and Xenopus chromosomes. For each chromosome, these values of B and Y are consistent with those expected for a simple elastic rod, B ≈ YR4, where R is the chromosome cross-section radius. Our measurements rule out the possibility that chromosome stretching and bending elasticity are principally due to a stiff central core region and are instead indicative of an internal structure, which is essentially homogeneous in its connectivity across the chromosome cross-section.
INTRODUCTION
Cell division involves the compaction of interphase chromosomes into condensed, mitotic chromosomes. This process is critical for the successful separation of the two copies of the chromosomes into the two daughter cells (Koshland, 1994). An open question about chromosome condensation is how mitotic chromosomes are structured (Koshland and Strunnikov, 1996). There are a number of proposed folding schemes, based on a variety of experimental results. These include chromatin loops tethered to a protein-rich core (Paulson and Laemmli, 1977) and a hierarchical organization of fibers (Belmont et al., 1987). In this paper, we use a fundamental physical property of mitotic chromosomes—their elasticity—to infer features of their internal structure.
Recent biophysical studies of metaphase chromosomes have revealed that they have remarkable elastic properties. Eukaryote mitotic chromosomes display well-defined reversible stretching elasticity over a fivefold range of stretching. This elasticity is characterized by the force scale of about a nanonewton (nN), which is the force needed to elongate mitotic chromosomes by about a factor of two. This is roughly the force that the mitotic spindle can generate during cell division, and correspondingly, mitotic chromosomes are often stretched during the cell division process (Nicklas, 1983). The stretching elasticity of chromosomes is thought to be important for successful chromosome sorting during mitosis (Nicklas, 1997, Joglekar and Hunt, 2001).
Chromosomes are also bent during mitosis, and thus chromosome bending rigidity is relevant to the biomechanics of cell division. However, bending rigidity can also give information about chromosome structure. First, mapping of the variation of bending rigidity with position along a mitotic chromosome provides information about the degree of homogeneity of chromatin packing. Second, comparison of bending and stretching elasticity can provide information about the cross-sectional organization of mitotic chromosomes (Houchmandzadeh and Dimitrov, 1999). For example, a homogeneous elastic rod has a well known quantitative relation between its bending stiffness and stretching elasticity, distinct from that of a rod with a core with an inhomogeneous cross-section (e.g. a scaffold-and-loop model of a chromosome with a stiff central core region surrounded by a soft halo). Thus, quantitative study of chromosome stretching and bending elasticity provides information about chromosome structure.
In this paper, we first report measurements of the bending stiffnesses of single newt and Xenopus chromosomes removed from mitotic cells, using micromanipulation techniques. For each chromosome studied, a stretch modulus was also determined. An important result is that each chromosome studied behaves, within the accuracy of our experiments, as an elastic rod with apparently uniform bending stiffness along its length. Although we observe that the bending modulus varies from chromosome to chromosome over an appreciable (roughly threefold) range, we see no evidence along one chromosome for local regions that are more easily bent. In particular, we observe that the kinetochore region has no less bending stiffness than the nearby chromosome arms.
In addition to the study of two species, we also directly compare mechanical properties of extracted chromosomes to those of chromosomes in vivo. Our in vivo measurements are bending fluctuation/measurement experiments on newt chromosomes inside metaphase-arrested cells. While intrinsically less precise than the measurements on isolated newt chromosomes, the in vivo measurements are in good agreement with the measurements on extracted chromosomes, and both are in good accord with available data on chromosome elastic properties measured in other experiments (Nicklas, 1983, Poirier et al., 2000). The similar bending moduli obtained from measurements in vivo and on isolated chromosomes indicate that the extraction and change of buffer does not dramatically alter chromosome mechanical properties. Our results are the first that compare physical properties of mitotic chromosomes in cells to those of chromosomes extracted into intracellular buffer; they are also the first measurements of both bending and stretching elasticity done on the same chromosomes.
Comparing bending and stretching properties of newt and Xenopus chromosomes, we find the bending and stretching elasticity to be quantitatively related in the way that would be expected for rods of homogeneous cross-section. This relation between bending and stretching properties holds to within about a factor of two. Thus the large-scale stretching and bending of a given mitotic chromosome can be characterized by a single elastic modulus, as if its internal structure were essentially homogeneous across its cross-section. This constrains potential models for higher order mitotic chromosome structure, in particular ruling out the possibility that the structural and elastic properties of mitotic chromosomes are due to a thin central, stiff organizing core from which tethered loops of chromatin are hung.
MATERIALS AND METHODS
Cell Culture
TVI newt (N. viridescens) epithelial cells (Reese, 1976) and A6 Xenopus cells (ATCC) were grown in 75 ml cell culture flasks (Falcon, Franklin Lakes, NJ) in 10 ml of cell culture medium (Poirier et al., 2000). The culture medium was replaced every four days for TVI and every two days for A6. At 90% confluence, the cells were subcultured into new flasks with 0.15% trypsin in 60% HBSS (Cellgro, Herndon, VA). Experiments were done in custom made culture dishes, with a diameter of 20 mm and a depth of 2 mm. These dishes are made of two teflon rings stacked on a 40-mm diameter #1 cover slide and attached by paraffin. The cells were subcultured into 1.8 ml of culture medium and grown to about 70% confluence in the small dishes. Micromanipulation experiments were done in these dishes while the cells were between 70% and 100% confluent. Growing the cultures to a point where adjacent cells provided mechanical support to one another was important, as this allowed the appreciable forces necessary for chromosome removal to be applied to mitotic cells without dislodging them.
Experimental Setup
Chromosomes were imaged by an inverted light microscope (IX-70 Olympus, Melville, NJ) with a 60×, 1.4 NA objective using either phase contrast or differential interference contrast (DIC) imaging. The culture dish was positioned by a 3-axis focus control stage (Prior Scientific, Rockland, MA). Chromosome extraction and manipulation were done with two motorized XYZ micromanipulators (MP-285 Sutter, Novato, CA) mounted on opposite sides of the microscope. A 233-MHz Pentium PC with Labview (National Instruments, Austin, TX) was used to control the micromanipulators and image acquisition. The images were recorded by a CCD video camera (Panasonic, Secaucus, NJ) and were captured with an NI-IMAQ PCI-1408 card and NI-IMAQ (National Instruments, Austin, TX) software onto a PC.
Chromosome Isolation
Two micropipettes, each attached to a micromanipulator, were used to isolate a newt or Xenopus mitotic chromosome. Micropipettes with a bending stiffness of about 10 nN/μm and an inner diameter of 2 μm or 1 μm were used for newt or Xenopus chromosome isolation, respectively. They were fabricated from borosilicate glass pipettes (WPI, Sarasota, FL) as described in Poirier et al., (2000). One pipette is filled with 0.05% Triton-X (FisherBiotech, Pittsburgh, PA) in 60% PBS (Biowhittaker, Walkersville, MD), while a second pipette is filled with 60% PBS. After a cell between prometaphase and metaphase is located, the first pipette is positioned within a few microns of the edge of the mitotic cell. The Triton-PBS solution is then flowed out of the cell with 5000 Pa of pressure. After 30 to 60 seconds a 5- to 10-μm hole in the cell membrane appears, and the chromosomes flow out of the cell. Usually the chromosomes are attached to each other and to the cell, but in about 1 in 100 attempts a chromosome floats completely free. When this occurs, the second pipette is positioned within 1 μm of the end of the free chromosome and is aspirated into the pipette with about 50 Pa of pressure. The chromosome tip permanently adheres to the inner wall of the pipette after about 10 sec of contact, via nonspecific adhesion of chromatin to untreated glass. The cell is then moved away from the isolated chromosome, and the chromosome is positioned about 40 μm above the glass surface.
Xenopus Chromatid Isolation
The technique used to isolate a Xenopus chromatid is similar to the technique described above for chromosome isolation. The difference is that the triton-PBS solution is sprayed during early anaphase when the chromatids are being pulled to the spindle poles. The chromatids flow out in two groups, but are attached to each other by end attachments. We were unable to repeatedly extract isolated chromatids with a free end, which is required for measuring the bending modulus. Only one Xenopus chromatid was isolated by this technique. We were not able to isolate single newt chromatids.
Stretching Elasticity
The stretching (Young's) modulus of an elastic rod can be determined by measurement of the force needed to lengthen it. For small enough extensions, the force needed to stretch a rod will be a force constant (f0) times the fractional change in length (change in length divided by unstressed length). Dividing f0 by the cross-sectional area of the rod converts f0 to the stretching or Young's modulus Y, which is a measure of stretching elasticity that is independent of the rod cross-section. The units of Young's modulus are those of force per area, or pressure; we will use the MKS unit of Pascals (1 Pa = 1 N/m2).
For newt chromosomes, f0 ≈ 1 nanonewton (nN) (N. viridescens, Houchmandzadeh et al., 1997; Poirier et al., 2000). Based on the observed cross-section radius of 0.8 μ, this gives a Young's modulus of about 500 Pa, similar to the Y = 430 Pa reported for grasshopper chromosomes inside cells (Nicklas, 1983). Similar stretching elasticity was recently reported by Houchmandzadeh and Dimitrov (1999) for Xenopus chromatids assembled in vitro using mitotic egg extracts and sperm chromatin.
Bending Elasticity
The bending flexibility of an elastic rod is described by a stiffness B with dimensions of force times length-squared (equivalently energy times length). For a rod of length ℓ, B/ℓ2 gives approximately the force that must be applied at the rod ends to deform it into a U-shape. The utility of the bending stiffness B is that it provides a length-independent measure of rigidity. However, the bending modulus of a rod does depend on its cross section.
For a rod composed of an ideal, isotropic elastic medium, B = π/4 YR4, where R is the radius and Y is the Young's modulus. The bending modulus thus has a very strong dependence on the cross-sectional thickness; doubling R increases B by 16 times. We will occasionally mention the Young's modulus inferred from bending modulus, YB = 4B/πR4, to compare bending moduli of chromosomes in a way that removes the dependence of B on chromosome radius expected for simple elastic materials.
For example, bending modulus measurements for chromosomes assembled in Xenopus mitotic egg extracts, B = 1.2 × 10−26 N · m2 (Houchmandzedah and Dimitrov, 1999), lead to YB = 0.6 Pa, given the radius of 0.4 μm. Recent measurements of B = 6 × 10−25 N · m2 for metaphase chromosomes in colchicine arrested Drosophila embryo cells (Marshall et al., 2001) lead to a value of YB = 40 Pa.
Measurement of the Bending Rigidity for Chromosomes Extracted From Cells
The bending modulus was measured by observation of thermal fluctuations of chromosome shape, in a manner similar to that used by Houchmandzadeh and Dimitrov (1999). In our experiments, we acquired a 150-sec time series of 1500 frames at different points along the chromosome. The resulting images were analyzed to determine chromosome shape fluctuations. The result is the average of the square of the deflection 〈u2〉, at a series of points along the chromosome. We can resolve fluctuations as small as 10 nm, much less than the light diffraction limit of our optics (60× Olympus objective, 1.4 N.A.). This is possible because we are measuring the motion of a single isolated object against a smooth optical background. The center of the resulting smooth density distribution that we observe can be located to a much higher accuracy than its width, given low-noise image data.
It is important to note that the correlation time of these fluctuations is 1 second at most, so each time series contains many time constants. For the extracted chromosomes the time series are typically 100 times longer than this correlation time. This is sufficient to reduce the statistical errors in determination of the fluctuation amplitudes to a level below that introduced by mechanical drifts.
The accuracy of the thermal fluctuation technique is limited in our case by mechanical noise coupled to the pipette by motion of the air-water interface. To eliminate slow drifts caused by evaporation-driven motion of the air-water interface, it was necessary to precisely level the culture dish. Experiments can be carried out for roughly 2 hr before evaporation makes it necessary to add water to the culture dish.
Thermal Fluctuation Experiment Analysis
The bending modulus can be determined from the root-mean-square amplitude of thermal bending fluctuations, and the absolute temperature of the surrounding medium. This approach has been used, for example, by Gittes et al. (1993) to measure bending stiffnesses of microtubules and actin filaments. In brief, we measure the amount of fluctuation of a chromosome along its length. The chromosomes are held at one end in a micropipette, and near to this point, the fluctuation is small. The fluctuation becomes larger at positions progressively closer to the free end. Thus we acquire data for mean-squared positional fluctuation 〈u2〉, as a function of distance x from the pipette that holds the chromosome. In the Appendix, we show how for our experimental situation thermal excitation of the bending modes of a stiff filament (Landau and Lifshitz, 1986) gives rise to the following relationship between fluctuations and position:
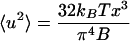 |
1 |
where kBT = 4.1 × 10−21 J is the thermal energy unit at room temperature. The plot of 〈u2〉 vs. x on a log-log scale should be linear with a slope of 3, with y-intercept related to bending modulus. Thermal fluctuations of the chromosome are insensitive to the presence of the pipette apart from its role in immobilizing the chromosome end.
Measurement of the Bending Modulus for Chromosomes in Colchicine Arrested Cells
Newt cells were grown to confluency and then incubated in culture medium with 0.1 mg/ml colchicine for 60 min. The mitotic cells become arrested in prometaphase/metaphase and chromosome movement stops. The cell culture is then scanned for cells, which have a 4- to 5-μm segment of a metaphase chromosome projected in the plane of the microscope. A 100-sec time series was acquired at a frame rate of 10 frames per second. Changes in cell shape, which occur on the minute time scale, cause a change in chromosome shape. To reduce the effect of the fluctuations of the cell shape, about 20 sec of the 100-sec time series were used for data analysis. Three points along the chromosome were tracked that parameterized the chromosome segment into 2 lines. A change in angle, Δθ, between the lines was computed vs. time.
As in the experiments on extracted chromosomes, the time correlation for the in vivo fluctuations are less than 1 sec. Therefore the typically 20-sec time series are long enough to accurately sample the fluctuation distribution, which is what we need to determine its width (see Fig. 4B for a typical in-vivo fluctuation distribution). Even for these shorter time series, statistical sampling error does not limit the accuracy of our measurements.
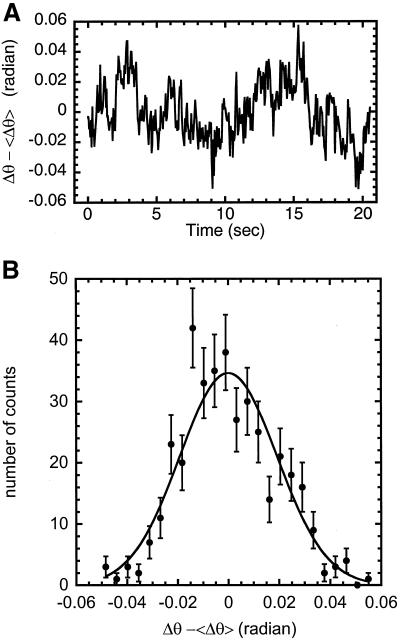
Figure 4.
(A) Change in angle (radians) vs. time for 5 μm chromosome segment in a colchicine arrested cell. (B) Histogram of the number of time points for binned values of Δθ (radians), which ranged from −0.1 to 0.1. A normalized Gaussian distribution (equation 2) is used for the 1 parameter fit, where 〈Δθ2〉 = 3.7 × 10−4 radian2. Using equation 3, we find B = 5 × 10−23 N · m2.
The bending modulus can be calculated from 〈Δθ2〉. The bending energy of the chromosome segment is E = B/2L Δθ2, where L is the line segment. The bending angle fluctuations will have a Maxwell-Boltzmann distribution in thermal equilibrium.
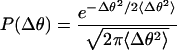 |
2 |
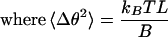 |
3 |
P(Δθ) is the probability (per unit angle) of the rod segment having a bending angle fluctuation Δθ. 〈Δθ2〉 can be determined directly from the time series or from a 1-parameter fit of equation 2 to a normalized histogram of Δθ2.
Stretching Experiments
After each bending modulus measurement, the chromosome stretching elastic response was measured. To quantify the chromosome force constant, the force needed to double its length, a third pipette is fabricated with an inner diameter of 2 μm for a newt chromosome or 1 μm for a Xenopus chromosome, each with a force constant of about 0.5 nN/μm. This pipette is positioned within 1 μm of the free end of the isolated chromosome, which is then aspirated with 50 Pa of pressure. The pipettes are then positioned antiparallel to each other and perpendicular to the chromosome (Fig. 1). A Labview program on the computer then moves one pipette out and back at a strain rate of 0.01 sec−1 (strain rate is the inverse of the time taken to double the chromosome's length), periodically capturing images to disk. The bending deflection of the stationary pipette provides a measure of the force applied to the chromosome during its extension.
Figure 1.
DIC images of a single-chromosome stretching experiment where the right pipette is translated 0, 5, 10, 15 and 20 μm. The left pipette is not moved but deflects and is calibrated so the deflection is converted into a force. Bar = 10 μm.
After such an experiment, the images were analyzed to measure length of the chromosome as a function of deflection of the stationary pipette. Pipette deflection is converted to a force by measuring the force constant of the stationary pipette by pushing it against a previously calibrated pipette (Poirier et al., 2000) after the experiment. The force constant of the chromosome f0 can then be determined from the slope of the force vs. extension plot and can be converted to a Young's (stretching) modulus (Landau and Lifshitz, 1986) by dividing by the cross-sectional area of the chromosome.
Note that after a stretching measurement, a bending measurement according to the methods described above is impossible, because both ends of the chromosome are permanently attached to pipettes. Therefore, the bending measurements are always done before the stretching measurements.
RESULTS
TVI Chromosomes Display the Same Elastic Response as Chromosomes from Explanted Cells
Our previous study of chromosome stretching elasticity (Poirier et al., 2000) used primary cultures of lung epithelial tissue taken from newts (N. viridescens). Two changes in our method, the use of TVI cell cultures, and use of 0.05% Triton-X in 60% PBS to soften the cell membrane, greatly facilitated non-damaging extractions of single chromosomes. A TVI cell culture has a large number of mitotic cells in the culture at any particular time, providing many more opportunities for chromosome isolation than occur in an explant culture. However, we needed to check that there were no significant differences between the elastic properties of chromosomes as previously studied (Houchmanzadeh et al., 1997, Poirier et al., 2000) and the TVI chromosomes extracted using diluted Triton-X.
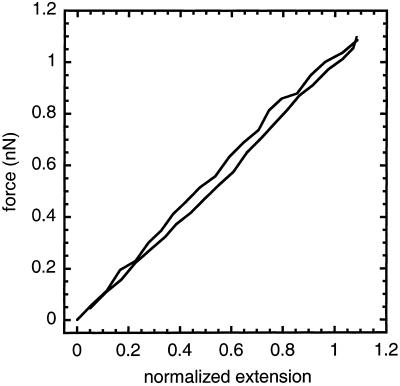
Three sets of stretching experiments were done, where the chromosomes were extended to 2 times the native length at strain rates of less then 0.01 sec−1 (Table 1). Fig. 2 shows the response of a TVI chromosome during an extension-retraction cycle. The response is linear out to three times its native length, with a characteristic force of 1.0 ± 0.1 nN to double the length, and the extension and retraction curves overlap. This response is similar to that of newt chromosomes from explanted cells (Houchmandzadeh et al., 1997, Poirier et al., 2000). For this chromosome, the force constant converts to a Young's Modulus of 500 ± 50 Pa by dividing by the cross-sectional area. The modulus is consistent with earlier results on newt chromosomes (Houchmandzedeh et al., 1997) and Xenopus artificial chromatids (Houchmandzadeh and Dimitirov, 1999). Also, the chromosome-to-chromosome variation in the Young's modulus is much larger then the experimental uncertainty, which has been previously reported by Houchmandzedah et al., 1997 and Poirier et al., 2000.
Table 1.
Elastic properties of mitotic chromosomes
| Chromosome type | Bending modulus, B (N · m2) | Young's modulus, Y (Pa) | Calculated Young's modulus, YB (Pa) |
|---|---|---|---|
| Newt chromosome, extracted | 100 ± 10 × 10−24 | 500 ± 50 | 500 ± 100 |
| Newt chromosome, extracted | 150 ± 30 × 10−24 | 400 ± 40 | 500 ± 200 |
| Newt chromosome, extracted | 300 ± 30 × 10−24 | 1000 ± 100 | 1500 ± 300 |
| Newt chromosome, extracted | 300 ± 100 × 10−24 | 300 ± 30 | 900 ± 500 |
| Newt chromosome, In vivo | 50 ± 50 × 10−24 | N.D. | 200 ± 200 |
| Newt chromosome, In vivo | 30 ± 30 × 10−24 | N.D. | 90 ± 90 |
| Newt chromosome, In vivo | 20 ± 20 × 10−24 | N.D. | 100 ± 100 |
| Newt chromosome, In vivo | 20 ± 20 × 10−24 | N.D. | 100 ± 100 |
| Xenopus chromosome, extracted | 5 ± 3 × 10−24 | 300 ± 30 | 200 ± 150 |
| Xenopus chromosome, extracted | 6 ± 2 × 10−24 | N.D. | 500 ± 200 |
| Xenopus chromosome, extracted | 10 ± 5 × 10−24 | 800 ± 80 | 400 ± 200 |
| Xenopus chromosome, extracted | 20 ± 10 × 10−24 | 200 ± 20 | 1300 ± 700 |
| Xenopus chromosome, extracted | 20 ± 4 × 10−24 | 400 ± 40 | 2000 ± 500 |
| Xenopus chromatid, extracted | 5 ± 5 × 10−24 | 300 ± 30 | 1500 ± 1500 |
N.D. indicates the experiment could not be done on that chromosome.
Figure 2.
Force vs. extension for the chromosome in Fig. 1a extended and retracted at a strain rate of 0.01 sec−1. The response is reversible and linear with a characteristic force of f0 = 1 nN to double the length of the chromosome.
Bending Modulus of Extracted Newt Chromosomes
Our measurement of B is based on measurement of the amount of thermal bending that occurs along a newt chromosome, following the method of Houchmandzadeh and Dimitrov (1999). One pipette holds a single chromosome about 50 μm above the glass surface. While held at one end in the cell buffer (Fig. 3A), the free end of the extracted chromosome undergoes submicron fluctuations.
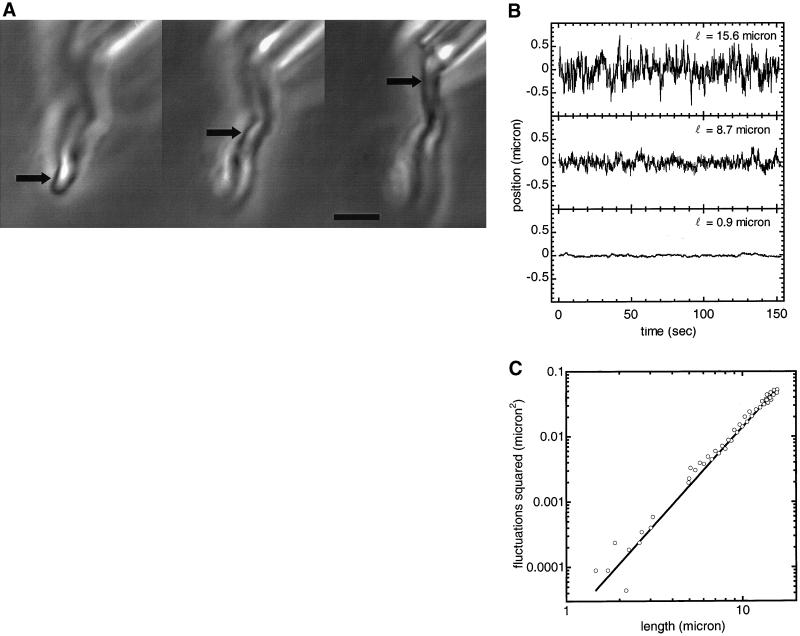
Figure 3.
(A) Phase-contrast images of different segments of a chromosome on which thermal bending fluctuations were measured. Arrows show where the fluctuations were measured, 15.6 μm, 8.7 μm, and 0.9 μm from the pipette tip. Bar = 4 μm. (B) Deflection (μm) vs. time (sec) for the chromosome segments shown in Fig. 3A. The fluctuation amplitudes increase with distance from the pipette. The fluctuations very near to the pipette are nonthermal in character and give an estimate of mechanical noise. (C) Mean square fluctuations (μm2) vs. position (μm) along the chromosome of Fig. 3A. This log-log plot shows the expected cubic dependence of mean-squared fluctuations on distance to the pipette. The measured positions have an uncertainty of ±0.1 μm and the measured mean-squared fluctuations have an uncertainty of ±10%. The data are fitted to 〈u2〉 = Cx3, with C = 1.4 × 10−5 μm−1, giving a bending modulus of 1 × 10−22 N · m2.
To quantify the fluctuation amplitude, we acquired two 150 sec time series at 10 frames per second of phase-contrast video photomicrographs at different points along the chromosome. The resulting photographs were digitally analyzed to determine the chromosome fluctuations relative to the anchored end. Three of the resulting time series are shown in Fig. 3B. The top and middle panels show the relatively large fluctuations occurring near the free end and near the middle of the chromosome.
The bottom time series in Fig. 3B shows the relatively low-amplitude fluctuations 0.9 μm from the pipette. These fluctuations are different in character from the much ‘noisier’ ones those further down the chromosome, and are non-thermal fluctuations of the pipette, i.e. mechanical noise. The slow and smooth variations are most likely slow drifts caused by lab temperature variations and air currents. Observation of this low fluctuation amplitude near the pipette is important as it indicates that we have reduced the level of mechanical noise to where it does not move the pipette relative to the rest of the microscope by more than ∼0.01 microns, allowing thermal bending fluctuations to dominate. This low remnant mean-squared mechanical noise was subtracted from the other mean-square amplitudes.
The thermal fluctuation amplitudes as a function of length are shown in Fig. 3C on a log-log plot. This is fit with the functional form 〈u2〉 = Cx3. The one fit parameter is C = 1.8 × 10−5 μm−1. Using Eq. (1) with kBT = 4.1 × 10−21 J, we find a bending modulus B of 1.0 ± 0.1 × 10−22 N · m2, which gives a calculated Young's modulus, YB = 500 ± 50 Pa. Following the thermal fluctuation measurements, the characteristic force was measured via an extension experiment to be 1.0 nN, which converts to a Young modulus of 500 ± 50 Pa. We repeated the thermal fluctuation measurements three times on different chromosomes, each time obtaining a bending modulus B ≈ 10−22 N · m2 (Table 1). The uncertainty of the bending rigidity measurements of extracted newt chromosomes is 10% and is due to the determination of the absolute position along the chromosome. The fluctuations along the chromosome length are a measure of change in position, which can be determined more accurately. The average squared fluctuations at the free end of the chromosome is three orders of magnitude larger then at clamped end (Fig. 3B, C).
Bending Modulus of Newt Chromosomes in Colchicine Arrested Cells
The bending fluctuations for chromosomes extracted from cells show exactly the expected relationship between amplitude and distance from the anchor point and provide a reliable measure of the bending modulus of extracted chromosomes. However, the extracted chromosome has been moved from the in vivo environment to the cell culture buffer. This change in buffer may induce a change in chromosome structure and its physical properties. To check this, we measured chromosome fluctuations inside cells arrested in prometaphase/metaphase by colchicine in the manner of experiments carried out by Marshall et al., 2001. Colchicine treatment blocks polymerization of microtubules, eliminating the mitotic spindle. However, chromosome condensation is essentially unaffected. Thus we obtain mitotic chromosomes, while eliminating their large-amplitude mechanical bending by the mitotic spindle. Only small-amplitude thermal bending fluctuations remain.
Bending fluctuations of mitotic newt chromosomes inside metaphase arrested cells were measured for four separate chromosomes. Figure 4A shows the time series for one of these chromosomes. The time series for the other three chromosomes give the same result. We were concerned that the other chromosomes and the cell membrane would restrict bending fluctuations: to check this, we show a histogram of the bending amplitudes extracted from one of the time series (Figure 4B, 25 bins). Unconstrained thermal bending fluctuations will have a Gaussian distribution according to Eq. 2. Alternately, if the fluctuations are constrained, the tails of this distribution should be suppressed, making the distribution more ‘square’.
We used Eq. 2 to fit the histogram with one parameter, 〈Δθ2〉 = 3.7 × 10−4 radian2. The tails of the histogram fit well to this distribution, indicating that the bending fluctuations are unconstrained. Eq. 3 is then used to calculate the bending modulus, B = 5 ± 5 × 10−23 N · m2 using the thermal energy, kBT = 4.1 × 10−21 J and the length of the segment of chromosome analyzed, L = 2.3 μm. The bending moduli of the three other chromosomes examined in this manner are listed in Table 1.
This analysis assumes that all of the fluctuations measured are thermal, a hypothesis made reasonable by the expected shape of the fluctuation distribution (Fig. 4B), and the reasonable value of B thereby obtained. However, there are likely sources of mechanical agitation remaining which give additional contributions to the measured fluctuations. Slow changes in cell shape and the other chromosomes within the cells distort the image of the chromosome in focus causing the bending fluctuation to be over estimated. These additional fluctuations cause the measured bending modulus to be less then its true value. Therefore, the in vivo results provide a lower limit on the actual bending modulus. However, based on examination of the time series, we estimate that the true value of B in vivo is within a factor of 2 of our measured value.
Effects of Using PBS to Extract Chromosomes
The bending measurements within metaphase arrested cells indicates chromosome elastic properties are not dramatically altered by the 60% PBS used during the extraction and the cell culture medium. To directly address this concern, we extracted a TVI mitotic chromosome using a buffering solution of 50 mM Tris and 100 mM glutamic acid monopotassium salt with a pH of 7.8. The chromosome Young's modulus was then measured in the cell culture medium and while flowing the above buffering solution with a third pipette around the chromosome. The tris-glutamic acid solution caused a 10% increase in the chromosome's relaxed length and a 20% increase in the Young's Modulus. This indicates the PBS and the cell culture medium do not dramatically alter the chromosome.
Elastic and Bending Moduli of Extracted Xenopus Chromosomes
We also measured the Young's and bending moduli for chromosomes removed from Xenopus cells. The Young's modulus was measured by the same technique as newt chromosomes for four separate A6 chromosomes (Table 1). These values are similar to previous measured chromosome moduli (Houchmandzedeh et al., 1997, Poirier et al., 2000) and to moduli of Xenopus chromatids assembled in egg extract (Houchmandzedeh and Dimitrov, 1999). We used the same technique to measure the bending modulus as with newt chromosomes by measuring thermal fluctuations along the length of the chromosome. The bending modulus was measured for five chromosomes with values all about 10−23 N · m2 (Table 1). The uncertainty of the bending rigidity measurements of extracted Xenopus chromosomes is larger than extracted newt chromosome uncertainty. This is a result of the smaller fluctuations along the length of the chromosome, which is due to their shorter length of about 5 μ long as compared to the newt chromosome length of about 20 μ long. The mean square of the fluctuations at the end of a chromosome is about five times larger then at the clamped (pipette) end and combines with the absolute position uncertainty to give a total uncertainty of about 30%.
Elastic Response and Bending Modulus of an Extracted Xenopus Chromatid
Chromosomes extracted during metaphase are composed of two chromatids. A direct measurement of the bending modulus of a single chromatid extracted from a cell in anaphase would test whether connections between the two chromatids in the single chromosome significantly contribute to the chromosome bending stiffness. We attempted this by extracting chromatids during anaphase. One Xenopus chromatid was completely isolated, for which a Young's modulus of 300 ± 30 Pa and a bending modulus of 5 ± 5 × 10−24 N · m2 was measured, similar to the elastic constants found for Xenopus chromosomes. Although we were only able to completely isolate an anaphase chromatid once, we could repeatedly extract clusters of anaphase chromatids; we recorded the bending fluctuations of chromatids sticking out of three separate clusters. Analysis of fluctuation time series gave bending stiffnesses of about 10−24 N · m2, confirming the result for the one completely isolated chromatid. The error of the measurements for the chromatid clusters is large, since the lengths of the segments of chromatids analyzed were only 0.5 to 0.7 μ. The magnitude of the fluctuations observed for this length of chromatid is similar to the nonthermal fluctuations of the pipette holding the cluster. Therefore, the value 10−24 N · m2 is a lower limit which confirms the more precise single chromatid measurement of 5 ± 5 × 10−24 N · m2.
DISCUSSION
Bending Moduli of Chromosomes in vivo and Extracted into Culture Medium are Similar
The measurements of chromosome elastic properties of chromosomes inside and outside the cell have advantages and disadvantages that complement each other. Measurements inside the cell allow us to study the native in vivo structure. A problem with these measurements is that other components of the cell may add noise to the supposed thermal fluctuation measurement. On the other hand, chromosomes extracted from a cell allow more precise measurements that are unaffected by the mechanical limitations of the in vivo experiments. Also, extracellular measurements are much more precise because the position of the chromosome is measured against an optically smooth background. An essential point of this study is that there is quite good agreement between bending moduli measured by these two approaches, indicating that the effects of cell-generated forces in vivo, and the change to the extracellular buffer, are both small.
We find a bending rigidity between 3 × 10−22 and 1 × 10−22 N · m2 for newt chromosomes removed from cells (Table 1). The bending modulus of chromosomes in newt colchicine arrested cells was measured to be between 5 × 10−23 and 2 × 10−23 N · m2 (Table 1). The bending modulus for chromosomes removed from cells and in metaphase arrested cells are within an order of magnitude of each other, indicating that removing a chromosome from the cell and exposing it to cell culture buffer does not drastically alter the bending rigidity. Because the measurements in metaphase arrested cells provide a lower limit on of the bending modulus, we conclude that our measurements on extracted chromosomes are relevant to chromosomes in vivo.
It is also possible that extracted chromosomes are up to five times stiffer then in vivo chromosomes. This is supported by the experiments of Marshall et al., 2001. They measured a bending modulus of 6 × 10−25 N · m2 for Drosophila embryo chromosomes, which gives YB = 40 Pa. This is about 10 times less then our measurements. However, Marshall et al. (2001) suggest that Drosophila embryo chromosomes may be less tightly compacted, explaining this 1 order of magnitude difference. Therefore, we interpret our mechanical measurement of chromosomes removed from a cell as representative of the in vivo chromosome bending modulus of ∼1022 N · m2.
Bending and Stretching Elasticity of Mitotic Chromosomes Are Related as for a Uniform Elastic Rod
The stretching and bending elastic constants can be used to extract information about the structures responsible for the elastic response. In general, rod-shaped biopolymers and biopolymer complexes have bending moduli B, which are approximately related to their elongational force constant f0 by the formula (Landau and Lifshitz, 1986) B = f0r2/4, where r is the radius of the rod cross-section. For example, for dsDNA with r = 1 × 10−9 m, f0 ≈ 1 nN (Smith et al., 1996), giving B = 2.5 × 10−28 N · m2, within 25% of the bending stiffness measured for dsDNA. Note that DNA bending stiffness is usually described in terms of its persistence length, which is just B/kBT ≈ 50 nm (Hagerman, 1988, Bustamante et al., 1994).
A newt chromosome was measured to have a bending modulus of B = 1.0 ± 0.1 × 10−22 N · m2, a force constant of f0 = 1.0 ± 0.1 nN and a radius of 0.8 ± 0.1 μm. This gives a Young's modulus of Y = 500 ± 50 Pa and a Young's modulus calculated from the bending modulus of YB = 500 ± 100 Pa, the same value. The other two newt chromosomes have similar calculated and measured bending moduli (Table 1). Xenopus chromosomes also roughly obey the elastic rod relation between force constant and bending modulus (Table 1). Therefore, chromosomes can be thought of, to a rough approximation, as being composed of a uniform elastic medium. The simplest way to imagine how this can occur is simply to suppose that the chromatin inside mitotic chromosomes is interconnected throughout the chromosome volume. Our results are inconsistent with a model where the chromosome is composed of chromatin loops anchored at their bases to a central axis or “scaffold.”
Mitotic Chromosomes Are Not Hinged at the Kinetochore
The kinetochore is the region of a mitotic chromosome that functions as the major point for microtubule attachment and is important for ensuring that the correct number of chromosomes are separated into each daughter cell (Nicklas, 1997). The structure around the kinetochore is different than the rest of the mitotic chromosome (Reider and Salmon, 1998). Given this, a different elastic behavior might be observed for this region of the chromosome. During anaphase, mitotic chromosomes are mostly bent at the kinetochore; suggesting the region around the kinetochore is very flexible and creates a hinge in the chromosomes. However, Figure 3C shows that the fluctuations along the length of the chromosome scale with a power law of nearly three, which is predicted for a homogeneous rod. Fluctuations of a hinged chromosome would not fit to this power law of three, showing that the kinetochore region of mitotic chromosomes is not a hinge that is much more flexible than the chromosome arms.
Chromosomes From Cells Are Much Stiffer than Chromatids Assembled in Xenopus Egg Extract
Houchmandzadeh and Dimitrov (1999) have carried out a precise and elegant study of the bending rigidity and stretching elasticity of chromatids assembled in vitro using Xenopus egg extracts. These artificial chromosomes are a powerful system for the study of chromosome structure independent of the many complications inherent to live cells. However, many questions remain regarding the relationship of structure of artificial chromosomes to their in-vivo counterparts.
Houchmandzadeh and Dimitrov found the stretching behavior of artificial chromosomes to be described by a force constant f0 ≈ 0.6 nN, corresponding to a Young's modulus Y = 1000 Pa. These are values similar to those for newt and Xenopus chromosomes. Compared to this, artificial chromosomes were found to have a very low bending stiffness, B = 1.2 × 10−26 N · m2. This bending stiffness indicates a calculated Young's modulus YB = 0.4 Pa, three orders of magnitude smaller then the YB found for newt and Xenopus chromosomes. Houchmandzadeh and Dimitrov made the reasonable inference that if the chromatids were homogeneous along their length, then they must have a thin internal core to provide the bending stiffness and stretching elasticity.
This 1000-fold difference in bending stiffness suggests there are important structural differences between chromosomes assembled in somatic cells and chromatids assembled in Xenopus egg extract. The differences must allow the egg extract chromatids to be much more easily bent than chromosomes in somatic cells, while giving the two systems similar stretching elasticity. A possible origin for the difference in bending stiffness is that the in vivo chromosomes contain two tethered chromatids, while the egg extract chromosomes are single chromatids. Possibly the egg extract chromatids lack interchromatid attachments, which could generate the increase in bending stiffness through the coupling of chromosome bending to chromatid stretching. Candidates for the interchromatid attachments are protein complexes formed of cohesins. These have been found in different species, such as S. cerevisiae (Guacci et al., 1997) and Xenopus (Losada et al., 1998), and are required for maintaining connections between sister chromatids until anaphase (Michaelis et al., 1997). However, this explanation is contradicted by our estimates of the bending moduli of individual Xenopus chromatids from observation of fluctuations of groups of isolated chromatids, and measurement of the bending modulus of a chromatid extracted from an anaphase Xenopus cell. We find that anaphase chromatids do not have a very different bending stiffness from metaphase chromosomes, and therefore that the main origin of chromosome bending stiffness is not the part of the interchromatid linkages that is removed at anaphase.
Our preferred explanation is that the 1000-fold-different bending stiffnesses of the in vivo and egg-extract chromatids is due to differences in chromatin structure in these two systems. The origins of these differences may be biological: chromatids from Xenopus egg extracts may represent an embryonic chromosome structure different from our somatic tissue culture cells. Alternately, this difference may stem from the fact that there is no DNA replication in the egg extract reaction, and no sister-chromatid-resolution process. Given that it is thought that condensation and resolution are coupled (Biggins and Murray, 1998), the in vivo and egg-extract systems may simply organize chromatin differently. A third possibility is that the egg extract reaction may produce chromatids that are incompletely condensed, with small but highly flexible regions along the chromatid length. If such uncondensed regions were small and closely spaced, they would be unobservable in the light microscope except through the flexibility they would impart to the chromatids.
A further experiment could address the above explanations. Two-chromatid chromosomes can be produced in vitro, by the use of mitotic or cycling extracts, which actually carry out nuclear assembly, DNA replication, and then chromosome condensation (Smythe and Newport, 1991). A measurement of the bending rigidity of such chromosomes would be extremely interesting. However, preliminary results communicated to us by E. Salmon show large bending fluctuations of chromosomes in cycled extracts, relative to those observed during mitosis in Xenopus cells. This suggests that in vitro chromosomes are anomolously flexible even after one cycle.
In summary, we measured the bending rigidity for newt and Xenopus mitotic chromosomes both in vivo and extracted into cell culture buffer. We find the bending modulus of newt chromosomes to be ∼10−22 N · m2 and for Xenopus chromosomes to be ∼10−23 N · m2. These values are consistent with the elastic rod model, B ≈ YR4, given the measured radius and Young's modulus of each type of chromosome. This indicates mitotic chromosomes can be thought of as being made of a roughly isotropic elastic medium, and that a uniform elastic rod model may be used to estimate their mechanical properties in vivo.
ACKNOWLEDGMENTS
We thank S. Dimitrov (Inst. Albert Bonnoit, La Tronche, France), H. Funabiki (Rockefeller, New York, NY), R. Heald (U. California, Berkeley, CA), T. Hirano (Cold Spring Harbor Laboratories, Cold Spring Harbor, NY), B. Houchmandzadeh (CNRS, Grenoble, France), W. Marshall (Yale, New Haven, CT), E. Salmon (U. North Carolina, Chapel Hill, NC), and J. Sedat (U.C.S.F., San Francisco, CA) for helpful discussions. We are indebted to D. Reese for generously sending us the TVI cells used in this study. This work was supported in part by a Biomedical Engineering Research Grant from the Whitaker Foundation, by Grant DMR-9734178 from the National Science Foundation, by a Research Innovation Grant from Research Corporation, and by an AC Grant from the Petroleum Research Foundation of the American Chemical Society.
Appendix
Here we show how the bending rigidity is related to thermal fluctuations, in the limit where those fluctuations are small. This discussion is included for completeness. However, it is not critical for understanding the results of this paper. The point is that the thermal fluctuations of an elastic rod clamped at one end and free at the other obey 〈u2〉 = 32kBTx3/π4B (Eq. 1).
The chromosome is considered to be a uniform straight rod of length L that lies along the x-axis and undergoes small fluctuations u (u ≪ L) in the y direction. Fluctuations in the z-direction play no role in our analysis and may be ignored. The position of the rod is described by the vector, r⃗(s), where s is the position along the rod. For the case that u ≪ L, s ≈ x, the tangent vector t̂ ≈ x̂ and the curvature κ ≈ d2u/dx2. The rod's normal bending modes can be shown to satisfy the equation d4u(x)/dx4 = k4/L4 u(x) (Rayleigh, 1945, Gittes et al., 1993). The general form of the solution of this equation is:
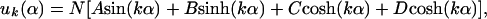 |
4 |
where α = x/L and N is the normalization constant.
To find the normal modes relevant to our situation, we must apply the appropriate boundary conditions. We are considering a straight rod that is clamped at x = 0 and free at x = L and has the four boundary conditions (B.C.):
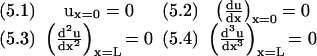 |
These boundary conditions determine A, B, C and D. It is easier to see how to satisfy the boundary conditions if we rewrite Eq. (4) as
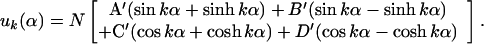 |
6 |
Right away one sees that B.C. (5.1) and (5.2), require A′ and C′ to be zero. After some arithmetic, one finds B.C. (5.3) and (5.4) set B′ = (sin(k) − sinh(k)) and D′ = [cos(k) + cosh(k)] where k has discrete values determined by
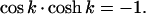 |
7 |
The first six values of k are k1 = 1.8751, k2 = 4.6941, k3 = 7.8548, k4 = 10.9955, k5 = 14.1372 and k6 = 17.2788 (Raleigh, 1945), and for large kn, it becomes (2n − 1)π/2. Therefore,
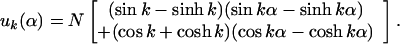 |
8 |
We now suppose the rod to be subjected to thermal fluctuations.
We can write down the shape of a deformed rod deformed as a sum of the
normal modes, u = ∑k
akuk. The bending energy is described by
E = B/2 ∫ ds κ2 ≈
B/2 ∫
ds κ2 ≈
B/2 ∫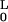 dx (d2u/dx2).
After plugging in for the curvature, we find
dx (d2u/dx2).
After plugging in for the curvature, we find
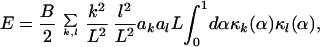 |
9 |
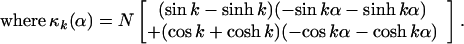 |
10 |
κk is orthonormal, so
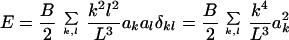 |
11 |
Because the energy is quadratic for each bending mode,
k, the equipartition theorem (Doi and Edwards,
1988) tells us that 〈a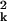 〉 =
kBTL3/Bk4 and
〈akal〉 = 0 for k ≠
l. We can now calculate 〈u2〉:
〉 =
kBTL3/Bk4 and
〈akal〉 = 0 for k ≠
l. We can now calculate 〈u2〉:
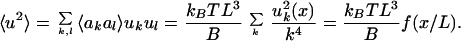 |
12 |
Numerical analysis shows that the function f(x/L) is within 1.5% of 32x3/π4L3 for 0 < x < L. We can therefore approximate Eq. (12) with 〈u2〉 = 32kBTx3/π4B.
Footnotes
Article published online ahead of print. Mol. Biol. Cell 10.1091/mbc.01–08–0401. Article and publication date are at www.molbiolcell.org/cgi/doi/10.1091/mbc.01–08–0401.
REFERENCES
- Biggins S, Murray AW. Sister chromatid cohesion in mitosis. Curr Opin Cell Biol. 1998;10:769–775. doi: 10.1016/s0955-0674(98)80120-8. [DOI] [PubMed] [Google Scholar]
- Bustamente C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;256:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- Belmont AS, Sedat JW, Agard DA. A three-dimensional approach to mitotic chromosome structure: evidence for a complex hierarchical organization. J Cell Biol. 1987;105:77–92. doi: 10.1083/jcb.105.1.77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi M, Edwards SF. Theory of Polymer Dynamics. Oxford: Oxford University Press; 1988. [Google Scholar]
- Gittes F, Mickey B, Nettleton J, Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guacci V, Koshland D, Strunnikov A. A direct link between sister chromatid cohesion and chromosome condensation revealed through the analysis of MCD1 in S. cerevisiae. Cell. 1997;91:47–57. doi: 10.1016/s0092-8674(01)80008-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagerman PJ. Flexibility of DNA. Annu Rev Biophys Bio. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- Houchmandzadeh B, Marko JF, Chatenay D, Libchaber A. Elasticity and structure of eukaryote chromosomes. J Cell Biol. 1997;138:1–12. doi: 10.1083/jcb.139.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houchmandzadeh B, Dimitrov S. Elasticity measurements show the existence of thin rigid cores inside mitotic chromosomes. J Cell Biol. 1999;145:215–223. doi: 10.1083/jcb.145.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar, A., and Hunt, A.J. (2002). A simple mechanistic model for directional instability during mitotic chromosome movement. Biophys. J. In press. [DOI] [PMC free article] [PubMed]
- Koshland D. Mitosis: back to the basics. Cell. 1994;77:951–954. doi: 10.1016/0092-8674(94)90432-4. [DOI] [PubMed] [Google Scholar]
- Koshland D, Strunnikov A. Mitotic chromosome condensation. Annu Rev Cell Dev Biol. 1996;12:305–333. doi: 10.1146/annurev.cellbio.12.1.305. [DOI] [PubMed] [Google Scholar]
- Landau LD, Lifshitz EM. Theory of Elasticity. New York: Pergamon Press; 1986. [Google Scholar]
- Losada A, Hirano M, Hirano T. Identification of Xenopus SMC protein complexes required for sister chromatid cohesion. Genes & Dev. 1998;12:1986–1997. doi: 10.1101/gad.12.13.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelis C, Ciock R, Nasmyth K. Cohesins: chromosomal proteins that prevent premature separation of sister chromatids. Cell. 1997;91:35–45. doi: 10.1016/s0092-8674(01)80007-6. [DOI] [PubMed] [Google Scholar]
- Marshall WF, Marko JF, Agard DA, Sedat JW. Chromosome elasticity and mitotic polar ejection force measured in living Drosophila embryos by four-dimensional microscopy-based motion analysis. Curr Biol. 2001;11:1–20. doi: 10.1016/s0960-9822(01)00180-4. [DOI] [PubMed] [Google Scholar]
- Nicklas RB. Measurements of the force produces by the mitotic spindle in anaphase. J Cell Biol. 1983;97:542–548. doi: 10.1083/jcb.97.2.542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicklas RB. How cells get the right chromosomes. Science. 1997;275:632–637. doi: 10.1126/science.275.5300.632. [DOI] [PubMed] [Google Scholar]
- Paulson JR, Laemmli UK. The structure of histone-depleted metaphase chromosomes. Cell. 1977;12:817–828. doi: 10.1016/0092-8674(77)90280-x. [DOI] [PubMed] [Google Scholar]
- Poirier MG, Eroglu S, Chatenay D, Marko JF. Reversible and irreversible unfolding of mitotic newt chromosomes by applied force. Mol Biol Cell. 2000;11:269–276. doi: 10.1091/mbc.11.1.269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayleigh JWS. The Theory of Sound. New York: Dover; 1894. pp. 256–305. [Google Scholar]
- Rieder CL, Salmon ED. The vertebrate cell kinetochore and its roles during mitosis. Trends Cell Biol. 1998;8:310–318. doi: 10.1016/s0962-8924(98)01299-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese DH, Yamada T, Moret R. An Established Cell Line from the Newt Notophthalmus viridescens. Differentiation. 1976;6:75–81. doi: 10.1111/j.1432-0436.1976.tb01472.x. [DOI] [PubMed] [Google Scholar]
- Smith SB, Cui YJ, Bustamnte C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- Smythe C, Newport JW. Systems for the study of nuclear assembly, DNA replication, and nuclear breakdown in Xenopus laevis egg extracts. Methods Cell Biol. 1991;35:449–468. doi: 10.1016/s0091-679x(08)60583-x. [DOI] [PubMed] [Google Scholar]