Abstract
The main objective of this work is to study the mathematical model that combines stem cell therapy and chemotherapy for cancer cells. We study the model using the fractal fractional derivative with the Mittag-Leffler kernel. In the analytical part, we study the existence of the solution and its uniqueness, which was studied based on the fixed point theory. The equilibrium points were also studied and discussed after stem cell therapy, and the approximate solutions for the given model were obtained using the Adam Bashford method, which depends on interpolation with Lagrange polynomials. Finally, the model was simulated using the Mathematica software, and through the figures, we found that the components of the model approach the equilibrium point, which indicates the stability of the model at the equilibrium point. Also, the result of the numerical simulation and graphic for the concentration of cells over time indicate the effects of the therapies on the decay rate of tumor cells and the growth rate of effector cells to modify the cancer patient’s immune system. It is worth noting that we simulated all the model components with different fractional orders, confirming the effect of stem cell therapy and chemotherapy on the cells and the decay of cancer cells.
Keywords: Mathematical model, Fractional derivative, Matignon criterion, Adams-Bashforth method
Subject terms: Cancer, Mathematics and computing
Introduction
Despite remarkable advancements in science and technology, cancer continues to pose a formidable challenge to human health. While conventional treatment approaches like surgery, radiation, chemotherapy, hormone therapy, and gene therapy have made progress, the core methods for tackling cancer have not transformed significantly. However, mathematical modeling offers a powerful tool to gain valuable insights into the intricate dynamics of cancer progression, immune responses, and potential therapeutic interventions1,2. In3,4, researchers have increasingly explored mathematical frameworks to enhance our understanding of cancer biology and develop more effective treatment strategies. Several studies have employed models to investigate the interactions between T-cells, particularly effector T-cells, and tumor cells, elucidating how these interactions influence cancer development; these quantitative models provide a comprehensive perspective that complements experimental research on the complex immune dynamics as in5–8.
The authors in9,10 clarified that stem cells have revolutionized the treatment of numerous diseases due to their remarkable ability to differentiate and proliferate. The researchers confirmed in11,12 that studying stem cells mathematically has excellent importance for considering their therapeutic potential; mathematical modeling of stem cell growth dynamics can help medical scientists determine optimal screening and treatment protocols since stem cell therapies are costly. Quantitative analyses of stem cell behavior through modeling provide the key insights that complement experimental stem cell research, highlighting promising directions for medical applications of stem cells. Fractional calculus and its various applications have recently witnessed remarkable developments as many fractional differential operators have emerged, such as Riemann-Liouville,Caputo,Grunwald-Letnikov, Atangana-Baleanu, Conformable Fractional, and Opsi Hilfer. For more information about these operators, see13–15. Furthermore, numerical and analytical methods have been formulated to meet the challenges of fractional calculus16–19. The power of fractional or non-classical calculus has been effectively harnessed across a wide range of disciplines, including computer science, physics, biology, social sciences, economics, engineering, epidemiology, and beyond20–26. A key advantage of employing fractional calculus with its various differential and integral operators lies in the ability to utilize fractional operators of arbitrary order, a flexibility not afforded by conventional derivatives of integer order. In recent years, there has been increased interest in mathematically modeling infectious diseases using fractional-order systems of equations. Fractional-order models are more accurate than integer-order models in representing memory effects over time and nonlocal phenomena in space. Overall, fractional calculus allows more precise modeling of infectious disease dynamics. A key benefit of fractional-order models is reducing errors from omitting parameters in natural processes see,27–33. In34, the authors apply time-fractional derivatives to model tumor growth dynamics involving cancer stem cells, generalizing an integer-order model previously analyzed. The aim is to investigate the sensitivity of the cancer growth paradox to differing mortality rates of non-stem cancer cells. It demonstrates that the paradox occurs across various parameter values in the proposed fractional-order model. A mathematical model of stem cells and chemotherapy for cancer treatment using fractional-order differential equations with the Caputo sense is used to represent the model by Özköse et al.35.
In34, the authors apply time-fractional derivatives to model tumor growth dynamics involving cancer stem cells, generalizing an integer-order model previously analyzed. The aim is to investigate the sensitivity of the cancer growth paradox to differing mortality rates of non-stem cancer cells. It demonstrates that the paradox occurs across various parameter values in the proposed fractional-order model. A mathematical model of stem cells and chemotherapy for cancer treatment using fractional-order differential equations with the Caputo sense is used to represent the model by Özköse et al.35.
In 2017, Atangana36 introduced a new class of operators called fractal–fractional operators (FFOs), combining concepts from fractional and fractal calculus. A recently developed fractal–fractional operator holds promise for addressing such mathematical challenges37,38. Furthermore, the fractal–fractional formulation allows us to account for biological systems’ inherent complexities and memory effects, potentially leading to more accurate and realistic predictions. Over the past few years, a growing number of researchers have applied this fractal–fractional operator to model various real-world scenarios, demonstrating its potential for capturing complex system behaviors, see39–46. Farman et al.47 proposed a fractional order model to study the sustainable approach for cancer treatment with chemotherapy by utilizing a fractional operator. The model incorporated the fractal–fractional Mittag-Leffler operator with non-integer order derivatives to capture the complex dynamics and memory effects of cancer progression and treatment response. We developed a mathematical model of stem cells and chemotherapy for cancer treatment using a mathematical fractal–fractional model via the generalized Mittag-Leffler-type kernel. The model provides insights into how stem cells support effector cells that combat tumor cells, thereby boosting the immune system of cancer patients. At the same time, the model incorporates chemotherapy, killing infected cancer cells. By modeling the dynamics of stem cells, immune cells, and chemotherapy, it is possible to understand their complex interactions during cancer treatment. The quantitative framework enables predicting how stem cell therapies and chemotherapy could be optimized to improve outcomes for cancer patients. Overall, the mathematical modeling approach furthers comprehension of combination therapies involving immune system modulation through stem cells and direct tumor cell cytotoxicity from chemotherapy. Overall, this work highlights the potential of mathematical modeling in guiding the development of innovative and effective cancer treatment approaches, paving the way for future experimental studies and clinical applications.
This research paper consists of seven sections. The second section presents a set of fundamental definitions, while the third section discusses the mathematical model. The fourth section addresses the existence and unit of a solution to the mathematical model. The fifth section examines stability and then calculates the approximate solution in the sixth section. The seventh section is dedicated to discussing the results.
Preliminaries
Here are some fundamental ideas that will be used in this study:
Definition 1
48 Let  be continuous in (a, b) , if
be continuous in (a, b) , if  is fractal differentiable on (a, b) with order
is fractal differentiable on (a, b) with order 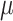 then, the fractal–fractional derivative of
then, the fractal–fractional derivative of 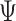 of order
of order 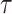 in the Riemann-Liouville sense using the generalized Mittag-Leffler kernel is given as
in the Riemann-Liouville sense using the generalized Mittag-Leffler kernel is given as
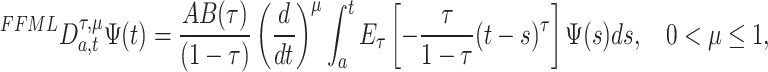 |
1 |
where  , and
, and 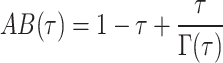 ,
, 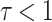 and
and 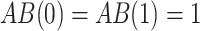 .
.
Definition 2
36 If 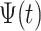 is continuous in an opened interval (a, b) , then the fractal–fractional integral of
is continuous in an opened interval (a, b) , then the fractal–fractional integral of 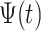 with order
with order 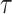 is defined as:
is defined as:
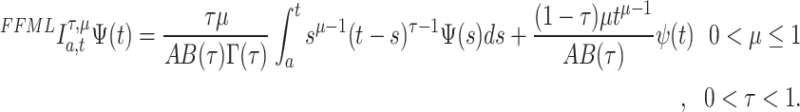 |
The formulation of the model
Before starting our study, we will take this model that the authors presented in1, which includes three distinct patterns of cell division. Specifically,they assume that stem cells (denoted S) can either:
Undergo symmetric self-renewing divisions with probability
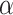 , generating two new stem cell daughters.
, generating two new stem cell daughters.Divide asymmetrically with probability
 , resulting in one stem cell and one differentiated progeny that lacks stemness.
, resulting in one stem cell and one differentiated progeny that lacks stemness.Or differentiate symmetrically into two non-stem daughters with probability
 . We constrain the relative probabilities such that
. We constrain the relative probabilities such that  Furthermore, we define the rates of stem cell division and cell death as k and
Furthermore, we define the rates of stem cell division and cell death as k and 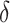 , respectively. Given that the stem cell pool can be replenished via both asymmetric and symmetric differentiating divisions, we derive an equation to capture the time evolution of stem cell numbers. This theoretical framework allows us to make quantitative predictions about how different division modalities influence net stem cell expansion or depletion. By fitting our model to experimental data, we can potentially infer the probabilities governing cell fate choices in vivo.
, respectively. Given that the stem cell pool can be replenished via both asymmetric and symmetric differentiating divisions, we derive an equation to capture the time evolution of stem cell numbers. This theoretical framework allows us to make quantitative predictions about how different division modalities influence net stem cell expansion or depletion. By fitting our model to experimental data, we can potentially infer the probabilities governing cell fate choices in vivo.
Initially, Alqudah et al.1, developed a mathematical model to explore the potential of stem cell therapy in treating cancer. The model considers the interactions between three cell populations over time:
E(t) effector immune cells,
T(t) tumor cells,
S(t) therapeutic stem cells.
To capture the downstream impact of stem cell activity, they introduced an amplification factor A. Using these elements, we derived a simplified system of ordinary differential equations (ODEs) describing how effector cells, tumour cells, and amplified stem cell signals modulate one another. We can predict the efficacy of stem-cell-based approaches by analyzing this theoretical model under different conditions. Fitting this model to preclinical/clinical data could help refine the quantitative assumptions regarding stem cell amplification effects and immune system activation. Overall, this general modelling framework provides a means to theoretically investigate anti-cancer stem cell therapies before experimental testing.
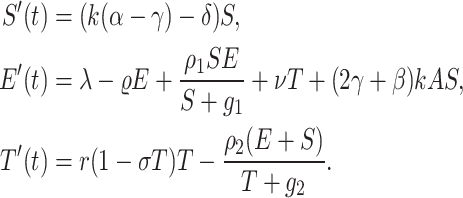 |
2 |
In building upon the model presented in equation (2), they propose an extension incorporating combination therapy with both chemotherapy and stem cell treatment for cancer as:
 |
3 |
where  ,
,
subject to  and
and  , where U(t) is chemotherapy concentration drug. In our current work, we present the model (3) on a mathematical fractal–fractional model via the generalized Mittag-Leffler-type kernel because this operator gives accurate results for describing models and phenomena that describe real-world biological systems, such as memory effects, long-range interactions, and anomalous dynamics. So, the model (3) become as
, where U(t) is chemotherapy concentration drug. In our current work, we present the model (3) on a mathematical fractal–fractional model via the generalized Mittag-Leffler-type kernel because this operator gives accurate results for describing models and phenomena that describe real-world biological systems, such as memory effects, long-range interactions, and anomalous dynamics. So, the model (3) become as
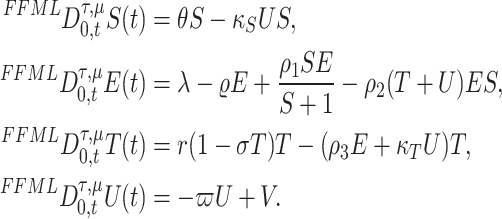 |
4 |
The first equation in model (4) captures the interplay between the stem cell population (S) and chemotherapy drug concentration (U) over time  . Furthermore, the model incorporates a decline in viable stem cells directly induced by the chemotherapeutic agent, occurring at rate
. Furthermore, the model incorporates a decline in viable stem cells directly induced by the chemotherapeutic agent, occurring at rate 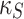 .
.
The second equation represents the dynamics of effector cells. These cells have a constant source rate  , which is the sum of a natural source rate
, which is the sum of a natural source rate 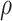 and a rate
and a rate 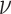 derived from the transformation of stem cells. The equation accounts for the death rate of effector cells
derived from the transformation of stem cells. The equation accounts for the death rate of effector cells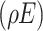 , their proliferation stimulated by stem cells, and their interaction with tumour cells and chemotherapy drugs at rates
, their proliferation stimulated by stem cells, and their interaction with tumour cells and chemotherapy drugs at rates 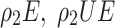 respectively.
respectively.
The third equation shows the rate of cancer cell production minus the amount of decrease in it as a result of the interaction between the responding cells and the chemical drug with rates 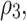 and
and  respectively. The last equation represents the rate of change in the concentration of the chemical drug.
respectively. The last equation represents the rate of change in the concentration of the chemical drug.
Existence and uniqueness of solution
Establishing the existence and uniqueness of solutions plays a crucial role in validating the outcomes of a study. It ensures the robustness and stability of the analyses performed and facilitates meaningful comparisons with other research endeavours. Furthermore, these results provide a solid theoretical foundation, guiding the applicability and broader generalization of the findings. Consequently, emphasizing the importance of existence and uniqueness within the study context helps reinforce the reliability and significance of the research conclusions drawn. In this section, we prove the existence of a solution for model (4) by using fixed point theory. Let  be a non empty set in Banach space, s.t
be a non empty set in Banach space, s.t 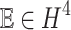 where
where 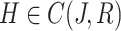 with norm
with norm 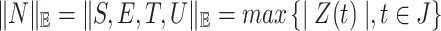 . For
. For 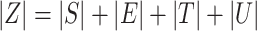 .
.
Now, we rewrite the R.H.S of model (4) as following
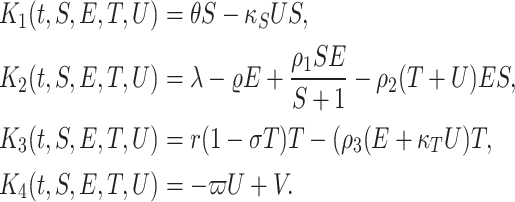 |
5 |
By Using definition 1
 |
6 |
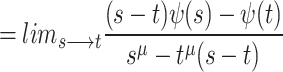 |
7 |
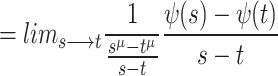 |
8 |
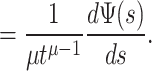 |
9 |
Then
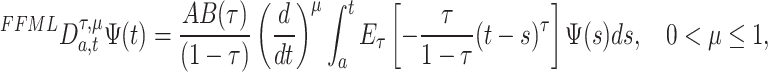 |
10 |
become
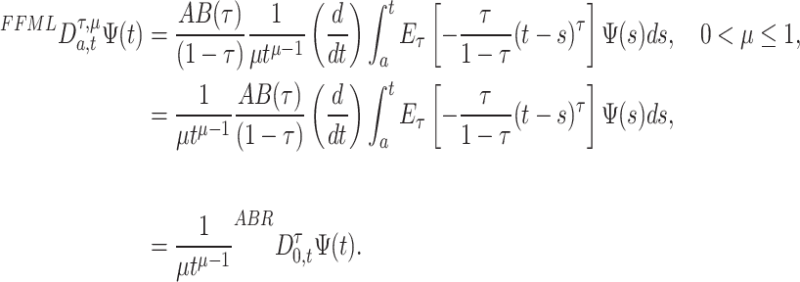 |
11 |
So the fractal–fractional Atangana-Baleanu of (4) in the Riemann-Liouville sense is become as:
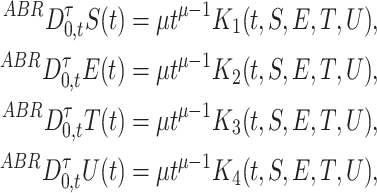 |
12 |
also, we can rewrite (12) in form of initial value problem as the following
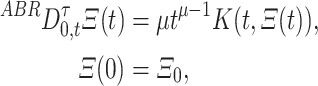 |
13 |
where  and
and 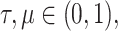
and
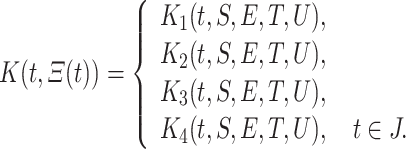 |
14 |
By definition 1 and equation (13) we get
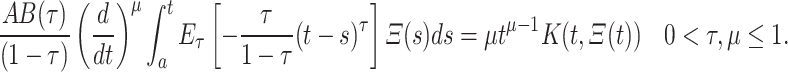 |
15 |
By taking the fractal-fractionl Atangana- Baleanu integral on (15) we obtain
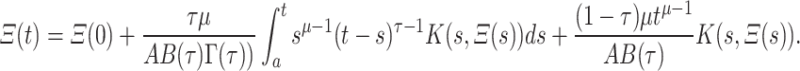 |
16 |
Now we extend the (16) as
 |
17 |
We defined the oprator 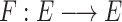 to derive a fixed-point problem as
to derive a fixed-point problem as
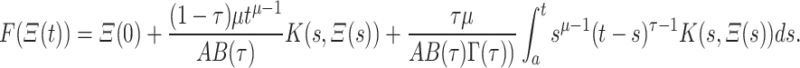 |
18 |
Theorem 1
49
Let
E
be a Banach space,
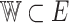 a convex closed bounded set,
a convex closed bounded set,
 an open set, and
an open set, and
 . Then for the continuous and compact map
. Then for the continuous and compact map
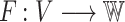 either:
either:
 s.t.
s.t.
 or
or and
and
 s.t.
s.t.
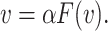
Theorem 2
Let
 . Assume:
. Assume:
- (
 )
)  and
and
 s.t.
s.t.
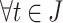 and
and
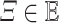 ,
,  .
.- (
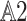 )
) 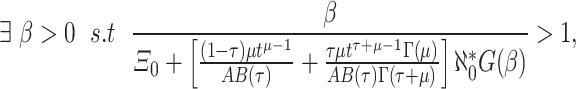
19
with
 .
.
Proof
Let  and assume
and assume  . Evidently, as K is continuous, so too is F. From (A1) we obtain
. Evidently, as K is continuous, so too is F. From (A1) we obtain
 |
for 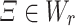 . Then
. Then
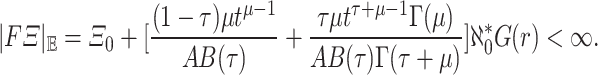 |
20 |
Thus F is uniformly bounded on 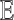 . Now, take
. Now, take  s.t.
s.t.  and
and  . and let
. and let 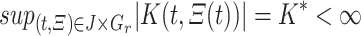 , we find
, we find
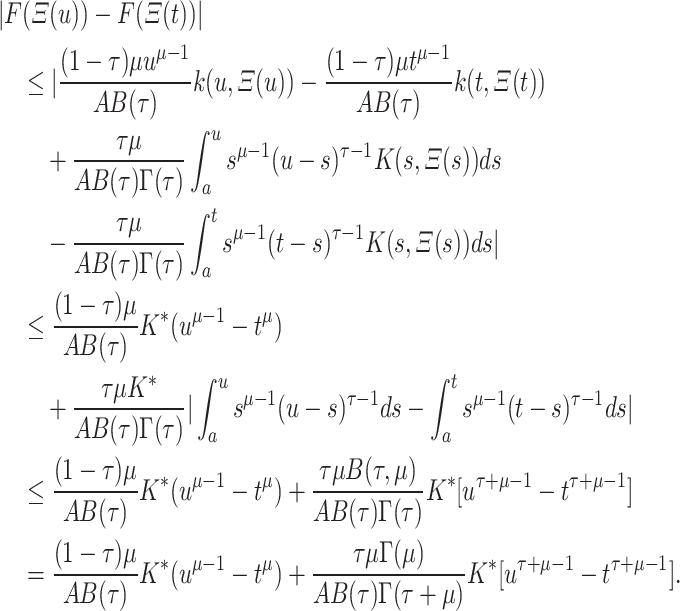 |
Now when 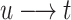 , we see that the expression
, we see that the expression
 when
when  . This gives the equicontinuity of F and, accordingly, the compactness of F on
. This gives the equicontinuity of F and, accordingly, the compactness of F on  by the Arzela-Ascoli thoerem. Since all conditions of Theorem 1 are fulfilled on F, we have one of (1) or (2). From (
by the Arzela-Ascoli thoerem. Since all conditions of Theorem 1 are fulfilled on F, we have one of (1) or (2). From (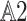 ), we set
), we set  for some
for some 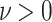 s.t.
s.t.
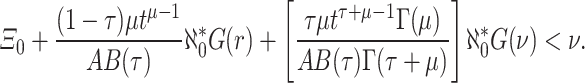 |
Form (A1) and (20), we get
 |
21 |
Assume that there are 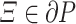 and
and 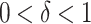 such that.
such that. 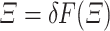 . Then, by the above inequality, we obtain
. Then, by the above inequality, we obtain
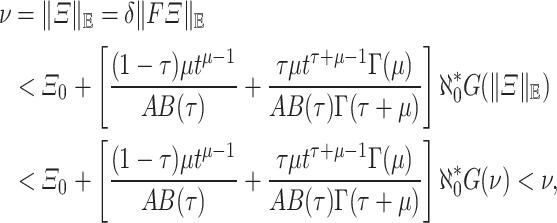 |
this contradiction with our hypthesis (A2), then F has a fixed point in P by Theorem 1. This demonstrates a solution to the model (4) exists. 
Now, we prove the uniqueness of the solution of the model (4).
Lemma 1
Let
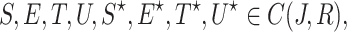 and let
and let
 , where
, where
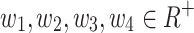 .
.
Then the kernels
 and
and
 defined in (5) are satisfies the Lipschitz condition.
defined in (5) are satisfies the Lipschitz condition.
Proof
For  , we take
, we take 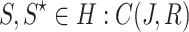 , and we get
, and we get
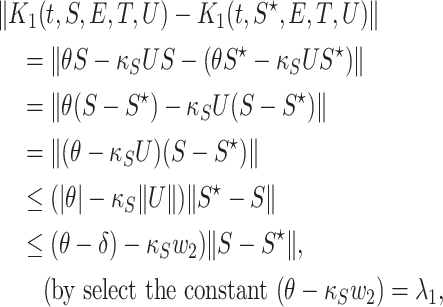 |
we obtain
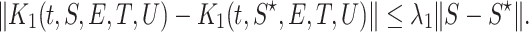 |
Then  satisfy the Lipschitze condition w.r.t. S. Similarly we can prove that
satisfy the Lipschitze condition w.r.t. S. Similarly we can prove that 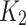 satisfy the Lipschitz condition w.r.t. U as the following:
satisfy the Lipschitz condition w.r.t. U as the following:
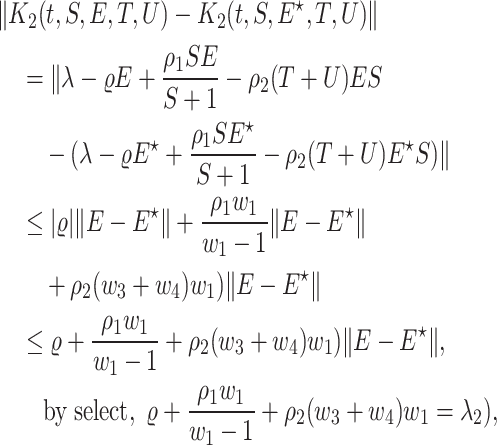 |
we get
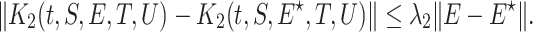 |
Now, we can prove that  satisfy the Lipschitz condition w.r.t. E as the following:
satisfy the Lipschitz condition w.r.t. E as the following:
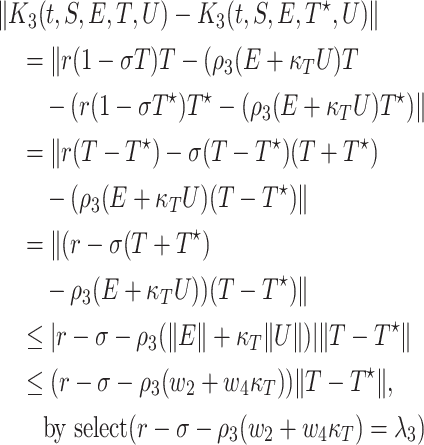 |
we obtain
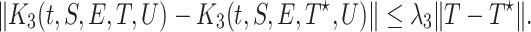 |
Finally, we can prove that 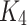 satisfy the Lipschitz condition w.r.t. A as the following:
satisfy the Lipschitz condition w.r.t. A as the following:
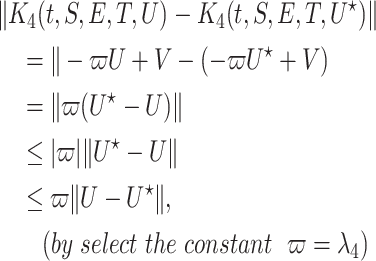 |
we obtain
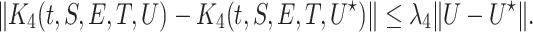 |
Consequently,  and
and 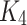 are satisfying the Lipschitz condition.
are satisfying the Lipschitz condition. 
Theorem 3
Assume that lemma 1be hold. Then the model (4) has exactly one solution if
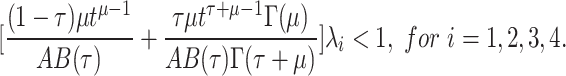 |
22 |
Proof
Suppose that there is an other solution for the model (4), namely  with the initial condition
with the initial condition  .
.
So by using the model (17)
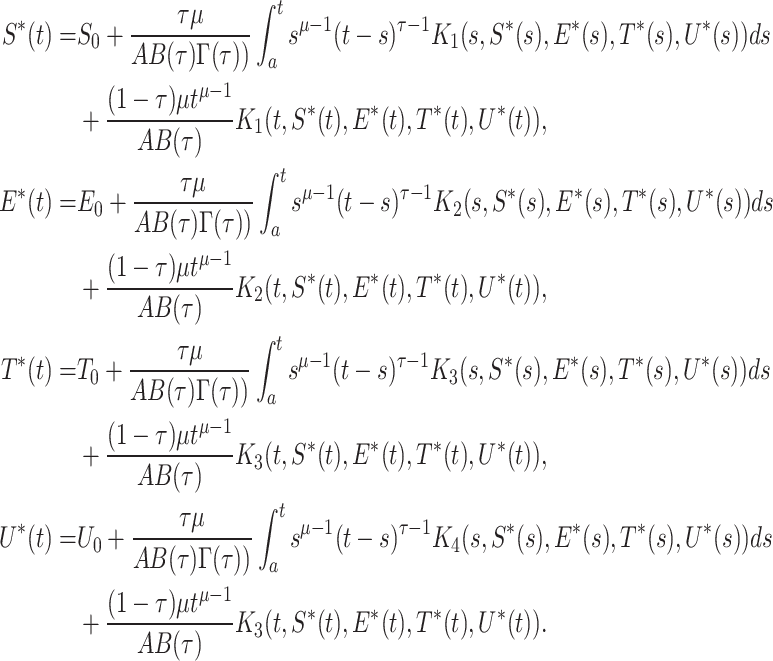 |
Now, we calculate
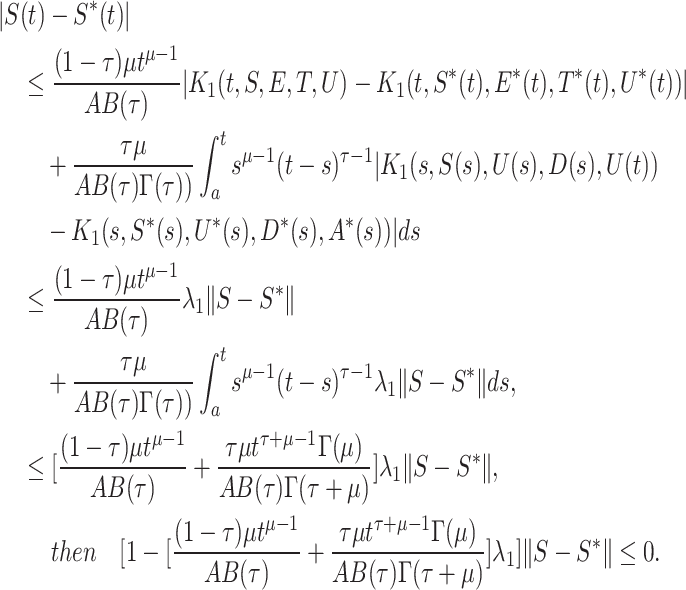 |
We can say the above inequality holds if  or
or 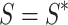 by the same way we can prove that
by the same way we can prove that  ,
,  and
and 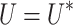 .
.
Then  . Then the model (4) has a unique solution.
. Then the model (4) has a unique solution. 
Equilibrium point
Stability theories play a significant role in understanding the long-term dynamics of our model. They provide a theoretical framework that predicts whether a system will converge to a steady state, oscillate, or diverge under small perturbations. We perform numerical simulations using the Adams-Bashforth method to validate these theoretical predictions, as detailed in Section 6. These simulations not only confirm the stability or instability of the equilibrium points but also provide insight into the behavior of the system under initial conditions. In this segment, we initiate our inquiries by conducting a local stability analysis within the framework of fractional-order derivatives. The conventional approach employed for examining local stability using the Jacobian matrix differs from that of the fractional context. The Matignon criterion50 is utilized in fractional scenarios. The equilibrium point 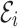 for the fractional differential equation
for the fractional differential equation 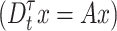 is considered locally stable only when the following condition is met50 :
is considered locally stable only when the following condition is met50 :
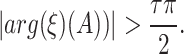 |
23 |
The approach for local stability analysis in the fractional context is detailed in51. This method involves several steps, starting with calculating the Jacobian matrix using integer-order derivatives. Subsequently, the characteristic polynomial is determined through the standard process, and the eigenvalues are computed using algebraic methods. The final step involves testing all eigenvalues against the Matignon criterion (23), incorporating the fractional order. Initially, equilibrium points for the fractional (4) are derived by solving the equations.
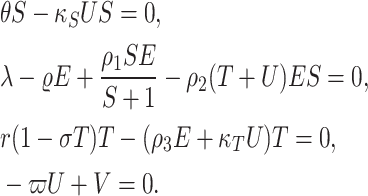 |
24 |
Following the calculations, the obtained equilibrium points are as follows:
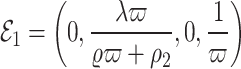 ,
,
 ,
,
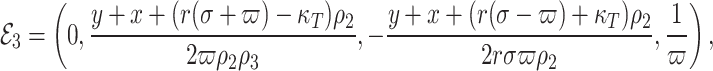
where
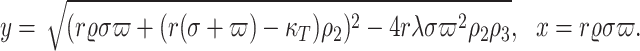
Now, we calculate the Jacobian matrix of the model (4) as the following :
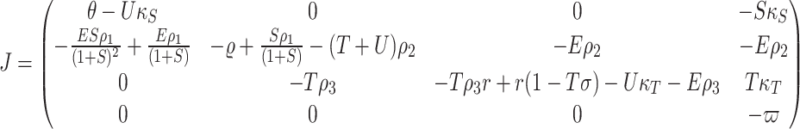 |
25 |
To simplify, we directly utilize the values of the parameters as outlined in Table 1. So 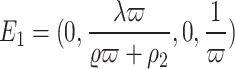 become
become  , the Jacobian matrix at the point
, the Jacobian matrix at the point 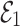 is given by
is given by
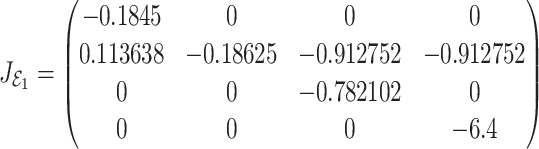 |
26 |
After performing the calculations, the characteristic polynomial of the Jacobian matrix is expressed in the following form:
 |
27 |
The eigenvalues of the 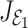 are given by
are given by 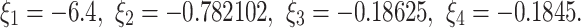 We note that
We note that
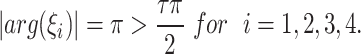 |
This fulfills the Matignon criterion,then the equilibrium point  is locally stable.
is locally stable.
Table 1.
Parameters description and values.
| Parameter | Description | Value/ Unit.day |
|---|---|---|
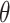 |
Stem cell therapy attrition rate | − 0.028251 |
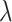 |
Effector cell turnover rate | 0.171 |
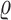 |
Attrition rate due to natural death of effecror cells | 0.031 |
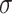 |
Ability to destroy cancer cells |
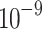 1 1
|
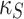 |
Attrition rate of stem cells by Chemotherapy | 11 |
| r | Tumor growth rate | 0.181 |
 |
Maximum effect of effector cells | 0.12451 |
 |
Attrition rate due to cancer and Chemotherapy of effector cells | 11 |
 |
FDeath rate due to Chemotherapy of cancer cells | 0.91 |
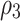 |
Attrition rate of cancer cells due to effector cells | 0.91 |
 |
Decomposition rate of chemotherapy | 6.41 |
| V | The rate of the Chemotherapy entering the system at a specific schedule | 11 |
 , the Jacobian matrix at the point
, the Jacobian matrix at the point  is given by
is given by
 |
28 |
After performing the calculations, the characteristic polynomial of the Jacobian matrix is expressed in the following form:
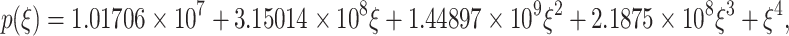 |
29 |
The eigenvalues of the 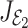 are given by
are given by 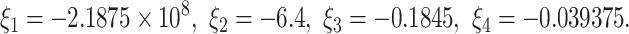 We note that
We note that
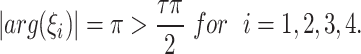 |
This fulfills the Matignon criterion,then the equilibrium point 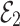 is locally stable.
is locally stable.
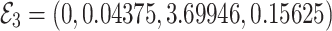 , the Jacobian matrix at the point
, the Jacobian matrix at the point 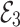 is given by
is given by
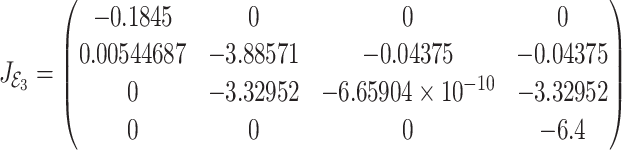 |
30 |
After performing the calculations, the characteristic polynomial of the Jacobian matrix is expressed in the following form:
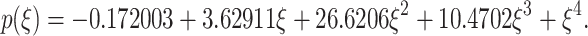 |
31 |
The eigenvalues of the 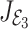 are given by
are given by  We note that
We note that
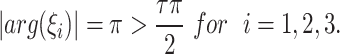 |
but
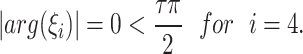 |
This not fulfills the Matignon criterion,then the equilibrium point 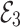 is unstable.
is unstable.
Numerical treatment
In this part, we develop a numerical approach for the fractal–fractional model (4). We use the fractional Adams-Bashforth approach based on two-step Lagrange interpolation polynomials to do this. This method offers a potent combination of accuracy, efficiency, and user-friendliness. Notably, it exhibits rapid convergence to the precise solution, even when employing a substantial discretization step (h), thereby streamlining the overall30,52. We redefine fractal fractional integral equations (17) at 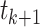 . In reality, these integrals (17) for
. In reality, these integrals (17) for 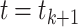 are discretized as follows:
are discretized as follows:
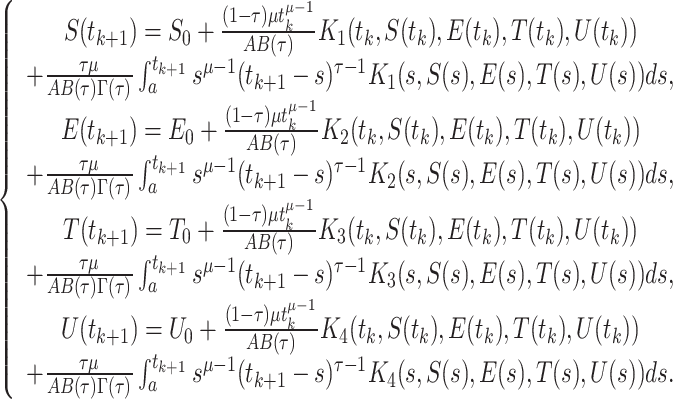 |
32 |
The formulation of the approximation of the integrals mentioned above is as follows:
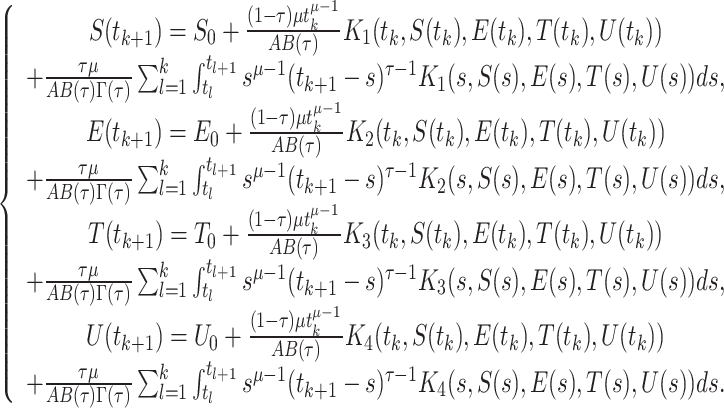 |
After that we use two-step Lagrange interpolation polynomial to approximate 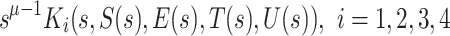 on the interval
on the interval 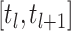 with step size
with step size 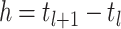 as the following:
as the following:
 |
33 |
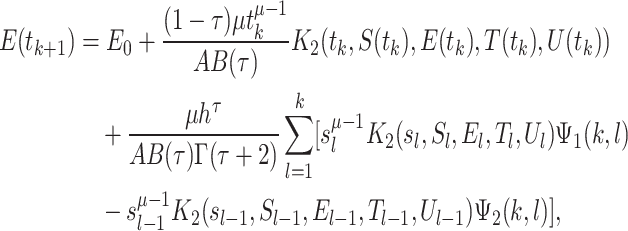 |
34 |
 |
35 |
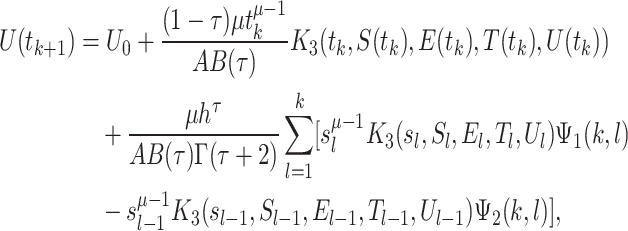 |
36 |
where
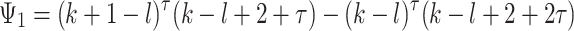 ,
,
 .
.
Discussion and numerical findings
Here, the actual data for initial values  ,
, 
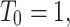 and the parameters in the table is utilized. Table 1 assumed by1 to simulate and describe the dynamic behaviors of the fractals model (4).
and the parameters in the table is utilized. Table 1 assumed by1 to simulate and describe the dynamic behaviors of the fractals model (4).
The study investigates the dynamic behavior of the approximate solution of the model (4) under the influence of various fractional orders, specifically  , through applying the Adams-Bashforth method. When we implemented the algorithms in Mathematica, we got the solution almost as shown in the figures above where: In Fig. 1, we notice that the stem cells decrease and return to the initial value very quickly in the first moments. They decrease until they reach equilibrium, indicating the stem cells’ depletion by chemotherapy. In contrast, in Fig. 2, we notice that the immune cells responding to the treatment decrease in the first days, and then these cells begin to increase until they reach the value 0.9, representing the equilibrium point for this component. In addition, Fig. 3 shows the behavior of cancer cells, as we notice a rapid decrease in cancer cells until they disappear, which is a positive indicator of the response to therapy by chemotherapy and stem cells. In Fig. 4, we notice at the beginning the fluctuation of the concentration of chemotherapy so that it increases very quickly inside the cancer cells, leading to stability. Furthermore, in Figs. 1, 2, 3, and 4, we notice that higher values of
, through applying the Adams-Bashforth method. When we implemented the algorithms in Mathematica, we got the solution almost as shown in the figures above where: In Fig. 1, we notice that the stem cells decrease and return to the initial value very quickly in the first moments. They decrease until they reach equilibrium, indicating the stem cells’ depletion by chemotherapy. In contrast, in Fig. 2, we notice that the immune cells responding to the treatment decrease in the first days, and then these cells begin to increase until they reach the value 0.9, representing the equilibrium point for this component. In addition, Fig. 3 shows the behavior of cancer cells, as we notice a rapid decrease in cancer cells until they disappear, which is a positive indicator of the response to therapy by chemotherapy and stem cells. In Fig. 4, we notice at the beginning the fluctuation of the concentration of chemotherapy so that it increases very quickly inside the cancer cells, leading to stability. Furthermore, in Figs. 1, 2, 3, and 4, we notice that higher values of 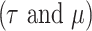 influence how quickly the system approaches equilibrium, representing a more realistic memory.
influence how quickly the system approaches equilibrium, representing a more realistic memory.
Fig. 1.
This figure shows the approximate solution of function S(t) under the influence of different values of the fractional orders 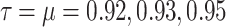 .
.
Fig. 2.
This figure shows the approximate solution of function E(t) under the influence of different values of the fractional orders  .
.
Fig. 3.
This figure shows the approximate solution of function T(t) under the influence of different values of the fractional orders 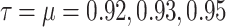 .
.
Fig. 4.
This figure shows the approximate solution of function U(t) under the influence of different values of the fractional orders  .
.
The Fig. 1 highlights the pivotal role of stem cells in fortifying the immune system against cancer by facilitating the regeneration of healthy tissues. Additionally, the effectiveness of chemotherapy in directly targeting and eradicating cancer is visually evident in Figs. 3 and 4. It is noteworthy that chemotherapy, while instrumental in cancer eradication, initially exerts a suppressive effect on the immune system. However, immune cell counts gradually rebound, as depicted in Fig. 2. The model emphasizes the importance of achieving a delicate balance between stem cell-based therapies and chemotherapy to combat cancer while concurrently supporting immune functionality effectively. These simulations confirm the stabilization or stabilization of equilibrium points and provide insight into the system’s behavior under initial conditions.
The visual representations reveal how the stem cells aid in replenishing the effector cell population, enabling a sustained immune response against the tumour cells. Concurrently, the chemotherapy agent exerts cytotoxic effects on the tumour cells, potentially reducing their population. However, as mentioned earlier, chemotherapy can initially suppress the immune system, leading to a temporary decrease in effector cell numbers.
The study’s findings underscore the importance of carefully balancing the stem cell-based immunotherapy and chemotherapy components to maximize their synergistic effects. By leveraging stem cells’ regenerative capabilities and chemotherapy’s direct tumor-killing properties, the model suggests an optimized treatment strategy can be developed, potentially leading to improved cancer management and patient outcomes.
Conclusion
Mathematical modelling is vital in understanding, anticipating, and mitigating the devastating societal impacts of infectious diseases throughout history. Fractional-order derivatives have emerged as a more prevalent and insightful framework for capturing the intricate dynamics of real-world phenomena compared to classical integer-order models. We have presented an integer-order and fractional-order mathematical model describing the interactions between stem cells, immune effector cells, tumour cells, and chemotherapy over time. The theoretical model provides insights into how the introduction of stem cells could potentially boost anti-cancer immune responses while chemotherapy acts to kill tumour cells directly. By fitting the model to experimental data in future work, the contributions of stem cell effects on immune activation could be parsed out from the direct tumoricidal impacts of chemotherapy. Additionally, the fractional-order model enables more precise dynamics capturing than traditional integer-order modelling. Our stability analysis of the fractional system revealed that the equilibrium points are locally stable under the Matignon criterion. To facilitate numerical simulations and explore the model’s dynamics, we employed the Adams-Bashforth method, which is based on two-step Lagrange polynomials to approximate the solutions of the system. The numerical simulation was done using Mathematica. Overall, the quantitative modelling approach presented here furthers understanding of the complex interplay between combination stem cell and chemotherapy treatments, highlighting promising new therapeutic avenues for combating cancer. In the future, continued theoretical developments combined with experimental validation will aid the development of potent immuno-oncology therapies harnessing the power of stem cells. A key avenue for future research involves investigating the controllability of the cancer model, specifically by incorporating the effects of chemotherapy treatment. This would enable the design and analysis of feedback control strategies, where the therapeutic input (chemotherapy dosing) is dynamically adjusted based on the observed response of the system. Also, in the future, it would be interesting to determine whether manipulating external signals can modulate  and
and 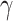 , thereby providing a means to control stem cell self-renewal versus differentiation programmatically.
, thereby providing a means to control stem cell self-renewal versus differentiation programmatically. 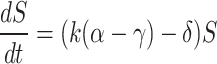 . The research results emphasize the critical need to carefully balance stem cell-based immunotherapy and chemotherapy components to optimize their combined effects. The study demonstrates that by harnessing the regenerative abilities of stem cells in conjunction with the tumor-targeting efficacy of chemotherapy, an optimized treatment strategy can be achieved, potentially improving cancer management and patient outcomes.
. The research results emphasize the critical need to carefully balance stem cell-based immunotherapy and chemotherapy components to optimize their combined effects. The study demonstrates that by harnessing the regenerative abilities of stem cells in conjunction with the tumor-targeting efficacy of chemotherapy, an optimized treatment strategy can be achieved, potentially improving cancer management and patient outcomes.
Author contributions
E.S. and B.S.:Conceptualized the study, developed the mathematical model, and contributed to the theoretical analysis. A.H.: Performed numerical simulations and stability analysis. H.E. and A.K.: Interpreted the results and provided guidance for model validation.
Funding
No funding.
Data availability
No datasets were generated or analysed during the current study.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Alqudah, M. A. Cancer treatment by stem cells and chemotherapy as a mathematical model with numerical simulations. Alex. Eng. J.59(4), 1953–1957 (2020). [Google Scholar]
- 2.Kirschner, D. & Panetta, J. C. Modeling immunotherapy of the tumor-immune interaction. J. Math. Biol.37, 235–252 (1998). [DOI] [PubMed] [Google Scholar]
- 3.Makhlouf, A. M. et al. Mathematical modelling for the role of CD4 + T cells in tumor-immune interactions. Comput. Math. Methods Med.2020 (2020). [DOI] [PMC free article] [PubMed]
- 4.Umar, M., Sabir, Z., Amin, F., Guirao, J. L. & Raja, M. A. Z. Stochastic numerical technique for solving HIV infection model of CD4 + T cells. Eur. Phys. J. Plus135, 1–19 (2020). [Google Scholar]
- 5.Ndenda, J., Njagarah, J. & Shaw, S. Role of immunotherapy in tumor-immune interaction: Perspectives from fractional-order modelling and sensitivity analysis. Chaos Solitons Fractals148, 111036 (2021). [Google Scholar]
- 6.Robertson-Tessi, M., El-Kareh, A. & Goriely, A. A mathematical model of tumor-immune interactions. J. Theor. Biol.294, 56–73 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Zhang, L. et al. Fractal-fractional anthroponotic cutaneous leishmania model study in sense of Caputo derivative. Alex. Eng. J.61(6), 4423–4433 (2022). [Google Scholar]
- 8.Yu, J.-L. & Jang, S.R.-J. A mathematical model of tumor-immune interactions with an immune checkpoint inhibitor. Appl. Math. Comput.362, 124523 (2019). [Google Scholar]
- 9.Ma, X., Luan, Z. & Li, J. Inorganic nanoparticles-based systems in biomedical applications of stem cells: Opportunities and challenges. Int. J. Nanomed. 143–182 (2023). [DOI] [PMC free article] [PubMed]
- 10.Ossanna, R. et al. Multilineage-differentiating stress-enduring cells (muse cells): An easily accessible, pluripotent stem cell niche with unique and powerful properties for multiple regenerative medicine applications. Biomedicines11(6), 1587 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pedersen, R. K. et al. Hsc niche dynamics in regeneration, pre-malignancy, and cancer: Insights from mathematical modeling. Stem Cells41(3), 260–270 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Uçar, E., Özdemir, N. & Altun, E. Qualitative analysis and numerical simulations of new model describing cancer. J. Comput. Appl. Math.422, 114899 (2023). [Google Scholar]
- 13.Miller, K. S. & Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations (Wiley, 1993). [Google Scholar]
- 14.Salah, E. Y. et al., Conformable fractional-order modeling and analysis of HIV/AIDS transmission dynamics. Int. J. Differ. Equ.2024 (2024).
- 15.Khan, H., Gomez-Aguilar, J. F., Abdeljawad, T. & Khan, A. Existence results and stability criteria for ABC-fuzzy-Volterra integro-differential equation. Fractals28(08), 2040048 (2020). [Google Scholar]
- 16.Yadav, P., Jahan, S. & Nisar, K. S. Shifted fractional order Gegenbauer wavelets method for solving electrical circuits model of fractional order. Ain Shams Eng. J.14(11), 102544 (2023). [Google Scholar]
- 17.Khan, H., Khan, A., Chen, W. & Shah, K. Stability analysis and a numerical scheme for fractional Klein-Gordon equations. Math. Methods Appl. Sci.42(2), 723–732 (2019). [Google Scholar]
- 18.Farman, M., Shehzad, A., Akgül, A., Baleanu, D. & De la Sen, M. Modelling and analysis of a measles epidemic model with the constant proportional Caputo operator. Symmetry15(2), 468 (2023). [Google Scholar]
- 19.Hadhoud, A. R., Srivastava, H. M. & Rageh, A. A. Non-polynomial B-spline and shifted Jacobi spectral collocation techniques to solve time-fractional nonlinear coupled Burgers’ equations numerically. Adv. Differ. Equ.2021(1), 439 (2021). [Google Scholar]
- 20.Ravichandran, C., Logeswari, K., Khan, A., Abdeljawad, T. & Gómez-Aguilar, J. F. An epidemiological model for computer virus with Atangana-Baleanu fractional derivative. Results Phys.51, 106601 (2023). [Google Scholar]
- 21.Khan, A., Abdeljawad, T. & Alqudah, M. A. Neural networking study of worms in a wireless sensor model in the sense of fractal fractional. AIMS Math.8(11), 26406–26424 (2023). [Google Scholar]
- 22.Hadhoud, A. R., Agarwal, P. & Rageh, A. A. Numerical treatments of the nonlinear coupled time-fractional Schrödinger equations. Math. Methods Appl. Sci.45(11), 7119–7143 (2022). [Google Scholar]
- 23.Liu, X., Arfan, M., Ur Rahman, M. & Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Engin.26(1), 98–112 (2023). [DOI] [PubMed] [Google Scholar]
- 24.Khan, M. A., DarAssi, M. H., Ahmad, I., Seyam, N. M. & Alzahrani, E. The transmission dynamics of an infectious disease model in fractional derivative with vaccination under real data. Comput. Biol. Med.181, 109069 (2024). [DOI] [PubMed] [Google Scholar]
- 25.Meetei, M. Z. et al. Analysis and simulation study of the HIV/AIDS model using the real cases. Plos One19(6), e0304735 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Addai, E. et al. A nonlinear fractional epidemic model for the Marburg virus transmission with public health education. Sci. Rep.13(1), 19292 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Agarwal, P., Ramadan, M. A., Rageh, A. A. & Hadhoud, A. R. A fractional-order mathematical model for analyzing the pandemic trend of COVID-19. Math. Methods Appl. Sci.45(8), 4625–4642 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li, B., Eskandari, Z. & Avazzadeh, Z. Dynamical behaviors of an SIR epidemic model with discrete time. Fractal Fract.6(11), 659 (2022). [Google Scholar]
- 29.ur Rahman, M., Althobaiti, A., Riaz, M. B. & Al-Duais, F. S. A theoretical and numerical study on fractional order biological models with Caputo Fabrizio derivative. Fractal Fract.6(8), 446 (2022). [Google Scholar]
- 30.Yadav, P., Jahan, S. & Nisar, K. S. Fractional order mathematical model of Ebola virus under Atangana-Baleanu-Caputo operator. Results Control Optim.13, 100332 (2023). [Google Scholar]
- 31.Yadav, P., Jahan, S., Shah, K., Peter, O. J. & Abdeljawad, T. Fractional-order modelling and analysis of diabetes mellitus: Utilizing the Atangana-Baleanu Caputo (ABC) operator. Alex. Eng. J.81, 200–209 (2023). [Google Scholar]
- 32.Ahmed, S., Jahan, S. & Nisar, K. S. Hybrid Fibonacci wavelet method to solve fractional-order logistic growth model. Math. Methods Appl. Sci.46(15), 16218–16231 (2023). [Google Scholar]
- 33.Nisar, K. S., Farman, M., Abdel-Aty, M. & Cao, J. A review on epidemic models in sight of fractional calculus. Alex. Eng. J.75, 81–113 (2023). [Google Scholar]
- 34.Aliasghari, G., Mesgarani, H., Nikan, O. & Avazzadeh, Z. On fractional order model of tumor growth with cancer stem cell. Fractal Fract.7(1), 27 (2022). [Google Scholar]
- 35.Özköse, F., Şenel, M. T. & Habbireeh, R. Fractional-order mathematical modelling of cancer cells-cancer stem cells-immune system interaction with chemotherapy. Math. Model. Numer. Simul. Appl.1(2), 67–83 (2021). [Google Scholar]
- 36.Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals102, 396–406 (2017). [Google Scholar]
- 37.Atangana, A. & Goufo, E. F. D. Some misinterpretations and lack of understanding in differential operators with no singular kernels. Open Phys.18(1), 594–612 (2020). [Google Scholar]
- 38.Asamoah, J. K. K. Fractal-fractional model and numerical scheme based on Newton polynomial for Q fever disease under Atangana-Baleanu derivative. Results Phys.34, 105189 (2022). [Google Scholar]
- 39.Haidong, Q. et al. Fractal–fractional dynamical system of Typhoid disease including protection from infection. Eng. Comput. 1–10 (2021).
- 40.Khan, H., Li, Y., Khan, A. & Khan, A. Existence of solution for a fractional-order Lotka-Volterra reaction-diffusion model with Mittag-Leffler kernel. Math. Methods Appl. Sci.42(9), 3377–3387 (2019). [Google Scholar]
- 41.Li, B., Zhang, T. & Zhang, C. Investigation of financial bubble mathematical model under fractal-fractional Caputo derivative. Fractals31(05), 1–13 (2023). [Google Scholar]
- 42.Shah, K., Abdalla, B., Abdeljawad, T. & Alqudah, M. A. A fractal-fractional order model to study multiple sclerosis: A chronic disease. Fractals 2440010 (2024).
- 43.Rezapour, S. et al. On the fractal-fractional Mittag-Leffler model of a COVID-19 and Zika Co-infection. Results Phys.55, 107118 (2023). [Google Scholar]
- 44.Kanwal, T. et al. Dynamics of a model of polluted lakes via fractal-fractional operators with two different numerical algorithms. Chaos Solitons Fractals181, 114653 (2024). [Google Scholar]
- 45.Rezapour, S., Etemad, S., Avcı, İ, Ahmad, H. & Hussain, A. A study on the fractal-fractional epidemic probability-based model of SARS-CoV-2 virus along with the Taylor operational matrix method for its Caputo version. J. Funct. Spaces2022(1), 2388557 (2022). [Google Scholar]
- 46.Farman, M., Sarwar, R. & Akgul, A. Modeling and analysis of sustainable approach for dynamics of infections in plant virus with fractal fractional operator. Chaos Solitons Fractals170, 113373 (2023). [Google Scholar]
- 47.Farman, M., Batool, M., Nisar, K. S., Ghaffari, A. S. & Ahmad, A. Controllability and analysis of sustainable approach for cancer treatment with chemotherapy by using the fractional operator. Results Phys.51, 106630 (2023). [Google Scholar]
- 48.Jan, R., Razak, N. N. A., Qureshi, S., Ahmad, I. & Bahramand, S. Modeling Rift Valley fever transmission: Insights from fractal-fractional dynamics with the Caputo derivative. Math. Model. Control4(2), 163–177 (2024). [Google Scholar]
- 49.Atangana, A. & Araz, S. I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications (Academic Press, 2021). [Google Scholar]
- 50.Matignon, D. Stability results on fractional differential equations with applications to control. In Proceedings of Computational Engineering in Systems and Application Multiconference, vol. 2 9633–968.
- 51.Ahmed, E., El-Sayed, A. & El-Saka, H. A. On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A358(1), 1–4 (2006). [Google Scholar]
- 52.Toufik, M. & Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus132, 1–16 (2017). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets were generated or analysed during the current study.






