Eutrophication of aquatic ecosystems: Bistability and soil phosphorus

Abstract

Eutrophication (the overenrichment of aquatic ecosystems with nutrients leading to algal blooms and anoxic events) is a persistent condition of surface waters and a widespread environmental problem. Some lakes have recovered after sources of nutrients were reduced. In others, recycling of phosphorus from sediments enriched by years of high nutrient inputs causes lakes to remain eutrophic even after external inputs of phosphorus are decreased. Slow flux of phosphorus from overfertilized soils may be even more important for maintaining eutrophication of lakes in agricultural regions. This type of eutrophication is not reversible unless there are substantial changes in soil management. Technologies for rapidly reducing phosphorus content of overenriched soils, or reducing erosion rates, are needed to improve water quality.

Limnologists have long studied the processes that cause some lakes to have low concentrations of algae (oligotrophic) and others to become highly turbid due to algae blooms, or eutrophic (1, 2). This research has led to understanding of eutrophication, a significant environmental problem. Consequences of eutrophication include excessive plant production, blooms of harmful algae, increased frequency of anoxic events, and fish kills. Economic losses attributed to eutrophication include costs of water purification for human use, losses of fish and wildlife production, and losses of recreational amenities (3). Eutrophication has become a global problem that is likely to intensify in coming decades because of increases in human population, demand for food, land conversion, fertilizer use, and nitrogen deposition (4).

Eutrophication of lakes is caused by overenrichment with nutrients, principally phosphorus (5). Excess phosphorus inputs to lakes usually come from sewage, industrial discharges, and runoff from agriculture, construction sites, and urban areas. Over time, many countries have regulated point sources of nutrients, such as municipal and industrial discharges. Nonpoint sources of nutrients, such as runoff from agricultural or urban lands, have replaced point sources as the driver of eutrophication in many regions (6). An important driver of nonpoint nutrient input is excessive application of fertilizer or manure, which causes phosphorus to accumulate in soils (7). Phosphorus-rich soils are washed into lakes, where some of the phosphorus dissolves and stimulates growth of phytoplankton and aquatic plants.

Oligotrophic conditions are usually stable, because the return of phosphorus from sediments is low, thereby limiting the growth of algae. Similarly, the eutrophic condition is stabilized by recycling of phosphorus from sediments within the lake. But many shallow (thermally unstratified) lakes display alternate stable states. One is a clear water state, with low algae but abundant rooted aquatic plants, whereas the other is a turbid state where shading by abundant algae suppresses rooted plants (8, 9). Some lakes change between these states from time to time, whereas others persist for years in either the clear water or turbid state. The reasons for the differences in stability have been the subject of many investigations (8). In deeper (thermally stratified) lakes, the stabilization can involve several factors, including biogeochemistry of the deep layer of water (hypolimnion), temperature of the hypolimnion, shape of the lake basin, abundance of rooted plants, and food web structure (10, 11). Regardless of lake depth, recycling can under some conditions maintain a persistent eutrophic regime. In principle, and sometimes in practice, the eutrophic regime can be destabilized by management interventions, thereby changing the lake toward the clear-water regime (9, 12, 13).

Lake eutrophication has proven to be a stubborn environmental problem (6, 12). Instead of alternating regimes, many lakes remain eutrophic for extended periods of time. Causes of slow recovery, or nonrecovery, from eutrophication are multiple and not entirely understood. Persistent eutrophication could be due to internal recycling from a large pool of phosphorus in sediments, leading to alternative stable states. Chronic release of phosphorus from enriched soils may also explain persistent eutrophication. This paper evaluates the roles of internal recycling and slow dynamics of soil phosphorus, using a general model of phosphorus dynamics in stratified lakes and their watersheds. Results suggest that dynamics of soil phosphorus may control alternate stable states, potentially causing eutrophication to last for centuries. Viewed from the perspective of a human lifetime, eutrophication is often a one-way trip.

Soil and Sediment Phosphorus: Role in Eutrophication

Phosphorus enters the biosphere by weathering or mining. At present, the annual global mining flux (≈18.5 Tg·y^-1 and weathering flux (15-20 Tg·y^-1) are similar in magnitude (7). Although the river-borne flux of phosphorus to the sea has tripled since preindustrial times, much of the additional phosphorus input to the biosphere is accumulating in continental ecosystems. At present, continental ecosystems are accumulating 10.5-15.5 Tg·y^-1 of phosphorus (7). Most of this accumulation occurs in agricultural soils as a consequence of fertilizer application in excess of crop needs (7). Phosphorus accumulation appears to be patchy, leading to large variance in soil phosphorus among different regions. In regions with high soil phosphorus concentrations, erosion of soil particles into streams and lakes is an important driver of eutrophication.

Phosphorus that enters lakes tends to accumulate in the sediments and the biota. Phosphorus can be recycled to lake water from sediments (14) and consumers (15). Recycling from sediments varies with annual cycles of mixing, and also over longer time horizons of decades to millennia as sediments build up in lakes. Recycling from consumers varies over shorter periods of days to years. At these shorter time scales, alternate regimes of phosphorus cycling could perhaps exist in lakes. Here, I focus on longer-term dynamics associated with sediment and soil phosphorus.

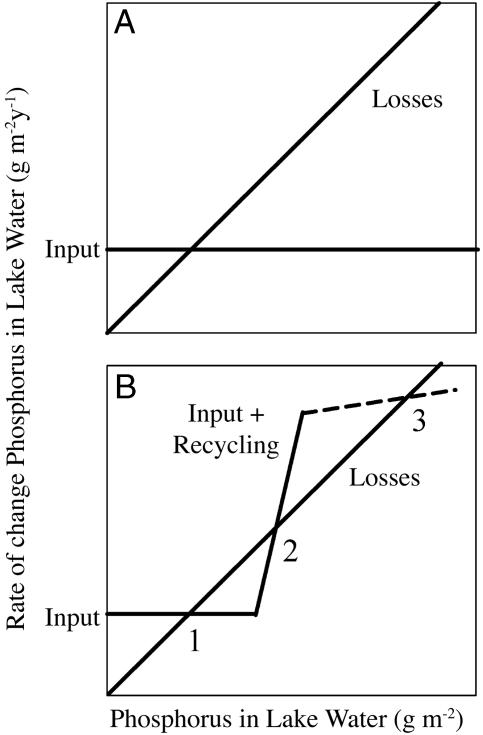
If recycling is negligible compared to loss rates of phosphorus from the lake water, then lake phosphorus cycles are expected to have one stable equilibrium point (e.g., the intersection of the two lines in Fig. 1A). Such a lake could have high levels of phosphorus in the water if inputs were high, but phosphorus levels could be decreased immediately by decreasing the inputs. Examples are known from experimental lakes (16). Some eutrophic lakes with slow recycling rates have responded rapidly to remediation of phosphorus inputs, as suggested by Fig. 1A (12, 17).

Fig. 1.

Rate of change of phosphorus in lake water (g·m^-2·y^-1) versus density of phosphorus in lake water (g·m^-2) in hypothetical situations with no recycling (A) or recycling faster than losses over some range of phosphorus in lake water (B).

If the recycling rate increases more steeply than the loss rates over some range of phosphorus, an unstable equilibrium can occur (intersection 2 in Fig. 1B). Eventually, the rate of recycling may level off due to declining amounts of recyclable phosphorus or some other factor (dashed line in Fig. 1B), leading to a second stable equilibrium (intersection 3 in Fig. 1B). If the phosphorus cycle was near intersection 3, returning it to intersection 1 might require extreme reductions of input, long time delays, or manipulations to cross the unstable equilibrium at point 2, depending on details of rate curves (18). Rapid recycling rates are known from some enriched lakes (14, 19). Various mechanisms for increased phosphorus release from enriched sediments of different lakes have been investigated (14, 19-22). Some eutrophic lakes have failed to respond, or responded with long delays, to decreases in phosphorus input because of rapid recycling from sediments (12, 17, 23-25), thereby demonstrating the effectiveness of recycling in maintaining a eutrophic state.

Model and Simulations

I used a model to compare the roles of soil and sediment phosphorus in eutrophication. The model, which was modified slightly from previous papers (10, 18, 26), is a system of differential equations for phosphorus density (g·m^-2) in soil (U), lake water (P), and surface sediment (M). The differential equations are

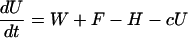[1]

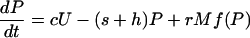[2]

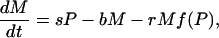[3]

where

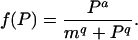[4]

Parameters of the model are defined in Table 1. Soil phosphorus density is expressed per unit lake area to facilitate comparisons with phosphorus densities in lake water and sediment. Previous research has addressed the stochastic version of the model, in which the flux from watershed to lake cU_t is subjected to random shocks. This paper sets the shocks to zero to focus on the deterministic skeleton of the model. Values of the parameters were estimated for the watershed of Lake Mendota, Wisconsin (10, 27). These parameters are consistent with estimates of presettlement phosphorus inputs (28) and modern measurements of phosphorus inputs (29).

Table 1. Model parameters, nominal values, and source.

Symbol	Definition	Units	Nominal value	Source
h	Permanent burial rate of sediment P	y−1	0.001	10
c	P runoff coefficient	y−1	0.00115	Calculated from ref. 27
F	Annual agricultural import of P to the watershed per unit lake area	g·m−2·y−1	31.6	27
h	Outflow rate of P	y−1	0.15	10
H	Annual export of P from the watershed in farm products, per unit lake area	g·m−2·y−1	18.6	27
m	P density in the lake when recycling is 0.5 r	g·m−2	2.4	10
r	Maximum recycling rate of P	g·m−2·y−1	0.019	10
q	Parameter for steepness of f(P) near m	Unitless	8	10
s	Sedimentation rate of P	g·m−2·y−1	0.7	10
W	Nonagricultural inputs of P to the watershed prior to disturbance, per unit lake area	g·m−2·y−1	0.147	Calculated from ref. 27
WD	Nonagricultural inputs of P to the watershed after distrubance, per unit lake area	g·m−2·y−1	1.55	Calculated from ref. 27

Areal unit; are based on the area of the lake, not the area of the watershed.

Two simulations were calculated to illustrate changes of the system over time. The first 250 years of each simulation are a highly simplified representation of the history of Lake Mendota and other lakes in agricultural regions (30). The remaining years of each simulation illustrate contrasting management policies for soil phosphorus. Simulations were initiated at stable equilibrium values calculated with F = H = 0 and W for undisturbed conditions. These represent presettlement conditions, and were maintained for years 0-100. For years 100-200, W was changed to the value for disturbed conditions (W_D, Table 1), representing the advent of agriculture in the region. For years 200-250, F and H were increased to the values estimated for a period of intensive industrialized agriculture in the Lake Mendota watershed, and W was maintained at W_D (Table 1). After year 250, the simulations were different. Simulation 1 represents management to balance the phosphorus budget of agriculture. In this simulation, after year 250 F = H and W is maintained at W_D. Simulation 2 represents management to balance the phosphorus budget of agriculture and decrease W. In this simulation, after year 250, F = H and W is set at the predisturbance value.

Equilibria were calculated numerically using matlab. Turnover times (y) near stable equilibria U^*, P^*, and M^* were estimated as 1/c, P^*/(cU^*), and M^*/(sP^*), respectively. Simulations were calculated by using the fourth-order Runge-Kutta method. During the simulations, stability of the lake water-sediment subsystem was determined by holding U constant and solving for roots of equations 2 and 3. These indicate the transient status of the lake subsystem (one clear-water attractor, one turbid-water attractor, or bistable).

Results

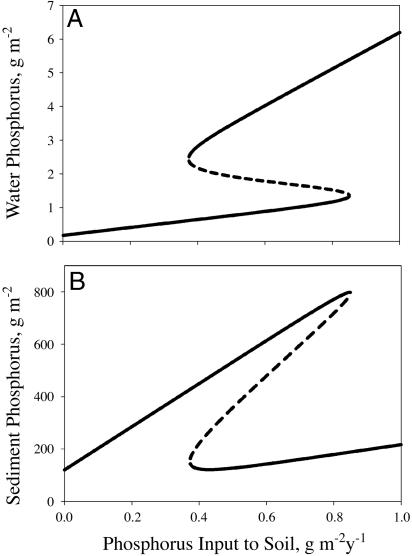
The model was bistable for soil fertilization rates of ≈0.38-0.85 g·P·y^-1·m^-2 lake area (Fig. 2). Under predisturbance conditions (W = 0.147), there was one stable equilibrium with relatively low levels of phosphorus in the water, corresponding to a clear-water state. After disturbance (W_D = 1.55), but with no net input from agriculture (F = H), there was one stable equilibrium with relatively high levels of phosphorus in the water, corresponding to a turbid state. At intermediate levels of phosphorus input to the soil, there were two stable equilibria separated by an unstable equilibrium. Note that levels of phosphorus input during intensive agriculture (W+ F - H, Table 1) are far to the right of the x axis of Fig. 2. Under such heavily enriched conditions, the model has only one turbid-water equilibrium.

Fig. 2.

Equilibria of the model with nominal parameter values versus net rate of phosphorus input to soil W + F - H. Solid lines are stable points, dashed lines are repellors. (A) P density in water (g·m^-2). (B) P density in surface sediment (g·m^-2).

The turnover time for soil phosphorus was ≈870 years. Turnover times for water and sediment phosphorus depend on whether the lake is in the clear or turbid condition. In the clear state, turnover time for water phosphorus was ≈1.2 years, whereas that for sediment phosphorus was ≈1,000 years. In the turbid state, the water and sediment turnover times became more similar: ≈5.4 years for water phosphorus and ≈50 years for sediment phosphorus.

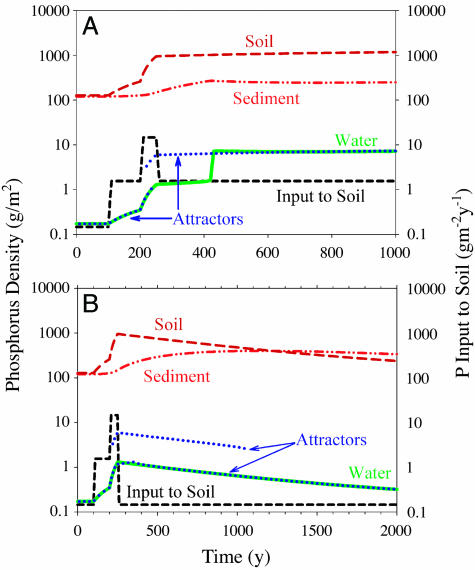
Simulations illustrated the slow recovery of the system from over-enrichment (Fig. 3). In both simulations, lake water phosphorus increased gradually when W increased in year 100, and rose more steeply after agriculture became intensive in year 200. The lake subsystem had one clear-water attractor from years 0-220, two attractors from years 220-240, and one turbid-water attractor from years 240-250. After year 250, the simulations were different.

Fig. 3.

Phosphorus density (g·m^-2) in soil (brown), sediment (red), and water (green), and phosphorus input rate to soil (black, g·m^-2·y^-1) versus time in two simulations. Attractors (blue) are shown for water phosphorus density. Note log scale of the y axes, and different x axis scales of the two plots. (A) Simulation 1. (B) Simulation 2.

In simulation 1 (Fig. 3A), the phosphorus budget of agriculture was balanced after year 250, but other inputs remained at the postdisturbance rate. Soil phosphorus remained nearly constant at a relatively high value. After year 240, the lake subsystem had only one turbid-water attractor for the remainder of the simulation. Near year 400, sediment phosphorus peaked and water phosphorus rose sharply to a high value near the turbid-water attractor. The high level of water phosphorus was sustained for the remainder of the simulation.

In simulation 2 (Fig. 3B), the phosphorus budget of agriculture is balanced after year 250, and phosphorus inputs to the soil return to the predisturbance rate. After year 250, the decline of water phosphorus parallels that of soil phosphorus for the remainder of the simulation. Sediment phosphorus is maximal near year 1100. The lake subsystem had one attractor from years 240 to 350, two attractors from years 350 to 1060, and one attractor after year 1060. The lake did not switch to the turbid attractor during the period of bistability.

Discussion

Although the model presented here is relatively simple, it represents the process of lake eutrophication and the most common mitigation strategies. Watershed soils are linked to nonpoint phosphorus inputs. Direct discharges of phosphorus (point inputs) can be considered by adding a constant input to Eq. 2. Stochastic inputs can be considered (10, 18, 26). The most common methods of mitigating eutrophication (13) can be represented, for example, watershed management practices (modify W, F, H, or c), flushing (increase h), chemical immobilization of sediment phosphorus (decrease r), or food web manipulation (increase s).

Parameters for recycling are constrained only weakly by existing data (10, 18). Analyses presented here should be regarded as an illustration of what may happen, according to one parameter set and one model. Despite these uncertainties, it appears that slow dynamics of soil phosphorus can set the tempo of eutrophication for lakes in agricultural watersheds. Slow recovery of water phosphorus, in parallel with slow dynamics of soil phosphorus, occurs even in simple linear analyses of watershed-lake systems (31). This paper focused on thermally stratified lakes, but the same effects of soil phosphorus should apply to shallow lakes.

The eutrophic state persisted for hundreds of years in this model. Although recycling from sediments caused bistability, it was slow depuration of soil phosphorus that retarded recovery from eutrophication. In the bistable condition, there is risk of switching from the clear-water attractor to the turbid one after a perturbation. However, bistability also opens the possibility of accelerating the lake's recovery from eutrophication in certain situations. A bistable eutrophic system could be moved to the clear-water equilibrium by a stochastic event (32) or a deliberate management intervention to reduce recycling (13).

Eutrophication can be caused by point inputs of phosphorus (such as sewage discharges) or nonpoint inputs of phosphorus (such as runoff from agriculture). Trajectories of eutrophication and recovery may differ, depending on whether most of the phosphorus comes from point or nonpoint inputs. In developed nations, most freshwater eutrophication is caused by nonpoint phosphorus inputs, principally from agriculture (6). In developing nations, the situation is mixed but trends in fertilizer use suggest that nonpoint phosphorus inputs will grow (4, 7). In these situations, decreasing soil phosphorus is an important step toward mitigation of eutrophication. Simply balancing the agricultural phosphorus budget is not sufficient to decrease soil phosphorus and mitigate eutrophication (Fig. 3A). Soil phosphorus density must decline to improve water quality. Once soil phosphorus is decreasing, other useful interventions may include steps to decrease transport of phosphorus in surface waters and manipulations to decrease phosphorus recycling within lakes (6, 13).

Widespread eutrophication by anthropogenic nutrient inputs is a relatively recent environmental problem. Intensive fertilization of agricultural soils and associated nonpoint inputs of phosphorus increased through the middle of the 20th century (6, 7). Analyses presented here show that it could take 1,000 years or more to recover from eutrophication caused by agricultural overenrichment of soils. In principle, eutrophication is reversible, but from the perspective of a human lifetime, lake eutrophication can appear to be permanent unless there are substantial changes in soil management. Technologies for rapidly reducing the phosphorus content of overenriched soils, or reducing erosion rates, could greatly accelerate improvements in water quality.