Evolution through genetically controlled allometry space

Abstract

Understanding evolutionary change requires phenotypic differences between organisms to be placed in a genetic context. However, there are few cases where it has been possible to define an appropriate genotypic space for a range of species. Here we address this problem by defining a genetically controlled space that captures variation in shape and size between closely related species of Antirrhinum. The axes of the space are based on an allometric model of leaves from an F₂ of an interspecific cross between Antirrhinum majus and Antirrhinum charidemi. Three principal components were found to capture most of the genetic variation in shape and size, allowing a three-dimensional allometric space to be defined. The contribution of individual genetic loci was determined from QTL analysis, allowing each locus to be represented as a vector in the allometric space. Leaf shapes and sizes of 18 different Antirrhinum taxa, encompassing a broad range of leaf morphologies, could be accurately represented as clouds within the space. Most taxa overlapped with, or were near to, at least one other species in the space, so that together they defined a largely interconnected domain of viable forms. It is likely that the pattern of evolution within this domain reflects a combination of directional selection and evolutionary tradeoffs within a high dimensional space.

Many of the morphological differences between species involve modifications in shape and size, yet the basis of these changes is poorly understood. Addressing this problem requires a quantitative genetic framework that allows differences between species to be evaluated in relation to gene action. Such a framework should incorporate allometric relationships, as changes in size are often accompanied by changes in shape (1), reflecting an interaction between developmental and selective constraints. Much progress has been made in quantifying shape or size variation between species, ecotypes, and varieties by using numerical methods (2–6), and in some cases genes underlying this variation have been defined by QTL analysis (7–9). However, so far, these approaches have not been combined to allow variation between a range of species to be placed in a genetic context. Here we address this problem for the case of interspecific variation in Antirrhinum.

There are ≈20 different Antirrhinum species closely related to the model plant, Antirrhinum majus. These species grow in southwestern Europe, and show considerable phenotypic divergence including substantial variation in the shape and size of their organs (10, 11). With the exception of Antirrhinum siculum, all can be crossed with each other and with cultivated A. majus to give fertile hybrids, allowing analysis of F₂ populations. The close relationship between these species is further supported by available molecular phylogenies (12). Given their close relationship, it is arguable that many of these species represent subspecies or races. However, for convenience and simplicity, we will refer to them as species throughout this paper, reflecting their divergent appearances and ecologies. Unlike many domesticated species, the morphology of cultivated A. majus does not differ greatly from that of its closest wild relatives, presumably reflecting the shorter period of domestication and lack of intense artificial selection.

To create a genetic framework for evaluating species differences, we have chosen Antirrhinum charidemi as a convenient species for crosses with A. majus (Fig. 1). A. charidemi is endemic to a single rocky outcrop on the southern coast of Spain and has relatively small flowers and leaves. The species is effectively isolated from other populations of Antirrhinum by an extensive, inhospitable plain. Sequence analysis indicates that A. charidemi forms a well defined sister-group to other Antirrhinum species (ref. 12 and our unpublished results). The small organ size of A. charidemi is thought to reflect an adaptation to drought: this species lives in the driest place in Europe with an annual rainfall of only 122 mm and a climate of the warm desert type (13).

Fig. 1.

Comparison between A. charidemi (Left) and A. majus (Right). (A) Individual flowers in side view. (B) Leaves from node 4. (C) Whole plants. (Scale bars, 1 cm in A and B and 10 cm in C.)

Several approaches have been used to quantify and genetically map variation in shape and size of biological structures. One is to use key measurements, such as area, length, and width (14–16). This method has the advantage of simplicity, but does not enable shape reconstruction from the data. Therefore, it is unclear whether all of the relevant shape information has been captured. Moreover, correlations between different measurements are not automatically assessed, so the final metrics may not be the most economical for describing the variation. Another approach is to use numerical methods to align objects and then capture their shape and size with a set of parameters, such as coordinate values (17, 18) or descriptors from elliptic Fourier analysis (reviewed in refs. 4, 6, 7, and 19). Principal component analysis (PCA) on the parameters then allows the major sources of variation to be identified. If this method is applied to a genetically segregating population, it should automatically identify the major components relating to genetic variation.

Here we apply numerical shape and size analysis to leaves from a mapped F₂ population derived from a cross between A. majus and A. charidemi. We show that three principal components (PCs) account for most of the shape and size variation in the F₂, reflecting the action of at least 15 QTL. This finding allows a three-dimensional allometric space to be defined in which each species of Antirrhinum can be represented as a cloud of points. Even though A. majus and A. charidemi do not differ greatly in shape, the allometric space can capture most of the shape variation between species, suggesting that the genetic control systems defined are representative of the species group as a whole. The species clouds form a largely interconnected region, defining a domain of allometric space through which evolution has occurred. The genetic and environmental factors that may constrain and drive evolution within this domain are discussed.

Methods

Plant Material. An F₂ population of 204 plants originating from a single F₁ hybrid of A. majus (JIC stock 7) × A. charidemi plant were grown together in controlled glasshouse conditions. All species accessions came from seeds harvested in the wild (for each species, a single wild capsule was sown), so it is possible that some variation between species reflects maternal effects. Accession locations, references, and numbers of sampled plants are summarized in Table 2, which is published as supporting information on the PNAS web site.

Data Capture and Measurements. Fully expanded node 4 leaves were sampled ≈4 months after sowing, when plants had fully flowered (cotyledons are at node 1). Leaves were removed from the plants, glued onto paper, and either scanned or photographed with a scale bar.

Allometry Model. All images were scaled to the same resolution (6 pixels per mm) and rotated to make every leaf horizontal. A leaf point model was created in matlab, with a function pmcreate in the Visicast package (available on request, see Supporting Text, which is published as supporting information on the PNAS web site). Nineteen points were placed around and within the leaf silhouette (Fig. 2). Point coordinates were saved as a separate array file for each leaf. A point distribution model was then built from the coordinates by PCA using the buildpdm function from Visicast without distinction between primary and secondary points.

Fig. 2.

Points used to capture leaf shape. Primary points (black circles) are placed at key landmarks and secondary points (white circles) are automatically spaced at equal intervals between primary points.

Genetic Map of the F₂ Population Between A. majus and A. charidemi. A genetic map was constructed by genotyping all members of the F₂ population for 237 dominant and 54 codominant markers (unpublished data). Redundant information from markers mapping at the same position in coupling was eliminated and dominant markers in repulsion converted to synthetic codominant loci. The resulting map resolved the eight Antirrhinum chromosomes and consisted of 96 codominant and 78 dominant loci, with an average interval of 4.0 cM.

QTL affecting PC values were identified by step-wise regression in QTL Express (20), allowing for both additive and dominance effects of QTL alleles. The significance of the QTL was assessed by the Churchill and Doerge method (21) implemented in QTL Express. At each stage, the most significant QTL was fixed as a cofactor and the genome rescanned until no further QTL could be detected with at least 95% confidence. The position, effect, and likelihood of each QTL were then recalculated with all other QTL affecting the same PC fixed as cofactors. To represent each QTL as a vector, its effect on all three PC values was estimated. To reduce the effects of linked QTL on these estimates, they were calculated by regression in QTL Express under conditions in which all other QTL affecting the PC were fixed as cofactors. Each QTL effect on PC values represents the mean effect of substituting both A. charidemi alleles at the most likely position for the QTL with alleles from A. majus.

Results

The outlines of leaves from an F₂ population of A. majus × A. charidemi were captured from digital images. For each image, the coordinates of 19 points along the leaf margin and mid-vein were recorded (Fig. 2). These included six primary points, which were manually placed at recognizable landmarks: one at the base of the petiole, two at the base of the lamina, two at the points of the maximum leaf width, and one at the tip of the leaf. The other 13 points, termed secondary points, were placed in between the landmarks and automatically spaced at equal intervals (Fig. 2).

Joining the 19 points with straight lines captured the main features of the leaf outline. Thus, 38 coordinate values (two per point) provided a numerical summary of the shape and size of the leaf. Data for each leaf were manually rotated such that the mid-vein was horizontal and automatically centered by using the centroid of the coordinate values. This procedure was applied to each of two leaves from node 4 of 173 F₂ plants, giving a data set of 38 × 173 × 2 = 13,148 coordinate values.

The coordinate values showed much greater variation between than within genotypes. For example, the variance in coordinate values taken at the widest point of the leaf was ≈32 times greater between plants than between leaf pairs of the same plants, suggesting that up to 95% of the variation had a genetic basis. The values showed near normal distributions on either absolute or logarithmic scales, compatible with both additive and multiplicative gene effects (data not shown).

The coordinates define a 38 dimensional space in which each axis represents variation in one of the coordinate values. Each leaf shape can be represented as a single point in this space, and therefore all of the leaf shapes in the F₂ together define a cloud of points. The means of each of the 38 coordinate values defines the center of the cloud, corresponding to the mean leaf shape. To facilitate further analysis, the 38 mean values were subtracted from the data so that the mean leaf shape was centered at the origin. Therefore, the position of each leaf shape corresponded to its deviation from the mean.

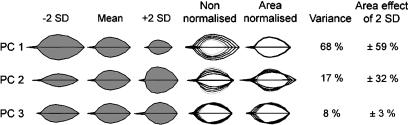
Because the points along the leaf outlines are correlated, most of the F₂ variation can be captured with far fewer than 38 axes. This smaller set of axes was defined through PCA, which uses linear correlations between data to define orthogonal axes that capture maximal trait variance. PCA revealed that 92% of the variation could be captured with three orthogonal axes, termed PCs. PCs were numbered according to the amount of variation they captured, so that PC1 accounted for 68%, PC2 accounted for 17%, and PC3 accounted for 8% of the variation. These PCs constitute an allometric leaf model, which efficiently captures the variation in leaf shape and size. Using this model, each leaf shape could be described with three PC values, corresponding to the deviation from the mean along each PC. The three PCs therefore defined axes of a three-dimensional space, in which each leaf could be represented as a point. We refer to this space as allometric leaf space.

Variation in values along each PC was significantly greater between than within genotypes, indicating that this variation was under genetic control (up to 97% of the variance was explained by genotype). The contribution of each PC to leaf shape and size is illustrated in Fig. 3. Variation in PC1 values had a major effect on area and a slight effect on shape. Variation in PC2 values had an allometric effect, influencing both shape and area. As the value of PC2 was changed from low to high, leaf shape changed from lanceolate to deltoid and leaves became larger. Varying PC3 values also had an allometric effect, although proportionate effect on size was less than for PC2 values. Because growth occurs exponentially during much of development, the PCs were also calculated after first transforming the data to a logarithmic scale. This gave qualitatively similar results (data not shown).

Fig. 3.

Leaf shapes and sizes described by variation along the first three PCs of the leaf allometry model. For each PC, the mean outlines together with outlines corresponding to PC values deviating by -2 standard deviations (-2 SD) or +2 standard deviations (+2SD) from the mean are shown in gray. Leaf outlines corresponding to -2, -1, 0, +1, +2 standard deviations from the mean are also shown overlaid with or without normalization to the same area. For each PC, the percentage variance explained and the effect on leaf area of varying the PC value by 2 standard deviations is shown on the right.

To map the genes controlling leaf shape, the PC values for each leaf were used as traits for QTL mapping. The positions of the loci underlying variation along each PC are shown in Table 1 and Fig. 7, which is published as supporting information on the PNAS web site. This analysis showed that four loci could account for 43% of variation along PC1, four loci for 54% of the variation along PC2, and three loci for 23% of the variation along PC3. Three minor effect loci were found to account for a further 12% of the variance along PC1 and one minor effect locus for a further 2.8% of the variance along PC2. Loci were named according to the PC values they mainly affected (e.g., LF1 refers to a locus affecting mainly PC1 values) and according to the magnitude of the effect (e.g., LF2.1 is the locus explaining the most variance along PC2). A. majus alleles at the loci were over-dominant (one case), dominant (four cases), acted additively (eight cases), or were recessive (two cases). For PC1, all QTL alleles acted in the same direction as the parental difference (positive direction), whereas for PC2 and PC3, alleles acted in both positive and negative directions. Epistatic interactions were detected between loci, but there were no consistent trends so that overall the effects of these interactions tended to cancel each other out.

Table 1. Mapping variation in PC values by QTL analysis.

				Variance explained, %‡			Additive effect, ×2§
QTL	Position*	LOD	Dominance effect†	PC1	PC2	PC3	PC1	PC2	PC3	Angle¶, °
LF1.1	7:25	16.0	0.02	19.9	0.01	0.05	–1.40	0.18	0.35	16
LF1.2	4:55	10.0	–0.31	12.2	0.99	1.31	–0.90	–0.46	–0.32	32
LF1.3	3:55	8.3	–0.39	8.57	0.23	1.05	–1.02	0.20	–0.28	19
LF1.4	1:24	5.2	–0.12	4.98	0.34	0.79	–0.65	0.20	0.01	17
LF1.5	8:72	4.6	–0.24	4.21	0.23	1.83	–0.58	0.09	0.40	35
LF1.6	8:32	4.3	–0.37	4.50	0.23	0.79	–0.40	0.15	0.04	21
LF1.7	1:82	3.8	0.10	3.43	0.69	1.83	–0.58	0.29	–0.47	43
LF2.1	2:45	16.1	0.18	0.21	18.7	0.26	0.17	1.22	0.27	15
LF2.2	4:39	12.5	0.25	0.64	17.0	0.79	–0.41	–1.13	–0.41	27
LF2.3	8:34	9.4	0.26	0.45	10.6	0.52	–0.03	1.00	0.15	9
LF2.4	6:5	6.9	0.25	0.21	9.94	0.52	–0.01	–0.95	–0.32	19
LF2.5	6:44	3.0	0.01	0.43	3.09	0.52	0.17	0.70	–0.01	13
LF3.1	7:47	6.0	–0.45	0.35	0.91	8.90	–0.10	0.33	1.23	16
LF3.2	6:31	4.0	–0.45	0.05	0.46	6.81	–0.01	0.01	–1.20	1
LF3.3	4:17	2.7	0.23	0.19	0.11	4.19	–0.14	–0.23	–0.65	23
Total				60.3	63.5	30.1	–5.90	1.58	–1.21

LOD, log of the likelihood ratio.

^*The first digit indicates the chromosome, and the number after the colon represents the most likely position of the QTL in cM (e.g. 7:25 is 25 cM from the top of chromosome 7)

^†Dominance effect is the difference in the direction of the A. majus allele between the means of the homozygotes in the F₂ population and plants heterozygous at the QTL estimated from regression-based interval mapping (see Methods). It refers only to the main PC affected by each locus and is expressed in units of standard deviation. Loci with a dominance/additive effect ratio >1 were classed as overdominant (LF1.6), between 0.67 and 1 as dominant (LF1.2, LF1.3, LF1.5, LF3.2), between 0.67 and –0.67 as additive (LF1.1, LF1.4, LF1.7, LF2.1 to LF2.5), and below –0.67 as recessive (LF3.1 and LF3.3)

^‡The percentage variance in each PC explained by a locus was calculated by regression in which all other loci relevant to the PC were fixed as cofactors (see Methods)

^§The additive effect of each locus represents half the effect on the value of each PC (in units of standard deviation) of replacing both alleles from A. majus with alleles from A. charidemi. Twice the additive effect therefore estimates the average difference between the two homozygotes. The values for the effects of each locus on the three PCs define a vector in three-dimensional allometry space

^¶Angle between the vector and the mainly affected PC axis

Although loci were classified according to the PC values they mainly affected, each locus typically had minor effects on the other PC values (Table 1). Each QTL could therefore be represented as a vector, with components corresponding to the effects along each PC axis. If each locus affected variation along only one PC, then its vector would be perfectly aligned with that PC axis. The observed angle between the vectors and the major PC axis they affected was, on average, 20°. There are several reasons that each locus need not act parallel to its corresponding PC axis. One is that the PCs are based on the collective effect of several genes, so each individual gene may affect values along other PCs slightly. Second, if two loci affecting values of different PCs are linked, then it may not be possible to separate fully their effects on the same PC in QTL analysis, depending on the number of recombination events and markers between them.

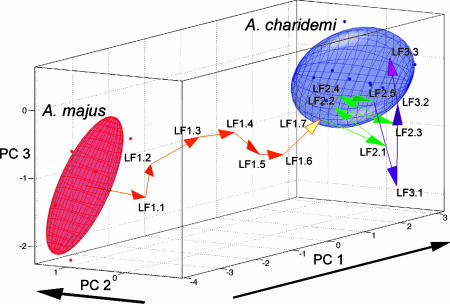
Each species in the allometric space could be represented by a cloud of points based on leaves from several individuals. The clouds could be summarized with ellipsoids that encapsulated most of the points. Because the individuals used were derived from a single location for each species, the size of each ellipsoid is likely to be an underestimate of the variation throughout the geographical range of each species. If the QTL analysis captured all genetic variation between A. majus and A. charidemi and all loci acted additively, laying the QTL vectors end to end, should traverse the gap from one species to the other. The path of vectors traversed 88% of the gap between A. majus and A. charidemi (Fig. 4, the order of vectors is arbitrary).

Fig. 4.

A. majus and A. charidemi species clouds displayed in allometric space with all QTL vectors laid end to end, starting from the center of A. majus. Arrowheads point in the direction of the A. charidemi allele effect for each QTL. Vectors are colored according to the PC values they mainly affect. Note that the order of the vectors is arbitrary. Overall, 88% of the distance between the species is traversed by the sequence of vectors. The separation between the means of A. charidemi and A. majus are (6.11, -0.82, 0.83) measured in standard deviations for PC1, PC2, and PC3 respectively.

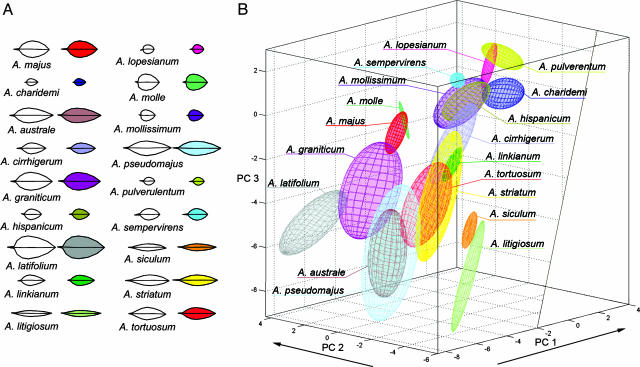
Leaf outlines from several individuals of 16 additional species were also recorded. The three-dimensional allometric model based on the A. majus and A. charidemi F₂ was able to capture most of the shape and size variation between species very effectively (Fig. 5A). This allowed the species to be accurately represented as clouds within the three-dimensional allometric space (Fig. 5B). Most species clouds overlapped with or were near to at least one other species.

Fig. 5.

Size and shape of leaves from 18 Antirrhinum species captured by the allometric model. (A) Average leaf outlines recorded for each Antirrhinum species (white) compared to the outline expressed with the three PCs of the allometric model (colored). (B) Representation of each species as a cloud in allometric space based on the F₂ between A. majus and A. charidemi. Each ellipsoid is based on leaf outlines from 2–14 individuals from each species. The unfilled region to the right corresponds to leaves with negative area and therefore does not represent a realistic part of the space.

Leaves of some species had PC values that extended beyond the range observed in the F₂ between A. majus and A. charidemi. This may partly reflect the limited size of the F₂, so that some homozygous combinations of alleles would not have been created, leading to an underestimate of the range of phenotypic variation. However, it is also likely that additional genes, or stronger alleles than those represented in the F₂, are involved in distinguishing many of the species. The direction of action of these additional factors is nevertheless likely to conform to the pattern observed in the F₂, because all leaf shapes of the sampled species can be accurately captured within the allometric space.

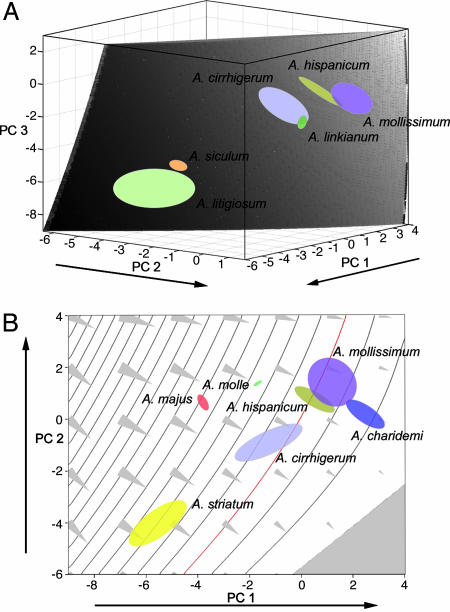
The allometric space allows genetic variation to be viewed in relation to characters that may be considered important for evaluating fitness. For example, leaf area is considered to be a major factor in controlling rates of water loss (22, 23). Using the allometric model, it is possible to compute the leaf area for each position in the allometric space. Leaves with the same area correspond to a subset of points in the space, which forms a surface (an area isosurface). Fig. 6A shows the isosurface, which includes all leaves with an area of 600 mm². This surface is slightly tilted from the vertical for the orientation of axes shown in Fig. 6B and intersects several species (i.e., Antirrhinum cirrhigerum, Antirrhinum hispanicum, Antirrhinum siculum, Antirrhinum litigiosum, Antirrhinum linkianum, and Antirrhinum mollissimum). As all these species have leaves with a similar area, the different positions of the intersections in the isosurface reflect variation in leaf shape. For example, species in the top right corner of the isosurface (A. cirrhigerum, A. linkianum, A. hispanicum, and A. mollissimum) have a rounder shape, whereas those at the bottom left (A. siculum and A. litigiosum) have a more elongated shape (Fig. 6A).

Fig. 6.

Assessment of leaf size within genetically controlled allometric space. (A) Isosurface corresponding to leaves with an area of 600 mm², showing intersection with several species. (B) Slice of allometric space for PC3 =-0.6. The slice intersects several species and a range of area isosurfaces to give a series of contours of constant leaf area (gray lines from 0 to 4,000 mm² in intervals of 200 mm²). Red line, 600 mm² corresponding to a section through the isosurface shown in A. Triangles indicate the steepest gradients in area and point toward smaller leaf size. Gray region indicates leaves with negative area that do not represent realistic part of the space.

The pattern of variation in leaf area can be viewed by taking slices through the allometric space that cut through the area isosurfaces. An example is shown in Fig. 6B, which shows a slice corresponding to a PC3 value of -0.6 (the slice is parallel to the top surface for the orientation of axes shown in Fig. 6B). The slice cuts through several leaf area isosurfaces (the intersections form area contours) and several species clouds (i.e., those which include leaves with PC3 =-0.6). The steepest gradient in area change is at right angles to the area contours (arrow in Fig. 6B).

Discussion

We have defined a genetically controlled allometric space that captures most of the variation in leaf shape and size between two species, A. majus and A. charidemi. A leaf corresponds to a point in this allometric space, whereas the additive effect of a gene (QTL) corresponds to a vector. The direction of this vector should reflect the developmental mechanism underlying the effect of the gene. The allometric space can also be used to display leaves of an individual species as a cloud of points. By mapping a range of closely related species into the space, it is possible to define a broad domain that reflects the paths of evolution in this species group. Therefore, the space provides a quantitative framework for relating genetic variation to evolutionary changes in shape and size.

Most of the leaf shape and size variation in the F₂ from A. majus and A. charidemi can be represented with three dimensions. These dimensions correspond to three PCs, each of which is under strong genetic control. Variation in PC1 values mainly affects size while varying values for PC2 or PC3 affects both shape and size. Altogether, 15 loci accounted for 43% of the total variance in shape and size in the F₂. By comparison, other studies on shape variation defined 25 QTL for the mouse mandible (17), 18 QTL for mouse molars (24), and at least eight QTL for Drosophila male genitalia (7).

Leaf shapes and sizes for each of the Antirrhinum species could be accurately represented within the three-dimensional allometric space. This finding suggests that, since divergence from a common ancestor, A. majus and A. charidemi have accumulated a series of genetic differences in directions that broadly capture the type of variation within the species group as a whole. These genetic differences can be represented by the zigzag path of the QTL vectors laid end to end (Fig. 4). Even though A. majus and A. charidemi do not differ greatly in shape, variation in shape is captured in the allometric space because of the QTL vectors with complementary components along PC axes influencing shape (PC2 and PC3). Complementary effects of QTL (leading to transgression in progeny) have similarly been described for several other interspecific crosses (25–28).

Most of the species occupy regions of allometric space that overlap with, or are near to, regions occupied by at least one other species. Taken together, the species form a largely interconnected region. This region defines a domain of viable forms within which evolution has occurred to generate diversity within the species group. This raises the questions of what constrains and drives evolutionary change within this domain.

One factor is likely to be selection on leaf area, because different species occupy regions that differ greatly in water limitation (from near-desert to montane climates). Water limitation has been shown to be a significant factor in natural plant populations, with smaller leaves increasing fitness in dry environments (22, 23, 29). Although selection on leaf size has not been directly assessed for Antirrhinum, species with small leaves (e.g., A. charidemi, A. microphyllum, and A. mollisimum) are found in the driest habitats encountered by the group, consistent with water limitation playing a role. Moreover, all seven QTL influencing values of PC1, the PC with the major effect on leaf area, act in the same direction as that of the parental difference, consistent with their having been subject to directional selection (30–32). The expected directions of size selection can be visualized in allometric space as vectors with major components at right angles to (normal to) the area isosurfaces (Fig. 6; ref. 33). Because the isosurfaces lie diagonally, these vectors will have components along axes capturing shape variation (e.g., PC2) as well as size variation. Thus, if selection was acting on size alone it would also be expected to bring about associated changes in shape. Moreover, multiple genes would likely be involved as many QTL vectors have significant components along the directions of size selection.

It is less clear how directional selection could account for shape variation for leaves of the same size. As shown in Fig. 6A, leaves with the same area can have a range of different shapes. Leaf shape would be expected to be important in relation to factors such as leaf support, supply and shading of other leaves (34, 35). Why then do leaves with the same area not all have the same optimized shape?

One possibility is that leaf shape variation reflects evolutionary tradeoffs. The effects of factors, such as shading, depends on other features of the plant, such as internode length and growth habit. Narrow leaves, for example, will not shade leaves below them as much as wide leaves, but this effect is less important when internodes are long or when the plant has a procumbent habit (e.g., growing along a rock surface). Each of these additional features can be considered as contributing one or more further dimensions to the relevant phenotypic space. Thus, fitness of particular leaf shapes can only be considered in a higher dimensional space that incorporates features in addition to leaf size and shape. The genetic structure of this space would depend on the specific and pleiotropic effects of genes on relevant features. It has been shown that higher dimensional spaces of this type are likely to contain paths of high fitness, which allow evolution to proceed in a nearly neutral but constrained manner (36, 37). Thus, variation in leaf shape could be brought about by evolution along such paths, reflecting essentially neutral walks among a range of possible tradeoffs in high dimensional space. Projection of these paths onto leaf allometry space would not be expected to give simple linear trajectories, consistent with QTL influencing leaf shape having a mixture of positive and negative effects.

Although potentially linked by viable forms in leaf allometric space, any two species taken alone may nevertheless be separated by gaps. If this pattern is extended to further traits, major divides in high dimensional space could separate lineages that diverged recently from a common ancestor. This could lead to the evolution of reproductive isolation if some of these traits reduce or prevent gene flow between lineages. Most European Antirrhinum species live in geographically separate areas, so it is difficult to evaluate the extent of this kind of reproductive isolation. However, in some cases, species can be found living in close proximity. For example, populations of A. molle and A. pseudomajus, two species that differ greatly in leaf as well as floral traits, can be found within a few kilometers distance with little evidence of gene flow, presumably because of barriers to reproduction (e.g., brought about by differences in pollinators or microhabitat). In other cases, contact between parapatric species can lead to the formation of hybrid zones in which there is a partial exchange of genes (e.g., A. striatum and A. pseudomajus). These situations can be compared to what has been proposed for ring species, in which there is a gradual shift in morphology along a chain of races or subspecies, which may lead to abrupt differences and reproductive isolation when terminal species meet (38, 39). Although the Antirrhinum species are not distributed as an obvious ring or chain, the processes underlying divergence and speciation may be comparable, with the practical difference that the Antirrhinum system is genetically tractable. In the longer term, it may therefore be possible to identify the QTL involved in Antirrhinum variation and further analyze their role in development and evolution.