Abstract
Understanding how the collective activity of neural populations relates to computation and ultimately behavior is a key goal in neuroscience. To this end, statistical methods which describe high-dimensional neural time series in terms of low-dimensional latent dynamics have played a fundamental role in characterizing neural systems. Yet, what constitutes a successful method involves two opposing criteria: (1) methods should be expressive enough to capture complex nonlinear dynamics, and (2) they should maintain a notion of interpretability often only warranted by simpler linear models. In this paper, we develop an approach that balances these two objectives: the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method builds on previous work modeling the latent state evolution via a stochastic differential equation whose nonlinear dynamics are described by a Gaussian process (GP-SDEs). We propose a novel kernel function which enforces smoothly interpolated locally linear dynamics, and therefore expresses flexible – yet interpretable – dynamics akin to those of recurrent switching linear dynamical systems (rSLDS). Our approach resolves key limitations of the rSLDS such as artifactual oscillations in dynamics near discrete state boundaries, while also providing posterior uncertainty estimates of the dynamics. To fit our models, we leverage a modified learning objective which improves the estimation accuracy of kernel hyperparameters compared to previous GP-SDE fitting approaches. We apply our method to synthetic data and data recorded in two neuroscience experiments and demonstrate favorable performance in comparison to the rSLDS.
1. Introduction
Computations in the brain are thought to be implemented through the dynamical evolution of neural activity. Such computations are typically studied in a controlled experimental setup, where an animal is engaged in a behavioral task with relatively few relevant variables. Consistent with this, empirical neural activity has been reported to exhibit many fewer degrees of freedom than there are neurons in the measured sample during such simple tasks [1]. These observations have driven the use of latent variable models to characterize low-dimensional structure in high-dimensional neural population activity [2, 3]. In this setting, neural activity is often modeled in terms of a low-dimensional latent state that evolves with Markovian dynamics [4–14]. It is thought that the latent state evolution is related to the computation of the system, and therefore, insights into how this evolution is shaped through a dynamical system can help us understand the mechanisms underlying computation [15–21].
In practice, choosing an appropriate modeling approach for a given task requires balancing two key criteria. First, statistical models should be expressive enough to capture potentially complex and nonlinear dynamics required to carry out a particular computation. On the other hand, these models should also be interpretable and allow for straightforward post-hoc analyses of dynamics. One model class that strikes this balance is the recurrent switching linear dynamical system (rSLDS) [8]. The rSLDS approximates arbitrary nonlinear dynamics by switching between a finite number of linear dynamical systems. This leads to a powerful and expressive model which maintains the interpretability of linear systems. Because of their flexibility and interpretability, variants of the rSLDS have been used in many neuroscience applications [19, 22–28] and are examples of a general set of models aiming to understand nonlinear dynamics using compact and interpretable components [29, 30].
However, rSLDS models suffer from several limitations. First, while the rSLDS is a probabilistic model, typical use cases do not capture posterior uncertainty over inferred dynamics. This makes it difficult to judge the extent to which particular features of a fitted model should be relied upon when making inferences about their role in neural computation. Second, the rSLDS often suffers from producing oscillatory dynamics in regions of high uncertainty in the latent space, such as boundaries between linear dynamical regimes. This artifactual behavior can significantly impact the interpretability and predictive performance of the rSLDS. Lastly, the rSLDS does not impose smoothness or continuity assumptions on the dynamics due to its discrete switching formulation. Such assumptions are often natural and useful in the context of modeling realistic neural systems.
In this paper, we improve upon the rSLDS by introducing the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method extends prior work on the Gaussian process stochastic differential equation (GP-SDE) model, a continuous-time method that places a Gaussian process (GP) prior on latent dynamics. By developing a novel GP kernel function, we enforce locally linear, interpretable structure in dynamics akin to that of the rSLDS. Our framework addresses the aforementioned modeling limitations of the rSLDS and contributes a new class of priors in the GP-SDE model class. Our paper is organized as follows. Section 2 provides background on GP-SDE and rSLDS models. Section 3 presents our new gpSLDS model and an inference and learning algorithm for fitting these models. In Section 4 we apply the gpSLDS to a synthetic dataset and two datasets from real neuroscience experiments to demonstrate its practical use and competitive performance. We review related work in Section 5 and conclude our paper with a discussion in Section 6.
2. Background
2.1. Gaussian process stochastic differential equation models
Gaussian processes (GPs) define nonparametric distributions over functions. They are a popular choice in machine learning due to their ability to capture nonlinearities and encode reasonable prior assumptions such as smoothness and continuity [31]. Here, we review the GP-SDE, a Bayesian generative model that leverages the expressivity of GPs for inferring latent dynamics [10].
Generative model
In a GP-SDE, the evolution of the latent state is modeled as a continuous-time SDE which underlies observed neural activity at time-points . Mathematically, this is expressed as
| (1) |
The drift function describes the system dynamics, is a noise covariance matrix, and is a Wiener process increment. Parameters and define an affine mapping from latent to observed space, which is then passed through a pre-specified inverse link function .
A GP prior is used to model each output dimension of the dynamics independently. More formally, if , then
| (2) |
where is the kernel for the GP with hyperparameters .
Interpretability
GP-SDEs and their variants can infer complex nonlinear dynamics with posterior uncertainty estimates in physical systems across a variety of applications [32–34]. However, one limitation of using this method with standard GP kernels, such as the radial basis function (RBF) kernel, is that its expressivity leads to dynamics that are often challenging to interpret. In Duncker et al. [10], this was addressed by conditioning the GP prior of the dynamics on fixed points and their local Jacobians , and subsequently learning the fixed-point locations and the locally-linearized dynamics as model parameters. This approach allows for direct estimation of key features of . However, due to its flexibility, it is also prone to finding more fixed points than those included in the prior conditioning, which undermines its overall interpretability.
2.2. Recurrent switching linear dynamical systems
The rSLDS models nonlinear dynamics by switching between different sets of linear dynamics [8]. Accordingly, it retains the simplicity and interpretability of linear dynamical systems while providing much more expressive power. For these reasons, variations of the rSLDS are commonly used to model neural dynamics [19, 22–29].
Generative model
The rSLDS is a discrete-time generative model of the following form:
| (3) |
where dynamics switch between distinct linear systems with parameters . This is controlled by a discrete state variable , which evolves via transition probabilities modeled by a multiclass logistic regression,
| (4) |
The “recurrent” nature of this model comes from the dependence of eq. (4) on latent space locations . As such, the rSLDS can be understood as learning a partition of the latent space into linear dynamical regimes seprated by linear decision boundaries. This serves as important motivation for the parametrization of the gpSLDS, as we describe later.
Interpretability
While the rSLDS has been successfully used in many applications to model nonlinear dynamical systems, it suffers from a few practical limitations. First, it often produces unnatural artifacts of modeling nonlinear dynamics with discrete switches between linear systems. For example, it may oscillate between discrete modes with different discontinuous dynamics when a trajectory is near a regime boundary. Next, common fitting techniques for rSLDS models with non-conjugate observations typically treat dynamics as learnable hyperparameters rather than as probabilistic quantities [26], which prevents the model from being able to capture posterior uncertainty over the learned dynamics. Inferring a posterior distribution over dynamics is especially important in many neuroscience applications, where scientists often draw conclusions from discovering key features in latent dynamics, such as fixed points or line attractors.
3. Gaussian process switching linear dynamical systems
To address these limitations of the rSLDS, we propose a new class of models called the Gaussian Process Switching Linear Dynamical System (gpSLDS). The gpSLDS combines the modeling advantages of the GP-SDE with the structured flexbility of the rSLDS. We achieve this balance by designing a novel GP kernel function that defines a smooth, locally linear prior on dynamics. While our main focus is on providing an alternative to the rSLDS, the gpSLDS also contributes a new prior which allows for more interpretable learning of dynamics and fixed points than standard priors in the GP-SDE framework (e.g., the RBF kernel). Our implementation of the gpSLDS is available at: https://github.com/lindermanlab/gpslds.
3.1. The smoothly switching linear kernel
The core innovation of our method is a novel GP kernel, which we call the Smoothly Switching Linear (SSL) kernel. The SSL kernel specifies a GP prior over dynamics that maintains the switching linear structure of rSLDS models, while allowing dynamics to smoothly interpolate between different linear regimes.
For every pair of locations , , the SSL kernel with linear regimes is defined as,
| (5) |
where , is a diagonal positive semi-definite matrix, , and with . To gain an intuitive understanding of the SSL kernel, we will separately analyze each of the two terms in the summands.
The first term, , is a standard linear kernel which defines a GP distribution over linear functions [31]. The superscript denotes that it is the linear prior on the dynamics in regime . controls the variance of the function’s slope in each input dimension, and is such that the variance of the function achieves its minimum value of at . We expand on the relationship between the linear kernel and linear dynamical systems in Appendix A.
The second term is what we define as the partition kernel, , which gives the gpSLDS its switching structure. We interpret as parametrizing a categorical distribution over linear regimes akin to the discrete switching variables in the rSLDS. We model as a multiclass logistic regression with decision boundaries , where is any feature transformation of . This yields random functions which are locally constant and smoothly interpolate at the decision boundaries. More formally,
| (6) |
where . The hyperparameter controls the smoothness of the decision boundaries. As , approaches a one-hot vector which produces piecewise constant functions with sharp boundaries, and as the boundaries become more uniform. While we focus on the parametrization in eq. (6) for the experiments in this paper, we note that in principle any classification method can be used, such as another GP or a neural network.
The SSL kernel in eq. (5) naturally combines aspects of the linear and partition kernels via sums and products of kernels, which has an intuitive interpretation [35]. The product kernel enforces linearity in regions where is close to 1. Summing over regimes then enforces linearity in each of the regimes, leading to a prior on locally linear functions with knots determined by . We note that our kernel is reminiscent of the one in Pfingsten et al. [36], which uses a GP classifier as a prior for and applies their kernel to a GP regression setting. Here, our work differs in that we explicitly enforce linearity in each regime and draw a novel connection to switching models like the rSLDS.
Figure 1A depicts 1D samples from each kernel. Figure 1B shows how a SSL kernel with linear regimes separated by decision boundary (top) produces a structured 2D flow field consisting of two linear systems, with - and - directions determined by 1D function samples (bottom).
Figure 1:
SSL kernel and generative model. A. 1D function samples, plotted in different colors, from GPs with five kernels: two linear kernels with different hyperparameters, partition kernels for each of the two regimes, and the SSL kernel. B. (top) An example in 2D and (bottom) a sample of dynamics from a SSL kernel in 2D with as hyperparameters. The - and - directions of the arrows are given by independent 1D samples of the kernel. C. Schematic of the generative model. Simulated trajectories follow the sampled dynamics. Each trajectory is observed via Poisson process or Gaussian observations.
3.2. The gpSLDS generative model
The full generative model for the gpSLDS incorporates the SSL kernel in eq. (5) into a GP-SDE modeling framework. Instead of placing a GP prior with a standard kernel on the system dynamics as in eq. (2), we simply plug in our new SSL kernel so that
| (7) |
where the kernel hyperparameters are . We then sample latent states and observations according to the GP-SDE via eq. (1). A schematic of the full generative model is depicted in fig. 1C.
Incorporating inputs
In many modern neuroscience applications, we are often interested in how external inputs to the system, such as experimental stimuli, influence latent states. To this end, we also consider an extension of the model in eq. (1) which incorporates additive inputs of the form,
| (8) |
where is a time-varying, known input signal and maps inputs linearly to the latent space. The latent path inference and learning approaches presented in the following section can naturally be extended to this setting, with updates for available in closed form. Further details are provided in Appendix B.3–B.6.
3.3. Latent path inference and parameter learning
For inference and learning in the gpSLDS, we apply and extend a variational expectation-maximization (vEM) algorithm for GP-SDEs from Duncker et al. [10]. In particular, we propose a modification of this algorithm that dramatically improves the learning accuracy of kernel hyperparameters, which are crucial to the interpretability of the gpSLDS. We outline the main ideas of the algorithm here, though full details can be found in Appendix B.
As in Duncker et al. [10], we consider a factorized variational approximation to the posterior,
| (9) |
where we have augmented the model with sparse inducing points to make inference of tractable [37].
The inducing points are located at and take values . Standard vEM maximizes the evidence lower bound (ELBO) to the marginal log-likelihood by alternating between updating the variational posterior and updating model hyperparameters [38]. Using the factorization in eq. (9), we will denote the ELBO as , , ).
For inference of , we follow the approach first proposed by Archambeau et al. [39] and extended by Duncker et al. [10]. Computing the ELBO using this approach requires computing variational expectations of the SSL kernel, which we approximate using Gauss-Hermite quadrature as they are not available in closed form. Full derivations of this step are provided in Appendix B.3. For inference of , we follow Duncker et al. [10] and choose a Gaussian variational posterior for , which admits closed-form updates for the mean and covariance given and . Duncker et al. [10] perform these updates before updating via gradient ascent on the ELBO in each vEM iteration.
In our setting, this did not work well in practice. The gpSLDS often exhibits strong dependencies between and , which makes standard coordinate-ascent steps in vEM prone to getting stuck in local maxima. These dependencies arise due to the highly structured nature of our GP prior; small changes in the decision boundaries can lead to large (adverse) changes in the prior, which prevents vEM from escaping suboptimal regions of parameter space. To overcome these difficulties, we propose a different approach for learning : instead of fixing and performing gradient ascent on the ELBO, we optimize by maximizing a partially optimized ELBO,
| (10) |
Due to the conjugacy of the model, the inner maximization can be performed analytically. This approach circumvents local optima that plague coordinate ascent on the standard ELBO. While other similar approaches exploit model conjugacy for faster vEM convergence in sparse variational GPs [37, 40] and GP-SDEs [41], our approach is the first to our knowledge that leverages this structure specifically for learning the latent dynamics of a GP-SDE model. We empirically demonstrate the superior performance of our learning algorithm in Appendix C.
3.4. Recovering predicted dynamics
It is straightforward to obtain the approximate posterior distribution over evaluated at any new location . Under the assumption that only depends on the inducing points, we can use the approximation which can be computed in closed-form using properties of conditional Gaussian distributions. For a batch of points , this can be computed in time. The full derivation can be found in Appendix B.4.
This property highlights an appealing feature of the gpSLDS over the rSLDS. The gpSLDS infers a posterior distribution over dynamics at every point in latent space, even in regions of high uncertainty. Meanwhile, as we shall see later, the rSLDS expresses uncertainty by randomly oscillating between different sets of most-likely linear dynamics, which is much harder to interpret.
4. Results
4.1. Synthetic data
We begin by applying the gpSLDS to a synthetic dataset consisting of two linear rotational systems, one clockwise and one-counterclockwise, which combine smoothly at (fig. 2A). We simulate 30 trials of latent states from an SDE as in eq. (1) and then generate Poisson process observations given these latent states for output dimensions (i.e. neurons) over T = 2.5 seconds (Fig. 2B). To initialize and , we fit a Poisson LDS [4] to data binned at 20ms with identity dynamics. For the rSLDS, we also bin the data at 20ms. We then fit the gpSLDS and rSLDS models with linear states using 5 different random initializations for 100 vEM iterations, and choose the fits with the highest ELBOs in each model class.
Figure 2:
Synthetic data results. A. True dynamics and latent states used to generate the dataset. Dynamics are clockwise and counterclockwise linear systems separated by x1 = 0. Two latent trajectories are shown on top of a kernel density estimate of the latent states visited by all 30 trials. B. Poisson process observations from an example trial. C. True vs. inferred latent states for the gpSLDS and rSLDS, with 95% posterior credible intervals. D. Inferred dynamics (pink/green) and two inferred latent trajectories (gray) corresponding to those in Panel A from a gpSLDS fit with 2 linear regimes. The model finds high-probability fixed points (purple) overlapping with true fixed points (stars). E. Analogous plot to D for the GP-SDE model with RBF kernel. Note that this model does not provide a partition of the dynamics. F. rSLDS inferred latents, dynamics, and fixed points (pink/green dots). G. (top) Sampled latents and corresponding dynamics from the gpSLDS, with 95% posterior credible intervals. (bottom) Same, but for the rSLDS. The pink/green trace represents the most likely dynamics at the sampled latents, colored by discrete switching variable. H. MSE between true and inferred latents and dynamics for gpSLDS, GP-SDE with RBF kernel, and rSLDS while varying the number of trials in the dataset. Error bars are ±2SE over 5 random initializations.
We find that the gpSLDS accurately recovers the true latent trajectories (fig. 2C) as well as the true rotation dynamics and the decision boundary between them (fig. 2D). We determine this decision boundary by thresholding the learned at 0.5. In addition, we can obtain estimates of fixed point locations by computing the posterior probability for a small ; the locations with high probability are shaded in purple. This reveals that the gpSLDS finds high-probability fixed points which overlap significantly with the true fixed points, denoted by stars. In comparison, both the rSLDS and the GP-SDE with RBF kernel do not learn the correct decision boundary nor the fixed points as accurately (fig. 2E–F). Of particular note, the RBF kernel incorrectly extrapolates and finds a superfluous fixed point outside the region traversed by the true latent states.
Figure 2G illustrates the differences in how the gpSLDS and the rSLDS express uncertainty over dynamics. To the left of the dashed line, we sample latent states starting from and plot the corresponding true dynamics. To the right, we simulate latent states from the fitted model and plot the true dynamics (in gray) and the learned most likely dynamics (in color) at . For a well-fitting model, we would expect the true and learned dynamics to overlap. We see that the gpSLDS produces smooth simulated dynamics that match the true dynamics at (top). By contrast, the rSLDS expresses uncertainty by oscillating between the two linear dynamical systems, hence producing uninterpretable dynamics at (bottom). This region of uncertainty overlaps with the boundary, suggesting that the rSLDS fails to capture the smoothly interpolating dynamics present in the true system.
Next, we perform quantitative comparisons between the three competing methods (fig. 2H). We find that both continuous-time methods consistently outperform the rSLDS on both metrics, suggesting that these methods are likely more suitable for modeling Poisson process data. Moreover, the gpSLDS better recovers dynamics compared to the RBF kernel, illustrating that the correct inductive bias can yield performance gains over a more flexible prior, especially in a data-limited setting.
Lastly, we note that the gpSLDS can achieve more expressive power than the rSLDS by learning nonlinear decision boundaries between linear regimes, for instance by incorporating nonlinear features into in eq. (6). We demonstrate this feature for a 2D limit cycle in Appendix D.
4.2. Application to hypothalamic neural population recordings during aggression
In this section, we revisit the analyses of Nair et al. [27], which applied dynamical systems models to neural recordings during aggressive behavior in mice. To do this, we reanalyze a dataset which consists of calcium imaging of ventromedial hypothalamus neurons from a mouse interacting with two consecutive intruders. The recording was collected from 104 neurons at 15 Hz over ∼343 seconds (i.e. 5140 time bins). Nair et al. [27] found that an rSLDS fit to this data learns dynamics that form an approximate line attractor corresponding to an aggressive internal state (fig. 3A). Here, we supplement this analysis by using the gpSLDS to directly assess model confidence about this finding.
Figure 3:
Results on hypothalamic data from Nair et al. [27]. In each of the panels A-C, flow field arrow widths are scaled by the magnitude of dynamics for clarity of visualization. A. rSLDS inferred latents and most likely dynamics. The presumed location of the line attractor from [27] is marked with a red box. B. gpSLDS inferred latents and most likely dynamics in latent space. Background is colored by posterior standard deviation of dynamics averaged across latent dimensions, which adjusts relative to the presence of data in the latent space. C. Posterior probability of slow points in gpSLDS, which validates line-attractor like dynamics, as marked by a red box. D. Comparison of in-sample forward simulation R2 between gpSLDS, rSLDS, and GP-SDE with RBF kernel. To compute this, we choose initial conditions uniformly spaced 100 time bins apart in both trials, simulate latent states k steps forward according to learned dynamics (with k ranging from 100–1500), and evaluate the R2 between predicted and true observations as in Nassar et al. [23]. Error bars are ±2SE over 5 different initializations.
For our experiments, we z-score and then split the data into two trials, one for each distinct intruder interacting with the mouse. Following Nair et al. [27], we choose linear regimes to compare the gpSLDS and rSLDS. We choose latent dimensions to aid the visualization of the resulting model fits; we find that even in such low dimensions, both models still recover line attractor-like dynamics. We model the calcium imaging traces as Gaussian emissions on an evenly spaced time grid and initialize and using principal component analysis. We fit models with 5 different initializations for 50 vEM iterations and display the runs with highest forward simulation accuracy (as described in the caption of fig. 3).
In fig. 3A–B, we find that both methods infer similar latent trajectories and find plausible flow fields that are parsed in terms of simpler linear components. We further demonstrate the ability of the gpSLDS to more precisely identify the line attractor from Nair et al. [27]. To do this, we use the learned to compute the posterior probability of slow dynamics on a dense (80×80) grid of points in the latent space using the procedure in Section 3.4. The gpSLDS finds a high-probability region of slow points corresponding to the approximate line attractor found in Nair et al. [27] (fig. 3C). This demonstrates a key advantage of the gpSLDS over the rSLDS: by modeling dynamics probabilistically using a structured GP prior, we can validate the finding of a line attractor with further statistical rigor. Finally, we compare the gpSLDS, rSLDS, and GP-SDE with RBF kernel using an in-sample forward simulation metric (fig. 3D). All three methods retain similar predictive power 500 steps into the future. After that, the gpSLDS performs slightly worse than the RBF kernel; however, it gains interpretability by imposing piecewise linear structure while still outperforming the rSLDS.
4.3. Application to lateral intraparietal neural recodings during decision making
In neuroscience, there is considerable interest in understanding how neural dynamics during decision making tasks support the process of making a choice [26, 34, 42–47]. In this section, we use the gpSLDS to infer latent dynamics from spiking activity in the lateral intraparietal (LIP) area of monkeys reporting decisions about the direction of motion of a random moving dots stimulus with varying degrees of motion coherence [42, 43]. The animal indicated its choice of net motion direction (either left or right) via a saccade. On some trials, a 100ms pulse of weak motion, randomly oriented to the left or right, was also presented to the animal. Here, we model the dynamics of 58 neurons recorded across 50 trials consisting of net motion coherence strengths in {−.512, −.128, 0.0, .128, .512}, where the sign corresponds to the net movement direction of the stimulus. We only consider data 200ms after motion onset, corresponding to the start of decision-related activity.
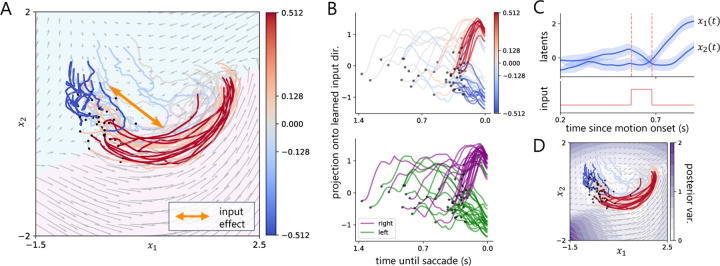
To capture potential input-driven effects, we fit a version of the gpSLDS described in eq. (8) with K = 2 latent dimensions and J = 2 linear regimes over 50 vEM iterations. We encoded the input signal as ±1 with sign corresponding to pulse direction. In Figure 4A, we find that not only does the gpSLDS capture a distinct visual separation between trials by motion coherence, but it also learns a precise separating decision boundary between the two linear regimes. Our finding is consistent with previous work on a related task, which found that average LIP responses can be represented by a 2D curved manifold [48], though here we take a dynamical systems perspective. Additionally, our model learns an input-driven effect which appears to define a separating axis. To verify this, we project the inferred latent states onto the 1D subspace spanned by the input effect vector. Figure 4B shows that the latent states separate by coherence (top) and by choice (bottom), further suggesting that the pulse input relates to meaningful variation in evidence accumulation for this task. Fig. 4C shows an example latent trajectory aligned with pulse input; during the pulse there is a noticeable change in the latent trajectory. Lastly, in Fig. 4D we find that the gpSLDS expresses high confidence in learned dynamics where latent trajectories are present and low confidence in areas further from this region.
Figure 4:
Results on LIP spiking data from a decision-making task in Stine et al. [42]. A. gpSLDS inferred latents colored by coherence, inferred dynamics with background colored by most likely linear regime, and the learned input-driven direction depicted by an orange arrow. B. Projection of latents onto the 1D input-driven axis from Panel A, colored by coherence (top) and choice (bottom). C. Inferred latents with 95% credible intervals and corresponding 100ms pulse input for an example trial. D. Posterior variance of dynamics produced by the gpSLDS.
5. Related work
There are several related approaches to learning nonlinear latent dynamics in discrete or continuous time. Gaussian process state-space models (GP-SSMs) [49–53] can be considered a discrete-time analogue to GP-SDEs. In a GP-SSM, observations are assumed to be regularly sampled and latent states evolve according to a discretized dynamical system with a GP prior. Wang et al. [49] and Turner et al. [50] learned the dynamics of a GP-SSM using maximum a posteriori estimation. Frigola et al. [51] and Eleftheriadis et al. [52] employed a variational approximation with sparse inducing points to infer the latent states and dynamics in a fully Bayesian fashion. In our work, we use a continuous-time framework that more naturally handles irregularly sampled data, such as point-process observations commonly encountered in neural spiking data. Neural ODEs and SDEs [54, 55] use deep neural networks to parametrize the dynamics of a continuous-time system, and have emerged as prominent tools for analyzing large datasets, including those in neuroscience [33, 56–58]. While these methods can represent flexible function classes, they are likely to overfit to low-data regimes and may be difficult to interpret. In addition, unlike the gpSLDS, neural ODEs and SDEs do not typically quantify uncertainty of the learned dynamics.
In the context of dynamical mixture models, Köhs et al. [59, 60] proposed a continuous-time switching model in a GP-SDE framework. This model assumes a latent Markov jump process over time which controls the system dynamics by switching between different SDEs. The switching process models dependence on time, but not location in latent space. In contrast, the gpSLDS does not explicitly represent a latent switching process and rather models switching probabilities as part of the kernel function. The dependence of the kernel on the location in latent space allows for the gpSLDS to partition the latent space into different linear regimes.
While our work has followed the inference approach of Archambeau et al. [61] and Duncker et al. [10], other methods for latent path inference in nonlinear SDEs have been proposed [32, 41, 62, 63]. Verma et al. [41] parameterized the posterior SDE path using an exponential family-based description. The resulting inference algorithm showed improved convergence of the E-step compared to Archambeau et al. [39]. Course and Nair [32, 62] proposed an amortization strategy that allows the variational update of the latent state to be parallelized over sequence length. In principle, any of these approaches could be applied to inference in the gpSLDS and would be an interesting direction for future work.
6. Discussion
In this paper, we introduced the gpSLDS to infer low-dimensional latent dynamical systems from high-dimensional, noisy observations. By developing a novel kernel for GP-SDE models that defines distributions over smooth locally-linear functions, we were able to relate GP-SDEs to rSLDS models and address key limitations of the rSLDS. Using both simulated and real neural datasets, we demonstrated that the gpSLDS can accurately infer true generative parameters and performs favorably in comparison to rSLDS models and GP-SDEs with other kernel choices. Moreover, our real data examples illustrate the variety of potential practical uses of this method. On calcium imaging traces recorded during aggressive behavior, the gpSLDS reveals dynamics consistent with the hypothesis of a line attractor put forward based on previous rSLDS analyses [27]. On a decision making dataset, the gpSLDS finds latent trajectories and dynamics that clearly separate by motion coherence and choice, providing a dynamical systems view consistent with prior studies [42, 48].
In our experiments, we demonstrated the ability of the gpSLDS to recover ground-truth dynamical systems and key dynamical features using fixed settings of hyperparameters: the latent dimensionality K and the number of regimes J. For simulated data, we set hyperparameters to their true values; for real data, we chose hyperparameters based on prior studies and did not further optimize these values. However, for most real neural datasets, we do not know the true underlying dimensionality or optimal number of regimes. To tune these hyperparameters, we can resort to standard techniques for model comparison in the neural latent variable modeling literature. Two common evaluation metrics are forward simulation accuracy [23, 27] and co-smoothing performance [6, 64, 65].
While these results are promising, we acknowledge a few limitations of the gpSLDS. First, the memory cost scales exponentially with the size of the latent dimension due to using quadrature methods to approximate expectations of the SSL kernel, which are not available in closed form. This computational limitation renders it difficult to fit the gpSLDS with many (i.e. greater than 3) latent dimensions. One potential direction for future work would be to instead use Monte Carlo methods to approximate kernel expectations for models with larger latent dimensionality. In addition, while both the gpSLDS and rSLDS require choosing a discretization timestep for solving dynamical systems, in practice we find that the gpSLDS requires smaller steps for stable model inference. This allows the gpSLDS to more accurately approximate dynamics with continuous-time likelihoods, at the cost of allocating more time bins during inference. Finally, we acknowledge that traditional variational inference approaches – such as those employed by the gpSLDS– tend to underestimate posterior variance due to the KL-divergence-based objective [38]. Carefully assessing biases introduced by our variational approximation to the posterior would be an important topic for future work.
Overall, the gpSLDS provides a general modeling approach for discovering latent dynamics of noisy measurements in an intepretable and fully probabilistic manner. We expect that our model will be a useful addition to the rSLDS and related methods on future analyses of neural data.
Supplementary Material
Acknowledgments and Disclosure of Funding
This work was supported by grants from the NIH BRAIN Initiative (U19NS113201, R01NS131987, & RF1MH133778) and the NSF/NIH CRCNS Program (R01NS130789), as well as fellowships from the Simons Collaboration on the Global Brain, the Wu Tsai Neurosciences Institute, the Alfred P. Sloan Foundation, and the McKnight Foundation. We thank Barbara Engelhardt, Julia Palacios, and the members of the Linderman Lab for helpful feedback throughout this project. The authors have no competing interests to declare.
Funding Statement
This work was supported by grants from the NIH BRAIN Initiative (U19NS113201, R01NS131987, & RF1MH133778) and the NSF/NIH CRCNS Program (R01NS130789), as well as fellowships from the Simons Collaboration on the Global Brain, the Wu Tsai Neurosciences Institute, the Alfred P. Sloan Foundation, and the McKnight Foundation. We thank Barbara Engelhardt, Julia Palacios, and the members of the Linderman Lab for helpful feedback throughout this project. The authors have no competing interests to declare.
Contributor Information
Amber Hu, Stanford University.
David Zoltowski, Stanford University.
Aditya Nair, Caltech & Howard Hughes Medical Institute.
David Anderson, Caltech & Howard Hughes Medical Institute.
Lea Duncker, Columbia University.
Scott Linderman, Stanford University.
References
- [1].Gao Peiran and Ganguli Surya. On simplicity and complexity in the brave new world of large-scale neuroscience. Current Opinion in Neurobiology, 32:148–155, 2015. [DOI] [PubMed] [Google Scholar]
- [2].Cunningham John P and Yu Byron M. Dimensionality reduction for large-scale neural recordings. Nature Neuroscience, 17(11):1500–1509, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Saxena Shreya and Cunningham John P. Towards the neural population doctrine. Current Opinion in Neurobiology, 55:103–111, 2019. [DOI] [PubMed] [Google Scholar]
- [4].Smith Anne C and Brown Emery N. Estimating a state-space model from point process observations. Neural Computation, 15(5):965–991, 2003. [DOI] [PubMed] [Google Scholar]
- [5].Paninski Liam, Ahmadian Yashar, Ferreira Daniel Gil, Koyama Shinsuke, Rad Kamiar Rahnama, Vidne Michael, Vogelstein Joshua, and Wu Wei. A new look at state-space models for neural data. Journal of Computational Neuroscience, 29:107–126, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Macke Jakob H, Buesing Lars, Cunningham John P, Yu Byron M, Shenoy Krishna V, and Sahani Maneesh. Empirical models of spiking in neural populations. Advances in Neural Information Processing Systems, 24, 2011. [Google Scholar]
- [7].Archer Evan, Park Memming Il, Buesing Lars, Cunningham John, and Paninski Liam. Black box variational inference for state space models. arXiv preprint arXiv:1511.07367, 2015. [Google Scholar]
- [8].Linderman Scott, Johnson Matthew, Miller Andrew, Adams Ryan, Blei David, and Paninski Liam. Bayesian learning and inference in recurrent switching linear dynamical systems. In Artificial Intelligence and Statistics, pages 914–922. PMLR, 2017. [Google Scholar]
- [9].Pandarinath Chethan, O’Shea Daniel J, Collins Jasmine, Jozefowicz Rafal, Stavisky Sergey D, Kao Jonathan C, Trautmann Eric M, Kaufman Matthew T, Ryu Stephen I, Hochberg Leigh R, et al. Inferring single-trial neural population dynamics using sequential auto-encoders. Nature Methods, 15(10):805–815, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Duncker Lea, Bohner Gergo, Boussard Julien, and Sahani Maneesh. Learning interpretable continuous-time models of latent stochastic dynamical systems. In International Conference on Machine Learning, pages 1726–1734. PMLR, 2019. [Google Scholar]
- [11].Schimel Marine, Kao Ta-Chu, Jensen Kristopher T, and Hennequin Guillaume. ilqr-vae: control-based learning of input-driven dynamics with applications to neural data. In International Conference on Learning Representations, 2021. [Google Scholar]
- [12].Genkin Mikhail, Hughes Owen, and Tatiana A Engel. Learning non-stationary langevin dynamics from stochastic observations of latent trajectories. Nature Communications, 12(1): 5986, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Langdon Christopher and Engel Tatiana A. Latent circuit inference from heterogeneous neural responses during cognitive tasks. bioRxiv, pages 2022–01, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Dowling Matthew, Zhao Yuan, and Park Memming Il. Large-scale variational gaussian state-space models. arXiv preprint arXiv:2403.01371, 2024. [Google Scholar]
- [15].Vyas Saurabh, Golub Matthew D, Sussillo David, and Shenoy Krishna V. Computation through neural population dynamics. Annual Review of Neuroscience, 43:249–275, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Duncker Lea and Sahani Maneesh. Dynamics on the manifold: Identifying computational dynamical activity from neural population recordings. Current Opinion in Neurobiology, 70: 163–170, 2021. [DOI] [PubMed] [Google Scholar]
- [17].Sussillo David and Barak Omri. Opening the black box: low-dimensional dynamics in high-dimensional recurrent neural networks. Neural Computation, 25(3):626–649, 2013. [DOI] [PubMed] [Google Scholar]
- [18].O’Shea Daniel J, Duncker Lea, Goo Werapong, Sun Xulu, Vyas Saurabh, Trautmann Eric M, Diester Ilka, Ramakrishnan Charu, Deisseroth Karl, Sahani Maneesh, et al. Direct neural perturbations reveal a dynamical mechanism for robust computation. bioRxiv, pages 2022–12, 2022. [Google Scholar]
- [19].Soldado-Magraner Joana, Mante Valerio, and Sahani Maneesh. Inferring context-dependent computations through linear approximations of prefrontal cortex dynamics. Science Advances, 10(51):eadl4743, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Vinograd Amit, Nair Aditya, Kim Joseph, Linderman Scott W, and Anderson David J. Causal evidence of a line attractor encoding an affective state. Nature, pages 1–3, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Mountoufaris George, Nair Aditya, Yang Bin, Kim Dong-Wook, Vinograd Amit, Kim Samuel, Linderman Scott W, and Anderson David J. A line attractor encoding a persistent internal state requires neuropeptide signaling. Cell, 187(21):5998–6015, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Petreska Biljana, Yu Byron M, Cunningham John P, Santhanam Gopal, Ryu Stephen, Shenoy Krishna V, and Sahani Maneesh. Dynamical segmentation of single trials from population neural data. Advances in Neural Information Processing Systems, 24, 2011. [Google Scholar]
- [23].Nassar Josue, Linderman Scott, Bugallo Monica, and Park Memming Il. Tree-structured recurrent switching linear dynamical systems for multi-scale modeling. In International Conference on Learning Representations, 2018. [Google Scholar]
- [24].Taghia Jalil, Cai Weidong, Ryali Srikanth, Kochalka John, Nicholas Jonathan, Chen Tianwen, and Menon Vinod. Uncovering hidden brain state dynamics that regulate performance and decision-making during cognition. Nature Communications, 9(1):2505, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Costa Antonio C, Ahamed Tosif, and Stephens Greg J. Adaptive, locally linear models of complex dynamics. Proceedings of the National Academy of Sciences, 116(5):1501–1510, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Zoltowski David, Pillow Jonathan, and Linderman Scott. A general recurrent state space framework for modeling neural dynamics during decision-making. In International Conference on Machine Learning, pages 11680–11691. PMLR, 2020. [Google Scholar]
- [27].Nair Aditya, Karigo Tomomi, Yang Bin, Ganguli Surya, Schnitzer Mark J, Linderman Scott W, Anderson David J, and Kennedy Ann. An approximate line attractor in the hypothalamus encodes an aggressive state. Cell, 186(1):178–193, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Liu Mengyu, Nair Aditya, Coria Nestor, Linderman Scott W, and Anderson David J. Encoding of female mating dynamics by a hypothalamic line attractor. Nature, pages 1–3, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Smith Jimmy, Linderman Scott, and Sussillo David. Reverse engineering recurrent neural networks with Jacobian switching linear dynamical systems. Advances in Neural Information Processing Systems, 34:16700–16713, 2021. [Google Scholar]
- [30].Mudrik Noga, Chen Yenho, Yezerets Eva, Rozell Christopher J, and Charles Adam S. Decomposed linear dynamical systems (dlds) for learning the latent components of neural dynamics. Journal of Machine Learning Research, 25(59):1–44, 2024. [Google Scholar]
- [31].Williams Christopher KI and Rasmussen Carl Edward. Gaussian processes for machine learning, volume 2. MIT press; Cambridge, MA, 2006. [Google Scholar]
- [32].Course Kevin and Nair Prasanth B. State estimation of a physical system with unknown governing equations. Nature, 622(7982):261–267, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Kim Timothy Doyeon, Zhihao Thomas Luo, Can Tankut, Krishnamurthy Kamesh, Pillow Jonathan W, and Brody Carlos D. Flow-field inference from neural data using deep recurrent networks. bioRxiv, 2023. [Google Scholar]
- [34].Luo Thomas Zhihao, Kim Timothy Doyeon, Gupta Diksha, Bondy Adrian G, Kopec Charles D, Elliot Verity A, DePasquale Brian, and Brody Carlos D. Transitions in dynamical regime and neural mode underlie perceptual decision-making. bioRxiv, pages 2023–10, 2023. [DOI] [PubMed] [Google Scholar]
- [35].Duvenaud David. Automatic model construction with Gaussian processes. PhD thesis, 2014. [Google Scholar]
- [36].Pfingsten Tobias, Kuss Malte, and Rasmussen Carl Edward. Nonstationary gaussian process regression using a latent extension of the input space. In Eighth World Meeting of the International Society for Bayesian Analysis (ISBA 2006), 2006. [Google Scholar]
- [37].Titsias Michalis. Variational learning of inducing variables in sparse gaussian processes. In Artificial Intelligence and Statistics, pages 567–574. PMLR, 2009. [Google Scholar]
- [38].Blei David M, Kucukelbir Alp, and McAuliffe Jon D. Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518):859–877, 2017. [Google Scholar]
- [39].Archambeau Cedric, Cornford Dan, Opper Manfred, and Shawe-Taylor John. Gaussian process approximations of stochastic differential equations. In Gaussian Processes in Practice, pages 1–16. PMLR, 2007. [Google Scholar]
- [40].Adam Vincent, Chang Paul, Khan Mohammad Emtiyaz E, and Solin Arno. Dual parameterization of sparse variational gaussian processes. Advances in Neural Information Processing Systems, 34:11474–11486, 2021. [Google Scholar]
- [41].Verma Prakhar, Adam Vincent, and Solin Arno. Variational gaussian process diffusion processes. In International Conference on Artificial Intelligence and Statistics, pages 1909–1917. PMLR, 2024. [Google Scholar]
- [42].Stine Gabriel M, Trautmann Eric M, Jeurissen Danique, and Shadlen Michael N. A neural mechanism for terminating decisions. Neuron, 111(16):2601–2613, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Roitman Jamie D and Shadlen Michael N. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience, 22(21): 9475–9489, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Ditterich Jochen. Stochastic models of decisions about motion direction: behavior and physiology. Neural Networks, 19(8):981–1012, 2006. [DOI] [PubMed] [Google Scholar]
- [45].Gold Joshua I and Shadlen Michael N. The neural basis of decision making. Annu. Rev. Neurosci., 30:535–574, 2007. [DOI] [PubMed] [Google Scholar]
- [46].Latimer Kenneth W, Yates Jacob L, Meister Miriam LR, Huk Alexander C, and Pillow Jonathan W. Single-trial spike trains in parietal cortex reveal discrete steps during decision-making. Science, 349(6244):184–187, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Genkin Mikhail, Shenoy Krishna V, Chandrasekaran Chandramouli, and Engel Tatiana A. The dynamics and geometry of choice in premotor cortex. bioRxiv, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Okazawa Gouki, Hatch Christina E, Mancoo Allan, Machens Christian K, and Kiani Roozbeh. Representational geometry of perceptual decisions in the monkey parietal cortex. Cell, 184(14): 3748–3761, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Wang Jack, Hertzmann Aaron, and Fleet David J. Gaussian process dynamical models. Advances in Neural Information Processing Systems, 18, 2005. [Google Scholar]
- [50].Turner Ryan, Deisenroth Marc, and Rasmussen Carl. State-space inference and learning with gaussian processes. In Artificial Intelligence and Statistics, pages 868–875. JMLR Workshop and Conference Proceedings, 2010. [Google Scholar]
- [51].Frigola Roger, Chen Yutian, and Rasmussen Carl Edward. Variational gaussian process state-space models. Advances in Neural Information Processing Systems, 27, 2014. [Google Scholar]
- [52].Eleftheriadis Stefanos, Nicholson Tom, Deisenroth Marc, and Hensman James. Identification of gaussian process state space models. Advances in Neural Information Processing Systems, 30, 2017. [Google Scholar]
- [53].Bohner Gergo and Sahani Maneesh. Empirical fixed point bifurcation analysis. arXiv preprint arXiv:1807.01486, 2018. [Google Scholar]
- [54].Chen Ricky TQ, Rubanova Yulia, Bettencourt Jesse, and Duvenaud David K. Neural ordinary differential equations. Advances in Neural Information Processing Systems, 31, 2018. [Google Scholar]
- [55].Rubanova Yulia, Chen Ricky TQ, and Duvenaud David K. Latent ordinary differential equations for irregularly-sampled time series. Advances in Neural Information Processing Systems, 32, 2019. [Google Scholar]
- [56].Kim Timothy D, Luo Thomas Z, Pillow Jonathan W, and Brody Carlos D. Inferring latent dynamics underlying neural population activity via neural differential equations. In International Conference on Machine Learning, pages 5551–5561. PMLR, 2021. [Google Scholar]
- [57].Kim Timothy Doyeon, Can Tankut, and Krishnamurthy Kamesh. Trainability, expressivity and interpretability in gated neural odes. In International Conference on Machine Learning, pages 16393–16423, 2023. [Google Scholar]
- [58].Versteeg Christopher, Sedler Andrew R, McCart Jonathan D, and Pandarinath Chethan. Expressive dynamics models with nonlinear injective readouts enable reliable recovery of latent features from neural activity. arXiv preprint arXiv:2309.06402, 2023. [Google Scholar]
- [59].Köhs Lukas, Alt Bastian, and Koeppl Heinz. Variational inference for continuous-time switching dynamical systems. Advances in Neural Information Processing Systems, 34:20545–20557, 2021. [Google Scholar]
- [60].Köhs Lukas, Alt Bastian, and Koeppl Heinz. Markov chain monte carlo for continuous-time switching dynamical systems. In International Conference on Machine Learning, pages 11430–11454. PMLR, 2022. [Google Scholar]
- [61].Archambeau Cédric, Opper Manfred, Shen Yuan, Cornford Dan, and Shawe-Taylor John. Variational inference for diffusion processes. Advances in Neural Information Processing Systems, 20, 2007. [Google Scholar]
- [62].Course Kevin and Nair Prasanth. Amortized reparametrization: Efficient and scalable variational inference for latent sdes. Advances in Neural Information Processing Systems, 36, 2024. [Google Scholar]
- [63].Cseke Botond, Schnoerr David, Opper Manfred, and Sanguinetti Guido. Expectation propagation for continuous time stochastic processes. Journal of Physics A: Mathematical and Theoretical, 49(49):494002, 2016. [Google Scholar]
- [64].Wu Anqi, Pashkovski Stan, Datta Sandeep R, and Pillow Jonathan W. Learning a latent manifold of odor representations from neural responses in piriform cortex. Advances in Neural Information Processing Systems, 31, 2018. [Google Scholar]
- [65].Keeley Stephen, Aoi Mikio, Yu Yiyi, Smith Spencer, and Pillow Jonathan W. Identifying signal and noise structure in neural population activity with gaussian process factor models. Advances in Neural Information Processing Systems, 33:13795–13805, 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.