Changes in physical characteristics of extreme rainfall events during the Indian summer monsoon based on downscaled and bias-corrected CMIP6 models

Abstract

We identified a set of bias-corrected and downscaled Coupled Model Intercomparison Project 6 (CMIP6) models capable of accurately simulating the observed mean Indian summer monsoon rainfall, extreme rain events (EREs) and their respective interannual variability. The future changes in EREs projected by these models for four climate change scenarios—Shared Socioeconomic Pathways (SSPs), 1–2.6, 2–4.5, 3–7.0 and 5–8.5 were estimated using percentile thresholds. Under the highest emission scenario, SSP5-8.5, at the end of the century, summer monsoon season total rainfall exhibits a 1.1-fold increase, while extreme rainfall intensity demonstrates a more substantial rise of 1.3-fold. The spatial variability of seasonal total rainfall increases by 1.2-fold compared to the baseline period, with an even more pronounced 2.1-fold increase in the spatial variability of extreme rainfall (R99p). These findings underscore the significant amplification of rainfall variability and intensity under the most extreme climate scenario. The intensity and frequency of very extreme rainfall events (vEREs) were also found to increase, though with a substantial inter-model spread. Under SSP5-8.5, extreme rainfall intensity scales with temperature at 1.5 to 2 times the Clausius-Clapeyron (CC) rate. While mid-century scenarios show minimal variations in extreme rainfall intensity from the historical period, end-century projections reveal significant shifts; an increase in north India and a decrease in south India due to cloud-induced cooling effects.

Introduction

Climate change significantly impacts a region’s general hydrology with intensification of hydrological events such as floods, droughts, and extreme precipitation events^1,2. Extreme rainfall events (EREs) result in substantial losses of life, property and agricultural productivity across India^3–5. The quantum of extreme rainfall is largely determined by temperature and other meteorological parameters (like pressure, wind and humidity), with the latter determining the moisture supply. Human activities have disrupted the climate equilibrium, creating an energy imbalance in the Earth’s system, observable through changes in the water cycle¹. Effective water resource management, including initiatives like linking river basins⁶, requires information about future water surpluses and deficits. Extreme event attribution is, therefore, necessary to link the effects of global climate change to people’s lives and property.

While studies indicate a dominance of extreme dry spells over the Indian region^7–9, extreme wet spells also significantly impact human life and economic stability⁷. In the tropics, the relative changes in extreme precipitation rate often exceed those of mean precipitation^10,11, posing severe socio-economic risks. Over the central Indian region as well as in its homogeneous rainfall zones, an increasing trend in heavy rainy days and a declining trend of moderate rainfall events have been observed^12,13, and has been linked to the rising sea surface temperature in the tropical Indian Ocean^14,15. There is a statistically increasing trend in annual maximum rainfall, with spatial heterogeneity influenced by factors such as topography, urbanization, and population growth¹⁶. Between 1951 and 2011, there has been a shift in precipitation patterns, with more intense wet spells and frequent less intense dry spells⁷, alongside significant spatiotemporal variability in precipitation extremes, including an increase in intensity during the summer monsoon season⁹.

Numerous studies explored the changing intensity and frequency of EREs¹⁷ over India, and the trends therein. However, recent studies^18,19 suggest that thermodynamic state of the atmosphere is also important for the changes in extreme rainfall characteristics. These studies strive to unravel the physics behind these changes, particularly with respect to the global warming. Briefly, according to Clausius-Clapeyron (CC) scaling, the atmospheric water vapour increases by approximately 7.5% per degree Celsius²⁰ of warming. This rise in water vapor content, driven by global warming, influences the precipitation amount and its type. Stronger updrafts are estimated to increase the precipitation extremes at rates similar to CC scaling or even more rapidly²¹. Studies suggest that the tropical precipitation events, which are largely driven by latent heat release, particularly undergo in super CC scaling²².

Over India, more than 80% of EREs occur during the summer monsoon season (June–September, JJAS), and studies have indicated a negative relationship between surface air temperature and precipitation extremes²³. In addition to aforementioned few observation-based studies, models have also been employed to understand the evolution of EREs in the background of global warming. Indeed, general circulation models (GCMs), vital for studying event detection, attribution and the origins of many climatic occurrences²⁴, also provide a critical handle in conjecturing how the extreme rainfall potentially scales with probable future warming. Critically, the limitations of current GCMs, including coarse resolution and biases, have been already discussed^8,25 and high-resolution GCMs have better captured EREs and their scaling with surface air temperature²⁶.

The Coupled Model Intercomparison Project (CMIP) serves as a global initiative to advance climate modelling by enabling comparisons of results from various models, thereby enhancing our understanding of climate variability and change. The latest Phase 6, known as CMIP6, represents a significant advancement in climate modelling, incorporating higher resolution and improved physics to address complex climate phenomena²⁷. The CMIP6 preparation were designed to address three broad scientific questions²⁸, which are mostly on how the models respond to the forcing, the origin and impacts of model biases and the assessment of future climate changes, provided the inherent uncertainties in scenario simulations. While CMIP6 models show significant improvements over its predecessor CMIP5, biases persist^25,29, hence necessitating the use of the Multi-Model Ensemble (MME) mean approach to enhance reliability. Ensemble-based probabilistic method was found to be advantageous^25,30 for predicting climate change, provided each ensemble member differs not just in terms of initial state but also in the representation of climate (concerning its physics scheme, land scheme, radiation scheme, etc.), thereby giving an estimate of the model’s inherent uncertainty. For studies on extreme event attribution, the models need to be good in simulating the updrafts with the right parameterization that will resolve the regional scale moist convection, among other requirements. The dependence of model simulations to resolution was identified³¹ and found that high-resolution models can simulate the daily extreme rainfall over the Asian monsoon region with better reliability³², highlighting the importance of using MME averages to better capture spatial variations across India by enhancing the signal-to-noise ratio. Studies using CMIP6 models³³ predict an increase in heavy precipitation events and a decline in light precipitation events under warming scenarios, an inference also made with CMIP3 models³⁴. The increase in wet days has also been linked to the rising occurrence of very wet seasons and the projected increase in Indian Summer Monsoon (ISM) rainfall³⁵. There are large differences in the physical and dynamical schemes among CMIP6 models³⁶. Hence, it is highly essential to choose the best and most consistent models of CMIP6 as ensemble members in the evaluation of future projections²⁵.

Many studies are already done in identifying future changes in EREs over India using CMIP6 models^37–40. However, a significant limitation in using CMIP6 models directly for such analysis is that their coarse resolution tends to underrepresent fine-scale processes, leading to biases. Alternative methods such as statistical downscaling, may be employed to obtain localized future projections⁴¹ to reduce the computational cost. Downscaled and bias corrected CMIP6 data is widely used for such impact assessment studies^39,40.

This study leverages the bias-corrected and downscaled NASA Earth Exchange (NEX) Global Daily Downscaled Projections (GDDP) CMIP6 (NEX-GDDP-CMIP6) dataset⁴² to evaluate and select models based on their better ability in reproducing observed spatial patterns and interannual variability of mean and extreme rainfall during the present-day ISM. Using these models, we project future climate changes and analyse the physical characteristics of extreme events across India’s homogeneous rainfall zones. The scope of the study includes changes in seasonal total mean and extreme rainfall, their variability, intensity, frequency, and scaling with temperature under different climate change scenarios.

Results and discussion

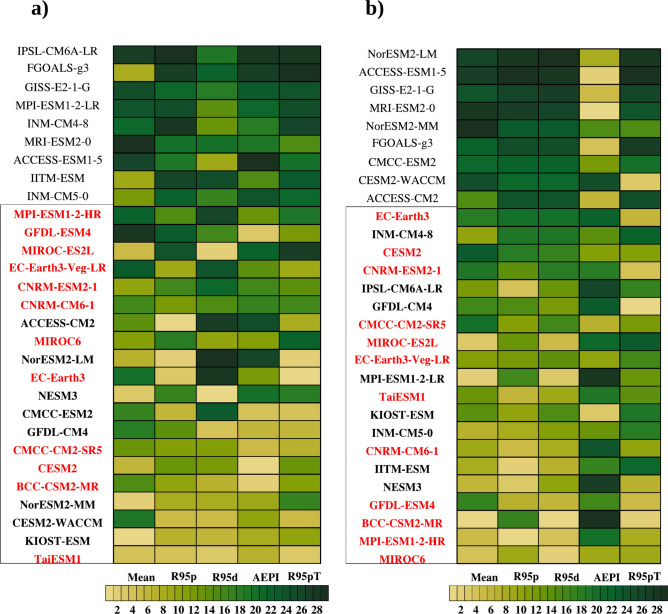
We selected the NEX-GDDP-CMIP6 models for their ability to accurately simulate the spatial patterns and interannual variability of mean and extreme indices, as shown in Fig. 1. The shortlisted models include BCC-CSM2-MR, CESM2, CMCC-CM2-SR5, CNRM-CM6-1, CNRM-ESM2-1, EC-Earth3, EC-Earth3-Veg-LR, GFDL-ESM4, MIROC6, MIROC-ES2L, MPI-ESM1-2-HR and TaiESM1. The detailed methodology used for shortlisting the models is provided in the Data and Methodology section. From the bias and RMSE values (Supplementary Tables S1–S5), it is evident that the models perform better at capturing rainfall frequency (R95d) than intensity (R95p). The least bias is observed for the climatological JJAS mean. The models exhibit greater consistency in simulating spatial patterns compared to temporal variability. For instance, a model that accurately represents the spatial pattern of one index, generally performs similarly for other indices (as in TaiESM1 or KIOST-ESM). However, when assessing temporal variability, significant disparities are evident in a model’s ability to simulate different indices (Supplementary Tables S6–S10). Future climate projection scenarios corresponding to Shared Socioeconomic Pathways (SSP) 1–2.6, 2–4.5, 3–7.0 and 5–8.5 are analysed for mid-century (2030–2064) and end-century (2065–2099) time periods. To ensure an equal sample size for comparison, the base period is fixed as 1980–2014 for analysing future changes.

Fig. 1.

The models shortlisted based on metrics evaluating the spatial pattern and interannual variability of mean and extreme rainfall are displayed. Panel (a) ranks the models by their ability to simulate the spatial pattern of mean rainfall and extreme rainfall indices (R95p, R95d, AEPI, and R95pT) using Taylor statistics. Panel (b) ranks the models based on their simulation of interannual variability for these indices using the Interannual Variability Score (IVS). The best 20 models are highlighted in the box, whereas the models common to both rankings (shown in red) are selected for future projection analysis.

The ISM system is generally stable, exhibiting a seasonal mean interannual fluctuation of approximately 10% relative to its long-term mean⁴³. Observations reveal that regions with the lowest JJAS climatological total rainfall exhibit the highest interannual variability during base-period, indicating a heightened vulnerability for the arid regions in the western part of India (Fig. 2a,b). Next, we examined the variability of extreme rainfall intensity. The mean of R95p (Fig. 2c), which represents the average of daily extreme rainfall during summer monsoon reason, closely resembles the total JJAS rainfall but exhibits an enhanced signal, particularly over the Western Ghats, as well as central and western India. The coefficient of variability for R95p (Fig. 2d) indicates a significantly amplified magnitude compared to the variability of total rainfall, with pronounced variability observed in specific pockets of the Western Ghats and in Leh. This implies that, unlike total rainfall, regions experiencing seasonal heavy rainfall also exhibit high vulnerability, highlighting their susceptibility to the adverse impacts of EREs.

Fig. 2.

The climatological accumulated JJAS rainfall (mm) (a), (e), (i) and its coefficient of variation (%) (b), (f), (j) and the R95p rainfall (mm) (c), (g) (k) and its coefficient of variation (%) (d), (h), (l) from observation (a–d), and from the corresponding MME mean of best NEX-GDDP-CMIP6 models for present-day (e–h) and end-century SSP5-8.5 scenario (i–l).

The variability associated with seasonal mean rainfall has been extensively studied and well-documented⁴⁴. However, variability in extreme rainfall demands greater attention. In this study, we utilize the NEX-GDDP-CMIP6 models, to analyse the variability linked to the best-performing models. Consequently, we examined the variability of JJAS precipitation under the selected SSPs and their corresponding Representative Concentration Pathways (RCPs).

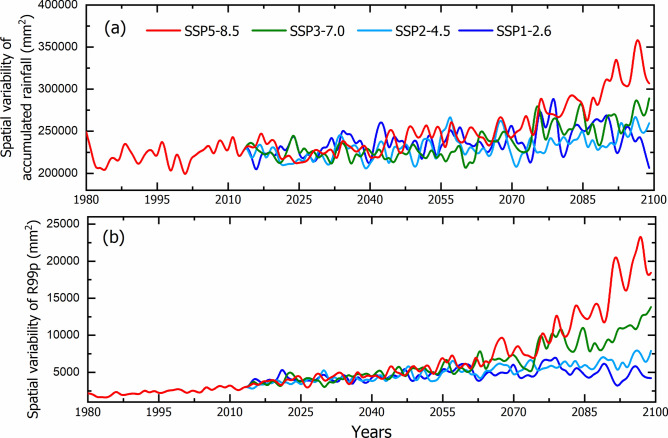
Figure 2e,i illustrates the spatial distribution of JJAS total rainfall for present-day and for the end-century simulation under the SSP5-8.5 scenario, presented as the MME mean of the best twelve NEX-GDDP-CMIP6 models. The mean JJAS total rainfall simulated by the MME of the selected models (Fig. 2e) closely aligns with the observed rainfall distribution (Fig. 2a). Notably, the selected models demonstrate reasonable accuracy in capturing rainfall over the core monsoon region. In general, the CMIP5 and CMIP6 model data exhibit a significant underestimation of rainfall over central India³¹. However, this negative bias is substantially reduced when the bias-corrected and downscaled NEX-GDDP-CMIP6 data is used⁴⁵. In present-day simulations, the models exhibit significant biases in representing R95p (Fig. 2g), notwithstanding the bias correction. Additionally, the high variability observed over the Western Ghats is poorly captured (Fig. 2f). These biases, evident in the models’ ability to simulate season total rainfall, its coefficient of variation, R95p, and its coefficient of variation (Fig. 2e–h), appear to persist in future projections across both time slices (Supplementary Figs. S1–S3). Our analysis reveals an increase in the mean JJAS total rainfall, R95p, and their associated variability under the SSP5-8.5 scenario (Fig. 2i–l). This indicates that warming intensifies the variability linked to JJAS rainfall, particularly towards the end of the twenty-first century. The simulated JJAS total rainfall from MME of selected models is projected to increase from 787 mm in the baseline period to 847 mm, 860 mm, 900 mm, and 930 mm by the end of the century under the SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 scenarios, respectively. Similarly, extreme rainfall intensity is expected to rise from 220 to 231 mm, 245 mm, 275 mm, and 290 mm for the same scenarios. The change in JJAS total rainfall thus represents an increase of 1.1 times, while extreme rainfall intensity shows a larger increase of 1.3 times to the end of the twenty-first century under the highest emission scenario. Our analysis highlights substantial increase in variability in EREs from the present to the future. However, the extent of their spatial variability remains uncertain. This aspect requires further investigation, as it holds significant implications for regional hydrological planning.

The changes in mean summer rainfall over India have been extensively studied and documented^46,47. However, spatial trends in mean rainfall are hardly looked upon. Understanding these trends is essential for assessing how the spatial distribution of water availability varies across regions. Such insights are crucial for planning extensive river interlinking projects and implementing river basin-scale water management strategies^48,49. Previous studies have identified an increase in spatial variability for extreme rainfall, while a decrease has been observed for mean rainfall⁴⁸. Our analysis of spatial variability of JJAS total rainfall and extreme rainfall indicates that by the end of the twenty-first century, both JJAS total rainfall and extreme rainfall exhibit increased variability across India (Fig. 2).

This finding aligns with our detailed examination of future projections, which further explores the spatial variability trends under different climate scenarios. Figure 3a shows the spatial variability of JJAS total rainfall from 1980–2100 for the four SSP scenarios. Each line corresponds to one of the SSP scenarios. Figure 3b illustrates the same but for the R99p extreme precipitation. Supplementary Figs. S4 and S5 respectively shows the same with inclusion of model spread. Our analysis reveals a substantial inter-model spread in the simulation of extreme rainfall, particularly towards the end of the century under the SSP5-8.5 scenario. Figure 3 illustrates that JJAS total rainfall also shows an increase in spatial variability by the end of the twenty-first century. Compared to the base period, the end-century spatial variability of JJAS total rainfall under the SSP5-8.5 scenario increases by a factor of 1.2, while the spatial variability of extreme rainfall (R99p) exhibits a more pronounced increase, reaching 2.1 times. This significant increase in the spatial variability of R99p extremes indicates a heightened vulnerability in terms of water resource management, emphasizing the need for adaptive and region-specific strategies. The high-resolution data enables the assessment of spatial variability within the rainfall homogeneous zones of India. The classification of these homogeneous zones has been described in previous studies^26,50 and will not be discussed here. Figure S6 illustrates the spatial variability of JJAS total rainfall across different homogeneous zones of India. Except for the peninsular region, all other zones show amplified spatial variability in JJAS total rainfall. Similarly, Fig. S7 illustrates that the spatial variability of R99p is amplified across all homogeneous zones. However, the magnitude of this amplification is lower compared to the variability observed for the whole of India (Fig. 3), likely due to the moderating effect of homogeneity within the zones. Our analysis provides preliminary insights into spatial variability under climate change scenarios. Further research using higher resolution model at regional scales is essential to better understand how this variability affects the local hydrology and to support the development of more effective planning and mitigation strategies. Building on this, our next objective is to examine the changes in the frequency and intensity of extreme events under different climate change scenarios. This analysis will provide valuable insights into shifts in the rarity and magnitude of these events.

Fig. 3.

The spatial variability of (a) JJAS total rainfall and (b) R99p extreme rainfall during JJAS over Indian land region for the period 1980–2100 from the MME means of twelve best NEX-GDDP-CMIP6 models. The four bold lines show the four climate change scenarios, SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5 respectively.

Previous studies have provided valuable insights into event rareness and precipitation changes under warming scenarios, showing that the rarity of extreme events nearly doubles with each degree of warming⁵¹. They also reported that total precipitation doubles due to an increase in the frequency of events, with minimal changes in intensity. Similar work has been conducted for the Indian region, focusing on annual rainfall⁵². Both the studies were done for annual rainfall over the respective regions and highlights comparable trends. These findings motivated us to explore the future rarity of EREs and analyse changes in their intensity over the Indian region.

We analysed the changes in intensity and frequency of six extreme rainfall thresholds, namely, 95th, 99th, 99.7th, 99.9th, 99.95th and 99.97th percentile. These indices were calculated for three time period: present-day (1980–2014), mid-century (2030–2064) and end-century (2065–2099), with the percentile thresholds defined based on the first ten years of present-day period. The differences were computed between the mid-century and present-day, as well as between the end-century and present-day. The changes were then normalized by the corresponding changes in surface air temperature for the entire Indian region, as the underlying driver of changes in both frequency and intensity is the increase in temperature. Expressing these changes per unit increase in temperature provides a standardized metric. This approach also enables a consistent inter-comparison of the response to unit forcing across different climate scenarios. Building on this concept, we expressed the changes in both frequency and intensity as relative percentages of the baseline period. This approach facilitates the evaluation of whether changes in frequency or intensity are more pronounced in relative terms. Additionally, such comparisons provide valuable insights for conducting relative risk assessments.

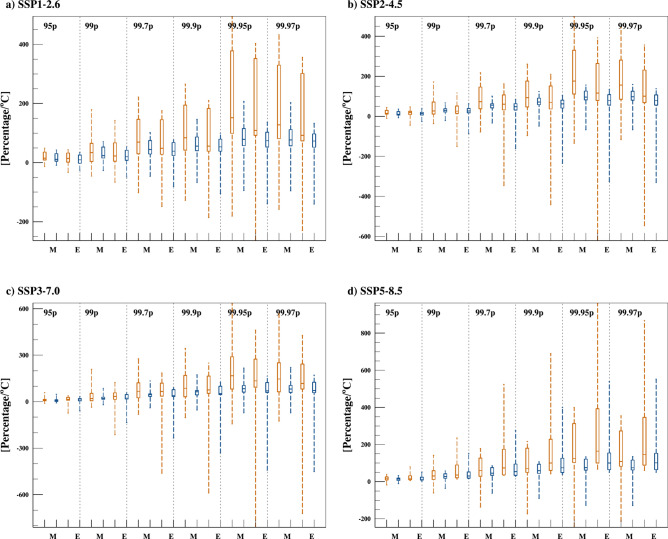
Figure 4 presents a Box and Whisker plot, where the box represents the interquartile range (25th and 75th percentile), the midline indicates the median (50th percentile), and the whiskers extend to the first and last percentile values of the selected models. Across all scenarios, the most extreme rainfall event, corresponding to 99.97th percentile (very extreme rainfall events (vEREs)), exhibits the largest changes in both intensity and frequency, with the highest magnitude of change observed under the SSP5-8.5 scenario. Rainfall intensities are increasing at a much higher rate than rainfall frequencies, a trend already established in previous studies on RCP scenarios²⁶. The large values depicted in Fig. 4 represents the inter-model spread in rainfall intensity and frequency per unit change in temperature. The figure highlights substantial inter-model uncertainty in the frequency and intensity of vEREs, particularly for thresholds R99.9p, R99.95p, and R99.97p. In contrast, the inter-model spread is significantly lower for lower thresholds such as R95p and R99p, with more robust inter-model agreement. Additionally, there is relatively better agreement among models regarding the frequencies of extreme events. Notably, the models also exhibit closer agreement in the median values of extreme intensities and frequencies. This suggests that, despite the inter-model spread, using median statistics could provide a reliable approach for understanding future changes in EREs. By the end of the century, the median normalized change in extreme intensity (95th percentile) is ~ 15%, while the change in extreme frequency is ~ 10%. For vEREs (99.97th percentile), the median change in intensity rises to 92%, and the frequency increases by 73%. Further, we examined the scaling of EREs with temperature to delineate the projected changes under future climate change scenarios.

Fig. 4.

Box-and-Whisker plot illustrating the changes in intensity and frequency of various extreme rainfall indices (95p, 99p, 99.7p, 99.9p, 99.95p and 99.97p) under different SSP scenarios: (a) SSP1-2.6, (b) SSP2-4.5, (c) SSP3-7.0 and (d) SSP5-8.5. The whiskers represent the first and last percentile values, the box indicates the interquartile range (lower and upper quartiles), and the middle line denotes the median value. The orange box represents changes in intensity, while the blue box represents changes in frequency. “M” and “E” denote changes for the mid-century and end-century, respectively, relative to the base period (1980–2014). All changes are normalized by the corresponding changes in surface air temperature.

As global temperatures rise, the amount of moisture in the air increases because relative humidity remains roughly constant, and warmer air can hold more water. This leads to an intensification of the water cycle, including increased global precipitation and a stronger hydrologic cycle⁵³. The Clausius Clapeyron (CC) equation indicates that the atmosphere’s moisture-holding capacity increases by a factor of 6–7% per °C. Consequently, the extreme precipitation events are expected to intensify at a similar rate. While extreme precipitation is primarily influenced by the total moisture content in the atmospheric column leading to a CC scaling rate^20,54,55, mean precipitation is constrained by the energy budget, resulting in a lower scaling rate of about 2% per °C⁵⁶. However, studies have highlighted significant spatiotemporal variability in the scaling of extreme precipitation with temperature^23,57.

A previous study²³ has identified super-CC scaling for maximum daily precipitation and dew point temperature, with the southern region of India showing a stronger relationship compared to northern India. The CC scaling applies under conditions of no moisture limitation, such as when the air is nearly saturated. However, as temperature rise, the increase in specific humidity with temperature slows down, leading to a reduction in relative humidity. This results in a negative CC scaling over the Indian region at higher temperatures^58,59.

The scaling of percentage change in R95p rainfall intensity with respect to change in temperature is checked (Fig. 5a,b). They roughly follow a straight line with a slope close to 1.5 times CC scaling, which is significantly higher than the 7% per °C as predicted by the CC relation. Figure 5a illustrates the scaling for the mid-century, where the curves generally exhibit 1.5 to 2 times the CC scaling, particularly at higher temperature changes. Notably, the scaling approaches negative values for smaller temperature changes. The end-century changes in scaling rates reveal a clear distinction between the scenarios, with scaling rates approaching twice the CC rate, particularly under the SSP5-8.5 scenario. Subsequently, the variation of R95p rainfall intensity with increasing temperatures is analysed using a scatter plot (Fig. 5c,d). The LOWESS-smoothed curve illustrates that the relationship between R95p rainfall intensity and temperature initially increases with rising temperatures but transitions to negative scaling at higher temperature levels (peak-point temperatures as indicated in Fig. 5c,d). This behaviour is primarily attributed to atmospheric cooling caused by monsoon rains, which limits the capacity for further moisture retention and intensification of precipitation at higher temperatures⁵⁹. The variation remains consistent across different scenarios. However, a significant shift in rainfall intensity is observed for the end-of-century scenarios (Fig. 5d), while all mid-century scenarios cluster closely together, indicating minimal differences among them (Fig. 5c). The north Indian region (latitude north of 23°N) exhibits variation patterns similar to those of the entire Indian region (Fig. S8a,b). However, the south Indian region (latitude south of 23°N) displays distinctly different behaviour (Fig. S8c,d). In the south, the variation shows a much more negative trend, indicating significant cooling induced by monsoon rains, which counteracts the effect of rising temperatures.

Fig. 5.

Scaling of R95p rainfall intensity for the Indian region. Panels (a) and (b) depict the scaling for mid-century and end-century scenarios, respectively. Panels (c) and (d) illustrate the variation in rainfall intensities with surface air temperature for mid-century and end-century periods, respectively. Different coloured lines represent the non-parametric fitting using LOWESS smoothing for various climate change scenarios. In (a) and (b), three reference lines indicate typical CC scaling (dots), 1.5 times CC scaling (dash) and 2 times CC scaling (dot-dash). The peak-point temperature for each scenario is highlighted in (c) and (d).

Several studies have reported super-CC scaling of EREs with temperature, which occurs due to the additional latent heat release that enhances atmospheric instability and moisture convergence. However, the total precipitation is constrained by energy availability, which can reduce the frequency or duration of precipitation events, resulting in longer dry spells⁶⁰. Our analysis of surface specific humidity supports this observation, showing an increase across all SSP scenarios, with amplified and distinct changes evident in the end-century simulations (Fig. S9). This increase in specific humidity ultimately contributes to extreme rainfall over the Indian subcontinent, as also corroborated by previous studies²⁶.

Summary and conclusions

This study identifies, through a comprehensive statistical evaluation, the most effective models among the NEX-GDDP-CMIP6 ensemble for simulating observed mean rainfall and extreme rainfall events over the Indian region. Using bias-corrected and downscaled data from 29 models, 12 were selected based on their ability to reproduce spatial patterns and interannual variability, evaluated through Taylor statistics and interannual variability scores. The identified best performing models are BCC-CSM2-MR, CESM2, CMCC-CM2-SR5, CNRM-CM6-1, CNRM-ESM2-1, EC-Earth3, EC-Earth3-Veg-LR, GFDL-ESM4, MIROC6, MIROC-ES2L, MPI-ESM1-2-HR and TaiESM1.

The Multi Model Ensemble (MME) mean of best performing NEX-GDDP-CMIP6 models closely matches observations for JJAS total rainfall with reasonable accuracy in capturing rainfall over the core monsoon region. However, the coefficient of variation fails to represent the large variability observed over Western Ghats. Additionally, biases are noted in the simulation of R95p by the MME mean, which may persist in future climate change scenarios. Our analysis projects increased spatial variability in JJAS total and extreme rainfall by the end of the twenty-first century. While total rainfall shows a slight increase, R99p variability is significantly amplified, especially under the SSP5-8.5 scenario (~ 4 times higher than total rainfall). Homogeneous rainfall zones also exhibit amplified variability in extreme events, reflecting consistent trends across India.

Extreme rainfall thresholds analyzed for mid and end-century periods show significant increases in both intensity and frequency, particularly under SSP5-8.5. The normalized increase in intensity (~ 15% for 95th percentile, 92% for 99.97th percentile) exceeds that of frequency (~ 10% and 73%, respectively). However, the large inter-model spread limits accurate simulation of very extreme rainfall events due to differences in model parameterization and physics schemes.

The scaling of R95p intensity with temperature shows a slope up to twice the Clausius-Clapeyron (CC) rate, exceeding the predicted 7%/°C. Mid-century scaling ranges from 1.5 to 2 times the CC rate, while end-century scaling is distinctly higher under SSP5-8.5. At high temperatures, scaling turns negative due to atmospheric cooling from monsoon rains. Regional analysis reveals that northern India follows a trend similar to whole India, while southern India shows negative scaling due to monsoon-induced cooling. Surface-specific humidity increases under all SSP scenarios, amplifying extreme rainfall by the end of the century.

Anthropogenic activities have significantly impacted the hydrological cycle, underscoring the need to understand its dynamics for accurate monsoon rainfall projections. Simulating EREs remains challenging due to the short timescales and complexity of convective systems, compounded by model sensitivity to boundary conditions and parameterizations.

With warming, increased atmospheric moisture leads to greater latent heat release and a more stable upper atmosphere, which can weaken the large-scale overturning circulations, as highlighted by many studies^26,46,61. The occurrences of floods and droughts are also largely influenced by the ENSO cycles, especially over the tropics, emphasizing the need to investigate future changes in precipitation extremes in the light of varying ENSO frequency and intensity, and also the natural decadal variations^62,63.

To document uncertainties more comprehensively, future studies may be carried out to explore additional climate change scenarios (beyond those used in this study). A limitation of this study is the reliance on statistically downscaled products for extreme event attribution. In this context, using dynamically downscaled datasets could provide further insights. Finally, the study highlights changes in the physical characteristics of precipitation under different climate scenarios, necessitating a deeper understanding of the mechanisms driving these projected changes.

Data and methodology

The daily gridded rainfall data with a horizontal resolution of 0.25° × 0.25° was developed using observations from 6995 rain gauge stations across India and obtained from the IMD for the period 1980–2014⁶⁴.

For the present-day historical simulations of Phase 6 of the Coupled Model Intercomparison Project (CMIP6), we utilised the NASA Earth Exchange Global Daily Downscaled Projections (NEX-GDDP-CMIP6) dataset⁴². This dataset employs the Bias-Correction Spatial Disaggregation (BCSD) method to bias-correct and statistically downscale the CMIP6 data into a fine resolution of 0.25° × 0.25° covering the period 1980–2100. The projections span various Tier 1 scenarios from CMIP6 ScenarioMIP model runs^65,66, including SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5. Our study utilises climate projections from 29 GCMs (Fig. 1). This dataset is shown to have better fidelity in simulating the ISM rainfall⁴⁵. This high-resolution global dataset enables a more detailed evaluation of the impacts of climate change at finer-scales.

A single realisation from each model was selected for analysis. The NEX-GDDP-CMIP6 dataset is accessible at https://nex-gddp-cmip6.s3.us-west-2.amazonaws.com/index.html. Figure 1 lists the models used in this study. These models were validated against IMD rainfall data for both mean and extreme rainfall, and the best-performing models were identified. For future climate analysis, 20 models were chosen based on their ability to accurately simulate the observed patterns of mean and extreme ISM rainfall, and another 20 models were selected for effectively capturing the interannual variability of mean and extreme ISM rainfall. The models common to both sets were then identified for further analysis.

This study focuses on the Indian summer monsoon season, spanning June–September (JJAS). Extreme events were identified using high percentiles of daily precipitation. The definition of extreme precipitation indices used-R95p, R95d, AEPI and R95pT-are given in Table 1 and are adapted from Tang et al.⁶⁷, with modifications. Unlike their method, which computes indices annually, we apply the methodology to the JJAS season, using a threshold defined at the 95th percentile of the first 10 years instead of the average of 95th percentile across all the years. This approach also facilitates the identification of the warming signal for the present-day period.

Table 1.

Extreme precipitation indices used in this study.

Extreme precipitation index	Description	Definition	Units
R95p	Precipitation due to very wet days	Seasonal total precipitation at each grid points when daily precipitation exceeds the extreme 95th percentile threshold R95 is the 95th percentile threshold, and Rw is daily rainfall	mm
R95d	Number of very wet days	Seasonal total number of days at each grid point when daily precipitation exceeds the extreme 95th percentile threshold Rd is rainy day when Rwi > 1 mm	days
AEPI	Extreme precipitation intensity	The absolute intensity of extreme precipitation defined as the ratio of extreme precipitation to extreme precipitation days, i.e., R95p/R95d	mm/day
R95pT	Ratio of extreme precipitation	Ratio of seasonal extreme precipitation to seasonal rainfall from rainy days	No units

For validation, the indices were computed for 1980–2014, corresponding to the end of historical simulations. Only wet days (precipitation > 1 mm/day) were considered in the calculation of extreme precipitation indices. This ensures that each individual model uses its own threshold, addressing model-specific biases^36,68.

The Taylor statistics were used to assess the ability of the models to simulate the spatial patterns of mean and extreme precipitation indices. These metrics include pattern correlation, ratio of spatial standard deviation, percentage of bias and root mean square error (RMSE). Supplementary Tables S1–S5 provide the Taylor statistics for each model, and a Taylor diagram summarizing these values is presented in Supplementary Fig. S10. A pattern correlation and spatial standard deviation ratio closer to 1 indicate higher model reliability, while bias and RMSE values closer to 0 suggest better model performance.

Each model was ranked based on these metrics: models with pattern correlation and spatial standard deviation ratio close to 1 and bias and RMSE values near 0 were assigned a rank of 1. The sum of all ranks determined the overall performance, with the models having the lowest ranks considered the most accurate. These top-performing models are arranged in ascending order (from below) in Fig. 1a, with the best 20 models highlighted within the box.

To evaluate interannual variability (temporal variation), we utilized the interannual variability score (IVS), following the methodology of Chen et al.⁶⁹ as follows:

where STD_M and STD_O are interannual standard deviations of the model and observation respectively. This method is widely used to evaluate the interannual variability of the models^69,70. We assessed the IVS for both mean and extreme rainfall indices, with the results for each model presented in Supplementary Tables S6–S10. IVS values approach 0 as the standard deviation of the model aligns more closely with observations. Consequently, models with the lowest IVS values are considered better at simulating interannual variability. These models are ranked in ascending order in Fig. 1b with the best 20 models highlighted within the box.

Using the two metrics of spatial patterns and temporal variability, we shortlisted 20 models for each, based on their performance in simulating the climatological spatial patterns and interannual variability of mean and extreme rainfall indices. From Fig. 1, the common models among the two sets of 20 models, those best simulating the spatial patterns and interannual variability are MIROC6, MIROC-ES2L, BCC-CSM2-MR, TaiESM1, CMCC-CM2-SR5, GFDL-CM4, CESM2, EC-Earth3, EC-Earth3-Veg-LR, CNRM-CM6-1, CNRM-ESM2-1, KIOST-ESM, NESM3, GFDL-ESM4, and MPI-ESM1-2-HR. Among these, future Shared Socio-economic Pathways (SSP) scenarios of SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5 are available for twelve models: BCC-CSM2-MR, CESM2, CMCC-CM2-SR5, CNRM-CM6-1, CNRM-ESM2-1, EC-Earth3, EC-Earth3-Veg-LR, GFDL-ESM4, MIROC6, MIROC-ES2L, MPI-ESM1-2-HR and TaiESM1. These twelve models were subsequently shortlisted for further analysis of future changes in spatial variability and precipitation extremes.

The four SSPs available from CMIP6, namely, SSP1, SSP2, SSP3 and SSP5 represent a range from aggressive mitigation to scenarios with continued emission growth. This study focuses on the Tier 1 scenarios, viz., SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5^65,66 as they encompass a wide spectrum of uncertainty associated with future socioeconomic and climatic forcing pathways which can define global development. Thus, the SSPs selected in this study range from a very high emissions scenario to a very low emissions scenario.

Spatial variability was determined by calculating the variance across each grid point for every year, estimated for both JJAS total and extreme R99p rainfall. The accumulated R99p rainfall, calculated with a base period of the first 10 years (1980–1989) is identified as an extreme rainfall amount for each JJAS season. For our analysis, we use the historical period (starting from 1980) followed by each climate change scenario as this approach allows us to examine the continuous interannual variability rather than focusing on discrete time slices. To assess the scaling of extreme rainfall intensity with surface air temperature, we evaluated the percentage changes in R95p rainfall intensity with changes in temperature at each grid point. Non-parametric fitting using LOWESS smoothing was applied to identify the scaling patterns for different climate change scenarios.

All datasets are in a common resolution of 0.25° × 0.25°. The analysis was conducted over the land regions of India (6°N–38°N and 66°E–100°E).

Author contributions

S.J.V., K.A. and S.P. conceived the idea and designed analysis. S.J.V. carried out the data analysis and visualisation. S.J.V., S.P. and K.A. interpreted the results. S.J.V., T.P. and P.G. wrote the paper. All authors reviewed the manuscript.

Data availability

The authors declare that the data are freely available and can be accessed at https://nex-gddp-cmip6.s3.us-west-2.amazonaws.com/index.html. The IMD gridded rainfall is available at https://www.imdpune.gov.in/cmpg/Griddata/Rainfall_25_NetCDF.html. The Python and NCL codes used for the study are available in the https://github.com/Stellajes/SR_manuscript repository.

Declarations

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-87949-x.